Modeling Water Flow and Phosphorus Sorption in a Soil Amended with Sewage Sludge and Olive Pomace as Compost or Biochar
Abstract
:1. Introduction
- Conduct a controlled set of column experiments on two common agricultural soils to determine how two amendments (biochar and compost) from two waste sources (sewage sludge and olive pomace) applied at two concentrations (a guideline rate and (10×) higher) affect soil hydraulic properties and P sorption and mobility;
- Simulate water flow and use inverse modelling to estimate the P sorption coefficient (Kd) in each treatment;
- Analyze the results to determine how the amendments impact the soil hydraulic functions and P mobility.
2. Materials and Methods
2.1. Soil Types and Amendments
2.2. Experimental Set-Up
2.3. Column Leaching Experiment and Chemical Analysis
2.4. Soil Hydraulic Parameters Estimation
2.5. Numerical Modeling of Water Flow and P Transport
2.6. Inverse P Dynamics Modeling
3. Results and Discussion
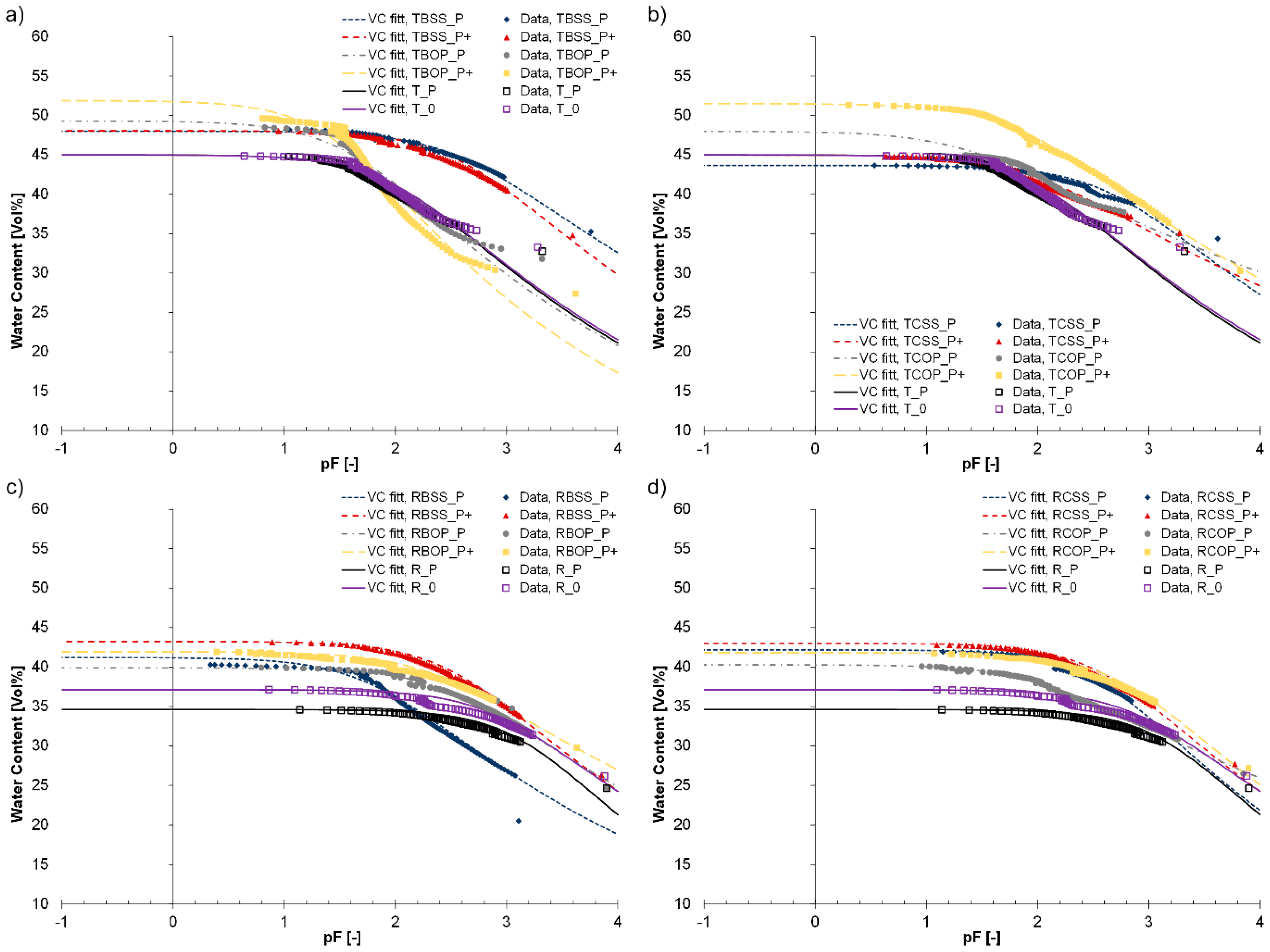
3.1. Impact of Amendments on Soil Water Retention and Hydraulic Properties
3.2. Soil Amendments and PO4-P Leaching Potential
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Diacono, M.; Montemurro, F. Long-term effects of organic amendments on soil fertility. A review. Agron. Sustain. Dev. 2010, 30, 401–422. [Google Scholar] [CrossRef] [Green Version]
- Marks, E.A.N.; Mattana, S.; Alcañiz, J.M.; Pérez-Herrero, E.; Domene, X. Gasifier biochar effects on nutrient availability, organic matter mineralization, and soil fauna activity in a multi-year Mediterranean. Agric. Ecosyst. Environ. 2016, 215, 30–39. [Google Scholar] [CrossRef]
- Ye, S.; Zeng, G.; Wu, H.; Liang, J.; Zhang, C.; Dai, J.; Xiong, W.; Song, B.; Wu, S.; Yu, J. The effects of activated biochar addition on remediation efficiency of co-composting with contaminated wetland soil. Resour. Conserv. Recycl. 2019, 140, 278–285. [Google Scholar] [CrossRef]
- Razzaghi, F.; Obour, P.B.; Arthur, E. Does biochar improve soil water retention? A systematic review and meta-analysis. Geoderma 2020, 361, 114055. [Google Scholar] [CrossRef]
- Wang, B.; Gao, B.; Fang, J. Recent advances in engineered biochar productions and applications. Crit. Rev. Environ. Sci. Technol. 2017, 47, 2158–2207. [Google Scholar] [CrossRef]
- Wu, H.P.; Lai, C.; Zeng, G.M.; Liang, J.; Chen, J.; Xu, J.J.; Dai, J.; Li, X.D.; Liu, J.F.; Chen, M.; et al. The interactions of composting and biochar and their implications for soil amendment and pollution remediation: A review. Crit. Rev. Biotechnol. 2017, 37, 754–764. [Google Scholar] [CrossRef] [PubMed]
- Mukherjee, A.; Lal, R. Biochar impacts on soil physical properties and greenhouse gas emissions. Agronomy 2013, 3, 313–339. [Google Scholar] [CrossRef] [Green Version]
- Mukherjee, A.; Zimmerman, A.R. Organic carbon and nutrient release from a range of laboratory-produced biochars and biochar–soil mixtures. Geoderma 2013, 193, 122–130. [Google Scholar] [CrossRef]
- Munoz, C.; Gongora, S.; Zagal, E. Use of biochar as a soil amendment: A brief review. Chil. J. Agric. Anim. Sci. 2016, 32, 37–47. [Google Scholar]
- Yu, H.; Zou, W.; Chen, J.; Chen, H.; Yu, Z.; Huang, J.; Tang, H.; Wei, X.; Gao, B. Biochar amendment improves crop production in problem soils: A review. J. Environ. Manag. 2019, 232, 8–21. [Google Scholar] [CrossRef]
- Kranz, C.N.; McLaughlin, R.A.; Johnson, A.; Miller, G.; Heitman, J.L. The effects of compost incorporation on soil physical properties in urban soils—A concise review. J. Environ. Manag. 2020, 261, 110209. [Google Scholar] [CrossRef] [PubMed]
- Lal, R. Restoring soil quality to mitigate soil degradation. Sustainability 2015, 7, 5875–5895. [Google Scholar] [CrossRef] [Green Version]
- Rizzardini, C.B.; Goi, D. Sustainability of domestic sewage sludge disposal. Sustainability 2014, 6, 2424–2434. [Google Scholar] [CrossRef] [Green Version]
- Toková, L.; Igaz, D.; Horák, J.; Aydin, E. Effect of Biochar Application and Re-Application on Soil Bulk Density, Porosity, Saturated Hydraulic Conductivity, Water Content and Soil Water Availability in a Silty Loam Haplic Luvisol. Agronomy 2020, 10, 1005. [Google Scholar] [CrossRef]
- Sun, Y.; Gao, B.; Yao, Y.; Fang, J.; Zhang, M.; Zhou, Y.; Chen, H.; Yang, L. Effects of feedstock type, production method, and pyrolysis temperature on biochar and hydrochar properties. Chem. Eng. J. 2014, 240, 574–578. [Google Scholar] [CrossRef]
- Villagra-Mendoza, K.; Horn, R. Effect of biochar addition on hydraulic functions of two textural soils. Geoderma 2018, 326, 88–95. [Google Scholar] [CrossRef]
- Mohawesh, O.; Durner, W. Effects of Bentonite, Hydrogel and Biochar Amendments on Soil Hydraulic Properties from Saturation to Oven Dryness. Pedosphere 2019, 29, 598–607. [Google Scholar] [CrossRef]
- Zhuo, A.; He, L.; Zhao, H. Effect of organic acids on inorganic phosphorus transformation in soils and its readily available phosphate. Acta Ecol. Sin. 2009, 29, 4061–4069. [Google Scholar]
- Cordell, D.; White, S. Peak phosphorus: Clarifying the key issues of a vigorous debate about long-term phosphorus security. Sustainability 2011, 3, 2027–2049. [Google Scholar] [CrossRef] [Green Version]
- McDowell, R.; Sharpley, A. Approximating phosphorus release from soils to surface runoff and subsurface drainage. J. Environ. Qual. 2001, 30, 508–520. [Google Scholar] [CrossRef] [Green Version]
- Morrison, J.; Madramootoo, C.A.; Chikhaoui, M. Modeling the influence of tile drainage flow and tile spacin g on phosphorus losses from two agricultural fields in southern Quebec. Water Qual. Res. J. Can. 2013, 48, 279–293. [Google Scholar] [CrossRef]
- Van der Salm, C.; Dupas, R.; Grant, R.; Heckrath, G.; Iversen, B.V.; Kronvang, B.; Levi, C.; Rubaek, G.H.; Schoumans, O.F. Predicting phosphorus losses with the PLEASE model on a local scale in Denmark and the Netherlands. J. Environ. Qual. 2011, 40, 1617–1626. [Google Scholar] [CrossRef] [PubMed]
- Larsson, M.H.; Persson, K.; Ulen, B.; Lindsjo, A.; Jarvis, N. A dual porosity model to quantify phosphorus losses from macroporous soils. Ecol. Model. 2007, 205, 123–134. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Development and applications of the HYDRUS and STANMOD software packages and related codes. Vadose Zone J. 2008, 7, 587–600. [Google Scholar] [CrossRef] [Green Version]
- Kadyampakeni, D.M.; Nkedi-Kizza, P.; Morgan, K.T.; Schumann, A.W. Characterizing sorption and modeling phosphorus movement on Candler and Immokalee fine sand. J. Soil Water Sci. 2017, 1, 8–14. [Google Scholar] [CrossRef]
- Ben-Gal, A.; Dudley, L.M. Phosphorus availability under continuous point source irrigation. Soil Sci. Soc. Am. J. 2003, 67, 1449–1456. [Google Scholar] [CrossRef]
- Elmi, A.; Abou Nohra, J.S.; Madramootoo, C.A.; Hendershot, W. Estimating phosphorus leachability in reconstructed soil columns using HYDRUS-1D model. Environ. Earth Sci. 2011, 65, 1751–1758. [Google Scholar] [CrossRef]
- Naseri, A.A.; Hoseini, Y.; Moazed, H.; Abbasi, F.; Samani, H.M.V.; Sakebi, S.A. Phosphorus Transport Through a Saturated Soil Column: Comparison Between Physical Modeling and HYDRUS-3D Outputs. J. Appl. Sci. 2011, 11, 815–823. [Google Scholar] [CrossRef] [Green Version]
- Nakhaei, M.; Šimůnek, J. Parameter estimation of soil hydraulic and thermal property functions for unsaturated porous media using the HYDRUS-2D code. J. Hydrol. Hydromech. 2014, 62, 7–15. [Google Scholar] [CrossRef] [Green Version]
- Hopmans, J.W.; Šimůnek, J.; Romano, N.; Durner, W. Inverse methods. In Methods of Soil Analysis. Part 4; SSSA Book Series, No. 5; Dane, J.H., Topp, G.C., Eds.; SSSA: Madison, WI, USA, 2002; pp. 963–1008. [Google Scholar] [CrossRef]
- Filipović, V.; Weninger, T.; Filipović, L.; Schwen, A.; Bristow, K.L.; Zechmeister-Boltenstern, S.; Leitner, S. Inverse estimation of soil hydraulic properties and water repellency following artificially induced drought stress. J. Hydrol. Hydromech. 2018, 66, 170–180. [Google Scholar] [CrossRef] [Green Version]
- Vrugt, J.A.; Stauffer, P.H.; Wöhling, T.; Robinson, B.A.; Vesselinov, V. Inverse modeling of subsurface flow and transport properties: A review with new developments. Vadose Zone J. 2008, 7, 843–864. [Google Scholar] [CrossRef]
- Filipović, V.; Cambier, P.; Filipović, L.; Coquet, Y.; Pot, V.; Bodineau, G.; Jaulin, A.; Mercier, V.; Houot, S.; Benoit, P. Modeling Copper and Cadmium Mobility in an Albeluvisol Amended with Urban Waste Composts. Vadose Zone J. 2016, 15, 1–15. [Google Scholar] [CrossRef]
- Filipović, V.; Coquet, Y.; Pot, V.; Houot, S.; Benoit, P. Modeling water and isoproturon dynamics in a soil profile with different urban waste compost application considering local heterogeneities. Geoderma 2016, 268, 29–40. [Google Scholar] [CrossRef] [Green Version]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014. Update 2015: International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports No. 106; FAO: Rome, Italy, 2015; p. 192. [Google Scholar]
- Černe, M.; Palčić, I.; Pasković, I.; Major, N.; Romić, M.; Filipović, V.; Igrc, M.D.; Perčin, A.; Goreta Ban, S.; Zorko, B.; et al. The effect of stabilization on the utilization of municipal sewage sludge as a soil amendment. Waste Manag. 2019, 94, 27–38. [Google Scholar] [CrossRef]
- Canet, R.; Pomares, F.; Cabot, B.; Chaves, C.; Ferrer, E.; Ribó, M.; Albiach, M.R. Composting of olive mill pomace and other residues from rural southeastern Spain. Waste Manag. 2008, 28, 2585–2592. [Google Scholar] [CrossRef]
- EPA. U.S. Environmental Protection Agency. Method 1684; EPA: Washington, DC, USA, 2001.
- Cornelissen, G.; Pandit, N.R.; Taylor, P.; Pandit, B.H.; Sparrevik, M.; Schmidt, H.P. Emissions and Char Quality of Flame-Curtain “Kon Tiki” Kilns for Farmer-Scale Charcoal/Biochar Production. PLoS ONE 2016, 11, e0154617. [Google Scholar] [CrossRef] [Green Version]
- Gee, G.W.; Or, D. Particle-size analysis. In Methods of Soil Analysis. Part 4; SSSA Book Series, No. 5; Dane, J.H., Topp, G.C., Eds.; SSSA: Madison, WI, USA, 2002; pp. 1381–1402. [Google Scholar]
- Schindler, U.; Durner, W.; von Unold, G.; Müller, L. Evaporation method for measuring unsaturated hydraulic properties of soils: Extending the measurement range. Soil Sci. Soc. Am. J. 2010, 74, 1071–1083. [Google Scholar] [CrossRef]
- Vogel, T.; Císlerová, M. On the reliability of unsaturated hydraulic conductivity calculated from the moisture retention curve. Transp. Porous Med. 1988, 3, 1–15. [Google Scholar] [CrossRef]
- Luckner, L.; van Genuchten, M.T.; Nielsen, D.R. A consistent set of parametric models for the two-phase flow of immiscible fluids in the subsurface. Water Resour. Res. 1989, 25, 2187–2193. [Google Scholar] [CrossRef]
- Šimůnek, J.; Angulo-Jaramillo, R.; Schaap, M.G.; Vandervaere, J.P.; van Genuchten, M.T. Using an inverse method to estimate the hydraulic properties of crusted soils from tension disc infiltrometer data. Geoderma 1998, 86, 61–81. [Google Scholar] [CrossRef]
- González, M.G.; Ramos, T.B.; Carlesso, R.; Paredes, P.; Petry, M.T.; Martins, J.D.; Aires, N.P.; Pereira, L.S. Modelling soil water dynamics of full and deficit drip irrigated maize cultivated under a rain shelter. Biosyst. Eng. 2015, 132, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Šimůnek, J.; van Genuchten, M.T.; Šejna, M. Recent developments and applications of the HYDRUS computer software package. Vadose Zone J. 2016, 15, 25. [Google Scholar] [CrossRef] [Green Version]
- Pote, D.H.; Daniel, T.C. Analyzing for Dissolved reactive phosphorus in water samples. In Methods of Phosphorus Analysis for Soils, Sediments, Residuals, and Waters; Pierzynski, G.M., Ed.; North Carolina State University: Raleigh, NC, USA, 2000; pp. 91–93. [Google Scholar]
- Pote, D.H.; Daniel, T.C. Analyzing for total phosphorus and total dissolved phosphorus in water samples. In Methods of Phosphorus Analysis for Soils, Sediments, Residuals, and Waters; Pierzynski, G.M., Ed.; North Carolina State University: Raleigh, NC, USA, 2000; pp. 94–97. [Google Scholar]
- Qiao, S.Y. Modeling Water Flow and Phosphorus Fate and Transport in a Tile Drained Clay Loam Soil Using HYDRUS 2D/3D. Master’s Thesis, McGill University, Montreal, QC, Canada, 2014. [Google Scholar]
- Marquardt, D.W. An algorithm for least-squares estimation of nonlinear parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Hopmans, J.W.; Šimůnek, J. Review of inverse estimation of soil hydraulic properties. In Characterization and Measurement of the Hydraulic Properties of Unsaturated Porous Media; Van Genuchten, M.T., Leij, F.J., Wu, L., Eds.; University of California: Riverside, CA, USA, 1999; pp. 643–659. [Google Scholar]
- Clausnitzer, V.; Hopmans, J.W. Non-Linear Parameter Estimation: LM_OPT. General-Purpose Optimization Code Based on the Levenberg-Marquardt Algorithm. Land, Air and Water Resources Paper; No. 100032; University of California: Davis, CA, USA, 1995. [Google Scholar]
- Karbout, N.; Moussa, M.; Brahim, N.; Bol, R.; Bounina, H. Effect of Combined Application of Mineral Fertilizer in Soil Hydraulic Properties; Kallel, A., Ed.; Springer: Cham, Switzerland, 2018; pp. 269–272. [Google Scholar] [CrossRef]
- Schneider, S.; Coquet, Y.; Vachier, P.; Labat, C.; Roger-Estrade, J.; Benoit, P.; Pot, V.; Houot, S. Effect of urban waste compost application on soil near-saturated hydraulic conductivity. J. Environ. Qual. 2009, 38, 772–781. [Google Scholar] [CrossRef] [PubMed]
- Mohanty, B.P.; Bowman, R.S.; Hendrickx, J.M.H.; van Genuchten, M.T. New piecewise-continuous hydraulic functions for modeling preferential flow in an intermittent-flood-irrigated field. Water Resour. Res. 1997, 33, 2049–2063. [Google Scholar] [CrossRef]
- Zhang, X.; Zhu, J.; Wendroth, O.; Matocha, C.; Edwards, D. Effect of Macroporosity on Pedotransfer Function Estimates at the Field Scale. Vadose Zone J. 2019, 18, 1–15. [Google Scholar] [CrossRef]
- Vogeler, I.; Carrick, S.; Cichota, R.; Lilburne, L. Estimation of soil subsurface hydraulic conductivity based on inverse modelling and soil morphology. J. Hydrol. 2019, 574, 373–382. [Google Scholar] [CrossRef]
- De Pinho, R.E.C.; de Miranda, J.H. Evaluation of HYDRUS-1D to simulate water and potassium transport in two laboratory tropical soil columns. Eng. Agric. Jaboticabal 2014, 34, 899–911. [Google Scholar] [CrossRef] [Green Version]
- Muwamba, A.; Nkedi-Kizza, P.; Morgan, K.T. Determination of sorption coefficient of phosphorus applied for sugarcane production in southwestern Florida. J. Environ. Qual. 2016, 45, 1760–1768. [Google Scholar] [CrossRef]
- Kadlec, R.H.; Knight, R.L. Treatment Wetlands, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1996. [Google Scholar]
- Grosse, W.; Wissing, F.; Perfler, R. Biotechnological Approach to Water Quality Improvement in Tropical and Subtropical Areas for Reuse and Rehabilitation of Aquatic Ecosystems; European Commission: Cologne, Germany, 1999. [Google Scholar]
- Zhang, J.Z.; Huang, X.L. Relative importance of solid-phase phosphorus and iron on the sorption behavior of sediments. Environ. Sci. Technol. 2007, 41, 2789–2795. [Google Scholar] [CrossRef]
- Iyamuremye, F.; Dick, R.P. Organic amendments and phosphorus sorption. Adv. Agron. 1996, 56, 139–185. [Google Scholar] [CrossRef]
- Guppy, C.N.; Menzies, N.W.; Moody, P.W.; Blamey, F.P.C. Competitive sorption reactions between phosphorus organic matter in soil: A review. Aust. J. Soil Res. 2005, 43, 189–202. [Google Scholar] [CrossRef]
- Agbenin, J.O.; Igbokwe, S.O. Effect of soil– dung manure incubation on the solubility and retention of applied phosphate by a weathered tropical semi-arid soil. Geoderma 2006, 133, 191–203. [Google Scholar] [CrossRef]
- Gichangi, E.M.; Mnkeni, P.N.S. Effects of goat manure and lime addition on phosphate sorption by two soils from the Transkei Region, South Africa. Commun. Soil Sci. Plan. 2009, 40, 3335–3347. [Google Scholar] [CrossRef]
- Eduah, J.O.; Nartey, E.K.; Abekoe, M.K.; Henriksen, S.W.; Andersen, M.N. Mechanism of orthophosphate (PO4-P) adsorption onto different biochars. Environ. Technol. Innov. 2020, 17, 100572. [Google Scholar] [CrossRef]
- Zhu, X.M.; Chen, B.L.; Zhu, L.Z.; Xing, B.S. Effects and mechanisms of biocharmicrobe interactions in soil improvement and pollution remediation: A review. Environ. Pollut. 2017, 227, 98–115. [Google Scholar] [CrossRef]
- Gondek, K.; Mierzwa-Hersztek, M.; Kopeć, M.; Sikora, J.; Głąb, T.; Szczurowska, K. Influence of biochar application on reduced acidification of sandy soil, increased cation exchange capacity, and the content of available forms of K, Mg, and P. Pol. J. Environ. Stud. 2019, 28, 1–9. [Google Scholar] [CrossRef]




| Treatment Abbreviation | Soil | Treatment Method | Waste Type | P-Level |
|---|---|---|---|---|
| TBSS_P | Terra Rossa | biochar | sewage sludge | P-regulation |
| TBSS_P+ | Terra Rossa | biochar | sewage sludge | P-10× higher |
| TBOP_P | Terra Rossa | biochar | olive pomace | P-regulation |
| TBOP_P+ | Terra Rossa | biochar | olive pomace | P-10× higher |
| TCSS_P | Terra Rossa | compost | sewage sludge | P-regulation |
| TCSS_P+ | Terra Rossa | compost | sewage sludge | P-10× higher |
| TCOP_P | Terra Rossa | compost | olive pomace | P-regulation |
| TCOP_P | Terra Rossa | compost | olive pomace | P-10× higher |
| T_P | Terra Rossa | / | / | P-regulation |
| T_0 | Terra Rossa | / | / | 0 |
| Treatment Abbreviation | Soil | Treatment Method | Waste Type | P-Level |
|---|---|---|---|---|
| RBSS_P | Rendzina | biochar | sewage sludge | P-regulation |
| RBSS_P+ | Rendzina | biochar | sewage sludge | P-10× higher |
| RBOP_P | Rendzina | biochar | olive pomace | P-regulation |
| RBOP_P+ | Rendzina | biochar | olive pomace | P-10× higher |
| RCSS_P | Rendzina | compost | sewage sludge | P-regulation |
| RCSS_P+ | Rendzina | compost | sewage sludge | P-10× higher |
| RCOP_P | Rendzina | compost | olive pomace | P-regulation |
| RCOP_P | Rendzina | compost | olive pomace | P-10× higher |
| R_P | Rendzina | / | / | P-regulation |
| R_0 | Rendzina | / | / | 0 |
| Treatment Abbreviation | Total P Concentration in Soil (mg kg−1) | Irrigation Volume (mL) | Treatment Abbreviation | Total P Concentration in Soil (mg kg−1) | Irrigation Volume (mL) |
|---|---|---|---|---|---|
| TBSS_P | 323.2 | 500 (3×) | RBSS_P | 270.4 | 500 (3×) |
| TBSS_P+ | 474.1 | 500 (3×) | RBSS_P+ | 366.9 | 500 (3×) |
| TBOP_P | 308.4 | 500 (3×) | RBOP_P | 249.8 | 500 (3×) |
| TBOP_P+ | 317.7 | 500 (3×) | RBOP_P+ | 258.9 | 500 (3×) |
| TCSS_P | 312.8 | 500 (3×) | RCSS_P | 254.8 | 500 (3×) |
| TCSS_P+ | 350.9 | 500 (3×) | RCSS_P+ | 294.4 | 500 (3×) |
| TCOP_P | 313.1 | 500 (3×) | RCOP_P | 247.7 | 500 (3×) |
| TCOP_P+ | 358.7 | 500 (3×) | RCOP_P+ | 333.2 | 500 (3×) |
| T_P | 422.8 | 500 (3×) | R_P | 490.5 | 500 (3×) |
| T_0 | 320.6 | 500 (3×) | R_0 | 251.5 | 500 (3×) |
| Treatment Abbreviation | θs (cm3 cm−3) | α (cm−1) | n (-) | Ks (cm d−1) | l (-) | θk (cm3 cm−3) | Kk (cm d−1) |
|---|---|---|---|---|---|---|---|
| TBSS_P | 0.480 | 0.00247 | 1.12 | 7.07 | −4.80 | 0.480 | 0.019 |
| TBSS_P+ | 0.481 | 0.00238 | 1.15 | 6.68 | −4.51 | 0.480 | 0.022 |
| TBOP_P | 0.493 | 0.0234 | 1.16 | 5.72 | −5.08 | 0.457 | 0.282 |
| TBOP_P+ | 0.519 | 0.032 | 1.19 | 7.07 | −3.57 | 0.437 | 0.759 |
| TCSS_P | 0.437 | 0.00195 | 1.16 | 6.59 | −3.57 | 0.437 | 0.026 |
| TCSS_P+ | 0.450 | 0.011 | 1.10 | 6.68 | 4.89 | 0.448 | 0.047 |
| TCOP_P | 0.480 | 0.0461 | 1.08 | 6.94 | 10.00 | 0.441 | 0.525 |
| TCOP_P+ | 0.515 | 0.0135 | 1.11 | 6.11 | −6.00 | 0.513 | 0.158 |
| T_P | 0.450 | 0.00895 | 1.17 | 6.37 | 4.59 | 0.434 | 0.575 |
| T_0 | 0.450 | 0.00914 | 1.16 | 6.81 | 3.99 | 0.446 | 0.093 |
| Treatment Abbreviation | θs (cm3 cm−3) | α (cm−1) | n (-) | Ks (cm d−1) | l (-) | θk (cm3 cm−3) | Kk (cm d−1) |
|---|---|---|---|---|---|---|---|
| RBSS_P | 0.412 | 0.015 | 1.16 | 5.97 | −0.15 | 0.398 | 0.537 |
| RBSS_P+ | 0.432 | 0.00272 | 1.17 | 4.71 | −6.00 | 0.432 | 0.029 |
| RBOP_P | 0.400 | 0.0018 | 1.18 | 7.07 | −6.00 | 0.399 | 0.024 |
| RBOP_P+ | 0.420 | 0.0043 | 1.12 | 6.94 | −6.00 | 0.419 | 0.065 |
| RCSS_P | 0.422 | 0.0023 | 1.21 | 7.16 | −5.95 | 0.420 | 0.047 |
| RCSS_P+ | 0.430 | 0.00219 | 1.18 | 6.94 | −5.80 | 0.429 | 0.019 |
| RCOP_P | 0.403 | 0.0093 | 1.10 | 7.07 | −6.00 | 0.397 | 0.525 |
| RCOP_P | 0.418 | 0.00146 | 1.19 | 7.24 | −6.00 | 0.418 | 0.019 |
| R_P | 0.372 | 0.00107 | 1.18 | 6.94 | −6.00 | 0.371 | 0.014 |
| R_0 | 0.346 | 0.00062 | 1.25 | 6.94 | −6.00 | 0.346 | 0.005 |
| TBSS_P | TBSS_P+ | TBOP_P | TBOP_P+ | TCSS_P | TCSS_P+ | TCOP_P | TCOP_P+ | T_P | T_0 | ||
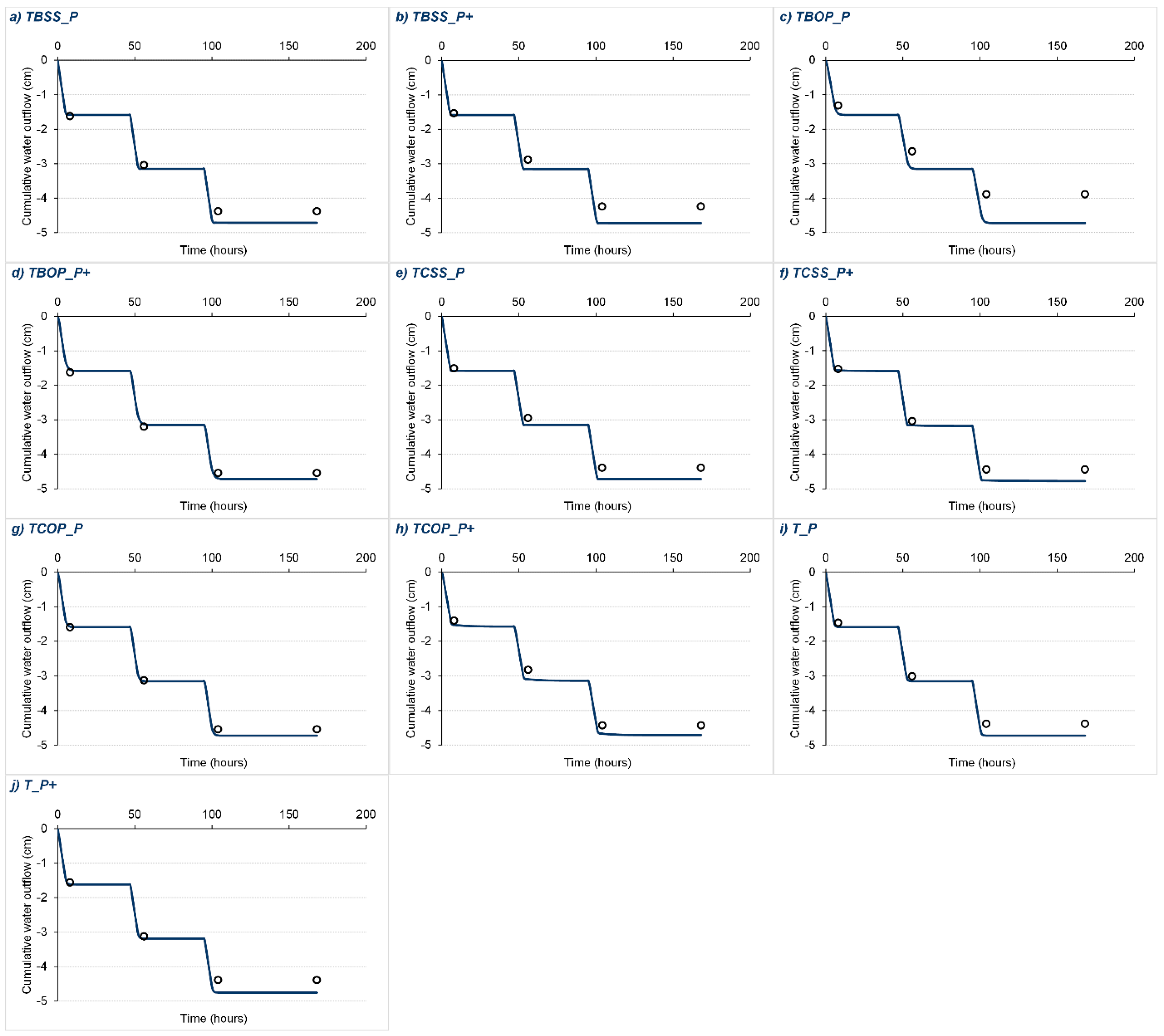
| Terra Rosa | Measured vol. (cm) | 4.38 | 4.24 | 3.89 | 4.54 | 4.39 | 4.44 | 4.54 | 4.43 | 4.38 | 4.39 |
| Simulated vol. (cm) | 4.71 | 4.72 | 4.72 | 4.72 | 4.72 | 4.72 | 4.71 | 4.71 | 4.72 | 4.72 | |
| R2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | |
| RBSS_P | RBSS_P+ | RBOP_P | RBOP_P+ | RCSS_P | RCSS_P+ | RCOP_P | RCOP_P+ | R_P | R_0 | ||
| Rendzina | Measured vol. (cm) | 4.46 | 4.13 | 4.55 | 4.09 | 4.33 | 4.56 | 4.71 | 4.54 | 4.65 | 4.44 |
| Simulated vol. (cm) | 4.72 | 4.72 | 4.73 | 4.72 | 4.72 | 4.73 | 4.73 | 4.73 | 4.72 | 4.72 | |
| R2 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 | 0.99 |
| TBSS_P | TBSS_P+ | TBOP_P | TBOP_P+ | TCSS_P | TCSS_P+ | TCOP_P | TCOP_P+ | T_P | T_0 | ||
| Terra Rosa | Kd | 35.13 | 53.68 | 27.27 | 22.51 | 28.34 | 26.48 | 26.23 | 23.07 | 29.98 | 37.57 |
| R2 | 0.99 | 0.98 | 0.98 | 0.99 | 0.98 | 0.95 | 0.96 | 0.92 | 0.99 | 0.96 | |
| RBSS_P | RBSS_P+ | RBOP_P | RBOP_P+ | RCSS_P | RCSS_P+ | RCOP_P | RCOP_P+ | R_P | R_0 | ||
| Rendzina | Kd | 34.67 | 30.01 | 27.11 | 34.41 | 25.22 | 28.38 | 21.24 | 44.89 | 52.83 | 30.64 |
| R2 | 0.99 | 0.99 | 0.93 | 0.94 | 0.99 | 0.93 | 0.99 | 0.97 | 0.96 | 0.93 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Filipović, V.; Černe, M.; Šimůnek, J.; Filipović, L.; Romić, M.; Ondrašek, G.; Bogunović, I.; Mustać, I.; Krevh, V.; Ferenčević, A.; et al. Modeling Water Flow and Phosphorus Sorption in a Soil Amended with Sewage Sludge and Olive Pomace as Compost or Biochar. Agronomy 2020, 10, 1163. https://doi.org/10.3390/agronomy10081163
Filipović V, Černe M, Šimůnek J, Filipović L, Romić M, Ondrašek G, Bogunović I, Mustać I, Krevh V, Ferenčević A, et al. Modeling Water Flow and Phosphorus Sorption in a Soil Amended with Sewage Sludge and Olive Pomace as Compost or Biochar. Agronomy. 2020; 10(8):1163. https://doi.org/10.3390/agronomy10081163
Chicago/Turabian StyleFilipović, Vilim, Marko Černe, Jiří Šimůnek, Lana Filipović, Marija Romić, Gabrijel Ondrašek, Igor Bogunović, Ivan Mustać, Vedran Krevh, Anja Ferenčević, and et al. 2020. "Modeling Water Flow and Phosphorus Sorption in a Soil Amended with Sewage Sludge and Olive Pomace as Compost or Biochar" Agronomy 10, no. 8: 1163. https://doi.org/10.3390/agronomy10081163
APA StyleFilipović, V., Černe, M., Šimůnek, J., Filipović, L., Romić, M., Ondrašek, G., Bogunović, I., Mustać, I., Krevh, V., Ferenčević, A., Robinson, D., Palčić, I., Pasković, I., Goreta Ban, S., Užila, Z., & Ban, D. (2020). Modeling Water Flow and Phosphorus Sorption in a Soil Amended with Sewage Sludge and Olive Pomace as Compost or Biochar. Agronomy, 10(8), 1163. https://doi.org/10.3390/agronomy10081163












