Impact of Climate Change on Groundwater Management in the Northwestern Part of Uzbekistan
Abstract
:1. Introduction
2. Materials and Methods
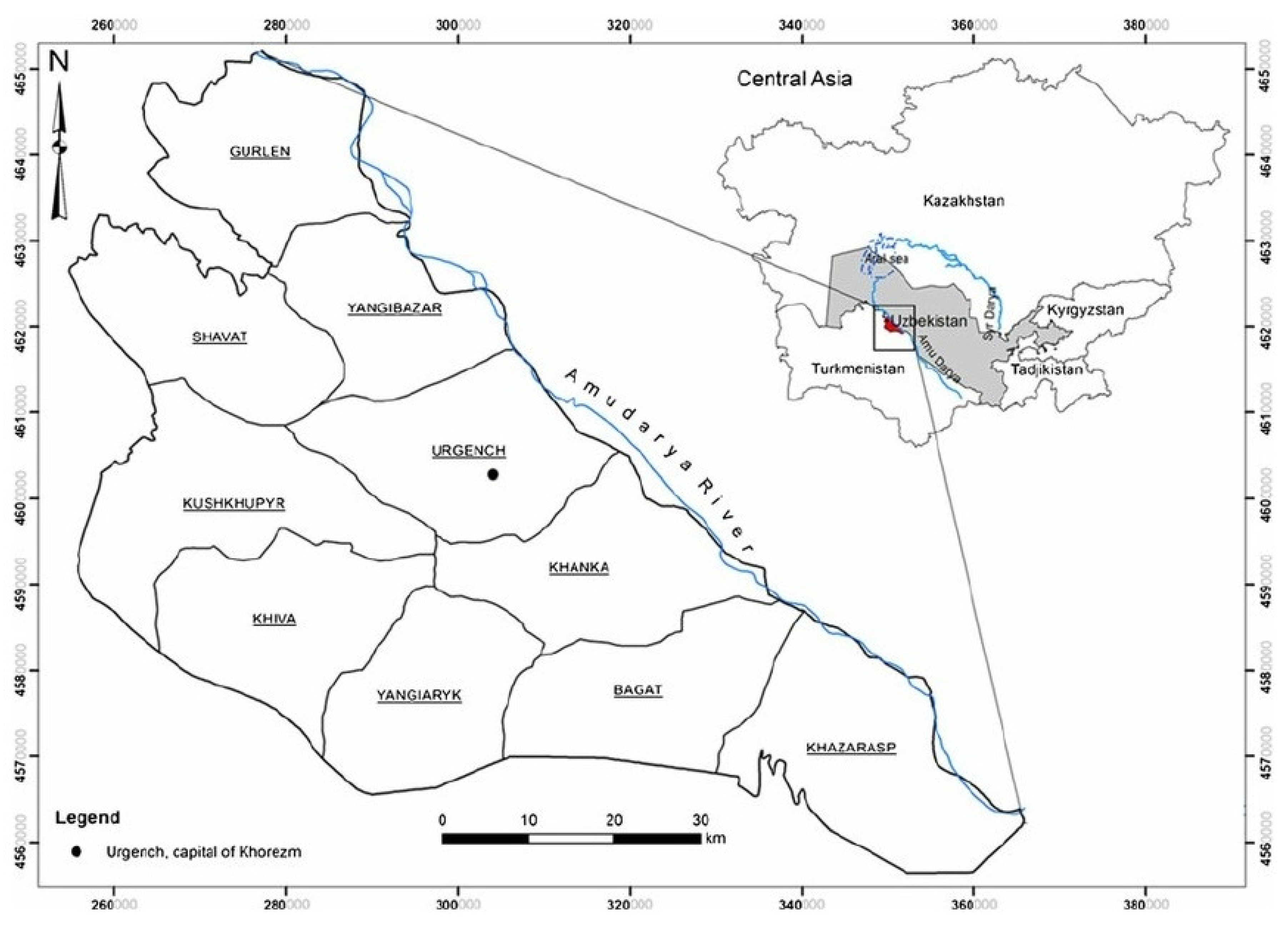
2.1. Case Study Area
2.2. Linear Regression Model
2.3. Mann–Kendall Trend Test
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hamidov, A.; Helming, K.; Balla, D. Impact of agricultural land use in Central Asia: A review. Agron. Sustain. Dev. 2016, 36, 6. [Google Scholar] [CrossRef] [Green Version]
- Unger-Shayesteh, K.; Vorogushyn, S.; Farinotti, D.; Gafurov, A.; Duethmann, D.; Mandychev, A.; Merz, B. What do we know about past changes in the water cycle of Central Asian headwaters? A review. Glob. Planet Chang. 2013, 110, 4–25. [Google Scholar] [CrossRef]
- Reyer, C.P.O.; Otto, I.M.; Adams, S.; Albrecht, T.; Baarsch, F.; Cartsburg, M.; Coumou, D.; Eden, A.; Ludi, E.; Marcus, R.; et al. Climate change impacts in Central Asia and their implications for development. Reg. Environ. Chang. 2017, 17, 1639–1650. [Google Scholar] [CrossRef]
- Jie, J.; Tianjun, Z.; Xiaolong, C.; Lixia, Z. Future changes in precipitation over Central Asia based on CMIP6 projections. Environ. Res. Lett. 2020, 15, 054009. [Google Scholar]
- Chub, V.E.; Spectorman, T.Y. Climate Trends in Uzbekistan. In Climate Change, Reasons, Impacts and Response Measures; Bulletin: Tashkent, Uzbekistan, 2016; pp. 5–16. [Google Scholar]
- Arora, N.K. Impact of climate change on agriculture production and its sustainable solutions. Environ. Sustain. 2019, 2, 95–96. [Google Scholar] [CrossRef] [Green Version]
- Musayev, S.; Musaev, I. Climate change impact on agriculture in Central Asia. Sci. -Tech. J. 2018, 22, 57–60. [Google Scholar]
- Xu, Y.; Ramanathan, V. Well below 2 °C: Mitigation strategies for avoiding dangerous to catastrophic climate changes. Proc. Natl. Acad. Sci. USA 2017, 114, 10315–10323. [Google Scholar] [CrossRef] [Green Version]
- Gruza, G.V.; Rankova, E.Y.; Aristova, L.N.; Kleschenko, L.K. On the uncertainty of some scenario climate forecasts of air temperature and precipitation in Russia. Meteorol. Hydrol. 2007, 10, 5–23. [Google Scholar]
- Israel, Y.A. An effective way to preserve climate at the present level is the main goal of solving the climate problem. Meteorol. Hydrol. 2005, 10, 5–9. [Google Scholar]
- Zhukov, V.A. Stochastic modeling and forecasting of agroclimatic resources during adaptation of agriculture to regional climate changes in Russia. Meteorol. Hydrol. 2000, 1, 100–109. [Google Scholar]
- Ivanov, V.V. Study of variations in mean monthly air temperature using sequential spectra. Meteorol. Hydrol. 2006, 5, 39–45. [Google Scholar]
- Konovalova, N.V.; Korobov, V.B.; Vasiliev, L.Y. Interpolation of climate data using GIS technology. Meteorol. Hydrol. 2006, 5, 46–53. [Google Scholar]
- Hamidov, A.; Helming, K.; Bellocchi, G.; Bojar, W.; Dalgaard, T.; Ghaley, B.B.; Hoffmann, C.; Holman, I.; Holzkämper, A.; Krzeminska, D.; et al. Impacts of climate change adaptation options on soil functions: A review of European case-studies. Land Degrad. Dev. 2018, 29, 2378–2389. [Google Scholar] [CrossRef] [PubMed]
- Huntington, T.G. Evidence for intensification of the global water cycle: Review and synthesis. J. Hydrol. 2006, 319, 83–95. [Google Scholar] [CrossRef]
- Wilby, R.L.; Whitehead, P.G.; Wade, A.J.; Butterfield, D.; Davis, R.J.; Watts, G. Integrated modelling of climate change impacts on water resources and quality in a lowland catchment: River Kennet, UK. J. Hydrol 2006, 330, 204–220. [Google Scholar] [CrossRef]
- IPCC. Climate Change 2007: The Physical Science Basis; Contribution of Working Group 1 to the Forth Assessment Report of the Intergovernmental Panel on Climate Change; Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K.B., Tignor, M., Miller, H.L., Eds.; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- IPCC. Summary for Policymakers. In Climate Change 2013: The Physical Science Basis; Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Zhao, Z.; Jia, Z.; Guan, Z.; Xu, C. The Effect of Climatic and Non-climatic Factors on Groundwater Levels in the Jinghuiqu Irrigation District of the Shaanxi Province, China. Water 2019, 11, 956. [Google Scholar] [CrossRef] [Green Version]
- Gallardo, A.H. Groundwater levels under climate change in the Gnangara system, Western Australia. J. Water Clim. Chang. 2013, 4, 52–62. [Google Scholar] [CrossRef]
- Lee, J.; Jung, C.; Kim, S.; Kim, S. Assessment of Climate Change Impact on Future Groundwater-Level Behavior Using SWAT Groundwater-Consumption Function in Geum River Basin of South Korea. Water 2019, 11, 949. [Google Scholar] [CrossRef] [Green Version]
- Chung, I.-M.; Kim, J.; Lee, J.; Chang, S.W. Status of Exploitable Groundwater Estimations in Korea. J. Eng. Geol. 2015, 25, 403–412. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.-Y. Lessons from three groundwater disputes in Korea: Lack of comprehensive and integrated investigation. Int. J. Water 2017, 11, 59. [Google Scholar] [CrossRef]
- Adane, Z.; Zlotnik, V.A.; Rossman, N.R.; Wang, T.; Nasta, P. Sensitivity of Potential Groundwater Recharge to Projected Climate Change Scenarios: A Site-Specific Study in the Nebraska Sand Hills, USA. Water 2019, 11, 950. [Google Scholar] [CrossRef] [Green Version]
- Terrell, B.L.; Johnson, P.N.; Segarra, E. Ogallala aquifer depletion: Economic impact on the Texas high plains. Water Policy 2002, 4, 33–46. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Hamidov, A.; Beltrao, J.; Neves, A.; Khaydarova, V.; Khamidov, M. Apocynum Lancifolium and Chenopodium Album—potential species to remediate saline soils. Wseas Trans. Environ. Dev. 2007, 3, 123–128. [Google Scholar]
- Vargas, R.; Pankova, E.I.; Balyuk, S.A.; Krasilnikov, P.V.; Khasankhanova, G.M. Handbook for Saline Soil Management; FAO: Rome, Italy, 2018; p. 144. [Google Scholar]
- Global Environment Facility (GEF). The GEF Small Grants Programme. Available online: http://sgp.uz/projects/desertification/73 (accessed on 10 April 2020).
- Ishchanov, J. Analysis and Projections of the Impacts of Environmental and Climate Changes on Ameliorative Conditions of Lands in the Khorezm Region. Ph.D. Thesis, Tashkent Institute of Irrigation and Agricultural Mechnaization Engineers (TIIAME), Tashkent, Uzbekistan, 2020; p. 106. [Google Scholar]
- Ibrakhimov, M.; Maritius, C.; Lamers, J.P.A.; Tischbein, B. The dynamics of groundwater table and salinity over 17 years in Khorezm. Agric. Water Manag. 2011, 101, 52–61. [Google Scholar] [CrossRef]
- Hamidov, A.; Beltrao, J.; Costa, C.; Khaydarova, V.; Sharipova, S. Environmentally useful technique—Portulaca Oleracea golden purslane as a salt removal species. WSEAS Trans. Environ. Dev. 2007, 3, 117–122. [Google Scholar]
- Hbirkoua, C.; Martius, C.; Khamzina, A.; Lamers, J.P.A.; Welp, G.; Amelung, W. Reducing topsoil salinity and raising carbon stocks through afforestation in Khorezm, Uzbekistan. J. Arid Environ. 2011, 75, 146–155. [Google Scholar] [CrossRef]
- Devkota, M.; Gupta, R.K.; Martius, C.; Lamers, J.P.A.; Devkota, K.P.; Sayre, K.D.; Vlek, P.L.G. Soil salinity management on raised beds with different furrow irrigation modes in salt-affected lands. Agric. Water Manag. 2015, 152, 243–250. [Google Scholar] [CrossRef]
- Khamzina, A.; Lamers, J.P.A.; Martius, C.; Worbes, V.; Vlek, P.L.G. Potential of nine multipurpose tree species to reduce saline groundwater tables in the lower Amu Darya River region of Uzbekistan. Agroforest Syst 2006, 68, 151–165. [Google Scholar] [CrossRef]
- Malik, A.; Shah, A.R. Crop Production and Productivity Variations in Uzbekistan with Special Reference to Grain Crops. J. Cent. Asian Stud. 2017, 24, 121-II. [Google Scholar]
- Panda, A.; Sahu, N. Trend analysis of seasonal rainfall and temperature pattern in Kalahandi, Bolangir and Koraput districts of Odisha, India. Atmos. Sci. Lett. 2019, 20, 932. [Google Scholar] [CrossRef] [Green Version]
- Addisu, S.; Selassie, Y.G.; Fissha, G.; Gedif, B. Time series trend analysis of temperature and rainfall in lake Tana sub-basin, Ethiopia. Environ. Syst. Res. 2015, 4, 25. [Google Scholar] [CrossRef] [Green Version]
- Bhutiyani, M.R.; Kale, V.S.; Pawar, N.J. Long-term trends in maximum, minimum and mean annual air temperatures across the Northwestern Himalaya during the twentieth century. Clim. Chang. 2007, 85, 159–177. [Google Scholar] [CrossRef]
- Tabari, H.; Talaee, P. Analysis of trends in temperature data in arid and semi-arid regions of Iran. Glob. Planet. Chang. 2011, 79, 1–10. [Google Scholar] [CrossRef]
- Gil-Alana, L.A. Maximum and minimum temperatures in the United States: Time trends and persistence. Atmos. Sci. Lett. 2018, 19, 810. [Google Scholar] [CrossRef]
- Conrad, C.; Dech, S.; Dubovyk, O.; Fritsch, S.; Klein, D.; Low, F.; Zeidler, J. Derivation of temporal windows for accurate crop discrimination in heterogeneous croplands of Uzbekistan using multitemporal Rapid Eye images. Comput. Electron. Agric. 2014, 103, 63–74. [Google Scholar] [CrossRef]
- Djumaboev, K.; Hamidov, A.; Anarbekov, O.; Gafurov, Z.; Tussupova, K. Impact of institutional change on irrigation management: A case study from southern Uzbekistan. Water 2017, 9, 419. [Google Scholar] [CrossRef] [Green Version]
- Simonett, O.; Novikov, V. Land Degradation and Desertification in Central Asia: Central Asian Countries Initiative for Land Management, Analysis of the current state and recommendation for the future. Zoï Environ. Netw. Swiss Gef Counc. Memb. Geneva 2010, 1–19. [Google Scholar]
- Uzbekistan State Committee. Urban and Rural Population by Regions for 2017. Available online: https://www.stat.uz/uz/statinfo/demografiya-va-mehnat/statistik-jadvallar-demografiya/220-ofytsyalnaia-statystyka-uz/demografiya-i-trud-uz/demograficheskie-pokazateli-uz/2399-hududlar-bo-yicha-shahar-va-qishloq-aholisi-soni-yil-boshiga-ming-kishi (accessed on 1 May 2020).
- Hamidov, A.; Kasymov, U.; Salokhiddinov, A.; Khamidov, M. How can intentionality and path dependence explain change in water-management institutions in Uzbekistan? Int. J. Commons 2020, 14, 16–29. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Su, X. Linear Regression Analysis: Theory and Computing; World Scientific Publishing: Hackensack, NJ, USA, 2009; p. 348. [Google Scholar]
- Warne, R.T. Beyond multiple regression: Using commonality analysis to better understand R2 results. Gift. Child Q. 2011, 55, 313–318. [Google Scholar] [CrossRef]
- Ratner, B. The correlation coefficient: Its values range between +1/−1, or do they? J. Target. Meas. Anal. Mark. 2009, 17, 139–142. [Google Scholar] [CrossRef] [Green Version]
- Lakin, G.F. Biometrics, 4th ed.; Higher School: Moscow, Russia, 1990; p. 352. [Google Scholar]
- Patle, G.T.; Singh, D.K.; Sarangi, A.; Rai, A.; Khanna, M.; Sahoo, R.N. Time series analysis of groundwater levels and projection of future trend. J. Geol. Soc. India 2015, 2, 232–242. [Google Scholar] [CrossRef]
- Allen, D.M. Historical trends and future projections of groundwater levels and recharge in costal British Columbia, Canada. In Proceedings of the SWIM 21-21st Salt Water Intrusion meeting 2010, Azores, Portugal, 21–26 June 2010; pp. 267–270. [Google Scholar]
- Chaudhuri, S.; Dutta, D. Mann–Kendall trend of pollutants, temperature and humidity over an urban station of India with forecast verification using different ARIMA models. Environ. Monit. Assess. 2014, 186, 4719–4742. [Google Scholar] [CrossRef] [PubMed]
- Emami, F.; Masiol, M.; Hopke, P.K. Air pollution at Rochester, NY: Long-term trends and multivariate analysis of upwind SO2 source impacts. Sci. Total Environ. 2018, 612, 1506–1515. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Hung, H.; Tian, C.; Kallenborn, R. Revolatilization of persistent organic pollutants in the Arctic induced by climate change. Nat. Clim. Chang. 2011, 1, 255–260. [Google Scholar] [CrossRef] [Green Version]
- Vanguelova, E.I.; Benham, S.; Pitman, R.; Moffat, A.J.; Broadmeadow, M.; Nisbet, T.; Durrant, D.; Barsoum, N.; Wilkinson, M.; Bochereau, F.; et al. Chemical fluxes in time through forest ecosystems in the UK–soil response to pollution recovery. Environ. Pollut. 2010, 158, 1857–1869. [Google Scholar] [CrossRef] [PubMed]
- Mann, H.B. Nonparametric tests against trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods; Griffin: London, UK, 1975. [Google Scholar]
- Jaiswal, A.; Samuel, C.; Kadabgaon, V.M. Statistical trend analysis and forecast modeling of air pollutants. Glob. J. Environ. Sci. 2018, 4, 427–438. [Google Scholar]
- Hirsch, R.M.; Slack, J.R. A Nonparametric Trend Test for Seasonal Data with Serial Dependence. Water Resour. Res. 1984, 20, 727–732. [Google Scholar] [CrossRef] [Green Version]
- Panda, D.K.; Mishra, A.; Kumar, A. Quantification of trends in groundwater levels of Gujarat in western India. Hydrol. Sci. J. 2012, 7, 1325–1336. [Google Scholar] [CrossRef]
- Biswas, B.; Jain, S.; Rawat, S. Spatio-temporal analysis of groundwater levels and projection of future trend of Agra city, Uttar Pradesh, India. Arab. J. Geosci. 2018, 11, 278. [Google Scholar] [CrossRef]
- Conrad, C.; Schorcht, G.; Tischbein, B.; Davletov, S.; Sultonov, M.; Lamers, J.P.A. Agro-Meteorological Trends of Recent Climate Development in Khorezm and Implications for Crop Production; Martius, C., Rudenko, I., Lamers, J.P.A., Vlek, P.L.G., Eds.; Cotton, Water, Salts and Soums—Economic and Ecological Restructuring in Khorezm, Uzbekistan; Springer: Berlin, Germany, 2012; pp. 25–36. [Google Scholar]
- Qian, C.; Zhang, X.; Li, Z. Linear trends in temperature extremes in China, with an emphasis on non-Gaussian and serially dependent characteristics. Clim. Dyn. 2019, 53, 533–550. [Google Scholar] [CrossRef] [Green Version]
- Nazir Zaz, S.; Ahmad Romshoo, S.; Thokuluwa Krishnamoorthy, R.; Viswanadhapalli, Y. Analyses of temperature and precipitation in the Indian Jammu and Kashmir region for the 1980-2016 period: Implications for remote influence and extreme events. Atmos. Chem. Phys. 2019, 19, 15–37. [Google Scholar]
- He, M.; Russo, M.; Anderson, M.; Fickenscher, P.; Whitin, B.; Schwarz, A.; Lynn, E. Changes in extremes of temperature, precipitation, and Runoff in California’s Central Valley During 1949–2010. Hydrology 2018, 5, 1. [Google Scholar] [CrossRef] [Green Version]




| Variable | Number of Years | Minimum | Maximum | Mean | Standard Deviation |
|---|---|---|---|---|---|
| Average annual air temperature | 90 | 10.558 | 14.983 | 12.961 | 1.020 |
| Sen’s Slope | Air Temperature | Absolute Humidity, mm | Relative Humidity, % | Land Surface Temperature | Precipitation, mm | Wind Speed, m·s−1 | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Max | Min | Mean | Max | Min | |||||
| Period = 10 years | 0.284 | 0.246 | 0.423 | 0.252 | 0.451 | 0.506 | −0.708 | 0.17 | −0.617 | −0.224 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hamidov, A.; Khamidov, M.; Ishchanov, J. Impact of Climate Change on Groundwater Management in the Northwestern Part of Uzbekistan. Agronomy 2020, 10, 1173. https://doi.org/10.3390/agronomy10081173
Hamidov A, Khamidov M, Ishchanov J. Impact of Climate Change on Groundwater Management in the Northwestern Part of Uzbekistan. Agronomy. 2020; 10(8):1173. https://doi.org/10.3390/agronomy10081173
Chicago/Turabian StyleHamidov, Ahmad, Mukhamadkhan Khamidov, and Javlonbek Ishchanov. 2020. "Impact of Climate Change on Groundwater Management in the Northwestern Part of Uzbekistan" Agronomy 10, no. 8: 1173. https://doi.org/10.3390/agronomy10081173
APA StyleHamidov, A., Khamidov, M., & Ishchanov, J. (2020). Impact of Climate Change on Groundwater Management in the Northwestern Part of Uzbekistan. Agronomy, 10(8), 1173. https://doi.org/10.3390/agronomy10081173







