Banana Biomass Estimation and Yield Forecasting from Non-Destructive Measurements for Two Contrasting Cultivars and Water Regimes
Abstract
1. Introduction
2. Materials and Methods
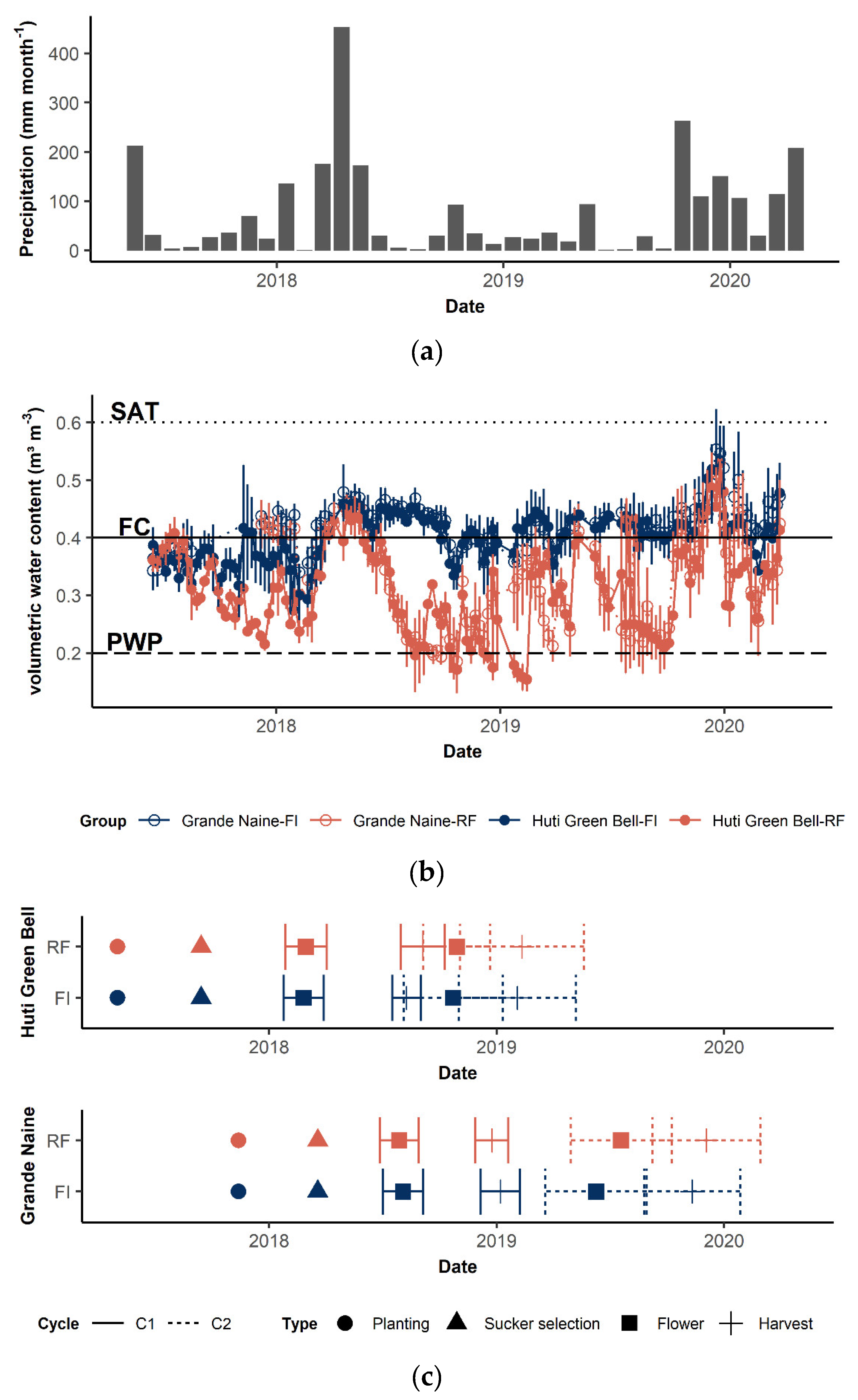
2.1. Experimental Design
2.2. Plant Data Collection
2.3. Moisture Effect on Plant Growth
2.4. Allometric Regression
2.4.1. Non-Destructive Vegetative Biomass Estimation
2.4.2. Bunch Fresh Weight Forecast
2.4.3. Regression Approach
3. Results
3.1. Moisture Effect on Phenology, Vegetative Growth, and Bunch Parameters
3.1.1. Difference in Moisture
3.1.2. Effect on Phenology
3.1.3. Effect on Vegetative Growth
3.1.4. Effect on Bunch Growth
3.1.5. Effect on Growth Rates
3.2. Aboveground Vegetative Dry Matter Estimation
3.3. Corm Dry Matter Estimation
3.4. Bunch Weight Forecast
4. Discussion
4.1. Effect of Moisture on Vegetative and Bunch Growth
4.2. ABGVD Estimation from Non-Destructive Observations
4.3. CormD Estimation from Non-Destructive Observations
4.4. Bunch Yield Forecast
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| C1, C2, and C3 | Cycle 1, 2, and 3 |
| EAHB | East African Highland Banana |
| FI | Full irrigation |
| GN | Cavendish–Grande Naine |
| HG | Mchare-Huti Green Bell |
| IITA | International Institute of Tropical Agriculture |
| NM-AIST | Nelson Mandela African Institution of Science and Technology |
| RF | Rainfed |
| RFH | Ratio of moisture received to ET0 between flowering and harvest |
| RPF | Ratio of moisture received to ET0 between planting and flowering |
| RPH | Ratio of moisture received to ET0 between planting and harvest |
| WLS | Weighted least squares regression |
References
- FAOSTAT. Banana And Plantain Production Data. Available online: http://www.fao.org/faostat/en/#data/ (accessed on 14 August 2020).
- Robinson, J.C.; Galán Saúco, V. Bananas and Plantains, 2nd ed.; Longmans: London, UK, 2010; ISBN 9781845936587. [Google Scholar]
- Swennen, R.; Langhe, E.D. Growth Parameters of Yield of Plantain (Musa cv. AAB). Ann. Bot. 1985, 197–204, 197–204. [Google Scholar] [CrossRef]
- Mukasa, H.H.; Ocan, D.; Rubaihayo, P.R.; Blomme, G. Relationships between bunch weight and plant growth characteristics of Musa spp. assessed at farm level. MusAfrica 2005, 16, 2–3. [Google Scholar]
- Nyombi, K.; Van Asten, P.J.A.; Leffelaar, P.A.; Corbeels, M.; Kaizzi, C.K.; Giller, K.E. Allometric growth relationships of East Africa highland bananas (Musa AAA-EAHB) cv. Kisansa and Mbwazirume. Ann. Appl. Biol. 2009, 155, 403–418. [Google Scholar] [CrossRef]
- Niklas, K.J. Plant allometry: Is there a grand unifying theory? Biol. Rev. 2004, 79, 871–889. [Google Scholar] [CrossRef] [PubMed]
- Picard, N.; Saint-André, L.; Henry, M. Manual for Building Tree Volume and Biomass Allometric Equations: From Field Measurement to Prediction; Food and Agricultural Organization of the United Nations, Rome, and Centre de Coopération Internationale en Recherche Agronomique pour le Développement: Rome, Italy, 2012. [Google Scholar]
- Negash, M.; Starr, M.; Kanninen, M. Allometric equations for biomass estimation of Enset (Ensete ventricosum) grown in indigenous agroforestry systems in the Rift Valley escarpment of southern-eastern Ethiopia. Agrofor. Syst. 2013, 571–581. [Google Scholar] [CrossRef]
- Wairegi, L.W.I.; van Asten, P.J.A.; Tenywa, M.; Bekunda, M. Quantifying bunch weights of the East African Highland bananas (Musa spp. AAA-EA) using non-destructive field observations. Sci. Hortic. 2009, 121, 63–72. [Google Scholar] [CrossRef]
- Yamaguchi, J.; Araki, S. Biomass production of banana plants in the indigenous farming system of the East African Highland A case study on the Kamachumu Plateau in northwest Tanzania. Agric. Ecosyst. Environ. 2004, 102, 93–111. [Google Scholar] [CrossRef]
- Swennen, R. A Physiological Study of the Suckering Behaviour in Plantain (Musa cv. AAB). Part II Observations and Experiments. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 1984; pp. 21–113. [Google Scholar]
- Soares, J.D.R.; Pasqual, M.; Lacerda, W.S.; Silva, S.O.; Donato, S.L.R. Comparison of techniques used in the prediction of yield in banana plants. Sci. Hortic. 2014, 167, 84–90. [Google Scholar] [CrossRef]
- Woomer, P.L.; Bekunda, M.A.; Nkalubo, S.T. Estimation of Banana Yield Based on Bunch Phenology. Afr. Crop Sci. J. 1999, 7, 341–347. [Google Scholar] [CrossRef]
- Taulya, G. Ky’osimba Onaanya: Understanding Productivity of East African Highland Banana. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, 2015. [Google Scholar]
- Tixier, P.; Malézieux, E.; Dorel, M.; Wery, J. SIMBA, a model for designing sustainable banana-based cropping systems. Agric. Syst. 2008, 97, 139–150. [Google Scholar] [CrossRef]
- Nyine, M.; Uwimana, B.; Akech, V.; Brown, A.; Ortiz, R.; Doležel, J.; Lorenzen, J.; Swennen, R. Association genetics of bunch weight and its component traits in East African highland banana (Musa spp. AAA group). Theor. Appl. Genet. 2019. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Guan, K.; Tang, J.; Ainsworth, E.A.; Asseng, S.; Bernacchi, C.J.; Cooper, M.; Delucia, E.H.; Elliott, J.W.; Ewert, F.; et al. Towards a multiscale crop modelling framework for climate change adaptation assessment. Nat. Plants 2020, 6, 338–348. [Google Scholar] [CrossRef] [PubMed]
- Carr, M.K.V. The water relations and irrigation requirements of banana (Musa spp.). Exp. Agric. 2009, 45, 333–371. [Google Scholar] [CrossRef]
- Van Asten, P.J.A.; Fermont, A.M.; Taulya, G. Drought is a major yield loss factor for rainfed East African highland banana. Agric. Water Manag. 2011, 98, 541–552. [Google Scholar] [CrossRef]
- Fortescue, J.A.; Turner, D.W.; Romero, R. Evidence that banana (Musa spp.), a tropical monocotyledon, has a facultative long-day response to photoperiod. Funct. Plant Biol. 2011, 38, 867–878. [Google Scholar] [CrossRef]
- Holder, G.D.; Gumbs, F.A. Effects of irrigation at critical stages of ontogeny of the banana cv. “Robusta” on growth and yield. Trop. Agric. 1982, 59, 221–226. [Google Scholar]
- Weiner, J. Allocation, plasticity and allometry in plants. Perspect. Plant Ecol. Evol. Syst. 2004, 6, 207–215. [Google Scholar] [CrossRef]
- Taulya, G. East African highland bananas (Musa spp. AAA-EA) “worry” more about potassium deficiency than drought stress. Field Crop. Res. 2013, 151, 45–55. [Google Scholar] [CrossRef]
- Robinson, J.C.; Nel, D.J. Plant density studies with banana (cv. Williams) in a subtropical climate. II. Components of yield and seasonal distribution of yield. J. Hortic. Sci. 1989, 64, 211–222. [Google Scholar] [CrossRef]
- Stevens, B.; Diels, J.; Vanuytrecht, E.; Brown, A.; Bayo, S.; Rujweka, A.; Richard, E.; Alois, P.; Swennen, R. Canopy cover evolution, diurnal patterns and leaf area index relationships in a Mchare and Cavendish banana cultivar under different soil moisture regimes. Sci. Hortic. 2020, 267, 109328. [Google Scholar] [CrossRef]
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014. International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Report No. 106; FAO: Rome, Italy, 2014; ISBN 9789251083697. [Google Scholar]
- FAO. Agro-Ecological Zoning Guidelines. FAO Soils Bulletin 73. Available online: http://www.fao.org/3/W2962E/W2962E00.htm (accessed on 20 August 2020).
- Robinson, J.C.; Alberts, A.J. Growth and yield Responses of Banana (Cultivar ‘Williams’) to drip irrigation under Drought and Normal Rainfall Conditions in the Subtropics. Sci. Hortic. 1986, 30, 187–202. [Google Scholar] [CrossRef]
- Varma, V.; Bebber, D.P. Climate change impacts on banana yields around the world. Nat. Clim. Chang. 2019, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Perrier, X.; Jenny, C.; Bakry, F.; Karamura, D.; Kitavi, M.; Dubois, C.; Hervouet, C.; Philippson, G.; Langhe, E. De East african diploid and triploid bananas: A genetic complex transported from south-east Asia. Ann. Bot. 2019, 123, 19–36. [Google Scholar] [CrossRef]
- Ploetz, R.C.; Kepler, A.K.; Daniells, J.; Nelson, S.C. Banana and plantain—An overview with emphasis on Pacific island cultivars. Musaceae (banana family). Species Profiles Pac. Isl. Agrofor. 2007, 1, 7–12. [Google Scholar]
- Meya, A.I.; Ndakidemi, P.A.; Mtei, K.M.; Swennen, R.; Merckx, R. Optimizing soil fertility management strategies to enhance banana production in volcanic soils of the Northern Highlands, Tanzania. Agronomy 2020, 289, 1–21. [Google Scholar]
- Banana Production Manual; NARO: Kampala, Uganda, 2001.
- Van Gaelen, H. Evaluating Agricultural Management from Field to Catchment Scale Development of a Parsimonious Agro-Hydrological Model. Ph.D. Thesis, KU Leuven, Leuven, Belgium, 2016. [Google Scholar]
- Kallarackal, J.; Milburn, J.; Baker, D. Water Relations of the Banana. III. Effects of Controlled Water Stress on Water Potential, Transpiration, Photosynthesis and Leaf Growth. Aust. J. Plant Physiol. 1990, 17, 79. [Google Scholar] [CrossRef]
- Thomas, D.S.; Turner, D.W. Leaf gas exchange of droughted and irrigated banana cv. Williams (Musa spp.) growing in hot, arid conditions. J. Hortic. Sci. Biotechnol. 1998, 73, 419–429. [Google Scholar] [CrossRef]
- Taiz, L.; Zeiger, E. Plant Physiology; Sinauer: Sunderland, MA, USA, 2002; ISBN 0878938230. [Google Scholar]
- Mahouachi, J. Growth and mineral nutrient content of developing fruit on banana plants (Musa acuminata AAA, ’Grand Nain’) subjected to water stress and recovery. J. Hortic. Sci. Biotechnol. 2007, 82, 839–844. [Google Scholar] [CrossRef]
- Turner, D.W.; Fortescue, J.A.; Thomas, D.S. Environmental physiology of the bananas (Musa spp.). Braz. J. Plant Physiol. 2007, 19, 463–484. [Google Scholar] [CrossRef]
- Taulya, G.; van Asten, P.J.A.; Leffelaar, P.A.; Giller, K.E. Phenological development of East African highland banana involves trade-offs between physiological age and chronological age. Eur. J. Agron. 2014, 60, 41–53. [Google Scholar] [CrossRef]
- Henry, M.; Picard, N.; Trotta, C.; Manlay, R.J.; Valentini, R.; Bernoux, M.; Saint-André, L. Estimating tree biomass of sub-Saharan African forests: A review of available allometric equations. Silva Fenn. 2011, 45, 477–569. [Google Scholar] [CrossRef]
- Kebede, B.; Soromessa, T. Allometric equations for aboveground biomass estimation of Olea europaea L. subsp. cuspidata in Mana Angetu Forest. Ecosyst. Health Sustain. 2018, 4, 1–12. [Google Scholar] [CrossRef]
- Eisenhauer, J.G. Regression through the Origin. Teach. Stat. 2003, 25, 76–80. [Google Scholar] [CrossRef]
- Lassoudière, A. Le Bananier et sa Culture; Savoir Faire: Montpellier, France, 2007; ISBN 978-2-7592-0046-7. [Google Scholar]
- Rodrigo, V.H.L.; Stirling, C.M.; Teklehaimanot, Z.; Nugawela, A. The effect of planting density on growth and development of component crops in rubber/banana intercropping systems. Field Crop. Res. 1997, 52, 95–108. [Google Scholar] [CrossRef]
- Stover, R.H.; Simmonds, N.W. Bananas; Longman Scientific & Technical: Harlow, UK, 1987; ISBN 0582463572. [Google Scholar]
- Dens, K.R.; Romero, R.A.; Swennen, R.; Turner, D.W. Removal of bunch, leaves, or pseudostem alone, or in combination, influences growth and bunch weight of ratoon crops in two banana cultivars. J. Hortic. Sci. Biotechnol. 2008, 83, 113–119. [Google Scholar] [CrossRef]




| Parameter | Explanation |
|---|---|
| Non-Destructive | |
| Phenology | |
| Days to flowering, DTF (days) | From planting/selection to flowering |
| Days to harvest, DTH (days) | From planting/selection to harvest |
| Flower cycle duration, FCD (days) | Days from flowering C1 to flowering C2 |
| Harvest cycle duration, HCD (days) | Days from harvest C1 to flowering C2 |
| Vegetative growth data, periodic | |
| Height of pseudostem, H (cm) | Measured until petiole divergence on the top |
| Girth of pseudostem at base, Gbase (cm); Girth of pseudostem at mid, Gmid (cm) | Measured at base; measured at middle |
| Radius of pseudostem at base, Rbase (cm); Radius of pseudostem at top, Rup (cm) | Measured at base; measured at petiole divergence |
| Functional leaves, functL (no.) | Leaves with less than 3/4 necrotic area |
| Dead leaves, deadL (no.) | Leaves with more than 3/4 necrotic area |
| Leaf length of third functional leaf, LL3 (cm) | Leaf length of third leaf along midrib |
| Leaf width of third functional leaf, LW3 (cm) | Leaf length of third leaf perpendicular to midrib |
| Pseudostem volume, Vpseudo (L) | |
| Pseudostem growth rate, Vrate (L day−1) | |
| Leaf area of ith leaf, LAleaf,i (m2) | (laf from [25]) |
| Leaf area of plant, LAplant (m2) | (from ith to nth leaf) |
| Leaf area index, LAI (m2m−2) | |
| Bunch growth data | |
| Bunch maturity grade, Grade (1–5) | Bunch maturity grade as specified in [33] |
| Number of hands on bunch, Nhand (no.) | Counted hands on a bunch |
| Number of fingers on bunch, Nfinger (no.) | Counted fingers on a bunch |
| Finger length, Lfinger (cm); Finger radius, rfinger (cm) | Average length/radius of individual finger |
| Volume of a finger, Vfinger (cm3) | |
| Ratio rfinger to Lfinger, Ratiofinger (-) | |
| Destructive data | |
| Leaf dry weight, leafD (kg plant−1); petiole dry weight, petioleD (kg plant−1); pseudostem dry weight, pseudostemD (kg plant−1) | Calculated from fresh weight and dry matter % |
| Aboveground vegetative dry weight, ABGVD (kg plant−1) | Sum of leafD, petioleD and pseudostemD |
| Corm dry weight, cormD (kg plant−1) | Calculated from fresh weight and dry matter % |
| Bunch fresh weight, bunchF (kg plant−1) | Measured bunch weight of plants in the field |
| Bunch growth rate, Brate (kg day−1) | |
| Individual finger weight, fingerF (g plant−1) | Average weight of individual finger on second hand |
| Huti Green Bell | Grande Naine | |||||||
|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C1 | C2 | |||||
| FI | RF | FI | RF | FI | RF | FI | RF | |
| Moisture and ET0 Ratios | ||||||||
| RPF (-) | 0.743(±0.0343) TC | 0.638(±0.0404) TC | 1.29 (±0.0408) TC | 0.807(±0.0791) TC | 1.44 (±0.0213) TC | 1.26 (±0.0448) TC | 1.33 (±0.0334) TC | 0.687(±0.0373) TC |
| RFH (-) | 2.17 (±0.210) TC | 1.47 (±0.182) TC | 0.920 (±0.107) TC | 0.333 (±0.194) TC | 1.08 (±0.106) TC | 0.329 (±0.0239) TC | 1.54 (±0.154) TC | 0.950 (±0.222) TC |
| RPH (-) | 1.19 (±0.0172) T | 0.902(±0.0372) TC | 1.17 (±0.0396) T | 0.661(±0.0436) TC | 1.30 (± 0.0404) TC | 0.873 (±0.0323) TC | 1.38 (±0.0211) TC | 0.742(±0.0247) TC |
| Growth Data | ||||||||
| Height † (cm) | 304.5 (±18.1) TC | 272.6 (±14.4) TC | 476.3 (±22.6) TC | 451.4 (±22.5) TC | 264.1 (±12.1) C | 265.1 (±18.0) C | 277.6 (±19.1) TC | 234.2 (±20.3) TC |
| Gbase † (cm) | 77.3 (±3.57) TC | 66.7 (±3.46) TC | 100.9 (±5.05) TC | 97.0 (±6.09) TC | 91.7 (±4.43) C | 93.2 (±6.07) C | 82.3 (±5.36) TC | 72.5 (±5.06) TC |
| Height ‡ (cm) | 305.3 (±20.8) TC | 272.0 (±23.3) TC | 457.5 (±39.1) TC | 424.2 (±32.7) TC | 258.5 (±18.2) C | 255.4 (±17.2) C | 277.6 (±28.7) TC | 236.7 (±37.3) TC |
| Gbase ‡ (cm) | 68.0 (±5.42) TC | 55.7 (±5.56) TC | 87.0 (±11.6) TC | 75.2 (±12.9) TC | 82.0 (±7.25) C | 78.4 (±8.21) C | 82.5 (±7.42) TC | 72.4 (±7.16) TC |
| ABGVD ‡ (kg plant−1) | 3.49 (±0.374) TC | 2.41 (±0.46) TC | 7.49 (±1.43) TC | 5.18 (±0.897) TC | 4.65 (±0.884) TC | 4.04 (±0.845) T | 6.16 (±1.78) TC | 3.73 (±1.22) T |
| BunchF ‡ (kg plant−1) | 25.4 (±3.87) TC | 19.6 (±3.96) T | 40.8 (±8.02) TC | 24.4 (±0.636) T | 49.6 (±7.61) T | 33.2 (±9.1) T | 52.4 (±15.2) T | 33.3 (±9.9) T |
| Nhand ‡ (no.) | 9.69 (±0.535) TC | 8.94 (±0.583) TC | 11 (±1.49) C | 10.8 (±2.5) C | 10.8 (±1.01) | 10.5 (±0.987) | 11 (±1.56) T | 10.2 (±1.67) T |
| Nfinger ‡ (no.) | 151 (±12.0) TC | 128 (±13.7) TC | 195 (±50.1) TC | 163 (±42.3) TC | 202 (±21.5) | 202 (±18.3) C | 204 (±57.7) T | 174 (±43.3) TC |
| fingerF ‡ (g finger−1) | 180 (±27.7) TC | 160 (±30.7) T | 227 (±41.3) TC | 139 (±50.5) T | 253 (±3.53) TC | 166 (±4.75) TC | 222 (±5.84)TC | 149 (±4.63) TC |
| Vfinger ‡ (cm3) | 354 (±54.7) TC | 325 (±76.8) TC | 434 (±91.6) TC | 305 (±116.00) TC | 417 (± 48.90) TC | 280 (±74.9) TC | 467 (±67.3) TC | 359 (±81.9) TC |
| Ratiofinger ‡ (-) | 0.073 (±0.004) TC | 0.078 (±0.01) TC | 0.068 (±0.005) C | 0.072 (±0.007) C | 0.078 (±0.015) T | 0.081 (±0.005) T | 0.078 (±0.005) T | 0.082 (±0.007) T |
| Phenology | ||||||||
| DTF (days) | 293 (±14.8) TC | 297 (±17.8) TC | 405 (±87.1) C | 406 (±57.6) C | 264 (±32) TC | 258 (±31) TC | 447 (±81)TC | 487 (±80)TC |
| DTH (days) | 474 (±6.03) TC | 511 (±103) TC | 546 (±113) TC | 662 (±164) TC | 420 (±31.2) C | 410 (±31.8) C | 612 (±54)TC | 636 (±56)TC |
| Growth Rates | ||||||||
| Vrate (L day−1) | 0.203(±0.0331) TC | 0.156(±0.0251) TC | 0.398(±0.0874) TC | 0.297(±0.0698) TC | 0.308(±0.0418) TC | 0.320(±0.0520) TC | 0.183(±0.0491) TC | 0.111(±0.0307) TC |
| Brate (kg day−1) | 0.144(±0.0271) T | 0.103(±0.0201) T | 0.266 (±0.0856) TC | 0.167 (±0.141) | 0.333 (±0.0419) TC | 0.193(±0.0460) TC | 0.315(±0.0462)TC | 0.205 (±0.0369) TC |
| Huti Green Bell | Grande Naine | |||||||
| Cycle Duration (C1 to C2) | ||||||||
| HG-FI | HG-RF | GN-FI | GN-RF | |||||
| FCD (C2-C1) (days) | 243 (±82.8) C | 237 (±55.2) C | 307 (±69) TC | 360 (±78) TC | ||||
| HCD (C2-C1) (days) | 222 (126) TC | 282 (53.7) TC | 315 (±43.1) TC | 332 (±59.0) TC | ||||
| Model Coefficients | Goodness of Fit Characteristics | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Vrate Models | ||||||||||||||||
| Data | Cultivar | Cycle | Parameters | Intercept (a) | 95%CI | Coefficient (b) | 95%CI | Coefficient (c) | 95%CI | n | df | R2adj | AIC | RMSE | RRMSE | p-Value |
| P | Huti Green | Both | RPF | −0.06 | (−0.11; −0.01) | 0.36 | (0.28; 0.43) | 66 | 2 | 0.59 | −238.86 | 0.041 | 0.20 | 3.09 × 10−14 | ||
| S | C1 | RPF | ns | 0.26 | (0.25; 0.27) | 54 | 1 | 0.97 | −220.75 | 0.031 | 0.17 | 2.57 × 10−43 | ||||
| S | C2 | RPF | ns | 0.30 | (0.27; 0.34) | 12 | 1 | 0.97 | −27.72 | 0.065 | 0.19 | 1.41 × 10−9 | ||||
| P | Grande Naine | Both | RPF | −0.04 | (−0.07; −0.01) | 0.22 | (0.19; 0.25) | 99 | 2 | 0.65 | −273.66 | 0.067 | 0.31 | 4.88 × 10−24 | ||
| S | C1 | RPF | 0.41 | (0.19; 0.64) | ns | 40 | 2 | −0.00 | −129.28 | 0.045 | 0.14 | 3.65 × 10−1 | ||||
| S | C2 | RPF | 0.03 | (0; 0.06) | 0.11 | (0.08; 0.14) | 59 | 2 | 0.49 | −219.96 | 0.038 | 0.26 | 4.45 × 10−10 | |||
| Brate Models | ||||||||||||||||
| Cultivar | Cycle | Parameters | Intercept (a) | 95%CI | Coefficient (b) | 95%CI | Coefficient (c) | 95%CI | n | df | R2adj | AIC | RMSE | RRMSE | p-Value | |
| P | Huti Green | Both | Vrate, RFH | ns | 0.73 | (0.70; 0.77) | ns | 65 | 1 | 0.96 | −233.43 | 0.053 | 0.38 | 4.34 × 10−48 | ||
| S | C1 | Vrate, RFH | ns | 0.53 | (0.37; 0.69) | 0.01 | (0; 0.03] | 54 | 2 | 0.97 | −264.12 | 0.020 | 0.16 | 2.91 × 10−42 | ||
| S | C2 | Vrate, RFH | ns | 0.58 | (0.39; 0.77) | ns | 11 | 1 | 0.80 | −13.63 | 0.120 | 0.60 | 4.91 × 10−05 | |||
| P | Grande Naine | Both | Vrate, RFH | ns | 0.56 | (0.50; 0.65) | 0.14 | (0.12; 0.15) | 99 | 2 | 0.98 | −340.63 | 0.043 | 0.17 | 2.32 × 10−85 | |
| S | C1 | Vrate, RFH | ns | 0.42 | (0.34; 0.50) | 0.19 | (0.16; 0.22) | 40 | 2 | 0.98 | −139.73 | 0.004 | 0.14 | 3.92 × 10−33 | ||
| S | C2 | Vrate, RFH | 0.05 | (0.02; 0.09) | 0.91 | (0.76; 1.06) | 0.06 | (0.03; 0.08) | 59 | 3 | 0.78 | −232.16 | 0.323 | 0.13 | 9.58 × 10−20 | |
| Huti Green Bell | Grande Naine | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ABGVD | |||||||||||||
| Model | Parameters | n | df | R2adj | AIC | RRMSE | p-Value | n | df | R2adj | AIC | RRMSE | p-Value |
| Lm.1 x | Vpseudo | 91 | 2 | 0.92 | 221.22 | 0.14 | 5.62 × 10−52 | 221 | 2 | 0.88 | 480.4 | 0.14 | 7.30 × 10−102 |
| Lm.2 | LAI | 88 | 2 | 0.79 | 297.89 | 0.22 | 5.16 × 10−31 | 214 | 2 | 0.92 | 573.2 | 0.19 | 1.20 × 10−116 |
| Lm.3 | Vpseudo, LAI | 88 | 3 | 0.93 | 192.41 | 0.13 | 1.70 × 10−51 | 213 | 3 | 0.93 | 379.0 | 0.11 | 1.30 × 10−124 |
| Lm.4 | Nfinger, Nhand | 62 | 3 | 0.68 | 209.93 | 0.22 | 1.32 × 10−15 | 138 | 3 | 0.19 | 475.5 | 0.27 | 3.13 × 10−7 |
| Lm.5 | Vpseudo, Nfinger, Nhand | 62 | 3 | 0.99 | 111.47 | 0.12 | 1.16 × 10−60 | 138 | 3 | 0.99 | 308.1 | 0.14 | 4.81 × 10−124 |
| Lm.6 | Vfinger, Ratiofinger | 58 | 3 | 0.29 | 236.14 | 0.31 | 2.81 × 10−5 | 144 | 3 | 0.07 | 521.2 | 0.29 | 3.22 × 10−3 |
| Lm.7 | Vpseudo, Ratiofinger, Nfinger, Nhand | 56 | 4 | 0.90 | 116.74 | 0.12 | 3.59 × 10−27 | 137 | 4 | 0.90 | 116.7 | 0.17 | 3.59 × 10−27 |
| CormD | |||||||||||||
| Model | Parameters | n | df | R2adj | AIC | RRMSE | p-Value | n | df | R2adj | AIC | RRMSE | p-Value |
| Lm.1 x | Vpseudo | 21 | 2 | 0.94 | 72.73 | 0.24 | 1.80 × 10−13 | 36 | 2 | 0.54 | 210.38 | 0.33 | 2.19 × 10−7 |
| Lm.2 | LAI | 14 | 2 | 0.71 | 83.14 | 0.75 | 9.95 × 10−5 | 35 | 2 | 0.36 | 214.67 | 0.39 | 7.35 × 10−5 |
| Lm.3 | Vpseudo, LAI | 14 | 3 | 0.97 | 59.62 | 0.22 | 2.20 × 10−9 | 34 | 3 | 0.53 | 199.99 | 0.34 | 2.87 × 10−6 |
| BunchF | |||||||||||||
| Model | Parameters | n | df | R2adj | AIC | RRMSE | p-Value | n | df | R2adj | AIC | RRMSE | p-Value |
| Lm.1 x | Vpseudo,Flower | 40 | 2 | 0.70 | 228.08 | 0.12 | 1.42 × 10−11 | 54 | 2 | 0.43 | 372.01 | 0.15 | 4.50 × 10−8 |
| Lm.2 | LAIFlower | 41 | 2 | 0.62 | 258.56 | 0.17 | 6.17 × 10−10 | 54 | 2 | 0.22 | 383.2 | 0.17 | 1.96 × 10−4 |
| Lm.3 | DTF | 41 | 2 | 0.32 | 268.02 | 0.22 | 7.71 × 10−5 | 55 | 2 | −0.01 | 406.85 | 0.20 | 4.83 × 10−1 |
| Lm.4 | Vpseudo,Flower, DTF | 40 | 3 | 0.69 | 229.76 | 0.12 | 1.20 × 10−10 | 54 | 3 | 0.42 | 373.99 | 0.15 | 3.48 × 10−7 |
| Lm.5 | Vpseudo,Flower, DTF, LAIFlower | 38 | 4 | 0.60 | 220.54 | 0.13 | 1.93 × 10−7 | 54 | 4 | 0.57 | 360.48 | 0.13 | 5.90 × 10−10 |
| Lm.6 | Vpseudo,flowerS | 38 | 2 | −0.01 | 257.52 | 0.25 | 4.97 × 10−1 | 52 | 2 | −0.02 | 381.38 | 0.20 | 6.66 × 10−1 |
| Lm.7 | Vpseudo,flower,Vpseudo,flowerS | 38 | 3 | 0.63 | 218.83 | 0.14 | 1.24 × 10−8 | 52 | 3 | 0.48 | 361.57 | 0.14 | 4.22 × 10−8 |
| Lm.8 | Vpseudo,Flower, DTF, Nfinger, Nhand | 35 | 5 | 0.64 | 204.24 | 0.12 | 3.31 × 10−7 | 37 | 5 | 0.65 | 248.92 | 0.13 | 8.38 × 10−8 |
| Lm.9 | Vpseudo,Flower, Vfinger | 36 | 3 | 0.80 | 191.12 | 0.11 | 1.05 × 10−12 | 40 | 3 | 0.56 | 277.63 | 0.14 | 8.44 × 10−8 |
| Lm.10 | Vpseudo,Flower, Vfinger, Ratiofinger | 36 | 4 | 0.80 | 192.48 | 0.11 | 6.59 × 10−12 | 40 | 4 | 0.60 | 276.25 | 0.14 | 7.81 × 10−8 |
| Lm.11 | Vpseudo,Flower, DTF, Nfinger, Nhand, Vfinger | 34 | 6 | 0.81 | 183.17 | 0.10 | 3.92 × 10−10 | 37 | 6 | 0.78 | 234.28 | 0.10 | 1.88 × 10−10 |
| Model Coefficients | Goodness of Fit Characteristics | Chosen Model | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ABGVD Models | |||||||||||||||
| Data | Cultivar | Treatment | Parameters | Intercept (a) | 95%CI | Coefficient (b) | 95%CI | n | df | R2adj | AIC | RMSE | RRMSE | p-Value | |
| P | Both | Both | Vpseudo | 0.33 | (0.24; 0.43) | 6.02 × 10−2 | (0.06; 0.06) | 700 | 2 | 0.90 | 1571.50 | 0.78 | 0.18 | 1.18 × 10−203 | x |
| P | Huti Green | Both | Vpseudo | 0.54 | (0.38; 0.71) | 5.56 × 10−2 | (0.05; 0.06) | 187 | 2 | 0.92 | 407.46 | 0.77 | 0.16 | 1.80 × 10−105 | |
| S | FI | Vpseudo | 0.75 | (0.47; 1.04) | 5.54 × 10−2 | (0.05; 0.06) | 89 | 2 | 0.93 | 205.82 | 0.77 | 0.14 | 1.32 × 10−53 | ||
| S | RF | Vpseudo | 0.43 | (0.25; 0.6) | 5.51 × 10−2 | (0.05; 0.06) | 98 | 2 | 0.92 | 193.43 | 0.72 | 0.17 | 1.54 × 10−53 | ||
| P | Grande Naine | Both | Vpseudo | 0.22 | (0.11; 0.34) | 6.27 × 10−2 | (0.06; 0.06) | 513 | 2 | 0.89 | 1149.31 | 0.76 | 0.18 | 1.17 × 10−245 | |
| S | FI | Vpseudo | 0.26 | (0.06; 0.47) | 6.34 × 10−2 | (0.06; 0.07) | 266 | 2 | 0.89 | 656.39 | 0.82 | 0.17 | 2.28 × 10−126 | ||
| S | RF | Vpseudo | 0.32 | (0.18; 0.45) | 5.91 × 10−2 | (0.06; 0.06) | 247 | 2 | 0.88 | 468.21 | 0.66 | 0.19 | 7.13 × 10−113 | ||
| CormD Models | |||||||||||||||
| Data | Cultivar | Treatment | Parameters | Intercept (a) | 95%CI | Coefficient (b) | 95%CI | n | df | R2adj | AIC | RMSE | RRMSE | p-Value | |
| P | Both | Both | Vpseudo | 0.39 | (0.29; 0.49) | 1.74 × 10−2 | (0.02; 0.02) | 180 | 2 | 0.64 | 271.47 | 0.52 | 0.40 | 2.46 × 10−41 | |
| P | Huti Green | Both | Vpseudo | 0.16 | (0.1; 0.23) | 1.94 × 10−2 | (0.02; 0.02) | 45 | 2 | 0.89 | 6.50 | 0.32 | 0.26 | 7.89 × 10−23 | x |
| S | FI | Vpseudo | 0.13 | (0.05; 0.22) | 2.24 × 10−2 | (0.02; 0.03) | 23 | 2 | 0.92 | −2.59 | 0.26 | 0.24 | 4.00 × 10−13 | ||
| S | RF | Vpseudo | 0.26 | (0.18; 0.34) | 1.67 × 10−2 | (0.01; 0.02) | 22 | 2 | 0.90 | 9.25 | 0.31 | 0.21 | 1.44 × 10−11 | ||
| P | Grande Naine | Both | Vpseudo | 0.51 | (0.37; 0.65) | 1.57 × 10−2 | (0.01; 0.02) | 135 | 2 | 0.50 | 224.77 | 0.55 | 0.43 | 6.00 × 10−22 | x |
| S | FI | Vpseudo | 0.62 | (0.37; 0.86) | 1.62 × 10−2 | (0.01; 0.02) | 69 | 2 | 0.57 | 140.02 | 0.64 | 0.41 | 4.62 × 10−14 | ||
| S | RF | Vpseudo | 0.56 | (0.39; 0.72) | 1.08 × 10−2 | (0.01; 0.01) | 66 | 2 | 0.34 | 61.48 | 0.37 | 0.38 | 1.53 × 10−7 | ||
| BunchF Models | |||||||||||||||
| Data | Cultivar | Treatment | Parameters | Intercept (a) | 95%CI | Coefficient (b) | 95%CI | n | df | R2adj | AIC | RMSE | RRMSE | p-Value | |
| P | Both | Both | Vpseudo,flower | −0.42 | (−4.84; 4) | 5.21 × 10−1 | (0.45; 0.6) | 167 | 2 | 0.53 | 1235.75 | 13.27 | 0.35 | 7.27 × 10−29 | |
| P | Huti Green | Both | Vpseudo,flower | 11.69 | (9.17; 14.22) | 1.99 × 10−1 | (0.16; 0.24) | 68 | 2 | 0.57 | 389.73 | 4.34 | 0.17 | 5.30 × 10−14 | |
| S | FI | Vpseudo,flower | 15.20 | (11.88; 18.52) | 1.73 × 10−1 | (0.13; 0.22) | 38 | 2 | 0.60 | 217.29 | 4.06 | 0.13 | 7.55 × 10−9 | x | |
| S | RF | Vpseudo,flower | 13.29 | (10.36; 16.23) | 1.30 × 10−1 | (0.08; 0.18) | 30 | 2 | 0.47 | 158.86 | 3.09 | 0.15 | 1.92 × 10−5 | x | |
| P | Grande Naine | Both | Vpseudo,flower | −0.17 | (−6.97; 6.62) | 5.91 × 10−1 | (0.49; 0.69) | 99 | 2 | 0.56 | 726.68 | 9.79 | 0.23 | 2.02 × 10−19 | |
| S | FI | Vpseudo,flower | −7.28 | (−17.3; 2.74) | 7.37 × 10−1 | (0.6; 0.87) | 54 | 2 | 0.69 | 363.80 | 6.89 | 0.14 | 3.54 × 10−15 | x | |
| S | RF | Vpseudo,flower | 20.12 | (10.39; 29.85) | 5.21 × 10−1 | (0.04; 0.34) | 45 | 2 | 0.11 | 315.94 | 7.57 | 0.23 | 7.27 × 10−29 | x | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stevens, B.; Diels, J.; Brown, A.; Bayo, S.; Ndakidemi, P.A.; Swennen, R. Banana Biomass Estimation and Yield Forecasting from Non-Destructive Measurements for Two Contrasting Cultivars and Water Regimes. Agronomy 2020, 10, 1435. https://doi.org/10.3390/agronomy10091435
Stevens B, Diels J, Brown A, Bayo S, Ndakidemi PA, Swennen R. Banana Biomass Estimation and Yield Forecasting from Non-Destructive Measurements for Two Contrasting Cultivars and Water Regimes. Agronomy. 2020; 10(9):1435. https://doi.org/10.3390/agronomy10091435
Chicago/Turabian StyleStevens, Bert, Jan Diels, Allan Brown, Stanley Bayo, Patrick A. Ndakidemi, and Rony Swennen. 2020. "Banana Biomass Estimation and Yield Forecasting from Non-Destructive Measurements for Two Contrasting Cultivars and Water Regimes" Agronomy 10, no. 9: 1435. https://doi.org/10.3390/agronomy10091435
APA StyleStevens, B., Diels, J., Brown, A., Bayo, S., Ndakidemi, P. A., & Swennen, R. (2020). Banana Biomass Estimation and Yield Forecasting from Non-Destructive Measurements for Two Contrasting Cultivars and Water Regimes. Agronomy, 10(9), 1435. https://doi.org/10.3390/agronomy10091435






