Analysis of Four Delineation Methods to Identify Potential Management Zones in a Commercial Potato Field in Eastern Canada
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site
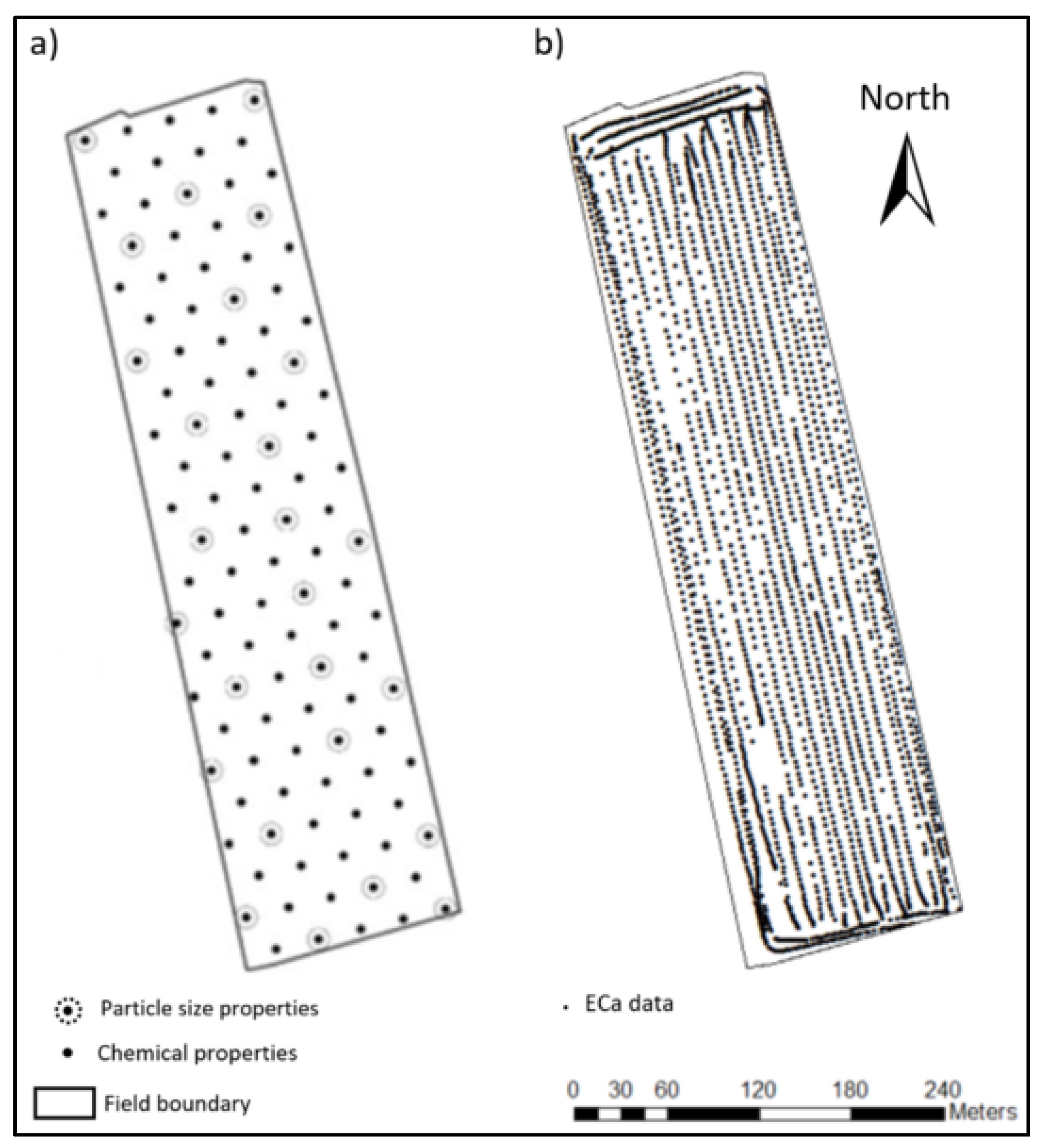
2.2. Soil Sampling and Analyses
2.3. Soil ECa Data
2.4. Statistical and Geostatistical Analysis
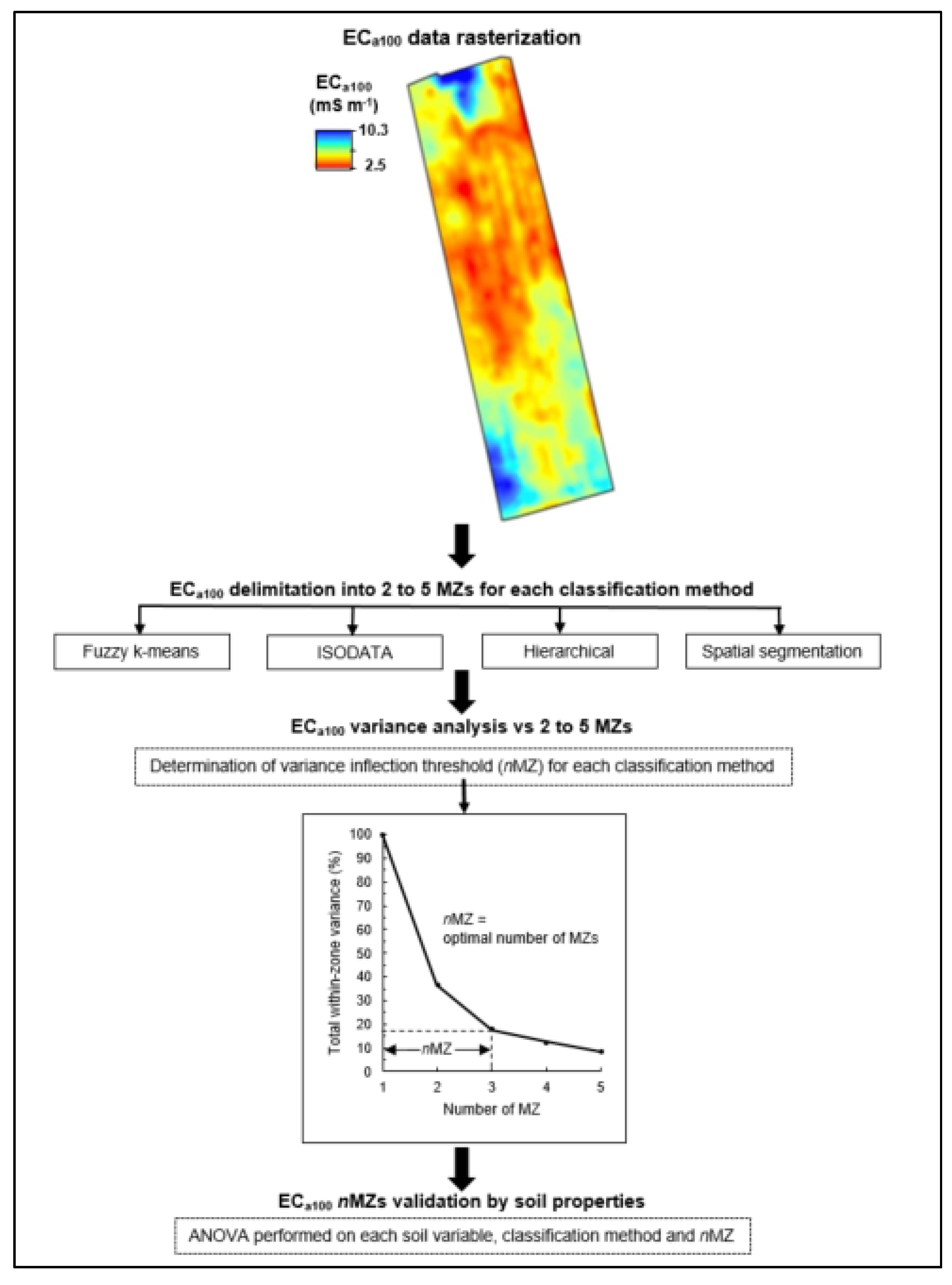
2.5. Delineation of Potential Management Zones
2.5.1. Fuzzy k-Means
2.5.2. ISODATA
2.5.3. Hierarchical
2.5.4. Spatial Segmentation
2.6. Determination and Validation of the Optimal Number of MZs
3. Results and Discussion
3.1. Variability of Soil Properties
3.2. Relationships between ECa and Soil Properties
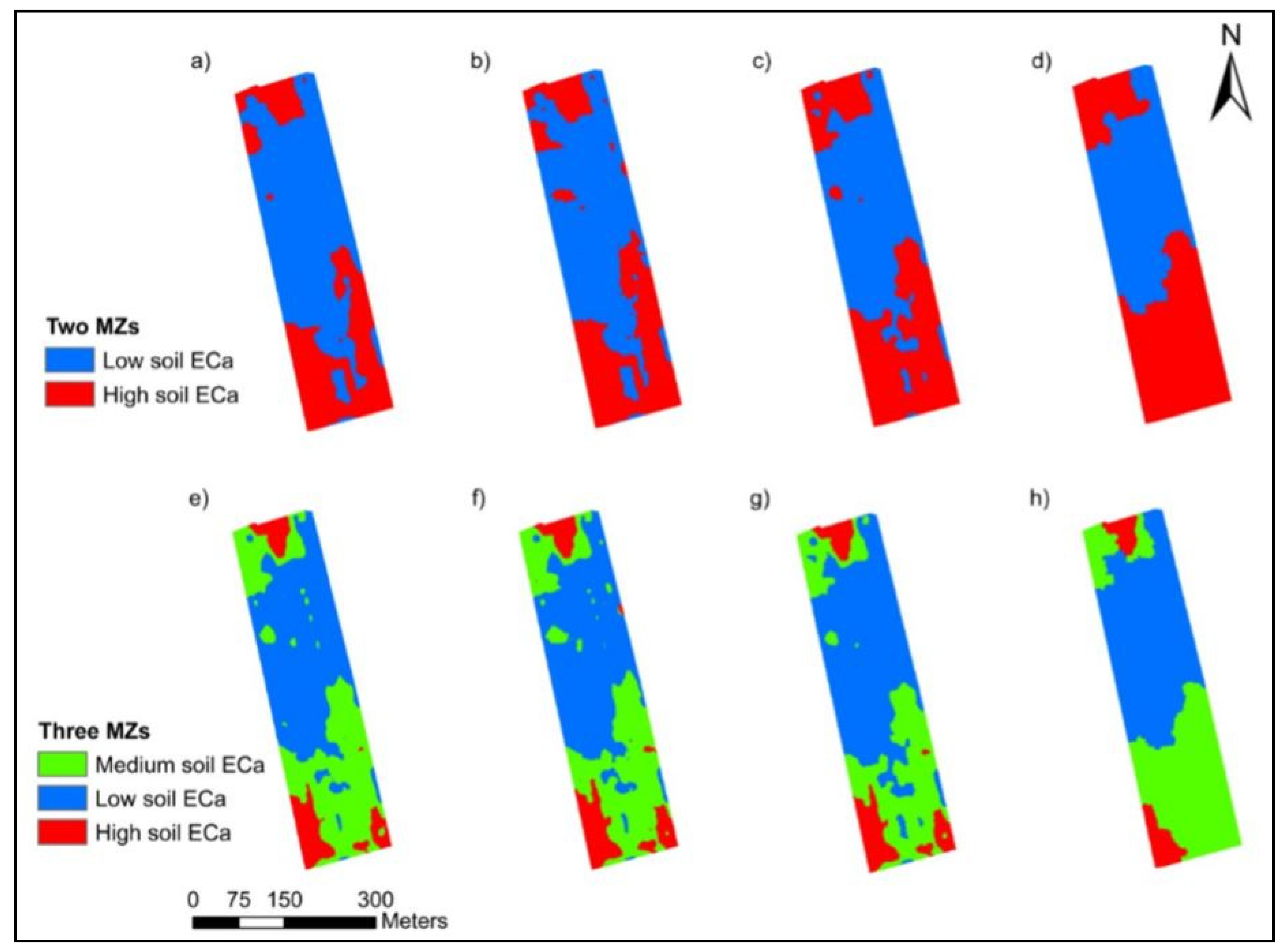
3.3. Reduction of Variance and Management Zone Delineation
3.4. Practical Implication of MZs
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Muschietti-Piana, M.D.P.; Cipriotti, P.A.; Urricariet, S.; Peralta, N.R.; Niborski, M. Using site-specific nitrogen management in rainfed corn to reduce the risk of nitrate leaching. Agric. Water Manag. 2018, 199, 61–70. [Google Scholar] [CrossRef]
- Haghverdi, A.; Leib, B.G.; Washington-Allen, R.A.; Ayers, P.D.; Buschermohle, M.J. Perspectives on delineating management zones for variable rate irrigation. Comput. Electron. Agric. 2015, 117, 154–167. [Google Scholar] [CrossRef]
- Oshunsanya, S.O.; Oluwasemire, K.O.; Taiwo, O.J. Use of GIS to Delineate Site-Specific Management Zone for Precision Agriculture. Commun. Soil Sci. Plant Anal. 2017, 48, 565–575. [Google Scholar] [CrossRef]
- Corwin, D.L.; Lesch, S.M. Delineating site-specific management units with proximal sensors. In Geostatistical Applications for Precision Agriculture; Oliver, M.A., Ed.; Springer: New York, NY, USA, 2010; pp. 139–165. [Google Scholar] [CrossRef]
- Cambouris, A.N.; Zebarth, B.J.; Ziadi, N.; Perron, I. Precision Agriculture in Potato Production. Potato Res. 2014, 57, 249–262. [Google Scholar] [CrossRef]
- Ahmad, A.; Ordoñez, J.; Cartujo, P.; Martos, V. Remotely Piloted Aircraft (RPA) in Agriculture: A Pursuit of Sustainability. Agronomy 2020, 11, 7. [Google Scholar] [CrossRef]
- Karydas, C.; Iatrou, M.; Iatrou, G.; Mourelatos, S. Management Zone Delineation for Site-Specific Fertilization in Rice Crop Using Multi-Temporal RapidEye Imagery. Remote. Sens. 2020, 12, 2604. [Google Scholar] [CrossRef]
- De Benedetto, D.; Castrignano, A.; Diacono, M.; Rinaldi, M.; Ruggieri, S.; Tamborrino, R. Field partition by proximal and remote sensing data fusion. Biosyst. Eng. 2013, 114, 372–383. [Google Scholar] [CrossRef]
- Fridgen, J.; Kitchen, R.; Sudduth, A. Variability of soil and landscape attributes within sub-field management zones. In Proceedings of the 5th International Conference on Precision Agriculture, Bloomington, MN, USA, 16–19 July 2000; Robert, P.C., Rust, R.H., Larson, W.E., Eds.; American Society of Agronomy: Madison, WI, USA; pp. 1–16. [Google Scholar]
- Peralta, N.R.; Costa, J.L. Delineation of management zones with soil apparent electrical conductivity to improve nutrient management. Comput. Electron. Agric. 2013, 99, 218–226. [Google Scholar] [CrossRef] [Green Version]
- Schenatto, K.; De Souza, E.G.; Bazzi, C.L.; Gavioli, A.; Betzek, N.M.; Beneduzzi, H.M. Normalization of data for delineating management zones. Comput. Electron. Agric. 2017, 143, 238–248. [Google Scholar] [CrossRef]
- Servadio, P.; Bergonzoli, S.; Verotti, M. Delineation of management zones based on soil mechanical-chemical properties to apply variable rates of inputs throughout a field (VRA). Eng. Agric. Environ. Food 2017, 10, 20–30. [Google Scholar] [CrossRef]
- Jiang, G.; Grafton, M.; Pearson, D.; Bretherton, M.; Holmes, A. Predicting spatiotemporal yield variability to aid arable precision agriculture in New Zealand: A case study of maize-grain crop production in the Waikato region. N. Z. J. Crop. Hortic. Sci. 2021, 1–22. [Google Scholar] [CrossRef]
- Memiaghe, J.D.N.; Cambouris, A.N.; Ziadi, N.; Karam, A.; Perron, I. Spatial Variability of Soil Phosphorus Indices Under Two Contrasting Grassland Fields in Eastern Canada. Agronomy 2020, 11, 24. [Google Scholar] [CrossRef]
- Viscarra Rossel, R.; Adamchuk, V.; Sudduth, K.; McKenzie, N.; Lobsey, C. Proximal soil sensing: An effective approach for soil measurements in space and time. Adv. Agron. 2011, 113, 243–291. [Google Scholar]
- Cambouris, A.; Nolin, M.; Zebarth, B.; Laverdière, M. Soil management zones delineated by electrical conductivity to characterize spatial and temporal variations in potato yield and in soil properties. Am. J. Potato Res. 2006, 83, 381–395. [Google Scholar] [CrossRef]
- Perron, I.; Cambouris, A.N.; Chokmani, K.; Gutierrez, M.V.; Zebarth, B.; Moreau, G.; Biswas, A.; Adamchuk, V. Delineating soil management zones using a proximal soil sensing system in two commercial potato fields in New Brunswick, Canada. Can. J. Soil Sci. 2018, 98, 724–737. [Google Scholar] [CrossRef]
- Córdoba, M.; Bruno, C.; Costa, J.; Balzarini, M. Subfield management class delineation using cluster analysis from spatial principal components of soil variables. Comput. Electron. Agric. 2013, 97, 6–14. [Google Scholar] [CrossRef]
- Gavioli, A.; De Souza, E.G.; Bazzi, C.L.; Schenatto, K.; Betzek, N.M. Identification of management zones in precision agriculture: An evaluation of alternative cluster analysis methods. Biosyst. Eng. 2019, 181, 86–102. [Google Scholar] [CrossRef]
- Ruspini, E.H. A new approach to clustering. Inf. Control. 1969, 15, 22–32. [Google Scholar] [CrossRef] [Green Version]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Moral, F.; Terrón, J.; Da Silva, J.M. Delineation of management zones using mobile measurements of soil apparent electrical conductivity and multivariate geostatistical techniques. Soil Tillage Res. 2010, 106, 335–343. [Google Scholar] [CrossRef]
- Kweon, G. Delineation of site-specific productivity zones using soil properties and topographic attributes with a fuzzy logic system. Biosyst. Eng. 2012, 112, 261–277. [Google Scholar] [CrossRef]
- Peralta, N.R.; Costa, J.L.; Balzarini, M.; Franco, M.C.; Córdoba, M.; Bullock, D. Delineation of management zones to improve nitrogen management of wheat. Comput. Electron. Agric. 2015, 110, 103–113. [Google Scholar] [CrossRef]
- Fridgen, J.J.; Kitchen, N.R.; Sudduth, K.A.; Drummond, S.T.; Wiebold, W.J.; Fraisse, C.W. Management zone analyst (MZA): Software for subfield Management zone delineation. Agron. J. 2004, 96, 100–108. [Google Scholar] [CrossRef]
- Fraisse, C.W.; Sudduth, K.A.; Kitchen, N.R. Delineation of Site-Specific Management Zones by Unsupervised Classification of Topographic Attributes and Soil Electrical Conductivity. Trans. ASAE 2001, 44, 155–166. [Google Scholar] [CrossRef] [Green Version]
- Tou, J.; González, R. Pattern recognition principles. Appl. Math. Comput. Reading (MA) Addison Wesley 1974, 57, 353–354. [Google Scholar] [CrossRef]
- Guastaferro, F.; Castrignanò, A.; De Benedetto, D.; Sollitto, D.; Troccoli, A.; Cafarelli, B. A comparison of different algorithms for the delineation of management zones. Precis. Agric. 2010, 11, 600–620. [Google Scholar] [CrossRef]
- Abbas, A.; Minalla, N.; Ahmad, N.; Abid, S.; Khan, M. K-means and ISODATA clustering algorithms for landcover classification using remote sensing. Sindh Univ. Res. J. SURJ (Sci. Ser.) 2016, 48, 315–318. [Google Scholar]
- Uribeetxebarria, A.; Arno, J.; Escola, A.; Martínez-Casasnovas, J.A. Apparent electrical conductivity and multivariate analysis of soil properties to assess soil constraints in orchards affected by previous parcelling. Geoderma 2018, 319, 185–193. [Google Scholar] [CrossRef] [Green Version]
- Arango, R.; Díaz, I.; Campos, A.; Combarro, E.; Canas, E. On the influence of temporal resolution on automatic delimitation using clustering algorithms. Appl. Math. Inform. Sci. 2015, 9, 339–347. [Google Scholar]
- Fleming, K.L.; Westfall, D.G.; Wiens, D.W.; Brodahl, M.C. Evaluating Farmer Defined Management Zone Maps for Variable Rate Fertilizer Application. Precis. Agric. 2000, 2, 201–215. [Google Scholar] [CrossRef]
- Ruß, G.; Kruse, R. Exploratory hierarchical clustering for management zone delineation in precision agriculture. In Industrial Conference on Data Mining. Advances in Data Mining; Applications and Theorical Aspects; ICDM 2011; Perner, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 161–173. [Google Scholar] [CrossRef]
- Benz, U.C.; Hofmann, P.; Willhauck, G.; Lingenfelder, I.; Heynen, M. Multi-resolution, object-oriented fuzzy analysis of remote sensing data for GIS-ready information. ISPRS J. Photogramm. Remote. Sens. 2004, 58, 239–258. [Google Scholar] [CrossRef]
- Blaschke, T.; Lang, S.; Lorup, E.; Strobl, J.; Zeil, P. Object-oriented image processing in an integrated GIS/remote sensing environment and perspectives for environmental applications. Environ. Inf. Plan. Politics Public 2000, 2, 555–570. [Google Scholar]
- Roudier, P.; Tisseyre, B.; Poilvé, H.; Roger, J.-M. Management zone delineation using a modified watershed algorithm. Precis. Agric. 2008, 9, 233–250. [Google Scholar] [CrossRef] [Green Version]
- Pedroso, M.; Taylor, J.; Tisseyre, B.; Charnomordic, B.; Guillaume, S. A segmentation algorithm for the delineation of agricultural management zones. Comput. Electron. Agric. 2010, 70, 199–208. [Google Scholar] [CrossRef]
- Statistics Canada. Area, Production and Farm Value of Potatoes; Statistics Canada; Government of Canada: Ottawa, ON, Canada, 2006. [CrossRef]
- Soil Classification Working Group. The Canadian System of Soil Classification, 3rd ed.; Publication 1646; Agriculture and Agri-Food Canada, NRC Research Press: Ottawa, ON, Canada, 1998; p. 187. [Google Scholar]
- Hendershot, W.; Lalande, H.; Duquette, M. Ion exchange and exchangeable cations. In Soil Sampling and Methods of Analysis; Carter, M.R., Ed.; Lewis Publisher: Boca Raton, FL, USA, 1993; pp. 167–176. [Google Scholar]
- Ziadi, N.; Tran, T.S. Mehlich 3-extractable elements. In Soil Sampling and Methods of Analysis, 2nd ed.; Carter, M.R., Gregorich, E.G., Eds.; CRC Press: Boca Raton, FL, USA, 2008; pp. 81–88. [Google Scholar]
- Kroetsch, D.; Wang, C. Particle size distribution. In Soil Sampling and Methods of Analysis, 2nd ed.; Carter, M.R., Gregorich, E.G., Eds.; CRC Press: Boca Raton, FL, USA, 2008; pp. 713–725. [Google Scholar]
- Sudduth, K.; Kitchen, N.; Wiebold, W.; Batchelor, W.; Bollero, G.; Bullock, D.; Clay, D.; Palm, H.; Pierce, F.; Schuler, R.; et al. Relating apparent electrical conductivity to soil properties across the north-central USA. Comput. Electron. Agric. 2005, 46, 263–283. [Google Scholar] [CrossRef]
- Sanches, G.M.; Magalhães, P.S.; Remacre, A.Z.; Franco, H.C. Potential of apparent soil electrical conductivity to describe the soil pH and improve lime application in a clayey soil. Soil Tillage Res. 2018, 175, 217–225. [Google Scholar] [CrossRef]
- SAS Institute Inc. Base SAS® 9.4 Procedures Guide: Statistical Procedures, 5th ed.; SAS Campus Drive: Cary, NC, USA, 2017. [Google Scholar]
- ESRI. ArcGIS for Desktop, Release 10.3; Environmental Systems Research Institute: Redlands, CA, USA, 2014. [Google Scholar]
- Minasny, B.; McBratney, A. FuzME Version 3.0. Australian Centre for Precision Agriculture; The University of Sydney: Sydney, Australia, 2002. [Google Scholar]
- Odeh, I.; Chittleborough, D.; McBratney, A. Soil Pattern Recognition with Fuzzy-c-means: Application to classification and soil-landform interrelationships. Soil Sci. Soc. Am. J. 1992, 56, 505–516. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Janrao, P.P.; Mishra, D.S.; Bharadi, V.A. A Median Strange Point algorithm for Delineation of Agricultural Management Zones. Int. J. Comput. Sci. Enginnering 2020, 8. [Google Scholar] [CrossRef]
- R Development Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2012. [Google Scholar]
- Fleming, K.L.; Heermann, D.F.; Westfall, D.G. Evaluating Soil Color with Farmer Input and Apparent Soil Electrical Conductivity for Management Zone Delineation. Agron. J. 2004, 96, 1581–1587. [Google Scholar] [CrossRef]
- Galambošová, J.; Rataj, V.; Prokeinová, R.; Prešinská, J. Determining the management zones with hierarchic and non-hierarchic clustering methods. Res. Agric. Eng. 2014, 60, S44–S51. [Google Scholar] [CrossRef] [Green Version]
- Trimble. eCognition Developer 8.64; Reference Book; Trimble Documention: München, Germany, 2011. [Google Scholar]
- Sena, N.; Chokmani, K.; Gloaguen, E.; Bernier, M. Analyse multi-échelles de la variabilité spatiale de l’équivalent en eau de la neige (EEN) sur le territoire de l’Est du Canada. Hydrolog. Sci. J. 2017, 62, 359–377. [Google Scholar] [CrossRef] [Green Version]
- Drǎguţ, L.; Tiede, D.; Levick, S.R. ESP: A tool to estimate scale parameter for multiresolution image segmentation of remotely sensed data. Int. J. Geogr. Inf. Sci. 2010, 24, 859–871. [Google Scholar] [CrossRef]
- Liu, H.; Qiu, Z.; Meng, L.; Xu, M.; Pan, Y.; Zhang, X. Delineation of site-specific management zone based on SPOT6/7 remote sensing image in black soil area, Northeast China. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5046–5049. [Google Scholar]
- Zebarth, B.; Rees, H.; Walsh, J.; Chow, L.; Pennock, D. Soil variation within a hummocky podzolic landscape under intensive potato production. Geoderma 2002, 110, 19–33. [Google Scholar] [CrossRef]
- Farooque, A.A.; Zaman, Q.U.; Schumann, A.W.; Madani, A.; Percival, D.C. Delineating Management Zones for Site Specific Fertilization in Wild Blueberry Fields. Appl. Eng. Agric. 2012, 28, 57–70. [Google Scholar] [CrossRef]
- Molin, J.P.; De Castro, C.N. Establishing management zones using soil electrical conductivity and other soil properties by the fuzzy clustering technique. Sci. Agricola 2008, 65, 567–573. [Google Scholar] [CrossRef] [Green Version]
- Sudduth, K.; Kitchen, N.; Bollero, G.; Bullock, D.; Wiebold, W. Comparison of electromagnetic induction and direct sensing of soil electrical conductivity. Agron. J. 2003, 95, 472–482. [Google Scholar] [CrossRef]
- Farahani, H.J.; Buchleiter, G.W. Temporal Stability of Soil Electrical Conductivity in Irrigated Sandy Fields in Colorado. Trans. ASAE 2004, 47, 79–90. [Google Scholar] [CrossRef]
- Tisseyre, B.; McBratney, A.B. A technical opportunity index based on mathematical morphology for site-specific management: An application to viticulture. Precis. Agric. 2008, 9, 101–113. [Google Scholar] [CrossRef]
- Barrett, R. Nutrient Management in PEI Potato Production. PEI Potato Board Factsheet, January 2018. Available online: http://peipotatoagronomy.com/wp-content/uploads/2018/01/Nutrient-Mgmt-Factsheet-Jan17.pdf (accessed on 23 February 2020).
- Khosla, R.; Fleming, K.; Delgado, J.; Shaver, T.; Westfall, D. Use of site-specific management zones to improve nitrogen management for precision agriculture. J. Soil Water Conser. 2002, 57, 513–518. [Google Scholar]

| Unit | Depth (m) | Mean | SD z | CV y (%) | |
|---|---|---|---|---|---|
| Particle size analyses (n = 23) | |||||
| Clay | g/kg | 0–0.15 | 83 | 14 | 17 |
| Silt | g/kg | 0–0.15 | 247 | 40 | 16 |
| Sand | g/kg | 0–0.15 | 669 | 54 | 8 |
| Chemical analyses (n = 104) | |||||
| Total C | % | 0–0.15 | 1.24 | 0.22 | 18 |
| Total N | % | 0–0.15 | 0.99 | 0.20 | 20 |
| pH | 0–0.15 | 6.2 | 0.2 | 3 | |
| P | mg/kg | 0–0.15 | 199 | 44 | 22 |
| K | mg/kg | 0–0.15 | 105 | 49 | 47 |
| Ca | mg/kg | 0–0.15 | 641 | 154 | 24 |
| Mg | mg/kg | 0–0.15 | 98 | 22 | 22 |
| Al | mg/kg | 0–0.15 | 1478 | 237 | 16 |
| Soil electrical conductivity measured by Veris (n = 1981) | |||||
| ECa30 x | mS/m | 0–0.30 | 5.2 | 1.3 | 25 |
| ECa100 w | mS/m | 0–1.00 | 5.3 | 1.4 | 27 |
| Pearson Correlations (r) | |||||
|---|---|---|---|---|---|
| ECa30 z | ECa100 y | ||||
| Particle size (0–0.15 m) | |||||
| Clay | 0.84 | *** x | 0.82 | *** | |
| Silt | 0.80 | *** | 0.79 | *** | |
| Sand | −0.83 | *** | −0.82 | *** | |
| Chemical properties (0–0.15 m) | |||||
| Total C | 0.42 | *** | 0.44 | *** | |
| Total N | 0.35 | *** | 0.36 | *** | |
| pH | 0.15 | NS w | 0.14 | NS | |
| P | 0.22 | * | 0.25 | * | |
| K | 0.34 | *** | 0.36 | *** | |
| Ca | 0.25 | ** | 0.28 | ** | |
| Mg | 0.16 | NS | 0.18 | NS | |
| Al | −0.26 | ** | −0.26 | ** | |
| Number of MZ | Soil Properties at 0–0.15 m Depth | ||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ECa100 y | Clay | Silt | Sand | Total C | Total N | pH | P | K | Ca | Mg | Al | ||||||||||||||
| Delineation Method | mS/m | g/kg | g/kg | g/kg | % | % | mg/kg | mg/kg | mg/kg | mg/kg | mg/kg | ||||||||||||||
| 2 MZ | Fuzzy k-means | 4.5 | B x | 76 | b | 229 | b | 695 | a | 1.15 | b | 0.09 | b | 6.22 | a | 193 | b | 92 | b | 614 | b | 95 | b | 1523 | a |
| 6.6 | a | 97 | a | 281 | a | 622 | b | 1.36 | a | 0.11 | a | 6.26 | a | 210 | a | 128 | a | 687 | a | 105 | a | 1402 | b | ||
| ISODATA | 4.4 | b | 74 | b | 224 | b | 703 | a | 1.16 | b | 0.09 | b | 6.22 | a | 191 | b | 90 | b | 614 | b | 94 | b | 1527 | a | |
| 6.5 | a | 96 | a | 278 | a | 626 | b | 1.35 | a | 0.11 | a | 6.26 | a | 211 | a | 127 | a | 680 | a | 105 | a | 1408 | b | ||
| Hierarchical | 4.3 | b | 73 | b | 222 | b | 705 | a | 1.13 | b | 0.09 | b | 6.23 | a | 193 | a | 92 | b | 614 | a | 95 | a | 1559 | a | |
| 6.3 | a | 94 | a | 275 | a | 631 | b | 1.35 | a | 0.11 | a | 6.24 | a | 206 | a | 120 | a | 669 | a | 102 | a | 1394 | b | ||
| Spatial segmentation | 4.2 | b | 72 | b | 217 | b | 711 | a | 1.12 | b | 0.09 | b | 6.22 | a | 194 | a | 90 | b | 604 | b | 94 | b | 1567 | a | |
| 6.1 | a | 92 | a | 271 | a | 637 | b | 1.35 | a | 0.11 | a | 6.25 | a | 204 | a | 121 | a | 677 | a | 103 | a | 1392 | b | ||
| 3 MZ | Fuzzy k-means | 4.2 | a | 76 | b | 234 | b | 690 | a | 1.12 | b | 0.09 | b | 6.23 | a | 192 | b | 90 | a | 613 | b | 95 | b | 1562 | a |
| 5.8 | b | 85 | b | 245 | b | 670 | a | 1.34 | a | 0.10 | a | 6.26 | a | 198 | b | 111 | b | 639 | b | 100 | ab | 1374 | b | ||
| 7.8 | c | 101 | a | 293 | a | 606 | b | 1.35 | a | 0.11 | a | 6.20 | a | 234 | a | 146 | c | 757 | a | 108 | a | 1467 | ab | ||
| ISODATA | 4.2 | a | 73 | a | 217 | b | 710 | a | 1.12 | b | 0.09 | b | 6.22 | a | 193 | b | 91 | a | 613 | b | 95 | b | 1568 | a | |
| 5.7 | b | 89 | b | 266 | a | 645 | b | 1.35 | a | 0.10 | a | 6.26 | a | 196 | b | 110 | b | 639 | b | 100 | ab | 1371 | b | ||
| 7.6 | c | 101 | c | 293 | a | 606 | b | 1.35 | a | 0.11 | a | 6.20 | a | 234 | a | 146 | c | 757 | a | 108 | a | 1467 | ab | ||
| Hierarchical | 4.3 | a | 73 | b | 222 | b | 705 | a | 1.13 | b | 0.09 | b | 6.23 | a | 193 | b | 92 | b | 614 | b | 95 | a | 1559 | a | |
| 5.9 | b | 91 | a | 265 | a | 644 | b | 1.35 | a | 0.11 | a | 6.25 | a | 198 | b | 113 | a | 645 | b | 101 | a | 1463 | ab | ||
| 7.7 | c | 101 | a | 293 | a | 606 | b | 1.34 | a | 0.11 | a | 6.23 | a | 238 | a | 143 | a | 757 | a | 107 | a | 1375 | b | ||
| Spatial segmentation | 4.3 | a | 72 | a | 217 | b | 712 | a | 1.10 | b | 0.09 | b | 6.20 | a | 196 | a | 90 | a | 609 | b | 94 | b | 1568 | a | |
| 5.9 | b | 88 | b | 262 | a | 651 | b | 1.37 | a | 0.11 | a | 6.28 | a | 198 | a | 113 | b | 654 | ab | 101 | ab | 1385 | b | ||
| 8.1 | c | 111 | c | 299 | a | 591 | c | 1.32 | a | 0.12 | a | 6.21 | a | 224 | a | 149 | c | 749 | a | 111 | a | 1458 | ab | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lajili, A.; Cambouris, A.N.; Chokmani, K.; Duchemin, M.; Perron, I.; Zebarth, B.J.; Biswas, A.; Adamchuk, V.I. Analysis of Four Delineation Methods to Identify Potential Management Zones in a Commercial Potato Field in Eastern Canada. Agronomy 2021, 11, 432. https://doi.org/10.3390/agronomy11030432
Lajili A, Cambouris AN, Chokmani K, Duchemin M, Perron I, Zebarth BJ, Biswas A, Adamchuk VI. Analysis of Four Delineation Methods to Identify Potential Management Zones in a Commercial Potato Field in Eastern Canada. Agronomy. 2021; 11(3):432. https://doi.org/10.3390/agronomy11030432
Chicago/Turabian StyleLajili, Abdelkarim, Athyna N. Cambouris, Karem Chokmani, Marc Duchemin, Isabelle Perron, Bernie J. Zebarth, Asim Biswas, and Viacheslav I. Adamchuk. 2021. "Analysis of Four Delineation Methods to Identify Potential Management Zones in a Commercial Potato Field in Eastern Canada" Agronomy 11, no. 3: 432. https://doi.org/10.3390/agronomy11030432
APA StyleLajili, A., Cambouris, A. N., Chokmani, K., Duchemin, M., Perron, I., Zebarth, B. J., Biswas, A., & Adamchuk, V. I. (2021). Analysis of Four Delineation Methods to Identify Potential Management Zones in a Commercial Potato Field in Eastern Canada. Agronomy, 11(3), 432. https://doi.org/10.3390/agronomy11030432









