Technologies for Forecasting Tree Fruit Load and Harvest Timing—From Ground, Sky and Time
Abstract
:1. Introduction
1.1. The Need for Fruit Load Forecast
1.2. Literature Base
1.3. Types of Models
2. Measurement of Fruit Number
2.1. Benchmarking
2.1.1. Reference Estimates
2.1.2. Evaluation Metrics
2.2. Tree Evaluation and Historical Knowledge
2.3. Manual Fruit Count
2.3.1. Sample Size and Variance
2.3.2. Sampling Approaches
2.3.3. Examples
2.4. Machine Vision Methods
2.4.1. Image Processing
2.4.2. Hardware and Imaging Platform
2.4.3. Implementation on Ground Vehicles
2.5. Correlative Methods
2.5.1. What Determines Tree Fruit Load?
2.5.2. Prediction of Yield in Cropping
2.5.3. Prediction Based on Correlation to within-Season Attributes
2.5.4. Correlation to Canopy Structural Attributes
2.5.5. Correlation to Spectral Indices
2.5.6. Prediction Based on Multiple Season Attributes
2.5.7. Prediction Based on Yield Across Multiple Seasons, Climatic Variables and Canopy Characteristics
3. Measurement of Fruit Size
3.1. Current (Manual) Methods
3.2. Machine Vision Methods
3.3. Prediction of Size at Harvest
4. Measurement of Fruit External Quality
5. Commercial Systems for Fruit Number, Size and External Quality
6. Measurement of Fruit Maturity
6.1. Thermal Time from Flowering
6.1.1. Heat Units/Growing Degree Days
6.1.2. Identifying Flowering Events
6.2. Fruit Attributes
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Scopus. Scopus Document Search. 2021. Available online: https://www.scopus.com/ (accessed on 1 April 2021).
- Koirala, A.; Walsh, K.; Wang, Z.; McCarthy, C. Deep learning for real-time fruit detection and orchard fruit load estimation: Benchmarking of ‘MangoYOLO’. Precis. Agric. 2019, 20, 1107–1135. [Google Scholar] [CrossRef]
- Marcelis, L.F.M.; Heuvelink, E.; Goudriaan, J. Modelling biomass production and yield of horticultural crops: A review. Sci. Hortic. 1998, 74, 83–111. [Google Scholar] [CrossRef]
- Rahmati, M.; Mirás-Avalos, J.M.; Valsesia, P.; Davarynejad, G.H.; Bannayan, M.; Azizi, M.; Lescourret, F.; Génard, M.; Vercambre, G. Assessing the effects of water stress on peach fruit quality and size using the QualiTree model. In Proceedings of the International Horticultural Congress IHC2018: International Symposium on Cultivars, Rootstocks and Management Systems of 1281, Istanbul, Turkey, 12–16 August 2018; pp. 539–546. [Google Scholar] [CrossRef]
- Normand, F.; Lauri, P.-E.; Legave, J.M. Climate change and its probable effects on mango production and cultivation. Acta Hortic. 2015, 1075, 21–31. [Google Scholar] [CrossRef]
- Boudon, F.; Persello, S.; Jestin, A.; Briand, A.-S.; Grechi, I.; Fernique, P.; Guédon, Y.; Léchaudel, M.; Lauri, P.-É.; Normand, F. V-Mango: A functional–structural model of mango tree growth, development and fruit production. Ann. Bot. 2020, 126, 745–763. [Google Scholar] [CrossRef] [PubMed]
- Dambreville, A.; Lauri, P.-É.; Trottier, C.; Guédon, Y.; Normand, F. Deciphering structural and temporal interplays during the architectural development of mango trees. J. Exp. Bot. 2013, 64, 2467–2480. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sarron, J.; Malézieux, É.; Sané, C.A.B.; Faye, É. Mango yield mapping at the orchard scale based on tree structure and land cover assessed by UAV. Remote Sens. 2018, 10, 1900. [Google Scholar] [CrossRef] [Green Version]
- Paliwal, A.; Jain, M. The accuracy of self-reported crop yield estimates and their ability to train remote sensing algorithms. Front. Sustain. Food Syst. 2020, 4, 25. [Google Scholar] [CrossRef] [Green Version]
- Dunn, G.M. Grape and Wine Research and Development Corporation. Yield Forecasting. 2010. Available online: https://www.wineaustralia.com/getmedia/5304c16d-23b3-4a6f-ad53-b3d4419cc979/201006_Yield-Forecasting.pdf (accessed on 20 April 2021).
- Koirala, A.; Walsh, K.B.; Wang, Z. Attempting to Estimate the Unseen—Correction for Occluded Fruit in Tree Fruit Load Estimation by Machine Vision with Deep Learning. Agronomy 2021, 11, 347. [Google Scholar] [CrossRef]
- Thompson, S.K. Sampling, 3rd ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-0-470-40231-3. [Google Scholar]
- Wulfsohn, D. Sampling techniques for plants and soil. Landbauforsch. Völkenrode 2010, 340, 3–30. [Google Scholar]
- Wulfsohn, D.; Zamora, F.A.; Téllez, C.P.; Lagos, I.Z.; García-Fiñana, M. Multilevel systematic sampling to estimate total fruit number for yield forecasts. Precis. Agric. 2012, 13, 256–275. [Google Scholar] [CrossRef]
- Anderson, N.; Underwood, J.; Rahman, M.; Robson, A.; Walsh, K. Estimation of fruit load in mango orchards: Tree sampling considerations and use of machine vision and satellite imagery. Precis. Agric. 2019, 20, 823–839. [Google Scholar] [CrossRef]
- Wolter, K.M. Introduction to Variance Estimation; Springer: New York, NY, USA, 1985; ISBN 978-0-387-35099-8. [Google Scholar]
- Wagenaar, W.A. Generation of random sequences by human subjects: A critical survey of literature. Psychol. Bull. 1972, 77, 65. [Google Scholar] [CrossRef]
- Jessen, R.J. Determining the fruit count on a tree by randomized branch sampling. Biometrics 1955, 11, 99–109. [Google Scholar] [CrossRef]
- Allen, R.D. Evaluating Procedures for Estimating Citrus Fruit Yield. Fruit Counts, Ground Photography, Remote Sensing. In Statistical Reporting Services; US Department of Agriculture: Washington, DC, USA, 1972. [Google Scholar]
- Forshey, C.G.; Elfving, D.C. Estimating yield and fruit numbers of apple trees from branch samples. J. Am. Soc. Hortic. Sci. 1979, 104, 897–900. [Google Scholar]
- Miranda, C.; Santesteban, L.G.; Urrestarazu, J.; Loidi, M.; Royo, J.B. Sampling stratification using aerial imagery to estimate fruit load in peach tree orchards. Agriculture 2018, 8, 78. [Google Scholar] [CrossRef] [Green Version]
- De Silva, H.N.; Hall, A.J.; Cashmore, W.M.; Tustin, D.S. Variation of fruit size and growth within an apple tree and its influence on sampling methods for estimating the parameters of mid-season size distributions. Ann. Bot. 2000, 86, 493–501. [Google Scholar] [CrossRef] [Green Version]
- Wulfsohn, D.; Maletti, M.; Toldam-Andersen, T.B. Unbiased estimator for the total number of flowers on a tree. In Proceedings of the VII International Symposium on Modelling in Fruit Research and Orchard Management, Copenhagen, Denmark, 20 June 2004; Volume 707, pp. 245–252. [Google Scholar] [CrossRef] [Green Version]
- Gardi, J.E.; Wulfsohn, D.; Nyengaard, J.R. handheld support system to facilitate stereological measurements and mapping of branching structures. J. Microsc. 2007, 227, 124–139. [Google Scholar] [CrossRef] [PubMed]
- Uribeetxebarria, A.; Martínez-Casasnovas, J.A.; Tisseyre, B.; Guillaume, S.; Escolà, A.; Rosell-Polo, J.R.; Arnó, J. Assessing ranked set sampling and ancillary data to improve fruit load estimates in peach orchards. Comput. Electron. Agric. 2019, 164, 104931. [Google Scholar] [CrossRef]
- Maletti, G.M.; Wulfsohn, D. Evaluation of variance models for fractionator sampling of trees. J. Microsc. 2006, 222, 228–241. [Google Scholar] [CrossRef]
- Stout, R.G. Estimating citrus production by use of frame count survey. J. Farm Econ. 1962, 44, 1037–1049. [Google Scholar] [CrossRef]
- Falivene, S.; Hardy, S. New South Wales Department of Primary Industries. Assessing Citrus Crop Load. 2008. Available online: http://www.dpi.nsw.gov.au/__data/assets/pdf_file/0007/247813/Assessing-citrus-crop-load.pdf (accessed on 1 March 2021).
- Lacey, K. Department of Primary Industries and Regional Development. Estimating Your Citrus Crop. 2019. Available online: https://www.agric.wa.gov.au/citrus/estimating-your-citrus-crop-load?page=0%2C1 (accessed on 26 April 2021).
- Martin, S.; Dunstone, R.; Dunn, G. Victoria Department of Primary Industries. How to Forecast Wine Grape Deliveries Using Grape Forecaster. 2003. Available online: https://www.fairport.com.au/fairport/Help/How%20to%20forecast%20wine%20grape%20deliveries%20Grape%20Forcaster.pdf (accessed on 12 April 2021).
- Olsen, J.; Goodwin, J. The methods and results of the Oregon Agricultural Statistics Service: Annual objective yield survey of Oregon hazelnut production. In Proceedings of the VI International Congress on Hazelnut, Davis, CA, USA, 15 July 2001; pp. 533–538. [Google Scholar] [CrossRef]
- Martinez Vega, M.V.; Wulfsohn, D.; Clemmensen, L.H.; Toldam-Andersen, T.B. Using multilevel systematic sampling to study apple fruit (Malus domestica Borkh.) quality and its variability at the orchard scale. Sci. Hortic. 2013, 161, 58–64. [Google Scholar] [CrossRef] [Green Version]
- Wulfsohn, D.; Lagos, I.Z. The use of a multirotor and high-resolution imaging for precision horticulture in Chile: An industry perspective. In Proceedings of the 12th International Conference on Precision Agriculture, Sacramento, CA, USA, 20–23 July 2014. [Google Scholar]
- Koirala, A.; Walsh, K.B.; Wang, Z.; McCarthy, C. Deep learning–Method overview and review of use for fruit detection and yield estimation. Comput. Electron. Agric. 2019, 162, 219–234. [Google Scholar] [CrossRef]
- Payne, A.B.; Walsh, K.B.; Subedi, P.P.; Jarvis, D. Estimation of mango crop yield using image analysis–segmentation method. Comput. Electron. Agric. 2013, 91, 57–64. [Google Scholar] [CrossRef]
- Stein, M.; Bargoti, S.; Underwood, J. Image based mango fruit detection, localisation and yield estimation using multiple view geometry. Sensors 2016, 16, 1915. [Google Scholar] [CrossRef] [PubMed]
- Underwood, J.P.; Hung, C.; Whelan, B.; Sukkarieh, S. Mapping almond orchard canopy volume, flowers, fruit and yield using lidar and vision sensors. Comput. Electron. Agric. 2016, 130, 83–96. [Google Scholar] [CrossRef]
- Dias, P.A.; Tabb, A.; Medeiros, H. Apple flower detection using deep convolutional networks. Comput. Ind. 2018, 99, 17–28. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Underwood, J.; Walsh, K.B. Machine vision assessment of mango orchard flowering. Comput. Electron. Agric. 2018, 151, 501–511. [Google Scholar] [CrossRef]
- Koirala, A.; Walsh, K.B.; Wang, Z.; Anderson, N. Deep Learning for Mango (Mangifera indica) Panicle Stage Classification. Agronomy 2020, 10, 143. [Google Scholar] [CrossRef] [Green Version]
- Fu, L.; Liu, Z.; Majeed, Y.; Cui, Y. Kiwifruit yield estimation using image processing by an Android mobile phone. IFAC-PapersOnLine 2018, 51, 185–190. [Google Scholar] [CrossRef]
- Faye, E.; Sarron, J.; Diatta, J.; Borianne, P. PixFruit: Un outil d’acquisition, de gestion, et de partage de données pour une normalisation de la filière Mangue en Afrique de l’Ouest aux services de ses acteurs. In Proceedings of the Symposium Agriculture Numérique en Afrique, Dakar, Senegal, 28–29 April 2019; Available online: https://hal.umontpellier.fr/hal-02311106 (accessed on 1 May 2021).
- Wijethunga, P.; Samarasinghe, S.; Kulasiri, D.; Woodhead, I. Digital image analysis based automated kiwifruit counting technique. In Proceedings of the 23rd International Conference Image and Vision Computing, Christchurch, New Zealand, 26–28 November 2008; pp. 1–6. [Google Scholar] [CrossRef] [Green Version]
- Vanbrabant, Y.; Delalieux, S.; Tits, L.; Pauly, K.; Vandermaesen, J.; Somers, B. Pear flower cluster quantification using RGB drone imagery. Agronomy 2020, 10, 407. [Google Scholar] [CrossRef] [Green Version]
- Apolo-Apolo, O.E.; Pérez-Ruiz, M.; Martínez-Guanter, J.; Valente, J. A cloud-based environment for generating yield estimation maps from apple orchards using UAV imagery and a deep learning technique. Front. Plant Sci. 2020, 11, 1086. [Google Scholar] [CrossRef]
- Chen, S.W.; Shivakumar, S.S.; Dcunha, S.; Das, J.; Okon, E.; Qu, C.; Taylor, C.J.; Kumar, V. Counting apples and oranges with deep learning: A data-driven approach. IEEE Robot. Autom. Lett. 2017, 2, 781–788. [Google Scholar] [CrossRef]
- Liu, X.; Chen, S.W.; Aditya, S.; Sivakumar, N.; Dcunha, S.; Qu, C.; Taylor, C.J.; Das, J.; Kumar, V. Robust fruit counting: Combining deep learning, tracking, and structure from motion. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1045–1052. [Google Scholar] [CrossRef] [Green Version]
- Liu, X.; Chen, S.W.; Liu, C.; Shivakumar, S.S.; Das, J.; Taylor, C.J.; Underwood, J.; Kumar, V. Monocular camera based fruit counting and mapping with semantic data association. IEEE Robot. Autom. Lett. 2019, 4, 2296–2303. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Walsh, K.; Koirala, A. Mango Fruit Load Estimation Using a Video Based MangoYOLO—Kalman Filter—Hungarian Algorithm Method. Sensors 2019, 19, 2742. [Google Scholar] [CrossRef] [Green Version]
- Gongal, A.; Karkee, M.; Amatya, S. Apple fruit size estimation using a 3D machine vision system. Inf. Process. Agric. 2018, 5, 498–503. [Google Scholar] [CrossRef]
- Nuske, S.; Gupta, K.; Narasimhan, S.; Singh, S. Modeling and calibrating visual yield estimates in vineyards. In Field and Service Robotics; Springer: Berlin/Heidelberg, Germany; Cham, Switzerland, 2014; pp. 343–356. [Google Scholar] [CrossRef] [Green Version]
- Cheng, H.; Damerow, L.; Sun, Y.; Blanke, M. Early yield prediction using image analysis of apple fruit and tree canopy features with neural networks. J. Imaging 2017, 3, 6. [Google Scholar] [CrossRef]
- Gongal, A.; Silwal, A.; Amatya, S.; Karkee, M.; Zhang, Q.; Lewis, K. Apple crop-load estimation with over-the-row machine vision system. Comput. Electron. Agric. 2016, 120, 26–35. [Google Scholar] [CrossRef]
- Font, D.; Tresanchez, M.; Martínez, D.; Moreno, J.; Clotet, E.; Palacín, J. Vineyard yield estimation based on the analysis of high resolution images obtained with artificial illumination at night. Sensors 2015, 15, 8284–8301. [Google Scholar] [CrossRef] [Green Version]
- Qureshi, W.S.; Payne, A.; Walsh, K.B.; Linker, R.; Cohen, O.; Dailey, M.N. Machine vision for counting fruit on mango tree canopies. Precis. Agric. 2017, 18, 224–244. [Google Scholar] [CrossRef]
- Linker, R. Machine learning based analysis of night-time images for yield prediction in apple orchard. Biosyst. Eng. 2018, 167, 114–125. [Google Scholar] [CrossRef]
- Bargoti, S.; Underwood, J.P. Image segmentation for fruit detection and yield estimation in apple orchards. J. Field Robot. 2017, 34, 1039–1060. [Google Scholar] [CrossRef] [Green Version]
- Kuznetsova, A.; Maleva, T.; Soloviev, V. Using YOLOv3 algorithm with pre-and post-processing for apple detection in fruit-harvesting robot. Agronomy 2020, 10, 1016. [Google Scholar] [CrossRef]
- Gan, H.; Lee, W.S.; Alchanatis, V.; Ehsani, R.; Schueller, J.K. Immature green citrus fruit detection using color and thermal images. Comput. Electron. Agric. 2018, 152, 117–125. [Google Scholar] [CrossRef]
- Xu, J.-X.; Ma, J.; Tang, Y.-N.; Wu, W.-X.; Shao, J.-H.; Wu, W.-B.; Wei, S.-Y.; Liu, Y.-F.; Wang, Y.-C.; Guo, H.-Q. Estimation of Sugarcane Yield Using a Machine Learning Approach Based on UAV-LiDAR Data. Remote Sens. 2020, 12, 2823. [Google Scholar] [CrossRef]
- Mizani, A.; Ibell, P.; Bally, I.S.E.; Wright, C.L.; Kolala, R. Effects of the percentage of terminal flowering on postharvest fruit quality in mango (Mangifera indica)’Calypso’™. In Proceedings of the XI International Mango Symposium, Darwin, Australia, 28 September–2 October 2015; pp. 181–186. [Google Scholar] [CrossRef]
- Braun, B.; Bulanon, D.M.; Colwell, J.; Stutz, A.; Stutz, J.; Nogales, C.; Hestand, T.; Verhage, P.; Tracht, T. A Fruit Yield Prediction Method Using Blossom Detection. In Proceedings of the 2018 ASABE Annual International Meeting; American Society of Agricultural and Biological Engineers, Detroit, MI, USA, 29 July–1 August 2018; p. 1. [Google Scholar]
- Bulanon, D.M.; Braddock, T.; Allen, B.; Bulanon, J.I. Predicting Fruit Yield Using Shallow Neural Networks. Preprints 2020. [Google Scholar] [CrossRef]
- Davenport, T. Floral manipulation in mangoes. In Proceedings of the Conference on Mango, Manoa, HI, USA, 9–11 March 1993; pp. 54–60. Available online: http://hdl.handle.net/10125/16483 (accessed on 1 May 2021).
- Winston, E.C. Evaluation of paclobutrazol on growth, flowering and yield of mango cv. Kensington Pride. Aust. J. Exp. Agric. 1992, 32, 97–104. [Google Scholar] [CrossRef]
- Zhao, Y.; Potgieter, A.B.; Zhang, M.; Wu, B.; Hammer, G.L. Predicting wheat yield at the field scale by combining high-resolution Sentinel-2 satellite imagery and crop modelling. Remote Sens. 2020, 12, 1024. [Google Scholar] [CrossRef] [Green Version]
- Zhao, D.; Reddy, K.R.; Kakani, V.G.; Read, J.J.; Koti, S. Canopy reflectance in cotton for growth assessment and lint yield prediction. Eur. J. Agron. 2007, 26, 335–344. [Google Scholar] [CrossRef]
- Sayago, S.; Bocco, M. Crop yield estimation using satellite images: Comparison of linear and non-linear models. AgriScientia 2018, 35, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Hammer, R.G.; Sentelhas, P.C.; Mariano, J.C.Q. Sugarcane yield prediction through data mining and crop simulation models. Sugar Tech. 2020, 22, 216–225. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Yadav, I.S.; Rao, N.K.S.; Reddy, B.M.C.; Rawal, R.D.; Srinivasan, V.R.; Sujatha, N.T.; Bhattacharya, C.; Rao, P.P.N.; Ramesh, K.S.; Elango, S. Acreage and production estimation of mango orchards using Indian Remote Sensing (IRS) satellite data. Sci. Hortic. 2002, 93, 105–123. [Google Scholar] [CrossRef]
- Zaman, Q.U.; Schumann, A.W.; Hostler, H.K. Estimation of citrus fruit yield using ultrasonically-sensed tree size. Appl. Eng. Agric. 2006, 22, 39–44. [Google Scholar] [CrossRef]
- Ye, X.; Sakai, K.; Asada, S.I.; Sasao, A. Inter-relationships between canopy features and fruit yield in citrus as detected by airborne multispectral imagery. Trans. ASABE 2008, 51, 739–751. [Google Scholar] [CrossRef]
- Sepulcre-Cantó, G.; Zarco-Tejada, P.J.; Jiménez-Muñoz, J.C.; Sobrino, J.A.; Soriano, M.A.; Fereres, E.; Vega, V.; Pastor, M. Monitoring yield and fruit quality parameters in open-canopy tree crops under water stress. Implications for ASTER. Remote Sens. Environ. 2007, 107, 455–470. [Google Scholar] [CrossRef]
- Maselli, F.; Chiesi, M.; Brilli, L.; Moriondo, M. Simulation of olive fruit yield in Tuscany through the integration of remote sensing and ground data. Ecol. Model. 2012, 244, 1–12. [Google Scholar] [CrossRef]
- Robson, A.; Rahman, M.M.; Muir, J. Using worldview satellite imagery to map yield in avocado (Persea americana): A case study in Bundaberg, Australia. Remote Sens. 2017, 9, 1223. [Google Scholar] [CrossRef] [Green Version]
- Rahman, M.M.; Robson, A.; Bristow, M. Exploring the potential of high resolution worldview-3 Imagery for estimating yield of mango. Remote Sens. 2018, 10, 1866. [Google Scholar] [CrossRef] [Green Version]
- Bai, T.; Zhang, N.; Mercatoris, B.; Chen, Y. Improving jujube fruit tree yield estimation at the field scale by assimilating a single landsat remotely-sensed LAI into the WOFOST model. Remote Sens. 2019, 11, 1119. [Google Scholar] [CrossRef] [Green Version]
- Chang, A.; Jung, J.; Yeom, J.; Maeda, M.M.; Landivar, J.A.; Enciso, J.M.; Avila, C.A.; Anciso, J.R. Unmanned Aircraft System-(UAS-) Based High-Throughput Phenotyping (HTP) for Tomato Yield Estimation. J. Sens. 2021. [Google Scholar] [CrossRef]
- Hoblyn, T.N.; Grubb, N.H.; Painter, A.C.; Wates, B.L. Studies in Biennial Bearing.—I. J. Pomol. Hortic. Sci. 1937, 14, 39–76. [Google Scholar] [CrossRef]
- Dahal, K.C.; Bhattarai, S.P.; Midmore, D.J.; Oag, D.R.; Walsh, K.B. Temporal yield variability in subtropical table grape production. Sci. Hortic. 2019, 246, 951–956. [Google Scholar] [CrossRef]
- Sakai, K.; Noguchi, Y.; Asada, S.-I. Detecting chaos in a citrus orchard: Reconstruction of nonlinear dynamics from very short ecological time series. Chaos Solitons Fractals 2008, 38, 1274–1282. [Google Scholar] [CrossRef]
- Zhang, Z.; Jin, Y.; Chen, B.; Brown, P. California almond yield prediction at the orchard level with a machine learning approach. Front. Plant Sci. 2019, 10, 809. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lampinen, B.D.; Udompetaikul, V.; Browne, G.T.; Metcalf, S.G.; Stewart, W.L.; Contador, L.; Negrón, C.; Upadhyaya, S.K. A mobile platform for measuring canopy photosynthetically active radiation interception in orchard systems. HortTechnology 2012, 22, 237–244. [Google Scholar] [CrossRef] [Green Version]
- Jin, Y.; Chen, B.; Lampinen, B.D.; Brown, P.H. Advancing agricultural production with machine learning analytics: Yield determinants for California’s almond orchards. Front. Plant Sci. 2020, 11, 290. [Google Scholar] [CrossRef] [Green Version]
- Peiris, T.S.G.; Hansen, J.W.; Zubair, L. Use of seasonal climate information to predict coconut production in Sri Lanka. Int. J. Climatol. A J. R. Meteorol. Soc. 2008, 28, 103–110. [Google Scholar] [CrossRef] [Green Version]
- Mayer, D.G.; Chandra, K.A.; Burnett, J.R. Improved crop forecasts for the Australian macadamia industry from ensemble models. Agric. Syst. 2019, 173, 519–523. [Google Scholar] [CrossRef]
- Brinkhoff, J.; Robson, A.J. Block-level macadamia yield forecasting using spatio-temporal datasets. Agric. Forest Meteorol. 2021, 303, 108369. [Google Scholar] [CrossRef]
- Marini, R.P.; Schupp, J.R.; Baugher, T.A.; Crassweller, R. Relationships between fruit weight and diameter at 60 days after bloom and at harvest for three apple cultivars. HortScience 2019, 54, 86–91. [Google Scholar] [CrossRef] [Green Version]
- Lakso, A.N.; Corelli Grappadelli, L.; Barnard, J.; Goffinet, M.C. An expolinear model of the growth pattern of the apple fruit. J. Hortic. Sci. 1995, 70, 389–394. [Google Scholar] [CrossRef]
- Ortega-Farias, S.; Flores, L.; León, L. Elaboration of a Predictive Table of Apple Diameter cv. Granny Smith Using Growing Degree Days. 2002. Available online: https://tspace.library.utoronto.ca/handle/1807/24073 (accessed on 1 May 2021).
- Verreynne, S. Fruit Size and Crop Load Prediction. Chapter 5, Part 7, Integrated Production Guidelines; Citrus Research International: Port Elizabeth, South Africa, 2010; Volume 2, Available online: https://www.citrusres.com/system/files/documents/production-guidelines/Ch%205-7%20Fruit%20size%20and%20crop%20load%20prediction%20Sep%202010.pdf (accessed on 12 April 2021).
- Ellis, R.; Moltchanova, E.; Gerhard, D.; Trought, M.; Yang, L. Using Bayesian growth models to predict grape yield. OENO ONE 2020, 54, 443–453. [Google Scholar] [CrossRef]
- Hall, A.J.; McPherson, H.G.; Crawford, R.A.; Seager, N.G. Using early-season measurements to estimate fruit volume at harvest in kiwifruit. N. Z. J. Crop Hortic. Sci. 1996, 24, 379–391. [Google Scholar] [CrossRef] [Green Version]
- Spreer, W.; Müller, J. Estimating the mass of mango fruit (Mangifera indica, cv. Chok Anan) from its geometric dimensions by optical measurement. Comput. Electron. Agric. 2011, 75, 125–131. [Google Scholar] [CrossRef]
- Wang, Z.; Walsh, K.B.; Verma, B. On-tree mango fruit size estimation using RGB-D images. Sensors 2017, 17, 2738. [Google Scholar] [CrossRef] [Green Version]
- Monselise, S.P.; Varga, A.; Bruinsma, J. Growth analysis of the tomato fruit, Lycopersicon esculentum Mill. Ann. Bot. 1978, 42, 1245–1247. [Google Scholar] [CrossRef]
- Caballero, B.; Trugo, L.C.; Finglas, P.M. Encyclopedia of Food Sciences and Nutrition; Academic Press: Cambridge, MA, USA, 2003; ISBN 012227055X. [Google Scholar]
- Miller, S.A.; Smith, G.S.; Boldingh, H.L.; Johansson, A. Effects of water stress on fruit quality attributes of kiwifruit. Ann. Bot. 1998, 81, 73–81. [Google Scholar] [CrossRef] [Green Version]
- Walsh, K.B.; Blasco, J.; Zude-Sasse, M.; Sun, X. Visible-NIR ‘point’spectroscopy in postharvest fruit and vegetable assessment: The science behind three decades of commercial use. Postharvest Biol. Technol. 2020, 168, 111246. [Google Scholar] [CrossRef]
- Li, J.B.; Huang, W.Q.; Zhao, C.J. Machine vision technology for detecting the external defects of fruits—A review. Imaging Sci. J. 2015, 63, 241–251. [Google Scholar] [CrossRef]
- Naik, S.; Patel, B. Machine vision based fruit classification and grading-a review. Int. J. Comput. Appl. 2017, 170, 22–34. [Google Scholar] [CrossRef]
- Guo, Z.; Zhang, M.; Lee, D.-J.; Simons, T. Smart Camera for Quality Inspection and Grading of Food Products. Electronics 2020, 9, 505. [Google Scholar] [CrossRef] [Green Version]
- Pothula, A.K.; Zhang, Z.; Lu, R. Design features and bruise evaluation of an apple harvest and in-field presorting machine. Trans. ASABE 2018, 61, 1135–1144. [Google Scholar] [CrossRef]
- Choi, D.; Lee, W.S.; Ehsani, R.; Schueller, J.; Roka, F.M. Detection of dropped citrus fruit on the ground and evaluation of decay stages in varying illumination conditions. Comput. Electron. Agric. 2016, 127, 109–119. [Google Scholar] [CrossRef]
- USDA. United States Department of Agriculture. Objective Yield Survey. 2020. Available online: https://www.nass.usda.gov/Surveys/Guide_to_NASS_Surveys/Objective_Yield/index.php (accessed on 13 April 2021).
- Wulfsohn, D.; Cohen, O.; Lagos, I.Z. OrchardMapper: Application for creating tree scale maps from high resolution orthomosaics. In Proceedings of the AgEng 2018, Wageningen, The Netherlands, 8–11 July 2018. [Google Scholar]
- Schrader, J.A.; Domoto, P.A.; Nonnecke, G.R.; Cochran, D.R. Multifactor Models for Improved Prediction of Phenological Timing in Cold-climate Wine Grapes. HortScience 2020, 1–14. [Google Scholar] [CrossRef]
- Henriod, R.; Sole, D. Development of maturity standards for a new Australian mango cultivar, ‘NMBP-1243’. In Proceedings of the XI International Mango Symposium, Darwin, Australia, 28 September–2 October 2015; pp. 17–22. [Google Scholar] [CrossRef]
- Hofman, P.; Macnish, A.; Duong, H.; Bryant, P.; Winston, T.; Scurr, R.; Joyce, D. Department of Agriculture and Fisheries, QLD. Improving Consumer Appeal of Honey Gold Mango by Reducing under Skin Browning and Red Lenticel Discolouration. 2017. Available online: http://era.daf.qld.gov.au/id/eprint/6545/1/MG13016%20final%20report-581.pdf (accessed on 1 March 2021).
- Moore, C. Northern Territory Government. Mango Heat Sums Instructions. 2013. Available online: https://nt.gov.au/__data/assets/pdf_file/0009/267678/heat-sum-instructions.pdf (accessed on 21 April 2021).
- Aggelopoulou, A.; Bochtis, D.; Fountas, S.; Swain, K.C.; Gemtos, T.; Nanos, G. Yield prediction in apple orchards based on image processing. Precis. Agric. 2011, 12, 448–456. [Google Scholar] [CrossRef]
- Farjon, G.; Krikeb, O.; Hillel, A.B.; Alchanatis, V. Detection and counting of flowers on apple trees for better chemical thinning decisions. Precis. Agric. 2019, 1–19. [Google Scholar] [CrossRef]
- Tian, Y.; Yang, G.; Wang, Z.; Li, E.; Liang, Z. Instance segmentation of apple flowers using the improved mask R–CNN model. Biosyst. Eng. 2020, 193, 264–278. [Google Scholar] [CrossRef]
- Wu, D.; Lv, S.; Jiang, M.; Song, H. Using channel pruning-based YOLO v4 deep learning algorithm for the real-time and accurate detection of apple flowers in natural environments. Comput. Electron. Agric. 2020, 178, 105742. [Google Scholar] [CrossRef]
- Darwin, B.; Dharmaraj, P.; Prince, S.; Popescu, D.E.; Hemanth, D.J. Recognition of Bloom/Yield in Crop Images Using Deep Learning Models for Smart Agriculture: A Review. Agronomy 2021, 11, 646. [Google Scholar] [CrossRef]
- Wang, Z.; Verma, B.; Walsh, K.B.; Subedi, P.; Koirala, A. Automated mango flowering assessment via refinement segmentation. In Proceedings of the 2016 International Conference on Image and Vision Computing New Zealand (IVCNZ), Palmerston North, New Zealand, 21–22 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Horticulture Innovation Australia, 2016 Mango Industry Quality Standards. Available online: https://www.horticulture.com.au/globalassets/hort-innovation/resource-assets/mg15002-2016-mango-industry-quality-standards.pdf (accessed on 1 March 2021).
- Peirs, A.; Tirry, J.; Verlinden, B.; Darius, P.; Nicolaï, B.M. Effect of biological variability on the robustness of NIR models for soluble solids content of apples. Postharvest Biol. Technol. 2003, 28, 269–280. [Google Scholar] [CrossRef]
- Clark, C.J.; McGlone, V.A.; Requejo, C.; White, A.; Woolf, A.B. Dry matter determination in ‘Hass’ avocado by NIR spectroscopy. Postharvest Biol. Technol. 2003, 29, 301–308. [Google Scholar] [CrossRef]
- Anderson, N.T.; Subedi, P.P.; Walsh, K.B. Manipulation of mango fruit dry matter content to improve eating quality. Sci. Hortic. 2017, 226, 316–321. [Google Scholar] [CrossRef]
- Tuccio, L.; Cavigli, L.; Rossi, F.; Dichala, O.; Katsogiannos, F.; Kalfas, I.; Agati, G. Fluorescence-sensor mapping for the in vineyard non-destructive assessment of crimson seedless table grape quality. Sensors 2020, 20, 983. [Google Scholar] [CrossRef] [Green Version]
- Balafoutis, A.T.; Evert, F.K.V.; Fountas, S. Smart Farming Technology Trends: Economic and Environmental Effects, Labor Impact, and Adoption Readiness. Agronomy 2020, 10, 743. [Google Scholar] [CrossRef]









| Crop | # of Records | % | Country | # of Records | % |
|---|---|---|---|---|---|
| Apple | 32 | 33 | China | 38 | 21 |
| Mango | 19 | 20 | United States | 34 | 19 |
| Citrus | 17 | 18 | Spain | 29 | 16 |
| Other | 16 | 16 | Australia | 20 | 11 |
| Kiwi | 4 | 4 | India | 16 | 9 |
| Grape | 3 | 3 | Germany | 14 | 8 |
| Olive | 3 | 3 | Brazil | 11 | 6 |
| Tomato | 3 | 3 | France | 11 | 6 |
| Italy | 9 | 5 | |||
| Method | # of records | % | Estimation level | # of records | % |
| MV RGB | 65 | 59 | image | 36 | 38 |
| Satellite | 10 | 9 | tree | 28 | 30 |
| MV Hyperspectral | 8 | 7 | orchard | 19 | 20 |
| Proximal indirect | 8 | 7 | region | 11 | 12 |
| UAV | 7 | 6 | |||
| Historical/climate | 6 | 5 | |||
| Manual | 6 | 5 |
| Term | Meaning | Equation |
|---|---|---|
| RMSE | The standard deviation of the prediction residuals | where is the estimated value, is the observed value and n is the sample size |
| RRMSE | RMSE relative to mean | |
| MSE | The average squared errors of prediction residuals | |
| R2 | The proportion of the variance of one variable that can be explained by the variance of the second variable | where is the mean of observed values |
| MAE | The average of the absolute values of prediction residuals | |
| MAPE | The average of the absolute values of prediction residuals divided by the actual values | |
| CCC | Interpreted similarly to R2, but used to compare two methods predictions or to measure repeatability of repeats of a single method | where represents the variability of either the observed value or another variable and and the variability and the mean of either the estimated value or another variable |
| RCV | The minimal significant difference between temporally different measurements | where is the quantile for the desired probability from a standard normal distribution |
| MCC | Measures the agreement of binary classifications | where TP is true positives, TN is true negatives, FP is false positives and FN is false negatives of binary classification |
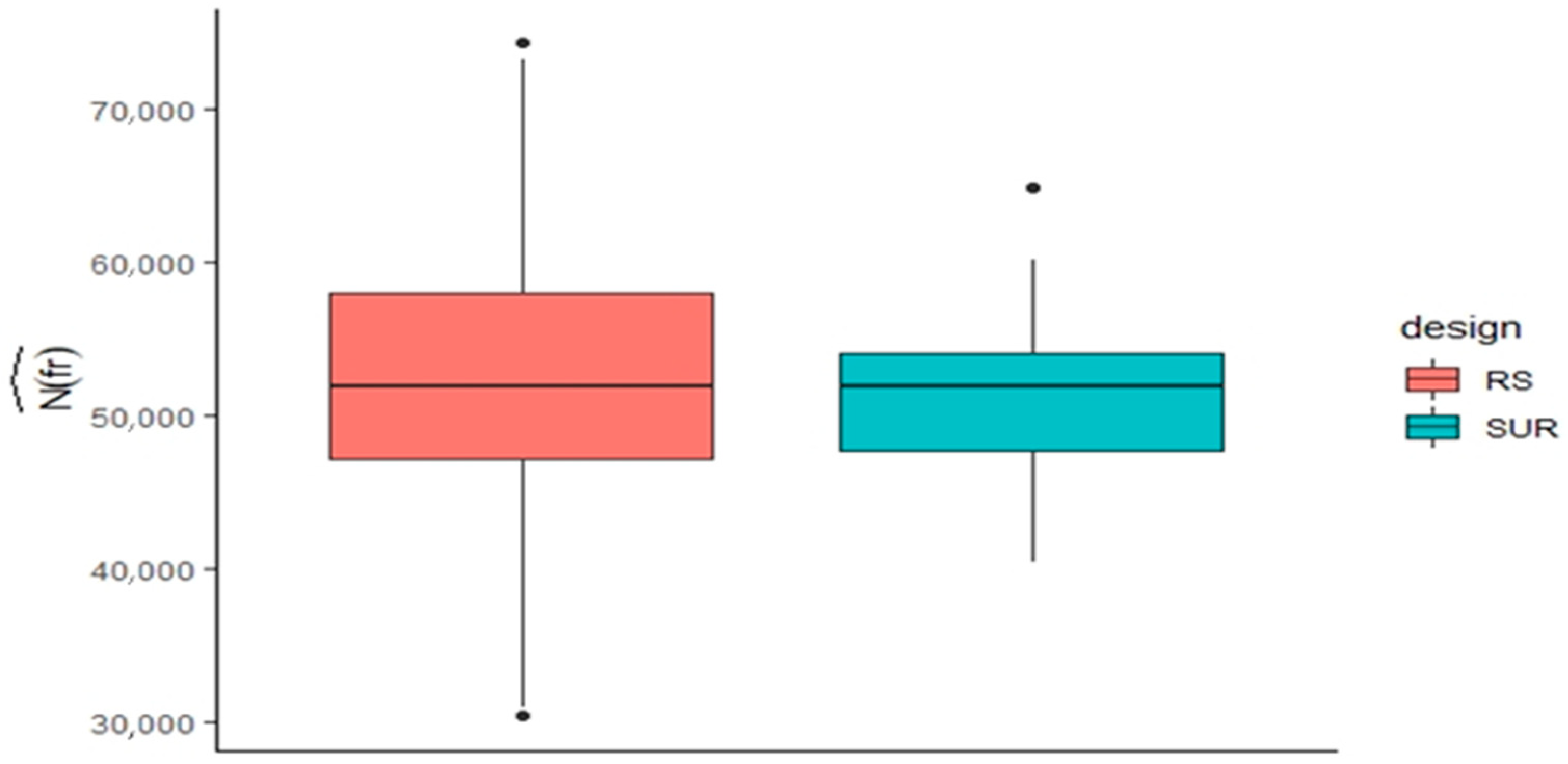
| Site | (# Trees) | Average (# Fruit/Tree) | (# Fruit/Tree) | (# Trees) Equation (3) | (# Trees) Equation (4) | |
|---|---|---|---|---|---|---|
| 1 | 469 | 88 | 82 | 234 | 156 | 33 |
| 2 | 486 | 259 | 102 | 42 | 38 | 8 |
| 3 | 1017 | 240 | 160 | 120 | 107 | 11 |
| 4 | 1100 | 80 | 34 | 49 | 47 | 4 |
| 5 | 224 | 59 | 36 | 100 | 69 | 31 |
| 6 | 1205 | 97 | 65 | 121 | 110 | 9 |
| 7 | 1091 | 201 | 55 | 20 | 20 | 2 |
| 8 | 1818 | 106 | 51 | 62 | 60 | 3 |
| 9 | 1176 | 77 | 61 | 169 | 148 | 13 |
| 10 | 1115 | 85 | 40 | 60 | 57 | 5 |
| Paper | Algorithm/Technique | Imaging Method | Validation Set | Result |
|---|---|---|---|---|
| Apple | ||||
| Gongal et al. [54] | Color and shape thresholding | DV on ground vehicle with row cover | 20 trees | 20% error on fruit in image, 18% error on fruits per tree |
| Bargoti and Underwood [58] | CNN | MV on ground vehicle, day imaging | 15 rows | 10.8% error on fruit counts per tree |
| Cheng et al. [53] | Color thresholding, neural network utilizing ancillary variables (foliage area, fruit area) | Single view on ground vehicle, day imaging | Multi season cross validations (2009–2011) 180 trees total. | 10.7 and 8.9% MAPE for estimations of fruit per tree after fruit drop and during ripening period, respectively |
| Linker [57] | Speeded Up Robust Features | DV (2014) and MV (2016 set) ground vehicle, night imaging | 10 grabs of 20 random trees (2014 and 2016 separately) | 2014: 4.8% error and 2016: 5.4% error (fruit/tree) |
| Kuznetsova et al. [59] | YOLOv3 | Single view on stationary platform | 552 images | 93% precision; 1% error on fruit count per image |
| Citrus | ||||
| Gan et al. [60] | FRCNN | Fusion of thermal and RGB, day imaging | 1658 images | 95.5% precision on fruit/image |
| Apolo-Apolo et al. [46] | FRCNN | DV on UAV | 20 trees, 3 seasons | 11.5, 4.3 and 5.8% error against harvested kg for 2016, 2017, and 2018, respectively |
| Grape | ||||
| Nuske et al. [52] | Shape, texture, color, occlusion correction | MV at 6 fps on ground vehicle; stereo camera for position | 1212 vines of 5 varieties on 4 trellis types, for 4 seasons. | 4% error in yield prediction with use of occlusion correction |
| Font et al. [55] | Color thresholding and area or volume modeling | Single view on ground vehicle | 25 bunches | 16–17% error on bunch weight. |
| Kiwifruit | ||||
| Wijethunga et al. [44] | Color thresholding | Single view on ground vehicle, night imaging | 78 gold 42 green images | 7.1 and 24.9% error for gold and green varieties, respectively, for fruit in image counts |
| Mango | ||||
| Stein et al. [37] | FRCNN | DV and MV on ground vehicle, day imaging | 16 trees | 1.4% error on fruit per tree (MV) |
| Qureshi et al. [56] | Texture and shape segmenting | DV ground vehicle, multiple light conditions | Multiple validations (10–74 trees) | Multiple validations from 0.5 to 40% error on fruit per tree estimate (mean = 18.6 and sd = 15.6%) |
| Anderson et al. [16] | FRCNN | DV and MV on ground vehicle, night imaging | 1 orchard | 9 and 6% error on packhouse count (DV and MV, respectively) |
| Koirala et al. [3] | MangoYOLOv3 | DV on ground vehicle; night imaging | 5 orchards | 3% error on packhouse count (5 orchards combined) |
| Publication | Commodity | Allometry between Weight and Lineal Dimensions | Prediction of Harvest Weight |
|---|---|---|---|
| Marini et al. [90] | Apple (Gala) | Quadratic W = 17.03 – (1.48 × d) + (0.046 × d2) R2 = 0.972 | Linear HW = −169.09 + (8.19 × W60 DAB) R2 = 0.79 |
| Lakso et al. [91] | Apple (Empire) | Linear 1.47 to 1.95 g/day | |
| Ortega-Farias et al. [92] | Apple (Granny Smith) | Logistic growth curve | |
| Verreynne [93] | Citrus (Navel Orange) | Linear 26.4 mm/day | |
| Ellis et al. [94] | Grape | Bayesian predicted double sigmoid growth curve | |
| Hall et al. [95] | Kiwifruit | Linear 0.42 mL/day from 50 DAB | |
| Spreer and Müller [96] | Mango (Chok Anan) | Linear W = 0.000539 × L × Wi × T R2 = 0.97 | |
| Wang et al. [97] | Mango (HoneyGold) | Linear W = 0.42 × L × Wi2 R2= 0.96 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, N.T.; Walsh, K.B.; Wulfsohn, D. Technologies for Forecasting Tree Fruit Load and Harvest Timing—From Ground, Sky and Time. Agronomy 2021, 11, 1409. https://doi.org/10.3390/agronomy11071409
Anderson NT, Walsh KB, Wulfsohn D. Technologies for Forecasting Tree Fruit Load and Harvest Timing—From Ground, Sky and Time. Agronomy. 2021; 11(7):1409. https://doi.org/10.3390/agronomy11071409
Chicago/Turabian StyleAnderson, Nicholas Todd, Kerry Brian Walsh, and Dvoralai Wulfsohn. 2021. "Technologies for Forecasting Tree Fruit Load and Harvest Timing—From Ground, Sky and Time" Agronomy 11, no. 7: 1409. https://doi.org/10.3390/agronomy11071409
APA StyleAnderson, N. T., Walsh, K. B., & Wulfsohn, D. (2021). Technologies for Forecasting Tree Fruit Load and Harvest Timing—From Ground, Sky and Time. Agronomy, 11(7), 1409. https://doi.org/10.3390/agronomy11071409







