Dynamic Energy Exchange Modelling for a Plastic-Covered Multi-Span Greenhouse Utilizing a Thermal Effluent from Power Plant
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Flow
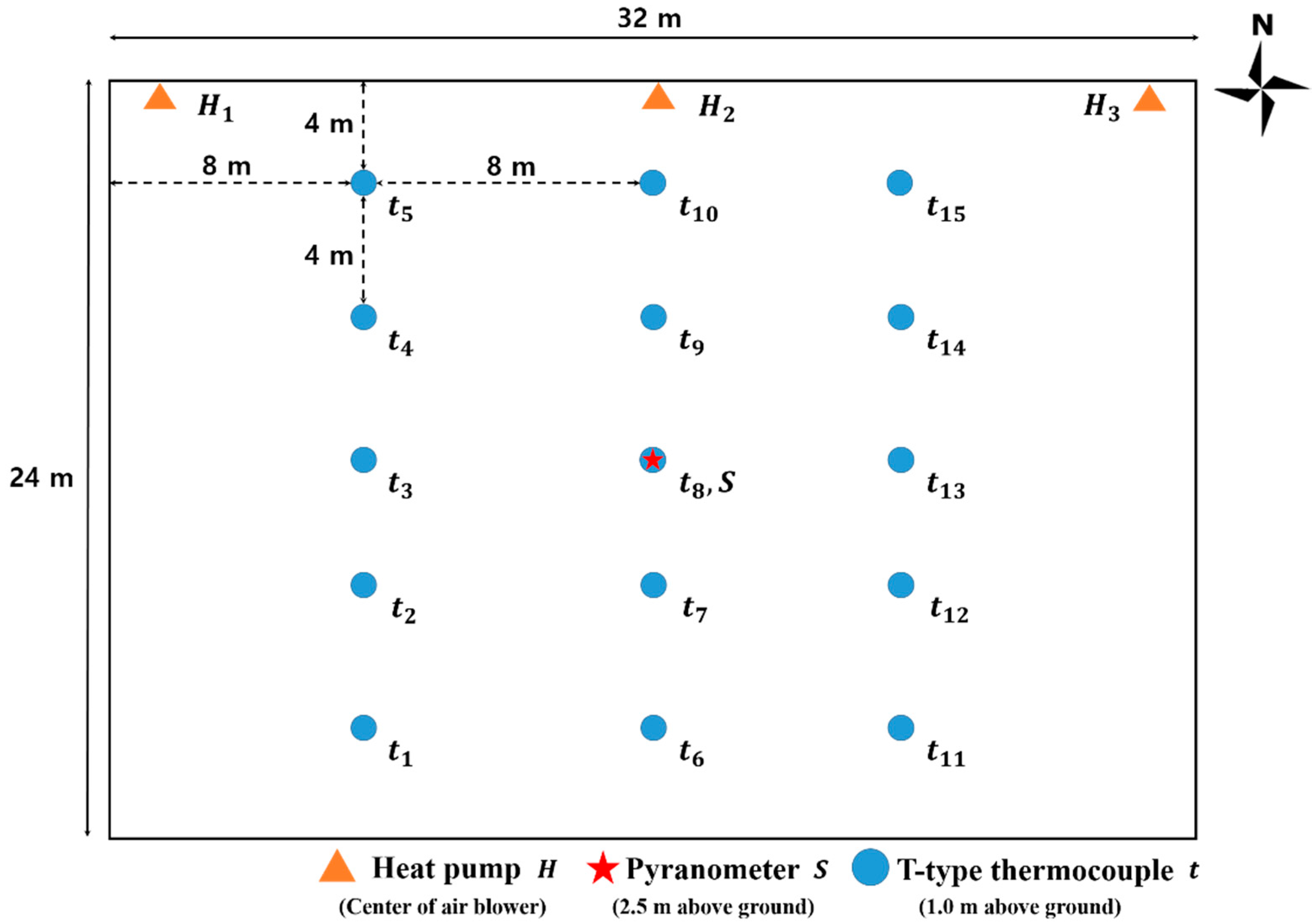
2.2. Experimental Greenhouse
2.3. Building Energy Simulation (BES)
2.4. Experimental Procedure
2.4.1. Field Experiments
Measurement of the Internal Environment in the Greenhouse
Measurement of the Stomatal Resistance and the Leaf Area Index of Crops
Measurement of Transpiration by Crops
2.4.2. Design of the Energy Exchange Model of the Greenhouse
2.4.3. Accuracy Evaluation Method for the BES Model
2.4.4. Analysis of the Greenhouse Energy Loads
3. Results and Discussion
3.1. Result of the Field Experiment
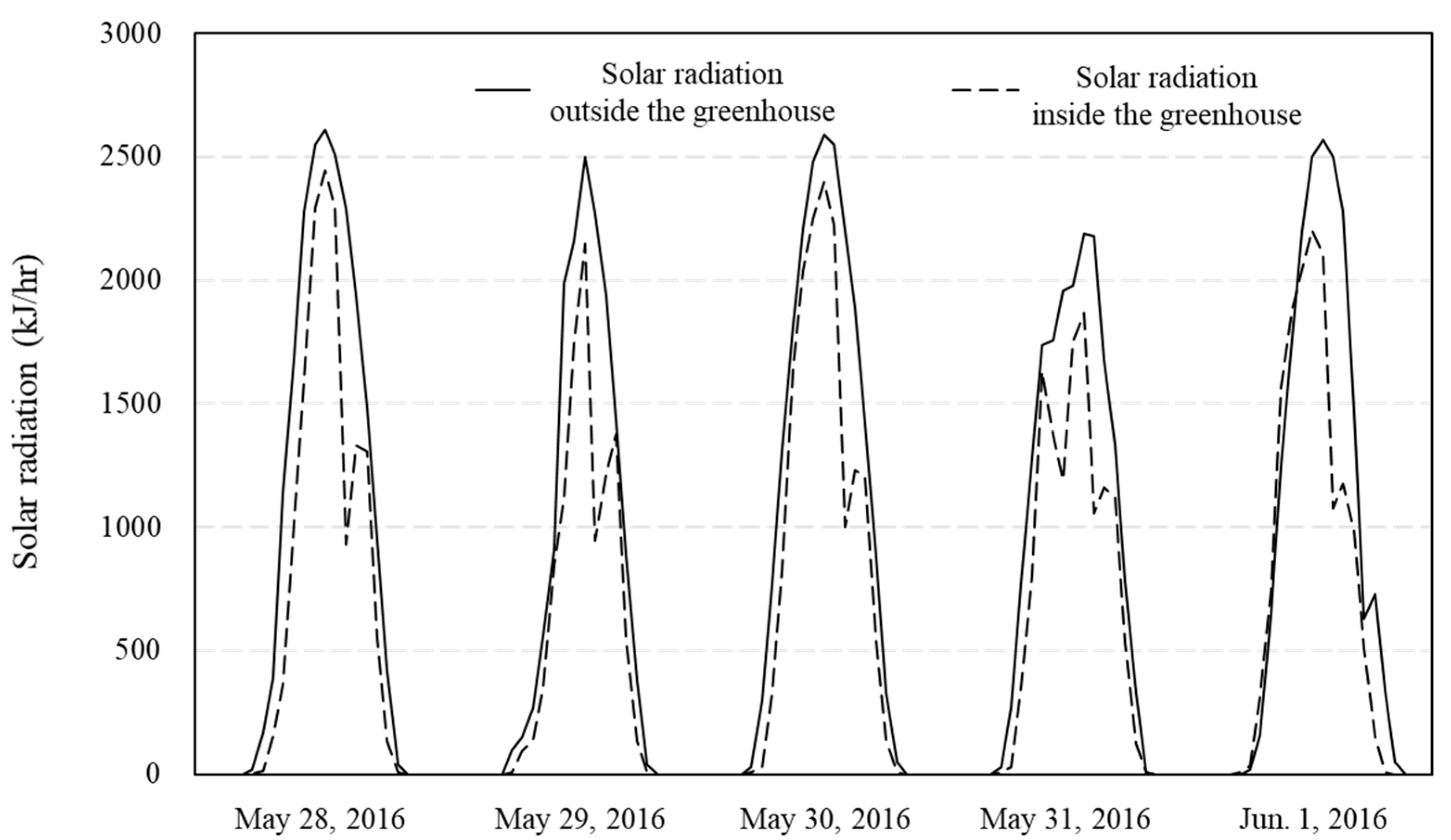
3.1.1. Analysis of the Internal Environmental Data
3.1.2. Stomatal Resistance and the Leaf Area Index of the Crops
3.2. Design of the Energy Exchange Model
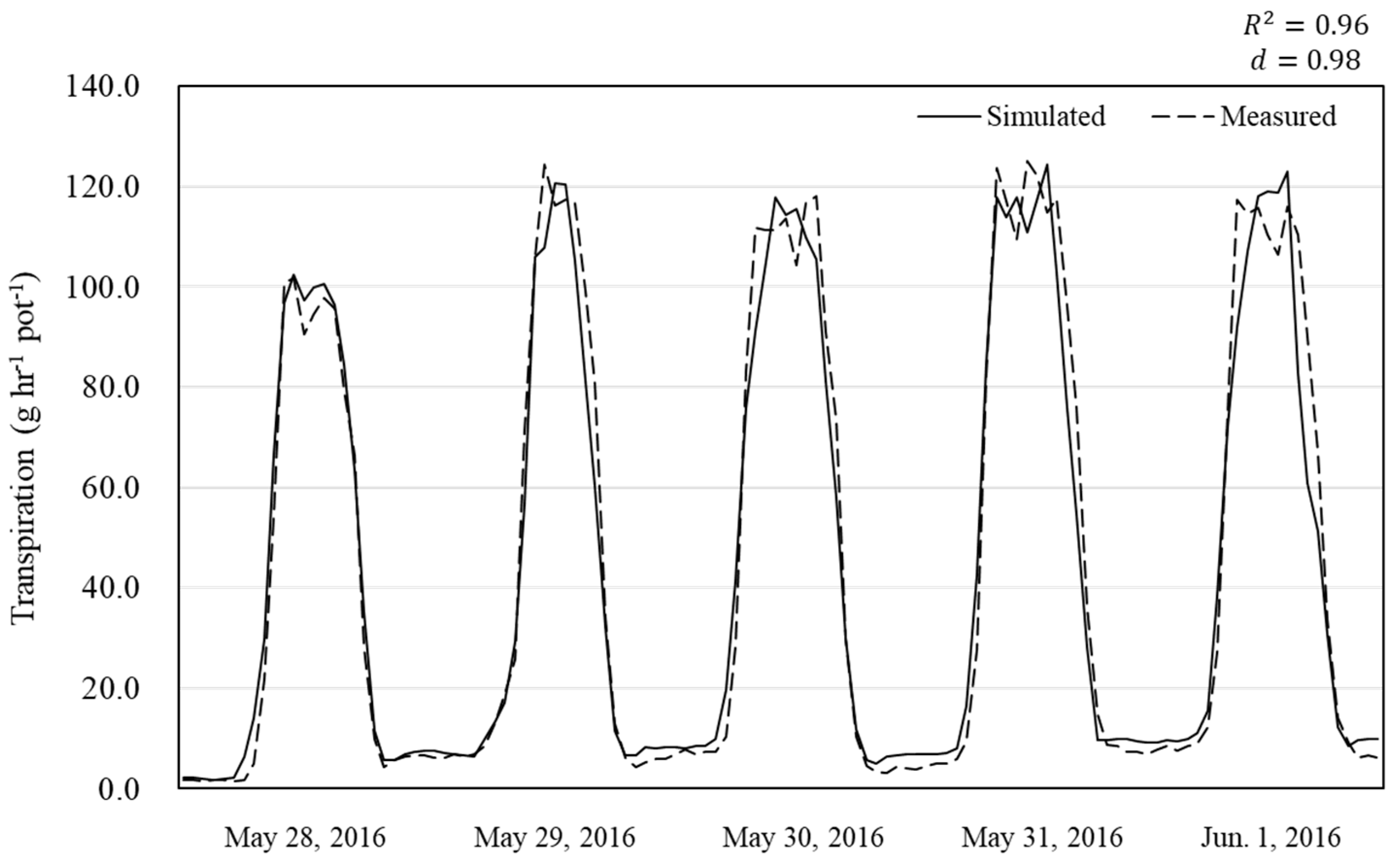
3.2.1. Validation of Transpiration of Crops
3.2.2. Validation of the Air Temperature inside the Greenhouse
3.2.3. Validation of the Air Temperature inside the Greenhouse
3.3. BES Computed Energy Load of the Experimental Greenhouse
3.3.1. Analysis of the Energy Load According to the Growth Stage
3.3.2. Analysis of the Energy Load with and without Internal Crops
3.3.3. Evaluation of the Design Capacities of the Heating and Cooling Systems
3.4. Comparative Analysis of the Energy Cost According to the Energy Source
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ministry of Agriculture Food and Rural Affairs. 2019 Greenhouse Status and Production of Vegetables; Ministry of Agriculture Food and Rural Affairs: Sejong, Korea, 2019. [Google Scholar]
- Roser, M.; Ritchie, R.; Ortiz-Ospina, E. World Population Growth. Our World in Data. 2013. Available online: https://ourworldindata.org/world-population-growth (accessed on 31 May 2021).
- Korea Energy Economics Institue. Yearbook of Regional Energy Statistics; Ministry of Trade, Industry &Energy: Sejong, Korea, 2019. [Google Scholar]
- Ministry of Agriculture Food and Rural Affairs. Guidelines for Implementing Agricultural Energy Efficiency Projects in 2015; Ministry of Agriculture Food and Rural Affairs: Sejong, Korea, 2015. [Google Scholar]
- Cho, S.H.; Kim, S.S.; Choi, C.Y. Study on the revision of HDD for 15 main cities of Korea. Korean J. Air-Cond. Refrig. Eng. 2010, 22, 436–441. [Google Scholar]
- Lee, H.W.; Diop, S.; Kim, Y.S. Variation of the overall heat transfer coefficient of plastic greenhouse covering material. Prot. Hortic. Plant Fact. 2011, 20, 72–77. [Google Scholar]
- Nam, S.W.; Shin, H.H. Development of a method to estimate the seasonal heating load for plastic greenhouses. J. Korean Soc. Agric. Eng. 2015, 57, 37–42. [Google Scholar]
- Song, S.Y.; Koo, B.K.; Lee, B.I. Analysis of Annual Heating Load Reduction Effect for Thermal Bridge-free Externally Insulated Apartment Buildings Using the Steady-state Method. J. Archit. Inst. Korea 2009, 25, 365–372. [Google Scholar]
- Al-Helal, I.M.; Abdel-Ghany, A.M. Energy partition and conversion of solar and thermal radiation into sensible and latent heat in a greenhouse under arid conditions. Energy Build. 2011, 43, 1740–1747. [Google Scholar] [CrossRef]
- Attar, I.; Farhat, A. Efficiency evaluation of a solar water heating system applied to the greenhouse climate. Sol. Energy 2015, 119, 212–224. [Google Scholar] [CrossRef]
- Candy, S.; Moore, G.; Freere, P. Design and modeling of a greenhouse for a remote region in Nepal. Procedia Eng. 2012, 49, 152–160. [Google Scholar] [CrossRef] [Green Version]
- Luo, W.; de Zwart, H.F.; DaiI, J.; Wang, X.; Stanghellini, C.; Bu, C. Simulation of greenhouse management in the subtropics, Part I: Model validation and scenario study for the winter season. Biosyst. Eng. 2005, 90, 307–318. [Google Scholar] [CrossRef]
- Ntinas, G.K.; Fragos, V.P.; Nikita-Martzopoulou, C. Thermal analysis of a hybrid solar energy saving system inside a greenhouse. Energy Convers. Manag. 2014, 81, 428–439. [Google Scholar] [CrossRef]
- Sethi, V.P. On the selection of shape and orientation of a greenhouse: Thermal modeling and experimental validation. Sol. Energy 2009, 83, 21–38. [Google Scholar] [CrossRef]
- Ha, T.H.; Lee, I.B.; Kwon, K.S.; Hong, S.W. Computation and field experiment validation of greenhouse energy load using building energy dimulation model. Int. J. Agric. Biol. Eng. 2015, 8, 116–127. [Google Scholar]
- Jiao, Z.; Yuan, J.; Farnham, C.; Emura, K. Deviation of design air-conditioning load based on weather database of reference weather year and actual weather year. Energy Built Environ. 2020, 1, 417–422. [Google Scholar] [CrossRef]
- Stanghellini, C. Transpiration of Greenhouse Crops: An Aid to Climate Management. Ph.D. Thesis, Wageningen University & Research, Wageningen, The Netherlands, 1987. [Google Scholar]
- Fynn, R.P.; Al-Shooshan, A.; Short, T.H.; McMahon, R.W. Evapotranspiration measurement and modeling for a potted chrysanthemum crop. Trans. ASAE 1993, 36, 1907–1913. [Google Scholar] [CrossRef]
- Monteith, J.L. Evaporation and environment. Symp. Soc. Exp. Biol. 1965, 19, 205–234. [Google Scholar] [PubMed]
- Willmott, C.J.; Ackleson, S.G.; Davis, R.E.; Feddema, J.J.; Klink, K.M.; Legates, D.R.; O’Donnell, J.; Rowe, C.M. Statistics for the evaluation and comparison of models. J. Geophys. Res. Oceans 1985, 90, 8995–9005. [Google Scholar] [CrossRef] [Green Version]
- Boulard, T.; Baille, A. Analysis of thermal performance of a greenhouse as a solar collector. Energy Agric. 1987, 6, 17–26. [Google Scholar] [CrossRef]
- Garzoli, K.V.; Blackwell, J. Response of a Glasshouse to High Solar Radiation and Ambient Temperature. J. Agric. Eng. Res. 1973, 18. [Google Scholar] [CrossRef]
- Kittas, C.; Karamanis, M.; Katsoulas, N. Air temperature regime in a forced ventilated greenhouse with rose crop. Energy Build. 2005, 37, 807–812. [Google Scholar] [CrossRef]
- Kittas, C.; Katsoulas, N.; Baille, A. Influence of an aluminized thermal screen on greenhouse microclimate and canopy energy balance. Trans. ASAE 2003, 46, 1653. [Google Scholar] [CrossRef]
- Rural Development Administration. Facility Gardening Energy Saving Guidebook; Rural Development Administration: Jeonju, Korea, 2008. [Google Scholar]
- Lee, S.B. Analysis and Validation of Dynamic Thermal Energy for Greenhouse with Geothermal System Using Field Data. Master’s Thesis, Seoul National University, Seoul, Korea, 2012. [Google Scholar]














| Icon | Module | Specification |
|---|---|---|
 | Data reader | Reads weather and sensor data to send input data to other modules |
 | Radiation processor | Interpolates radiation data, calculates several quantities that are related to the position of the sun and estimates the insolation on surfaces of either fixed or variable orientation |
 | Psychrometric calculator | Calculates moist air by accepting as input the dry bulb temperature and the relative humidity |
 | Sky temperature calculator | Determines the effective sky temperature for calculating the longwave radiation exchange between an arbitrary external surface and the atmosphere |
 | Multi-zone (greenhouse) | Models the thermal behavior inside a greenhouse (heating, cooling, ventilation, and infiltration) |
 | User-defined function | Calculates average greenhouse internal temperature as input data for the switch module, the sensible/latent heat flux by crops, and the energy production and power consumption of the heat pump |
 | Switch | Determines on/off signals for each device based on the external/internal weather conditions |
 | Heat pump | Models a single-stage liquid-source heat pump based on user-supplied data files that contain catalogue data for the capacity and power |
| Type | Material | Density (kg m−3) | Specific Heat (kJ kg−1 K−1) | Thermal Conductivity (kJ h−1 m−1 K−1) | Thickness (m) |
|---|---|---|---|---|---|
| Frame | Carbon steel | 7840 | 0.502 | 154.8 | 0.0254 |
| Floor | Gravel | 1800 | 1.000 | 7.2 | 0.2000 |
| Cotton | 1550 | 1.338 | 0.104 | 0.0100 |
| Cooling Performance | Heating Performance | |||||
|---|---|---|---|---|---|---|
| Water Temperature (°C) | Total Cooling Capacity (kW) | Sensible Cooling Capacity (kW) | Power Consumption (kW) | Water Temperature (°C) | Total Heating Capacity (kW) | Power Consumption (kW) |
| 1 | 41.38 | 33.93 | 4.92 | 1 | 30.08 | 8.42 |
| 5 | 39.00 | 31.98 | 5.92 | 5 | 37.77 | 8.47 |
| 10 | 37.10 | 30.42 | 6.72 | 10 | 43.92 | 8.52 |
| 15 | 35.20 | 28.86 | 7.52 | 15 | 51.00 | 8.60 |
| 20 | 33.30 | 27.31 | 8.32 | 20 | 59.01 | 8.71 |
| 25 | 31.30 | 25.67 | 9.24 | 25 | 68.15 | 8.85 |
| 30 | 29.30 | 24.03 | 10.30 | 30 | 77.29 | 8.99 |
| Stage | Period | Set Temperature (°C) | ||
|---|---|---|---|---|
| Heating | Cooling | Ventilation | ||
| Generative growth | 06/01–08/14 | 20 | 30 | 27 |
| Floral-initiation | 08/15–10/19 | 8 | 20 | 17 |
| Flowering | 10/20–12/31 | 18 | 25 | 22 |
| Fruit-bearing | 01/01–02/14 | 22 | 30 | 27 |
| Fruit-growing | 02/15–04/14 | 25 | 30 | 27 |
| Harvesting | 04/15–05/31 | 25 | 30 | 27 |
| Location | Average Temperature (°C) | Average Diurnal Temperature (°C) | Average Nocturnal Temperature (°C) |
|---|---|---|---|
| t1 | 29.5 | 33.3 | 25.0 |
| t2 | 29.4 | 33.1 | 25.1 |
| t3 | 29.8 | 33.5 | 25.4 |
| t4 | 29.6 | 33.3 | 25.2 |
| t5 | 29.3 | 33.1 | 24.8 |
| t6 | 30.2 | 34.2 | 25.5 |
| t7 | 30.0 | 33.6 | 25.7 |
| t8 | 29.3 | 32.5 | 25.5 |
| t9 | 29.2 | 32.6 | 25.2 |
| t10 | 29.6 | 33.3 | 25.4 |
| t11 | 31.1 | 35.5 | 25.9 |
| t12 | 30.5 | 34.4 | 25.9 |
| t13 | 29.3 | 32.5 | 25.7 |
| t14 | 30.5 | 34.8 | 25.5 |
| t15 | 30.4 | 34.8 | 25.2 |
| Average | 29.9 | 33.6 | 25.4 |
| Standard deviation | 0.57 | 0.92 | 0.30 |
| Growth Stage | External Weather Conditions | Periodic Energy Loads | ||||
|---|---|---|---|---|---|---|
| Average Air Temperature (°C) | Average Solar Radiation (kJ h−1) | Cooling Loads (MJ) | Heating Loads (MJ) | Total Energy Load (MJ) | Total Energy Load per Day (MJ day−1) | |
| Generative growth | 23.4 | 640 | 73,693 | 130 | 73,822 | 984 |
| Floral-initiation | 20.1 | 521 | 158,949 | 68 | 159,017 | 2409 |
| Flowering | 5.5 | 326 | 2351 | 231,717 | 234,068 | 3206 |
| Fruit-bearing | −2.1 | 326 | - | 248,483 | 248,483 | 5522 |
| Fruit-growing | 6.6 | 571 | 3390 | 254,554 | 257,944 | 4372 |
| Harvesting | 15.8 | 785 | 19,099 | 78,457 | 97,557 | 2076 |
| Total | - | - | 257,482 | 813,410 | 1,070,892 | 2934 |
| Stage | Maximum Cooling Loads | Maximum Heating Loads | ||||||
|---|---|---|---|---|---|---|---|---|
| Air Temperature (°C) | Solar Radiation (kJ h−1) | Cooling Loads (kJ h−1) | Occurrence | Air Temperature (°C) | Solar Radiation (kJ h−1) | Heating Loads (kJ h−1) | Occurrence | |
| Generative growth | 31.7 | 2360 | 353,853 | 30 July 2014 16:00 | 6.6 | 0 | 24,671 | 3 June 2014 05:00 |
| Floral-initiation | 29.9 | 2410 | 456,047 | 6 September 2014 15:00 | 4.4 | 0 | 20,763 | 17 October 2014 07:00 |
| Flowering | 13.9 | 2080 | 104,574 | 27 October 2014 13:00 | −7.7 | 0 | 343,879 | 22 December 2014 07:00 |
| Fruit-bearing | - | - | - | −9.5 | 0 | 409,285 | 8 January 2015 07:00 | |
| Fruit-growing | 18.6 | 2400 | 120,733 | 30 March 2015 14:00 | −6.7 | 0 | 402,428 | 5 March 2015 05:00 |
| Harvesting | 28.4 | 2870 | 281,886 | 27 May 2015 14:00 | 1.4 | 0 | 297,781 | 17 April 2015 05:00 |
| Year | Maximum Cooling Loads | Maximum Heating Loads | ||
|---|---|---|---|---|
| Cooling Loads (kJ h−1) | Occurrence | Cooling Loads (kJ h−1) | Occurrence | |
| 2014–2015 | 456,047 | 6 September 2014 15:00 | 409,285 | 8 January 2015 08:00 |
| 2015–2016 | 442,746 | 17 August 2015 15:00 | 467,526 | 24 January 2016 09:00 |
| 2016–2017 | 507,250 | 16 August 2016 15:00 | 471,388 | 18 February 2017 08:00 |
| 2017–2018 | 451,791 | 22 August 2017 15:00 | 463,709 | 27 January 2018 06:00 |
| 2018–2019 | 590,258 | 16 August 2018 15:00 | 455,211 | 17 February 2019 08:00 |
| Year | Boiler | Thermal Effluent—Heat Pump | Energy Saving Cost (KRW year−1) | ||
|---|---|---|---|---|---|
| Fuel Usage (L year−1) | Energy Cost (KRW year−1) | Electricity Usage (kWh year−1) | Energy Cost (KRW year−1) | ||
| 2010 | 20,225 | 21,534 | 211,814 | 8875 | 12,659 (58.79%) |
| 2011 | 19,883 | 25,507 | 150,627 | 6311 | 19,196 (75.26%) |
| 2012 | 21,391 | 29,793 | 211,755 | 8873 | 20,921 (70.22%) |
| 2013 | 21,147 | 29,075 | 210,668 | 8827 | 20,248 (69.64%) |
| 2014 | 18,940 | 24,610 | 205,459 | 8609 | 16,001 (65.02%) |
| Average | 20,317 | 26,104 | 198,065 | 8299 | 17,805 (68.21%) |
| Year | Tax-Free Oil Price (KRW L−1) | Temperature of the Sea Water (°C) | Temperature of the Thermal Effluent (°C) |
|---|---|---|---|
| 2010 | 1071 | 14.7 | 24.3 |
| 2011 | 1327 | 14.4 | 24.2 |
| 2012 | 1394 | 14.7 | 24.2 |
| 2013 | 1365 | 14.5 | 24.4 |
| 2014 | 1300 | 14.9 | 21.7 |
| Average | 1291 | 14.6 | 23.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.-y.; Lee, I.-b.; Lee, S.-n.; Yeo, U.-h.; Kim, J.-g.; Kim, R.-w.; Decano-Valentin, C. Dynamic Energy Exchange Modelling for a Plastic-Covered Multi-Span Greenhouse Utilizing a Thermal Effluent from Power Plant. Agronomy 2021, 11, 1461. https://doi.org/10.3390/agronomy11081461
Lee S-y, Lee I-b, Lee S-n, Yeo U-h, Kim J-g, Kim R-w, Decano-Valentin C. Dynamic Energy Exchange Modelling for a Plastic-Covered Multi-Span Greenhouse Utilizing a Thermal Effluent from Power Plant. Agronomy. 2021; 11(8):1461. https://doi.org/10.3390/agronomy11081461
Chicago/Turabian StyleLee, Sang-yeon, In-bok Lee, Seung-no Lee, Uk-hyeon Yeo, Jun-gyu Kim, Rack-woo Kim, and Cristina Decano-Valentin. 2021. "Dynamic Energy Exchange Modelling for a Plastic-Covered Multi-Span Greenhouse Utilizing a Thermal Effluent from Power Plant" Agronomy 11, no. 8: 1461. https://doi.org/10.3390/agronomy11081461
APA StyleLee, S.-y., Lee, I.-b., Lee, S.-n., Yeo, U.-h., Kim, J.-g., Kim, R.-w., & Decano-Valentin, C. (2021). Dynamic Energy Exchange Modelling for a Plastic-Covered Multi-Span Greenhouse Utilizing a Thermal Effluent from Power Plant. Agronomy, 11(8), 1461. https://doi.org/10.3390/agronomy11081461







