Next Article in Journal
Screening of Wheat Genotypes for Nitrogen Deficiency Tolerance Using Stress Screening Indices
Next Article in Special Issue
Vineyard Yield Estimation, Prediction, and Forecasting: A Systematic Literature Review
Previous Article in Journal
Paddy Rice Imagery Dataset for Panicle Segmentation
Previous Article in Special Issue
The Application of Multiple Linear Regression and Artificial Neural Network Models for Yield Prediction of Very Early Potato Cultivars before Harvest
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Agronomy
Volume 11
Issue 8
10.3390/agronomy11081543
agronomy-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effects of NP Fertilizer Placement Depth by Year Interaction on the Number of Maize (Zea mays L.) Plants after Emergence Using the Additive Main Effects and Multiplicative Interaction Model

by
Piotr Szulc
1,†,
Jan Bocianowski
2,*,†,
Kamila Nowosad
3,
Henryk Bujak
3,4,
Waldemar Zielewicz
5 and
Barbara Stachowiak
6
1
Department of Agronomy, Poznań University of Life Sciences, Dojazd 11, 60-632 Poznań, Poland
2
Department of Mathematical and Statistical Methods, Poznań University of Life Sciences, Wojska Polskiego 28, 60-637 Poznań, Poland
3
Department of Genetics, Plant Breeding and Seed Production, Wrocław University of Environmental and Life Sciences, Grunwaldzki 24A, 53-363 Wrocław, Poland
4
Research Center for Cultivar Testing (COBORU), Słupia Wielka 34, 63-022 Słupia Wielka, Poland
5
Department of Grassland and Natural Landscape Sciences, Poznań University of Life Sciences, Dojazd 11, 60-632 Poznań, Poland
6
Department of Food Technology of Plant Origin, Poznan University of Life Sciences, Wojska Polskiego 31, 60-624 Poznań, Poland
*
Author to whom correspondence should be addressed.
†
These authors contributed equally to this work.
Agronomy 2021, 11(8), 1543; https://doi.org/10.3390/agronomy11081543
Submission received: 24 June 2021 / Revised: 27 July 2021 / Accepted: 29 July 2021 / Published: 31 July 2021
(This article belongs to the Special Issue Crop Yield Prediction in Precision Agriculture)
Browse Figures
Review Reports Versions Notes

Abstract

:
Field experiments were carried out at the Department of Agronomy of the Poznań University of Life Sciences to determine the effect of the depth of NP fertilization placement in maize cultivation on the number of plants after emergence. The adopted assumptions were verified based on a six-year field experiment involving four depths of NP fertilizer application (A1—0 cm (broadcast), A2—5 cm (in rows), A3—10 cm (in rows), A4—15 cm (in rows)). The objective of this study was to assess NP fertilizer placement depth, in conjunction with the year, on the number of maize (Zea mays L.) plants after emergence using the additive main effects and multiplicative interaction model. The number of plants after emergence decreased with the depth of NP fertilization in the soil profile, confirming the high dependence of maize on phosphorus and nitrogen availability, as well as greater subsoil loosening during placement. The number of plants after emergence for the experimental NP fertilizer placement depths varied from 7.237 to 8.201 plant m−2 during six years, with an average of 7.687 plant m−2. The 61.51% of variation in the total number of plants after emergence was explained by years differences, 23.21% by differences between NP fertilizer placement depths and 4.68% by NP fertilizer placement depths by years interaction. NP fertilizer placement depth 10 cm (A3) was the most stable (ASV = 1.361) in terms of the number of plants after emergence among the studied NP fertilizer placement depths. Assuming that the maize kernels are placed in the soil at a depth of approx. 5 cm, the fertilizer during starter fertilization should be placed 5 cm to the side and below the kernel. Deeper NP fertilizer application in maize cultivation is not recommended. The condition for the use of agriculture progress, represented by localized fertilization, is the simultaneous recognition of the aspects of yielding physiology of new maize varieties and the assessment of their reaction to deeper seed placement during sowing.

1. Introduction

Recently, maize has grown in popularity and importance [1]. This is mainly due to its functional features. Nevertheless, they would not be sufficient to generalize cultivation without breeding participation, which would ensure access to varieties with suitable early maturation. Until recently, maize was mainly cultivated for silage from whole plants, while in recent years, the placement acreage was dominated by grain cultivation [2]. As part of the planned animal feeding systems, maize silage is a cheap source of starch and fiber, which is a good complement to grazing nutrition throughout the year [3]. This is due to maize cultivation for silage that has significantly increased the profitability of dairy production [3]. For the expansion of this species cultivation, it is important to develop a technology that would utilize sustainable technological and biological advances [4]. Domestic and foreign breeding programs led to the creation of many high-yielding and sufficiently early hybrid varieties that were well adapted to soil and climate conditions [5]. Unfortunately, the production potential of this species has not yet been fully exploited [6]. This is due to the lack of sufficient knowledge and skill resources, and frequent underestimation of the importance of punctuality and thoroughness in individual agriculture procedures [7]. Contrary to popular belief, maize, like other cereals, requires careful agriculture practices. Therefore, the primary aspect is to learn and implement a new technology of maize cultivation, and in particular to recognize the impact of the depth of starter (row) fertilization on the number of plants after emergence. This trait is very important in maize cultivation, because it determines the number of production ears per unit area, i.e., one of the elements of grain yield structure [8]. Previous studies clearly showed the beneficial effect of localized nitrogen and phosphorus fertilization on maize’s growth, development, and yielding [9,10]. This influence is particularly high in the early developmental stages, when the weather conditions in the initial growth period are often stressful for maize [11]. The positive effect of starter fertilization on maize in the initial growing season is also reflected in its yield [12].
Grain yields are significantly higher for the localized fertilizer placements performed concurrently with seed placement compared to traditional broadcast fertilization over the entire soil surface [13]. Grain moisture during harvest is a very important trait that determines the profitability of maize cultivation [14,15]. All studies carried out at the Department of Agronomy of the Poznań University of Life Sciences demonstrated that row application of fertilizers, compared to the traditional (broadcast) application, lowered water content in the grain [16]. Moreover, the row method of fertilizer placement allowed to reduce the level of mineral fertilization and extend maize placement period, especially by accelerating the placement, which is important in periodic soil moisture shortages in the early spring [17,18,19]. Therefore, the present results are of great applicatory importance and can improve the economy and organization of maize cultivation.
In published studies [20,21,22], the effectiveness of starter fertilization was usually assessed by placing the fertilizer at a distance of 5 cm to the side and below the seeds. Hence, a comparison of different depths of fertilizer placement in soil in relation to kernel and soil surface could suggest a deeper placement of the fertilizer in drought conditions that occur almost every year.
The number of plants after emergence is influenced by NP fertilizer placement depth (D), year (Y) and NP fertilizer placement depth-by-year (DY) interaction, but also many other climatic, biologic, and terrestrial factors.
Hence, phenotyping should be carried out in replicated, multi-year field trials to accurately assess this trait. DY interaction in the field trials of agricultural crops can be analyzed using the Additive Main effects and Multiplicative Interaction (AMMI) model [23]. The AMMI model determines NP fertilizer placement depths characterized by a high mean value of the observed trait and high adaptability to the desired area using the analysis of variance (ANOVA) and mega-year delineation. This model combines ANOVA with additive parameters and principal component analysis (PCA) with multiplicative parameters in a single analysis. As a result, the AMMI biplot simultaneously displays both the main and interaction effects for NP fertilizer placement depths and years, thereby enabling a single analysis of DY interaction. For this reason, AMMI is also known as interaction PCA (IPCA) [24,25]. The advantages of the AMMI model are that they use overall fitting, impose no restrictions on the multiplicative terms, and result in a least squares fit; within limits, any model may also be expected to fit data from which it was derived. The AMMI method is used for three main purposes. The first is that the model diagnoses other models; secondly, AMMI clarifies treatment × environment interaction and summarizes patterns and relationships of treatment and environment [23,26], and the third use is the accuracy of trait estimates [23,26]. The AMMI method is widely used in stability and adaptability analyses because it (i) provides an initial diagnosis of the model and is well-suited for data analysis with many environmental influences, (ii) allows greater unfolding of the treatment × environment interaction and summarizes the patterns and relationships between treatments [27,28,29,30,31,32,33].
Field studies at the Department of Agronomy of the Poznań University of Life Sciences were carried out to determine the effect of the depth of NP fertilization placement in maize cultivation on the number of plants after emergence. The objective of this study was to assess NP fertilizer placement depths by years interaction on the number of maize (Zea mays L.) plants after emergence using the additive main effects and multiplicative interaction model.

2. Materials and Methods

2.1. Soil and Climate Information

Maize placement was performed using a precision seeder, with a built-in granular fertilizer applicator (Monosem). Gross plot size was 24.5 m2 (length—8.75 m, width—2.8 m), while the plot size used to observe the number of plants after emergence was 12.25 m2. In the 3-leaf stage (BBCH 13), the plants in each row of the plot were carefully counted, and subsequently their sum was divided by its size, thus establishing the number of plants after emergence. The structure of the experimental field morphology was characteristic of the bottom moraine of the North Polish (Baltic) glaciation, the Poznań stadium. Sandy-loam formations constituted parental materials of the soil. Terrain configuration was slightly diversified, and the dominant area was flat and slightly undulating. Typologically, the soils in the test field were of the black-earth type, the cambic black-earth subtype that belonged to the black-earth order. These soils should be classified as Phaeozemes according to the international WRB classification [34], and as Mollisols according to the US Soil Taxonomy [35]. Humic horizon was homogeneous on the entire experimental field. The percentage content of the sand fraction of the Ap level showed little differentiation and ranged from 77–79%, while the average values for individual fertilization objects were almost identical for the depths of 0–0.15 m and 0.15–0.30 m. Dust content in these levels was also not very diverse and was within 17–18% for both depths. Clay content, relatively low, fluctuated in the top and deeper soil layers in a narrow range of 4–5%. Granulometric composition of the soils from the experimental field in the arable-humic horizons (Ap) was even in all the tested fertilization objects in this experimental field. All analyzed samples from the experimental objects belonged to one grain size group, i.e., loamy sands [36]. The experimental field was valuated as class IIIb. The black earth type are soils with direct impact of groundwater or heavy rainfall on the lower and partly central portions of the soil profile. Precipitation and water management dominate in the surface horizons and it can be somewhat modified through changes of water properties in the deeper parts of the soil profile (0–0.30 m, genetic horizon Ap). Soil abundance in nutrients and soil pH before establishing the experiment in maize growing seasons are presented in Table 1.
Air temperature and rainfall in the maize growing seasons are presented in Table 2. Definitely the warmest and driest growing season was recorded in 2018. In turn, the largest sum of precipitation in the initial period of maize growth was recorded in 2016. The lowest average daily temperature at the level of 12.8 °C was recorded in 2017. Generally, it should be said that thermal and rainfall in the initial maize vegetation varied considerably in individual growing seasons. The effect of temperature and humidity factors is best described in a comprehensive manner by the hydrothermal water supply index [K] according to Szulc et al. [37].
K = 10 · monthly precipitation total [mm]
Number of days · mean daily air temperature in a given month [°C]
Interpretation of the hydrothermal index according to Sielianinow: K > 1.5—excessive moisture for most plants, 1 < K < 1.5—sufficient moisture for most plants, 0.5 < K < 1.0—insufficient moisture for most plants, K < 0.5—drought.

2.2. Field Experiment

Field trial was carried out at the Department of Agronomy of the Poznań University of Life Sciences on the fields of the Gorzyń Experimental and Educational Unit, branch in Złotniki (52°26′ N; 16°45′ E), in the years 2015–2020. The experiments were carried out for six years as single-factor experiments in four field replications. The following variable was tested: A—NP fertilizer placement depth (A1—0 cm (broadcast), A2—5 cm (in rows), A3—10 cm (in rows), A4—15 cm (in rows)). The same level of mineral fertilization (100 kg N ha−1, 70 kg P2O5 ha−1 and 130 kg K2O ha−1) was applied in all experimental objects. Fertilization was balanced against phosphorus, which was applied at the whole required concentration in the form of ammonium phosphate (18% N, 46% P2O5). N and K fertilization was performed before maize placement using urea (46% N) and potassium salt (60%). Fertilizer coulters (on objects with starter fertilization) were set 5 cm aside from the seeds. The depth of NP fertilization application was regulated on the seeder frame (Figure 1). The maize variety P7905 was used in the experiment. Is this a commercial hybrid.

2.3. Statistical Analysis

Two-way analysis of variance was applied to determine the magnitude of the main effects of NP fertilizer placement depth and years as well as NP fertilizer placement depth by years interaction on the number of plants after emergence. The main effects of NP fertilizer placement depths and years were fixed; however, the effect of NP fertilizer placement depth by year interaction was random. In parallel, least-squares means were calculated for the AMMI model. The model first fitted the additive main effects of NP fertilizer placement depths (D) and years (Y), followed by the multiplicative effects of DY interaction by PCA. The AMMI model [24,38] was defined by the following equation:
y d e = μ + α d + β e + ∑ n = 1 N λ n γ d n δ e n + Q d e ,
where yde is the mean of NP fertilizer placement depth d in the year e, μ is the grand mean of the number of plants after emergence, αd is the mean deviation of NP fertilizer placement depth, βe is the year mean deviation, N is the number of PCA axes retained in the adjusted model, λn is the eigenvalue of the PCA axis n, γdn is NP fertilizer placement depth score for the PCA axis n, δen is the eigenvector score for the PCA axis n, and Qde is the residual, which includes AMMI noise and pooled experimental error. The expected distribution of Qde was found to be normal. The AMMI stability values (ASVs) were used to compare the stability of NP fertilizer placement depths as described by [39]:
A S V = [ S S I P C A 1 S S I P C A 2 ( I P C A 1 ) ] 2 + ( I P C A 2 ) 2 ,
where SS is the sum of squares, IPCA1 and IPCA2 are the first and the second interaction principal component axes, respectively; and the IPCA1 and IPCA2 scores were the NP fertilizer placement depth scores in the AMMI model. ASV is the distance from zero in a two-dimensional scatterplot of IPCA1 scores against IPCA2 scores. Since the IPCA1 score contributes more to the NP fertilizer placement depth by year sum of squares, it has to be weighted by the proportional difference between IPCA1 and IPCA2 scores to compensate for the difference in contribution. The distance from zero is then determined using Pythagoras’s theorem. The greater the IPCA score, either negative or positive, the more specifically adapted the NP fertilizer placement depth is to certain years. The higher the IPCA score (which can be negative or positive), the more accurately selected NP fertilizer placement depth in an individual year. Lower ASV score indicates more stable NP fertilizer placement depth across the year [29,31,33,38,40]. The level of significance in PCA analysis was tested with the F test.
The level of significance of PCA analysis was tested using the F test according to Gollob [41]. In the biplot, which is an efficient representation of the AMMI model, DY interactions are plotted on the vertical axis (IPCA 1), while means of NP fertilizer placement depth and year are plotted on the horizontal axis. The applied analytical procedures and result interpretation were based on the protocol of Gauch and Zobel [24]. All statistical analyses were conducted using the GenStat software package (v. 18) [42].

3. Results

Three sources of variation (NP fertilizer placement depth, year and DY interaction), were found to be significant for the number of plants after emergence. In ANOVA, the sum of squares for the main effect of the year represented 61.51% of the total variation in the number of plants after emergence, and this factor had the highest effect on the number of plants after emergence. The differences between NP fertilizer placement depths explained 23.21% of the total variation in the number of plants after emergence, while the effects of the DY interaction explained 4.68% of the variation (Table 3). The values of the two principal components were also statistically significant and jointly accounted for 91.87% of the whole effect on the variation in the number of plants after emergence. The first principal component (IPCA 1) explained 80.21% of the variation caused by interaction, while the second component (IPCA 2) accounted for 11.66% of the variation in the number of plants after emergence (Figure 2). Among the tested NP fertilizer placement depths, the A4 had the highest IPCA 1 value of 0.882, while the lowest value of IPCA 1 was −0.251 for A1. The values of IPCA 2 ranged from −0.147 (for A1) to 0.153 (for A3) (Figure 2, Table 4). Among the years of study, the 2018 had the highest IPCA 1 value of 0.231, while the lowest value of IPCA 1 was −0.360 in 2016. The values of IPCA 2 ranged from −0.249 (in 2019) to 0.125 (in 2018) (Figure 2, Table 4).
The number of plants after emergence for the tested NP fertilizer placement depths varied from 7.237 plant m−2 (for A4 in 2017) to 8.201 plant m−2 (for A1 in 2015) over the six years, with an average of 7.687 plant m−2 (Table 4). NP fertilizer placement depth A1 (0 cm—broadcast) had the highest average number of plants after emergence (7.828 plant m−2), while NP fertilizer placement depth A4 (15 cm in rows) resulted in the lowest number of plants after emergence (7.507 plants m−2). In addition, the average number of plants after emergence per year varied from 7.375 in 2017 to 8.051 plant m−2 in 2015 (Table 4). Variation of the number of plants after emergence, measured coefficient of variation—CV, was equal to 3.28%, across all four NP fertilizer placement depth and six years of study (Table 3). The highest variation of the number of plants after emergence was observed for A1 (CV = 3.17%), while the lowest for A3 (2.78%) (Table 4). Values of coefficient of variation for particular years of study varied from 1.34% (in 2018) to 3.03 (in 2016) (Table 4).
Stability of the analyzed NP fertilizer placement depths during six years with respect to the number of plants after emergence was visualized as a biplot (Figure 3). NP fertilizer placement depth A1 interacted positively with the year 2015, but negatively with the years 2017 and 2018 (Figure 2), while NP fertilizer placement depth A2 interacted positively with the years 2016 and 2020, but negatively with 2019. NP fertilizer placement depth A3 interacted positively with the years 2017 and 2018, but negatively with the year 2015, while NP fertilizer placement depth A4 interacted positively with the year 2019, but negatively with 2020 (Figure 2). The analysis indicated that some NP fertilizer placement depths exhibited a high level of adaptation; however, most of them showed a specific adaptation. The ASVs varied in the number of plants after emergence between four NP fertilizer placement depths tested (Table 4). NP fertilizer placement depths A3 and A2 with the ASV of 1.361 and 1.615, respectively, were the most stable, while NP fertilizer placement depths A4 and A1 with the ASV amounting to 1.999 and 1.745, respectively, were the least stable (Table 4).

4. Discussion

The number of plants after emergence per unit area is one of the most important agriculture factors in the cultivation of this plant for grain [43]. According to current recommendations, the number of plants after emergence in grain cultivation ranges from 8 to 10 pcs. m−2. In the present study, the number of plants after emergence decreased along with the increase of NP fertilizer placement depth in each of the six years of research. In turn, Szulc and Kruczek [44] showed no significant effect of the method of placement phosphorus and phosphorus-nitrogen fertilizers on plant emergence. Nevertheless, many authors have indicated that too high a concentration of the component in the immediate vicinity of seeds can cause disturbances in germinating seeds [10,12,45,46]. However, the latter authors have not provided the maximum nutrient concentration that can be used in the immediate vicinity of germinating seeds. The confirmation obtained in these studies [45] that even the maximum concentration of 130 kg P2O5 ha−1, applied in the immediate vicinity of the seeds, did not affect maize emergence, seemed to be a positive result. Consistent reproducibility of the lack of influence of fertilization of the on maize emergence in the following days of observation indicated that relationship [45]. To obtain more general conclusions, these authors standardized the intermediate values of subsequent emergence days to the average period of emergence, uniform for individual years. Logarithmic function most optimally reflected the emergence of maize, and its course for the tested fertilization methods was almost identical. Hence, the result obtained in these studies confirmed that the fertilization method did not differentiate maize by the number of plants after emergence. One can ask why the application of a lower phosphorus concentration of 70 kg P2O5 ha−1 (30.8 kg P ha−1) in the immediate vicinity of the seeds in the current study resulted in a reduction in plants’ quantity after emergence and before maize harvest along with an increase in depth fertilizer application. The increase in fertilizer placement depth using a fertilizer coulter most likely worked in the same manner as the use of a subsoiler (Figure 4 and Figure 5). Most probably, the subsoil was too loosened and water penetration was interrupted. Therefore, placing the seeds in such soil did not occur at the planned depth (4–5 cm), but deeper. This was confirmed by maize plant losses during the vegetation period that were in fact the lowest in objects with deep (15 cm) fertilizer placement during seed placement.
Other authors argued [47] that deeper sowing should be a common practice in the development of sustainable agriculture in arid and semi-arid areas of our globe. Nevertheless, most commercial maize varieties are not adapted to deeper sowing (>5 cm), which results in a disturbance of emergence dynamics [47] and reduction of the planned plant density. Therefore, scientists determined a recommended sowing depth, which is dependent on the type of soil, texture, pH and moisture conditions that vary for each crop species. However, arable fields are not uniform, therefore deeper sowing becomes a difficult task to solve. Deeper sowing is an alternative agricultural practice that has a strong influence on maize germination rate and consequently the final yield [48]. Hence, research should be focused on the selection of tolerant maize varieties in terms of increasing depth of their sowing. Strong hydrotropic reactions of new varieties should be the highest for its implementation in sustainable agriculture in times of the impending drought caused by the climate crisis [49]. This feature varies greatly from strong (>40°) to weak (<40°), which confirms the large genetic diversity among commercial maize varieties [50]. Therefore, the selection should use the genetic diversity of native, local maize varieties, which show a strong hydrotropic response and a greater mesocotyl elongation coefficient in deeper seed placement in soil during sowing [51].
In addition to the most important DY interactions, the AMMI biplot allows to visualize the major effects of NP fertilizer placement depths and individual years of cultivation. The present study found that the largest difference in the number of plants after emergence between A1 and A4 was obtained in 2016, which was characterized by the highest sum of atmospheric precipitation (218.4 mm) in the initial period of maize vegetation. On the other hand, the lowest difference between A1 and A4 in the number of plants after emergence occurred in 2018, which was characterized by the highest average daily air temperature (16.1 °C). The AMMI model has been extensively used in studies on numerous species [52,53,54,55,56,57,58,59,60,61,62,63,64]. The AMMI is more appropriate in the initial statistical analysis of yield trials because it provides an analytical tool to diagnose other models, such as subcases, when these are better for particular data sets and also have a good chance of predicting new depths and years, this is a real advance [65]. To our knowledge, this is the first report about using the additive main effects and multiplicative interaction model to analysis of NP fertilizer placement depth by year interaction on the number of maize (Zea mays L.) plants after emergence. The results obtained from AMMI analyses are very important in terms of the development and recommendation of most optimal NP fertilizer placement depths concerning the productivity in a specific year. The AMMI model is a useful tool for diagnosing DY interaction patterns and improving the accuracy of reaction assessments. It allows to group NP fertilizer placement depths based on the similarity of response features and determine potential trends over the years. The proposed strategy could extract more information from DY interactions, thereby helping researchers to determine specific NP fertilizer placement depths, which would contribute to competitive yields in different years.
The AMMI model does not provide for a quantitative stability measure and such a measure is essential to quantify and rank genotypes in terms of observed trait stability [66,67]. Therefore, the AMMI stability value (ASV) was proposed by Purchase et al. [39] to quantify and rank objects according to their observed trait stability. The AMMI stability value (ASV) identified NP fertilizer placement depth A3 (10 cm in rows) as a more stable depth, which also had high mean performance. Such an outcome could be regularly employed in the future to delineate predictive, more rigorous recommendation strategies, as well as to help define stability concepts for recommendations for maize.

5. Conclusions

The number of plants after emergence decreased with the depth of NP fertilization in the soil profile. Most probably, the main reason for this relationship was too deep placement, caused by excessive loosening of the subsoil during placement. NP fertilizer placement depths of 10 cm in rows (A3) and 5 cm in rows (A2) were found to be the most stable, while 15 cm in rows (A4) and 0 cm in broadcast (A1) were the least stable in terms of the number of plants after emergence. Based on the experiment, it seems reasonable to place the NP fertilizer granules at a maximum depth of 10 cm. A deeper application of fertilizer >10 cm can only be advisable with thin coulters that do not disturb the soil structure under the seed. Maize varieties for deeper application of mineral fertilizer in the soil profile >10 cm (row fertilization) should be more tolerant to deeper seed placement during sowing. AMMI analysis proved to be effective for determining DY interactions with respect to the number of plants after emergence. In order to most efficiently utilize the biological progress, represented by new maize varieties, it is very important to assess the correct depth of mineral fertilizer application and develop plant nutrition on this basis.

Author Contributions

Conceptualization, J.B.; methodology, J.B., P.S., K.N. and H.B.; software, J.B.; validation, J.B., P.S. and K.N.; formal analysis, J.B. and K.N.; investigation, J.B., P.S., K.N. and H.B.; resources, J.B. and P.S.; data curation, P.S.; writing—original draft preparation, J.B. and P.S.; writing—review and editing, J.B., P.S., K.N., W.Z. and B.S.; visualization, J.B. and K.N.; supervision, J.B.; project administration, J.B.; funding acquisition, H.B. and B.S. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are available on request from the corresponding authors.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Amnuaylojaroen, T.; Chanvichit, P.; Janta, R.; Surapipith, V. Projection of rice and maize productions in Northern Thailand under climate change scenario RCP8.5. Agriculture 2021, 11, 23. [Google Scholar] [CrossRef]
  2. Neumann, K.; Verburg, P.H.; Stehfest, E.; Mueller, C. The yield gap of global grain production: A spatial analysis. Agric. Syst. 2010, 103, 316–326. [Google Scholar] [CrossRef]
  3. Kolver, E.S.; Roche, J.R.; Miller, D.; Densley, R. Maize silage for dairy cows. Proc. N. Z. Assoc. 2001, 63, 195–201. [Google Scholar] [CrossRef]
  4. Paponov, I.A.; Sambo, P.; Erley, G.S.; Presterl, T.; Geiger, H.H.; Engels, C. Grain yield and kernel weight of two maize genotypes differing in nitrogen use efficiency at various levels on nitrogen and carbohydrate availability during flowering and grain filling. Plant Soil 2005, 272, 111–123. [Google Scholar] [CrossRef]
  5. Adamczyk, J.; Rogacki, J.; Cygert, H. The progress in maize breeding in Poland. Acta Sci. Pol. Agric. 2010, 9, 85–91. (In Polish) [Google Scholar]
  6. Baohua, L.; Xinping, C.; Qingfeng, M.; Haishun, Y.; Justin, V.W. Estimating maize yield potential and yield gap with agro-climatic zones in China-Distinguish irrigated and rainfed conditions. Agric. For. Meteorol. 2017, 239, 108–117. [Google Scholar] [CrossRef]
  7. Bänziger, M.; Edmeades, G.O.; Lafitte, H.R. Physiological mechanisms contributing to the increased N stress tolerance of tropical maize selected for drought tolerance. Field Crops Res. 2002, 75, 223–233. [Google Scholar] [CrossRef]
  8. Milander, J.J. Maize Yield and Components as Influenced by Environment and Agronomic Management. Master’s Thesis, University of Nebraska, Lincoln, NE, USA, 2015; p. 86. [Google Scholar]
  9. Szulc, P.; Barłóg, P.; Ambroży-Deręgowska, K.; Mejza, I.; Kobus-Cisowska, J. In-soil application of NP mineral fertilizer as a method of improving nitrogen yielding efficiency. Agronomy 2020, 10, 1488. [Google Scholar] [CrossRef]
  10. Szulc, P.; Barłóg, P.; Ambroży-Deręgowska, K.; Mejza, I.; Kobus-Cisowska, J.; Ligaj, M. Effect of phosphorus application technique on effectiveness indices of its use in maize cultivation. Plant Soil Environ. 2020, 66, 500–505. [Google Scholar] [CrossRef]
  11. Araus, J.L.; Slafer, G.A.; Royo, C.; Serret, M.D. Breeding for yield potential and stress adaptation in cereals. CRC Crit. Rev. Plant Sci. 2008, 27, 377–412. [Google Scholar] [CrossRef]
  12. Balawejder, M.; Szostek, M.; Gorzelany, J.; Antos, P.; Witek, G.; Małtok, N. A study on the potential fertilization effects of microgranule fertilizer based on the protein and calcined bones in maize cultivation. Sustainability 2020, 12, 1343. [Google Scholar] [CrossRef] [Green Version]
  13. Nkebiwe, P.M.; Weinmann, M.; Bar-Tal, A.; Müller, T. Fertilizer placement to improve crop nutrient acquisition and yield: A review and meta-analysis. Field Crops Res. 2016, 196, 389–401. [Google Scholar] [CrossRef]
  14. Zhang, H.L.; Ma, Q.; Fan, L.F.; Zhao, P.F.; Wang, J.X.; Zhang, X.D.; Zhu, D.H.; Huang, L.; Zhao, D.J.; Wang, Z.Y. Nondestructive in situ measurement method for kernel moisture content in corn ear. Sensor 2016, 16, 2196. [Google Scholar] [CrossRef] [Green Version]
  15. Weinberg, Z.G.; Yan, Y.; Chen, Y.; Finkelman, S.; Ashbell, G.; Navarro, S. The effect of moisture level on high-moisture maize (Zea mays L.) under hermetic storage conditions—In vitro studies. J. Stored Prod. Res. 2008, 44, 136–144. [Google Scholar] [CrossRef]
  16. Szulc, P. Starter fertilization of maize as a method to improve the efficiency of nutrient application. Pol. J. Natur. Sci. 2017, 32, 615–636. [Google Scholar]
  17. Ao, S.; Russelle, M.P.; Feyereisen, G.W.; Varga, T.; Coulter, J.A. Maize hybrid response to sustained moderate drought stress reveals clues for improved management. Agronomy 2020, 10, 1374. [Google Scholar] [CrossRef]
  18. Kruczek, A. Response of maize varieties to the method of fertilization with a two-component NP fertilizer depending on the date of sowing. Pamiętnik Puławski 2005, 140, 117–127. (In Polish) [Google Scholar]
  19. Jagła, M.; Szulc, P.; Ambroży-Deręgowska, K.; Mejza, I.; Kobus-Cisowska, J. Yielding of two types of maize cultivars in relation to selected agrotechnical factors. Plant Soil Environ. 2019, 65, 416–423. [Google Scholar] [CrossRef] [Green Version]
  20. Mandić, V.; Dordević, S.; Bikelić, Z.; Krnjaja, V.; Pantelić, V.; Simić, A.; Dragićević, V. Agronomic responses of soybean genotypes to starter nitrogen fertilizer rate. Agronomy 2020, 10, 535. [Google Scholar] [CrossRef] [Green Version]
  21. Rehm, G.W.; Lamb, J.A. Corn Response to Fluid Fertilizers Placed Near the Seed at Planting. Nutr. Manag. Soil Plant Anal. 2009, 73, 1427–1434. [Google Scholar] [CrossRef]
  22. Grzebisz, W.; Szczepaniak, W.; Bocianowski, J. Potassium fertilization as a driver of sustainable management of nitrogen in potato (Solanum tuberosum L.). Field Crops Res. 2020, 254, 107824. [Google Scholar] [CrossRef]
  23. Zobel, R.W.; Wright, M.J.; Gauch, H.G. Statistical analysis of yield trial. Agron. J. 1988, 80, 388–393. [Google Scholar] [CrossRef]
  24. Gauch, H.G.; Zobel, R.W. Imputing missing yield trial data. Theor. Appl. Genet. 1990, 79, 753–761. [Google Scholar] [CrossRef] [PubMed]
  25. Bocianowski, J.; Szulc, P.; Nowosad, K. Soil tillage methods by years interaction for dry matter of plant yield of maize (Zea mays L.) using additive main effects and multiplicative interaction model. J. Integr. Agric. 2018, 17, 2836–2839. [Google Scholar] [CrossRef] [Green Version]
  26. Crossa, J.; Gauch, H.G.; Zobel, R.W. Additive main effects and multiplicative interactions analysis of two international maize cultivar trials. Crop Sci. 1990, 30, 493–500. [Google Scholar] [CrossRef]
  27. Bocianowski, J.; Nowosad, K.; Szulc, P. Soil tillage methods by years interaction for harvest index of maize (Zea mays L.) using additive main effects and multiplicative interaction model. Acta Agric. Scand. B Soil Plant Sci. 2019, 69, 75–81. [Google Scholar] [CrossRef]
  28. Fotso, A.K.; Hanna, R.; Kulakow, P.; Parkes, E.; Iluebbey, P.; Ngome, F.A.; Suh, C.; Massussi, J.; Choutnji, I.; Wirnkar, V.L. AMMI analysis of cassava response to contrasting environments: Case study of genotype by environment effect on pests and diseases, root yield, and carotenoids content in Cameroon. Euphytica 2018, 214, 155. [Google Scholar] [CrossRef]
  29. Bocianowski, J.; Nowosad, K.; Tomkowiak, A. Genotype—Environment interaction for seed yield of maize hybrids and lines using the AMMI model. Maydica 2019, 64, M13. [Google Scholar]
  30. Padarewski, J.; Rodrigues, P.C. The usefulness of EM-AMMI to study the influence of missing data pattern and application to Polish post-registration winter wheat data. Aust. J. Crop Sci. 2014, 8, 640–645. [Google Scholar]
  31. Bocianowski, J.; Liersch, A.; Nowosad, K. Genotype by environment interaction for alkenyl glucosinolates content in winter oilseed rape (Brassica napus L.) using additive main effects and multiplicative interaction model. Curr. Plant Biol. 2020, 21, 100137. [Google Scholar] [CrossRef]
  32. Hassani, M.; Heidari, B.; Dadkhodaie, A.; Stevanato, P. Genotype by environment interaction components underlying variations in root, sugar and white sugar yield in sugar beet (Beta vulgaris L). Euphytica 2018, 214, 79. [Google Scholar] [CrossRef]
  33. Bocianowski, J.; Tratwal, A.; Nowosad, K. Genotype by environment interaction for main winter triticale varieties characteristics at two levels of technology using additive main effects and multiplicative interaction model. Euphytica 2021, 217, 26. [Google Scholar] [CrossRef]
  34. World Reference Base for Soil Resources; IUSS Working Group WRB, World Soil Res. Rep. 103; FAO: Rome, Italy, 2006.
  35. Soil Taxonomy. A Basic System of Soil Classification for Making and Interpreting Soil Surveys; Soil Survey Staff USDA-NRCS. Agri. Handb. 436; U.S. Gov. Printing Office: Washington, DC, USA, 1999. [Google Scholar]
  36. Dubas, A.; Drzymała, S.; Mocek, A.; Owczarzak, W.; Szulc, P. Impact of Reduced Tillage in Long-Term Maize Monoculture (Zea mays L.) on Soil Properties and Plant Vegetation and Yielding; University Publisher Poznań University of Life Sciences: Poznań, Poland, 2012; 74p; ISBN 978-83-7160-662-5. (In Polish) [Google Scholar]
  37. Szulc, P.; Jagła, M.; Nowosad, K.; Bocianowski, J.; Olejarski, P. Path analysis in assessment of cause and effect dependencies of yield structure components in maize cultivars differing in genetic profiles. Fresenius Environ. Bull. 2017, 26, 7309–7318. [Google Scholar]
  38. Nowosad, K.; Liersch, A.; Popławska, W.; Bocianowski, J. Genotype by environment interaction for seed yield in rapeseed (Brassica napus L.) using additive main effects and multiplicative interaction model. Euphytica 2016, 208, 187–194. [Google Scholar] [CrossRef]
  39. Purchase, J.L.; Hatting, H.; van Deventer, C.S. Genotype × environment interaction of winter wheat (Triticum aestivum L.) in South Africa: II. Stability analysis of yield performance. S. Afr. J. Plant Soil 2000, 17, 101–107. [Google Scholar] [CrossRef]
  40. Nowosad, K.; Liersch, A.; Poplawska, W.; Bocianowski, J. Genotype by environment interaction for oil content in winter oilseed rape (Brassica napus L.) using additive main effects and multiplicative interaction model. Indian J. Genet. Pl. Br. 2017, 77, 293–297. [Google Scholar] [CrossRef] [Green Version]
  41. Gollob, H.F. A statistical model which combines features of factor analytic and analysis of variance techniques. Psychometrika 1968, 33, 73–155. [Google Scholar] [CrossRef]
  42. Genstat, 18th ed.; v.18.2.0.18409; VSN International Ltd.: Hemel Hempstead, UK, 2016.
  43. Bocianowski, J.; Szulc, P.; Nowosad, K.; Rybus-Zając, M. Relationships between selected traits of maize cultivars differing in leaf blade senescence rates. Polish J. Agron. 2016, 26, 9–14. [Google Scholar]
  44. Szulc, P.; Kruczek, A. Change of the morphological features of maize in dependence on doses of phosphorus and methods of their usage. Roczniki AR w Poznaniu 2005, 64, 173–183. (In Polish) [Google Scholar]
  45. Ge, Z.; Rubio, G.; Lynch, J.P. The importance of root gravitropism for inter-root competition and phosphorus acquisition efficiency: Results from a geometric simulation model. Plant Soil 2000, 218, 159–171. [Google Scholar] [CrossRef] [PubMed]
  46. Kruczek, A.; Szulc, P. Effect of fertilization method on the uptake and accumulation of mineral components in the initial period of maize development. Int. Agrophys. 2006, 20, 11–22. [Google Scholar]
  47. Hardegree, S.P.; Jones, T.A.; Roundy, B.A.; Shaw, N.L.; Monaco, T.A. Assessment of range planting as a conservation practice. Rangel. Ecol. Manag. 2016, 69, 237–247. [Google Scholar] [CrossRef]
  48. Sáenz Rodrígueaz, M.N.; Cassab, G.I. Primary root and mesocotyl elongation in maize seedlings: Two organs with antagonistic growth below the soil surface. Plants 2021, 10, 1274. [Google Scholar] [CrossRef] [PubMed]
  49. Zhao, G.; Wang, J.H. Effect of auxin on mesocotyl elongation of dark-grown maize under different seeding depths. Russ. J. Plant Physiol. 2010, 57, 79–86. [Google Scholar] [CrossRef]
  50. Eapen, D.; Martinez, J.J.; Hernández, O.; Flores, L.; Nieto-Sotelo, J.; Cassab, G.I. Synergy between root hydrotropic response and root biomass in maize (Zea mays L.) enhances drought avoidance. Plant. Sci. 2017, 365, 87–99. [Google Scholar] [CrossRef]
  51. Vanhees, D.J.; Loades, K.W.; Bengough, A.G.; Mooney, S.J.; Lynch, J. Root anatomical traits contribute to deeper rooting of maize under compacted field conditions. J. Exp. Bot. 2020, 14, 4243–4257. [Google Scholar] [CrossRef]
  52. Bocianowski, J.; Radkowski, A.; Nowosad, K.; Radkowska, I.; Zieliński, A. The impact of genotype-by-environment interaction on the dry matter yield and chemical composition in timothy (Phleum pratense L.) examined by using the additive main effects and multiplicative interaction model. Grass Forage Sci. 2021. [Google Scholar] [CrossRef]
  53. Hristov, N.; Mladenov, N.; Djuric, V.; Kondic-Spika, A.; Marjanovic-Jeromela, A.; Simic, D. Genotype by environment interactions in wheat quality breeding programs in southeast Europe. Euphytica 2010, 174, 315–324. [Google Scholar] [CrossRef]
  54. Bocianowski, J.; Księżak, J.; Nowosad, K. Genotype by environment interaction for seeds yield in pea (Pisum sativum L.) using additive main effects and multiplicative interaction model. Euphytica 2019, 215, 191. [Google Scholar] [CrossRef] [Green Version]
  55. Berti, M.; Fischer, S.; Wilckens, R.; Hevia, F.; Johnson, B. Adaptation and genotype × environment interaction of flaxseed (Linum usitatissimum L.) genotypes in South Central Chile. Chil. J. Agric. Res. 2010, 70, 345–356. [Google Scholar]
  56. Nowosad, K.; Tratwal, A.; Bocianowski, J. Genotype by environment interaction for grain yield in spring barley using additive main effects and multiplicative interaction model. Cereal Res. Commun. 2018, 46, 729–738. [Google Scholar] [CrossRef]
  57. Abakemal, D.; Shimelis, H.; Derera, J. Genotype-by-environment interaction and yield stability of quality protein maize hybrids developed from tropical-highland adapted inbred lines. Euphytica 2016, 209, 757–769. [Google Scholar] [CrossRef]
  58. Bocianowski, J.; Niemann, J.; Nowosad, K. Genotype-by-environment interaction for seed quality traits in interspecific cross-derived Brassica lines using additive main effects and multiplicative interaction model. Euphytica 2019, 215, 7. [Google Scholar] [CrossRef] [Green Version]
  59. Edwards, J.W. Genotype×environment interaction for plant density response in maize (Zea mays L.). Crop Sci. 2016, 56, 1493–1505. [Google Scholar] [CrossRef] [Green Version]
  60. Bocianowski, J.; Warzecha, T.; Nowosad, K.; Bathelt, R. Genotype by environment interaction using AMMI model and estimation of additive and epistasis gene effects for 1000-kernel weight in spring barley (Hordeum vulgare L.). J. Appl. Genet. 2019, 60, 127–135. [Google Scholar] [CrossRef] [Green Version]
  61. Rea, R.; De Sousa-Vieira, O.; Díaz, A.; Ramón, M.; Briceño, R.; George, J.; Niño, M.; Balzano-Nogueira, L. Genotype-environment interaction, megaenvironments and two-table coupling methods for sugarcane yield studies in Venezuela. Sugar Tech. 2016, 18, 354–364. [Google Scholar] [CrossRef]
  62. Bocianowski, J.; Nowosad, K.; Liersch, A.; Popławska, W.; Łącka, A. Genotype-by-environment interaction for seed glucosinolate content in winter oilseed rape (Brassica napus L.) using an additive main effects and multiplicative interaction model. Biom. Lett. 2018, 55, 85–96. [Google Scholar] [CrossRef] [Green Version]
  63. Bocianowski, J.; Tratwal, A.; Nowosad, K. Genotype by environment interaction for area under the disease-progress curve (AUDPC) value in spring barley using additive main effects and multiplicative interaction model. Australas. Plant Pathol. 2020, 49, 525–529. [Google Scholar] [CrossRef]
  64. Liersch, A.; Bocianowski, J.; Nowosad, K.; Spasibionek, S.; Szała, L.; Cegielska-Taras, T.; Sosnowska, K.; Matuszczak, M.; Mikołajczyk, M.; Bartkowiak-Broda, I. Effect of Genotype × Environment Interaction for Seed Traits in Winter Oilseed Rape (Brassica napus L.). Agriculture 2020, 10, 607. [Google Scholar] [CrossRef]
  65. Gauch, H.G. Model selection and validation for yield trials with interaction. Biometrics 1988, 44, 705–715. [Google Scholar] [CrossRef]
  66. Gauch, H.G. Statistical Analysis of Regional Yield Trials: AMMI Analysis of Factorial Designs; Elsevier: Amsterdam, The Netherlands, 1992. [Google Scholar]
  67. Gauch, H.G.; Zobel, R.W. AMMI analyses of yield trials. In Genotype by Environment Interaction; Kang, M.S., Gauch, H.G., Eds.; CRC: Boca Raton, FL, USA, 1996; pp. 85–122. [Google Scholar]
Agronomy 11 01543 g001 550
Figure 1. Setting the depth of NP fertilizer placement (photo taken by Szulc P.).
Figure 1. Setting the depth of NP fertilizer placement (photo taken by Szulc P.).
Agronomy 11 01543 g001
Agronomy 11 01543 g002 550
Figure 2. Biplot for NP fertilizer placement depth by year interaction of the number of plants after emergence for four NP fertilizer placement depths of maize (Zea mays L.) during six years, showing the effects of primary and secondary components (IPCA 1 and IPCA 2, respectively) (A1—0 cm (broadcast), A2—5 cm (in rows), A3—10 cm (in rows), A4—15 cm (in rows)).
Figure 2. Biplot for NP fertilizer placement depth by year interaction of the number of plants after emergence for four NP fertilizer placement depths of maize (Zea mays L.) during six years, showing the effects of primary and secondary components (IPCA 1 and IPCA 2, respectively) (A1—0 cm (broadcast), A2—5 cm (in rows), A3—10 cm (in rows), A4—15 cm (in rows)).
Agronomy 11 01543 g002
Agronomy 11 01543 g003 550
Figure 3. Biplot for the interaction principal component (IPCA 1) and average number of plants after emergence (plants m−2). Vertical line in the biplot center is the grand mean (A1—0 cm (broadcast), A2—5 cm (in rows), A3—10 cm (in rows), A4—15 cm (in rows)).
Figure 3. Biplot for the interaction principal component (IPCA 1) and average number of plants after emergence (plants m−2). Vertical line in the biplot center is the grand mean (A1—0 cm (broadcast), A2—5 cm (in rows), A3—10 cm (in rows), A4—15 cm (in rows)).
Agronomy 11 01543 g003
Agronomy 11 01543 g004 550
Figure 4. View of the field after placement. A trace of a seed coulter is visible on the left, and a fertilizer coulter on the right (20 cm from kernels, depth—15 cm) (photo taken by Szulc P.).
Figure 4. View of the field after placement. A trace of a seed coulter is visible on the left, and a fertilizer coulter on the right (20 cm from kernels, depth—15 cm) (photo taken by Szulc P.).
Agronomy 11 01543 g004
Agronomy 11 01543 g005 550
Figure 5. View of the field after placement. A trace of a seed coulter is visible on the left, and a fertilizer coulter on the right (10 cm from kernels, depth—5 cm) (photo taken by Szulc P.).
Figure 5. View of the field after placement. A trace of a seed coulter is visible on the left, and a fertilizer coulter on the right (10 cm from kernels, depth—5 cm) (photo taken by Szulc P.).
Agronomy 11 01543 g005
Table
Table 1. Nutrient contents and soil pH before establishing the experiment in maize growing seasons.
Table 1. Nutrient contents and soil pH before establishing the experiment in maize growing seasons.
SpecificationYears
201520162017201820192020
P [mg P kg−1 dm of soil]40.0104.073.049.0155.0115.0
K [mg K kg−1 dm of soil]111.097.0108.0116.0122.0103.4
Mg [mg Mg kg−1 dm of soil]29.044.053.053.069.058.0
pH [1 mol dm−3 KCl]4.54.65.65.15.85.9
Nmin [kg ha−1] in soil, layer 0.0–0.6 m68.579.271.465.769.373.8
C, org. [%]1.010.990.990.981.021.00
Table
Table 2. Average monthly air temperatures and monthly total precipitation in individual growing season.
Table 2. Average monthly air temperatures and monthly total precipitation in individual growing season.
YearsTemperature [°C]
AprilMayJuneAverage/Sum
20159.313.916.913.4
20169.616.319.915.3
20177.313.717.412.8
201812.916.918.516.1
201910.511.922.014.8
20209.411.818.313.2
YearsRainfall [mm]
201517.627.266.6111.4
201647.347.312.8107.4
201740.656.868.2165.6
201836.217.425.679.2
20198.694.47.2110.2
20202.052.842.897.6
YearsValues of hydrothermal coefficient of water preservation [K] 1
20150.630.631.310.85
20161.640.932.071.54
20171.851.331.301.49
20180.930.330.460.57
20190.272.550.110.97
20200.071.440.770.76
1 according to Sielianinow [37].
Table
Table 3. Results of main effects and interaction from analysis of variance for the number of plants after emergence in relation to NP fertilizer placement depths as well as variability explained (in %). Coefficient of variation of the number of plants after emergence is equal to 3.28%.
Table 3. Results of main effects and interaction from analysis of variance for the number of plants after emergence in relation to NP fertilizer placement depths as well as variability explained (in %). Coefficient of variation of the number of plants after emergence is equal to 3.28%.
Source of Variationd.f.Sum of SquaresMean SquaresF StatisticVariability Explained (%)
Treatments235.4040.234924.09 ***89.40
NP Fertilizer Placement Depth (D)31.4030.467847.96 ***23.21
Year (Y)53.7180.7435117.19 ***61.51
DY Interaction150.2830.01891.93 *4.68
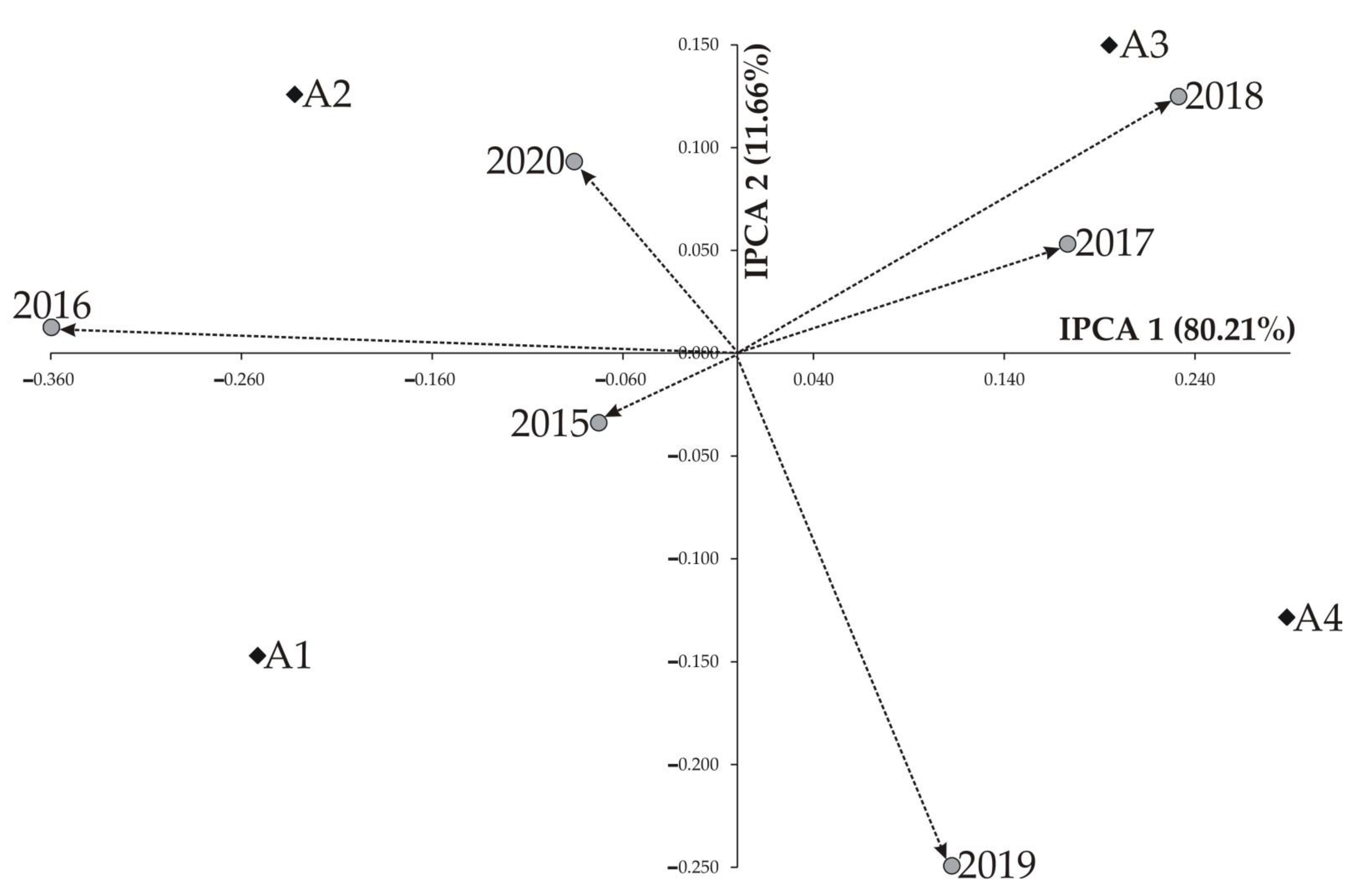
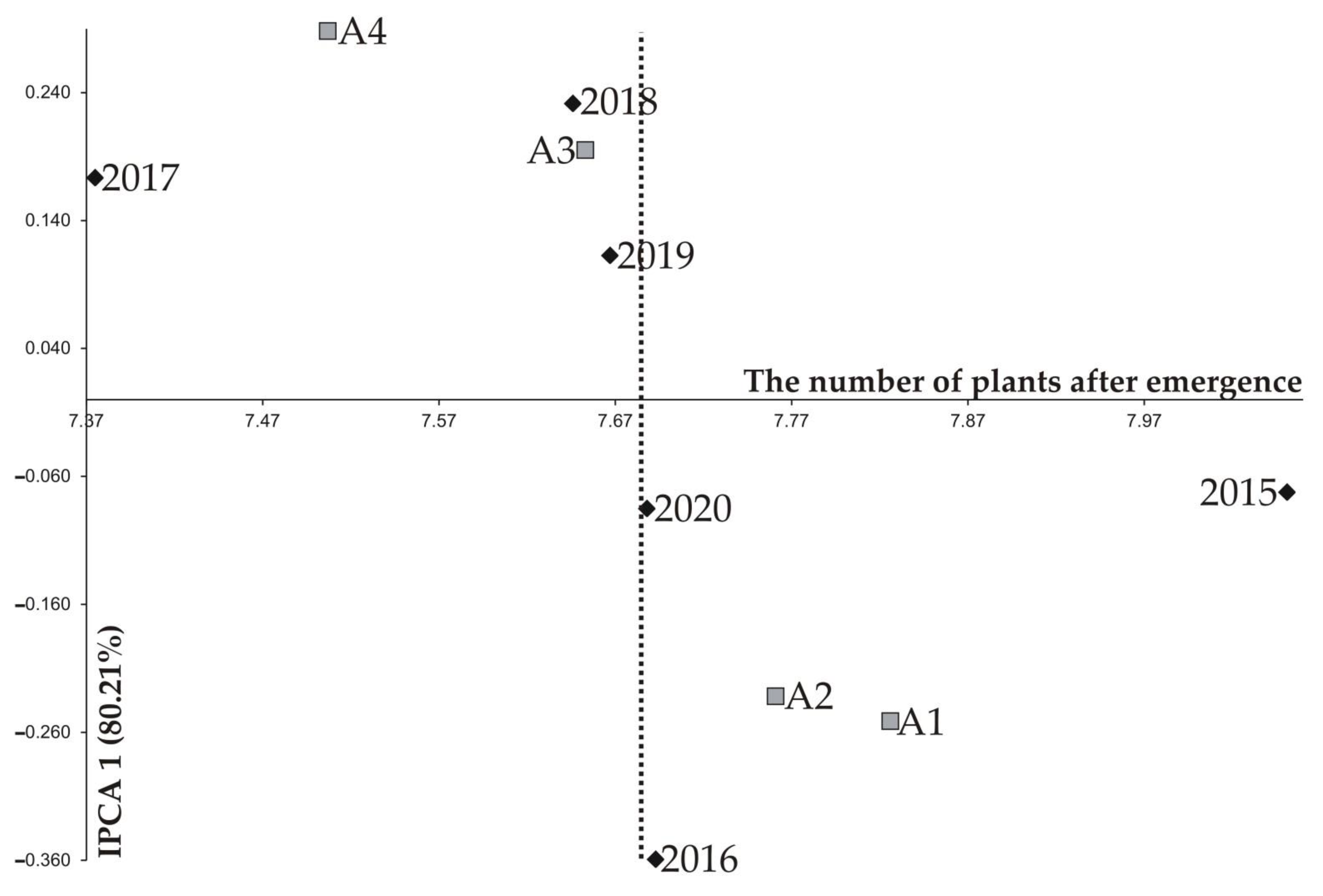
IPCA 1 70.2270.03243.32 **80.21
IPCA 250.0330.00660.67 *11.66
Residuals30.0230.00780.8 *8.13
Error540.5270.0098
* p < 0.05, ** p < 0.01, *** p < 0.001, d.f.—the number of degrees of freedom.
Table
Table 4. Average number of maize (Zea mays L.) plants after emergence (plant m−2), for NP fertilizer placement depths and years, principal component analysis values (IPCAg1, IPCAg2) and AMMI stability value (ASV).
Table 4. Average number of maize (Zea mays L.) plants after emergence (plant m−2), for NP fertilizer placement depths and years, principal component analysis values (IPCAg1, IPCAg2) and AMMI stability value (ASV).
YearNP Fertilizer Placement DepthIPCA 1IPCA 2
A1 1A2A3A4MeanStandard DeviationCoefficient of Variation
20158.201 a28.147 ab8.022 ab7.835 b8.0510.1612.00−0.073−0.034
20167.911 a7.862 a7.598 b7.402 b7.6930.2333.03−0.3600.012
20177.446 a7.432 a7.384 b7.237 c7.3750.1141.550.1730.053
20187.710 a7.688 ab7.637 ab7.548 b7.6460.1031.340.2310.125
20197.821 a7.665 b7.688 b7.496 c7.6670.1532.000.113−0.249
20207.867 a7.770 a7.590 b7.522 b7.6880.1682.18−0.0850.093
Mean7.826 a7.761 ab7.653 ab7.507 b7.6870.2523.28
Coefficient of variation3.173.082.782.59
IPCA 1−0.251−0.2320.1950.288
IPCA 2−0.1470.1260.150−0.128
ASV1.7451.6151.3611.999
1 A1—0 cm (broadcast), A2—5 cm (in rows), A3—10 cm (in rows), A4—15 cm (in rows). 2 Means in rows followed by the same letters are not significantly different.
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Szulc, P.; Bocianowski, J.; Nowosad, K.; Bujak, H.; Zielewicz, W.; Stachowiak, B. Effects of NP Fertilizer Placement Depth by Year Interaction on the Number of Maize (Zea mays L.) Plants after Emergence Using the Additive Main Effects and Multiplicative Interaction Model. Agronomy 2021, 11, 1543. https://doi.org/10.3390/agronomy11081543

AMA Style

Szulc P, Bocianowski J, Nowosad K, Bujak H, Zielewicz W, Stachowiak B. Effects of NP Fertilizer Placement Depth by Year Interaction on the Number of Maize (Zea mays L.) Plants after Emergence Using the Additive Main Effects and Multiplicative Interaction Model. Agronomy. 2021; 11(8):1543. https://doi.org/10.3390/agronomy11081543

Chicago/Turabian Style

Szulc, Piotr, Jan Bocianowski, Kamila Nowosad, Henryk Bujak, Waldemar Zielewicz, and Barbara Stachowiak. 2021. "Effects of NP Fertilizer Placement Depth by Year Interaction on the Number of Maize (Zea mays L.) Plants after Emergence Using the Additive Main Effects and Multiplicative Interaction Model" Agronomy 11, no. 8: 1543. https://doi.org/10.3390/agronomy11081543

APA Style

Szulc, P., Bocianowski, J., Nowosad, K., Bujak, H., Zielewicz, W., & Stachowiak, B. (2021). Effects of NP Fertilizer Placement Depth by Year Interaction on the Number of Maize (Zea mays L.) Plants after Emergence Using the Additive Main Effects and Multiplicative Interaction Model. Agronomy, 11(8), 1543. https://doi.org/10.3390/agronomy11081543

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop