Effect of Barley Sowing Density on the Integrated Weed Management of Lolium rigidum (Annual Ryegrass) in Mediterranean Dryland: A Modeling Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Lolium Rigidum Submodel
2.2. Barley Submodel
2.3. Weed–Crop System Analysis
2.4. Simulation Condition and Parameter Values
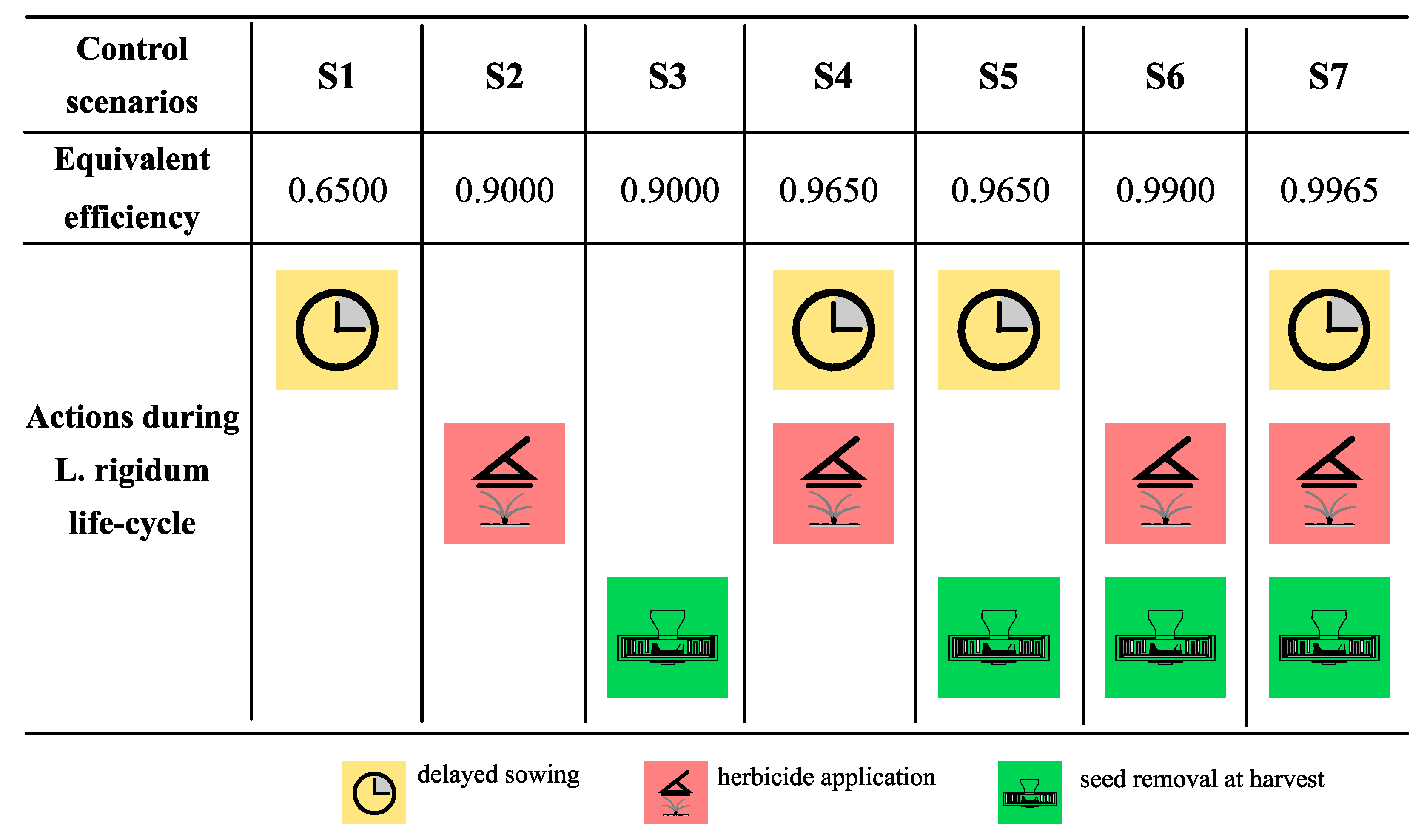
2.5. Control Programs
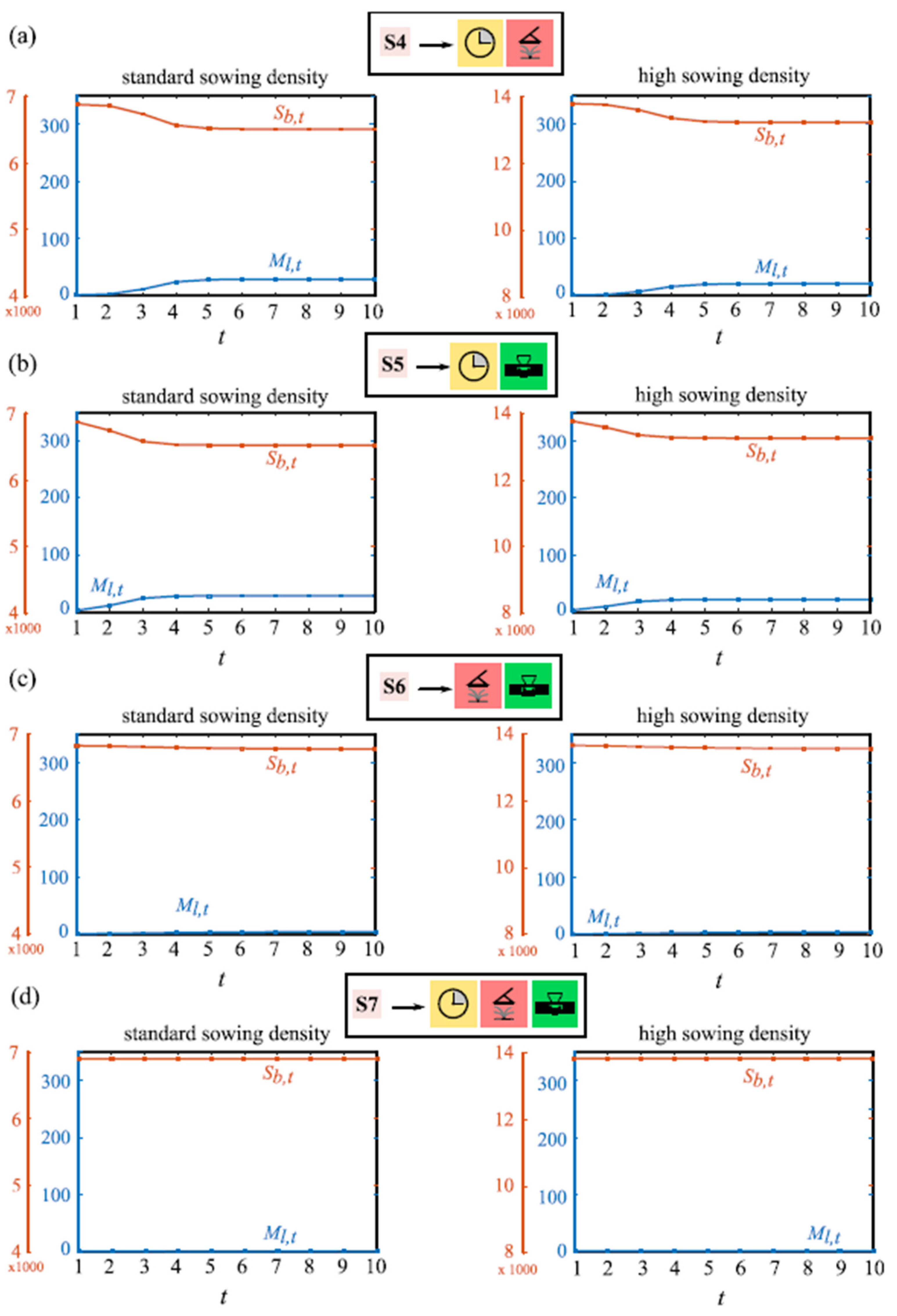
3. Results
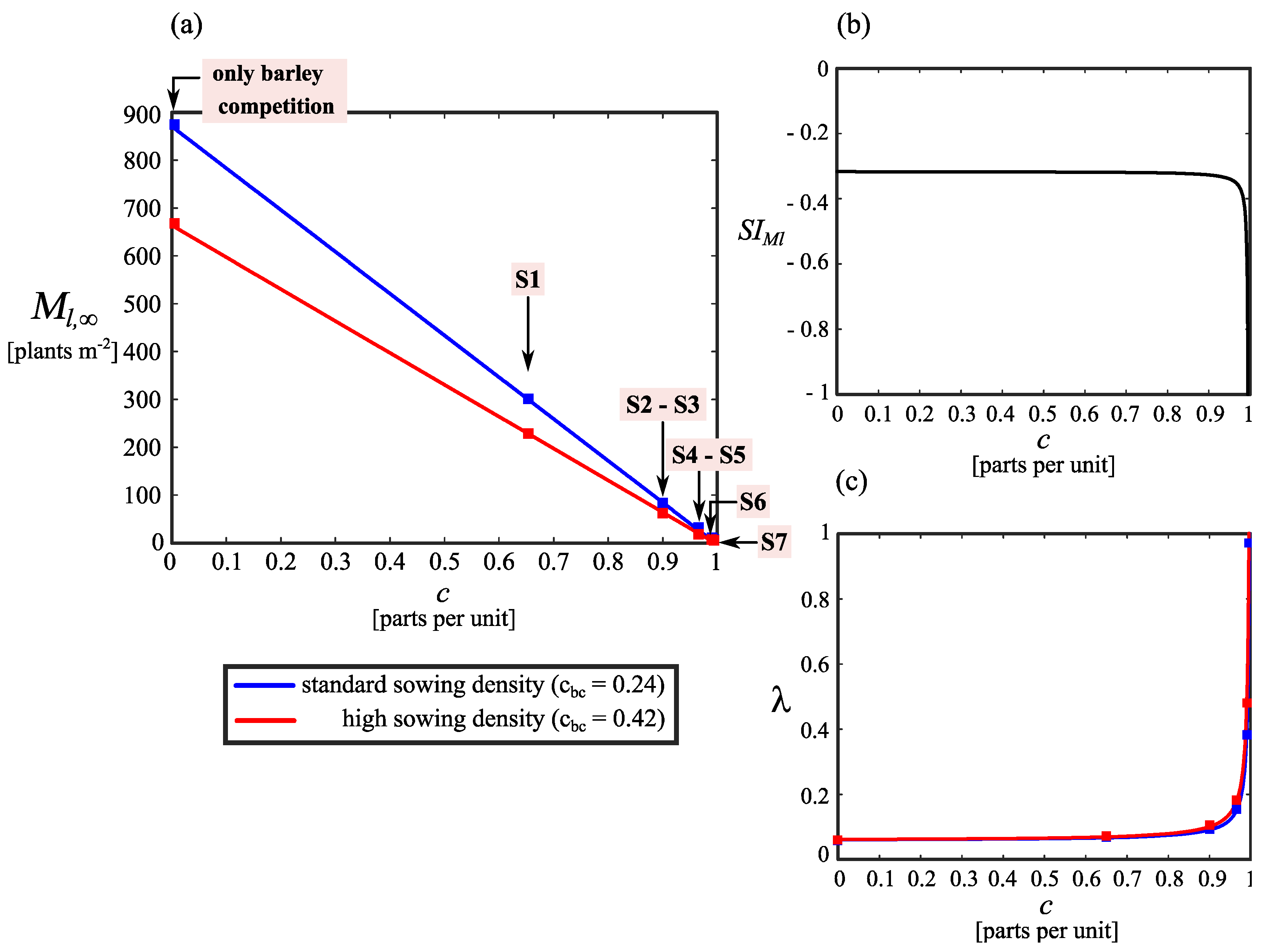
3.1. Lolium Rigidum Control
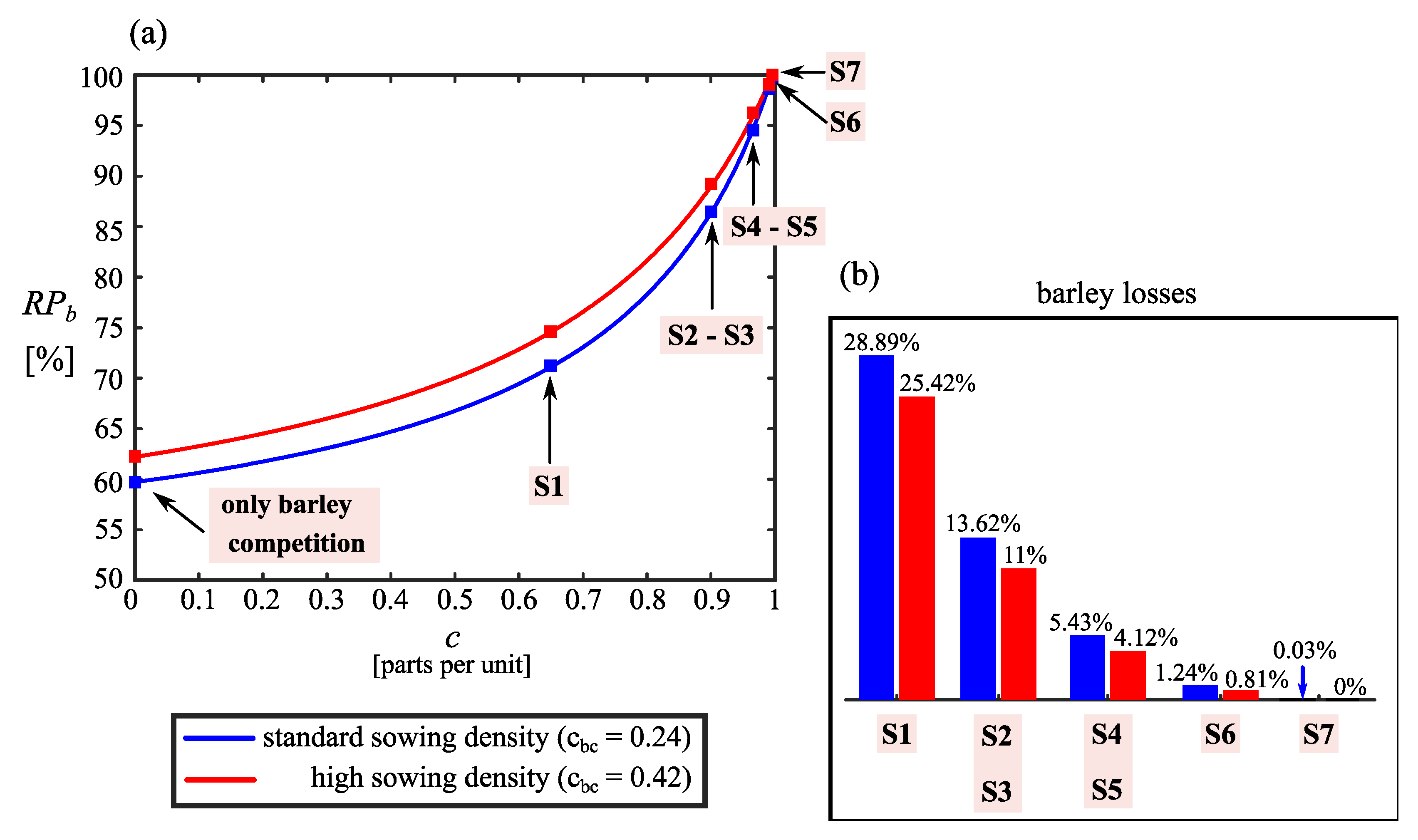
3.2. Impact on the Barley Seed Production
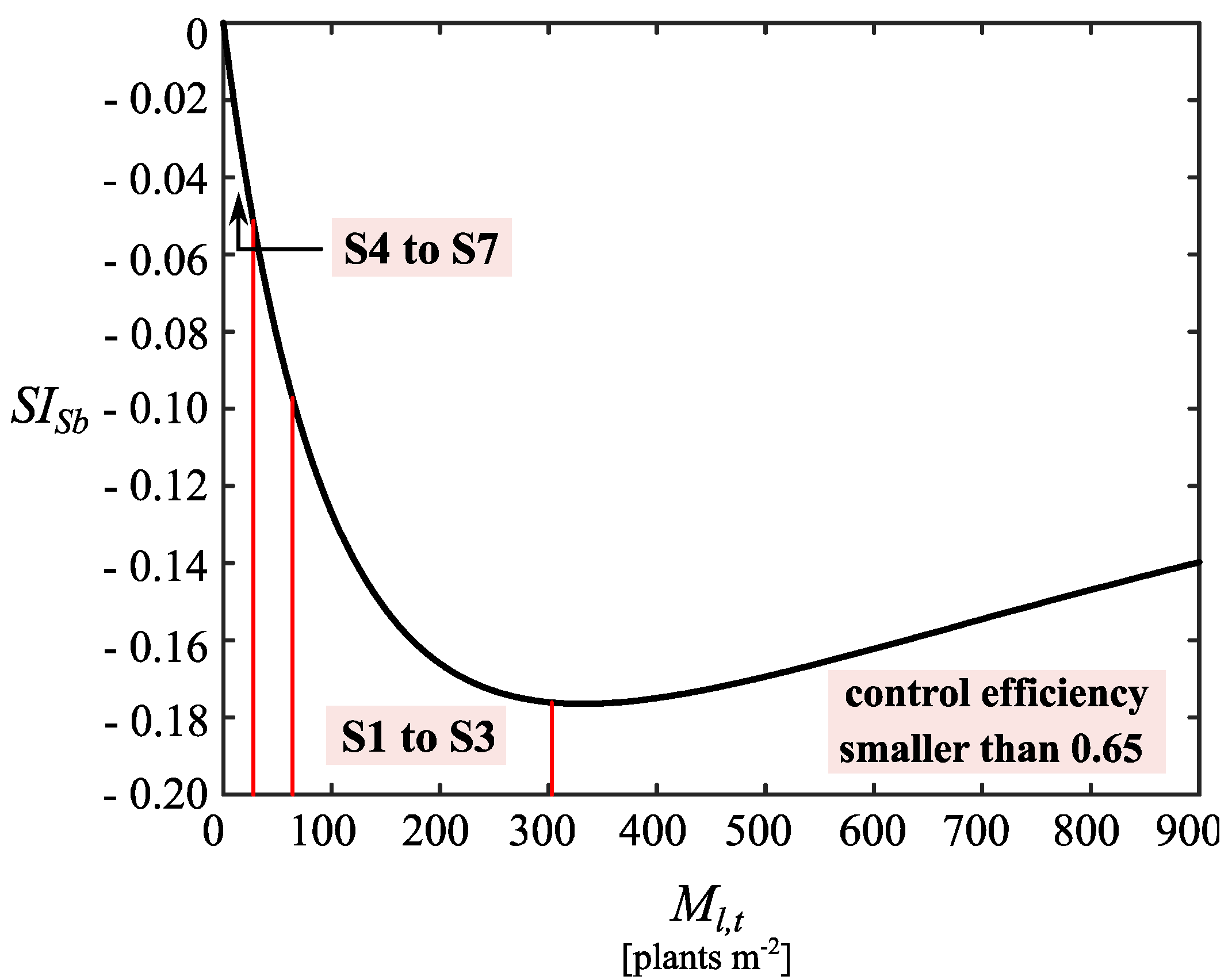
3.3. Dynamical Behavior of the Weed–Crop System
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhou, M. Barley production and consumption. In Genetics and Improvement of Barley Malt Quality; Zhang, G., Li, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 1–17. [Google Scholar]
- Izquierdo, J.; Recasens, J.; Fernández-Quintanilla, C.; Gille, G. Effects of crop and weed densities on the interactions between barley and Lolium rigidum in several mediterranean locations. Agronomie 2003, 23, 529–536. [Google Scholar] [CrossRef]
- Fernández-Quintanilla, C.; Barroso, J.; Recasens, J.; Sans, X.; Torner, C.; del Arco, M.J.S. Demography of Lolium rigidum in winter barley crops: Analysis of recruitment, survival and reproduction. Weed Res. 2000, 40, 281–291. [Google Scholar] [CrossRef]
- Gill, G.S.; Cousens, R.D.; Allan, M.R. Germination, growth, and development of herbicide resistant and susceptible populations of rigid ryegrass (Lolium rigidum). Weed Sci. 1996, 44, 252–256. [Google Scholar] [CrossRef]
- Gramshaw, D.; Stern, W.R. Survival of annual ryegrass (lolium rigidum gaud.) in a Mediterranean type environment. II Effects of short term burial on persistence of viable seed. Aust. J. Agric. Res. 1977, 28, 93–101. [Google Scholar] [CrossRef]
- Heap, I.M. The International Survey of Herbicide Resistant Weeds. Available online: http://www.weedscience.org (accessed on 5 June 2021).
- Boutsalis, P.; Gill, G.; Preston, C. Incidence of herbicide resistance in rigid ryegrass (Lolium rigidum) across Southeastern Australia. Weed Technol. 2012, 26, 391–398. [Google Scholar] [CrossRef]
- Borger, C.P.D.; Hashem, A.; Powles, S.B. Manipulating crop row orientation and crop density to suppress Lolium rigidum. Weed Res. 2016, 56, 22–30. [Google Scholar] [CrossRef]
- Olsen, J.; Kristensen, L.; Weiner, J. Effects of density and spatial pattern of winter wheat on suppression of different weed species. Weed Sci. 2005, 53, 690–694. [Google Scholar] [CrossRef]
- Champion, G.T.; Froud-Williams, R.J.; Holland, J.M. Interactions between wheat (Triticum aestivum L.) cultivar, row spacing and density and the effect on weed suppression and crop yield. Ann. Appl. Biol. 1998, 133, 443–453. [Google Scholar] [CrossRef]
- Paynter, H.H.; Hills, A.L. Barley and rigid ryegrass (Lolium rigidum) competition is influenced by crop cultivar and density. Weed Technol. 2009, 23, 40–48. [Google Scholar] [CrossRef]
- Lemerle, D.; Cousens, R.D.; Gill, G.S.; Peltzer, S.J.; Moerkerk, M.; Murphy, C.E.; Collins, D.J.; Cullis, B. Reliability of higher seeding rates of wheat for increased competitiveness with weeds in low rainfall environments. J. Agric. Sci. 2004, 142, 395–409. [Google Scholar] [CrossRef] [Green Version]
- González-Andújar, J.L.; Fernández-Quintanilla, C. Modelling the population dynamics of annual ryegrass (Lolium rigidum) under various weed management systems. Crop Prot. 2004, 23, 723–729. [Google Scholar] [CrossRef] [Green Version]
- Somerville, G.J.; Powles, S.B.; Walsh, M.J.; Renton, M. How do spatial heterogeneity and dispersal in weed population models affect predictions of herbicide resistance evolution? Ecol. Model. 2017, 362, 37–53. [Google Scholar] [CrossRef]
- D’Amico, M.B.; Calandrini, G.L.; González-Andújar, J.L.; Chantre, G.R. Analysis of different management strategies for annual ryegrass (Lolium rigidum) based on a population dynamic model under various weed management systems. Int. J. Bifurc. Chaos 2018, 28, 1830041. [Google Scholar] [CrossRef]
- Bagavathiannan, M.V.; Beckie, H.J.; Chantre, G.R.; González-Andújar, J.L.; Leon, R.G.; Neve, P.; Poggio, S.L.; Schutte, B.J.; Somerville, G.J.; Werle, R.; et al. Simulation models on the ecology and management of arable weeds: Structure, quantitative insights, and applications. Agronomy 2020, 10, 1611. [Google Scholar] [CrossRef]
- González-Díaz, L.; Bastidas, F.; González-Andújar, J.L. A bioeconomic model for the analysis of control strategies for Lolium rigidum and Avena sterilis ssp ludoviciana in winter wheat. Int. J. Plant Prod. 2020, 14, 37–42. [Google Scholar] [CrossRef]
- Sonderskov, M.; Somerville, G.J.; Lacoste, M.; Jensen, J.E.; Holst, N. DK-RIM: Assisting integrated management of Lolium multiflorum, italian ryegrass. Agronomy 2020, 10, 856. [Google Scholar] [CrossRef]
- Torra, J.; Monjardino, M. Ryegrass Integrated Management (RIM)–Based Decision Support System. In Decision Support Systems for Weed Management; Chantre, G., González-Andújar, J.L., Eds.; Springer: Cham, Switzerland, 2020; pp. 249–278. [Google Scholar]
- Briggs, D.E. Barley; Chapman and Hall: London, UK, 1978. [Google Scholar]
- Singh, M.; Kaur, S.; Chauhan, B.S. Weed Interference Models. In Decision Support Systems for Weed Management; Chantre, G., González-Andújar, J.L., Eds.; Springer: Cham, Switzerland, 2020; pp. 117–142. [Google Scholar]
- Moreno, A.; Moreno, M.; Ribas, F.; Cabello, M.J. Influencia de distintas dosis de siembra sobre el rendimiento de la cebada (Hordeum vulgare L.) para su aplicación en cultivo ecológico. In La Agricultura y Ganadería Ecológicas en un Marco de Diversificación y Desarrollo Solidario; Sociedad Española de Agricultura Ecológica: Gijón, Spain, 2002; Volume 1, pp. 685–689. [Google Scholar]
- Holst, N. Mathematical Models. In Decision Support Systems for Weed Management; Chantre, G., González-Andújar, J.L., Eds.; Springer: Cham, Switzerland, 2020; pp. 3–23. [Google Scholar]
- Cirujeda, A.; Taberner, A. Cultural control of herbicide-resistant Lolium rigidum Gaud. populations in winter cereal in Northeastern Spain. Span. J. Agric. Res. 2009, 7, 146–154. [Google Scholar] [CrossRef] [Green Version]
- Kolbe, W. Effect of weed control on grain yield of different winter barley cultivars with reference to sowing time, seed rate and seed size, in long-term trials at Hofchen and Laacherhof Experimental Stations (1968–1980). Pflanzenschutz-Nachr. Bayer 1980, 33, 203–219. [Google Scholar]
- Walsh, M.J.; Broster, J.C.; Schwartz-Lazaro, L.M.; Norsworthy, J.K.; Davis, A.S.; Tidemann, B.D.; Beckie, H.J.; Lyon, D.J.; Soni, N.; Neve, P.; et al. Opportunities and challenges for harvest weed seed control in global cropping systems. Pest Manag. Sci. 2018, 74, 2235–2245. [Google Scholar] [CrossRef]
- San Martin, C.; Lyon, D.J.; Gourlie, J.A.; Thorne, M.; Barroso, J. Seed retention of grass weeds at wheat harvest in the Pacific Northwest. Weed Sci. 2021, 69, 238–246. [Google Scholar] [CrossRef]
- Anderson, R. Managing weeds with a dualistic approach of prevention and control. A review. Agron. Sustain. Dev. 2007, 27, 13–18. [Google Scholar] [CrossRef] [Green Version]
- Liebman, M.; Gallandt, E.R. Many little hammers: Ecological management of crop-weed interactions. In Ecology in Agriculture; Jackson, L.E., Ed.; Academic Press: Cambridge, MA, USA, 1997; pp. 291–343. [Google Scholar]
- Lacasta, C.; Meco, R.; Estalrich, E.; Martín de Eugenio, L. Interacción de densidades de siembra de cebada y rotaciones de cultivo sobre la flora arvense y rendimientos de cultivos. In Proceedings of the VI SEAE Congress, Almería, Spain, 27 September–2 October 2004; pp. 1481–1496. [Google Scholar]
- Weiner, J.; Griepentrog, H.-W.; Kristensen, L. Suppression of weeds by spring wheat Triticum aestivum increases with crop density and spatial uniformity. J. Appl. Ecol. 2001, 38, 784–790. [Google Scholar] [CrossRef]
- González-Díaz, L.; Blanco-Moreno, J.M.; González-Andújar, J.L. Spatially-explicit bioeconomic model for weed management in cereals: Validation and evaluation of management strategies. J. Appl. Ecol. 2015, 52, 240–249. [Google Scholar] [CrossRef] [Green Version]


| Parameter | Model | Value | Reference | |
|---|---|---|---|---|
| Barley | Emergence (seedlings/seed) | 0.75 | [22] | |
| Seedling survivorship | 1 | [22] | ||
| (plants/seedlings) | ||||
| Fecundity (seed/plants) | 18.40 | (González-Andújar, personal communication) | ||
| Interspecific competition | ||||
| (m2/plant) | 0.0022 | [2] | ||
| (part per unit) | 0.5100 | [2] | ||
| L. rigidum | Emergence (seedlings/seed) | 0.64 | [3,13] | |
| Seedling survivorship | 0.76 | [3,13] | ||
| (plants/seedlings) | ||||
| Fecundity (seed/plants) | 935 | [3,13] | ||
| Area (m2/plant) | 0.34 | [3,13] | ||
| Seed bank mortality (parts per unit) | 0.84 | [3,13] | ||
| Biotic reduction (parts per unit) | 0.19 | [13] | ||
| Control | Crop competition (parts per unit) | [3,13] | ||
| Standard barley density | 0.24 | |||
| High barley density | 0.42 | |||
| Sowing delay (parts per unit) | 0.65 | [13] | ||
| Herbicide control (parts per unit) | 0.90 | [13] | ||
| Seed removal at harvest (parts per unit) | 0.90 | [13] |
| Control Scenarios | Equivalent Efficiency | Standard Sowing Density | High Sowing Density | Reduction [%] |
|---|---|---|---|---|
| without control | 0 | 871 | 664 | 23.7 |
| S1 | 0.6500 | 303 | 230 | 24.1 |
| S2–S3 | 0.9000 | 84 | 64 | 23.8 |
| S4–S5 | 0.9650 | 28 | 20 | 28.6 |
| S6 | 0.9900 | 6 | 4 | 33.3 |
| S7 | 0.9965 | 0.12 | Extinction | 100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
D’Amico, M.B.; Chantre, G.R.; Calandrini, G.L.; González-Andújar, J.L. Effect of Barley Sowing Density on the Integrated Weed Management of Lolium rigidum (Annual Ryegrass) in Mediterranean Dryland: A Modeling Approach. Agronomy 2021, 11, 1565. https://doi.org/10.3390/agronomy11081565
D’Amico MB, Chantre GR, Calandrini GL, González-Andújar JL. Effect of Barley Sowing Density on the Integrated Weed Management of Lolium rigidum (Annual Ryegrass) in Mediterranean Dryland: A Modeling Approach. Agronomy. 2021; 11(8):1565. https://doi.org/10.3390/agronomy11081565
Chicago/Turabian StyleD’Amico, María Belén, Guillermo R. Chantre, Guillermo L. Calandrini, and José L. González-Andújar. 2021. "Effect of Barley Sowing Density on the Integrated Weed Management of Lolium rigidum (Annual Ryegrass) in Mediterranean Dryland: A Modeling Approach" Agronomy 11, no. 8: 1565. https://doi.org/10.3390/agronomy11081565
APA StyleD’Amico, M. B., Chantre, G. R., Calandrini, G. L., & González-Andújar, J. L. (2021). Effect of Barley Sowing Density on the Integrated Weed Management of Lolium rigidum (Annual Ryegrass) in Mediterranean Dryland: A Modeling Approach. Agronomy, 11(8), 1565. https://doi.org/10.3390/agronomy11081565









