Evaluation and Development of Pedo-Transfer Functions for Predicting Soil Saturated Hydraulic Conductivity in the Alpine Frigid Hilly Region of Qinghai Province
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
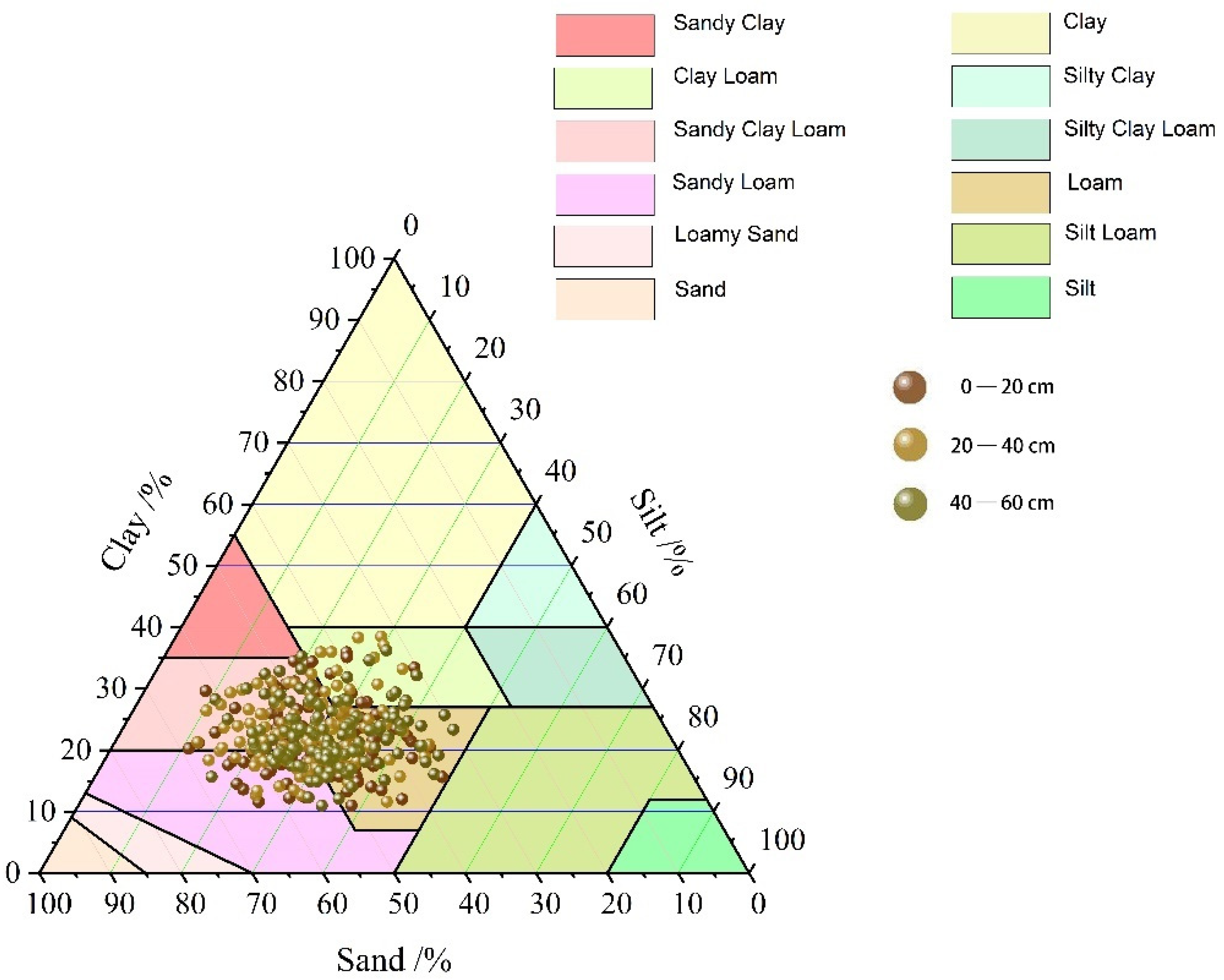
2.2. Soil Sample Collection
2.3. Laboratory Experiment
2.4. Data Analysis
2.4.1. Regression Analysis
2.4.2. Construction of BP Artificial Neural Network
2.5. Evaluation Criteria of Performance
3. Results and Discussion
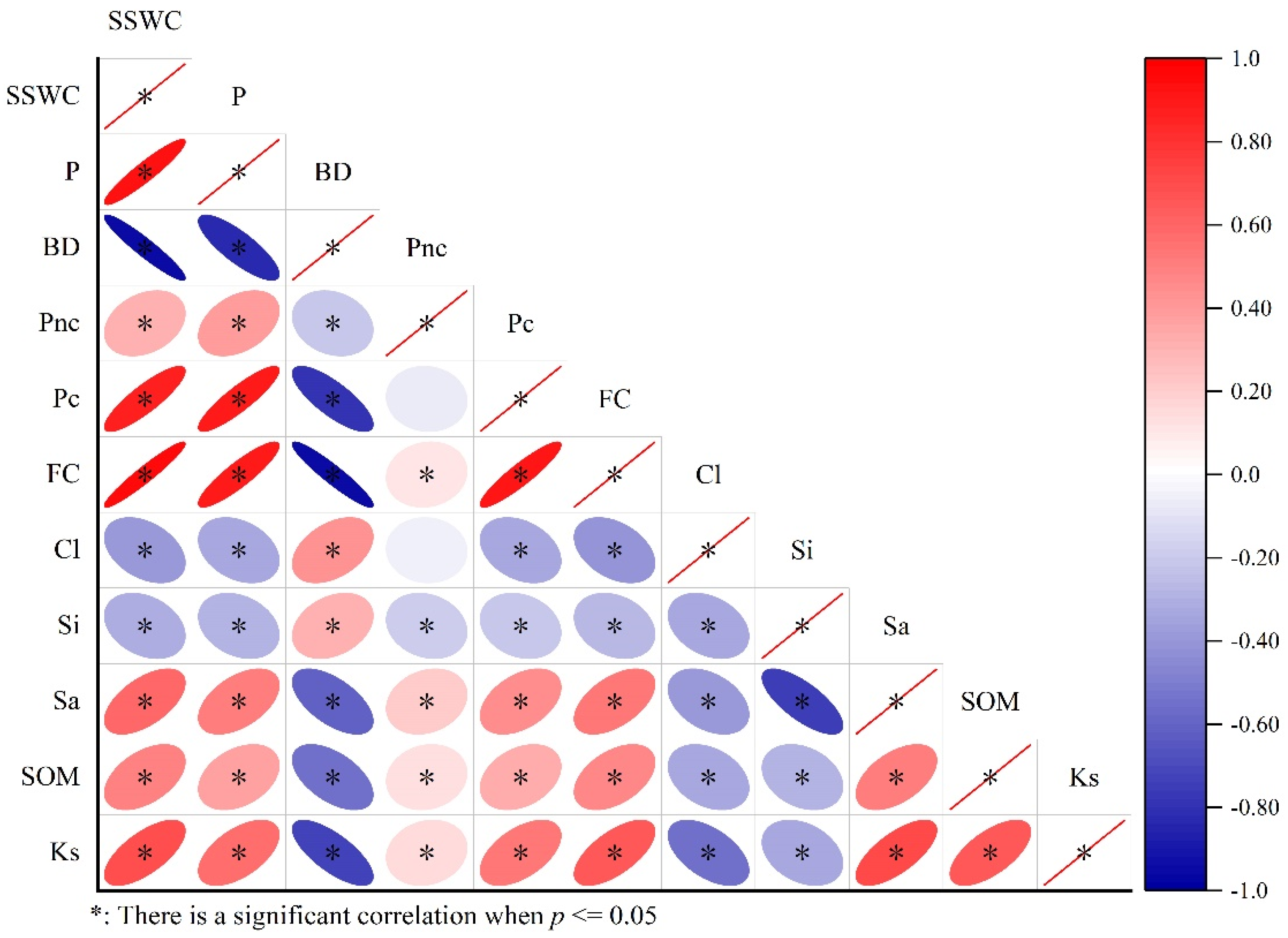
3.1. Descriptive Statistics
3.2. Characteristics of KS in Different Stand Types of the Study Area
3.3. Modification of the Published PTFs
3.4. Multiple Linear Regression
3.5. Development of BP Artificial Neural Network
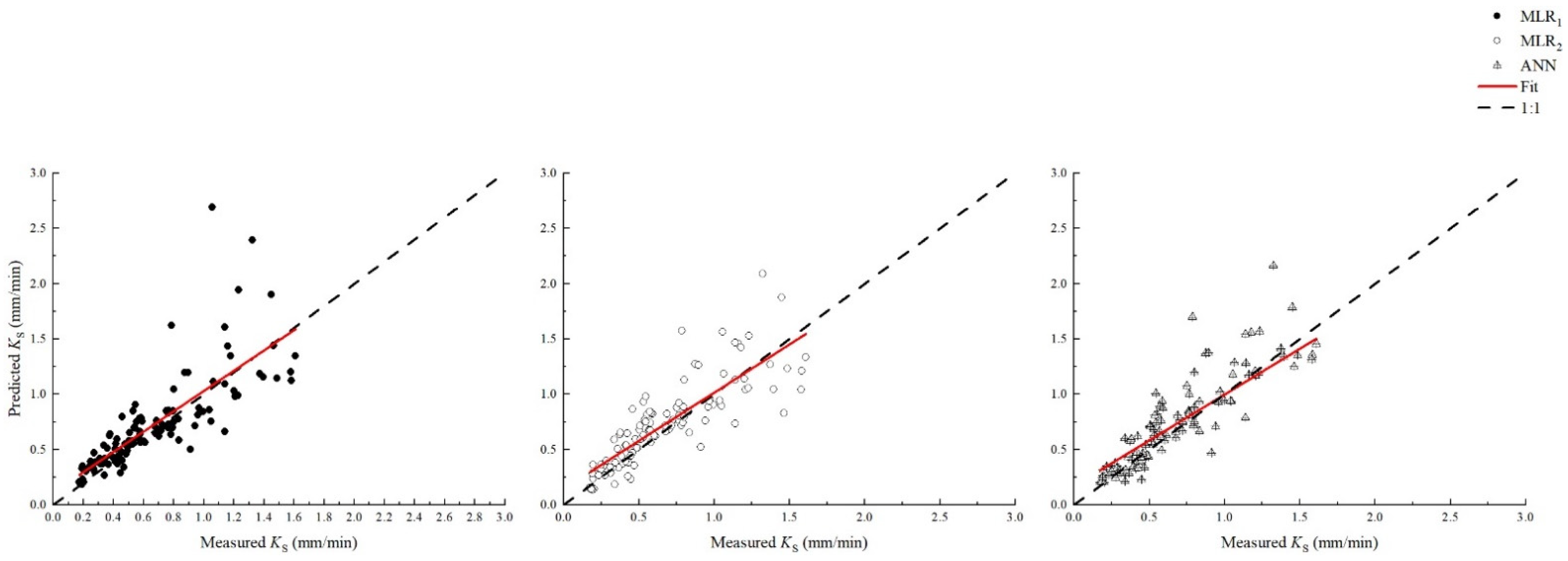
3.6. Evaluation of Prediction Performance of the Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Montzka, C.; Herbst, M.; Weihermüller, L.; Verhoef, A.; Vereecken, H. A global data set of soil hydraulic properties and sub-grid variability of soil water retention and hydraulic conductivity curves. Earth Syst. Sci. Data 2017, 9, 529–543. [Google Scholar] [CrossRef] [Green Version]
- Woolhiser, D.A.; Smith, R.E.; Giraldez, J.V. Effects of spatial variability of saturated hydraulic conductivity on hortonian overland flow. Water Resour. Res. 1996, 32, 671–678. [Google Scholar] [CrossRef]
- Noguchi, S.; Nik, A.R.; Kasran, B.; Tani, M.; Sammori, T.; Morisada, K. Soil physical properties and preferential flow pathways in tropical rain forest, bukit tarek, peninsular malaysia. J. For. Res. 1997, 2, 115–120. [Google Scholar] [CrossRef]
- Lee, J.H. The Role of Preferential Flow as a Mechanism for Groundwater Contamination; American Geophysical Union: New York, NY, USA, 1988. [Google Scholar]
- Shirmohammadi, A.; Montas, H.; Bergstrom, L.; Coyne, K.; Wei, S.; Gish, T. Deterministic and stochastic prediction of atrazine transport in soils displaying macropore flow. In Proceedings of the 2nd International Symposium, Ala Moana Hotel, Honolulu, HI, USA, 3–5 January 2001. [Google Scholar]
- Yao, R.-J.; Yang, J.-S.; Wu, D.-H.; Li, F.-R.; Gao, P.; Wang, X.-P. Evaluation of pedotransfer functions for estimating saturated hydraulic conductivity in coastal salt-affected mud farmland. J. Soils Sediments 2015, 15, 902–916. [Google Scholar] [CrossRef]
- Wösten, J.H.M.; Pachepsky, Y.A.; Rawls, W.J. Pedotransfer functions: Bridging the gap between available basic soil data and missing soil hydraulic characteristics. J. Hydrol. 2001, 251, 123–150. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Elrick, D.E. A method for simultaneous in situ measurement in the vadose zone of field-saturated hydraulic conductivity, sorptivity and the conductivity-pressure head relationship. Ground Water Monit. Remediat. 1986, 6, 84–95. [Google Scholar] [CrossRef]
- Klute, A. Hydraulic conductivity and diffusivity: Laboratory methods. Soil Phys. 1986, 5, 687–734. [Google Scholar]
- Abdelbaki, A.M. Evaluation of pedotransfer functions for predicting soil bulk density for U.S. Soils. Ain Shams Eng. J. 2018, 9, 1611–1619. [Google Scholar] [CrossRef]
- Zhang, Y.; Schaap, M.G. Estimation of saturated hydraulic conductivity with pedotransfer functions: A review. J. Hydrol. 2019, 575, 1011–1030. [Google Scholar] [CrossRef]
- Bouma, J. Transfer functions and threshold values: From soil characteristics to land qualities. In Proceedings of the Workshop on Quantified Land Evaluation Process, Washington, DC, USA, 27 April–2 May 1986; Volume 6. [Google Scholar]
- Gupta, S.C.; Larson, W.E. Estimating soil water retention characteristics from particle size distribution, organic matter percent, and bulk density. Water Resour. Res. 1979, 15, 1633–1635. [Google Scholar] [CrossRef]
- Rawls, W.J.; Brakensiek, D.L. An infiltration based runoff model for use with a design store. In Hydraulics & Hydrology in the Small Computer Age; American Society of Civil Engineers: Orlando, FL, USA, 2015. [Google Scholar]
- Nelson, M.C.; Illingworth, W.T. A Practical Guide to Neural Nets; Addison-Wesley Publishing Company, Inc.: Upper Saddle River, NJ, USA, 1991. [Google Scholar]
- Merdun, H.; Çınar, Ö.; Meral, R.; Apan, M. Comparison of artificial neural network and regression pedotransfer functions for prediction of soil water retention and saturated hydraulic conductivity. Soil Tillage Res. 2006, 90, 108–116. [Google Scholar] [CrossRef]
- Motaghian, H.R.; Mohammadi, J. Spatial estimation of saturated hydraulic conductivity from terrain attributes using regression, kriging, and artificial neural networks. Pedosphere 2011, 21, 170–177. [Google Scholar] [CrossRef]
- Zhao, C.; Shao, M.a.; Jia, X.; Nasir, M.; Zhang, C. Using pedotransfer functions to estimate soil hydraulic conductivity in the loess plateau of china. Catena 2016, 143, 1–6. [Google Scholar] [CrossRef]
- Lilly, A.; Nemes, A.; Rawls, W.J.; Pachepsky, Y.A. Probabilistic approach to the identification of input variables to estimate hydraulic conductivity. Soil Sci. Soc. Am. J. 2008, 72, 16–24. [Google Scholar] [CrossRef] [Green Version]
- De Vos, B.; Meirvenne, M.V.; Quataert, P.; Jozef, D.; Muys, B. Predictive quality of pedotransfer functions for estimating bulk density of forest soils. Soil Sci. Soc. Am. J. 2005, 69, 500–510. [Google Scholar] [CrossRef]
- Mcbratney, A.B.; Minasny, B.; Cattle, S.R.; Vervoort, R.W. From pedotransfer functions to soil inference systems. Geoderma 2002, 109, 41–73. [Google Scholar] [CrossRef]
- Kaur, R.; Kumar, S.; Gurung, H.P. A pedo-transfer function (ptf) for estimating soil bulk density from basic soil data and its comparison with existing ptfs. Aust. J. Soil Res. 2002, 40, 847–858. [Google Scholar] [CrossRef]
- C, Y.W.A.B.; B, M.A.S.; C, Z.L.; D, R.H. Regional-scale variation and distribution patterns of soil saturated hydraulic conductivities in surface and subsurface layers in the loessial soils of china. J. Hydrol. 2013, 487, 13–23. [Google Scholar]
- Hu, W.; Shao, M.A.; Si, B.C. Seasonal changes in surface bulk density and saturated hydraulic conductivity of natural landscapes. Eur. J. Soil Sci. 2012, 63, 820–830. [Google Scholar] [CrossRef]
- Gao, L.; Shao, M.; Wang, Y. Spatial scaling of saturated hydraulic conductivity of soils in a small watershed on the loess plateau, china. J. Soil Sediments 2012, 12, 863–875. [Google Scholar] [CrossRef]
- Simunek, J.; Nimmo, J.R. Estimating soil hydraulic parameters from transient flow experiments in a centrifuge using parameter optimization technique. Water Resour. Res. 2005, 41, 297–303. [Google Scholar] [CrossRef] [Green Version]
- Arshad, R.R.; Sayyad, G.; Mosaddeghi, M.; Gharabaghi, B. Predicting saturated hydraulic conductivity by artificial intelligence and regression models. Isrn Soil Sci. 2013, 2013, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Zeleke, T.B.; Si, B.C. Scaling relationships between saturated hydraulic conductivity and soil physical properties. Soil Sci. Soc. Am. J. 2005, 69, 1691–1702. [Google Scholar] [CrossRef]
- Seobi, T.; Anderson, S.H.; Udawatta, R.P.; Gantzer, C.J. Influence of grass and agroforestry buffer strips on soil hydraulic properties for an albaqualf. Soil Sci. Soc. Am. J. 2005, 69, 893–901. [Google Scholar] [CrossRef] [Green Version]
- Rachman, A.; Anderson, S.H.; Gantzer, C.J. Computed-tomographic measurement of soil macroporosity parameters as affected by stiff-stemmed grass hedges. Soil Sci. Soc. Am. J. 2005, 69, 1609–1616. [Google Scholar] [CrossRef]
- Hao, M.; Zhang, J.; Meng, M.; Chen, H.Y.H.; Guo, X.; Liu, S.; Ye, L. Impacts of changes in vegetation on saturated hydraulic conductivity of soil in subtropical forests. Sci. Rep. 2019, 9, 8372. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lim, H.; Yang, H.; Chun, K.W.; Choi, H.T. Development of pedo-transfer functions for the saturated hydraulic conductivity of forest soil in south korea considering forest stand and site characteristics. Water 2020, 12, 2217. [Google Scholar] [CrossRef]
- Burch, W.H.; Jones, R.H.; Mou, P.; Mitchell, R.J. Root system development of single and mixed plant functional type communities following harvest in a pine-hardwood forest. Can. J. For. Res. 1997, 27, 1753–1764. [Google Scholar] [CrossRef]
- Piaszczyk, W.; Lasota, J.; Błońska, E. Effect of organic matter released from deadwood at different decomposition stages on physical properties of forest soil. Forests 2019, 11, 24. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Huang, Y.; Sun, W. Using organic matter and ph to estimate the bulk density of afforested/reforested soils in northwest and northeast china. Pedosphere 2017, 27, 890–900. [Google Scholar] [CrossRef]
- Tietje, O.; Tapkenhinrichs, M. Evaluation of pedo-transfer functions. Soil Sci. Soc. Am. J. 2004, 57, 1088–1095. [Google Scholar] [CrossRef]
- Tietje, O.; Hennings, V. Accuracy of the saturated hydraulic conductivity prediction by pedo-transfer functions compared to the variability within fao textural classes. Geoderma 1996, 69, 71–84. [Google Scholar] [CrossRef]
- Tamari, S.; Wsten, J.H.M.; Ruiz-Suárez, J.C. Testing an artificial neural network for predicting soil hydraulic conductivity. Soil Sci. Soc. Am. J. 1996, 60, 1732–1741. [Google Scholar] [CrossRef]
- Yilmaz, I.; Marschalko, M.; Bednarik, M.; Kaynar, O.; Fojtova, L. Neural computing models for prediction of permeability coefficient of coarse-grained soils. Neural Comput. Appl. 2011, 21, 957–968. [Google Scholar] [CrossRef]
- Schaap, M.G.; Leij, F.J. Using neural networks to predict soil water retention and soil hydraulic conductivity. Soil Tillage Res. 1998, 47, 37–42. [Google Scholar] [CrossRef]
- Lamorski, K.; Pachepsky, Y.; Sławiński, C.; Walczak, R.T. Using support vector machines to develop pedotransfer functions for water retention of soils in poland. Soil Sci. Soc. Am. J. 2008, 72, 1243–1247. [Google Scholar] [CrossRef]
- Nemes, A.; Rawls, W.J.; Pachepsky, Y.A. Use of the nonparametric nearest neighbor approach to estimate soil hydraulic properties. Soil Sci. Soc. Am. J. 2006, 70, 327–336. [Google Scholar] [CrossRef]
- Mckenzie, N.; Jacquier, D. Improving the field estimation of saturated hydraulic conductivity in soil survey. Aust. J. Soil Res. 1997, 35, 803–827. [Google Scholar] [CrossRef]
- Souza, E.d.; Fernandes Filho, E.I.; Schaefer, C.E.G.R.; Batjes, N.H.; Santos, G.R.d.; Pontes, L.M. Pedotransfer functions to estimate bulk density from soil properties and environmental covariates: Rio doce basin. Sci. Agric. 2016, 73, 525–534. [Google Scholar] [CrossRef] [Green Version]
- Minasny, B.; Hartemink, A.E. Predicting soil properties in the tropics. Earth-Sci. Rev. 2011, 106, 52–62. [Google Scholar] [CrossRef]



| Data | Variables | Minimum | Maximum | Mean | SD | CV (%) |
|---|---|---|---|---|---|---|
| Total (n = 378) | SSWC (cm3 cm−3) | 0.26 | 0.60 | 0.43 | 0.07 | 15.80 |
| P (%) | 42.28 | 63.39 | 51.74 | 4.00 | 7.73 | |
| BD (g cm−3) | 0.89 | 1.56 | 1.22 | 0.11 | 8.98 | |
| PNc (%) | 0.31 | 18.46 | 3.70 | 1.74 | 46.92 | |
| PC (%) | 38.11 | 58.51 | 48.04 | 3.72 | 7.74 | |
| FC (%) | 16.89 | 60.88 | 39.81 | 7.03 | 17.65 | |
| Cl (%) | 10.97 | 38.47 | 22.33 | 5.44 | 24.36 | |
| Si (%) | 8.64 | 48.97 | 28.47 | 7.47 | 26.25 | |
| Sa (%) | 29.98 | 68.79 | 49.19 | 7.68 | 15.61 | |
| SOM (%) | 0.75 | 4.77 | 2.63 | 0.69 | 26.07 | |
| KS (mm min−1) | 0.17 | 2.17 | 0.94 | 0.49 | 52.45 | |
| Modeling (n = 264) | SSWC (cm3 cm−3) | 0.26 | 0.60 | 0.44 | 0.07 | 15.81 |
| P (%) | 42.28 | 63.39 | 52.15 | 4.11 | 7.88 | |
| BD (g cm−3) | 0.89 | 1.56 | 1.20 | 0.11 | 9.45 | |
| PNc (%) | 0.31 | 18.46 | 3.76 | 1.86 | 49.45 | |
| PC (%) | 38.11 | 58.51 | 48.39 | 3.80 | 7.85 | |
| FC (%) | 16.89 | 60.88 | 40.64 | 7.44 | 18.32 | |
| Cl (%) | 10.97 | 36.24 | 21.64 | 5.09 | 23.52 | |
| Si (%) | 8.64 | 46.69 | 28.09 | 7.31 | 26.03 | |
| Sa (%) | 29.98 | 68.79 | 50.27 | 7.51 | 14.94 | |
| SOM (%) | 1.08 | 4.57 | 2.75 | 0.65 | 23.57 | |
| KS (mm min−1) | 0.17 | 2.17 | 1.05 | 0.50 | 47.13 | |
| Test (n = 114) | SSWC (cm3 cm−3) | 0.26 | 0.57 | 0.41 | 0.06 | 14.43 |
| P (%) | 43.52 | 61.45 | 50.78 | 3.58 | 7.05 | |
| BD (g cm−3) | 1.01 | 1.41 | 1.26 | 0.09 | 6.97 | |
| PNc (%) | 1.39 | 12.95 | 3.56 | 1.41 | 39.50 | |
| PC (%) | 39.38 | 58.15 | 47.22 | 3.40 | 7.20 | |
| FC (%) | 24.20 | 57.40 | 37.90 | 5.52 | 14.57 | |
| Cl (%) | 13.36 | 38.47 | 23.94 | 5.89 | 24.60 | |
| Si (%) | 11.66 | 48.97 | 29.36 | 7.79 | 26.54 | |
| Sa (%) | 30.42 | 67.06 | 46.70 | 7.51 | 16.08 | |
| SOM (%) | 0.75 | 4.77 | 2.37 | 0.71 | 29.76 | |
| KS (mm min−1) | 0.17 | 1.61 | 0.67 | 0.37 | 54.28 |
| Soil Property | PC1 | PC2 | PC3 | PC4 | PC5 | |
|---|---|---|---|---|---|---|
| Component Matrix | SSWC | 0.922 | 0.189 | 0.139 | 0.191 | 0.163 |
| P | 0.916 | 0.16 | 0.099 | 0.256 | 0.108 | |
| BD | −0.865 | −0.219 | −0.19 | −0.121 | −0.25 | |
| PNC | 0.095 | 0.115 | 0.035 | 0.984 | 0.081 | |
| PC | 0.941 | 0.118 | 0.09 | −0.186 | 0.08 | |
| FC | 0.948 | 0.153 | 0.149 | −0.003 | 0.153 | |
| Cl | −0.267 | 0.067 | −0.95 | −0.041 | −0.14 | |
| Si | −0.166 | −0.914 | 0.344 | −0.086 | −0.105 | |
| Sa | 0.35 | 0.843 | 0.337 | 0.112 | 0.202 | |
| SOM | 0.289 | 0.204 | 0.144 | 0.095 | 0.917 | |
| Eigenvalue | 4.536 | 1.752 | 1.252 | 1.151 | 1.050 | |
| Cumulative variance contribution rate | 45.358 | 62.874 | 75.391 | 86.899 | 94.402 | |
| Established PTFs | Input Variables | Formulation |
|---|---|---|
| Cosby | Sa; Cl | |
| Saxton | Sa; Cl; SSWC | |
| Wosten 1997 | BD; SOM; Cl | |
| Wosten 1999 | Si; T; BD; Cl; SOM; | |
| Li | Sa; Cl; SOM; BD | |
| Pucket | Cl | |
| Campbell | BD; Si; Cl; Sa | |
| Vereecken | Cl; Sa; SOM; BD |
| Parameter | Cosby | Saxton | Wosten 1997 | Wosten 1999 | Li | Pucket | Campbell | Vereecken |
|---|---|---|---|---|---|---|---|---|
| a | 0.378 ± 0.017 | 1.801 ± 0.036 | 6.437 ± 0.327 | 5.916 ± 0.078 | 4.829 ± 0.131 | −0.028 ± 0.002 | −1.102 ± 0.064 | 6.018 ± 0.086 |
| b | 0.008 ± 0.001 | 0.003 ± 0.0007 | −0.75 ± 0.321 | −0.049 ± 0.016 | 0.141 ± 0.047 | −0.0095 ± 0.0047 | −0.176 ± 0.028 | |
| c | −0.026 ± 0.002 | 0.031 ± 0.006 | −1.121 ± 0.242 | 0.076 ± 0.05 | −0.234 ± 0.038 | −0.0003 ± 0.0055 | 0.148 ± 0.039 | |
| d | 0.017 ± 0.004 | −0.732 ± 0.435 | −1.18 ± 0.192 | −0.035 ± 0.05 | 0.055 ± 0.077 | 0.649 ± 0.065 | ||
| e | −0.077 ± 0.01 | 0.021 ± 0.046 | 0.00099 ± 0.00058 | 0.574 ± 0.114 | −2.889 ± 0.284 | −1.687 ± 0.137 | ||
| f | 0.001 ± 0.0002 | 0.957 ± 0.193 | 0.000424 ± 0.000289 | 0.134 ± 0.073 | ||||
| g | −0.004 ± 0.002 | −0.017 ± 0.01 | −0.406 ± 0.064 | |||||
| h | 0.599 ± 0.205 | −0.214 ± 0.028 | ||||||
| i | 0.344 ± 0.049 | |||||||
| j | 0.014 ± 0.022 | |||||||
| k | 0.128 ± 0.037 | |||||||
| l | 0.0062 ± 0.0059 | |||||||
| m | 0.0036 ± 0.0048 |
| Modified PTFs | R2 | RMSE | MRE (%) | ME | AIC |
|---|---|---|---|---|---|
| Cosby | 0.335 | 0.305 | 33.717 | −0.055 | 274.970 |
| Saxton | 0.460 | 0.335 | 34.954 | −0.177 | 302.794 |
| Wosten 1997 | 0.624 | 0.226 | 27.159 | −0.032 | 216.723 |
| Wosten 1999 | 0.654 | 0.270 | 25.022 | −0.152 | 267.629 |
| Li | 0.604 | 0.232 | 25.957 | −0.029 | 220.600 |
| Pucket | 0.561 | 0.346 | 42.628 | −0.115 | 299.691 |
| Campbell | 0.481 | 0.295 | 47.058 | −0.02 | 273.876 |
| Vereecken | 0.655 | 0.235 | 28.266 | −0.052 | 219.698 |
| New PTFs | R2 | RMSE | MRE | ME | AIC |
|---|---|---|---|---|---|
| MLR1 | 0.615 | 0.272 | 24.900 | 0.057 | 255.040 |
| MLR2 | 0.694 | 0.223 | 25.002 | 0.057 | 209.812 |
| ANN | 0.769 | 0.209 | 22.248 | 0.067 | 192.610 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, Y.; He, K. Evaluation and Development of Pedo-Transfer Functions for Predicting Soil Saturated Hydraulic Conductivity in the Alpine Frigid Hilly Region of Qinghai Province. Agronomy 2021, 11, 1581. https://doi.org/10.3390/agronomy11081581
Zuo Y, He K. Evaluation and Development of Pedo-Transfer Functions for Predicting Soil Saturated Hydraulic Conductivity in the Alpine Frigid Hilly Region of Qinghai Province. Agronomy. 2021; 11(8):1581. https://doi.org/10.3390/agronomy11081581
Chicago/Turabian StyleZuo, Yafan, and Kangning He. 2021. "Evaluation and Development of Pedo-Transfer Functions for Predicting Soil Saturated Hydraulic Conductivity in the Alpine Frigid Hilly Region of Qinghai Province" Agronomy 11, no. 8: 1581. https://doi.org/10.3390/agronomy11081581
APA StyleZuo, Y., & He, K. (2021). Evaluation and Development of Pedo-Transfer Functions for Predicting Soil Saturated Hydraulic Conductivity in the Alpine Frigid Hilly Region of Qinghai Province. Agronomy, 11(8), 1581. https://doi.org/10.3390/agronomy11081581





