Suitability of Image Analysis in Evaluating Air and Water Permeability of Soil

Abstract

A comprehensive understanding of the water and air permeability of soil is necessary for modelling the transport properties which depend on soil structure. We aimed to evaluate the suitability of image analysis to estimate gas and liquid transport in soil using resin-impregnated soil blocks. The soil texture, TOC, density, porosity, air capacity (VV), air permeability (logAP), and the saturated hydraulic conductivity (logK_S) of a Cambisol developed from loess were measured. To characterise the pores, using the soil structure images, we determined the macroporosity (AA), index of soil pore-network growth rate, percolation number (logn_PER), length of pore path/unit area (PLA), and relative volume of pores overlapping top and/or bottom edge of the image (VTB). logK_S and logAP related to morphometric parameters of soil structure derived from the image analysis. The main factor controlling the soil’s infiltration was the total volume of soil pores (VV and AA). AA, PLA, VTB, and logn_PER were equally useful for characterising the soil pore system. These results will contribute to more accurate estimations of gas and liquid transport in soils and allow to obtain historical hydraulic properties and model long-term trends in the soil water regime based on the existing collections of thin sections and polished blocks.

1. Introduction

A comprehensive understanding of the water and air permeability of soil is necessary for modelling transport properties that govern numerous environmental processes and functions, including groundwater horizontal and vertical flow, transport of dissolved nutrients and contaminants, and soil aeration. This is particularly useful in water management for assessing the water and air demand of vegetation, preventing environmental pollution, and irrigation practice, which is in line with the United Nations Sustainable Development Goal 6 [1].

Various methods have been used to obtain the water and air permeability of soil. A satisfactory alternative to costly and time-consuming direct measurements is pedotransfer functions that utilise easy-obtainable basic soil parameters, such as texture, soil organic matter content, and bulk density [2]. However, the water and air permeability of soil depend on its structure, which is shaped not only by soil properties, such as texture, organic matter, carbonates, clay minerals, and sesquioxides but also by external conditions [3]. This means that even if a soil has the same physical and physicochemical properties, different structures are possible if external factors affect the soil or act in a different way. The resulting arrangement of soil structural elements can be assessed by direct measurement methods, such as imaging techniques using computed tomography or resin-impregnated soil blocks and thin sections. Various studies have used these soil preparations when conducting soil structure assessments, e.g., [4,5,6,7,8,9,10,11,12,13]. Morphological and morphometric analyses of the soil structure can significantly improve the understanding of the retention and transport processes in soils, e.g., [14,15,16,17,18]. In particular, a morphometric analysis of soil structure images allows for the quantification of structural parameters, and the identification of relationships between structure and physical properties, such as air and water permeability, and water retention. Bouma et al. [19] quantified large thin sections by examining the impact of macropores on the saturated flow through clay soil. Vogel and Roth [20,21] investigated the applicability of pore-size distribution and pore connectivity in reconstructed three-dimensional representations of the pore space in order to predict essential characteristics of soil hydraulic properties. Pagliai et al. [22,23] and Pagliai and Kutílek [24] studied the correlations between saturated hydraulic conductivity (logK_S) and differently shaped pores in soils under various management practices. Quinton et al. [25] investigated the effects of active porosity and specific pore perimeters on the hydraulic conductivity of peat using a digital image analysis of resin-impregnated samples. Bryk [26] revealed mathematical relationships between air and water permeability pore and solid-phase element number, and area in compaction index classes. Fernández et al. [27] measured the macropore shape via image analysis of thin sections and found that hydraulic conductivity and infiltration rate increased with an increasing number of elongated and irregular macropores.

Although some of these studies indicated that the pore shape may affect air and water permeability, we believe that pore size and connectivity are decisive for soil transport properties. In our earlier study of the Chernozem [28], we developed a methodology for assessing soil transport properties using correlations between the laboratory-assessed water and air permeability and morphometric indices of a soil pore system obtained from large resin-impregnated blocks. This study aims to re-examine this approach for a Cambisol in order to further evaluate the suitability of image analysis for the estimation of gas and liquid transport in soil. We hypothesise that there are: (i) relationships between water and air permeability and structural parameters, and (ii) relationships between texture, particle and bulk density, total porosity, air capacity, total organic carbon and structural parameters. Based on this, the air and water permeability (AP and K_S), texture (c_S, c_SI, c_C), particle and bulk density (ρ_S and ρ_D), total porosity (P_O), air capacity (VV), and total organic carbon (TOC) of a forest Eutric Cambisol developed from loess were measured. To characterise the pores, we used soil structure images to determine the macroporosity (AA), index of soil pore-network growth rate (v_G), percolation number (logn_PER), length of pore path/unit area (PLA), and relative volume of pores overlapping the top and/or bottom edges of the image (VTB). The relationships among the morphometric, physical, and chemical parameters were examined using a linear regression model.

2. Materials and Methods

2.1. Material

This study was conducted on an Eutric Cambisol developed from loess, which contains a sequence of horizons O-A-AB-Bw-BC-C-Ck, located in Wola Gródecka (50°29′43″ N, 23°37′03″ E, SE Poland) in a mesophytic deciduous forest composed of oak Quercus robur and Q. petraea, hornbeam Carpinus betulus, and lime Tilia cordata–plant community Tilio-Carpinetum Tracz. 1962. The samples were collected in 2010 from seven soil layers representing distinguished genetic horizons at a depth of 0–146 cm (

Table 1. Selected physical and chemical properties of the studied Cambisol.

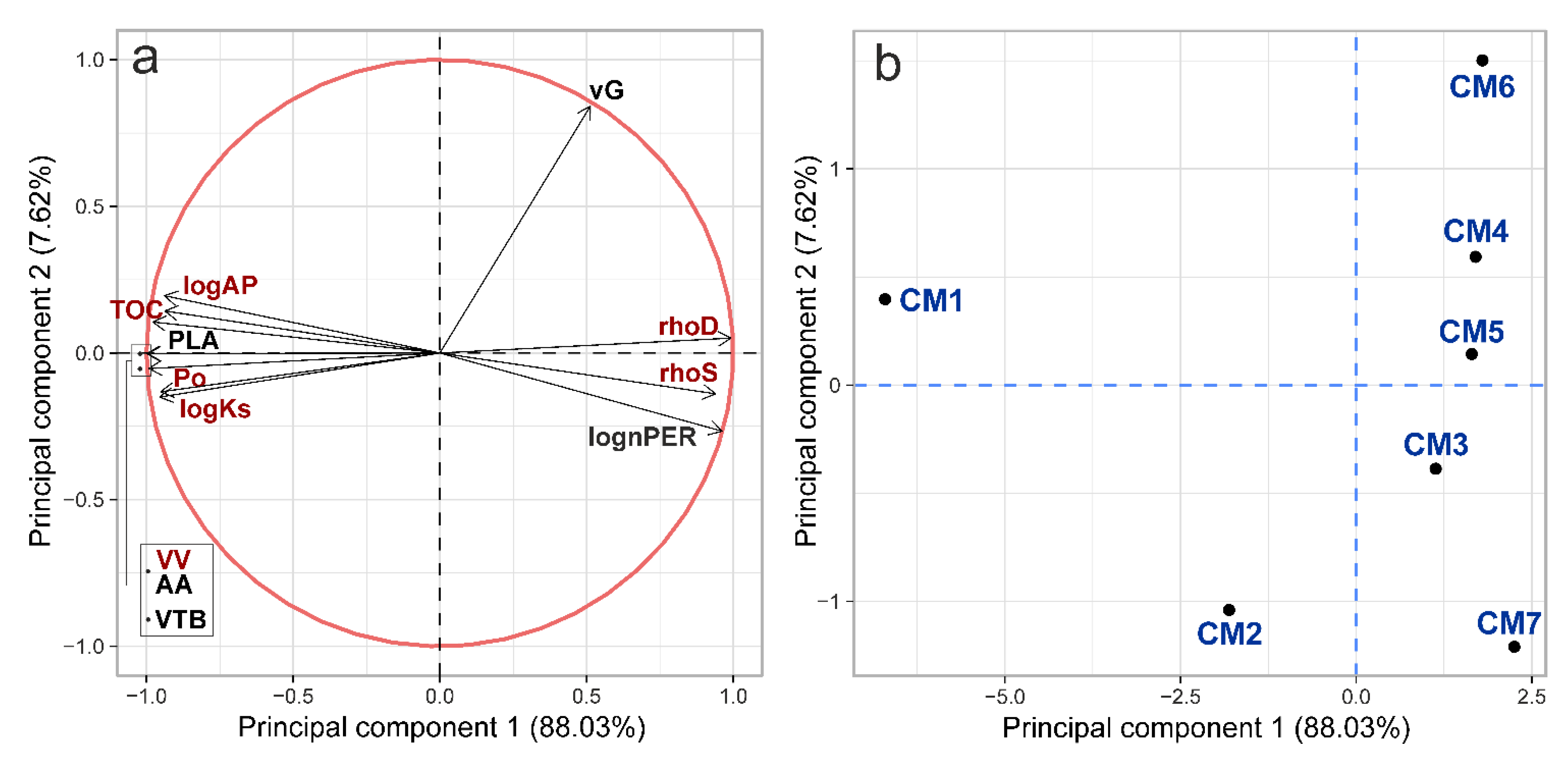
Layer	CM1	CM2	CM3	CM4	CM5	CM6	CM7
Horizon	O-A	A	AB	Bw	BC	C	Ck
Horizon depth (cm)	0–5 – 5–10/15	5–10/15	10/15–30/45	30/45–67	67–85	85–120/135	>120/135
Sampling depth (cm)	0–8	6–14	20–28	50–58 and 54–62	70–78 and 74–82	100–108	138–146
Sand, cS (g g−1)	–	0.210	0.180	0.180	0.170	0.180	0.130
Silt, cSI (g g−1)	–	0.720	0.720	0.590	0.650	0.665	0.750
Clay, cC (g g−1)	–	0.070	0.100	0.230	0.180	0.155	0.120
TOC (mg g−1)	316.8	26.3	6.3	2.9	2.9	1.6	3.5
CaCO3 (mg g−1)	0	0	0	0	0	0	110
pHH2O	5.68	5.72	4.77	5.51	6.07	6.52	8.17
pHKCl	5.37	5.21	4.06	4.16	4.71	5.03	7.95
Bulk density, ρD (g cm−3)	0.44 ± 0.10	0.90 ± 0.07	1.31 ± 0.04	1.44 ± 0.01	1.44 ± 0.01	1.38 ± 0.04	1.45 ± 0.03
Particle density, ρS (g cm−3)	1.48	2.55	2.61	2.62	2.66	2.66	2.65
Total porosity, PO (cm3 cm−3)	0.703	0.647	0.498	0.450	0.459	0.481	0.453

Note: ρ_D values are mean ± standard deviation, n = 6.

). We took the soil samples with disturbed structure (in bags), core samples (in metal cylinders, Figure 1a), and samples of preserved structure (in metal boxes, Figure 1b).

2.2. Laboratory Tests

Samples with a disturbed structure were used to determine the soil texture (sand 0.05–2 mm, c_S; silt 0.002–0.05 mm, c_SI; and clay <0.002 mm fraction content, c_C; g g⁻¹, by a combination of the hydrometer and the wet-sieve methods [29]), TOC, mg g⁻¹ [30], soil pH in distilled water and in a 1 mol dm⁻³ KCl [31], the amount of carbonates (CaCO₃, mg g⁻¹ [32], and particle density (ρ_S, Mg m⁻³ [33]).

From each of the seven soil layers, 12 soil samples with a preserved structure were collected vertically in metal cylinders with a volume of 100 cm³ (Figure 1a). Of the 12, 6 core samples were used to determine the dry soil bulk density (ρ_D, Mg m⁻³), the maximum soil water content (WV₀, cm³ cm⁻³), and soil water content at a potential of −15 kPa (WV, cm³ cm⁻³) while equilibrated on pressure ceramic plates. Next, the relative volume of the air-filled pores was determined, i.e., the share of macropores with equivalent diameters greater than approximately 20 μm (VV = WV₀ − WV; cm³ cm⁻³). In the same state of soil water saturation, AP was measured in a device designed to test the permeability of moulding sands (type LPiR-2e, Multiserw-Morek, Brzeźnica, Poland). During the measurements, pores with an equivalent diameter of less than approximately 20 μm were filled with water, and larger pores were accessible for air. As the measurements were conducted at a constant ambient temperature (20 ± 0.5 °C), the dynamic viscosity of the air was not considered. The results of the AP analysis are given in 10⁻⁸ m² Pa⁻¹ s⁻¹. Meanwhile, the remaining 6 core samples, were used to measure the K_S (cm d⁻¹) using the ICW laboratory permeameter (Eijkelkamp, Giesbeek, The Netherlands) via the constant head method. The P_O (cm³ cm⁻³) was calculated based on the ρ_D and ρ_S.

2.3. Preliminary Image Analysis

Based on the aforementioned layers (Table 1), two samples with a preserved structure were obtained from the vertical plane of the soil profile and placed into metal boxes measuring 8 cm × 9 cm × 4 cm (height × width × depth, Figure 1b), with the 8 cm × 9 cm side facing forward. Soil samples were dried at room temperature and then impregnated with a resin solution following a previously described method [28]. After hardening, each soil sample was cut twice to form approximately 8 cm × 9 cm × 1 cm slices, which revealed four inner surfaces that were then polished. Some sides were not suitable for image analysis because of damaged edges. For each tested layer CM2, CM4, CM5 and CM1, CM3, CM6, CM7, respectively eight and seven soil block faces of approximately 8 cm × 9 cm were obtained. Then, the soil block faces were scanned using an Epson Perfection 1200 Photo scanner at a resolution of 1200 dpi × 1200 dpi with 24-bit colour depth. Each image was approximately 4000 pixels × 4000 pixels. Pictures of the representative soil blocks for each layer are shown in Figure 2. Based on the soil blocks and their enlarged photos, a morphological structure analysis of the tested Cambisol was performed. The macrostructure was described using terminology provided by Aguilar et al. [34] and Słowińska-Jurkiewicz et al. [9].

In the next step, the blue channel was isolated from the colour images as it had the best contrast. The obtained images were recorded in 256 grey levels, with prior improvement of their contrast and intensity. The subsequent operations on the images were made using the image analysis program Aphelion [35]. First, the images were given thresholds, wherein the threshold level, which is the limit value of the grey level between the solid phase and pores, was selected manually based on the brightness histogram and visual evaluation of the enlarged soil block photo. In the obtained binary (black and white) images, the pores were marked with white, while the solid phase sections were marked with black. In total, 7–8 binary images were prepared for each layer (CM1–CM7). The white objects, which denote the pore cross-sections, were then subjected to a series of morphological operations.

First, the binary images were closed. The morphological closing operation was performed on 17 levels, i.e., which involved the square structuring elements sized from 1 to 17. For each image in each layer at each of the closed 0–17 levels, the soil macroporosity was measured as the ratio of the area occupied by the pore cross-sections over the area of the entire image. Then, for each soil layer (CM1–CM7) at each closing level (0–17), the mean macroporosity was calculated using seven or eight closed binary images. In this respect, under the laws of stereology [36], the relative area of the obtained macropores (AA) was equal to the relative volume of the macropores in the analysed soil samples. Therefore, the AA values would be further expressed in cm³ cm⁻³. The selected scanning resolution limited the minimum diameter of the measured object to 21.2 μm. Therefore, the AA value corresponded to the relative volume of the pores with an equivalent diameter greater than 21.2 μm. The AA could therefore be related to the macroporosity measured at a soil water potential of −15 kPa, which corresponds to the shares of pores with equivalent diameters above approximately 20 μm (VV). Then, for each soil layer, the mean AA at the 0–17 closing levels and VV were compared, wherein the closing level was selected to pair the most similar values of macroporosities obtained via image analysis, AA, and via laboratory measurement, VV. We obtained the following set of binary images representing the analysed layers of the Cambisol: CM1-c0, CM2-c0, CM3-c10, CM4-c4, CM5-c4, CM6-c4, and CM7-c17 (Figure 2), wherein the suffixes -c0, …, -c17 denote the level of closing.

2.4. Extended Image Analysis

For each image, the morphological operations and calculations were performed on the pore cross-sections and then the means for each layer were calculated. First, a series of dilations were performed by increasing the size of the square structuring element from k = 1 to n. The dilations began from the relevant image’s initial AA and terminated when macroporosity reached 1, in order to determine the number of dilations, n. This allowed us to calculate the v_G (cm³ cm⁻³), which reflects the spatial distribution of soil pores. The growth-rate index was calculated as: v_G = (1 − AA)/n.

Then, the number of dilation steps (n_PER) was assessed at which all the soil pores merged into a continuous network during the execution of a series of dilations, wherein the square structuring element was sized from k = 1 to n. This phenomenon was accompanied by changing the Euler’s number sign (connectivity number, ε) for the binary image from positive to negative [37,38,39]. The n_PER parameter depends on the arrangement of pore cross-sections. It was assumed that the n_PER [40,41] corresponded to ε = 0. To calculate the n_PER, the lowest positive ε_k value, the highest negative ε_k+1 value, and the corresponding n_k and n_k+1 values were determined. Subsequently, by solving the set of two linear equations with the two unknowns a, b: n_k = a·ε_k + b; n_k+1 = a·ε_k+1 + b; and assuming that for ε = 0 and n_PER = b, the following was calculated: n_PER = n_k − ε_k[(n_k+1 − n_k)/(ε_k+1 − ε_k)] = n_k − [ε_k/(ε_k+1 − ε_k)].

The length of the pore path/unit area (PLA, cm cm⁻²) was measured after determining the minimal skeleton of the pore systems in the images.

The volumes of the pores intersecting the 10-pixel-wide edge of the image were also calculated. As such pores may be construed as coming into contact with the external environment, they can introduce water and air into the soil sample. The VTB (cm³ cm⁻³) was also determined.

2.5. Statistical Analyses Laboratory Tests

A one-way analysis of variance (ANOVA) was used to compare the measured parameters for layers CM1–CM7. Subsequently, a Tukey’s honestly significant difference test was performed at p < 0.05. The soil parameters logK_S, logAP, and VV were measured with six replicates for each studied layer. The morphometric parameters AA, VTB, logn_PER, v_G, and PLA were assessed using the soil structure images, with seven replicates for the CM1, CM3, CM6, and CM7 layers, and eight replicates for the CM2, CM4, and CM5 layers. A principal component analysis (PCA) was performed to examine the relationships between the studied parameters and layers. Linear regressions were then calculated to further evaluate the parameter relationships obtained from image analysis, including AA, VTB, logn_PER, v_G, and PLA, as well as the values of the parameters obtained from laboratory measurements, including c_S, ρ_D, ρ_S, P_O, logK_S, logAP, VV. The regressions were estimated for seven pairs of variables (CM1–CM7), except for the relationships with c_S, in which six pairs of variables were tested (CM2–CM7). As there was a large range of air and water permeability values, logarithmic data were used. The statistical analyses were executed in the R software environment [42].

3. Results

3.1. Macrostructure

Representative images of the Cambisol macrostructure and their corresponding binary images are shown in Figure 2 (left and right panel, respectively). In the organic horizon O of the soil (the upper part of the CM1 layer), plant remnants (a) that were not fully decayed and loosely arranged were visible. The dark mineral horizon A (the lower part of the CM1 layer; CM2 layer), located directly underneath the organic layer, showed an aggregate structure with strongly-developed crumbs in the continuous pore space (b), wherein roots and plant remnants were also discernible (c). In some zones, the soil groundmass was separated by planes creating sub-angular blocks (d). The CM3 layer exhibited higher compaction, with zones of non-aggregate structure with biogenic channels (e) and tiny vughs typical of loess (<1 mm–Nadelstichporen, “pinholes”); (f). In these soil layers, plant remnants and tree roots were very abundant (c). The CM4 and CM5 soil layers revealed bioturbations caused by extensive soil fauna activity. Consequently, numerous channels were created, often characterised with large widths and filled with aggregates, including angular or sub-angular blocks or zoogenic crumbs (g). Therefore, the CM4 and CM5 layers had aggregate structures (h) with weakly, moderately, and strongly-developed aggregates. The CM6 and CM7 layers had a non-aggregate structure with tiny vughs (f). Further, in these layers, some effects of soil fauna activity were visible as rare channels of 10 mm in diameter created by earthworms (k).

3.2. Chemical and Physical Properties

Selected chemical and physical properties of the studied Cambisol are summarised in Table 1. The CM2–CM7 layers of the analysed Cambisol had a silt loam texture. The TOC was 316.8 mg g⁻¹ in the organic horizon and gradually decreased from 26.3 mg g⁻¹ to approximately 3 mg g⁻¹ in the mineral part of the soil profile. A total of 110 mg g⁻¹ of Carbonates was present in the Ck horizon below 120 cm. The ρ_S gradually increased with depth from 1.48 Mg m⁻³ in the organic horizon to 2.55–2.66 Mg m⁻³ in the lower horizons.

The Cambisol hydraulic conductivity was the highest in the O and A horizons (

Table 2. Water and air properties and morphometric parameters for the studied Cambisol. Results of 1-way ANOVA; for each parameter, different letters denote statistically different values between layers at p < 0.05 according to Tukey’s honestly significant difference test.

Layer	Horizon	Macroporosity by Image Analysis, AA (cm3 cm–3)	Air Capacity, VV (cm3 cm–3)	Air Permeability, logAP	Hydraulic Conductivity, logKS	Relative Length of Pore Path, PLA (cm cm–2)	Relative Volume of Pores overlapping the Top and Bottom Edge of the Image, VTB (cm3 cm–3)	Pore-Network Growth-Rate, vG (×10–3 cm3 cm–3)	Percolation Number, nPER
CM1	O-A	0.5183 ± 0.0379	0.332 ± 0.064	3.278 ± 0.609	3.710 ± 0.290	22.558 ± 0.600	0.4624 ± 0.0577	6.40 ± 1.36	0.26 ± 0.45
		c	c	c	c	d	c	ab	a
CM2	A	0.2905 ± 0.1038	0.224 ± 0.052	1.956 ± 1.046	3.092 ± 1.386	13.770 ± 4.383	0.1874 ± 0.1276	6.07 ± 1.93	3.93 ± 3.19
		b	b	b	bc	c	b	a	b
CM3	AB	0.1681 ± 0.0459	0.165 ± 0.016	1.354 ± 0.852	1.900 ± 0.860	3.835 ± 0.976	0.0482 ± 0.0472	8.51 ± 1.32	12.22 ± 2.67
		a	ab	ab	ab	ab	a	ab	d
CM4	Bw	0.1391 ± 0.0287	0.141 ± 0.016	1.603 ± 0.187	1.427 ± 0.854	5.168 ± 0.965	0.0093 ± 0.0101	10.91 ± 1.85	9.31 ± 1.61
		a	a	b	a	b	a	bc	cd
CM5	BC	0.1262 ± 0.0224	0.131 ± 0.008	1.329 ± 0.193	1.985 ± 1.110	4.960 ± 0.815	0.0030 ± 0.0019	9.99 ± 2.30	9.32 ± 1.63
		a	a	ab	ab	b	a	abc	cd
CM6	C	0.1341 ± 0.0216	0.135 ± 0.024	1.099 ± 0.396	1.611 ± 0.127	6.501 ± 0.853	0.0100 ± 0.0184	14.60 ± 2.55	6.72 ± 0.92
		a	a	ab	ab	b	a	c	bc
CM7	Ck	0.1179 ± 0.0288	0.117 ± 0.020	0.458 ± 0.046	1.514 ± 0.148	1.890 ± 0.257	0.0353 ± 0.0410	6.38 ± 1.18	23.25 ± 2.60
		a	a	a	a	a	a	ab	e

Note: values are mean ± standard deviation; n = 6 for VV, logAP, logK_S; n = 7 for AA, PLA, VTB, v_G, n_PER in CM1, CM3, CM6, CM7, and n = 8 for these parameters in CM2, CM4, CM5; AP in 10⁻⁸ m² Pa⁻¹ s⁻¹; K_S in cm d⁻¹.

). In the AB, Bw, and BC horizons, the mean hydraulic conductivities were comparable, showing relatively high variability, which was expressed through large standard deviations. The hydraulic conductivity in the C and Ck horizons was similar to those in the upper horizons, however the dispersion of the logK_S values in both horizons was much smaller.

The air permeability, logAP, in the Cambisol pedon was the highest in the superficial soil layer encompassing the O–A horizons. From a statistical perspective, the logAP values were similar in the other horizons. However, these values generally decreased with depth. The relative volume of air-filled pores at −15 kPa, VV, decreased slowly with depth and, similar to the aforementioned parameters, the largest values were observed in the upper horizons of O and A.

3.3. Morphometric Characteristics of Soil Pores and Their Relationship with Chemical and Physical Soil Properties

For the binary images (Table 2, Figure 2), the morphometric parameters were determined to characterise the volume and arrangement of the soil pores. The relationship between the image analysis results and the laboratory measurements of selected chemical and physical soil properties was verified using PCA (Figure 3) and linear regression equations (

Table 3. Relationships among physicochemical and morphometric parameters. ρ_S–particle density; ρ_D–bulk density; P_O–total porosity; c_S–sand; TOC–total organic carbon; VV–air capacity at −15 kPa; AP–air permeability at −15 kPa; K_S–hydraulic conductivity; AA–macroporosity by image analysis; PLA–relative length of pore path; n_PER–percolation number; VTB–relative volume of pores overlapping the top and bottom edge of the image.

Linear Regression Equations	R2	p	Linear Regression Equations	R2	p
VV = −0.163 ** ρS + 0.578 ***	0.823	0.0027	lognPER = 1.376 ** ρS − 2.640 **	0.869	0.0014
VV = −0.197 *** ρD + 0.413 ***	0.981	<0.0001	lognPER = 1.543 ** ρD − 1.097 *	0.856	0.0018
VV = 0.708 *** PO − 0.195 *	0.900	0.0007	lognPER = −5.356 ** PO + 3.571 **	0.720	0.0098
VV = 0.876 *** cS	0.977	<0.0001	lognPER = 5.271 ** cS	0.846	0.0021
VV = 6.0×10−4 ** TOC + 0.147 ***	0.811	0.0036	lognPER = −0.005 ** TOC + 1.009 ***	0.869	0.0014
logKS = −2.207 *** ρD + 4.813 ***	0.925	0.0003	AA = 1.911 *** VV − 0.126 ***	0.990	<0.0001
logKS = 8.290 *** PO − 2.194 **	0.948	0.0001	PLA = 92.370 *** VV − 8.046 **	0.930	0.0003
logKS = 11.077 *** cS	0.946	0.0001	PLA = 41.870 *** AA	0.965	<0.0001
logAP = −1.783 ** ρS + 5.972 **	0.734	0.0086	VTB = 2.169 *** VV − 0.278 ***	0.960	0.0001
logAP = −2.079 ** ρD + 4.066 ***	0.797	0.0043	VTB = 1.144 *** AA − 0.136 ***	0.988	<0.0001
logAP = 0.007 * TOC + 1.246 **	0.716	0.0102	VTB = 0.022 *** PLA − 0.078	0.897	0.0008
logAP = 7.623 *** cS	0.943	0.0002	lognPER = −7.875 *** VV + 2.147 ***	0.887	0.0010
AA = −0.320 ** ρS + 1.000 ***	0.872	0.0013	lognPER = −4.134 *** AA + 1.629 ***	0.903	0.0006
AA = −0.379 *** ρD + 0.666 ***	0.981	<0.0001	lognPER = −0.085 *** PLA + 1.456 ***	0.935	0.0002
AA = 1.345 ** PO − 0.496 **	0.880	0.0011	lognPER = −3.526 ** VTB + 1.127 ***	0.861	0.0016
AA = 0.947 *** cS	0.920	0.0004	logAP = 9.166 *** VV	0.968	<0.0001
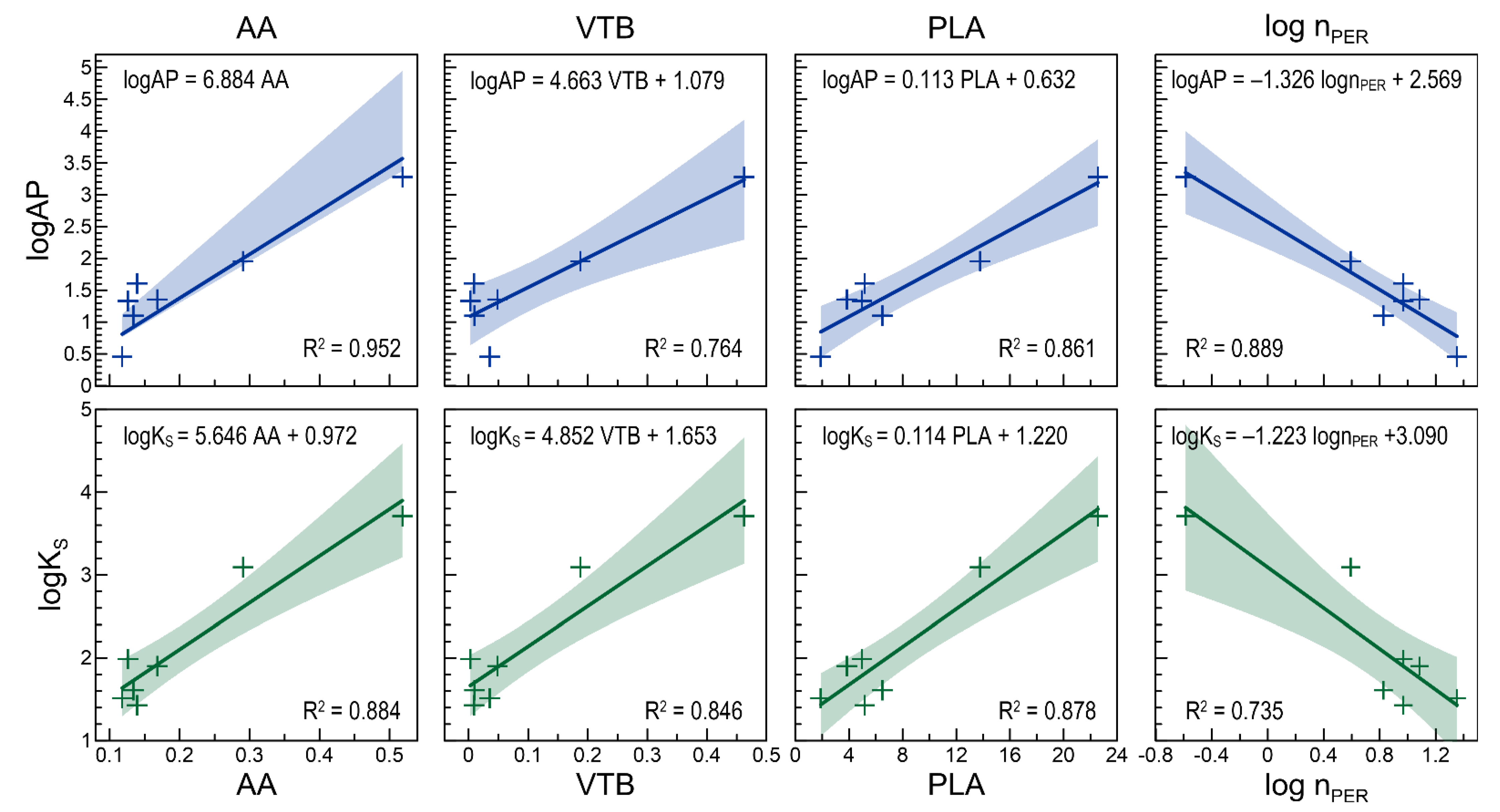
AA = 0.001 ** TOC + 0.152 **	0.864	0.0015	logAP = 6.884 *** AA	0.952	<0.0001
PLA = −14.918 ** ρS + 45.104 **	0.750	0.0073	logAP = 0.113 ** PLA + 0.632 *	0.861	0.0016
PLA = −18.486 *** ρD + 30.461 ***	0.946	0.0002	logAP = 4.663 ** VTB + 1.079 **	0.764	0.0063
PLA = 67.129 *** PO − 27.013 **	0.893	0.0008	logAP = −1.323 *** lognPER + 2.570 ***	0.891	0.0009
PLA = 36.191 ** cS	0.776	0.0055	logKS = 12.057 *** VV	0.985	<0.0001
PLA = 0.055 ** TOC + 5.542 *	0.749	0.0074	logKS = 5.646 ** AA + 0.972 **	0.872	0.0013
VTB = −0.370 *** ρS + 1.019 ***	0.889	0.0009	logKS = 0.114 ** PLA + 1.220 **	0.878	0.0012
VTB = −0.432 *** ρD + 0.624 ***	0.965	<0.0001	logKS = 4.852 ** VTB + 1.653 ***	0.846	0.0021
VTB = 1.527 ** PO − 0.697 **	0.852	0.0019	logKS = −1.223 ** lognPER + 3.090 ***	0.735	0.0085

*, **, *** significance levels for linear regression coefficients.

).

The PCA model of the physicochemical and morphometric parameter results explained 95.65% of the data variation, wherein the first principal component (PC1) explained that 88.03% of the variance was controlled by almost all variables, and the second component (PC2) explained 7.62% of the variance, in which the most important variable was the v_G.

The plot for the variable loadings (Figure 3a) revealed their correlation structure. In particular, three groups of variables were distinguishable. The first group included logAP, PLA, TOC, VV, AA, VTB, P_O, and logK_S, which were strongly negatively correlated with the PC1. The second group comprised ρ_D, ρ_S, and logn_PER which were strongly positively correlated with the PC1. Both of these groups were located on opposite sides of the graph, revealing a strong negative correlation between them. The third group comprised only v_G which was strongly positively correlated with the PC2, and weakly correlated with the other groups. The vectors of all the variables practically reached the unit circle, indicating their high impact on the PCs.

The score plot (Figure 3b) revealed three distinct groups of soil layers: CM1, CM2, and CM3–CM7. Specifically, the distant location of the organic CM1 was observable as it differed from other layers, particularly in terms of TOC and ρ_D. Further, the arrangement of the points on the plot reflected the TOC and ρ_D values for the layers tested. In particular, the points of the layers with high TOC or ρ_D values were located on the same side of the score plot as the TOC or ρ_D vector on the loading plot (Figure 3a), and those with low TOC or ρ_D values were located on the opposite side.

The linear regression equation results (Table 3) showed the quantitative relationships among the studied parameters. As a result of the intentional equalisation of the macroporosities, AA, and air capacities, VV, they were very strongly related. Similarly, the relative lengths of the pore path, PLA, were closely associated with the VV values, as the length of pores is strongly dependent on the relative area, as well as the volume, of the pore system.

The relative volume of the air-filled pores, VV, was strongly negatively related to the bulk density, ρ_D (Table 3). An opposite relationship was observed between VV and P_O because of the strong negative correlation between ρ_D and P_O (P_O = −0.264 *** ρ_D + 0.842 ***, R² = 0.953 at p = 0.0001). The volume of the air-filled pores increased with increasing sand (c_S), and increasing organic matter (TOC) or decreasing particle density (ρ_S) because the latter two parameters were correlated (TOC = −269.835 *** ρ_S + 715.650 ***, R² = 0.998 at p < 0.0001). As VV, AA, PLA, and VTB were strongly correlated, the relationships between VV and the physicochemical soil properties could be generally transferred to these morphometric parameters, and the relevant correlations listed in Table 3 do not require further discussion.

The Cambisol hydraulic conductivity, logK_S, was found to depend on the total soil pore volume, as described by P_O (Table 3). However, stronger relationships were noted between the air and water permeabilities, logK_S and logAP, and the air-filled pores, VV. Consequently, logK_S and logAP exhibited similar correlations as VV with ρ_D, ρ_S, and TOC.

Of particular interest were the relationships between the parameters characterising the soil’s ability to transport water and air (logK_S and logAP) and the pore-describing parameters obtained from the image analysis (Figure 4, Table 3). The logAP and logK_S had comparable relationships with the morphometric parameters of the soil structure. The image analysis revealed that the logK_S and logAP were strongly related to AA, PLA, VTB, and the logn_PER (Figure 4). In most cases, with the exception of VTB, the observed relationships were stronger for logAP than for logK_S.

For the efficient transport of fluids into the soil, the continuity of the pore system is important. The image analysis performed on the 2D soil blocks revealed that in 17 of the 52 images representing soil structure (CM1-c0 × 6, CM2-c0 × 2, CM4-c4 × 4, CM5-c4 × 2, CM6-c4 × 2, and CM7-c17 × 1) pores were detected that connected the top and bottom edges of the image, thereby forming continuous paths for vertical air or water movement in the soil. For the remaining 67% of images, the volume of such pores yielded zero, therefore this parameter was not applicable in further calculations. However, our previous studies [28] confirmed that the relative volume of pores overlapping the top and/or bottom edge of the image, VTB, was a good estimate of the volume of pores responsible for the vertical transport of water and air in the soil. Nevertheless, the correlations of logAP and logK_S with VTB were, contrary to expectations, weaker than those with the macroporosity by image analysis, AA (Figure 4).

Another parameter that characterises the soil pore system is the v_G (Table 2). The v_G index values gradually increased in the subsequent layers of the studied Cambisol, reaching a maximum in the CM6 layer. Further, low values were recorded in the CM1, CM2, CM3, and CM7 layers. The v_G index did not exhibit statistically significant linear relationships with logK_S or logAP.

The percolation number, n_PER, reflects the spatial distribution of soil pore cross-sections and is determined by the number of dilation steps required to obtain a continuous permeable pore system from the initial pore system shown in the binary images (right panel of Figure 2). The larger the distance between soil pores, the greater the n_PER, because more dilations must be performed to create a continuous pore network. The n_PER varied in the profile of the studied soil, in which its lowest value was recorded in the CM1 layer and its highest was–in the CM7 layer. Meanwhile, in the CM2–CM6 layers, the n_PER values did not exhibit a clear trend. Further, the dependence of the n_PER on the soil parameters measured in the laboratory as well as the morphometric parameters was analysed. Based on these analyses, many strong linear dependencies were revealed between the logn_PER and other parameters. In particular, the logn_PER correlated positively with ρ_D and ρ_S, and negatively with P_O, TOC, and VV (Table 3). Moreover, its relationships with PLA, AA, and VTB were negative and weaker than those recorded among AA, PLA, and VTB, even though the high R² (0.935) for the logn_PER–PLA correlation was noteworthy (Table 3). As the n_PER describes the arrangement of soil pore cross-sections, its relationships with water and logAP were of special interest. The results showed that the logAP value decreased significantly with increasing logn_PER, and the relationship between logn_PER and logK_S was similar, although slightly weaker (Figure 4).

4. Discussion

In this study, we aimed to assess the water and air permeability of a forest Cambisol using 2D image analyses. For the soil structure images, we determined the morphometric parameters that characterised the volume and arrangement of soil pores and then identified relationships between the image analysis results and the laboratory measurements of selected chemical and physical soil properties.

We obtained statistically significant linear relationships between the basic soil properties including: the bulk (ρ_D) and particle (ρ_S) density, total porosity (P_O), organic matter (TOC), and the sand (c_S), as well as between the studied morphometric structure parameters including: the macroporosity by image analysis (AA), length of pore path per unit area (PLA), the relative volume of pores overlapping the top and/or bottom edge of the image (VTB), and the percolation number (logn_PER). These associations confirmed that the soil structure is closely related to soil physicochemical properties. Soil bulk density is the ratio of the total mass of solids to the total volume of the soil and thus it reflects the state of soil compactness. The process of soil compaction first causes a decrease in the volume of the largest pores. Correspondingly, a smaller amount of macropores >20 μm (VV) was observed for the soil layers with higher bulk densities. The VV also increased with increasing c_S and increasing TOC or decreasing ρ_S, because the latter two parameters are correlated. The VV growth could be attributed to the ability of these soil components to reduce soil compactness, by lowering the mechanical stability of the large peds (sand) and by increasing the aggregate stability (organic matter), which in turn promoted the formation of pores.

The Cambisol water permeability (logK_S) correlated positively with P_O, while both air permeability (logAP) and logK_S correlated more strongly with VV. These relationships were justified because it was expected that, in general, the largest pores would govern the flow of air and water through the soil, thereby affecting the value of Ks and the logAP. Fernández et al. [27] also confirmed that P_O and AA were among the best indicators for water infiltration, filtering and storage.

Texture, organic matter content, and bulk density are generally considered when designing pedotransfer functions in order to calculate soil hydraulic conductivity. For example, based on these basic soil parameters, the Database of Hydraulic Properties of European Soils (HYPRES) was created [2]. Our study showed that both logK_S and logAP correlated with ρ_D, and that logAP also correlated with ρ_S and TOC, as indicated by the linear regression equations. Nevertheless, no statistically significant relationships were observed between logAP, logK_S and texture or between logK_S and TOC. Our results support the findings of Jarvis et al. [3], who reported that the hydraulic conductivity of the topsoil is only weakly related to texture, depending more on the bulk density. However, they stated that hydraulic conductivity was significantly related to organic carbon content. The limited or varying number of statistically valid relationships between soil permeability and basic physicochemical characteristics may cause difficulties in determining the soil transport properties via the aforementioned pedotransfer functions. Meanwhile, other factors may determine the permeability of the soil. The K_S can change rapidly in the soil profile in the presence of large pores, inducing preferential flow [43], or impermeable layers. The dominant factor controlling the flow processes in soil is, thus, its structure (e.g., [3]).

Consequently, it is challenging to model hydraulic conductivity with satisfactory predictive power using only basic soil physical parameters [43,44]. For this reason, as presented in a review by Patil and Singh [45], other soil parameters were included in the pedotransfer functions to improve their accuracy and reliability. The authors noted the application of data on water retention, clay mineralogy, mechanical properties (like the coefficient of linear extensibility), calcium carbonate content, and cation exchange capacity of clay soils. Another review on the estimation of saturated hydraulic conductivity with pedotransfer functions [46] indicated that soil structural effects on K_S were rarely considered in the estimation of K_S. As suggested by the authors, one of the reasons for this was that soil structure characteristics were generally difficult to measure and quantify. This issue was also earlier highlighted by Vereecken et al. [47], who suggested that hydrological databases should be supplemented with morphometric indices that reflect the arrangement of the soil structural components in order to enable further improvement of existing pedotransfer functions.

In our study on the Cambisol developed from loess of silt loam texture, we identified the correlations of logK_S and logAP with the morphometric parameters of soil structure derived from an image analysis. We found strong linear relationships of logK_S and logAP with AA, PLA, VTB, and logn_PER. Further, the main factor controlling the soil’s infiltration ability was the total volume of soil pores, as demonstrated by the laboratory measurement (VV) and image analysis (AA) results.

The index of soil pore-network growth rate (v_G), depending on the spatial distribution of pore cross-sections was, in general, smaller when there were larger initial pore volumes and lower pore numbers, indicating higher pore interconnectivity in the 2D images of the soil structure. Low v_G values were recorded in the O and A horizons as well as the Ck and AB horizons. These low values signify the continuous pore space and a relatively high pore volume in the upper Cambisol layers, which resulted from the aggregate soil structure. In addition, the low v_G values in the subsoil layers could be associated with the applied initial procedure of image transformation to equalise the AA and VV. In particular, the images representing the AB and Ck horizons, subjected to a relatively large number of closings, showed higher pore volumes and interconnectivities in the 2D image. It was stated that the v_G index did not exhibit statistically significant linear relationships with logK_S or logAP.

The percolation number (logn_PER) also reflects the arrangement of soil pore cross-sections. Its relationships with PLA, AA, and VTB were negative and weaker than those recorded among AA, PLA, and VTB, although there was a strong relationship between logn_PER and PLA. Further, the logn_PER was negatively correlated with logAP and logK_S.

The measured morphometric parameters, AA, PLA, VTB, and logn_PER, correlated strongly. As a result, they can be used interchangeably, even though each parameter describes a slightly different attribute of the soil pore system. For the studied Cambisol, all the proposed morphometric indices presented strong linear relationships with logK_S and logAP, with R² ≥ 0.735 at p < 0.01, which is consistent with the results of our previous research [28]. In comparison with the previously studied Chernozem, however, we observed a slightly different correlation between the air and water permeability and the indices of the spatial distribution of pore cross-sections (v_G, logn_PER). The robustness of the studied relationships between the structural characteristics and the soil transport data must therefore be further tested with a larger population of soils of various textures and structures.

Our study revealed that the image analysis using resin-impregnated soil blocks was useful in evaluating the air and water permeability of the soil. Thus, the methods employed herein will contribute to more accurate estimations of gas and liquid transport in soils and broaden the knowledge on sediment connectivity, a key issue to understand the hydrological cycle [48,49]. Despite the increasing recognition of X-ray computed tomography in soil structure research, resin-impregnated soil thin sections or polished blocks continue to be a valuable method for analysing the soil pore space and aggregates via direct geometric visualisation [50,51]. A review of the literature indicates that collections of resin-impregnated soil samples have existed in research centres globally for several decades. Recent studies show that such collections are continually being enlarged (Section 1). These durable soil structure samples can therefore be a potential source of current as well as historical information to evaluate site-specific soil hydraulic properties for modelling long-term trends in the soil water regime. According to Bayabil et al. [52], the soil parameter spatial variations have substantial implications for hydrological modelling and effectively planning land and water management practices. Thus, the availability of soil data that adequately represent actual field conditions is critical. We propose that the information regarding soil pore arrangement drawn from the soil structure images, as well as the basic soil physical and chemical parameters, can help to refine both current and past simulations of air and water permeabilities by accounting for specific local conditions and soil management types.

5. Conclusions

Our study revealed that an image analysis of soil structure using resin-impregnated soil blocks was useful in evaluating air and water permeability. We found that saturated hydraulic conductivity (logK_S) and air permeability at a potential of −15 kPa (logAP) had statistically significant relationships (R² ≥ 0.735 at p < 0.01) with morphometric soil structure parameters that were derived from image analysis, including macroporosity (AA), relative length of pore path (PLA), relative volume of pores contacting with top and bottom edge of the image (VTB), and percolation number (logn_PER). Further, the main factor controlling the soil’s infiltration ability was the total volume of soil pores, as demonstrated by the laboratory measurements of air-filled porosity (VV) and macroporosity by image analysis (AA).

Due to the strong relationships between AA, PLA, VTB, and logn_PER, the parameters proved to be equally useful for characterising the soil pore system, of which the first three indices refer to the pore volume, and the last denotes the arrangement of pore cross-sections. These parameters can be incorporated in the pedotransfer functions, contributing to more accurate estimations of gas and liquid transport in soils. The obtained relationships between the structural characteristics and the soil transport data constitute a valuable basis for further studies on a broader diversity of soil textures and structures. To build a useful database for hydrological models, we propose performing hydraulic conductivity and air permeability measurements in conjunction with soil structure assessments using direct visualisation methods. Moreover, the existing collections of thin sections and polished blocks offer the possibility of obtaining historical transport parameters for modelling long-term trends in the soil water regime.