The Dynamic Impacts of Weather Changes on Vegetable Price Fluctuations in Shandong Province, China: An Analysis Based on VAR and TVP-VAR Models
Abstract
:1. Introduction
2. Literature Review
3. Methodology and Data
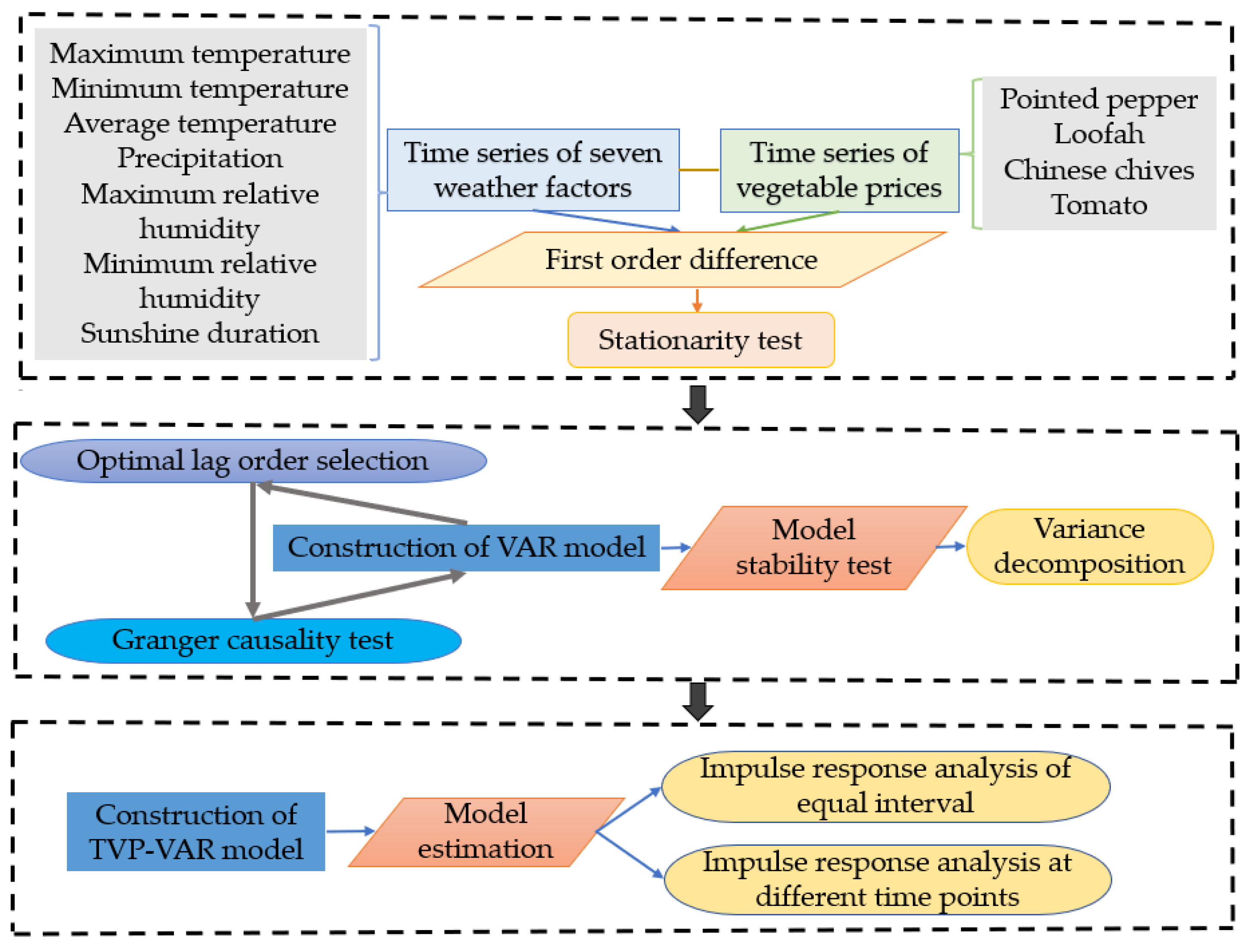
3.1. Research Framework
3.2. Methodology
3.3. Data
4. Results and Discussion
4.1. Granger Causality Analysis
4.2. Variance Decomposition Analysis
4.3. Impulse Response Analysis
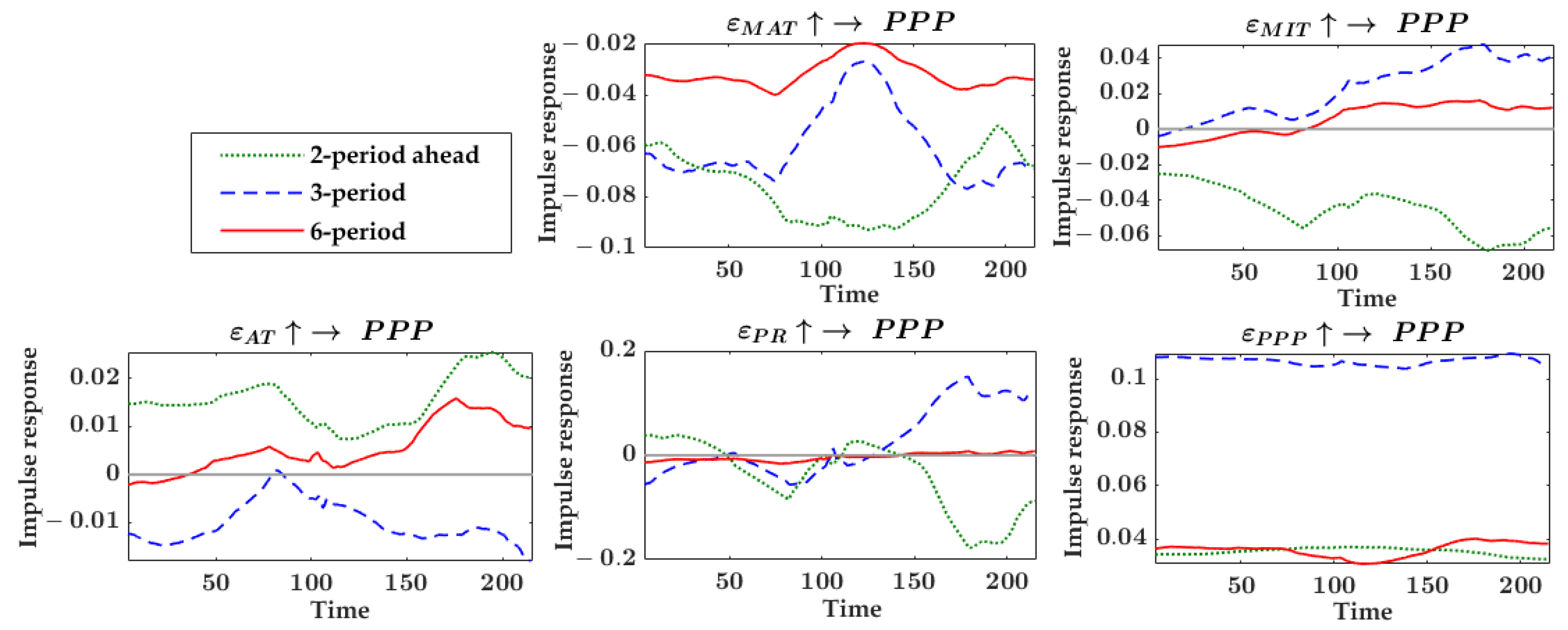
4.3.1. Pointed Pepper Analysis Unit
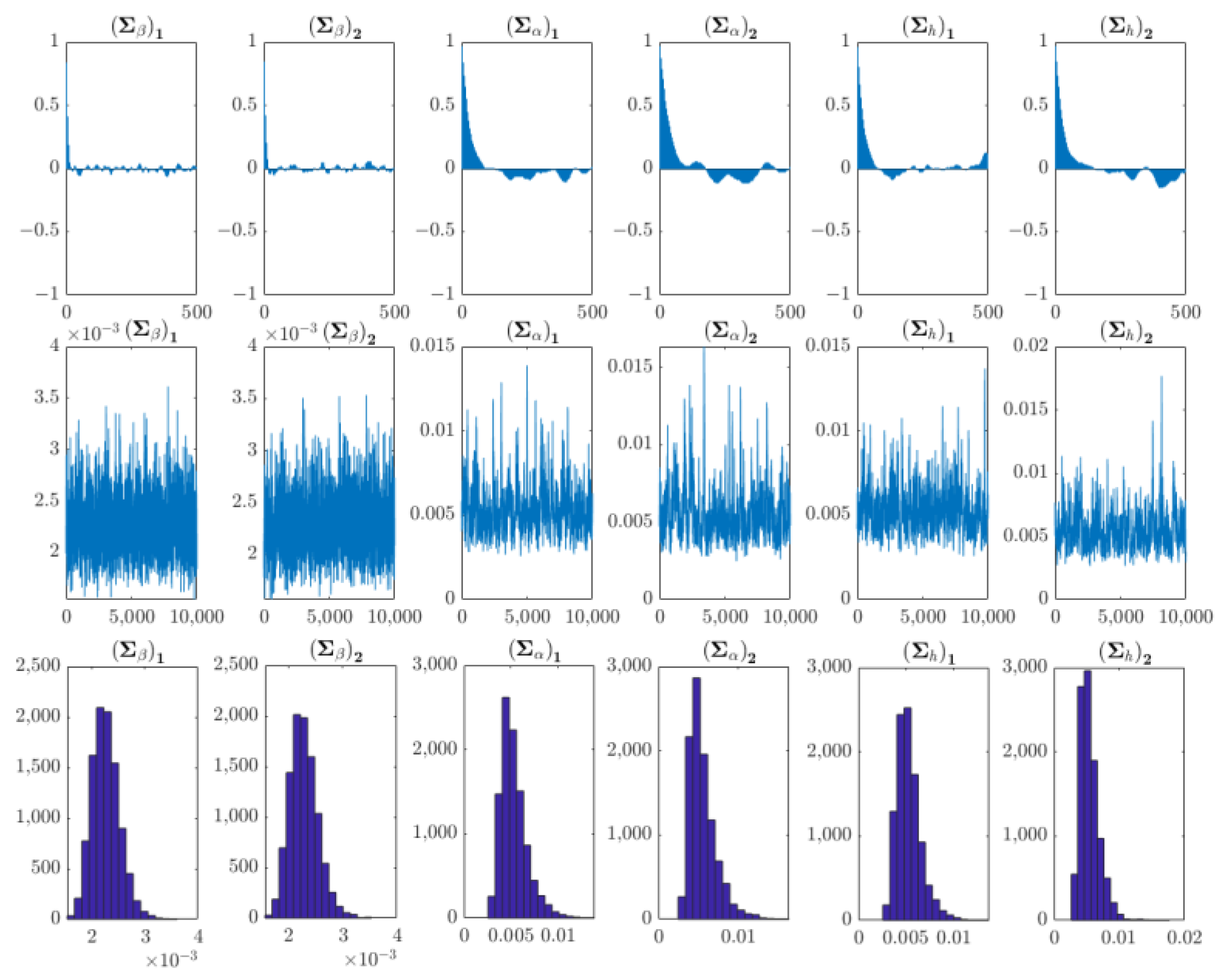
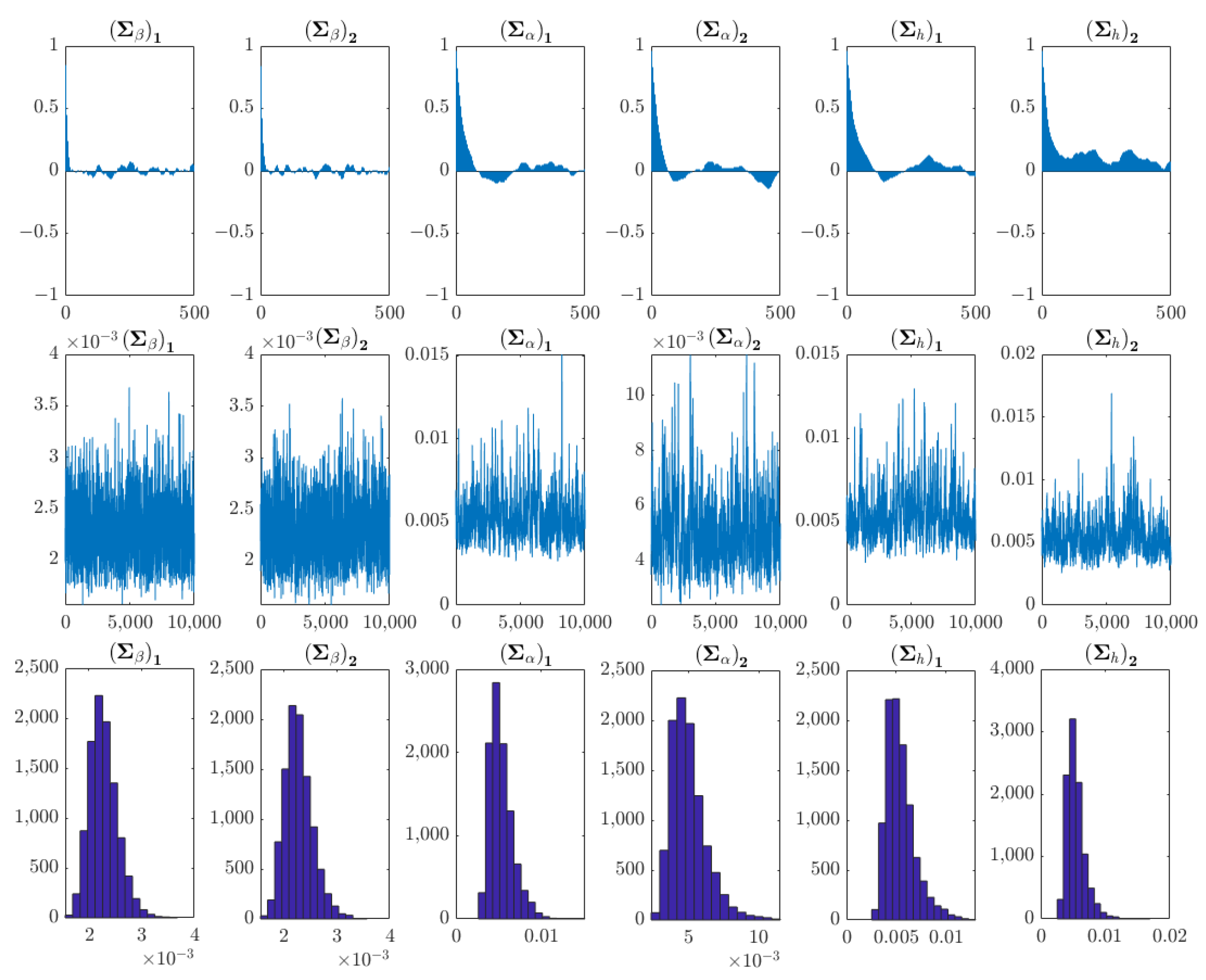
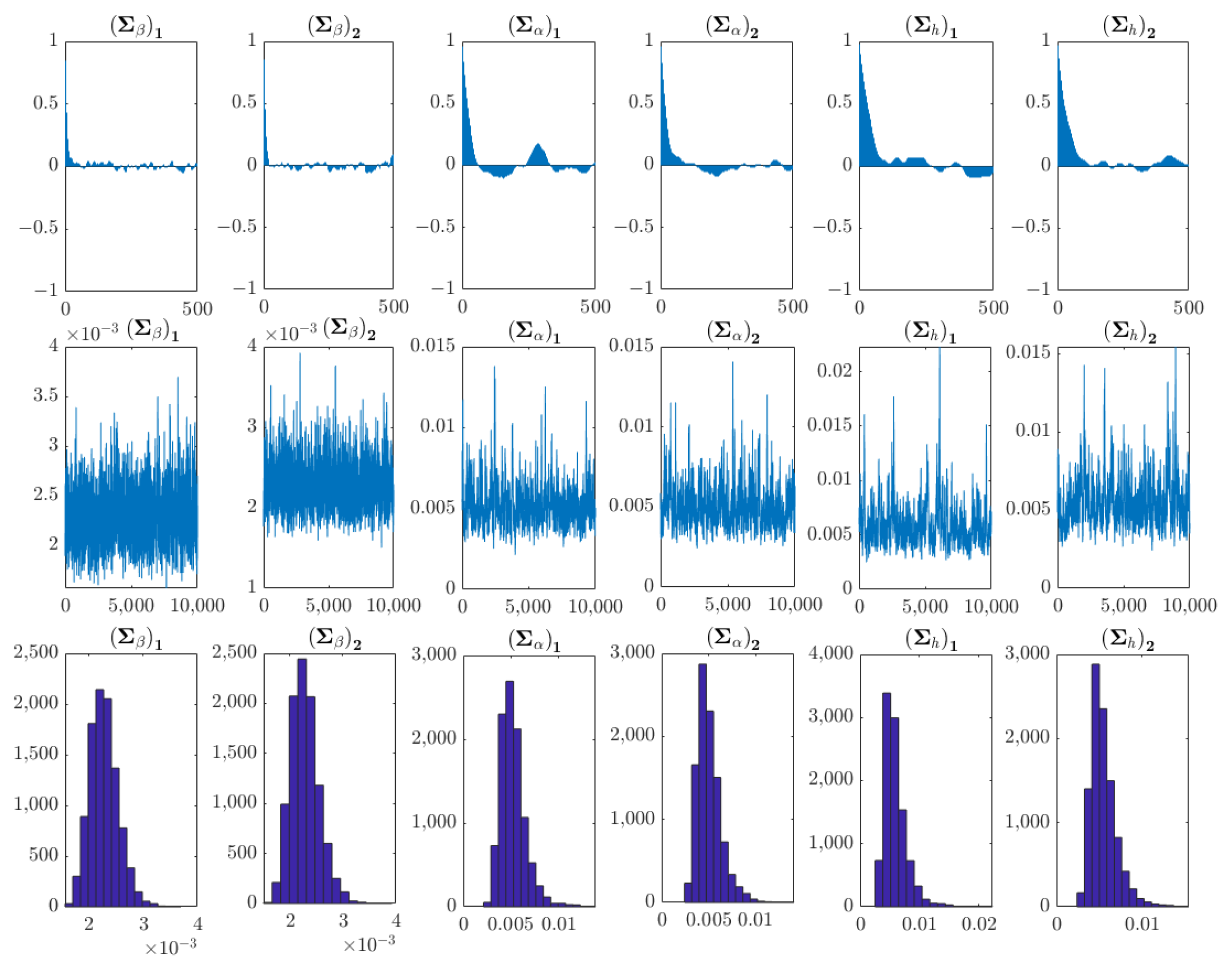
- Model Estimation and Parameter Test
- Impulse Response Analysis of Equal Interval
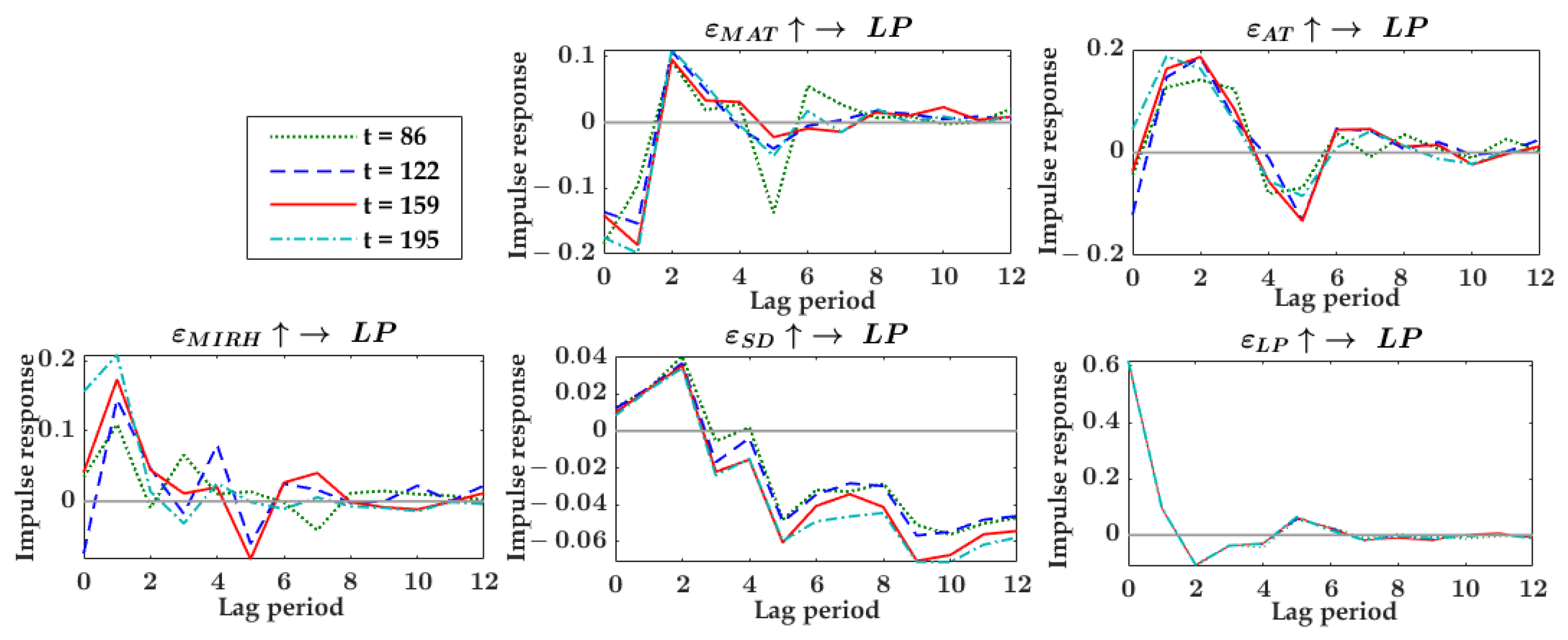
- Impulse Response Analysis at Different Time Points
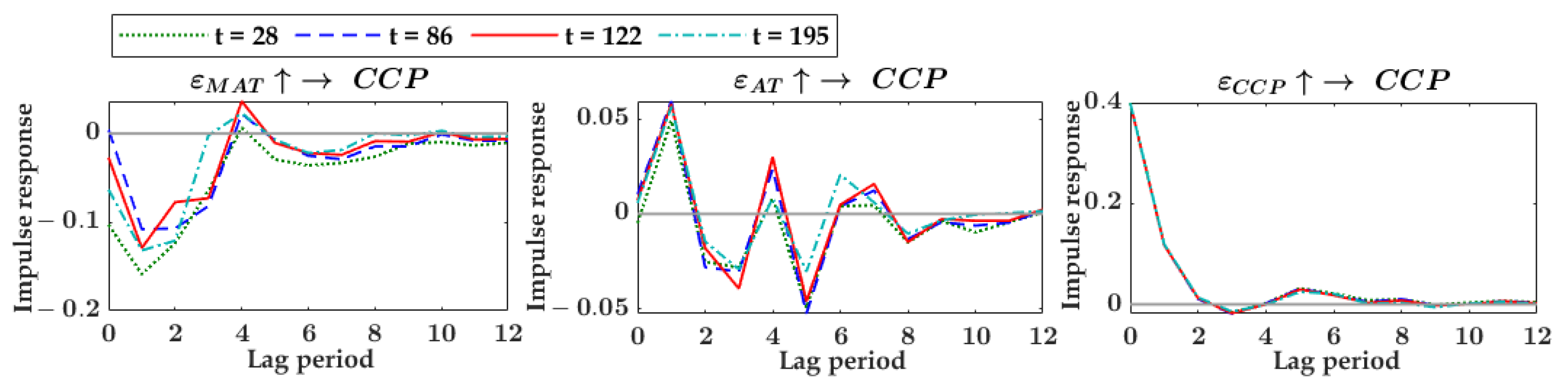
4.3.2. Loofah, Chinese Chives and Tomato Analysis Units
- Loofah
- 2.
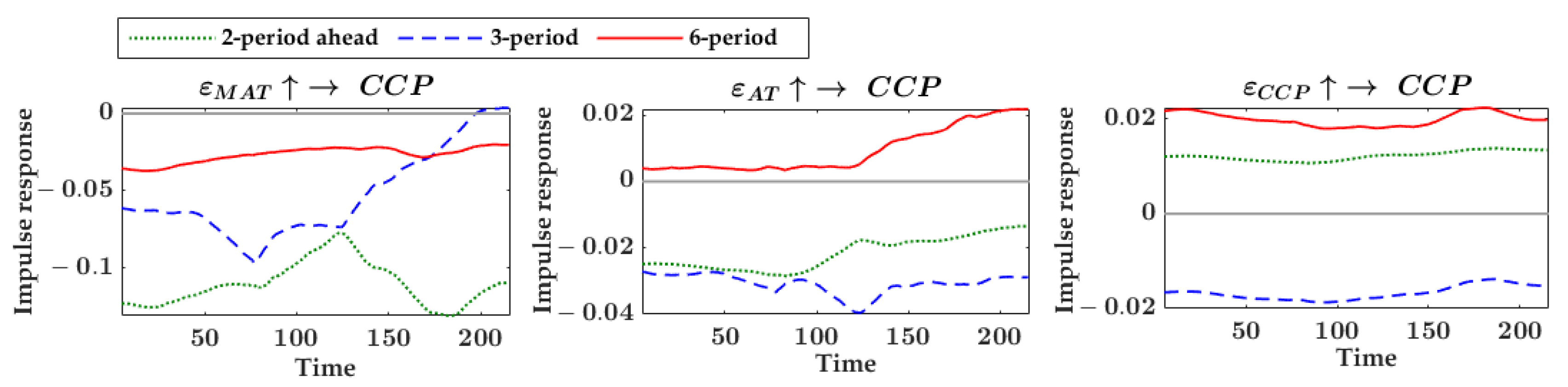
- Chinese Chives
- 3.
- Tomato
4.4. Discussion
5. Conclusions and Suggestions
5.1. Conclusions
5.2. Suggestions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| First-Level Variables | Secondary Variables | Code | ADF | PP | Conclusions | ||||
|---|---|---|---|---|---|---|---|---|---|
| Intercept | Trend and Intercept | None | Intercept | Trend and Intercept | None | ||||
| Vegetable prices | D pointed pepper price | PPP | −6.125867 *** | −6.110883 *** | −6.130357 *** | −14.37946 *** | −14.35091 *** | −14.39663 *** | Stationary |
| D loofah price | LP | −11.48933 *** | −11.47608 *** | −11.51571 *** | −11.62354 *** | −11.59984 *** | −11.65401 *** | Stationary | |
| D Chinese chives price | CCP | −10.19264 *** | −10.16857 *** | −10.21698 *** | −10.22133 *** | −10.19745 *** | −10.24536 *** | Stationary | |
| D tomato price | TP | −10.25838 *** | −10.25092 *** | −10.27605 *** | −10.25838 *** | −10.25092 *** | −10.27605 *** | Stationary | |
| Weather factors in Shouguang | D maximum temperature | MAT | −20.0715 *** | −20.08556 *** | −20.11769 *** | −19.10048 *** | −19.10710 *** | −19.13434 *** | Stationary |
| D minimum temperature | MIT | −5.24486 *** | −5.230246 *** | −5.256803 *** | −17.48307 *** | −17.49313 *** | −17.50212 *** | Stationary | |
| D average temperature | AT | −4.713818 *** | −4.709089 *** | −4.724847 *** | −18.54082 *** | −18.53967 *** | −18.5653 *** | Stationary | |
| D precipitation | PR | −14.19014 *** | −14.15539 *** | −14.22388 *** | −50.26337 *** | −50.37139 *** | −50.53741 *** | Stationary | |
| D maximum relative humidity | MARH | −11.97051 *** | −11.9637 *** | −11.99922 *** | −28.52883 *** | −28.92497 *** | −28.61517 *** | Stationary | |
| D minimum relative humidity | MIRH | −15.11913 *** | −15.10502 *** | −15.15052 *** | −26.97608 *** | −26.97608 *** | −27.44539 *** | Stationary | |
| D sunshine duration | SD | −5.946357 *** | −5.900428 *** | −5.961565 *** | −7.311444 *** | −7.312367 *** | −7.314433 *** | Stationary | |
| Weather factors in Changle | D maximum temperature | MAT | −20.71488 *** | −20.72627 *** | −20.7626 *** | −19.53424 *** | −19.54433 *** | −19.56966 *** | Stationary |
| D minimum temperature | MIT | −5.41871 *** | −5.396147 *** | −5.430856 *** | −18.45126 *** | −18.45187 *** | −18.47337 *** | Stationary | |
| D average temperature | AT | −4.601533 *** | −4.590126 *** | −4.612283 *** | −19.29557 *** | −19.29395 *** | −19.32213 *** | Stationary | |
| D precipitation | PR | −11.83259 *** | −11.80236 *** | −11.86127 *** | −78.47304 *** | −78.18714 *** | −78.80674 *** | Stationary | |
| D maximum relative humidity | MARH | −12.1011 *** | −12.10656 *** | −12.13014 *** | −24.22536 *** | −24.37019 *** | −24.29398 *** | Stationary | |
| D minimum relative humidity | MIRH | −14.43345 *** | −14.42353 *** | −14.46221 *** | −24.34848 *** | −24.40541 *** | −24.42056 *** | Stationary | |
| D sunshine duration | SD | −7.168282 *** | −7.125036 *** | −7.186744 *** | −5.259499 *** | −5.24769 *** | −5.263488 *** | Stationary | |
| Parameter | Mean | Std. Dev. | 95% L | 95% U | G. C. D. | I. F. |
|---|---|---|---|---|---|---|
| 0.0023 | 0.0003 | 0.0018 | 0.0028 | 0.989 | 8.71 | |
| 0.0023 | 0.0003 | 0.0018 | 0.0029 | 0.166 | 8.59 | |
| 0.0053 | 0.0014 | 0.0033 | 0.0089 | 0.392 | 42.96 | |
| 0.0055 | 0.0017 | 0.0034 | 0.0100 | 0.947 | 57.63 | |
| 0.0053 | 0.0013 | 0.0034 | 0.0084 | 0.128 | 36.21 | |
| 0.0055 | 0.0015 | 0.0034 | 0.0090 | 0.795 | 51.96 |
| Parameter | Mean | Std. Dev. | 95% L | 95% U | G. C. D. | I. F. |
|---|---|---|---|---|---|---|
| 0.0023 | 0.0003 | 0.0018 | 0.0029 | 0.167 | 10.48 | |
| 0.0023 | 0.0003 | 0.0018 | 0.0028 | 0.367 | 11.7 | |
| 0.0054 | 0.0015 | 0.0034 | 0.0091 | 0.283 | 61.77 | |
| 0.0049 | 0.0012 | 0.0033 | 0.0078 | 0.041 | 38.74 | |
| 0.0055 | 0.0016 | 0.0033 | 0.0092 | 0.284 | 69.18 | |
| 0.0056 | 0.0016 | 0.0034 | 0.0095 | 0.613 | 52.94 |
| Parameter | Mean | Std. Dev. | 95% L | 95% U | G. C. D. | I. F. |
|---|---|---|---|---|---|---|
| 0.0023 | 0.0003 | 0.0018 | 0.0029 | 0.509 | 9.46 | |
| 0.0023 | 0.0003 | 0.0018 | 0.0029 | 0.124 | 11.84 | |
| 0.0053 | 0.0014 | 0.0034 | 0.0087 | 0.028 | 39.97 | |
| 0.0050 | 0.0013 | 0.0033 | 0.0081 | 0.437 | 39.57 | |
| 0.0054 | 0.0015 | 0.0034 | 0.0093 | 0.000 | 56.85 | |
| 0.0054 | 0.0015 | 0.0034 | 0.0090 | 0.383 | 78.87 |
Appendix B




References
- Li, Y.; Zhang, M.; Liu, J.; Su, B.; Lin, X.; Liang, Y.; Bao, Y.; Yang, S.; Zhang, J. Research on the Disturbance Sources of Vegetable Price Fluctuation Based on Grounded Theory and LDA Topic Model. Agriculture 2022, 12, 648. [Google Scholar] [CrossRef]
- Li, Y.; Xia, J.; Li, C.; Zheng, M. Construction of an Early-Warning System for Vegetable Prices Based on Index Contribution Analysis. Sustainability 2015, 7, 3823–3837. [Google Scholar] [CrossRef] [Green Version]
- Illankoon, I.; Kumara, B. Analyzing the Influence of Various Factors for Vegetable Price using Data Mining. In Proceedings of the International Research Conference 2020 KDU, Ratmalana, Sri Lanka, 15–16 October 2020. [Google Scholar]
- Li, Y.; Liu, J.; Yang, H.; Chen, J.; Xiong, J. A Bibliometric Analysis of Literature on Vegetable Prices at Domestic and International Markets—A Knowledge Graph Approach. Agriculture 2021, 11, 951. [Google Scholar] [CrossRef]
- Ji, L.; Li, C.; Zhang, S. The spatial distribution of vegetable production in China and its impact on vegetable price volatility. Econ. Geogr. 2016, 36, 148–155. [Google Scholar]
- Adams, R.M.; Hurd, B.H.; Lenhart, S.; Leary, N. Effects of global climate change on agriculture: An interpretative review. Clim. Res. 1998, 11, 19–30. [Google Scholar] [CrossRef] [Green Version]
- Hatfield, J.L.; Boote, K.J.; Kimball, B.A.; Ziska, L.H.; Izaurralde, R.C.; Ort, D.; Thomson, A.M.; Wolfe, D. Climate impacts on agriculture: Implications for crop production. Agron. J. 2011, 103, 351–370. [Google Scholar] [CrossRef] [Green Version]
- Gordeev, R.V.; Pyzhev, A.I.; Zander, E.V. Does Climate Change Influence Russian Agriculture? Evidence from Panel Data Analysis. Sustainability 2022, 14, 718. [Google Scholar]
- Vermeulen, S.J.; Aggarwal, P.K.; Ainslie, A.; Angelone, C.; Campbell, B.M.; Challinor, A.J.; Hansen, J.W.; Ingram, J.S.; Jarvis, A.; Kristjanson, P. Options for support to agriculture and food security under climate change. Environ. Sci. Policy 2012, 15, 136–144. [Google Scholar] [CrossRef]
- Eigenbrod, C.; Gruda, N. Urban vegetable for food security in cities. A review. Agron. Sustain. Dev. 2015, 35, 483–498. [Google Scholar] [CrossRef] [Green Version]
- Tack, J.B.; Holt, M.T. Influence of weather extremes on the spatial correlation of corn yields. Clim. Chang. 2016, 134, 299–309. [Google Scholar] [CrossRef]
- Lesk, C.; Rowhani, P.; Ramankutty, N. Influence of extreme weather disasters on global crop production. Nature 2016, 529, 84–87. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jat, M.L.; Dagar, J.C.; Sapkota, T.B.; Govaerts, B.; Ridaura, S.L.; Saharawat, Y.S.; Sharma, R.K.; Tetarwal, J.P.; Jat, R.K.; Hobbs, H. Climate change and agriculture: Adaptation strategies and mitigation opportunities for food security in South Asia and Latin America. Adv. Agron. 2016, 137, 127–235. [Google Scholar]
- De Winne, J.; Peersman, G. The adverse consequences of global harvest and weather disruptions on economic activity. Nat. Clim. Chang. 2021, 11, 665–672. [Google Scholar] [CrossRef]
- Furuya, J.; Kobayashi, S. Impact of global warming on agricultural product markets: Stochastic world food model analysis. Sustain. Sci. 2009, 4, 71–79. [Google Scholar] [CrossRef]
- Wang, J.; Mendelsohn, R.; Dinar, A.; Huang, J.; Rozelle, S.; Zhang, L. The impact of climate change on China’s agriculture. Agric. Econ. 2009, 40, 323–337. [Google Scholar] [CrossRef]
- Seo, S.N. An essay on the impact of climate change on US agriculture: Weather fluctuations, climatic shifts, and adaptation strategies. Clim. Chang. 2013, 121, 115–124. [Google Scholar] [CrossRef]
- Cogato, A.; Meggio, F.; De Antoni Migliorati, M.; Marinello, F. Extreme weather events in agriculture: A systematic review. Sustainability 2019, 11, 2547. [Google Scholar] [CrossRef] [Green Version]
- Dalhaus, T.; Schlenker, W.; Blanke, M.M.; Bravin, E.; Finger, R. The effects of extreme weather on apple quality. Sci. Rep. 2020, 10, 1–7. [Google Scholar] [CrossRef]
- Cui, Q.; Ali, T.; Xie, W.; Huang, J.; Wang, J. The uncertainty of climate change impacts on China’s agricultural economy based on an integrated assessment approach. Mitig. Adapt. Strat. Glob. 2022, 27, 1–22. [Google Scholar] [CrossRef]
- Poudel, M.P.; Chen, S.E.; Huang, W.C. Pricing of rainfall index insurance for rice and wheat in Nepal. J. Agric. Sci. Technol. 2016, 18, 291–302. [Google Scholar]
- Elum, Z.A.; Nhamo, G.; Antwi, M.A. Effects of climate variability and insurance adoption on crop production in select provinces of South Africa. J. Water Clim. Change 2018, 9, 500–511. [Google Scholar] [CrossRef]
- Guo, J.; Jin, J.; Tang, Y.; Wu, X. Design of Temperature Insurance Index and Risk Zonation for Single-Season Rice in Response to High-Temperature and Low-Temperature Damage: A Case Study of Jiangsu Province, China. Int. J. Environ. Res. Public Health 2019, 16, 1187. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vishnoi, L.; Kumar, A.; Kumar, S.; Sharma, G.; Baxla, A.K.; Singh, K.K.; Bhan, S.C. Weather based crop insurance for risk management in agriculture. J. Agrometeorol. 2020, 22, 101–108. [Google Scholar] [CrossRef]
- Taşkin, D.; Cagli, E.C.; Evrim Mandaci, P. The impact of temperature anomalies on commodity futures. Energy Sources Part B Econ. Plan. Policy 2021, 16, 357–370. [Google Scholar] [CrossRef]
- Cao, G.; He, C.; Xu, W. Effect of weather on agricultural futures markets on the basis of DCCA cross-correlation coefficient analysis. Fluct. Noise Lett. 2016, 15, 1650012. [Google Scholar] [CrossRef]
- Letta, M.; Montalbano, P.; Pierre, G. Weather shocks, traders’ expectations, and food prices. Am. J. Agric. Econ. 2022, 104, 1100–1119. [Google Scholar] [CrossRef]
- Pustil Nik, L.; Yom Din, G. On possible influence of space weather on agricultural markets: Necessary conditions and probable scenarios. Astrophys. Bull. 2013, 68, 107–124. [Google Scholar] [CrossRef] [Green Version]
- Brown, M.E.; Kshirsagar, V. Weather and international price shocks on food prices in the developing world. Glob. Environ. Chang. 2015, 35, 31–40. [Google Scholar] [CrossRef]
- Hansen, J.W.; Jones, J.W.; Kiker, C.F.; Hodges, A.W. El Niño–Southern Oscillation impacts on winter vegetable production in Florida. J. Clim. 1999, 12, 92–102. [Google Scholar] [CrossRef]
- Moretti, C.L.; Mattos, L.M.; Calbo, A.G.; Sargent, S.A. Climate changes and potential impacts on postharvest quality of fruit and vegetable crops: A review. Food Res. Int. 2010, 43, 1824–1832. [Google Scholar] [CrossRef]
- Potopová, V.; Zahradníček, P.; Atěpánek, P.; Türkott, L.; Farda, A.; Soukup, J. The impacts of key adverse weather events on the field-grown vegetable yield variability in the Czech Republic from 1961 to 2014. Int. J. Climatol. 2017, 37, 1648–1664. [Google Scholar] [CrossRef]
- Bisbis, M.B.; Gruda, N.; Blanke, M. Potential impacts of climate change on vegetable production and product quality—A review. J. Clean. Prod. 2018, 170, 1602–1620. [Google Scholar] [CrossRef]
- Yoo, D.I. Developing vegetable price forecasting model with climate factors. Korean J. Agric. Econ. 2016, 57, 1–24. [Google Scholar]
- Yin, H.; Jin, D.; Gu, Y.H.; Park, C.J.; Han, S.K.; Yoo, S.J. STL-ATTLSTM: Vegetable price forecasting using STL and attention mechanism-based LSTM. Agriculture 2020, 10, 612. [Google Scholar] [CrossRef]
- Purohit, S.K.; Panigrahi, S.; Sethy, P.K.; Behera, S.K. Time series forecasting of price of agricultural products using hybrid methods. Appl. Artif. Intell. 2021, 35, 1388–1406. [Google Scholar] [CrossRef]
- Gu, Y.H.; Jin, D.; Yin, H.; Zheng, R.; Piao, X.; Yoo, S.J. Forecasting agricultural commodity prices using dual input attention LSTM. Agriculture 2022, 12, 256. [Google Scholar] [CrossRef]
- Nalwanga, R.; Belay, A. Fuzzy Logic based Vegetable Price prediction in IoT. Procedia Comput. Sci. 2022, 203, 807–812. [Google Scholar] [CrossRef]
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econom. J. Econom. Soc. 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Sims, C.A. Macroeconomics and reality. Econom. J. Econom. Soc. 1980, 48, 1–48. [Google Scholar] [CrossRef] [Green Version]
- Primiceri, G.E. Time varying structural vector autoregressions and monetary policy. Rev. Econ. Stud. 2005, 72, 821–852. [Google Scholar] [CrossRef]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Akaike, H. Fitting autoregressive models for prediction. Ann. Inst. Stat. Math. 1969, 21, 243–247. [Google Scholar] [CrossRef]
- Akaike, H. Statistical predictor identification. Ann. Inst. Stat. Math. 1970, 22, 203–217. [Google Scholar] [CrossRef]
- Huang, J.; Dong, X.; Chen, J.; Zhong, M. Do oil prices and economic policy uncertainty matter for precious metal returns? New insights from a TVP-VAR framework. Int. Rev. Econ. Financ. 2022, 78, 433–445. [Google Scholar] [CrossRef]
- Nakajima, J. Time-varying parameter VAR model with stochastic volatility: An overview of methodology and empirical applications. Monet. Econ. Stud. 2011, 29, 107–142. [Google Scholar]
- Nakajima, J.; Kasuya, M.; Watanabe, T. Bayesian analysis of time-varying parameter vector autoregressive model for the Japanese economy and monetary policy. J. Jpn. Int. Econ. 2011, 25, 225–245. [Google Scholar] [CrossRef]
- Gong, X.; Lin, B. Time-varying effects of oil supply and demand shocks on China’s macro-economy. Energy 2018, 149, 424–437. [Google Scholar] [CrossRef]
- Chen, J.; Zhu, X.; Li, H. The pass-through effects of oil price shocks on China’s inflation: A time-varying analysis. Energy Econ. 2020, 86, 104695. [Google Scholar] [CrossRef]
- Cao, Y.; Mohiuddin, M. Sustainable emerging country agro-food supply chains: Fresh vegetable price formation mechanisms in rural China. Sustainability 2019, 11, 2814. [Google Scholar] [CrossRef] [Green Version]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econom. J. Econom. Soc. 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Phillips, P.C.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, S.; Ye, D.; Tang, H.; Wang, F. Dynamic impact of negative public sentiment on agricultural product prices during COVID-19. J. Retail. Consum. Serv. 2022, 64, 102790. [Google Scholar] [CrossRef]

| D Pointed Pepper Price (PPP) | D Loofah Price (LP) | D Chinese Chives Price (CCP) | D Tomato Price (TP) | |
|---|---|---|---|---|
| Mean | 0.020 | 0.006 | 0.007 | 0.011 |
| Median | −0.001 | 0.003 | 0.042 | 0.023 |
| Maximum | 2.583 | 5.451 | 2.154 | 1.453 |
| Minimum | −1.920 | −3.624 | −1.967 | −1.186 |
| Std. Dev. | 0.602 | 0.906 | 0.460 | 0.392 |
| C.V. | 30.1 | 151 | 65.714 | 35.636 |
| Observations | 215 | 215 | 215 | 215 |
| D Maximum Temperature (MAT) | D Minimum Temperature (MIT) | D Average Temperature (AT) | D Precipitation (PR) | D Maximum Relative Humidity (MARH) | D Minimum Relative Humidity (MIRH) | D Sunshine Duration (SD) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sg | Cl | Sg | Cl | Sg | Cl | Sg | Cl | Sg | Cl | Sg | Cl | Sg | Cl | |
| Mean | −0.018 | −0.018 | −0.038 | −0.041 | −0.027 | −0.028 | −0.073 | −0.144 | 0.001 | −0.007 | −0.114 | −0.119 | −0.057 | −0.056 |
| Median | −0.264 | −0.243 | 0.071 | 0.143 | −0.268 | −0.285 | 0.000 | 0.000 | 0.571 | 0.143 | −0.857 | −0.714 | −0.160 | −0.117 |
| Maximum | 12.289 | 11.814 | 7.421 | 10.664 | 10.207 | 11.041 | 296.300 | 414.800 | 28.857 | 22.714 | 37.643 | 38.929 | 6.848 | 3.960 |
| Minimum | −10.771 | −10.829 | −7.729 | −8.368 | −8.514 | −9.745 | −252.700 | −408.000 | −30.250 | −29.893 | −29.045 | −37.375 | −4.898 | −3.510 |
| Std. Dev. | 3.590 | 3.682 | 2.521 | 2.867 | 2.854 | 3.023 | 41.653 | 57.713 | 8.626 | 8.127 | 11.974 | 12.144 | 1.717 | 1.619 |
| C.V. | −199.444 | −204.556 | −66.342 | −69.927 | −105.704 | −107.964 | −570.589 | −400.785 | 8626 | −1161 | −105.035 | −102.05 | −30.123 | −28.911 |
| Observations | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 | 215 |
| Analysis Units | The Null Hypothesis | Lag | p-Value | Conclusion |
|---|---|---|---|---|
| Pointed pepper | MAT does not Granger Cause PPP | Lag 3 | 0.0402 ** | Reject |
| MIT does not Granger Cause PPP | Lag 3 | 0.0218 ** | Reject | |
| AT does not Granger Cause PPP | Lag 3 | 0.0392 ** | Reject | |
| PR does not Granger Cause PPP | Lag 3 | 0.001 *** | Reject | |
| Loofah | MAT does not Granger Cause LP | Lag 5 | 0.0056 *** | Reject |
| AT does not Granger Cause LP | Lag 5 | 0.0347 ** | Reject | |
| MIRH does not Granger Cause LP | Lag 5 | 0.0232 ** | Reject | |
| SD does not Granger Cause LP | Lag 5 | 0.0026 *** | Reject | |
| Chinese chives | MAT does not Granger Cause CCP | Lag 4 | 0.0003 *** | Reject |
| AT does not Granger Cause CCP | Lag 4 | 0.0003 *** | Reject | |
| Tomato | MAT does not Granger Cause TP | Lag 8 | 0.0091 *** | Reject |
| AT does not Granger Cause TP | Lag 8 | 0.0129 ** | Reject | |
| SD does not Granger Cause TP | Lag 8 | 0.0158 ** | Reject |
| Period | MAT | MIT | AT | PR | PPP |
|---|---|---|---|---|---|
| 1 | 0.025882 | 1.278085 | 0.481557 | 1.988722 | 96.22575 |
| 2 | 0.319346 | 1.784059 | 0.538460 | 2.439580 | 94.91855 |
| 3 | 1.817316 | 4.227725 | 0.535714 | 5.886640 | 87.53260 |
| 4 | 2.027129 | 4.232233 | 0.532154 | 6.287928 | 86.92056 |
| 5 | 2.308690 | 4.550647 | 0.528686 | 6.268270 | 86.34371 |
| 6 | 2.304700 | 4.546859 | 0.54822 | 6.411144 | 86.18908 |
| 7 | 2.328718 | 4.569512 | 0.556427 | 6.417992 | 86.12735 |
| 8 | 2.328997 | 4.569192 | 0.559767 | 6.424172 | 86.11787 |
| 9 | 2.333007 | 4.568818 | 0.559853 | 6.434503 | 86.10382 |
| 10 | 2.333531 | 4.568789 | 0.559868 | 6.434861 | 86.10295 |
| Period | MAT | AT | MIRH | SD | LP |
|---|---|---|---|---|---|
| 1 | 2.092774 | 1.473740 | 0.604665 | 0.448184 | 95.38064 |
| 2 | 7.434745 | 2.310542 | 1.876440 | 1.402755 | 86.97552 |
| 3 | 7.361410 | 2.231838 | 2.064632 | 1.507659 | 86.83446 |
| 4 | 7.831818 | 2.175388 | 2.283457 | 2.021554 | 85.68778 |
| 5 | 7.801771 | 2.225018 | 2.276271 | 2.340149 | 85.35679 |
| 6 | 7.825930 | 2.218832 | 2.274204 | 2.480816 | 85.20022 |
| 7 | 7.842001 | 2.214767 | 2.271180 | 2.633050 | 85.03900 |
| 8 | 7.832383 | 2.212909 | 2.271098 | 2.739194 | 84.94442 |
| 9 | 7.826115 | 2.212392 | 2.271032 | 2.822922 | 84.86754 |
| 10 | 7.823346 | 2.211414 | 2.269919 | 2.881527 | 84.81379 |
| Period | MAT | AT | CCP |
|---|---|---|---|
| 1 | 1.631579 | 0.099920 | 98.26850 |
| 2 | 7.878212 | 0.800084 | 91.32170 |
| 3 | 10.39201 | 1.024730 | 88.58326 |
| 4 | 10.41237 | 1.048125 | 88.53950 |
| 5 | 10.52968 | 1.056555 | 88.41377 |
| 6 | 10.52946 | 1.063172 | 88.40736 |
| 7 | 10.53277 | 1.068477 | 88.39875 |
| 8 | 10.53277 | 1.069099 | 88.39813 |
| 9 | 10.53354 | 1.069275 | 88.39718 |
| 10 | 10.53361 | 1.069304 | 88.39709 |
| Period | MAT | AT | SD | TP |
|---|---|---|---|---|
| 1 | 0.016132 | 0.905924 | 0.000000 | 99.07794 |
| 2 | 0.411480 | 0.899718 | 0.002606 | 98.68620 |
| 3 | 3.078374 | 0.876355 | 0.428455 | 95.61682 |
| 4 | 3.192602 | 0.936708 | 1.466219 | 94.40447 |
| 5 | 3.180635 | 1.026650 | 2.627425 | 93.16529 |
| 6 | 3.177232 | 1.022940 | 3.213173 | 92.58666 |
| 7 | 3.180737 | 1.017473 | 3.743496 | 92.05829 |
| 8 | 3.171162 | 1.018726 | 4.141277 | 91.66883 |
| 9 | 3.171939 | 1.018343 | 4.464577 | 91.34514 |
| 10 | 3.170665 | 1.016833 | 4.713903 | 91.09860 |
| Parameter | Mean | Std. Dev. | 95% L | 95% U | G. C. D. | I. F. |
|---|---|---|---|---|---|---|
| 0.0023 | 0.0003 | 0.0018 | 0.0028 | 0.459 | 16.68 | |
| 0.0023 | 0.0003 | 0.0018 | 0.0029 | 0.226 | 9.47 | |
| 0.0052 | 0.0013 | 0.0033 | 0.0084 | 0.133 | 33.21 | |
| 0.0050 | 0.0013 | 0.0032 | 0.0083 | 0.212 | 37.49 | |
| 0.0059 | 0.0020 | 0.0034 | 0.0107 | 0.952 | 74.2 | |
| 0.0055 | 0.0015 | 0.0034 | 0.0092 | 0.015 | 66.81 |
| Analysis Units | Variables | Optimal Lag Order | Intervals | Time Points | |
|---|---|---|---|---|---|
| Dependent Variable | Independent Variables | ||||
| Pointed Pepper | PPP | MAT, MIT, AT, PR | 3 | 2, 3, 6 | 106th, 122nd, 157th, 195th |
| Loofah | LP | MAT, AT, MIRH, SD | 5 | 2, 4, 6 | 86th, 122nd, 159th, 195th |
| Chinese chives | CCP | MAT, AT | 4 | 2, 3, 6 | 28th, 86th, 122nd, 195th |
| Tomato | TP | MAT, AT, SD | 8 | 1, 3, 6 | 86th, 122nd, 185th, 195th |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Cao, Y.; Shi, Y.; Wu, Y.; Guo, W.; Fu, H.; Li, Y. The Dynamic Impacts of Weather Changes on Vegetable Price Fluctuations in Shandong Province, China: An Analysis Based on VAR and TVP-VAR Models. Agronomy 2022, 12, 2680. https://doi.org/10.3390/agronomy12112680
Yang H, Cao Y, Shi Y, Wu Y, Guo W, Fu H, Li Y. The Dynamic Impacts of Weather Changes on Vegetable Price Fluctuations in Shandong Province, China: An Analysis Based on VAR and TVP-VAR Models. Agronomy. 2022; 12(11):2680. https://doi.org/10.3390/agronomy12112680
Chicago/Turabian StyleYang, Hongyu, Yuanxin Cao, Yuemeng Shi, Yuling Wu, Weixi Guo, Hui Fu, and Youzhu Li. 2022. "The Dynamic Impacts of Weather Changes on Vegetable Price Fluctuations in Shandong Province, China: An Analysis Based on VAR and TVP-VAR Models" Agronomy 12, no. 11: 2680. https://doi.org/10.3390/agronomy12112680
APA StyleYang, H., Cao, Y., Shi, Y., Wu, Y., Guo, W., Fu, H., & Li, Y. (2022). The Dynamic Impacts of Weather Changes on Vegetable Price Fluctuations in Shandong Province, China: An Analysis Based on VAR and TVP-VAR Models. Agronomy, 12(11), 2680. https://doi.org/10.3390/agronomy12112680






