Comparison of Methane Emission Patterns from Dairy Housings with Solid and Slatted Floors at Two Locations
Abstract
:1. Introduction
2. Materials and Methods
2.1. Measurement Sites
2.1.1. Switzerland
2.1.2. Germany
2.2. Estimation of Ventilation Rate and Emission
2.2.1. Artificial Tracer Approach
2.2.2. Natural Tracer Approach
2.3. Data Collection
2.3.1. Swiss Study Site
2.3.2. German Study Site
2.4. Data Analysis
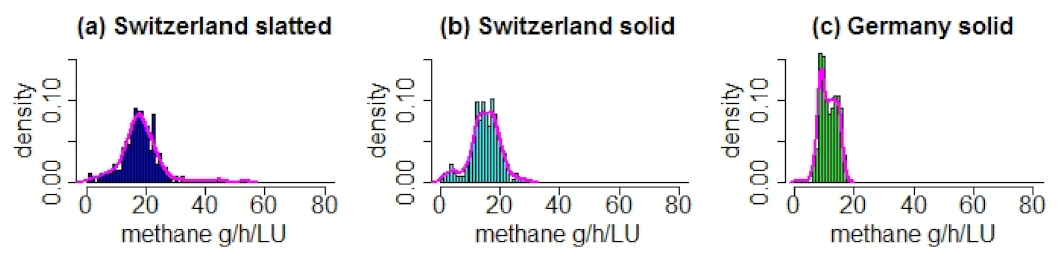
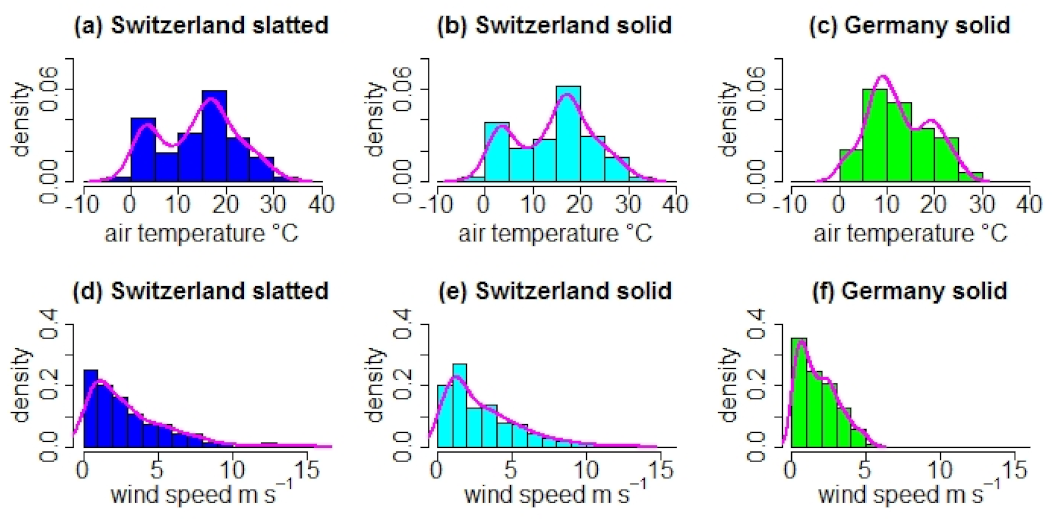
2.4.1. Histograms and Statistical Moments
2.4.2. Convection Regimes
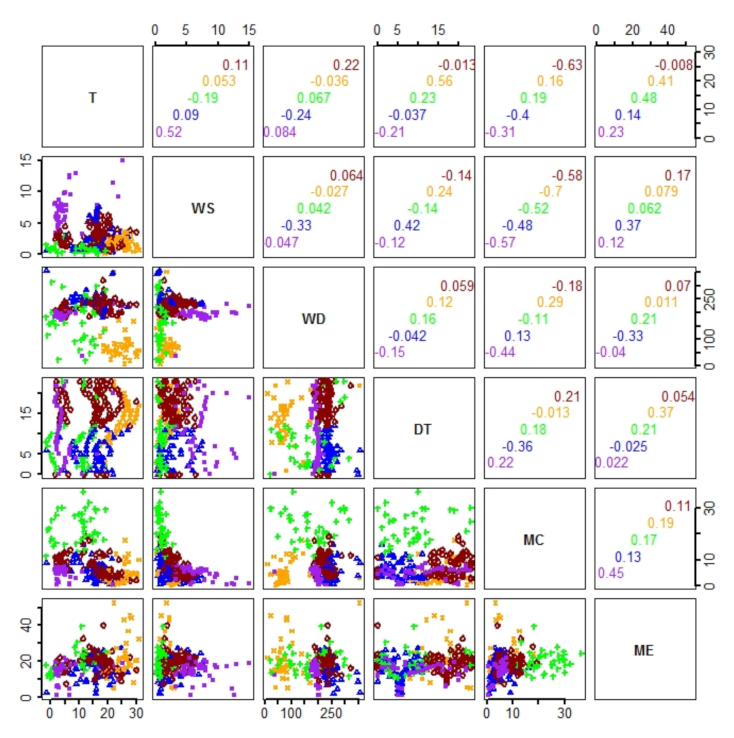
2.4.3. Pairwise Statistical Relations
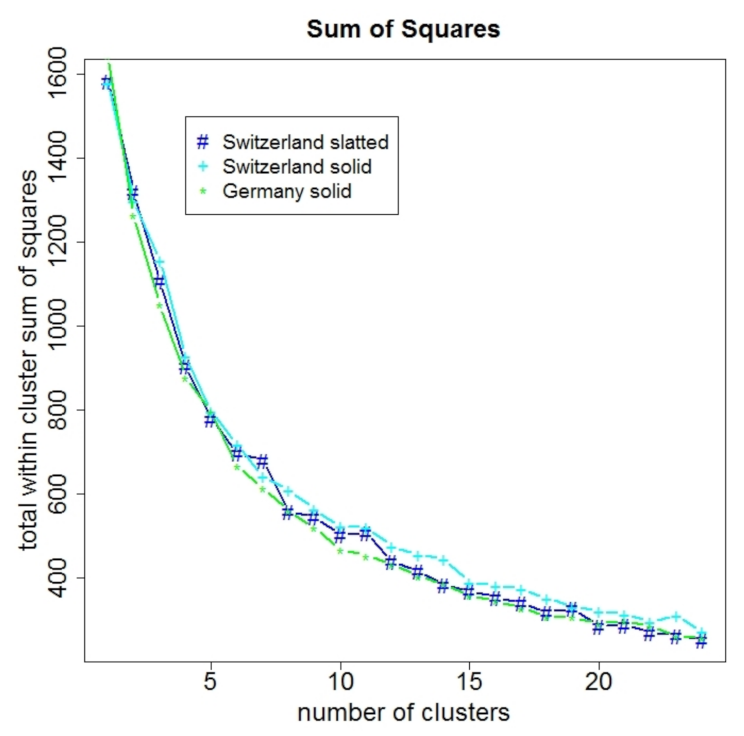
2.4.4. Clustering
3. Results
3.1. Individual Characteristics
3.1.1. Feeding and Milk Yield
3.1.2. CH Emissions
3.1.3. Environmental Conditions
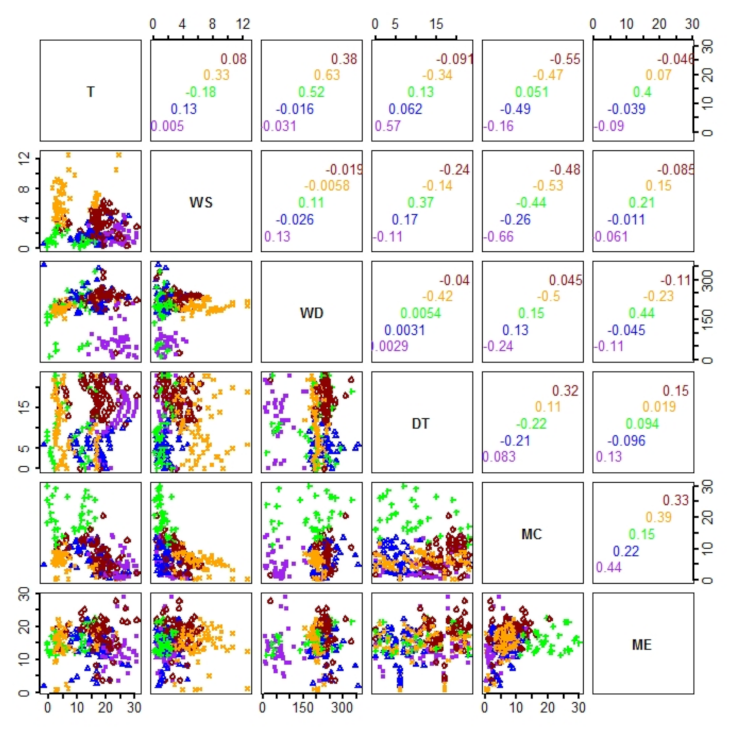
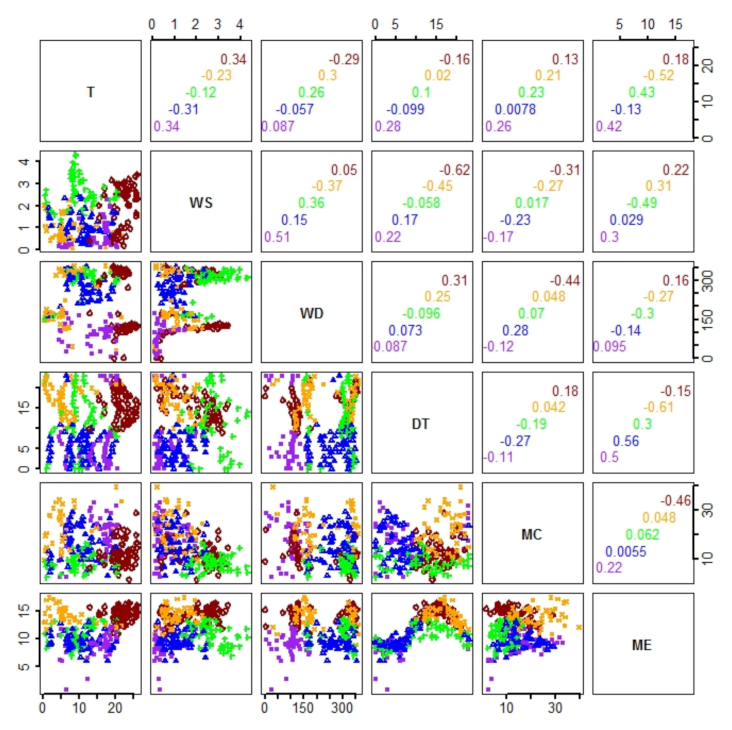
3.2. Pairwise Statistical Relations
3.3. Clustering
4. Discussion
4.1. Differences in CH Emissions between Farm Locations
4.2. Effect of Floor Type and Climate Parameters on CH Emissions
4.3. Statistical Association and Clustering
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| NVH | naturally ventilated housings |
| CH | methane |
| SF | sulfur hexafluoride |
| SFCF | trifluoromethylsulfurpentafluoride |
| CO | carbon dioxide |
| PTFE | polytetrafluorethylen (i.e., teflon) |
| FTIR | Fourier transform infrared |
| LU | livestock unit (500 kg body mass equivalent) |
| N | number of animals in the housing |
| P | carbon dioxide production |
| mass flow of tracer gas | |
| mass flow of target gas methane | |
| Q | ventilation rate |
| TC | concentration of tracer gas |
| MC | concentration of target gas methane |
| ME | normalized emission of target gas methane |
| T | ambient air temperature |
| inflow wind speed | |
| inflow wind direction | |
| hour of the day | |
| S | Swiss study site |
| G | German study site |
| R | Richardson number (ratio of buoyancy to shear forces) |
| Spearman’s rank correlation | |
| expectation value | |
| ranked set of random variables set X | |
| Kendall’s rank correlation | |
| ties in the set of random variables set X | |
| concordant pairs | |
| discordant pairs |
| possible number of pairs given n observations | |
| mutual information | |
| H | Shannon entropy |
| I | indicator (either , or MI) |
References
- WMO. WMO Statement on the State of the Global Climate in 2017; WMO-No.1212; Publications Board World Meteorological Organization (WMO), Ed.; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Sutton, M.A.; Bleeker, A.; Howard, C.; Erisman, J.; Abrol, Y.; Bekunda, M.; Datta, A.; Davidson, E.; de Vries, W.; Oenema, O.; et al. Our Nutrient World. The Challenge to Produce More Food & Energy with Less Pollution; Technical Report; Centre for Ecology & Hydrology: Edinburgh, UK, 2013. [Google Scholar]
- Masson-Delmotte, V.; Zhai, P.; Pörtner, H.O.; Roberts, D.; Skea, J.; Shukla, P.R.; Pirani, A.; Moufouma-Okia, W.; Péan, C.; Pidcock, R.; et al. Global Warming of 1.5 ∘C. An IPCC Special Report on the Impacts of Global Warming of 1.5 ∘C above Pre-Industrial Levels and Related Global Greenhouse Gas Emission Pathways, in the Context of Strengthening the Global Response to the Threat of Climate Change, Sustainable Development, and Efforts to Eradicate Poverty. Technical Report. Intergovernmental Panel on Climate Change (IPCC). 2018. Available online: https://www.ipcc.ch/site/assets/uploads/sites/2/2019/06/SR15_Full_Report_High_Res.pdf (accessed on 20 December 2021).
- Shukla, P.R.; Skea, J.; Calvo Buendia, E.; Masson-Delmotte, V.; Pörtner, H.O.; Roberts, D.C.; Zhai, P.; Slade, R.; Connors, S.; van Diemen, R.; et al. Climate Change and Land: An IPCC Special Report on Climate Change, Desertification, Land Degradation, Sustainable Land Management, Food Security, and Greenhouse Gas Fluxes in Terrestrial Ecosystems. Technical Report. Intergovernmental Panel on Climate Change (IPCC). 2019. Available online: https://www.ipcc.ch/site/assets/uploads/sites/4/2020/02/SRCCL-Complete-BOOK-LRES.pdf (accessed on 20 December 2021).
- Food and Agriculture Organization of the United Nations (FAO). The Future of Food and Agriculture—Trends and Challenges; Technical Report; FAO: Rome, Italy, 2017; 180p, Available online: http://www.fao.org/3/a-i6583e.pdf (accessed on 20 December 2021)ISBN 978-92-5-109551-5.
- Food and Agriculture Organization of the United Nations (FAO). World Livestock: Transforming the Livestock Sector through the Sustainable Development Goals—Full Report; Technical Report; FAO: Rome, Italy, 2018; 222p, Available online: http://www.fao.org/3/CA1201EN/ca1201en.pdf (accessed on 20 December 2021).
- Gerber, P.J.; Steinfeld, H.; Henderson, B.; Mottet, A.; Opio, C.; Dijkman, J.; Falcucci, A.; Tempio, G. Tackling Climate Change through Livestock—A Global Assessment of Emissions and Mitigation Opportunities; Technical Report; Food and Agriculture Organization of the United Nations (FAO): Rome, Italy, 2013; 26p, Available online: http://www.fao.org/3/i3437e/i3437e.pdf (accessed on 20 December 2021).
- Saunois, M.; Stavert, A.R.; Poulter, B.; Bousquet, P.; Canadell, J.G.; Jackson, R.B.; Raymond, P.A.; Dlugokencky, E.J.; Houweling, S.; Patra, P.K.; et al. The global methane budget 2000–2017. Earth Syst. Sci. Data 2020, 12, 1561–1623. [Google Scholar] [CrossRef]
- Bewley, J.; Robertson, L.; Eckelkamp, E. A 100-Year Review: Lactating dairy cattle housing management. J. Dairy Sci. 2017, 100, 10418–10431. [Google Scholar] [CrossRef] [PubMed]
- Galama, P.; Ouweltjes, W.; Endres, M.; Sprecher, J.; Leso, L.; Kuipers, A.; Klopčič, M. Symposium review: Future of housing for dairy cattle. J. Dairy Sci. 2020, 103, 5759–5772. [Google Scholar] [CrossRef] [PubMed]
- Hempel, S.; Menz, C.; Pinto, S.; Galán, E.; Janke, D.; Estellés, F.; Müschner-Siemens, T.; Wang, X.; Heinicke, J.; Zhang, G.; et al. Heat stress risk in European dairy cattle husbandry under different climate change scenarios—Uncertainties and potential impacts. Earth Syst. Dyn. 2019, 10, 859–884. [Google Scholar] [CrossRef] [Green Version]
- Poteko, J.; Zähner, M.; Schrade, S. Effects of housing system, floor type and temperature on ammonia and methane emissions from dairy farming: A meta-analysis. Biosyst. Eng. 2019, 182, 16–28. [Google Scholar] [CrossRef]
- Schrade, S.; Zeyer, K.; Gygax, L.; Emmenegger, L.; Hartung, E.; Keck, M. Ammonia emissions and emission factors of naturally ventilated dairy housing with solid floors and an outdoor exercise area in Switzerland. Atmos. Environ. 2012, 47, 183–194. [Google Scholar] [CrossRef]
- Ngwabie, N.M.; Vanderzaag, A.; Jayasundara, S.; Wagner-Riddle, C. Measurements of emission factors from a naturally ventilated commercial barn for dairy cows in a cold climate. Biosyst. Eng. 2014, 127, 103–114. [Google Scholar] [CrossRef]
- Monteny, G.; Groenestein, C.; Hilhorst, M. Interactions and coupling between emissions of methane and nitrous oxide from animal husbandry. Nutr. Cycl. Agroecosyst. 2001, 60, 123–132. [Google Scholar] [CrossRef]
- Monteny, G.J.; Bannink, A.; Chadwick, D. Greenhouse gas abatement strategies for animal husbandry. Agric. Ecosyst. Environ. 2006, 112, 163–170. [Google Scholar] [CrossRef]
- Beauchemin, K.; McGinn, S.; Benchaar, C.; Holtshausen, L. Crushed sunflower, flax, or canola seeds in lactating dairy cow diets: Effects on methane production, rumen fermentation, and milk production. J. Dairy Sci. 2009, 92, 2118–2127. [Google Scholar] [CrossRef]
- Ngwabie, N.; Jeppsson, K.H.; Gustafsson, G.; Nimmermark, S. Effects of animal activity and air temperature on methane and ammonia emissions from a naturally ventilated building for dairy cows. Atmos. Environ. 2011, 45, 6760–6768. [Google Scholar] [CrossRef]
- Saha, C.; Ammon, C.; Berg, W.; Fiedler, M.; Loebsin, C.; Sanftleben, P.; Brunsch, R.; Amon, T. Seasonal and diel variations of ammonia and methane emissions from a naturally ventilated dairy building and the associated factors influencing emissions. Sci. Total Environ. 2014, 468, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Hempel, S.; Saha, C.K.; Fiedler, M.; Berg, W.; Hansen, C.; Amon, B.; Amon, T. Non-linear temperature dependency of ammonia and methane emissions from a naturally ventilated dairy barn. Biosyst. Eng. 2016, 145, 10–21. [Google Scholar] [CrossRef] [Green Version]
- Yadav, B.; Singh, G.; Wankar, A.; Dutta, N.; Chaturvedi, V.; Verma, M.R. Effect of simulated heat stress on digestibility, methane emission and metabolic adaptability in crossbred cattle. Asian-Australas. J. Anim. Sci. 2016, 29, 1585. [Google Scholar] [CrossRef]
- Hempel, S.; Willink, D.; Janke, D.; Ammon, C.; Amon, B.; Amon, T. Methane emission characteristics of naturally ventilated cattle buildings. Sustainability 2020, 12, 4314. [Google Scholar] [CrossRef]
- Husted, S. An open chamber technique for determination of methane emission from stored livestock manure. Atmos. Environ. Part A. Gen. Top. 1993, 27, 1635–1642. [Google Scholar] [CrossRef]
- Im, S.; Petersen, S.O.; Lee, D.; Kim, D.H. Effects of storage temperature on CH4 emissions from cattle manure and subsequent biogas production potential. Waste Manag. 2020, 101, 35–43. [Google Scholar] [CrossRef]
- Schmithausen, A.J.; Schiefler, I.; Trimborn, M.; Gerlach, K.; Südekum, K.H.; Pries, M.; Büscher, W. Quantification of methane and ammonia emissions in a naturally ventilated barn by using defined criteria to calculate emission rates. Animals 2018, 8, 75. [Google Scholar] [CrossRef] [Green Version]
- Amon, B.; Kryvoruchko, V.; Fröhlich, M.; Amon, T.; Pöllinger, A.; Mösenbacher, I.; Hausleitner, A. Ammonia and greenhouse gas emissions from a straw flow system for fattening pigs: Housing and manure storage. Livest. Sci. 2007, 112, 199–207. [Google Scholar] [CrossRef]
- Cárdenas, A.; Ammon, C.; Schumacher, B.; Stinner, W.; Herrmann, C.; Schneider, M.; Weinrich, S.; Fischer, P.; Amon, T.; Amon, B. Methane emissions from the storage of liquid dairy manure: Influences of season, temperature and storage duration. Waste Manag. 2021, 121, 393–402. [Google Scholar] [CrossRef]
- Kori, R.K.; Hasan, W.; Jain, A.K.; Yadav, R.S. Cholinesterase inhibition and its association with hematological, biochemical and oxidative stress markers in chronic pesticide exposed agriculture workers. J. Biochem. Mol. Toxicol. 2019, 33, e22367. [Google Scholar] [CrossRef]
- Zetouni, L.; Kargo, M.; Norberg, E.; Lassen, J. Genetic correlations between methane production and fertility, health, and body type traits in Danish Holstein cows. J. Dairy Sci. 2018, 101, 2273–2280. [Google Scholar] [CrossRef]
- Van Gastelen, S.; Mollenhorst, H.; Antunes-Fernandes, E.; Hettinga, K.; van Burgsteden, G.; Dijkstra, J.; Rademaker, J. Predicting enteric methane emission of dairy cows with milk Fourier-transform infrared spectra and gas chromatography–based milk fatty acid profiles. J. Dairy Sci. 2018, 101, 5582–5598. [Google Scholar] [CrossRef] [Green Version]
- Ellis, J.; Kebreab, E.; Odongo, N.; McBride, B.; Okine, E.; France, J. Prediction of methane production from dairy and beef cattle. J. Dairy Sci. 2007, 90, 3456–3466. [Google Scholar] [CrossRef]
- Hempel, S.; Adolphs, J.; Landwehr, N.; Willink, D.; Janke, D.; Amon, T. Supervised Machine Learning to Assess Methane Emissions of a Dairy Building with Natural Ventilation. Appl. Sci. 2020, 10, 6938. [Google Scholar] [CrossRef]
- Bolboaca, S.D.; Jäntschi, L. Pearson versus Spearman, Kendall’s tau correlation analysis on structure-activity relationships of biologic active compounds. Leonardo J. Sci. 2006, 5, 179–200. [Google Scholar]
- Spearman, C. Footrule for measuring correlation. Br. J. Psychol. 1906, 2, 89. [Google Scholar] [CrossRef]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Duncan, T.E. On the calculation of mutual information. SIAM J. Appl. Math. 1970, 19, 215–220. [Google Scholar] [CrossRef] [Green Version]
- Gierlichs, B.; Batina, L.; Tuyls, P.; Preneel, B. Mutual information analysis. In Proceedings of the International Workshop on Cryptographic Hardware and Embedded Systems, Washington, DC, USA, 10–13 August 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 426–442. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond k-means. In Proceedings of the Joint European Conference on Machine Learning and Knowledge Discovery in Databases, Antwerp, Belgium, 15–18 September 2008; Springer: Berlin/Heidelberg, Germany, 2008; pp. 3–4. [Google Scholar]
- Mohn, J.; Zeyer, K.; Keck, M.; Keller, M.; Zähner, M.; Poteko, J.; Emmenegger, L.; Schrade, S. A dual tracer ratio method for comparative emission measurements in an experimental dairy housing. Atmos. Environ. 2018, 179, 12–22. [Google Scholar] [CrossRef]
- Poteko, J.; Zähner, M.; Steiner, B.; Schrade, S. Residual soiling mass after dung removal in dairy loose housings: Effect of scraping tool, floor type, dung removal frequency and season. Biosyst. Eng. 2018, 170, 117–129. [Google Scholar] [CrossRef]
- Leinweber, T.; Zähner, M.; Schrade, S. Evaluation of a dung-removal robot for use in dairy housing from an ethological and process-engineering point of view. Landtechnik 2019, 74, 55–68. [Google Scholar]
- Pedersen, S.; Sällvik, K. Climatization of Animal Houses. Heat and Moisture Production at Animal and House Levels; Danish Insitute of Agricultural Sciences: Horsens, Denmark, 2002; pp. 1–46. [Google Scholar]
- Willink, D.; Hempel, S.; Janke, D.; Amon, B.; Amon, T. High resolution long-term measurements of carbon dioxide, ammonia, and methane concentrations in two naturally ventilated dairy barns. Publisso ZB Med Repos. Life Sci. 2020. [Google Scholar] [CrossRef]
- Doumbia, E.M.; Janke, D.; Yi, Q.; Prinz, A.; Amon, T.; Kriegel, M.; Hempel, S. A parametric model for local air exchange rate of naturally ventilated barns. Agronomy 2021, 11, 1585. [Google Scholar] [CrossRef]
- Poteko, J.; Schrade, S.; Zeyer, K.; Mohn, J.; Zaehner, M.; Zeitz, J.O.; Kreuzer, M.; Schwarm, A. Methane emissions and milk fatty acid profiles in dairy cows fed linseed, measured at the group level in a naturally ventilated housing and individually in respiration chambers. Animals 2020, 10, 1091. [Google Scholar] [CrossRef]
- Aguerre, M.J.; Wattiaux, M.A.; Powell, J.; Broderick, G.A.; Arndt, C. Effect of forage-to-concentrate ratio in dairy cow diets on emission of methane, carbon dioxide, and ammonia, lactation performance, and manure excretion. J. Dairy Sci. 2011, 94, 3081–3093. [Google Scholar] [CrossRef]
- Benchaar, C.; Pomar, C.; Chiquette, J. Evaluation of dietary strategies to reduce methane production in ruminants: A modelling approach. Can. J. Anim. Sci. 2001, 81, 563–574. [Google Scholar] [CrossRef]
- Knapp, J.R.; Laur, G.; Vadas, P.A.; Weiss, W.P.; Tricarico, J.M. Invited review: Enteric methane in dairy cattle production: Quantifying the opportunities and impact of reducing emissions. J. Dairy Sci. 2014, 97, 3231–3261. [Google Scholar] [CrossRef] [Green Version]
- Olijhoek, D.; Løvendahl, P.; Lassen, J.; Hellwing, A.; Höglund, J.; Weisbjerg, M.; Noel, S.; McLean, F.; Højberg, O.; Lund, P. Methane production, rumen fermentation, and diet digestibility of Holstein and Jersey dairy cows being divergent in residual feed intake and fed at 2 forage-to-concentrate ratios. J. Dairy Sci. 2018, 101, 9926–9940. [Google Scholar] [CrossRef] [Green Version]
- van Gastelen, S.; Dijkstra, J.; Bannink, A. Are dietary strategies to mitigate enteric methane emission equally effective across dairy cattle, beef cattle, and sheep? J. Dairy Sci. 2019, 102, 6109–6130. [Google Scholar] [CrossRef] [Green Version]
- Qu, Q.; Groot, J.C.; Zhang, K.; Schulte, R.P. Effects of housing system, measurement methods and environmental factors on estimating ammonia and methane emission rates in dairy barns: A meta-analysis. Biosyst. Eng. 2021, 205, 64–75. [Google Scholar] [CrossRef]
- Edouard, N.; Mosquera, J.; van Dooren, H.J.; Mendes, L.B.; Ogink, N.W. Comparison of CO2- and SF6-based tracer gas methods for the estimation of ventilation rates in a naturally ventilated dairy barn. Biosyst. Eng. 2016, 149, 11–23. [Google Scholar] [CrossRef] [Green Version]
- Pereira, J.; Misselbrook, T.H.; Chadwick, D.R.; Coutinho, J.; Trindade, H. Effects of temperature and dairy cattle excreta characteristics on potential ammonia and greenhouse gas emissions from housing: A laboratory study. Biosyst. Eng. 2012, 112, 138–150. [Google Scholar] [CrossRef]
- D’Urso, P.R.; Arcidiacono, C.; Cascone, G. Environmental and Animal-Related Parameters and the Emissions of Ammonia and Methane from an Open-Sided Free-Stall Barn in Hot Mediterranean Climate: A Preliminary Study. Agronomy 2021, 11, 1772. [Google Scholar] [CrossRef]
- Doumbia, E.M.; Janke, D.; Yi, Q.; Zhang, G.; Amon, T.; Kriegel, M.; Hempel, S. On Finding the Right Sampling Line Height through a Parametric Study of Gas Dispersion in a NVB. Appl. Sci. 2021, 11, 4560. [Google Scholar] [CrossRef]
| Site | S | S | S | G | G | G |
|---|---|---|---|---|---|---|
| Season | Wi | Au | Su | Wi | Sp | Su |
| Energy-corrected | ||||||
| milk per cow (kg day) | 32.4 | 33.8 | 27.7 | 37.3 | 37.4 | 37.0 |
| Dry matter | ||||||
| intake per cow (kg day) | 21.1 | 21.6 | 20.9 | 26.6 | 26.0 | 26.7 |
| Percentage of concentrate | ||||||
| (% of dry matter) | 20.4 | 17.2 | 20.0 | 42.3 | 42.1 | 42.3 |
| Crude protein | ||||||
| (g kg of dry matter) | 168 | 168 | 163 | 173 | 166 | 167 |
| Neutral detergent fiber | ||||||
| (g kg of dry matter) | 362 | 360 | 445 | 292 | 338 | 346 |
| Netto energy lactation | ||||||
| (MJ kg of dry matter) | 6.6 | 6.6 | 6.3 | 7.2 | 7.2 | 7.1 |
| Parameter | Site | Floor Type | Mean | SD | CV | Skewness | Kurtosis |
|---|---|---|---|---|---|---|---|
| ME | Switzerland | Slatted | 18.23 | 6.79 | 0.37 | 1.13 | 7.68 |
| ME | Switzerland | Solid | 14.95 | 4.96 | 0.33 | −0.50 | 3.68 |
| ME | Germany | Solid | 11.44 | 2.84 | 0.25 | −0.11 | 2.68 |
| T | Switzerland | Slatted | 13.93 | 8.05 | 0.58 | −0.08 | 2.05 |
| T | Switzerland | Solid | 14.31 | 8.02 | 0.56 | −0.13 | 2.07 |
| T | Germany | Solid | 12.55 | 6.34 | 0.51 | 0.23 | 2.19 |
| WS | Switzerland | Slatted | 3.05 | 2.63 | 0.86 | 1.49 | 5.56 |
| WS | Switzerland | Solid | 3.01 | 2.41 | 0.80 | 1.27 | 4.53 |
| WS | Germany | Solid | 1.80 | 1.28 | 0.71 | 0.65 | 2.54 |
| Site | Floor Type | Forced Convection | Mixed Convection | Natural Convection |
|---|---|---|---|---|
| Switzerland | Slatted | 0.40 | 0.50 | 0.10 |
| Switzerland | Solid | 0.42 | 0.49 | 0.09 |
| Germany | Solid | 0.21 | 0.57 | 0.22 |
| Site | Floor | Regime | T, ME | T, MC | WS, ME | WS, MC |
|---|---|---|---|---|---|---|
| S | Slatted | All | 0.22 (p = 0.51) | −0.41 (p = 0.50) | −0.02 (p = 0.44) | −0.57 (p = 0.50) |
| Slatted | Forced | 0.28 (p = 0.50) | −0.48 (p = 0.51) | −0.25 (p = 0.50) | 0.01 (p = 0.44) | |
| S | Slatted | Mixed | 0.14 (p = 0.50) | −0.44 (p = 0.49) | −0.04 (p = 0.45) | −0.33 (p = 0.49) |
| S | Slatted | Natural | 0.24 (p = 0.48) | −0.43 (p = 0.50) | −0.22 (p = 0.47) | −0.06 (p = 0.43) |
| S | Solid | All | −0.08 (p = 0.48) | −0.49 (p = 0.50) | 0.12 (p = 0.50) | −0.39 (p = 0.51) |
| S | Solid | Forced | 0.00 (p = 0.44) | −0.55 (p = 0.48) | −0.01 (p = 0.45) | 0.06 (p = 0.45) |
| S | Solid | Mixed | −0.19 (p = 0.49) | −0.60 (p = 0.49) | 0.08 (p = 0.47) | −0.03 (p = 0.43) |
| S | Solid | Natural | 0.32 (p = 0.49) | −0.52 (p = 0.49) | −0.20 (p = 0.47) | −0.13 (p = 0.45) |
| G | Solid | All | 0.24 (p = 0.50) | 0.11 (p = 0.50) | 0.22 (p = 0.50) | 0.09 (p = 0.47) |
| G | Solid | Forced | 0.69 (p = 0.51) | 0.39 (p = 0.50) | −0.61 (p = 0.51) | −0.31 (p = 0.49) |
| G | Solid | Mixed | 0.14 (p = 0.50) | 0.07 (p = 0.47) | 0.02 (p = 0.44) | 0.03 (p = 0.44) |
| G | Solid | Natural | −0.09 (p = 0.45) | −0.04 (p = 0.43) | 0.26 (p = 0.50) | 0.01 (p = 0.45) |
| Site | Floor | Regime | T, ME | T, MC | WS, ME | WS, MC |
|---|---|---|---|---|---|---|
| S | Slatted | All | 0.15 (p = 0.51) | −0.27 (p = 0.50) | −0.02 (p = 0.44) | −0.39 (p = 0.50) |
| S | Slatted | Forced | 0.20 (p = 0.49) | −0.33 (p = 0.50) | −0.17 (p = 0.49) | 0.01 (p = 0.44) |
| S | Slatted | Mixed | 0.11 (p = 0.50) | −0.28 (p = 0.49) | −0.03 (p = 0.45) | −0.22 (p = 0.49) |
| S | Slatted | Natural | 0.17 (p = 0.48) | −0.32 (p = 0.50) | −0.15 (p = 0.47) | −0.02 (p = 0.43) |
| S | Solid | All | −0.05 (p = 0.47) | −0.34 (p = 0.50) | 0.08 (p = 0.49) | −0.28 (p = 0.51) |
| S | Solid | Forced | 0.00 (p = 0.43) | −0.40 (p = 0.49) | −0.01 (p = 0.45) | 0.01 (p = 0.44) |
| S | Solid | Mixed | −0.11 (p = 0.49) | −0.40 (p = 0.49) | 0.05 (p = 0.46) | −0.02 (p = 0.43) |
| S | Solid | Natural | 0.24 (p = 0.48) | −0.37 (p = 0.48) | −0.13 (p = 0.46) | −0.13 (p = 0.45) |
| G | Solid | All | 0.17 (p = 0.50) | 0.08 (p = 0.50) | 0.15 (p = 0.50) | 0.07 (p = 0.48) |
| G | Solid | Forced | 0.51 (p = 0.50) | 0.32 (p = 0.49) | −0.41 (p = 0.50) | −0.23 (p = 0.49) |
| G | Solid | Mixed | 0.10 (p = 0.50) | 0.06 (p = 0.48) | 0.01 (p = 0.44) | 0.03 (p = 0.44) |
| G | Solid | Natural | −0.06 (p = 0.45) | −0.07 (p = 0.45) | 0.17 (p = 0.50) | 0.02 (p = 0.46) |
| Site | Floor | Regime | T, ME | T, MC | WS, ME | WS, MC |
|---|---|---|---|---|---|---|
| S | Slatted | All | 0.18 (p < 0.01) | 0.22 (p < 0.01) | 0.12 (p = 0.06) | 0.31 (p < 0.01) |
| S | Slatted | Forced | 0.21 (p < 0.01) | 0.30 (p < 0.01) | 0.14 (p = 0.01) | 0.1 (p = 0.22) |
| S | Slatted | Mixed | 0.20 (p < 0.01) | 0.32 (p < 0.01) | 0.11 (p = 0.65) | 0.25 (p < 0.01) |
| S | Slatted | Natural | 0.17 (p = 0.24) | 0.23 (p = 0.08) | 0.21 (p = 0.15) | 0.09 (p = 0.98) |
| S | Solid | All | 0.15 (p < 0.01) | 0.25 (p < 0.01) | 0.09 (p = 0.47) | 0.27 (p < 0.01) |
| S | Solid | Forced | 0.10 (p = 0.18) | 0.27 (p < 0.01) | 0.09 (p = 0.29) | 0.14 (p = 0.01) |
| S | Solid | Mixed | 0.17 (p = 0.04) | 0.39 (p < 0.01) | 0.13 (p = 0.37) | 0.18 (p = 0.02) |
| S | Solid | Natural | 0.03 (p = 0.68) | 0.42 (p < 0.01) | 0.03 (p = 0.70) | 0.03 (p = 0.67) |
| G | Solid | All | 0.26 (p < 0.01) | 0.20 (p < 0.01) | 0.14 (p < 0.01) | 0.20 (p < 0.01) |
| G | Solid | Forced | 0.50 (p < 0.01) | 0.17 (p = 0.08) | 0.38 (p < 0.01) | 0.14 (p = 0.20) |
| G | Solid | Mixed | 0.21 (p < 0.01) | 0.12 (p = 0.06) | 0.12 (p = 0.06) | 0.15 (p < 0.01) |
| G | Solid | Natural | 0.21 (p = 0.03) | 0.24 (p = 0.01) | 0.25 (p = 0.01) | 0.21 (p = 0.03) |
| Site | Floor | Cluster Number | T | WS | WD | DT | MC | ME |
|---|---|---|---|---|---|---|---|---|
| S | Slatted | 1 | 3.6 | 7.1 | 195.6 (S) | 12 | 5.5 | 16.1 |
| S | Slatted | 2 | 16.1 | 1.6 | 234.9 (SW) | 4 | 4.1 | 16.1 |
| S | Slatted | 3 | 11.2 | 0.8 | 166.7 (S) | 10 | 21.7 | 18.6 |
| S | Slatted | 4 | 25.2 | 1.6 | 58.8 (NO) | 14 | 4.5 | 19.4 |
| S | Slatted | 5 | 16.0 | 2.8 | 231.5 (SW) | 15 | 6.4 | 19.6 |
| S | Solid | 1 | 24.2 | 1.5 | 48.4 (NO) | 23 | 4.1 | 12.5 |
| S | Solid | 2 | 17.0 | 1.3 | 229.6 (SW) | 4 | 5.9 | 14.7 |
| S | Solid | 3 | 7.7 | 1.0 | 198.6 (S) | 10 | 19.1 | 15.2 |
| S | Solid | 4 | 4.6 | 6.0 | 200.6 (S) | 1 | 5.9 | 15.8 |
| S | Solid | 5 | 16.90 | 3.3 | 234.8 (SW) | 21 | 6.7 | 18.4 |
| G | Solid | 1 | 17.1 | 0.4 | 111.1 (O) | 3 | 20.1 | 9.1 |
| G | Solid | 2 | 10.8 | 1.1 | 312.7 (NW) | 4 | 14.0 | 9.3 |
| G | Solid | 3 | 9.0 | 2.6 | 218.9 (SW) | 0 | 8.3 | 10.6 |
| G | Solid | 4 | 5.3 | 0.9 | 5.7 (N) | 21 | 23.1 | 14.0 |
| G | Solid | 5 | 22.0 | 2.3 | 1.8 (N) | 15 | 11.5 | 14.7 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hempel, S.; Janke, D.; Losand, B.; Zeyer, K.; Zähner, M.; Mohn, J.; Amon, T.; Schrade, S. Comparison of Methane Emission Patterns from Dairy Housings with Solid and Slatted Floors at Two Locations. Agronomy 2022, 12, 381. https://doi.org/10.3390/agronomy12020381
Hempel S, Janke D, Losand B, Zeyer K, Zähner M, Mohn J, Amon T, Schrade S. Comparison of Methane Emission Patterns from Dairy Housings with Solid and Slatted Floors at Two Locations. Agronomy. 2022; 12(2):381. https://doi.org/10.3390/agronomy12020381
Chicago/Turabian StyleHempel, Sabrina, David Janke, Bernd Losand, Kerstin Zeyer, Michael Zähner, Joachim Mohn, Thomas Amon, and Sabine Schrade. 2022. "Comparison of Methane Emission Patterns from Dairy Housings with Solid and Slatted Floors at Two Locations" Agronomy 12, no. 2: 381. https://doi.org/10.3390/agronomy12020381
APA StyleHempel, S., Janke, D., Losand, B., Zeyer, K., Zähner, M., Mohn, J., Amon, T., & Schrade, S. (2022). Comparison of Methane Emission Patterns from Dairy Housings with Solid and Slatted Floors at Two Locations. Agronomy, 12(2), 381. https://doi.org/10.3390/agronomy12020381









