Abstract
In this study, we provide a discretized system of a continuous dynamical model for enhancing crop production in the presence of insecticides and insects. Crops are assumed to grow logistically but are limited by an insect population that entirely depends on agriculture. To protect crops from insects, farmers use insecticides, and their overmuch use is harmful to human health. We assumed that external efforts are proportional to the gap between actual production and carrying capacity to increase the field’s development potential. We use the Levenberg–Marquardt algorithm (LMA) based on artificial neural networks (NNs) to investigate the approximate solutions for different insecticide spraying rates. “NDSolve” tool in Mathematica generated a data collection for supervised LMA. The NN-LMA approximation’s value is achieved by the training, validation, and testing reference data sets. Regression, error histograms, and complexity analysis help to validate the technique’s robustness and accuracy.
1. Introduction
Agriculture production is essential for meeting fundamental life demands and the needs of the industrial sector for raw materials, which enhances the country’s economy. Due to the increase in population, higher food production is essential (estimated to be over 10 billion by 2050). Because agricultural land is limited, increasing crop production can help increase agricultural production. Farmers utilize high-yield seed kinds, irrigation techniques, and mechanical equipment to increase production. Despite agricultural achievements, food insecurity continues to be a significant human health concern.
In 2018, 113 million people in 53 countries were food insecure, according to the Organization for Food and Agriculture [1]. Some insects strike on growing crops, destroying leaves, fruits, and roots. According to Oerke’s estimates [2], insects cause 26–29% loss in cotton, soybean, and wheat crops, loss in maize, loss in rice, and loss in potato crops. Insect damaging the crops is one of the significant variables affecting the quality and quantity of the crops. For this reason, managing insects population is vital for crop production.
An ecosystem-based approach to pest management, known as Integrated Pest Management (IPM), helps protect crops from insects. IPM strategies fall into two broad categories: Non-chemical and chemical controls. Non-chemical control involves killing insects without chemicals, such as crop rotations, antagonists, etc. On the other hand, chemical control involves chemicals such as insecticides to reduce insect density.
Biological control is a strategy that doesn’t use chemicals to get control of the incests population. It uses living organisms to reduce the number of insects [3]. Putting an infected insect on a crop field can help reduce the number of insects that eat it [4,5]. It is good that biological control methods are suitable for the environment and effective at controlling insect populations, but the process is prolonged. A biological approach to pest management is no longer sufficient for the constantly increasing insect population; a methodology that can quickly control insect population density is required. Insecticides are highly toxic to certain species of insects; they can significantly lower the insect population and help protect the crop. According to Wang et al., [6], it has been shown that periodic insecticides spraying with infected insects can effectively manage insect populations.
Tang et al. [7] used IPM approaches to develop and study a dynamical system that is state-dependent and impulsive between prey and predator. To keep the insect population at or below a predetermined level, a precise number of insecticides must be applied. Insect population density can be lowered by combining these two strategies [8].
Plants require specific nutrients, such as nitrogen, phosphorus, and potassium, to grow. There are a variety of nutrients that may be found in agricultural soil to preserve the soil’s fertility. Plants suffer from nutrient insufficiency when the nutrient level in the soil is low, and their growth is affected. Farmers use fertilizers in their fields to meet the needs of their crops. Adding fertilizer to the soil helps to ensure that it has the necessary amount of nutrients.
According to Lombin and Uyovbisere [9], to increase maize yields, soil nutrition needs to be optimized, which necessitates the use of fertilizers. The availability of agricultural land influences crop growth. Farmers recruit extra staff to prepare crop fields. The external effort includes both nutrition and extra labor. Several studies have shown the value of external effort in several domains. Misra et al. [10] devised and analysed an algal model to assess the effectiveness of external efforts in removing algae from lakes.
Models based on mathematics are usually used to show nonlinear physical phenomena. It is very rare for a mathematical model to have an analytical solution. So numerical methods are preferred to approximate it. There are various numerical techniques for solving nonlinear initial value problems, such as Euler, Adams-Bashforth, and Runge-Kutta (RK), but these strategies don’t always work [11]. There are several methods to avoid numerical discrepancies. Mickens developed a non-standard finite difference (NSFD) approach to prevent numerical instability [12,13]. Approximation of nonlinear terms by nonlocal approximation, he discretizes the continuous model and reconstructs dynamical variable derivatives. Equilibrium points are bounded, stable, and, positive much like a continuous system. There is a dynamically consistent solution for the continuous system using this technique. Continuous dynamical systems can be used to derive many different finite-difference strategies. An NSFD scheme keeps one of the following qualities:
- Nonlocal strategies are used to approximate nonlinear terms in continuous systems.
- During the derivatives of discretization procedure, is denominator function with a renormalized denominator used instead h a traditional denominator, as a result when , [14,15,16].
For logistic equations, Olabode and Obayomi [17] investigated non-standard and standard schemes and discovered that the non-standard scheme’s solution curve has more consistency with the analytical solution than the standard scheme. Similarly, numerous discretization techniques for nonlinear differential equations have been devised across several fields [18,19,20,21]. The following are some prominent elements of the presented study:
- We use the developed nonlinear computational model [8] to determine the effects of insecticides, insects, and external efforts on agricultural crop production in order to achieve optimal crop production.
- Using artificial neural networks, a Levenberg–Marquardt technique (LMT) trains hidden neurons and validates the reference data set obtained using the “NDSolve” tool in Mathematica for different insecticide spraying rates instances.
- Based on curve fitting, regression, the mean squared error (MSE), and total and absolute errors, the technique has to prove its convergence, accuracy, and processing cost through extensive graphical study.
2. Problem Formulation
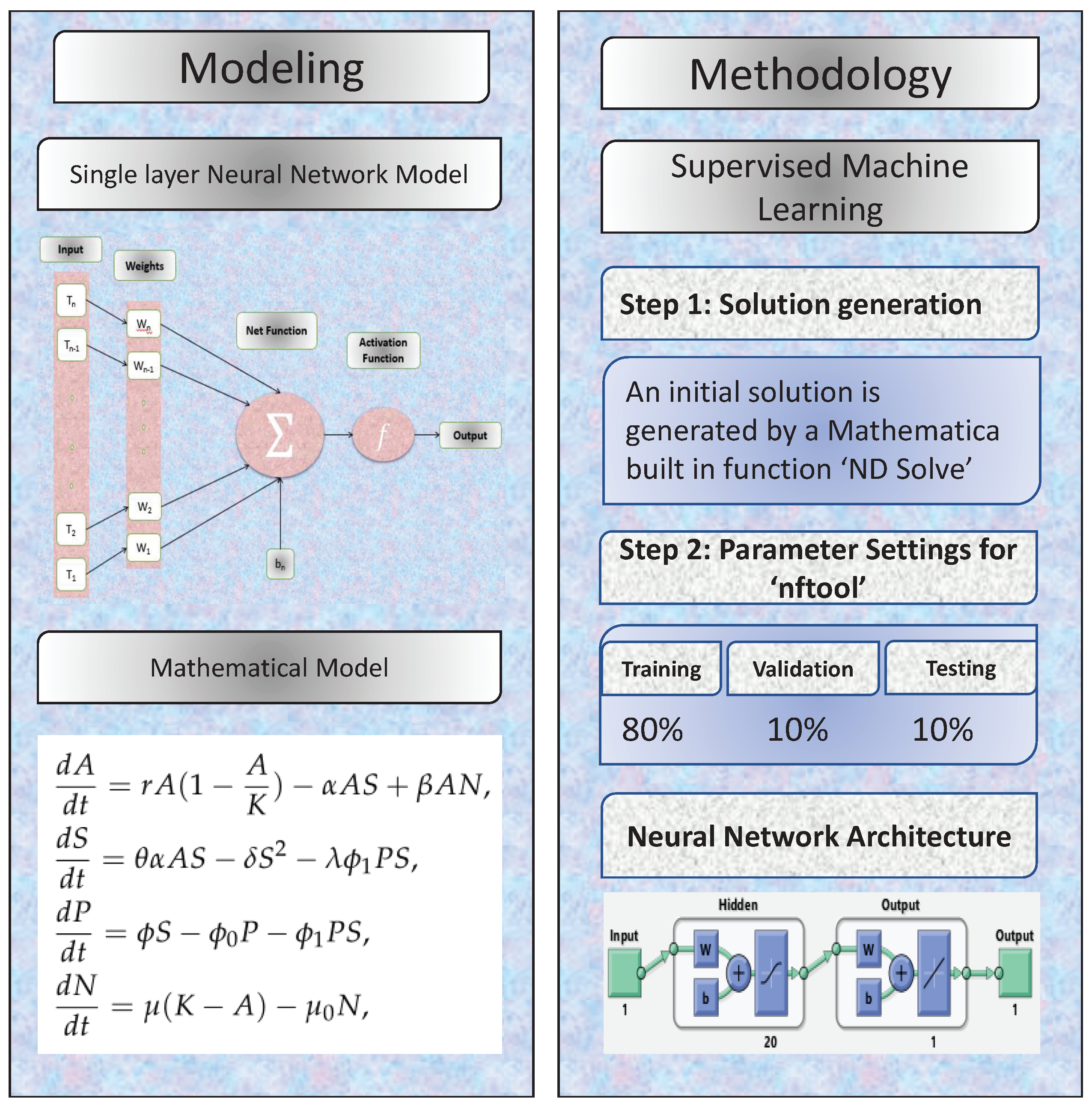
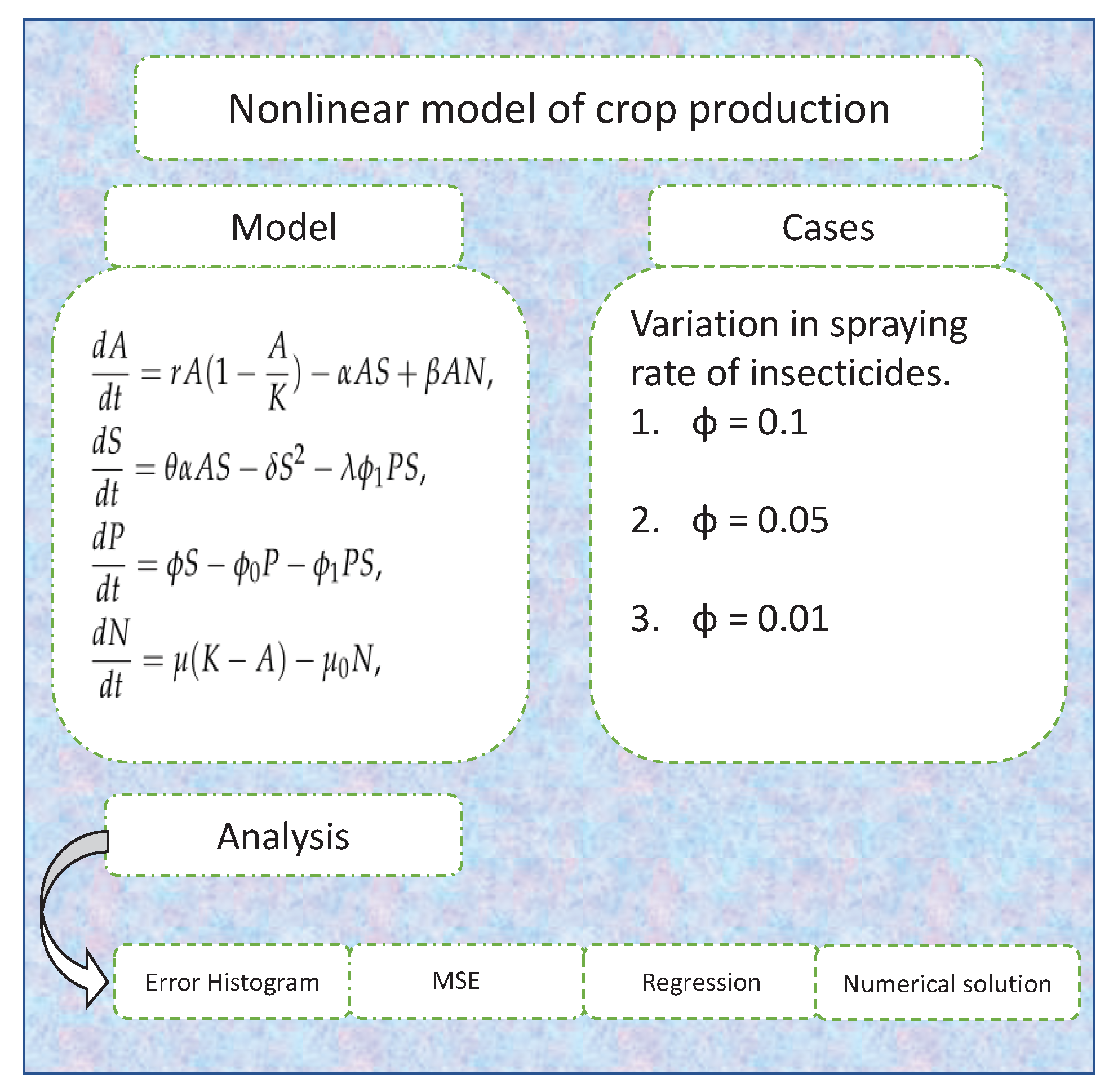
To defend the crop from pests using pesticides and improve agricultural production via external actions, we create a non-linear mathematical model. Let represent agricultural production, population of insects’ density, insecticide concentration, and external efforts at . We expect that consent the strategic development work with r the rate of inherent development and K the ecological conveying limit. The rate of crop consumed by insects is considered by . It lowers the pace of crop production by . It is anticipated that insect population density grows at a rate of ; this rise is due to the consumption of crops by insects, here signifies the conversion efficiency of insects. We have likewise accepted in the population of insects the intra-specific contest happens, resulting in the decrease in insects density at a rate , where the intra-specific competition rate is represented by . Insecticides are applied at a rate proportionate to the insects’ population density. The natural depletion rate of insecticides is denoted by . Insecticide normally exhausts relative to its fixation at the rate . It is believed that there is a decrease in the insecticides quantity owing to the population of incests uptake, which is comparable to insects density and the quantity of it (i.e., ), where the insecticides uptake rate by insects is represented by . The density of the insect population reduces by as a result of this uptake, here signifies the constant of proportionality. To boost productivity, farmers apply external efforts in the cultivation field. The external efforts are quantified by using fertilizers to provide nutrients for crop gro. External efforts are assumed to raise the proportional difference between the actual production of crop and carrying capacity (i.e., ) here the constant of proportionality is . The rate of increase in crop production, which comes as a result of applied external efforts, is represented by . External efforts are assumed to deplete proportionally to themselves (i.e., ), here the external efforts’ natural depletion rate is represented by . Thus, the following set of ODEs drives agricultural production dynamics with insect populations and insecticides:
where , , , and are initial conditions.
This is because the model system (1), insect population density, insecticide amount, and external efforts all drive agricultural crop production dynamics in a non-negative way. Table 1 shows the description, source of reference of parameters used in model (1) and their values for numerical simulations.

Table 1.
Parameter setting for the numerical simulation of model (1).
3. Design Methodology
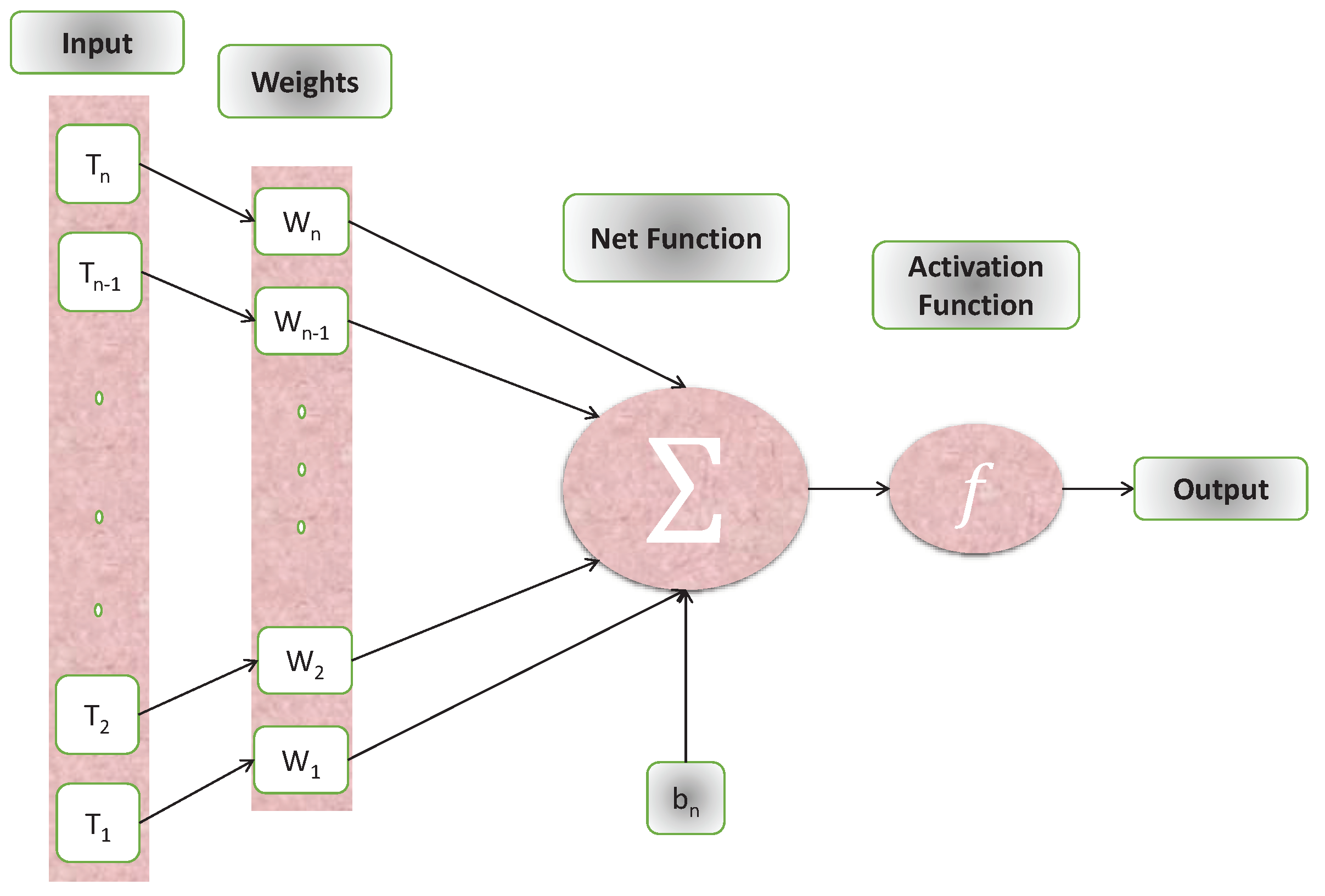
Artificial neural networks (ANN) are examined in this part, which presents a unique machine learning approach focused on the supervised methods of neurons. An ANN is an interconnected fundamental components network known as neurons that receives various inputs and produces only one output. The sum of a neuron’s inputs dictates its output. In this study, a multilayer perceptron (MLP) is used to optimize the number of hidden units. The connection weights and biases were also optimised. The standard MLP construction with one hidden layer is as follows:
where the inputs are represented by , and represent biased vectors and connection weights, respectively. The Feed-forward neural network model uses a log-sigmoid as an activation function given as,
It also explains how the design soft computing technique works. The proposed approach involves two phases.
- The “NDSolve” function in Mathematica is used to solve the model (1) numerically for the initial data collection.
- For different cases of the problem, the Levenberg Marquardt method uses neural networks with 20 hidden neurons to approximate answers. Figure 1 depicts the NN’s-LMT approach as a single neuron model.
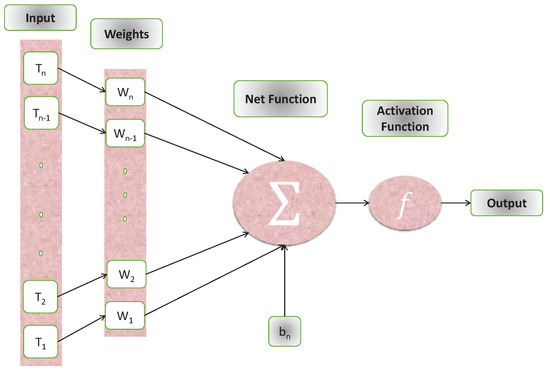 Figure 1. Architecture of artificial neural networks with single neuron.
Figure 1. Architecture of artificial neural networks with single neuron.
The Levenberg–Marquardt method uses the first step’s reference data set for supervised learning to process data for training, validation and, testing. Table 2 illustrate the parameter settings for the proposed approach.

Table 2.
Parameters settings for the execution of the design NN-LMT.
Performance measurements include mean square error, regression analysis, absolute and histograms errors to assess the design scheme’s convergence and accuracy. Figure 2 illustrate the working mechanism and a stepwise methodology for NN-LM technique.
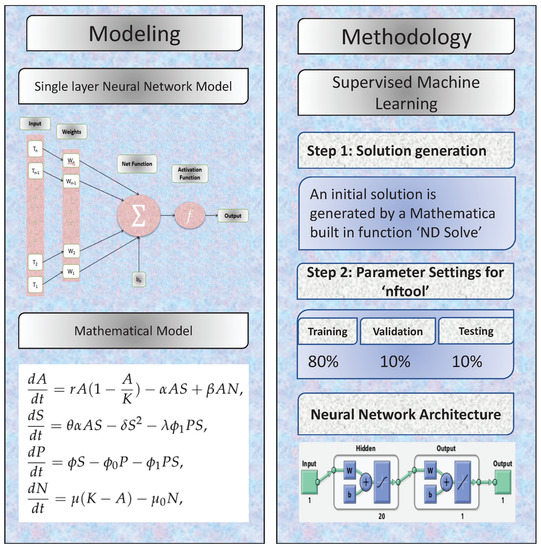
Figure 2.
The NNs–LM method for a mathematical model (1).
4. Results and Discussions
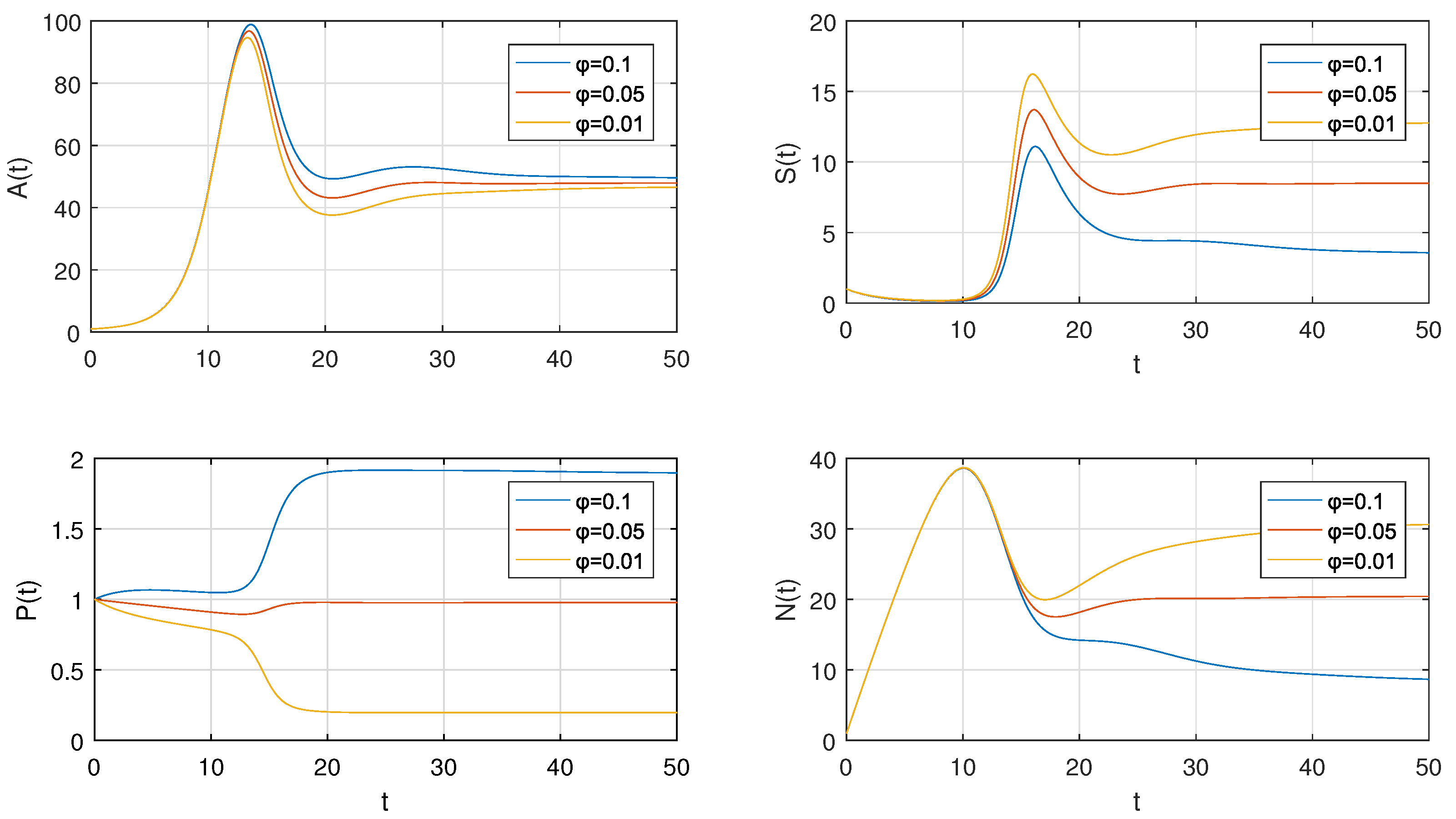
We did experiments in this section to see if the technique was correct and how the insecticide spraying rate affects a crop model. This model includes agricultural production, the concentration of insecticides, the density of insects, and the efforts. The cases are based on variation in the spraying rate of insecticides, i.e., the parameter. We consider the first case as [23]; to make the second and third cases, we slightly decrease the value of . Figure 3 illustrates the model and its different cases.
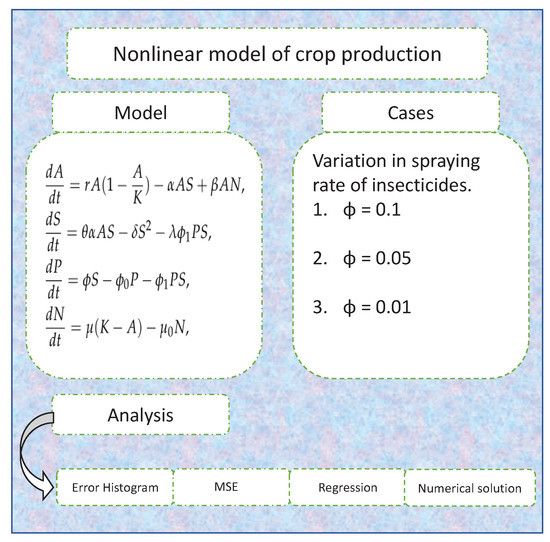
Figure 3.
Nonlinear model of crop production and its different cases.
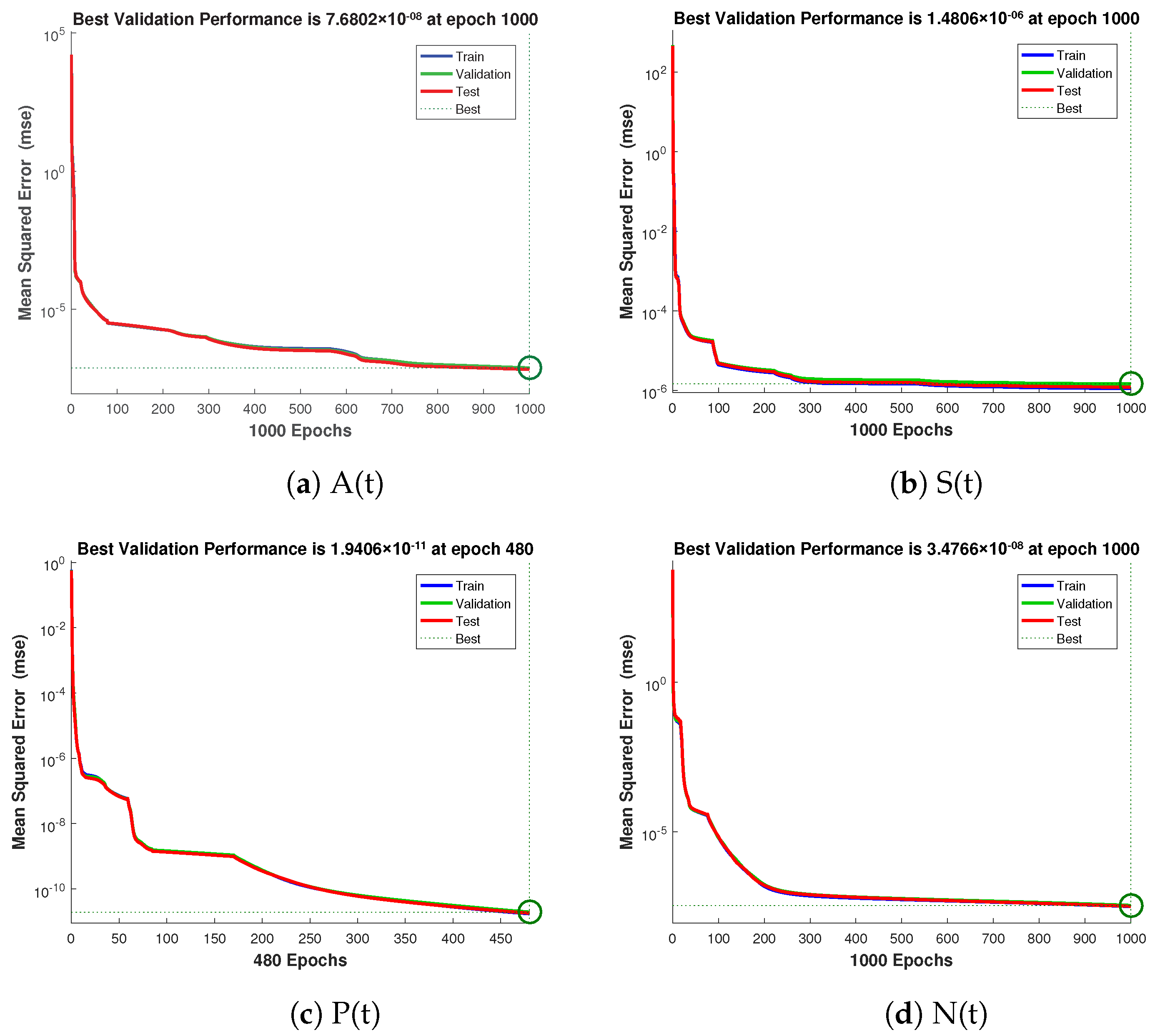
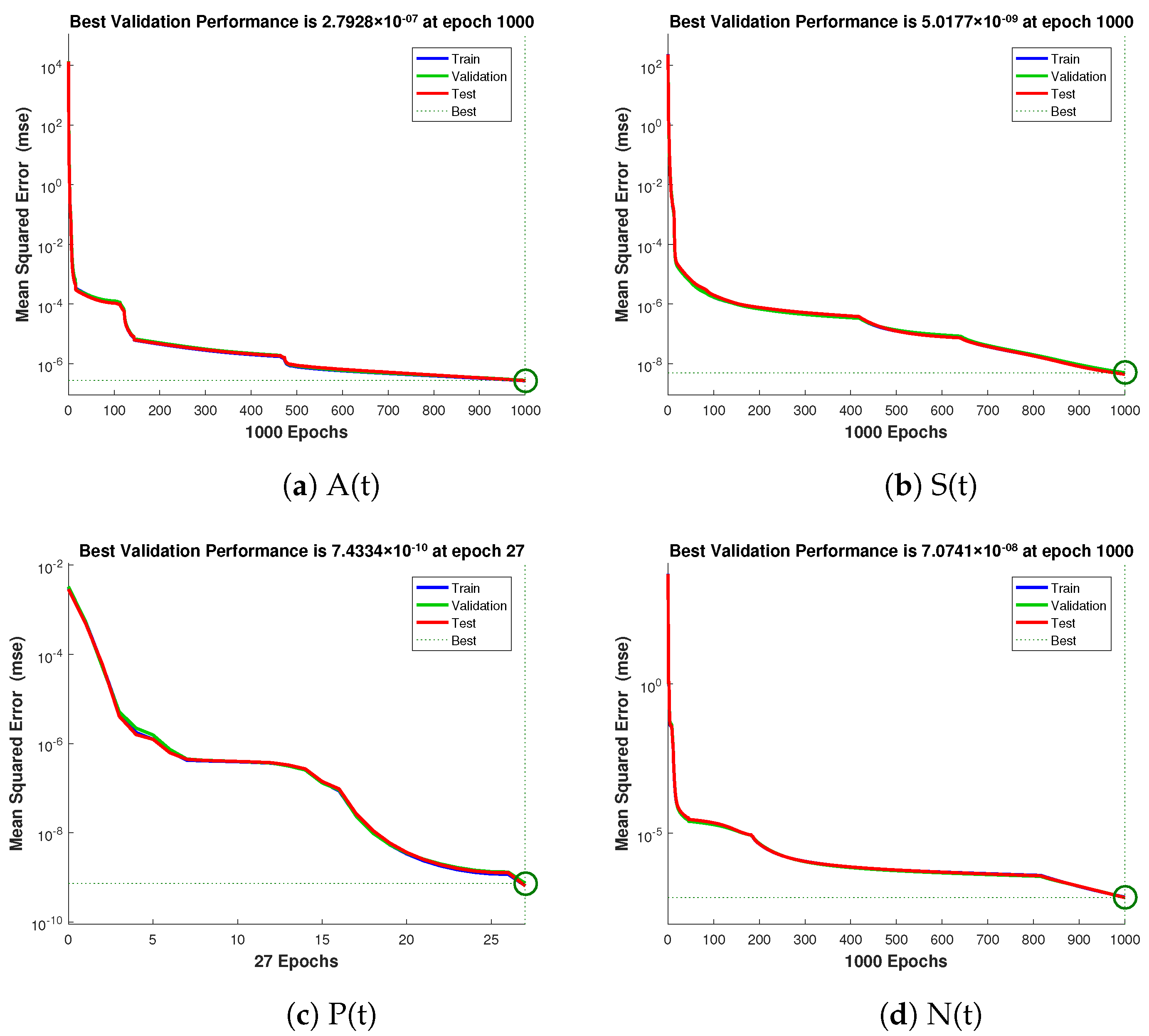
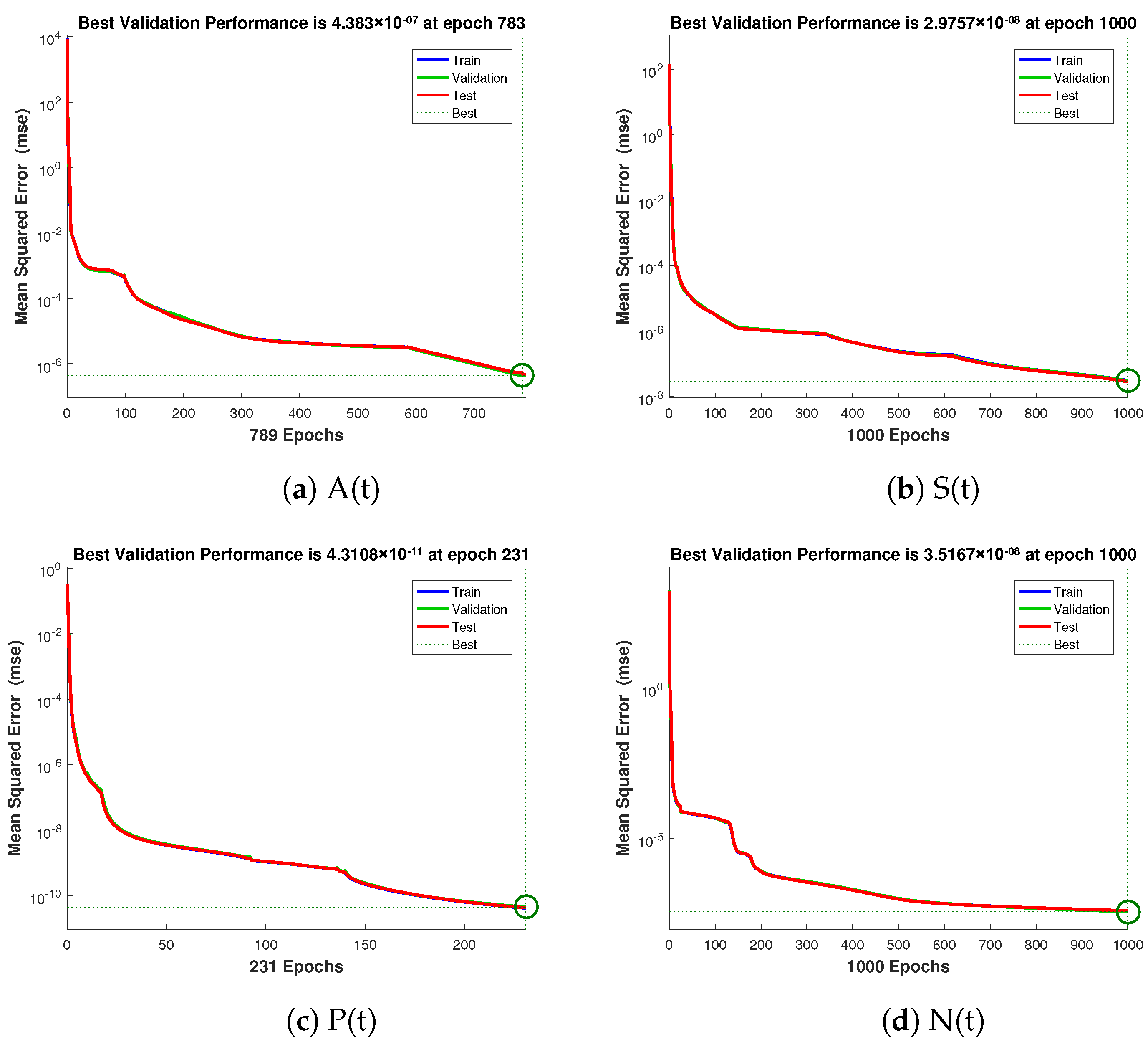
The numerical technique gives data set values that can be used to train, validate, and test data with 80%, 10%, and 10% probability. Each example’s mean square error (MSE) function convergence is shown graphically. Figure 4 shows the performance values for the case 1 which are in the range of , , and . Similarly Figure 5 and Figure 6 illustrate the performance values for case 2 and 3 respectively, which are in the range of , , , , , , and .
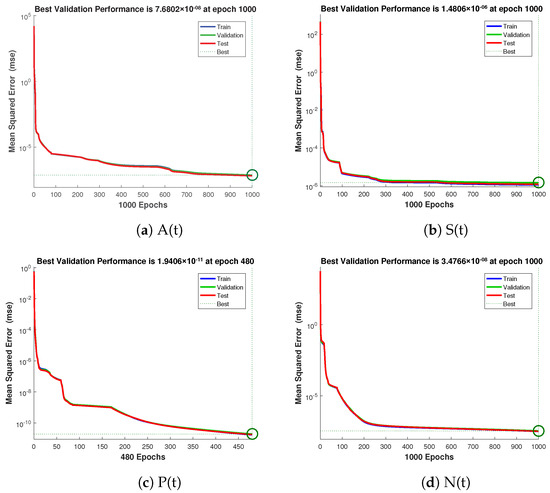
Figure 4.
Mean square error of NNs-LMT for crop production, insects density, insecticides concentration, and external effort of case 1.
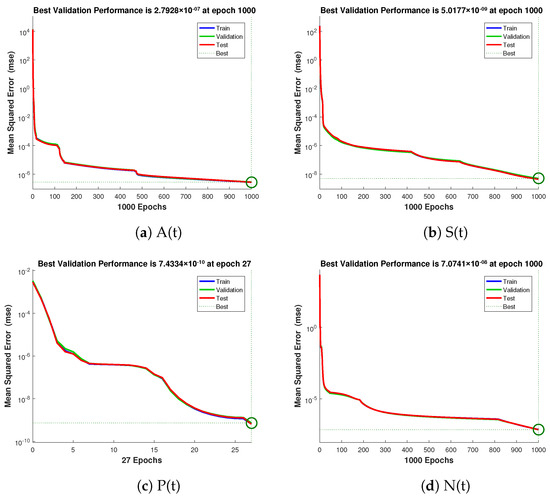
Figure 5.
Mean square error of NNs-LMT for crop production, insects density, insecticides concentration, and external effort of case 2.
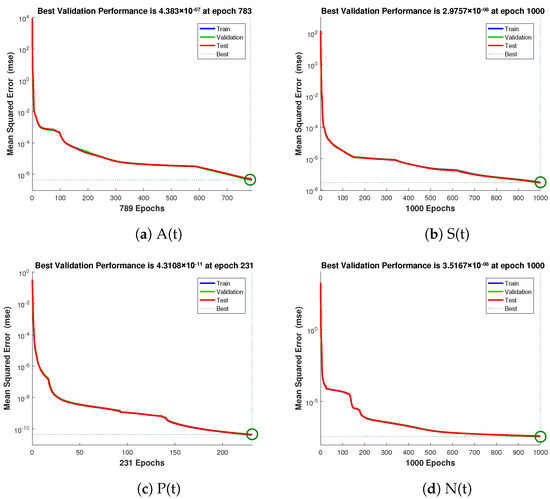
Figure 6.
Mean square error of NNs-LMT for crop production, insects density, insecticides concentration, and external effort of case 3.
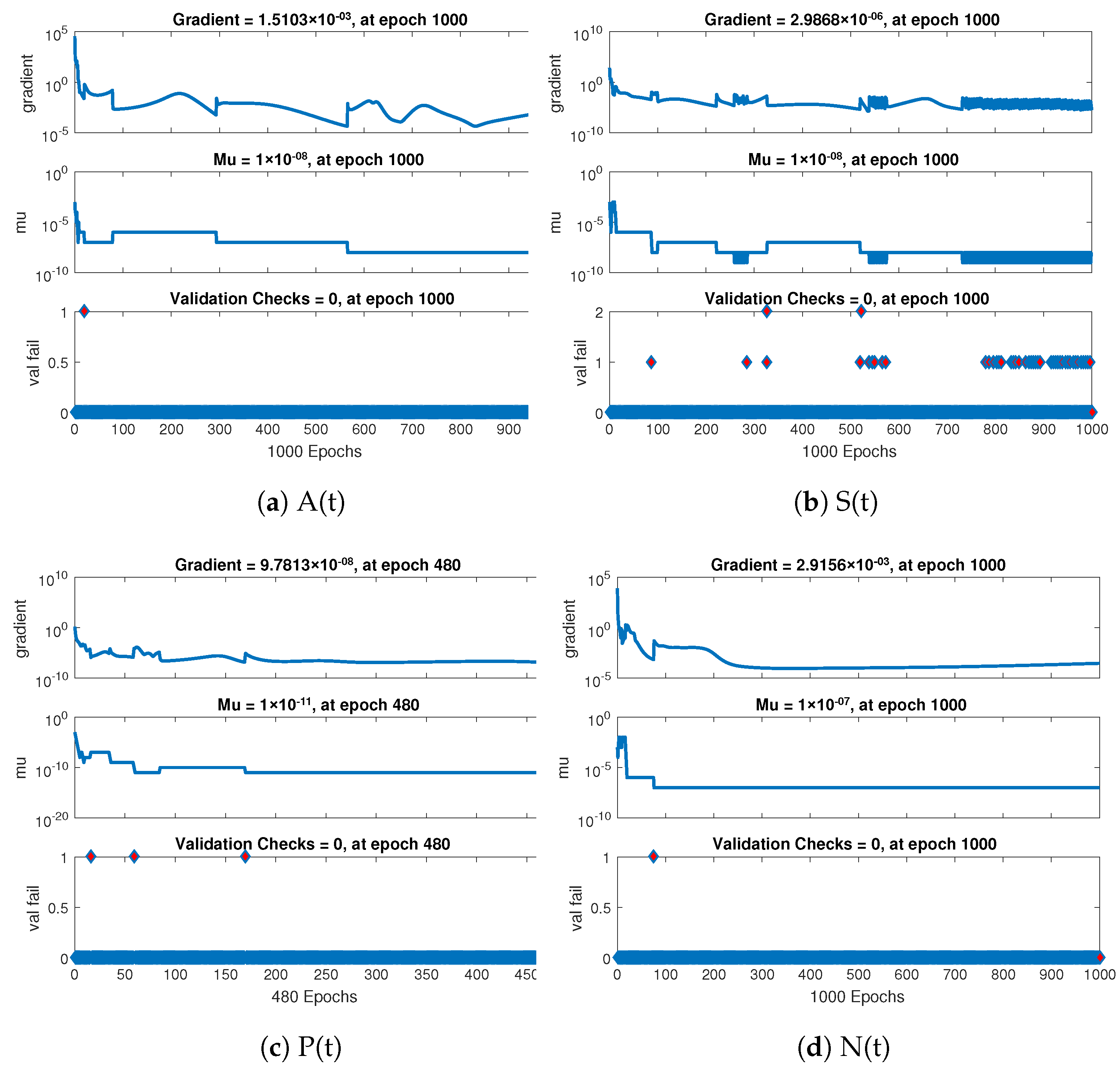
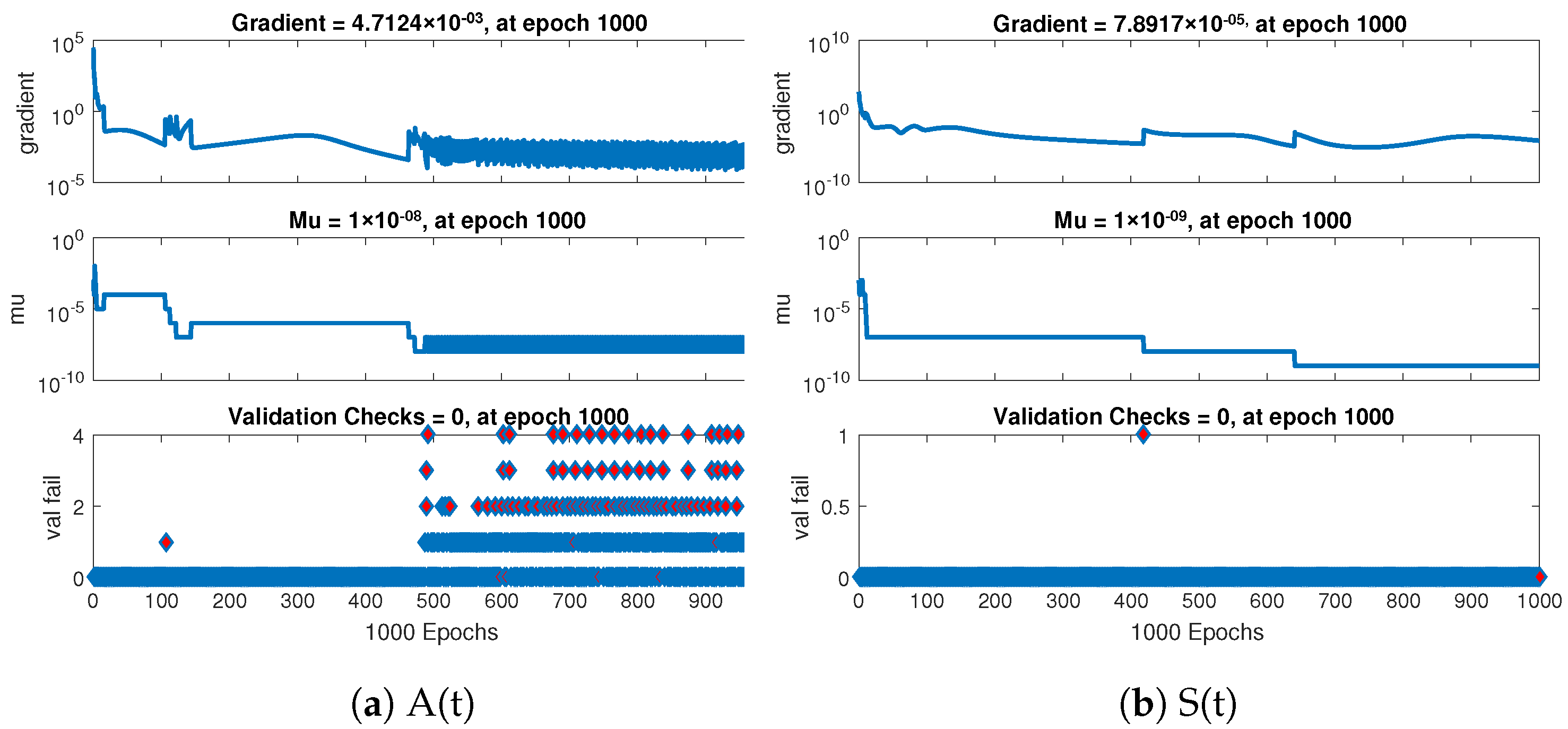
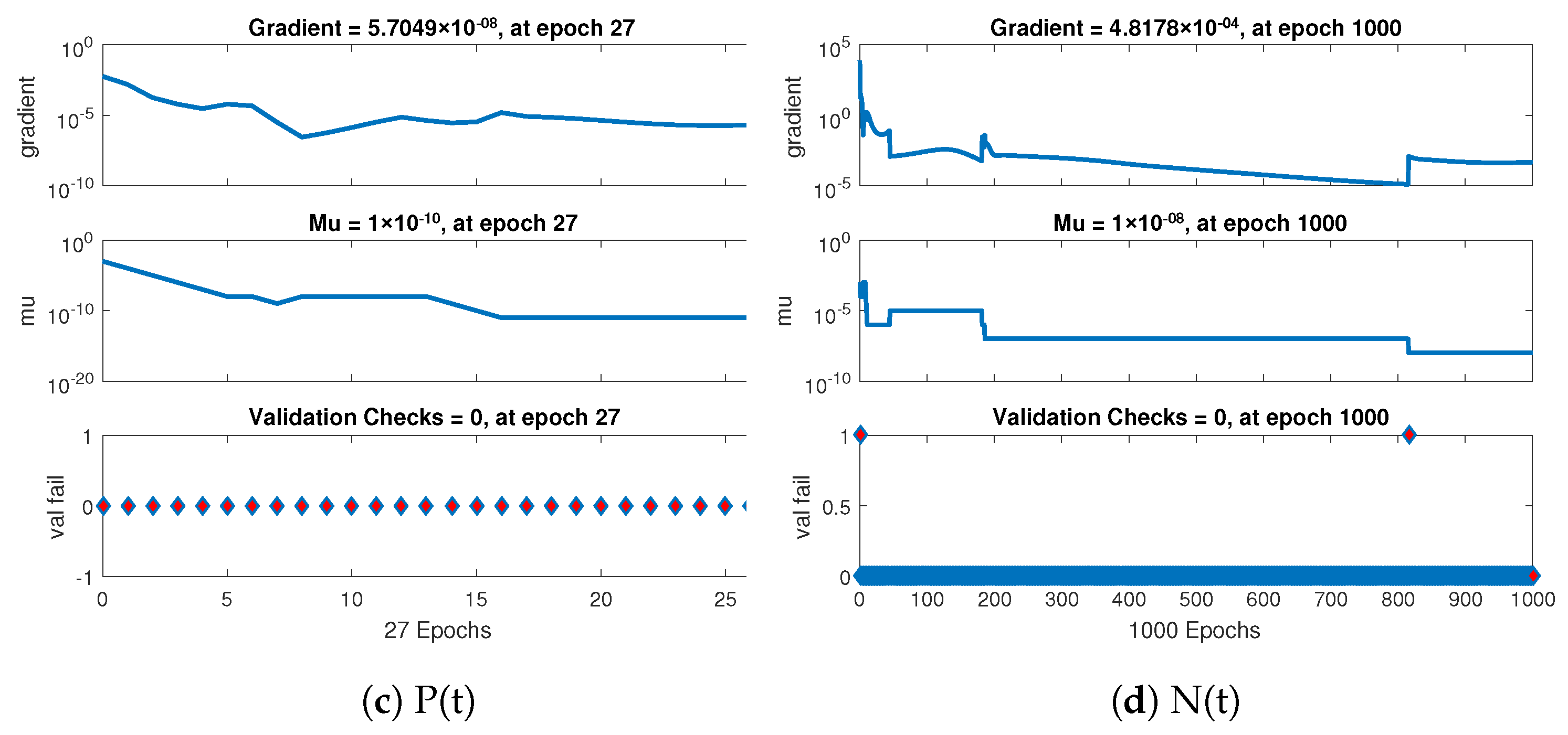
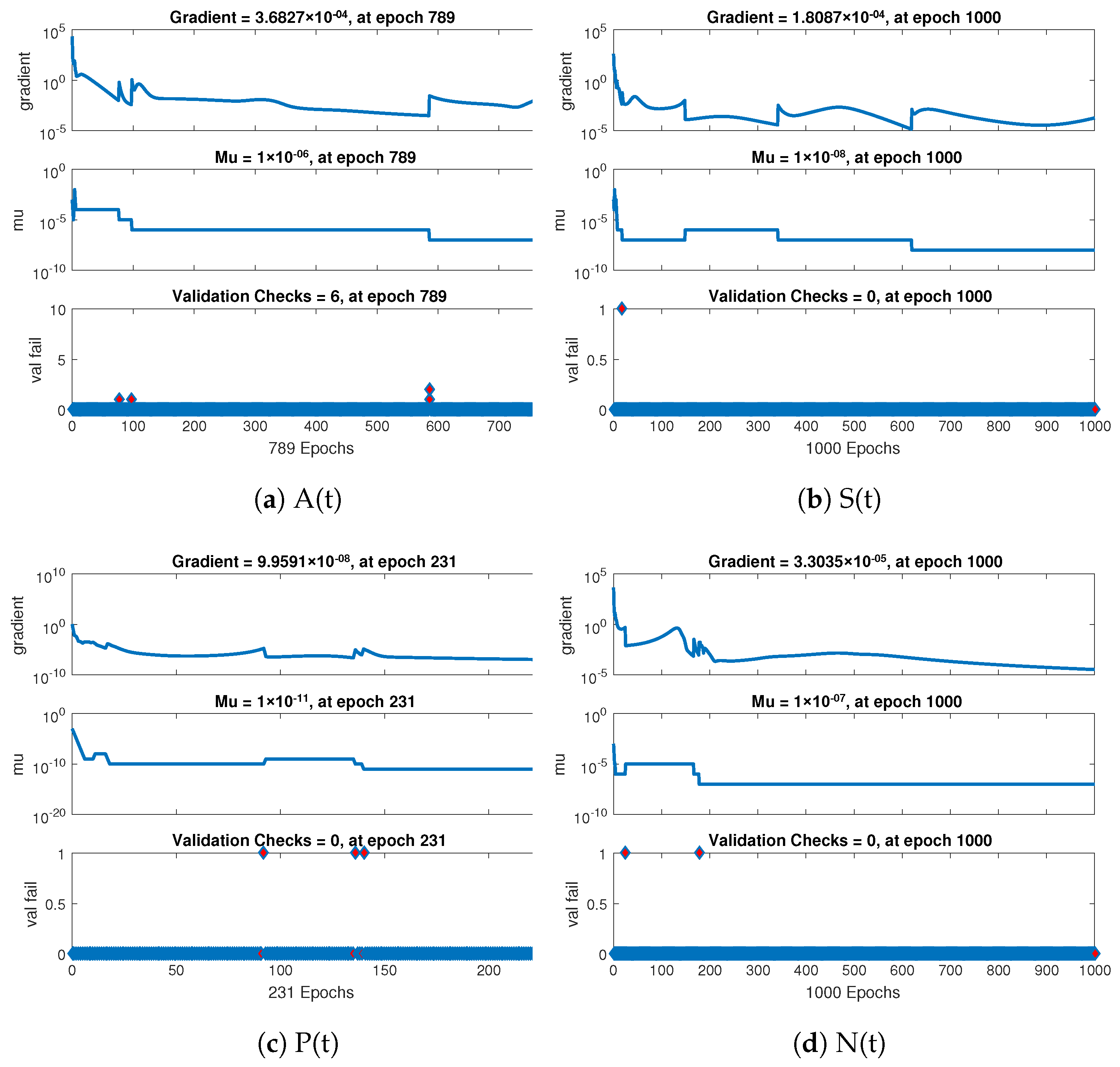
Further the statistical performance of gradient for case 1 are illustrated in Figure 7 and its gradient values are in the region , , and . Similarly for case 2 and 3 the statistical performance of gradient are illustrated in Figure 8 and Figure 9 respectively. Their gradient values are in the range of , , , and for case 2 and , , and for case 3. These figures also illustrate the mu, a control parameter for the algorithm to train the neural network and validation failure for all the cases of non-linear model of crop production. For all the cases the values of mu lies in between to .
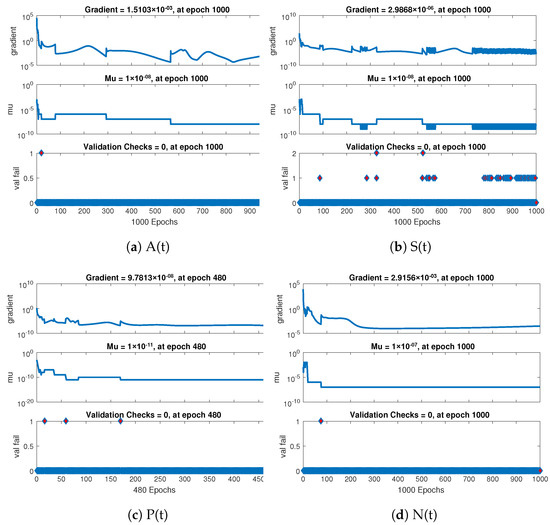
Figure 7.
Performance based on validations failure, mu, and gradient of NNs-LMT for case 1.
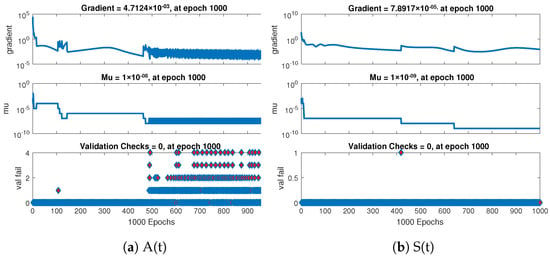
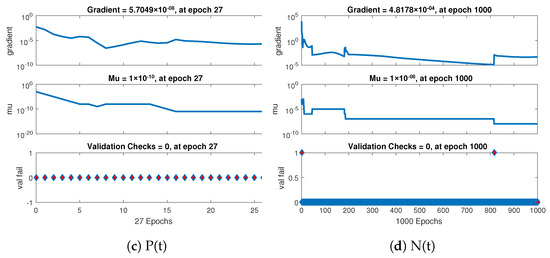
Figure 8.
Performance based on validations failure, mu, and gradient of NNs-LMT for case 2.
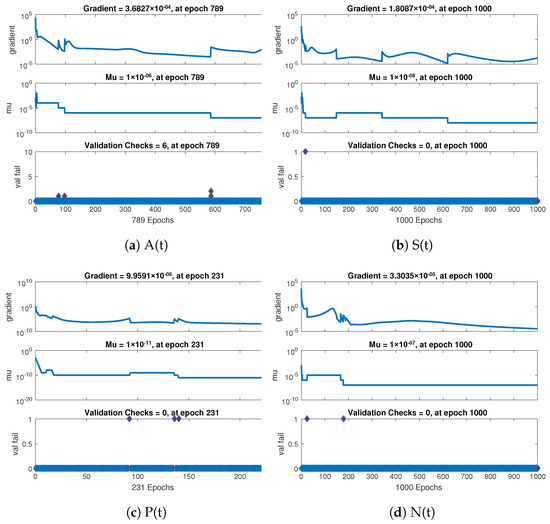
Figure 9.
Performance based on validations failure, mu, and gradient of NNs-LMT for case 3.
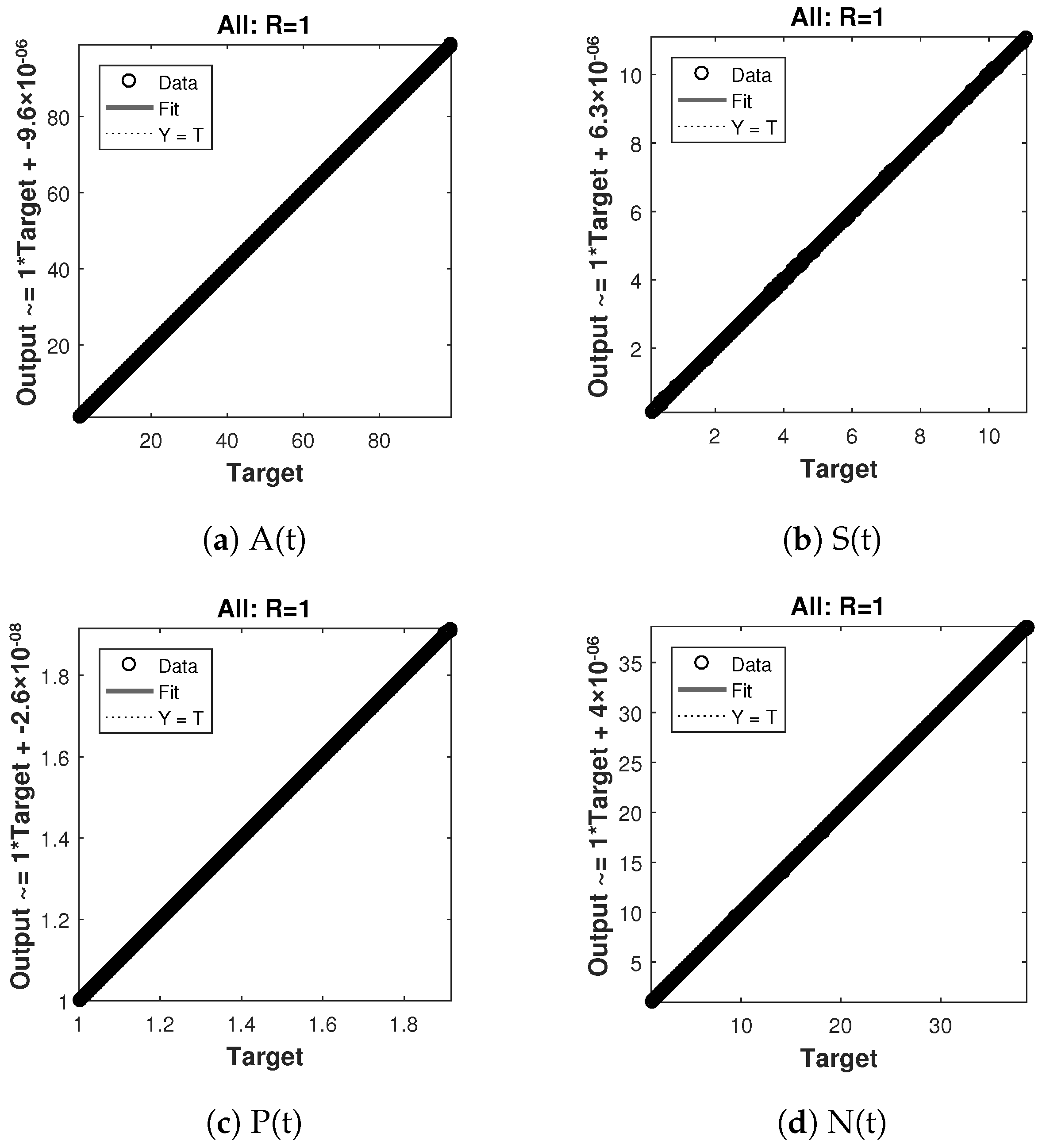
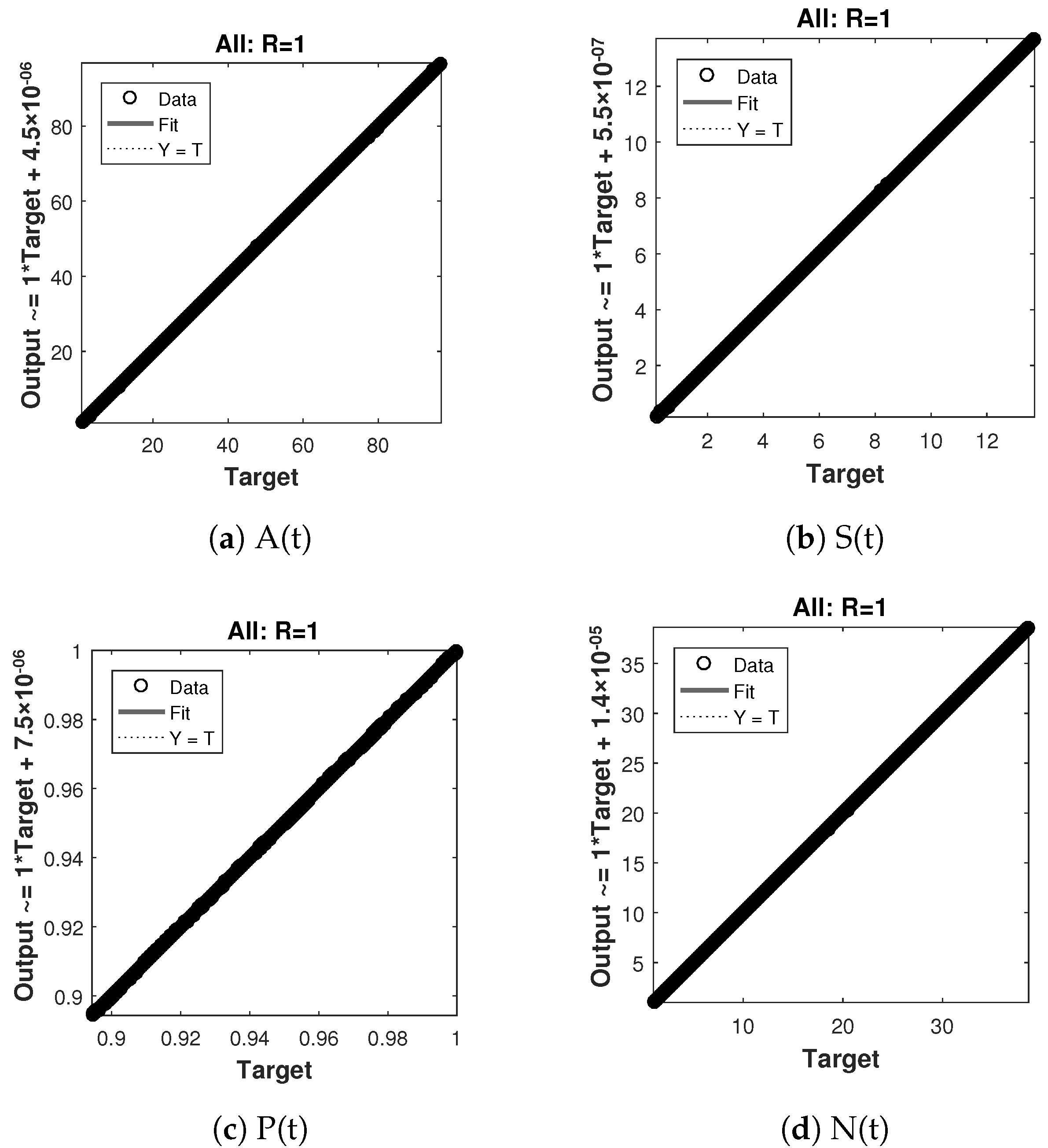
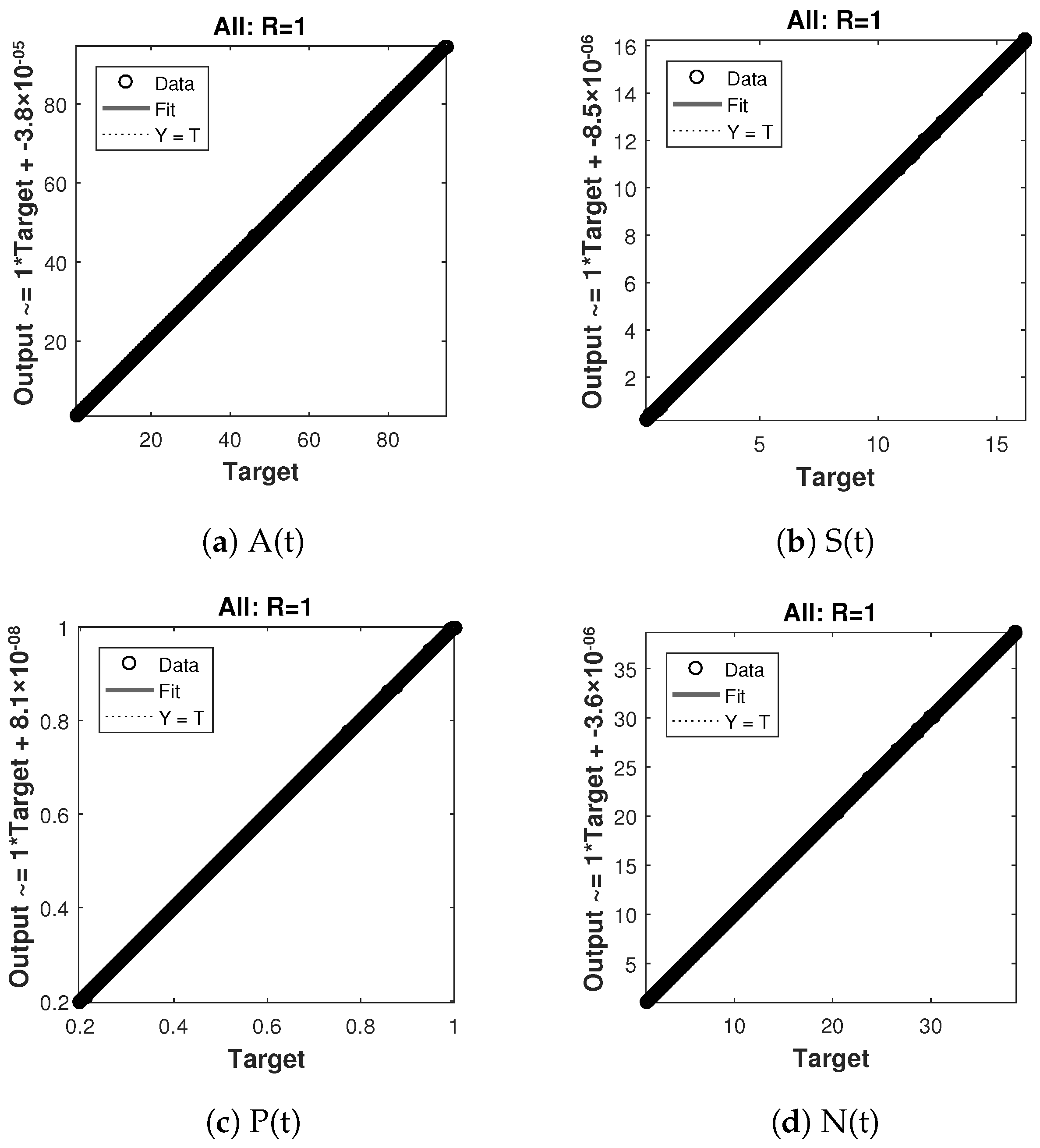
The regression analysis for case 1 is shown in Figure 10 and its value is 1, which shows a close relationship between outputs and targets. Similarly the regression analysis for case 2 and 3 are shown in Figure 11 and Figure 12 respectively, and they also shows a close relationship between the outputs and the targets by giving the value, .
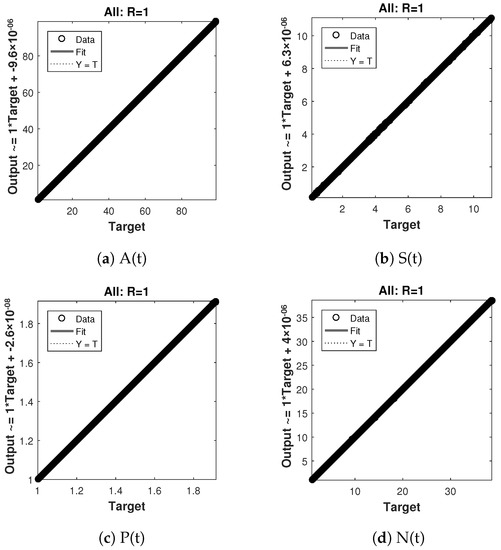
Figure 10.
Regression analysis of nonlinear model of crop production for case 1.
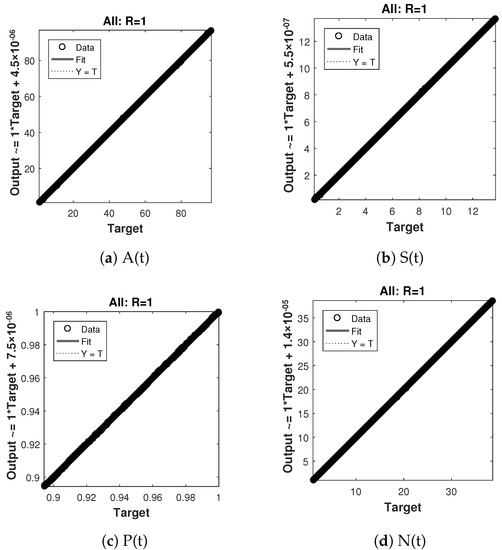
Figure 11.
Regression analysis of nonlinear model of crop production for case 2.
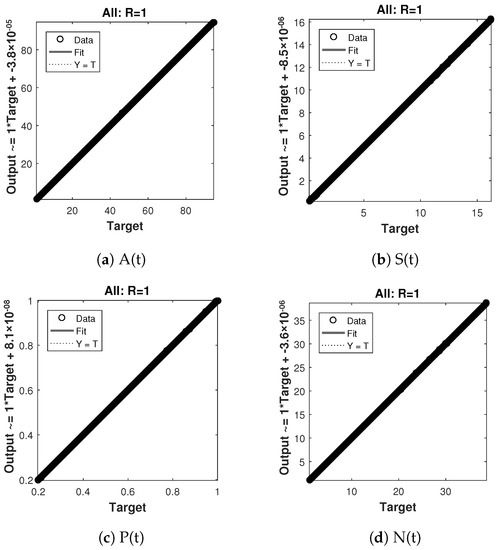
Figure 12.
Regression analysis of nonlinear model of crop production for case 3.
The tables below illustrate the data details discussed above, given by the computing system. Table 3 shows the details of the data for case 1, where Table 4 and Table 5 show the details of the data for cases 2 and 3, respectively. These tables also indicate the data details of validation, testing, the number of hidden neurons, and iterations and time spent by the computing system.

Table 3.
Gradient, MSE, number of iterations, mu, and time spent by the computing system to get solutions for Case 1.

Table 4.
Gradient, MSE, number of iterations, mu, and time spent by the computing system to get solutions for Case 2.

Table 5.
Gradient, MSE, number of iterations, mu, and time spent by the computing system to get solutions for Case 3.
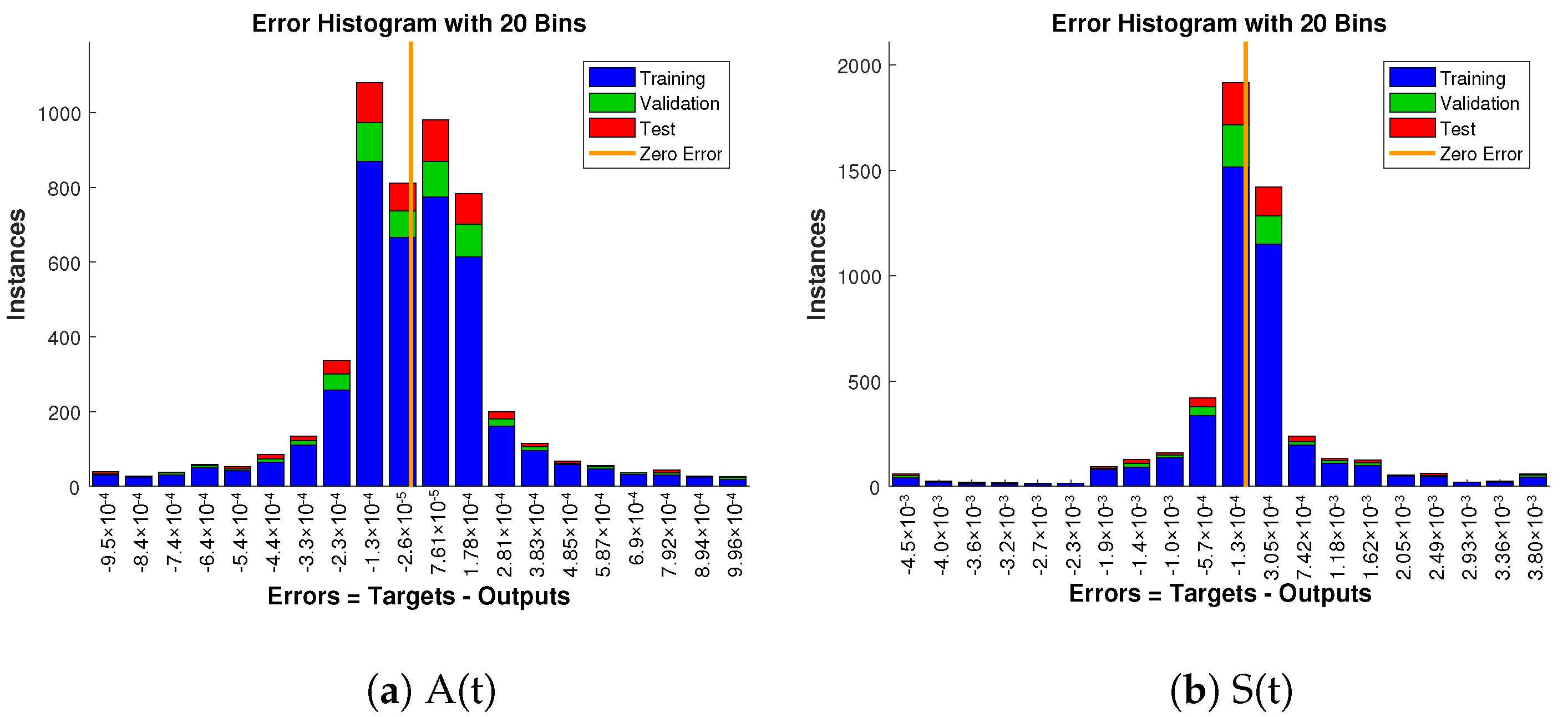
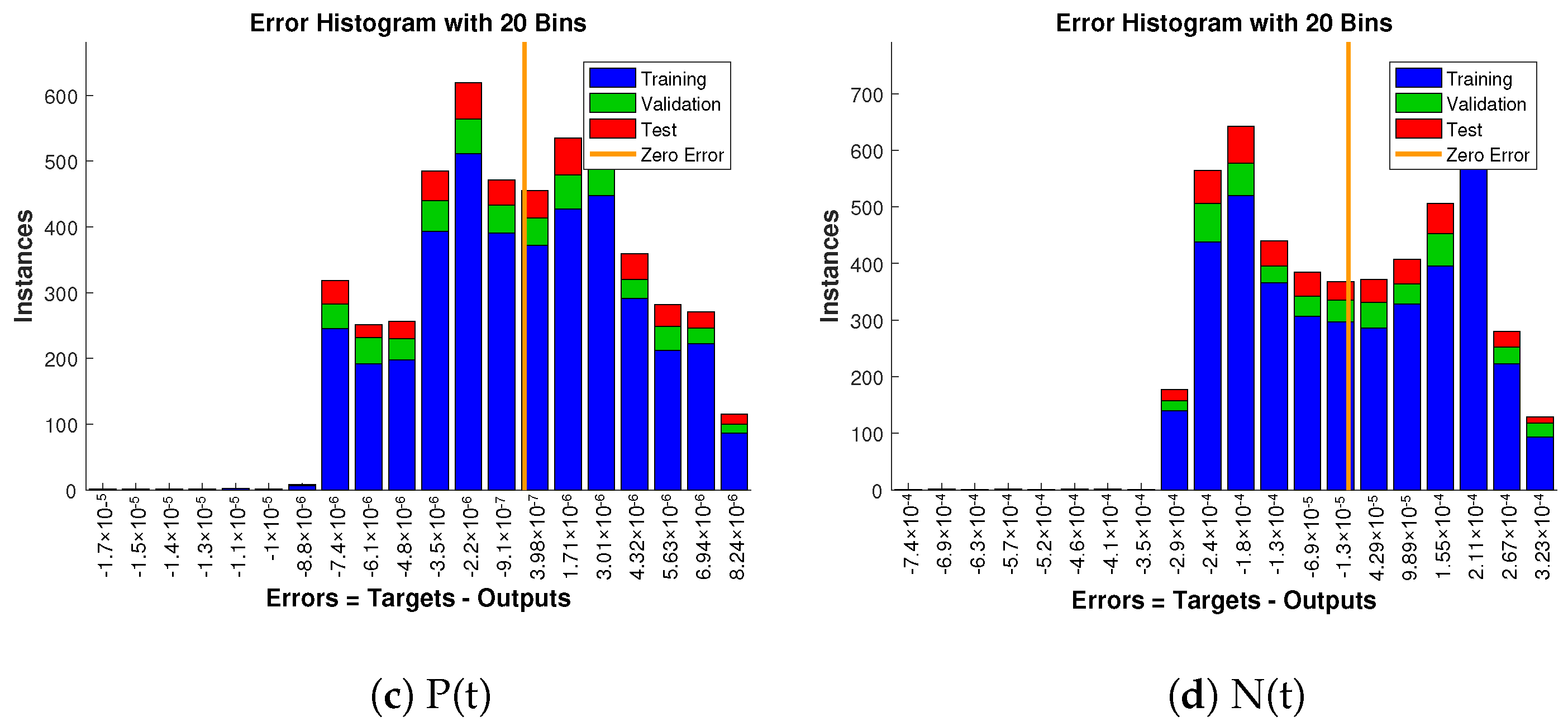
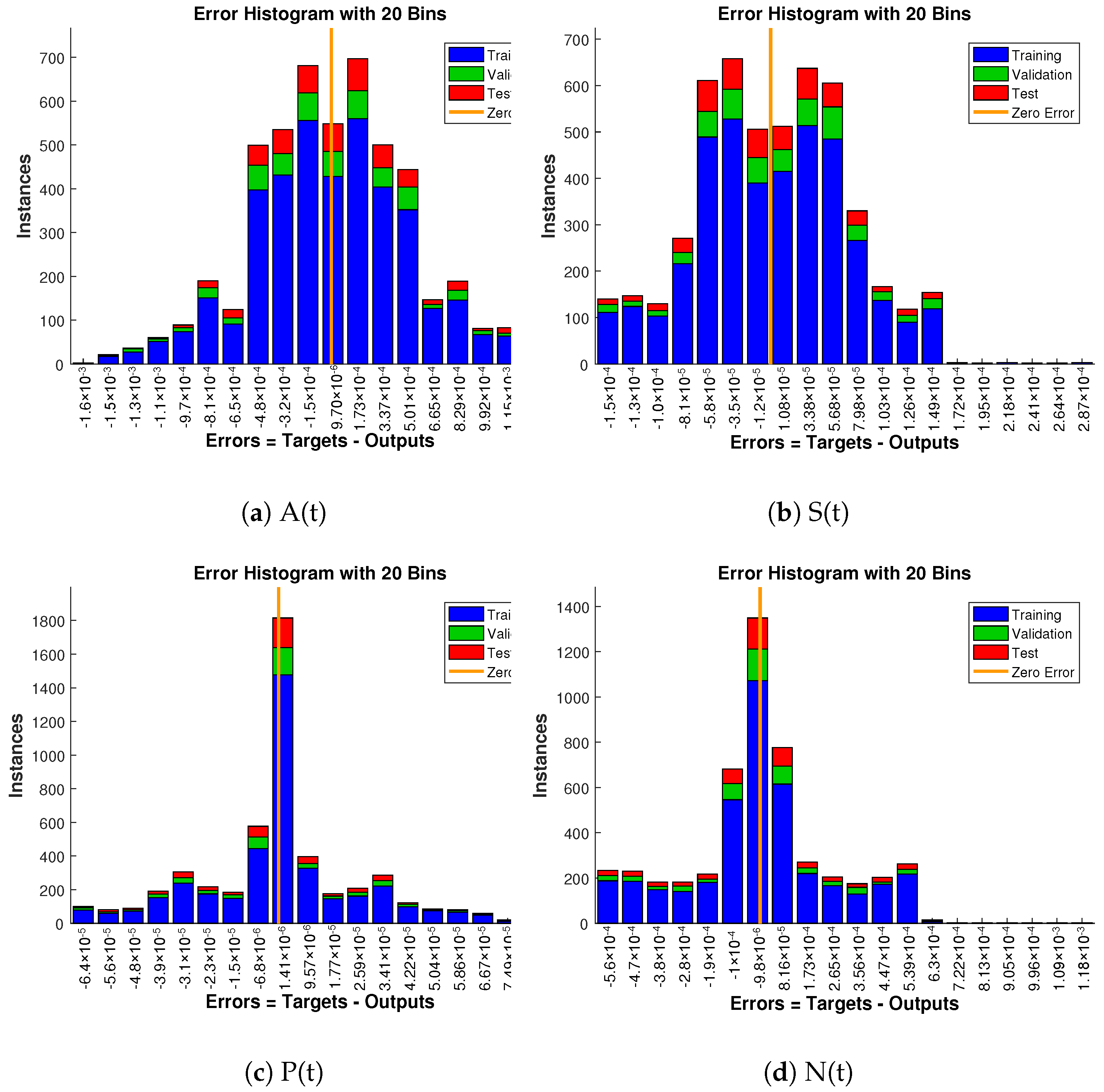
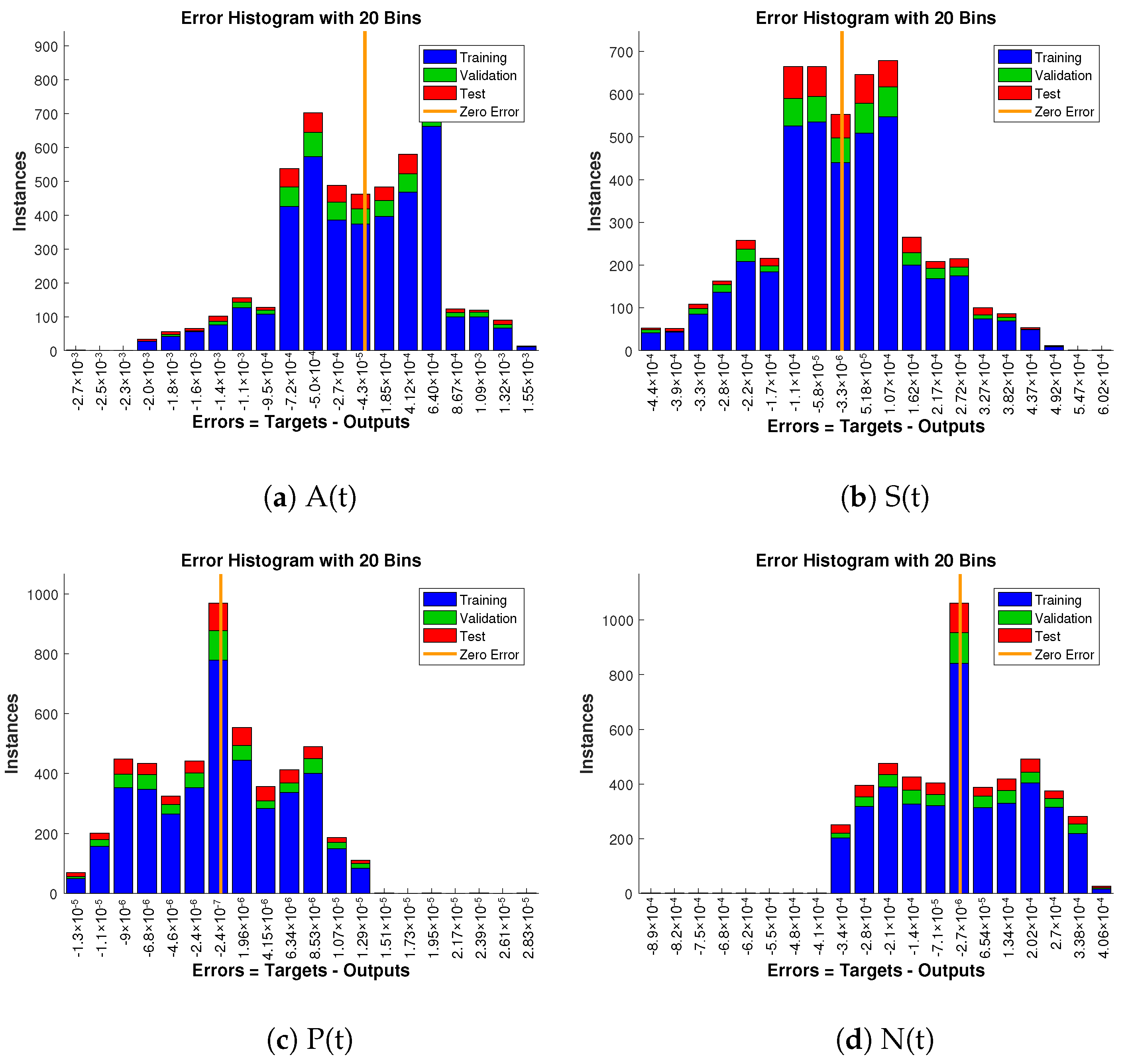
Approximate solution and targeted data fit together well and have the fewest absolute errors shown in the Figure 13, Figure 14 and Figure 15. The absolute error values of A(t) lie in the region of to , to and to ; for S(t) the values are in the range to , to and to . Similarly, for P(t) and N(t), the values are in between to , to , to , to , to and to .
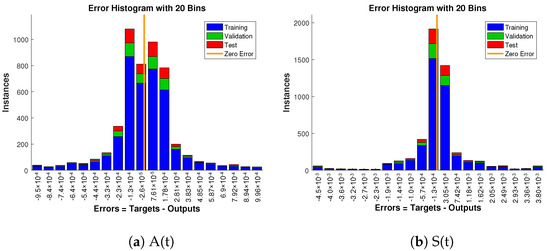
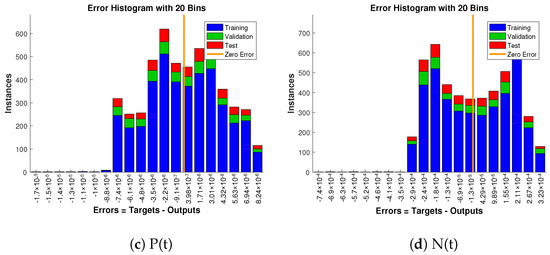
Figure 13.
Error histogram analysis in relation to the target data and the approximate solutions for case 1.
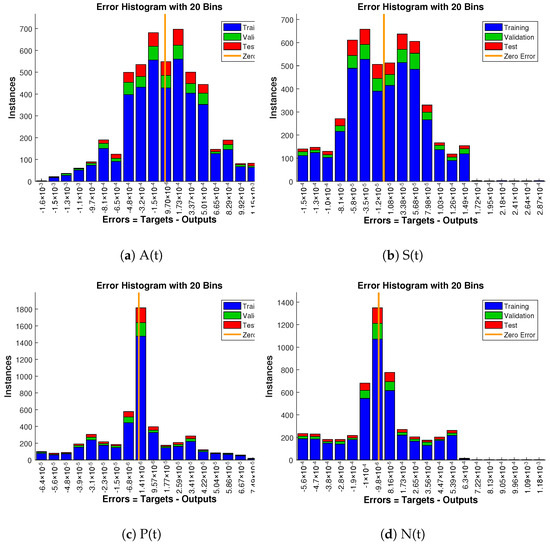
Figure 14.
Error histogram analysis in relation to the target data and the approximate solutions for case 2.
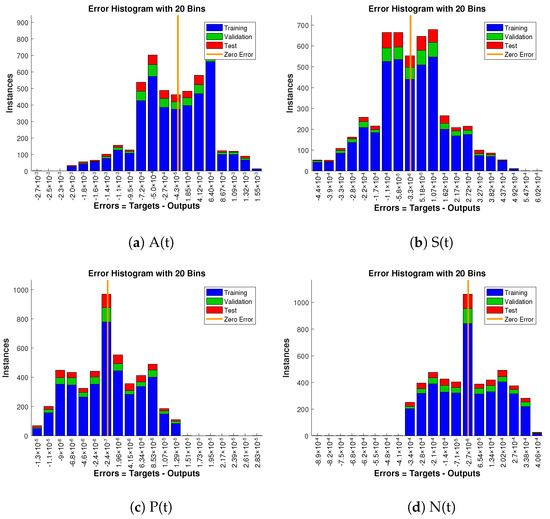
Figure 15.
Error histogram analysis in relation to the target data and the approximate solutions for case 3.
After solving the model (1) numerically for variation in spraying rate of insecticides, we see that the decrease in the spraying rate affects the crop production and concentration of insecticides directly and inversely affects the density of insects population and external efforts. The numerical solutions for different insecticide spraying rates are shown graphically in Figure 16.
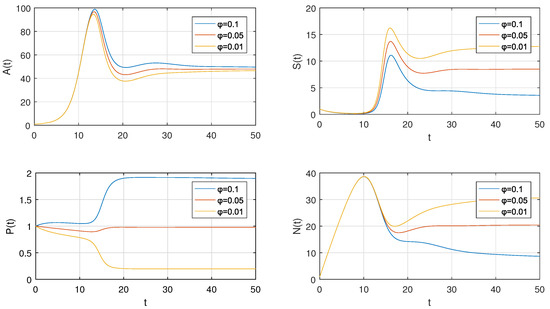
Figure 16.
Numerical solution of crop model for different insecticides spraying rate.
Table 6, Table 7 and Table 8 provide a comparison of the numerical solutions of the design algorithm with the results obtained from numerically solving the model using the “NDSolve” tool in Mathematica for cases 1, 2, and 3, respectively. The numerical simulations in the first two rows of each table represent comparisons of numerical solutions for agricultural crop production, followed by insect population density, insecticide concentration, and external efforts.

Table 6.
Comparative analysis of numerical solutions by NDSolve tool in Mathematica with the solutions obtained from NN-LMA for case 1.

Table 7.
Comparative analysis of numerical solutions by NDSolve tool in Mathematica with the solutions obtained from NN-LMA for case 2.

Table 8.
Comparative analysis of numerical solutions by NDSolve tool in Mathematica with the solutions obtained from NN-LMA for case 3.
5. Conclusions
In this paper, we investigated the non-linear dynamical model of crop production. The model was based on agricultural crop production in the presence of density of insects population, insecticides concentration, and some external efforts, which was given by a system of nonlinear differential equations. Moreover, a soft computing technique based on supervised learning of NNs-LM used to calculate the influence of variations in the spraying rate of insecticide on the nonlinear model of crop production.
- Results shows in the figure illustrate that the decrease in spraying rate of insecticides causes decrease in crop production and insecticides concentration while increases the insects density and external effort.
- To relate the sparing rate of insecticides with the given model is that it relates inversely with crop production and insecticides concentration while directly relates to incests density and external efforts.
- Thorough graphical analysis is performed using mean squared error, error histograms, absolute errors, regressions, and computing complexity to demonstrate the resilience, correctness, and efficiency of the developed system.
Author Contributions
Conceptualization, M.S. and M.U.; investigation, M.S., M.U. and K.N.; methodology, K.N.; validation, M.S., M.U., K.N., F.S.A.; visualization, M.S., K.N., M.U. and F.S.A.; writing—original draft, M.S. and M.U.; writing—review and editing, K.N. and F.S.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received funding support from the National Science, Research, and Innovation Fund (NSRF), Thailand.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
We would like to thank the referees for their valuable comments and helpful advice on our manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- FSIN: Global Report on Food Crises. 2019. Available online: https://www.wfp.org/publications/2019-global-report-food-crises (accessed on 15 December 2021).
- Oerke, E.C. Crop losses to pests. J. Agric. Sci. 2006, 144, 31–43. [Google Scholar] [CrossRef]
- Shankar, C.; Dhyani, S.K. Insect pest of Jatropha curcas L. and the potential for their management. Curr. Sci. 2006, 91, 162–163. [Google Scholar]
- Sun, S.; Chen, L. Mathematical modelling to control a pest population by infected pests. Appl. Math. Model. 2009, 33, 2864–2873. [Google Scholar] [CrossRef]
- Xiao, Y.N.; Chen, L.S. Modeling and analysis of a predator-prey model with disease in the prey. Math. Biosci. 2001, 171, 59–82. [Google Scholar] [CrossRef]
- Wang, X.; Tao, Y.; Song, X. Analysis of pest-epidemic model by releasing diseased pest with impulsive transmission. Nonlinear Dyn. 2011, 65, 175–185. [Google Scholar] [CrossRef]
- Tang, S.; Cheke, R.A. State-dependent impulsive models of integrated pest management (IPM) strategies and their dynamic consequences. J. Math. Biol. 2005, 50, 257–292. [Google Scholar] [CrossRef] [PubMed]
- Misra, A.K.; Jha, N.; Patel, R. Modeling the Effects of Insects and Insecticides with External Efforts on Agricultural Crops. Differ. Equ. Dyn. Syst. 2020, 28, 1–18. [Google Scholar] [CrossRef]
- Uyovbisere, E.O.; Lombim, G. Efficient fertilizer use for increased crop production: The sub-humid Nigeria experience. Fertil. Res. 1991, 29, 81–94. [Google Scholar] [CrossRef]
- Misra, A.K.; Tiwari, P.K.; Chandra, P. Modeling the control of algal bloom in a lake by applying some external efforts with time delay. Differ. Equ. Dyn. Syst. 2017, 29, 539–568. [Google Scholar] [CrossRef]
- Lambert, J.D. Numerical Methods for Ordinary Differential Systems: The Initial Value Problem; John Wiley and Sons: Chichester, UK, 1991. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: River Edge, NJ, USA, 1994. [Google Scholar]
- Mickens, R.E. Nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 2002, 8, 823–847. [Google Scholar] [CrossRef]
- Anguelov, R.; Lubuma, J.M.S. Contributions to the mathematics of the nonstandard finite difference method and applications. Numer. Methods Partial Differ. Equ. 2001, 17, 518–543. [Google Scholar] [CrossRef]
- Mickens, R.E. Dynamic consistency: A fundamental principle for constructing nonstandard finite difference schemes for differential equations. J. Differ. Equ. Appl. 2005, 11, 645–653. [Google Scholar] [CrossRef]
- Patidar, K.C. Nonstandard finite difference methods: Recent trends and further developments. J. Differ. Equ. Appl. 2016, 22, 817–849. [Google Scholar] [CrossRef]
- Obayomi, A.A.; Olabode, B.T. Comparative analysis of standard and non-standard finite difference schemes for the logistic equations. J. Emerg. Trends Eng. Appl. Sci. (JETEAS) 2013, 4, 317–321. [Google Scholar]
- Dimitrov, D.T.; Kojouharov, H.V. Positive and elementary stable nonstandard numerical methods with applications to predator-prey models. J. Comput. Appl. Math. 2006, 1–2, 98–108. [Google Scholar] [CrossRef]
- Chen-Charpentiera, B.M.; Dimitrovb, D.T.; Kojouharov, H.V. Combined nonstandard numerical methods for ODEs with polynomial right-hand sides. Math. Comput. Simul. 2006, 73, 105–113. [Google Scholar] [CrossRef]
- Anguelov, R.; Kama, P.; Lubuma, J.M.S. On non-standard finite difference models of reaction-diffusion equations. J. Comput. Appl. Math. 2005, 175, 11–29. [Google Scholar] [CrossRef][Green Version]
- Jansen, H.; Twizell, E.H. An unconditionally convergentdiscretization of the SEIR model. Math. Comput. Simul. 2002, 58, 147–158. [Google Scholar] [CrossRef]
- Basir, F.A.; Banerjee, A.; Ray, S. Role of farming awareness in crop pest management: A mathematical model. J. Theor. Biol. 2019, 461, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Misra, A.K.; Jha, N.; Patel, R. Modeling the effects of insects and insecticides on agricultural crops with NSFD method. J. Appl. Math. Comput. 2020, 63, 197–215. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).