A Path Optimization Algorithm for Multiple Unmanned Tractors in Peach Orchard Management

Abstract

In order to improve the management efficiency of peach orchards, this paper considers the cooperative operation scheme of multiple unmanned tractors. According to the actual situation, this paper constructs the path planning model of multiple unmanned tractors in a standard peach orchard, designs the objective function to optimize the total turning time and total operating time according to the tractor driving parameters, and solves it by improving the differential evolution algorithm. Aiming at the premature convergence problem, the permutation matrix is introduced to represent the driving paths of multiple unmanned tractors. Then, the dynamic parameters are adopted to make the parameters change with the number of iterations, and the elite selection strategy is used to eliminate the redundant feasible solutions. An Adaptive Elite Differential Evolution (AEDE) algorithm suitable for multi-tractor path optimization is proposed. The results show that, compared with the traditional Differential Evolution algorithm (Differential Evolution, DE), the total turning time and total operating time in the rectangular peach orchard optimized by AEDE are reduced by 3.34% and 0.87%, respectively. Compared with the block operation, the total turning time and total operating time of the AEDE-optimized rectangular peach orchard operation path were reduced by 37.37% and 9.47%, respectively. Experiments show that AEDE, which optimizes the operating path of multi-tractors in standard peach orchards, is able to improve the efficiency and reduce the operating time.

1. Introduction

The cultivation area of peaches in China is 55,317.23 (km²), and the planting scale ranks first in the world [1]. Peach orchard management includes weeding, ditching, fertilizing, and soil cultivation, which requires a large amount of labor, contradicting the increasingly serious aging of the rural labor force. At present, China is vigorously promoting the integration of agricultural machinery and agronomy and standardized farmland transformation. The integrated path planning systems of agricultural unmanned tractors can perceive and act independently [2]. By connecting different agricultural tools to carry out different operations in standard peach orchards, the labor force can be reduced and the planting management efficiency can be improved. Optimizing the driving path is a key to improving unmanned production efficiency and operation quality [3].

Spekken et al. mentioned that during agricultural machinery operation, most of the time was used for non-productive operations, such as turning in non-working areas. Reasonable path planning can reduce the working time of agricultural machinery and improve operation efficiency [4]. At present, the B-Pattern model [5] proposed by Bochtis was adopted as the path planning model in most studies. Based on the B-Pattern model, the tractor operation scheduling is optimized by intelligent optimization methods, such as genetic algorithm [6,7,8], simulated annealing algorithm [9,10], ant colony algorithm [11,12], domain search [13], tabu search algorithm [14,15], particle swarm optimization algorithm [16], and Clark–Wright algorithm [17,18]. In addition, there is research on operation path optimization based on probability. Utama et al. introduced domain search and elite selection to improve the effect of distribution estimation algorithms in agricultural machinery operation path planning [19].

Fabre et al. [20] transformed the path planning problem of agricultural machinery into a Hamiltonian problem and proposed a path optimization algorithm based on a greedy strategy to minimize the repetitive operation area. Jensen et al. transformed the path planning problem of agricultural machinery into a Traveling Salesman Problem (TSP) problem and proposed an algorithm based on the state-space search to reduce the length of non-operational paths [21]. Muthukumaran et al. adopted the hybrid dragonfly cuckoo search algorithm to optimize the path coverage based on the TSP model [22], and the computational efficiency and effect were better than most intelligent optimization algorithms. Postmes transformed the operation coverage optimization of agricultural machinery robots into VRP (Vehicle Routing Problem) and tried to solve the problem with various approximation algorithms [23]. In order to reduce the complexity of agricultural machinery path planning, Oksanenand et al. used trapezoidal decomposition and an incremental method to simplify the path coverage problem [24].

At present, the studies on autonomous driving path planning in farmland mainly focus on food production, including global path planning and local path planning. The traditional B-Pattern planning model is mainly used in the field where the spacing of operation lines is equal (operation line refers to the route that the tractor starts from one end of the orchard and ends at the opposite end, such as transplanting and harvesting in the field). When the unmanned driving system is applied to the management of a peach or-chard (such as ditching, weeding, fertilization, soil tillage), the operation is usually one-sided, resulting in uneven spacing between operation lines. Therefore, the path autonomous decision-making in the peach orchards cannot be directly applied to the B-Pattern model [25].

The spacing of operation lines in the peach orchard is unequal, and peach trees are densely distributed. This paper studies a multi-machine cooperative operation path optimization method that is suitable for standard peach orchard management, which provides a reference for the continuous and stable operation of unmanned systems.

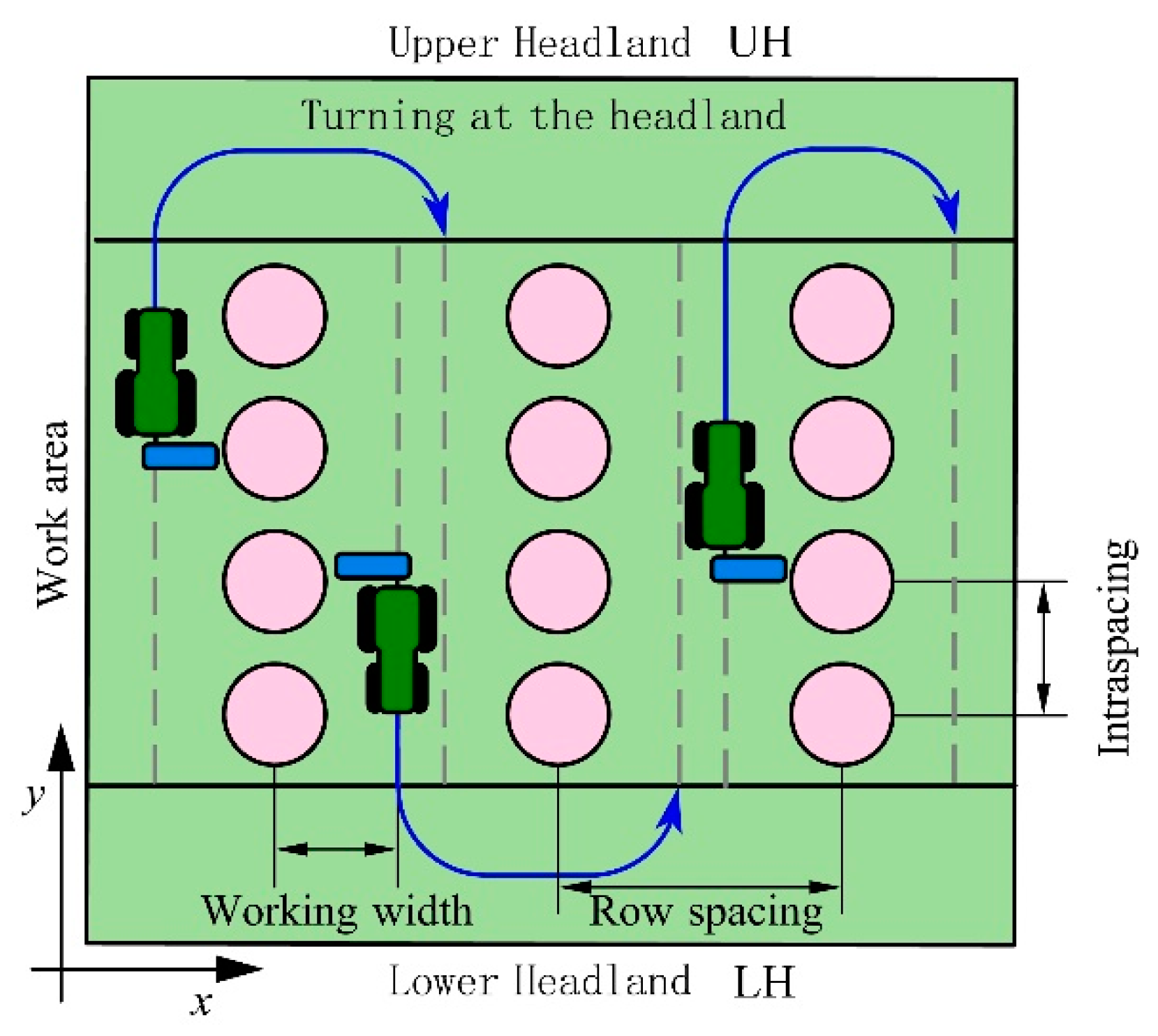
2. Path Optimization Model of Unmanned Tractor

The distribution of peach trees in the standard peach orchard is shown in Figure 1. The peach orchard is divided into Upper headland (UH), working area, and Lower headland (LH). The working area is the area where the tractors manage the peach trees, and the headland is the area where the tractor turns. Suppose there are n rows of peach trees in the peach orchard—vectors x^k and y^k represent the x-coordinate and y-coordinates of each peach tree in row k, respectively. Additionally, x_m^k represents the x-coordinate of the peach tree m in row k (counted from bottom to top, consistent with the positive direction of Y-axis), where 1 ≤ k ≤ n, 1 ≤ m ≤ n_k, n_k represents the number of peach trees in row k. The coordinates of peach trees at both ends of each row are represented by n × 2-dimensional matrices U and L, and U_k,1 and U_k,2 respectively represent the horizontal and vertical coordinates of peach trees at the junction of headland UH and working area in row k, i.e., $x_{n_k}^k$ and $y_{n_k}^k$. Similarly, L_k,1 and L_k,2 respectively represent the horizontal and vertical coordinates of the peach trees in row k at the junction of the headland LH and working area, i.e., $x_1^k$ and $x_1^k$. The boundary of the headland and the working area in the standard peach orchard can be determined according to the matrices U and L.

In order to ensure that peach trees have enough space for growth and management, the spacing of peach trees is much larger than the width of tractors. As shown in Figure 1, the tractor needs to be driven at least twice to manage a row of peach trees, and probably does not work in sequence on both sides of the peach trees. Therefore, when the tractor works in the standard peach orchard, the driving path is not the equidistant operation line in the traditional B-Pattern model. If the peach orchard has n rows of peach trees, the tractor needs to make at least 2n to complete the management of all peach trees. The dashed line in Figure 1 represents the track of the tractor when it is working in the standard peach orchard. Although it is also composed of several parallel lines, they are not equidistant from each other.

Unmanned tractors need to make turns in the field before working on the next row of peach trees. There are three main types of turns, including the Π-Turn, Ω-turn, and T-turn. As the T-turn requires the tractor to reverse and stop, it will not only consume time, but also aggravate the tractor wear. This paper considers only the Π-Turn and Ω-turn, as shown in Figure 2a,b. In Figure 2, w and d represent the horizontal and vertical distance of two adjacent rows of peach trees, respectively, and r represents the turning radius of the tractor.

Based on the above path planning model, this paper designs a path optimization scheme for multiple unmanned tractors. The design of a multi-tractor driving route can avoid incomplete operation or repeated operation. The simplest scheme is to divide the peach orchard into several sub areas, and then assign different tractors to operate in the divided areas. The schematic diagram of block operation is shown in Figure 3.

Block operation is the operation mode of an S-type operation for multiple tractors, which requires multiple turns and has low operation efficiency. Reasonably arranging the operation sequence of the tractor and reducing the Ω-turn is conducive to improving the overall operation efficiency.

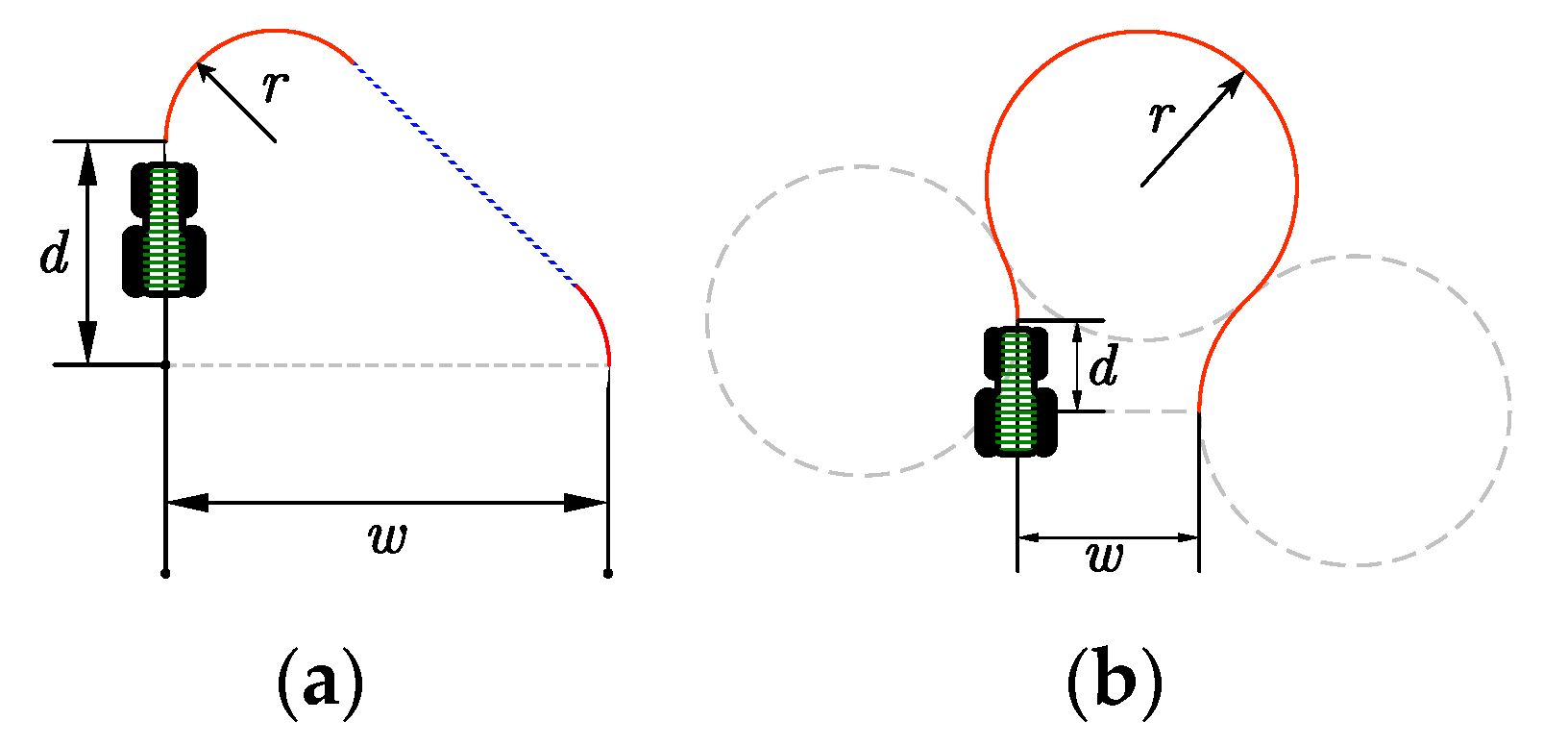
Optimization Model of Minimum Operating Time for Unmanned Tractor

The term “operation line” refers to the route that the tractor starts from one end of the orchard and ends at the opposite end. E represents the set of all operation lines, V is the set of end points of all operation lines, and the driving path is represented by a directed graph G = {V,E}. Graph G is mainly composed of vertices and connecting edges of parallel lines, so it is connected. $E_{v_i,v_j}$ represents the edge from the vertex v_i to v_j of the operation line, where v_i, v_j ∈ V. R represents the set of tractor paths, and R^k represents the driving path of the k-th tractor. R^k is composed of a vertex set <R₁^k, R₂^k, …, $R_{m_k}^k$>, where m_k represents the number of vertices of path R^k.

To improve the management efficiency of the standard peach orchard, it is considered to formulate a cooperative scheme for multiple tractors to ensure the shortest working time. As shown in Equation (1), this paper establishes an objective function to minimize the total turning time and working time of multiple tractors, which ignores the time of tractors entering and leaving the orchard.

$$t_{all}=\underset{t_{turn},t_{work}}{\min }z{t}_{turn}+\frac{(1-z)t_{work}}{M}$$

(1)

where,

t_turn—total turning time of multiple unmanned tractors

t_work—total operating time of unmanned tractors

M—the number of unmanned tractors

t_all—weighted average of total turning time and total operating time

z—the weight variable represents farmers’ attention to the total turning time and the total operating time

t_turn can be calculated according to Equation (2):

$$t_{turn}={\displaystyle \sum _{k=1}^M{\displaystyle \sum _{i=1}^{\left|R^k\right|-1}{c}_{R_i^k, R_{i+1}^k}^{\mathrm{D}}}}$$

(2)

where,

$c_{R_i^k, R_{i+1}^k}^{\mathrm{D}}$(D ∈ {UH,LH})—turning time for unmanned tractor to travel from R_i^k to R_i+1^k,

$c_{R_i^k, R_{i+1}^k}^{\mathrm{UH}}$—the time cost of changing an unmanned tractor from R_i^k to R_i+1^k in headland UH.

$c_{R_i^k, R_{i+1}^k}^{\mathrm{LH}}$—the time cost of changing an unmanned tractor from R_i^k to R_i+1^k in headland LH.

t_work can be calculated according to Equation (3):

$$t_{work}=\underset{k}{\max }({\displaystyle \sum _{i=1}^{\left|R^k\right|}{c}_{R_i^k,R_i^k}^{\mathrm{W}}}+{\displaystyle \sum _{i=1}^{\left|R^k\right|-1}{c}_{R_i^k, R_{i+1}^k}^{\mathrm{D}}})$$

(3)

where, $c_{R_i^k,R_i^k}^{\mathrm{W}}$—operating time of tractor in the i-th operation line, which is calculated by the operation line length and tractor speed.

Assuming that only one tractor is allowed to work in each operation line, each operation line is traversed once, and constraints (4) and (5) can be obtained. Under the constraint of this model, the number of operation lines is 2n, and the number of turning paths is 2n-M.

$$\underset{m=1}{\overset{M}{\cap }}{R}^m=0$$

(4)

$$E\subseteq \underset{m=1}{\overset{M}{\cup }}{R}^m$$

(5)

When an unmanned tractor enters the next operation line from one operation line, C_i,j describes the time cost of the tractor from line i to line j, and its definition is shown in Equations (6) and (7).

$$C_{i,j}=\left(\begin{array}{cc}{c}_{i.j}^{\mathrm{UH}}& \infty \\ \infty & c_{i.j}^{\mathrm{LH}}\end{array}\right) (i\ne j)$$

(6)

$$C_{i,j}=\left(\begin{array}{cc}{c}_{i.j}^{\mathrm{W}}& \infty \\ \infty & c_{i.j}^{\mathrm{W}}\end{array}\right) (i=j)$$

(7)

When i = j, C_i,j represents the work time in the i-th operation line. When i ≠ j, C_i,j means turning from the i-th operation line to the j-th operation line. At this time, there are two possibilities: ① the tractor changes the operation line at the headland UH; ② the tractor converts the operation line in the headland LH. Considering that peach trees may be asymmetrically distributed on both sides of the headland, the time cost of changing the operation line at headland UH may be different from that at headland LH; that is, c_i,j^UH may not be equal to c_i,j^LH. Based on the working time of the tractor in the operation line and the turning time of the tractor in the headland, the matrix C′ representing the time cost of the tractor changing the operation line is constructed in this paper:

$${\mathit{C}}^{\prime }=\left(\begin{array}{cccc}\begin{array}{cc}{c}_{1,1}^{\mathrm{W}}& \infty \\ \infty & c_{1,1}^{\mathrm{W}}\end{array}& \begin{array}{cc}{c}_{1,2}^{\mathrm{UH}}& \infty \\ \infty & c_{1,2}^{\mathrm{LH}}\end{array}& \cdots & \begin{array}{cc}{c}_{1,\left|E\right|}^{\mathrm{UH}}& \infty \\ \infty & c_{1,\left|E\right|}^{\mathrm{LH}}\end{array}\\ \begin{array}{cc}{c}_{2,1}^{\mathrm{UH}}& \infty \\ \infty & c_{2,1}^{\mathrm{LH}}\end{array}& \begin{array}{cc}{c}_{2,2}^{\mathrm{W}}& \infty \\ \infty & c_{2,2}^{\mathrm{W}}\end{array}& \cdots & \begin{array}{cc}{c}_{2,\left|E\right|}^{\mathrm{UH}}& \infty \\ \infty & c_{2,\left|E\right|}^{\mathrm{LH}}\end{array}\\ ⋮& ⋮& \ddots & ⋮\\ \begin{array}{cc}{c}_{\left|E\right|,1}^{\mathrm{UH}}& \infty \\ \infty & c_{\left|E\right|,1}^{\mathrm{LH}}\end{array}& \begin{array}{cc}{c}_{\left|E\right|,2}^{\mathrm{UH}}& \infty \\ \infty & c_{\left|E\right|,2}^{\mathrm{LH}}\end{array}& \cdots & \begin{array}{cc}{c}_{\left|E\right|,\left|E\right|}^{\mathrm{W}}& \infty \\ \infty & c_{\left|E\right|,\left|E\right|}^{\mathrm{W}}\end{array}\end{array}\right)$$

(8)

The calculation of c_i,j^UH and c_i,j^LH is related to the turning model used in path planning. In order to reduce turning time and improve operation efficiency, this paper adopts the Π-Turn model and Ω-Turn model. Assuming that c_i,j^D, D ∈ {UH,LH} represents the time cost of changing from line i to line j at the headland, and the time cost of the Π-Turn model and Ω-Turn model can be calculated by Equations (9) and (10), respectively.

$${\mathsf{\Pi }}_{i,j}^{\mathrm{D}}=\frac{\pi r}{v_t}+\frac{\sqrt{{(d_{i,j}^{\mathrm{D}})}^2+{(w_{i,j}^{\mathrm{D}}-2r)}^2}}{v_s}$$

(9)

$${\mathsf{\Omega }}_{i,j}^{\mathrm{D}}=\frac{(3\pi -\mathrm{a}\cos (1-\frac{{(d_{i,j}^{\mathrm{D}})}^2+{(w_{i,j}^{\mathrm{D}}-2r)}^2}{8r^2}))r}{v_t}$$

(10)

where,

d_i,j^D—vertical coordinate difference between the i-th operation line and the j-th operation line at the endpoint near the headland D.

w_i,j^D—abscissa coordinate difference between the i-th operation line and the j-th operation line at the endpoint near the headland D.

v_t—the turning speed of the tractor at the end of the headland.

v_s—the straight speed of the tractor at the end of the headland.

d_i,j^D can be calculated according to d_i,j^D = |X_i^D − X_j^D|. X_i^D and X_j^D represent the x-coordinate of the j-th operation line. After calculating all U_k,1 ± W(1 ≤ k ≤ n), X_i^U and X_j^U are sorted, and similarly, X_i^L is obtained, where W is the working width of the tractor.

According to W and r, c_i,j^D can be obtained:

$$c_{i.j}^{\mathrm{D}}=\{\begin{array}{c}{\mathsf{\Pi }}_{i,j}^{\mathrm{D}}\hspace{1em}{w}_{i,j}^{\mathrm{D}}\ge 2r\\ {\mathsf{\Omega }}_{i,j}^{\mathrm{D}}\hspace{1em}{w}_{i,j}^{\mathrm{D}}<2r\end{array}$$

(11)

Based on the number |E| of operation lines, the number M of unmanned tractors, and the cost matrix C′, the objective function is obtained as shown in Equation (1), where the set of traveled operation lines by each tractor is used as the variable.

A reasonable path optimization scheme for multi-unmanned tractors can reduce the total operating time and improve work efficiency [26]. However, this problem belongs to the TSP [27,28], and it is difficult to calculate the optimal solution in a short time. Differential evolution algorithm is an intelligent optimization algorithm based on population evolution proposed by Storn [29,30]. It has the characteristics of fewer operators and strong search ability. The solution can be obtained through mutation, crossover, and selection to update the population [31,32,33]. This paper designs a differential evolution algorithm to obtain multi-tractor paths.

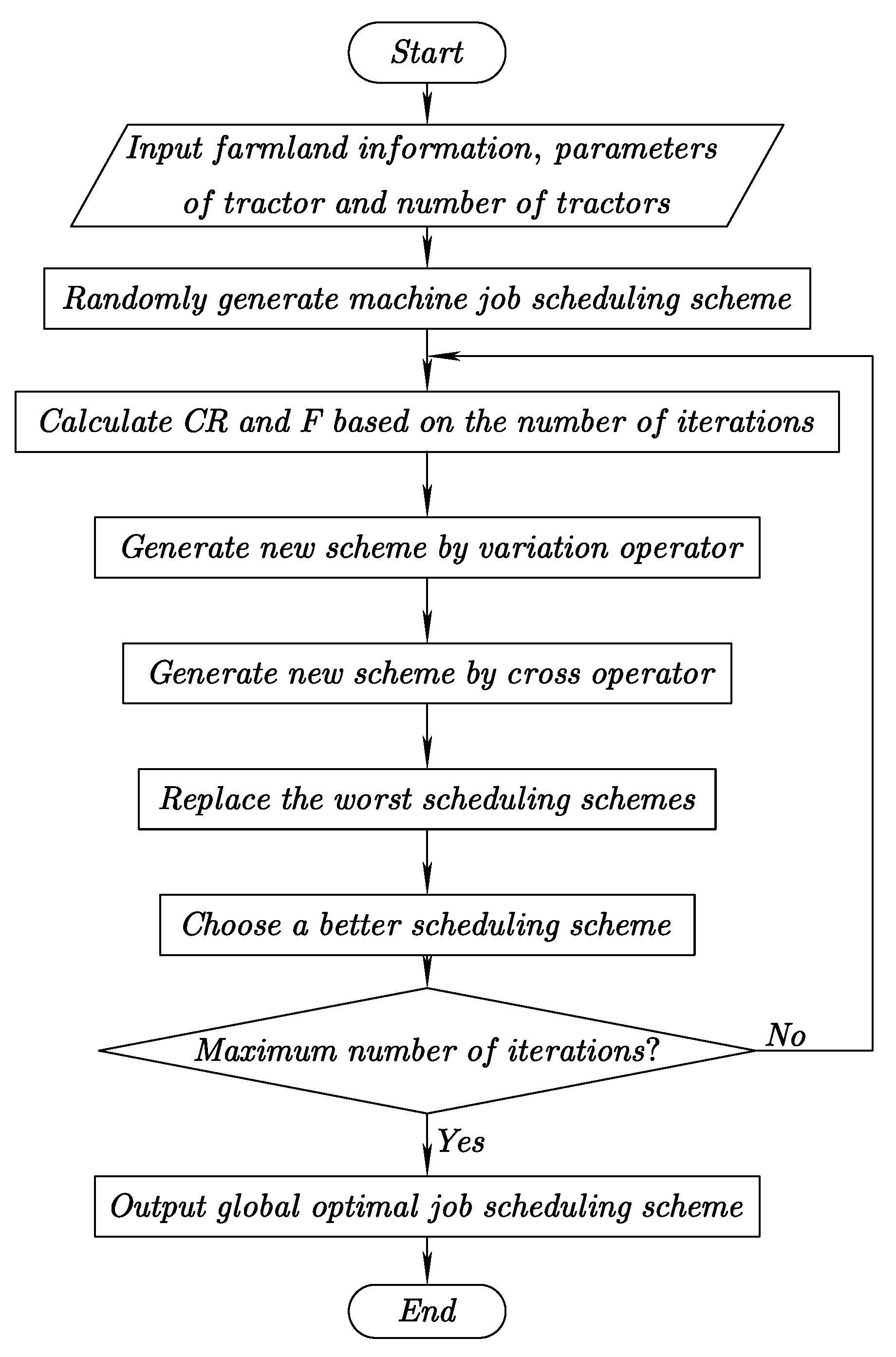
3. Multi-Tractor Path Optimization Algorithm

3.1. Differential Evolution Algorithm

Differential evolution algorithm needs to balance the global search and local search in the iterative process [34]. A global search is to search different spaces that have not appeared. A local search means the ability to improve the solution quality according to the information of the current solution. Differential evolution algorithms can obtain effective solutions through mutation and crossover operations. However, when differential evolution algorithm pays attention to local search, it is easy to fall into local optimization, resulting in premature convergence. On the other hand, if the differential evolution algorithm focuses on global search, the convergence will be very slow [35].

The mutation is also called mutation operator, which calculates the position of the new individual according to the individual position of the last iteration and the optimal position of all individuals. Differential evolution algorithm mainly has six mutation operators, and Equation (12) gives a common mutation operator [36].

$${\kappa }_i^{t+1}={\kappa }_i^t+F\cdot ({\kappa }_{best}^t-{\kappa }_i^t)+F\cdot ({\kappa }_{r_1}^t-{\kappa }_{r_2}^t)$$

(12)

where,

t—iteration number.

i—individual ID in algorithm population.

κ_i^t—the position of the i-th individual in the t-th iteration, |E|-dimensional column vector.

κ_best^t—the individual position with the best fitness in the t-th iteration, |E|-dimensional column vector.

F—a scaling factor that controls the scale of the difference.

The crossover of differential evolution algorithm is shown in Equation (13), where there is a random variable subject to the uniform distribution. When the random variable is less than the crossover probability, accept the mutation operation, otherwise, keep the original value.

$${\kappa }_{i,j}^{t+1}=\{\begin{array}{ll}{\kappa }_{i,j}^{t+1}& rand<CR\\ {\kappa }_{i,j}^t& \mathrm{otherwise}\end{array}$$

(13)

where,

CR—crossover probability.

rand—random number obeying uniform distribution [0,1).

The selection can be represented by Equation (14). If the fitness of the new solution is less than that of the original solution, the new solution is accepted, otherwise the original solution is retained.

$${\kappa }_i^{t+1}=\{\begin{array}{ll}{\kappa }_i^{t+1}& f(z_i^{t+1})<f(z_i^t)\\ {\kappa }_i^t& \mathrm{otherwise}\end{array}$$

(14)

where, f(κ)—objective function.

Although the differential evolution algorithm can obtain the minimum driving cost solution of the unmanned tractors in a limited time, it has the problem of premature convergence and insufficient exploration of solution space. In addition, the mutation operator generates a sequence of real numbers, not an integer sequence in a given range. Multi-tractor cooperation requires a finite number of integers to indicate the number of unmanned tractors and the current scheduling state. The traditional differential evolution algorithm cannot be directly used to solve the multi-tractor path optimization problem. When solving this kind of problem, they usually optimize the continuous variables first, and then indirectly obtain the discrete operation line travelling scheme through the round rather than directly optimizing the discrete operation line travelling scheme. Therefore, this paper provides a better balance between global search and local exploration by improving the mutation operator and crossover operator to optimize the differential evolution algorithm so as to obtain an efficient multi-tractor cooperative path optimization scheme.

3.2. Improved Differential Evolution Algorithm

3.2.1. Mutation Operator

A permutation matrix is not only an invertible matrix but also an orthogonal matrix. It can greatly reduce the convergence time by transposing when finding the inverse. In the cooperative path optimization problem for multi-tractors, the tractor sequence κ_i is one of the permutations composed of 1~|E|, and κ_i is a column vector. According to the definition of the permutation matrix, the column vector x_i obtained by left multiplying a permutation matrix is still one of the permutations composed of 1~|E|; that is, it is still a legal operation sequence after the transformation of the permutation matrix. Therefore, this paper introduces a permutation matrix to optimize the mutation operator.

Let the position κ of the i-th individual in the t iteration be:

$${\kappa }_i^t=P_i^t\cdot \alpha$$

(15)

where,

P_i^t—the permutation matrix of the individual i in the t-th iteration, with the size of |E|×|E|.

α—|E|-dimensional column vector, the expression is [1 2 … |E|]^T.

Substitute Equation (15) into mutation operator (Equation (12)). Since α is a non-zero vector, the simplified operator (16) is obtained:

$$P_i^{t+1}=P_i^t+F(P_{best}^t-P_i^t)+F(P_{r_1}^t-P_{r_2}^t)$$

(16)

However, when the permutation matrices are added or subtracted from each other, it is difficult to ensure the orthogonality of the matrix, so it can not be calculated directly by Equation (16).

Two permutation matrices are still permutation matrices after point multiplication, and the inverse cost is very low. Point multiplication can be used instead of plus; dot inverse matrix can be used instead of subtraction; let F = 1; Equation (16) can be rewritten as:

$$P_i^{t+1}=P_i^t\cdot (P_{best}^t{(P_i^t)}^{-1})\cdot (P_{r_1}^t{(P_{r_2}^t)}^{-1})$$

(17)

However, in Equation (17), the time complexity of calculating the inverse matrix is at least the cubic, and the calculation cost is large, which is not conducive to the fast acquisition of planning paths. The inverse operation of the orthogonal matrix is equivalent to the transpose operation, and the transpose operation is simpler. Therefore, this paper rewrites Equation (17) into Equation (18) with clearer mathematical meaning and less calculation:

$$P_i^{t+1}=P_i^t\cdot (P_{r_1}^t\cdot {(P_{r_2}^t)}^T)\cdot (P_{best}^t\cdot {(P_i^t)}^T)$$

(18)

This paper takes Equation (18) as the mutation operator of the improved differential evolution algorithm so as to optimize the operation path of the unmanned tractors.

3.2.2. Dynamic Parameters

In the traditional differential evolution algorithm, the crossover probability CR and scaling factor F are fixed and do not change with iteration. CR affects the probability of mutation. The smaller its value, the smaller the probability of mutation. Currently, the local search ability of the algorithm is strong. On the contrary, the greater the mutation probability, the stronger the global search ability of the algorithm. If F is fixed, the global search and local search cannot change adaptively, resulting in premature convergence and low search accuracy. As shown in Equation (19), the dynamic parameter scheme is adopted in this paper to make CR changes with the number of iterations. n is the number of operation lines, t is the current number of iterations, and T is the maximum number of iterations.

$$CR=\frac{1}{n}+(1-\frac{1}{n})\times (1-\frac{t}{T})$$

(19)

When t increases from 1 to T, the crossover probability CR gradually decreases to 1/n. The global search of the algorithm changes from strong to weak, and the local search changes from weak to strong. This can avoid premature convergence and improve search accuracy.

Similarly, too small a scaling factor F will also affect the search accuracy and convergence speed. This paper designs an adaptive function as shown in Equation (20). When t increases from 1 to T, the scaling factor F gradually increases to 1. The global search of the mutation operator changes from strong to weak, and the local search changes from weak to strong, which promotes the convergence of the algorithm.

$$F=0.2+\frac{0.8t}{T}$$

(20)

3.2.3. Elite Selection

Elite selection can improve the convergence speed and local search performance. It is assumed that κ_n−2^t, κ_n−1^t, κ_n^t are the first three individuals with the worst fitness in the t-th iteration and κ₁^t−1, κ₂^t−1, κ₃^t−1 are the first three individuals with the best fitness in the (t − 1)-th iteration. κ_n−2^t, κ_n−1^t, κ_n^t can be replaced by κ₁^t−1, κ₂^t−1, κ₃^t−1 to realize the elite selection.

This paper introduces the permutation matrix, adopts dynamic parameters and elite selection strategy to improve the differential evolution algorithm, and proposes an Adaptive Elite Differential Evolution (AEDE) Algorithm. The algorithm flow chart is shown in Figure 4.

The multi-tractor cooperative path optimization method studied in this paper firstly generates several feasible driving paths randomly according to the input orchard information, tractor parameters, and the number of tractors. Then, the crossover probability CR and scaling factor F of the current iteration are calculated, and the mutation operator and crossover operator designed in this paper are used to generate a new multi-tractor cooperative operation path optimization. Then, the solution with the worst fitness is eliminated through the elite selection, and the three schemes with the best fitness in the last iteration are introduced. The scheme with better fitness is selected through the selection operation to replace the current scheme until the termination condition is reached. This scheme with the best current fitness is output as the optimal multi machine cooperative path planning scheme solved by the algorithm.

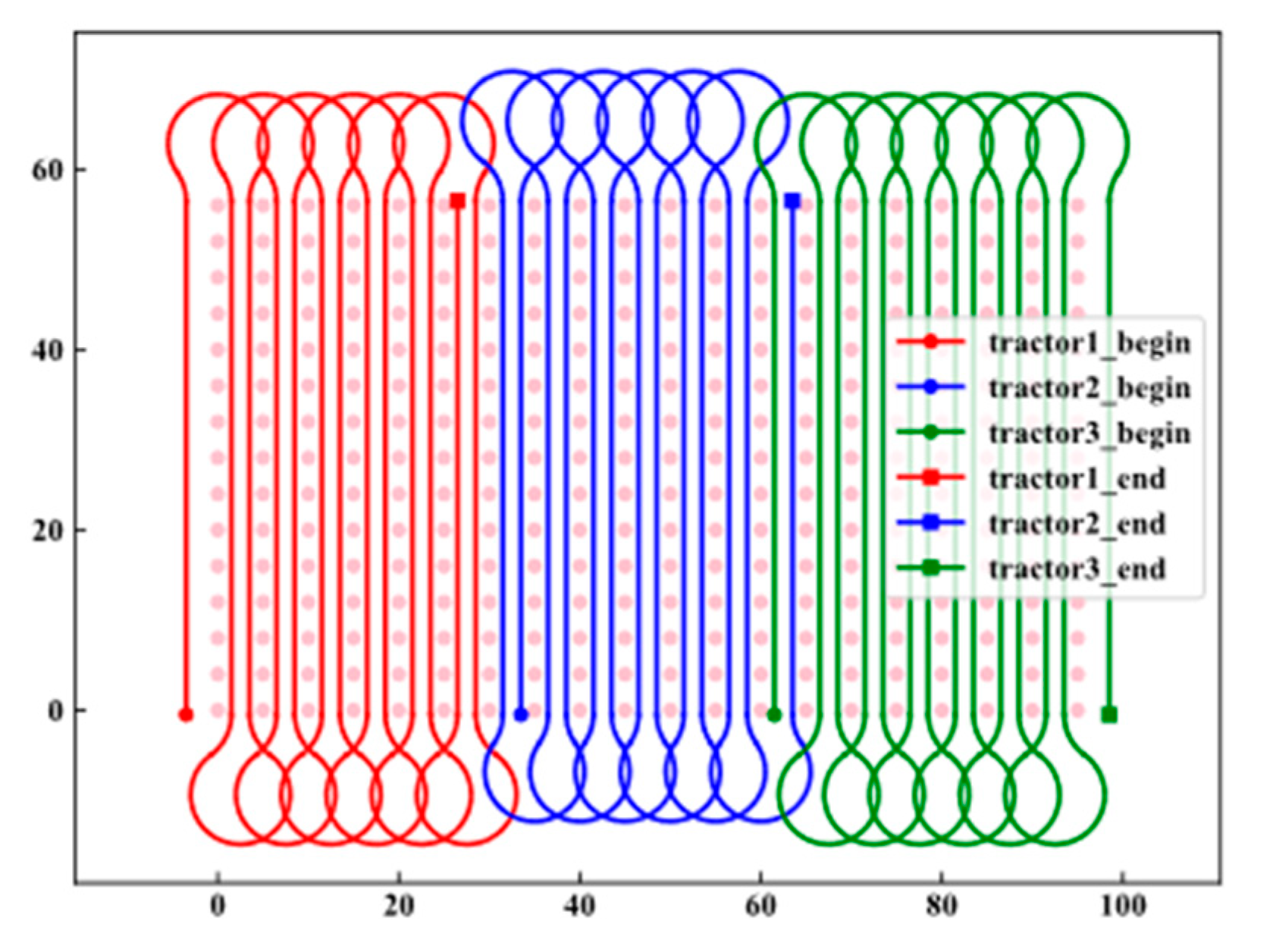
4. Experiment and Analysis

This paper took the John Deere 6B-1204 tractor commonly used in planting as the research object, and the total number of tractors was six. The working width of each tractor was W = 3.5 m, the minimum turning radius was r_min = 5.5 m, the working speed was v_w = 1 m·s⁻¹ in the working area, the straight speed was v_s = 5 m·s⁻¹ in the non-working area, and the turning speed was v_t = 2 m·s⁻¹. The peach orchard was rectangular, and the row spacing of peach trees was 4 × 5 m. As the peach tree distribution will affect the algorithm performance, this paper tests the path planning effect of the proposed model and the improved algorithm with different peach tree distributions. Figure 5 shows the distribution of peach trees in three rectangular standard peach orchards. Figure 5a shows the peach orchards with the rectangular distribution of peach trees. There were 20 rows of peach trees in the peach orchard, with 15 trees in each row. Figure 5b shows peach orchards with the approximately trapezoidal distribution of the peach trees, and Figure 5c shows peach orchards with an irregular distribution of peach trees. The experiment assumes that the tractor works in a peach orchard without obstacles and the driving process is continuous.

The parameters of the original differential evolution algorithm DE are as follows: population size N = 100, crossover probability CR = 0.1, scaling coefficient F = 0.5, and the maximum number of iterations is 500. Equation (1) is used as the fitness function. The experimental environment is Windows 10 and Python 3.7.

4.1. Analysis of Experimental Results

The evaluation indexes of the model adopt the total turning time decrease rate (TTTDR) and total operating time decrease rate (TOTDR). The higher the value, the better the optimization effect of the algorithm. TTTDR_n represents the reduction rate of total turning time between AEDE optimized and control group when n tractors work together. Similarly, TOTDR_n represents the reduction rate of operation time after AEDE optimization and comparison algorithms when n unmanned tractors work together. The calculation formulas of TTTDR_n and TOTDR_n are shown in Equations (21) and (22).

$$TTTD{R}_n=\frac{TTT{O}_n-TTT{I}_n}{TTT{O}_n}\times 100\%$$

(21)

$$TOTD{R}_n=\frac{TOT{O}_n-TOT{I}_n}{TOT{O}_n}\times 100\%$$

(22)

In addition, we also use the following indexes to evaluate the algorithm performance. TTTO_n is the total turning time of the n combined after control group optimization. TTTI_n is the total turning time of the n combined after AEDE optimization. TOTO_n is the total operating time of the n combined after control group optimization. TOTI_n is the total operating time of the n combined after AEDE optimization.

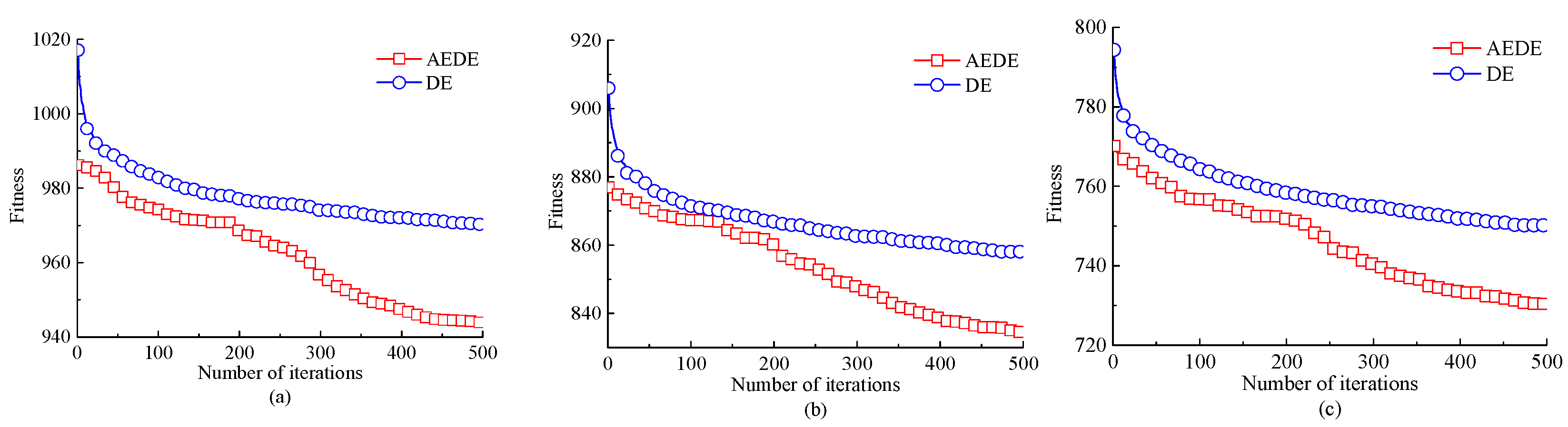
4.1.1. Performance Comparison of Elite Selection Algorithm

Using traditional DE as the control group, we compared it with the AEDE proposed in this paper in terms of total turning time and total operating time, respectively. Both DE and AEDE are intelligent evolutionary algorithms; different peach tree distributions do not affect the solution process. Therefore, this comparison is based on the rectangular distribution of peach trees. The results are shown in

Table 1. Performance comparision of algorithm.

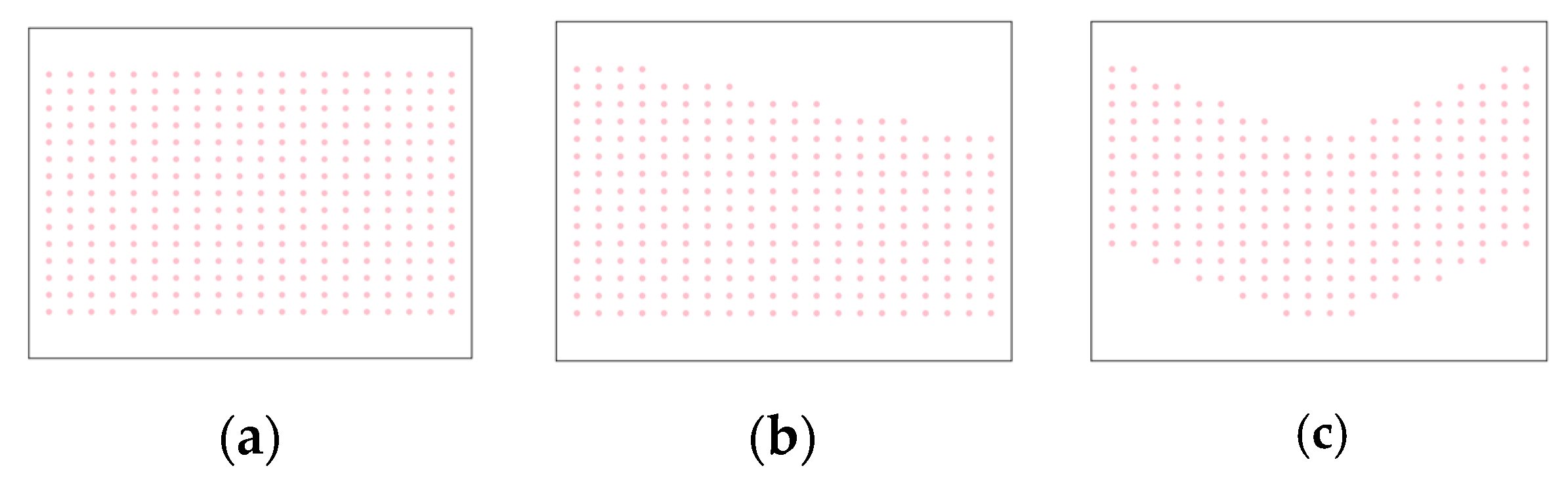
Number of Agricultural Machinery	Total Turning Time			Total Operating Time
	TTTOn(s)	TTTIn(s)	TTTDRn(%)	TOTOn(s)	TOTIn(s)	TOTDRn(%)
1	558.29	545.95	2.21	2838.29	2825.95	0.44
2	507.00	490.80	3.19	1417.89	1388.25	2.09
3	541.10	495.97	8.34	954.71	945.11	1.01
4	509.67	490.97	3.67	703.96	696.70	1.03
5	458.38	468.63	2.19	556.68	547.68	0.41
6	467.13	465.03	0.45	487.44	486.24	0.24
Mean	506.93	492.89	3.34	1159.83	1148.32	0.87

. According to Table 1, the total turning time of AEDE method proposed in this paper was reduced by 3.34%, and the total operating time was reduced by 0.87%. It shows that after improving DE, the total turning time and total operating time are optimized to a certain extent.

4.1.2. Comparison with Block Operation

Block is a common multi-tractor scheduling scheme, which divides orchards into different areas and is operated by a single tractor. Using block operation as the control group, this paper compares it with AEDE in terms of total turning time and total operating time, respectively. The results are shown in

Table 2. Comparison of total turning time and total operating time.

Peach Orchard	Number of Tractors	Total Turning Time			Total Operating Time
		TTTOn/s	TTTIn/s	TTTDRn/%	TOTOn/s	TOTIn/s	TOTDRn/%
Rectangle	1	839.3	536.8	36.0	3119.3	2816.8	9.7
	2	816.9	523.6	35.9	1548.4	1414.5	8.7
	3	794.5	492.5	38.0	1077.2	956.9	11.2
	4	772.0	489.7	36.6	763.0	698.4	8.5
	5	749.6	495.5	33.9	605.9	563.9	6.9
	6	732.5	468.4	36.1	528.3	488.3	7.6
	Mean	784.1	501.1	36.1	1273.7	1156.5	8.8
Trapezoid	1	839.3	560.5	33.2	2799.3	2520.5	10.0
	2	816.9	524.4	35.8	1484.4	1257.1	15.3
	3	794.5	527.7	33.6	1053.2	838.5	20.4
	4	772.0	530.9	31.2	755.0	633.5	16.1
	5	749.6	490.8	34.5	605.9	507.8	16.2
	6	732.1	506.0	30.9	528.3	434.2	17.8
	Mean	784.1	523.4	33.2	1204.4	1031.9	16.0
Irregular	1	837.8	572.0	31.7	2477.8	2212.0	10.7
	2	815.4	522.2	36.0	1227.7	1087.4	11.4
	3	793.1	520.8	34.3	852.8	751.5	11.9
	4	770.5	510.9	33.7	602.6	546.7	9.3
	5	748.8	501.7	33.0	477.9	433.4	9.3
	6	731.2	463.9	36.6	416.1	368.7	11.4
	Mean	782.8	515.2	34.2	1009.2	899.9	10.7

.

From Table 2, the total turning time of AEDE after optimization is reduced by more than 30%, and the total operating time is reduced by about 10%. This is because when working in block mode, the tractor needs to make frequent Ω-turns on the headland, which increases a lot of non-working time compared with the Π-Turn. AEDE avoids a lot of turning by optimizing the driving path of multiple tractors so as to reduce the total turning time and total operating time. In addition, AEDE can get good results whether the shape of the peach orchard is regular or irregular, which shows that AEDE is not sensitive to peach tree distribution and can be used to optimize peach orchard with complex peach tree distribution.

4.1.3. Comparison of Effective Operation Ability

Effective operation and average operation are important indexes to evaluate the cooperative operation efficiency of multiple tractors [37]. In a standard peach orchard, the effective operation refers to the ratio of the peach orchard area to the total operating time, and the average operation refers to the ratio of the effective operating capacity to the number of tractors. Figure 6 shows the changes of effective operating capacity and average effective operating capacity after block and AEDE optimization when the number of tractors working in rectangular orchards increases from two to six.

In Figure 7, the effective operating capacity shows an increasing trend because increasing the number of tractors reduces the total operating time in the orchard. AEDE reduces the total turning time by optimizing the turning path of the tractor, which in turn reduces the total operating time. When the number of tractor operations is two, the effective operation capacity and average effective operation capacity calculated by block operation are 0.0124 km²·h⁻¹ and 0.0062 km²·h⁻¹, respectively. The effective operation capacity and average effective operation capacity calculated by AEDE are 0.0138 km²·h⁻¹ and 0.0069 km·h⁻¹, respectively, which are 11.5% and 11.5% higher than block, respectively. When the number of tractors is six, the effective operation capacity and average effective operation capacity calculated by AEDE are increased by 8.6% and 8.6%, respectively, compared with block.

5. Conclusions

In order to improve the operating efficiency of tractors in standard peach orchards, this paper studies a path optimization algorithm based on differential evolution for multiple tractors.

(1) In the rectangular peach orchard, the total turning time and total operating time in the process of management operation are reduced by 3.34% and 0.87%, respectively. Compared with the non-optimized differential evolution algorithm, it shows that the performance of the algorithm studied in this paper is better.

(2) Compared with block operation, the total turning time and total operating time in the process of management operation obtained by this algorithm are reduced by 37.37% and 9.47%, and the effect is better. It not only improves the operation efficiency of the tractors in the standard peach orchard, but also reduces the operating loss of the tractors.

However, when the tractors meet in the turning area, they will automatically avoid obstacles by adjusting the path. As the adjusted path is shorter than the length of the turning path and working path, the mutual interference of tractors in the turning area is ignored in this paper. The time consumption of tractors entering and leaving the peach orchard is also not considered in the model. In further work, we plan to use the time window to construct the turning constraint so as to avoid the situation that tractors meet in the turning area. At the same time, a more accurate path optimization method for multi-tractor cooperative work is realized by setting fixed starting points and ending points of tractors.