Practical Implications of the Availability of Multiple Measurements to Classify Agricultural Soil Compaction: A Case-Study in The Netherlands
Abstract
:1. Introduction
2. Methods and Materials
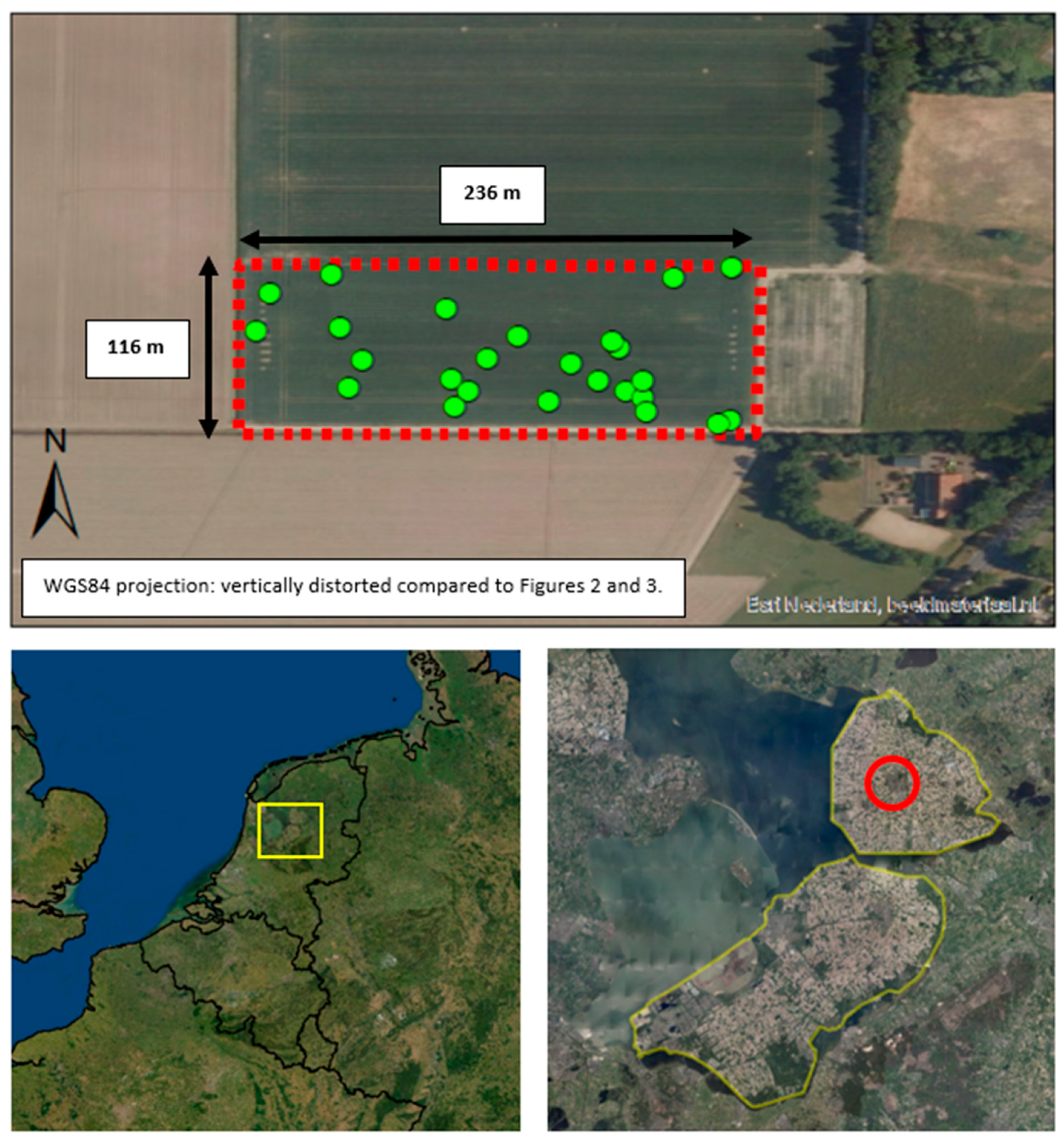
2.1. Study Area
2.2. Data Collection and Pre-Processing
2.3. Penetration Resistance (PR)
2.4. Dry Bulk Density (BDd)
2.5. Soil Moisture and Clay Content Estimation
2.6. Data Pre-Processing
2.7. State of Soil Compaction Using BDd and PR
2.8. Confusion Matrices
2.9. Accuracy Metrics
2.10. Misclassification Costs: Formula
2.11. False Negative Costs
2.12. False Positive Costs
3. Results
3.1. Confusion Matrices
3.2. Accuracy Metrics
3.3. Cost Functions
4. Discussion
4.1. Interpretation of Results
4.2. Broader Perspective
4.3. Limitations and Future Research
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Hartemink, A.E. Soils are back on the global agenda. Soil Use Manag. 2008, 24, 327–330. [Google Scholar] [CrossRef]
- Schjønning, P.; van den Akker, H.J.J.; Keller, T.; Greve, H.M.; Lamandé, M.; Simojoki, A.; Stettler, M.; Arvidsson, J.; Breuning-Madsen, H. Soil compaction. In Soil Threats in Europe—Status, Methods, Drivers and Effects on Ecosystem Services; Stolte, J., Tesfai, M., Øygarden, L., Kværnø, S., Keizer, J., Verheijen, F., Panagos, P., Ballabio, C., Hessel, R., Eds.; EUR 27607 EN; Publications Office of the European Union: Luxembourg, 2016; pp. 69–78. [Google Scholar] [CrossRef]
- Van-Camp, L.; Bujarrabal, B.; Gentile, A.R.; Jones, R.J.A.; Montanarella, L.; Olazabal, C.; Selvaradjou, S.-K. Reports of the Technical Working Groups Established under the Thematic Strategy for Soil Protection; EUR 21319 EN/5; Office for the official Publications of the European Communities: Luxembourg, 2004; p. 8722. Available online: https://ec.europa.eu/environment/archives/soil/pdf/vol5.pdf (accessed on 28 June 2018).
- Batey, T.; McKenzie, D.C. Soil compaction: Identification directly in the field. Soil Use Manag. 2006, 22, 123–131. [Google Scholar] [CrossRef]
- Batey, T. Soil compaction and soil management—A review. Soil Use Manag. 2009, 25, 335–345. [Google Scholar] [CrossRef]
- Ellis, S.; Atherton, J.K. Properties and development of soils on reclaimed alluvial sediments of the Humber estuary, eastern England. Catena 2003, 52, 129–147. [Google Scholar] [CrossRef]
- Soane, B.D.H.; Van Ouwerkerk, C. Soil Compaction in Crop Production. In Engineering, Developments in Agricultural 11; Soane, B.D., van Ouwerkerk, C., Eds.; Elsevier: Amsterdam, The Netherlands, 1994. [Google Scholar]
- Birkás, M.; Szemök, A.; Antos, G.; Neményi, M. Environmentally Sound Adaptable Tillage; Akadémiai Kiadó: Budapest, Hungary, 2008; ISBN 9789630586313. [Google Scholar]
- Douglas, J.T.; Koppi, A.J.; Crawford, C.E. Structural improvement in a grassland soil after changes to wheel-traffic systems to avoid soil compaction. Soil Use Manag. 1998, 14, 14–18. [Google Scholar] [CrossRef]
- Horton, R.; Ankeny, M.D.; Allmaras, R.R. Effects of Compaction on Soil Hydraulic Properties. In Soil Compaction in Crop Production; Soane, B.D., Van Ouwerkerk, C., Eds.; Elsevier: Amsterdam, The Netherlands, 1994; pp. 141–165. [Google Scholar] [CrossRef]
- Lipiec, J.; Stępniewski, W. Effects of soil compaction and tillage systems on uptake and losses of nutrients. Soil Tillage Res. 1995, 35, 37–52. [Google Scholar] [CrossRef]
- Mooney, S.J.; Nipattasuk, W. Quantification of the effects of soil compaction on water flow using dye tracers and image analysis. Soil Use Manag. 2003, 19, 356–363. [Google Scholar] [CrossRef]
- Massah, J.; Azadegan, B. Effect of chemical fertilizers on soil compaction and degradation. AMA Agric. Mech. Asia Afr. Lat. Am. 2016, 47, 44–50. [Google Scholar]
- Arvidsson, J.; Håkansson, I. Do effects of soil compaction persist after ploughing? Results from 21 long-term field experiments in Sweden. Soil Tillage Res. 1996, 39, 175–197. [Google Scholar] [CrossRef]
- Brus, D.J.; Van den Akker, J.J.H. How serious a problem is subsoil compaction in the Netherlands? A survey based on probability sampling. Soil 2018, 4, 37–45. [Google Scholar] [CrossRef] [Green Version]
- Van den Akker, J.J.H.; Hoogland, T. Comparison of risk assessment methods to determine the subsoil compaction risk of agricultural soils in The Netherlands. Soil Tillage Res. 2011, 114, 146–154. [Google Scholar] [CrossRef]
- Vermeulen, G.D.; Verwijs, B.R.; Van den Akker, J.J.H. Vergelijking van de Bodembelasting bij Agrarisch Veldwerk in 1980 en 2010; Comparison of the soil Stress during Agricultural Field Activities in 1980 and 2010; Report 501; Plant Research International: Wageningen, The Netherlands, 2013; Available online: https://edepot.wur.nl/258660 (accessed on 16 May 2022).
- Arvidsson, J. Subsoil compaction caused by heavy sugarbeet harvesters in southern Sweden: I. Soil physical properties and crop yield in six field experiments. Soil Tillage Res. 2001, 60, 67–78. [Google Scholar] [CrossRef]
- Håkansson, I.; Lipiec, J. A review of the usefulness of relative bulk density values in studies of soil structure and compaction. Soil Tillage Res. 2000, 53, 71–85. [Google Scholar] [CrossRef]
- Suzuki, L.E.A.S.; Reichert, J.M.; Reinert, D.J. Degree of compactness, soil physical properties and yield of soybean in six soils under no-tillage. Soil Res. 2013, 51, 311–321. [Google Scholar] [CrossRef]
- Van den Akker, J.J.H.; De Groot, W.J.M. Een Inventariserend Onderzoek Naar Ondergrondverdichting van Zandgronden en Lichte zavels; An Inventory Study into Soil Compaction of Sandy and Loamy Soils; Alterra-Report 1450; Alterra: Wageningen, The Netherlands, 2008; Available online: https://www.wur.nl/nl/Publicatie-details.htm?publicationId=publication-way-333637313733 (accessed on 28 June 2018).
- Huber, S.; Prokop, G.; Arrouays, D.; Banko, G.; Bispo, A.; Jones, R.J.A.; Kibblewhite, M.G.; Lexer, W.; Möller, A.; Rickson, R.J.; et al. Environmental Assessment of Soil for Monitoring Volume I: Indicators & Criteria. EUR 23490 EN/1; Office for the Official Publications of the European Communities: Luxembourg, 2008; p. 339. [Google Scholar] [CrossRef]
- Jones, R.J.A.; Spoor, G.; Thomasson, A.J. Vulnerability of subsoils in Europe to compaction: A preliminary analysis. Soil Tillage Res. 2003, 73, 131–143. [Google Scholar] [CrossRef] [Green Version]
- Renger, M. Uber den Einfluβ der Dränung auf das Gefüge und die Wasserdurchlässigkeit bindiger Böden [On the influence of drainage on the structure and water permeability of cohesive soils]. Mitt. Der Dtsch. Bodenkd. Ges. 1970, 11, 23–28. [Google Scholar]
- International Organization for Standardization. ISO 11272:2017. 2017. Available online: https://www.iso.org/standard/68255.html (accessed on 16 July 2021).
- Netherlands Standardisation Institute. NEN-EN-ISO 11272: Soil Quality—Determination of Dry Bulk Density. 2017. Available online: https://www.nen.nl/en/nen-en-iso-11272-2017-en-232321 (accessed on 19 July 2021).
- Wageningen Environmental Research. Bodemkundig Informatiesysteem (English: Soil Information System). 2021. Available online: http://maps.bodemdata.nl/bodemdatanl/index.jsp (accessed on 27 July 2021).
- Bengough, A.G.; Mullins, C.E. Mechanical impedance to root growth: A review of experimental techniques and root growth responses. J. Soil Sci. 1990, 41, 341–358. [Google Scholar] [CrossRef]
- Taylor, H.M.; Roberson, G.M.; Parker, J.J. Soil strength-root penetration relations to coarse-textured materials. Soil Sci. 1966, 102, 18–22. [Google Scholar] [CrossRef]
- Agostini, A.M.; Studdert, A.G.; San Martino, S.; Costa, L.J.; Balbuena, H.R. Crop residue grazing and tillage systems effects on soil physical properties and corn (Zea mays L.) performance. J. Soil Sci. Plant Nutr. 2012, 12, 271–282. [Google Scholar] [CrossRef] [Green Version]
- Gupta, S.C.; Allmaras, R.R. Models to Assess the Susceptibility of Soils to Excessive Compaction. In Advances in Soil Science; Stewart, B.A., Ed.; Springer: New York, NY, USA, 1987; Volume 6, pp. 65–100. [Google Scholar] [CrossRef]
- De Lima, R.P.; Tormena, C.A.; Figueiredo, G.C.; Anderson, R.; Rolim, M.M. Least limiting water and matric potential ranges of agricultural soils with calculated physical restriction thresholds. Agric. Water Manag. 2020, 240, 106299. [Google Scholar] [CrossRef]
- Da Silva, A.P.; Kay, B.D.; Perfect, E. Characterization of the Least Limiting Water Range of Soils. Soil Sci. Soc. Am. J. 1994, 58, 1775–1781. [Google Scholar] [CrossRef]
- Fabrizzi, K.P.; García, F.O.; Costa, J.L.; Picone, L.I. Soil water dynamics, physical properties and corn and wheat responses to minimum and no-tillage systems in the southern Pampas of Argentina. Soil Tillage Res. 2005, 81, 57–69. [Google Scholar] [CrossRef]
- Hamblin, A.P. The influence of soil structure on water movement, crop root growth, and water uptake. Adv. Agron. 1985, 38, 95–158. [Google Scholar] [CrossRef]
- Fernández, P.L.; Alvarez, C.R.; Taboada, M.A. Assessment of topsoil properties in integrated crop-livestock and continuous cropping systems under zero tillage. Soil Res. 2011, 49, 143–151. [Google Scholar] [CrossRef]
- Hernandez-Ramirez, G.; Lawrence-Smith, E.J.; Sinton, S.M.; Schwen, A.; Brown, H.E. Root Responses to Alterations in Macroporosity and Penetrability in a Silt Loam Soil. Soil Water Manag. Conserv. 2014, 78, 1392–1403. [Google Scholar] [CrossRef]
- Lapen, D.R.; Topp, G.C.; Gregorich, E.G.; Curnoe, W.E. Least limiting water range indicators of soil quality and corn production, eastern Ontario, Canada. Soil Tillage Res. 2004, 78, 151–170. [Google Scholar] [CrossRef]
- Greacen, E.L. Root response to soil mechanical properties. In Proceedings of the Transactions of the 13th Congress of International Society of Soil Science, Hamburg, Germany, 13–20 August 1986; Volume 5, pp. 20–47. [Google Scholar]
- Martins, R.N.; Fagundes Portes, M.; Fialho e Moraes, H.M.; Ribeiro Furtado Junior, M.; Fim Rosas, J.T.; Orlando Junior, W.D.A. Influence of tillage systems on soil physical properties, spectral response and yield of the bean crop. Remote Sens. Appl. Soc. Environ. 2021, 22, 100517. [Google Scholar] [CrossRef]
- Barbosa, L.C.; Magalhães, P.S.G.; Bordonal, R.O.; Cherubin, M.R.; Castioni, G.A.F.; Tenelli, S.; Franco, H.C.J.; Carvalho, J.L.N. Soil physical quality associated with tillage practices during sugarcane planting in south-central Brazil. Soil Tillage Res. 2019, 195, 104383. [Google Scholar] [CrossRef]
- Otto, R.; Silva, A.P.; Franco, H.C.J.; Oliveira, E.C.A.; Trivelin, P.C.O. High soil penetration resistance reduces sugarcane root system development. Soil Tillage Res. 2011, 117, 201–210. [Google Scholar] [CrossRef]
- Salem, H.M.; Valero, C.; Muñoz, M.Á.; Rodríguez, M.G.; Silva, L.L. Short term effects of four tillage practices on soil physical properties, soil water potential, and maize yield. Geoderma 2015, 237–238, 60–70. [Google Scholar] [CrossRef] [Green Version]
- Özgöz, E.; Günal, H.; Hüseyin, Ö.; Bayram, M.; Acir, N. Effect of Management on Spatial and Temporal Distribution of Soil Physical Properties. J. Agric. Sci. 2012, 18, 77–91. [Google Scholar] [CrossRef]
- Zaman, Q. Planning variable tillage practices based on spatial variation in soil physical conditions and crop yield using DGPS/GIS. Agric. Mech. Asia Afr. Lat. Am. 2002, 33, 41–44. [Google Scholar]
- Tebebu, T.Y.; Bayabil, H.K.; Stoof, C.R.; Giri, S.K.; Gessess, A.A.; Tilahun, S.A.; Steenhuis, T.S. Characterization of Degraded Soils in the Humid Ethiopian Highlands. Land Degrad. Dev. 2017, 28, 1891–1901. [Google Scholar] [CrossRef] [Green Version]
- Hamza, M.A.; Anderson, W.K. Soil compaction in cropping systems: A review of the nature, causes and possible solutions. Soil Tillage Res. 2005, 82, 121–145. [Google Scholar] [CrossRef]
- Taylor, H.M.; Gardner, H.R. Penetration of cotton seedling taproots as influenced by bulk density, moisture content, and strength of soil. Soil Sci. 1963, 96, 153–156. [Google Scholar] [CrossRef]
- Van Leeuwen, M.M.W.J.; Heuvelink, G.B.M.; Wallinga, J.; De Boer, I.J.M.; Van Dam, J.C.; Van Essen, E.A.; Moolenaar, S.W.; Verhoeven, F.P.M.; Stoorvogel, J.J.; Stoof, C.R. Visual soil evaluation: Reproducibility and correlation with standard measurements. Soil Tillage Res. 2018, 178, 167–178. [Google Scholar] [CrossRef]
- Wilson, M.G.; Sasal, M.C.; Caviglia, O.P. Critical bulk density for a Mollisol and a Vertisol using least limiting water range: Effect on early wheat growth. Geoderma 2013, 192, 354–361. [Google Scholar] [CrossRef]
- Wilson, M.G.; Paparotti, O.; Paz Gonzalez, A.; Díaz Ucha, E. Ecuaciones de ajuste entre la Resistencia Mecánica a la Penetración y el contenido hídrico en un lote en siembra directa. In Proceedings of the XX Congreso Argentino de la Ciencia del Suelo, Salta, Argentina, 19–22 September 2006. [Google Scholar]
- Alvarez, R.; Steinbach, H.S. A review of the effects of tillage systems on some soil physical properties, water content, nitrate availability and crops yield in the Argentine Pampas. Soil Tillage Res. 2009, 104, 1–15. [Google Scholar] [CrossRef]
- Coelho, M.B.; Mateos, L.; Villalobos, F.J. Influence of a compacted loam subsoil layer on growth and yield of irrigated cotton in Southern Spain. Soil Tillage Res. 2000, 57, 129–142. [Google Scholar] [CrossRef]
- Stock, O.; Bens, O.; Hüttl, R.F. The interrelationship between the cultivation of crops and soil-strength dynamics. J. Plant Nutr. Soil Sci. 2007, 170, 713–721. [Google Scholar] [CrossRef]
- Laboski, C.A.M.; Dowdy, R.H.; Allmaras, R.R.; Lamb, J.A. Soil strength and water content influences on corn root distribution in a sandy soil. Plant Soil 1998, 203, 239–247. Available online: http://www.jstor.org/stable/42949872 (accessed on 16 May 2022).
- Boone, F.R.; Nam der Werf, H.M.G.; Kroesbergen, B.; Ten Hag, B.A.; Boers, A. The effect of compaction of the arable layer in sandy soils on the growth of maize for silage. 1. Critical matric water potentials in relation to soil aeration and mechanical impedance. Neth. J. Agric. Sci. 1986, 34, 155–171. [Google Scholar] [CrossRef]
- Çelik, İ.; Günal, H.; Acar, M.; Acir, N.; Bereket, Z.; Budak, M. Strategic tillage may sustain the benefits of long-term no-till in a Vertisol under Mediterranean climate. Soil Tillage Res. 2019, 185, 17–28. [Google Scholar] [CrossRef]
- Bengough, A.G.; Bransby, M.F.; Hans, J.; McKenna, S.J.; Roberts, T.J.; Valentine, T.A. Root responses to soil physical conditions; growth dynamics from field to cell. J. Exp. Bot. 2005, 57, 437–447. [Google Scholar] [CrossRef] [Green Version]
- De Moraes Sá, J.C.; Tivet, F.; Lal, R.; Briedis, C.; Hartman, D.C.; dos Santos, J.Z.; dos Santos, J.B. Long-term tillage systems impacts on soil C dynamics, soil resilience and agronomic productivity of a Brazilian Oxisol. Soil Tillage Res. 2014, 136, 38–50. [Google Scholar] [CrossRef]
- Müller, M.M.L.; Tormena, C.A.; Genú, A.M.; Kramer, L.F.M.; Michalovicz, L.; Caires, E.F. Structural Quality of a No-Tillage Red Latosol 50 Months After Gypsum Aplication. Rev. Bras. Cienc. Solo 2012, 36, 1005–1013. [Google Scholar] [CrossRef]
- Tekeste, M.; Habtzghi, D.H.; Stroosnijder, L. Soil strength assessment using threshold probability approach on soils from three agro-ecological zones in Eritrea. Biosyst. Eng. 2007, 98, 470–478. [Google Scholar] [CrossRef]
- Bradfort, J.M. Penetrability. In Methods of Soil Analysis-Part 1: Physical and Mineralogical Methods, 2nd ed.; Klute, A., Ed.; American Society of Agronomy: Madison, WI, USA, 1986; pp. 463–478. [Google Scholar] [CrossRef]
- Barik, K.; Aksakal, E.L.; Islam, K.R.; Sari, S.; Angin, I. Spatial variability in soil compaction properties associated with field traffic operations. Catena 2014, 120, 122–133. [Google Scholar] [CrossRef]
- Kumar, A.; Chen, Y.; Sadek, A.; Rahman, S. Soil cone index in relation to soil texture, moisture content, and bulk density for no-tillage and conventional tillage. Agric. Eng. Int. CIGR J. 2012, 14, 26–37. [Google Scholar]
- Carrara, M.; Castrignanò, A.; Comparetti, A.; Febo, P.; Orlando, S. Mapping of penetrometer resistance in relation to tractor traffic using multivariate Geostatistics. Geoderma 2007, 142, 294–307. [Google Scholar] [CrossRef] [Green Version]
- Perdok, U.D.; Kroesbergen, B.; Hoogmoed, W.B. Possibilities for modelling the effect of compression on mechanical and physical properties of various Dutch soil types. Soil Tillage Res. 2002, 65, 61–75. [Google Scholar] [CrossRef]
- Vaz, C.M.P.; Manieri, J.M.; de Maria, I.C.; Tuller, M. Modeling and correction of soil penetration resistance for varying soil water content. Geoderma 2011, 166, 92–101. [Google Scholar] [CrossRef]
- Da Silva, W.M.; Bianchini, A.; Da Cunha, C.A. Modeling and correction of soil penetration resistance for variations in soil moisture and soil bulk density. J. Braz. Assoc. Agric. Eng. 2016, 36, 449–459. [Google Scholar] [CrossRef] [Green Version]
- Hernanz, J.L.; Peixoto, H.; Cerisola, C.; Sánchez-Girón, V. An empirical model to predict soil bulk density profiles in field conditions using penetration resistance, moisture content and soil depth. J. Terramech. 2000, 37, 167–184. [Google Scholar] [CrossRef]
- Van den Biggelaar, D.F.A.M. New Land, Old History: Past Landscapes and Hominin Activity Covering the Last 220,000 Years in Flevoland, The Netherlands [Vrije Universiteit Amsterdam]. 2017. Available online: https://research.vu.nl/en/publications/new-land-old-history-past-landscapes-and-hominin-activity-coverin (accessed on 16 May 2022).
- IUSS Working Group WRB. World Reference Base for Soil Resources 2014, Update 2015, International Soil Classification System for Naming Soils and Creating Legends for Soil Maps; World Soil Resources Reports 2015, No. 106; FAO: Rome, Italy, 2015. [Google Scholar]
- Minasny, B.; McBratney, A.B.A. conditioned Latin hypercube method for sampling in the presence of ancillary information. Comput. Geosci. 2006, 32, 1378–1388. [Google Scholar] [CrossRef]
- Walvoort, D.J.J.; Brus, D.J.; De Gruijter, J.J. An R package for spatial coverage sampling and random sampling from compact geographical strata by k means. Comput. Geosci. 2010, 36, 1261–1267. [Google Scholar] [CrossRef]
- Royal Eijkelkamp. Penetrologger—User Manual, (41 pp.). 2021. Available online: https://www.eijkelkamp.com/download.php?file=M0615SAe_Penetrologger_bd1b.pdf (accessed on 27 July 2021).
- Soil Survey Staff. Kellogg Soil Survey Laboratory Methods Manual. Soil Survey Investigations Report No. 42, Version 5.0. 2014. Available online: https://www.nrcs.usda.gov/wps/portal/nrcs/detail/soils/ref/?cid=nrcs142p2_054247 (accessed on 12 July 2021).
- Royal Eijkelkamp, Delta-T Devices Ltd. User Manual for the WET Sensor. 2018, p. 42. Available online: https://www.eijkelkamp.com/download.php?file=M1933e_Wet_sensor_b18b.pdf (accessed on 27 July 2021).
- Mome Filho, E.A.; Da Silva, A.P.; Figueiredo, G.C.; Gimenes, F.H.S.; Vitti, A.C. Compared performance of penetrometers and effect of soil water content on penetration resistance measurements. Rev. Bras. Ciência Solo 2014, 38, 744–754. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing. 2021. Available online: https://www.r-project.org/ (accessed on 12 November 2021).
- Wand, M.P.; Jones, M.C. Kernel Smoothing; CRC Press: Boca Raton, FL, USA, 1995; ISBN 0-412-55270-1. [Google Scholar]
- Wand, M.P.; Jones, M.C. KernSmooth: Functions for Kernel Smoothing (and Density Estimation). R-Package Version 2.23-20. 2021. Available online: https://cran.r-project.org/web/packages/KernSmooth/index.html (accessed on 27 July 2021).
- Tharwat, A. Classification assessment methods. Appl. Comput. Inform. 2021, 17, 168–192. [Google Scholar] [CrossRef]
- Wageningen Economic Research. BINternet Database. 2022. Available online: https://www.agrofoodportal.com/Binternet.aspx?ID=20&Lang=1 (accessed on 3 August 2021).
- De Wolf, P.; Dawson, A.; Klompe, K. Kosten En Baten Van Bodemmaatregelen: Grondbewerking, Organische Stofaanvoer En Tagetes Patula Als Aaltjesvanggewas; Cost and Benefit of Soil Management: Tillage, Supply of Organic Matter, and Tagetes Patula as Nematode Cover Crop; Report 2019, WPR-819; Wageningen Research, Wageningen Plant Research: Wageningen, The Netherlands, 2019. [Google Scholar] [CrossRef]
- Botta, G.F.; Jorajuria, D.; Balbuena, R.; Ressia, M.; Ferrero, C.; Rosatto, H.; Tourn, M. Deep tillage and traffic effects on subsoil compaction and sunflower (Helianthus annus L.) yields. Soil Tillage Res. 2006, 91, 164–172. [Google Scholar] [CrossRef]
- Drewry, J.J.A.; Paton, R.J.A.; Monaghan, R.M.A. Soil compaction and recovery cycle on a Southland dairy farm: Implications for soil monitoring. Aust. J. Soil Res. 2004, 42, 851–856. [Google Scholar] [CrossRef]
- CBS Statistics Netherlands. Aantal Boerderijen in Flevoland Daalt Minder Snel dan Elders [Number of Farms Decreasing More Slowly in Flevoland than Elsewhere]. Available online: https://www.cbs.nl/nl-nl/nieuws/2015/53/aantalboerderijen-in-flevoland-daalt-minder-snel-dan-elders (accessed on 10 November 2021).
- Tol-Leenders, D.; Knotters, M.; De Groot, W.; Gerritsen, P.; Reijneveld, A.; Van Egmond, F.; Wösten, H.; Kuikman, P. Koolstofvoorraad in de Bodem van Nederland (1998–2018): CC-NL; Carbon Stock in the Soil of the Netherlands (1998–2018): CC-NL; Report 2974; Wageningen Environmental Research: Wageningen, The Netherlands, 2018. [Google Scholar] [CrossRef] [Green Version]
- Klerkx, L.; Jakku, E.; Labarthe, P. A review of social science on digital agriculture, smart farming and agriculture 4.0: New contributions and a future research agenda. NJAS—Wagening J. Life Sci. 2019, 90–91, 100315. [Google Scholar] [CrossRef]
- Wolfert, S.; Ge, L.; Verdouw, C.; Bogaardt, M.J. Big Data in Smart Farming—A review. Agric. Syst. 2017, 153, 69–80. [Google Scholar] [CrossRef]
- Daydé, C.; Couture, S.; Garcia, F.; Martin-Clouaire, R. Investigating operational decision-making in agriculture. In Proceedings of the 7th Congress on Environmental Modelling and Software (IEMSS 2014), San Diego, CA, USA, 15–19 June 2014; Available online: https://hal.inrae.fr/hal-02739614/document (accessed on 16 May 2022).
- Van den Akker, J.J.H.; De Vries, F.; Vermeulen, G.D.; Hack-ten Broeke, M.J.D.; Schouten, T. Risico op Ondergrondverdichting in Het Landelijk Gebied in Kaart; Map of the Risk of Subsoil Compaction in the Rural Areas; Alterra-report 2409; Alterra: Wageningen, The Netherlands, 2013; Available online: https://research.wur.nl/en/publications/risico-op-ondergrondverdichting-in-het-landelijk-gebied-kaart (accessed on 28 June 2018).










| Threshold Value for Soil Compaction | Authors | Cited Source |
|---|---|---|
| Using a single threshold | ||
| 2.0 MPa | Agostini et al. [30] | Gupta & Allmaras [31] |
| De Lima et al. [32] | Da Silva et al. [33] | |
| Fabrizzi et al. [34] | Gupta & Allmaras [31]; Hamblin [35] | |
| Fernández et al. [36] | - | |
| Hernandez-Ramirez et al. [37] | Da Silva et al. [33] | |
| Lapen et al. [38] | Bengough & Mullins [28]; Greacen [39] | |
| Martins et al. [40] | Barbosa et al. [41]; Otto et al. [42]; Salem et al. [43] | |
| Özgöz et al. [44] | Zaman [45] | |
| Tebebu et al. [46] | Hamza & Anderson [47]; Taylor & Gardner [48] | |
| Van Leeuwen et al. [49] | - | |
| Wilson et al. [50] | Wilson et al. [51] | |
| 2.5 MPa | Alvarez & Steinbach [52] | - |
| 3.0 MPa | Coelho et al. [53] | Taylor & Gardner [48] |
| 4.2 MPa | Stock et al. [54] | - |
| Using a range of thresholds | ||
| 1.5 MPa to 3.0 MPa | Laboski et al. [55] | Boone et al. [56] |
| 2.0 MPa to 3.0 MPa | Çelik et al. [57] | Bengough et al. [58]; De Moraes Sá et al. [59] |
| Müller et al. [60] | Bengough & Mullins [28] | |
| Tekeste et al. [61] | Bradfort [62]; Taylor & Gardner [48] | |
| Metric | Formula | Interpretation |
|---|---|---|
| Accuracy | Ratio between number of correctly classified samples and total number of samples | |
| Sensitivity | Ratio of number of correctly classified positive samples to total number of positive samples | |
| Specificity | Ratio of number of correctly classified negative samples to total number of negative samples | |
| Balanced accuracy | Accuracy measure corrected for imbalance in the dataset |
| Crop | Revenue from Crop (€ ha−1 y−1) Mean over 2010–2019 | Estimated Revenue Loss of 10% in Case of Soil Compaction (€ ha−1 y−1) |
|---|---|---|
| Seed potatoes | 10.355 | 1036 |
| Onions | 6.744 | 674 |
| Sugar beets | 3.337 | 334 |
| Wheat | 1.641 | 164 |
| Crop | Cost of a False Positive (€ ha−1 y−1) | Cost of a False Negative (€ ha−1 y−1) |
|---|---|---|
| Seed potatoes | 380 | 1036 |
| Onions | 260 | 674 |
| Sugar beets | 146 | 334 |
| Wheat | 90 | 164 |
| Metric | Optimum Value (%) | Threshold at Which the Optimum Is Reached (MPa) |
|---|---|---|
| Accuracy | 84.1 | 3.0 |
| Sensitivity | 100 | 0.0–0.4 |
| Specificity | 100 | 4.3 |
| Balanced accuracy | 76.0 | 1.8–1.9 |
| Sensitivity (at max. balanced accuracy) | 76.9 | 1.8–1.9 |
| Specificity (at max. balanced accuracy) | 75.0 | 1.8–1.9 |
| Crop | Cost at 0.0 MPa (€ ha−1 y−1) | Cost at 4.3 MPa (€ ha−1 y−1) | Optimal Cost (€ ha−1 y−1) | Threshold at Optimal Cost (MPa) |
|---|---|---|---|---|
| Seed potatoes | 308 | 195 | 122 | 1.8–1.9 |
| Onions | 211 | 127 | 82 | 1.8–1.9 |
| Sugar beets | 118 | 63 | 44 | 2.6 |
| Wheat | 73 | 31 | 23 | 2.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Orsouw, T.L.; Mulder, V.L.; Schoorl, J.M.; Van Os, G.J.; Van Essen, E.A.; Pepers, K.H.J.; Heuvelink, G.B.M. Practical Implications of the Availability of Multiple Measurements to Classify Agricultural Soil Compaction: A Case-Study in The Netherlands. Agronomy 2022, 12, 1669. https://doi.org/10.3390/agronomy12071669
Van Orsouw TL, Mulder VL, Schoorl JM, Van Os GJ, Van Essen EA, Pepers KHJ, Heuvelink GBM. Practical Implications of the Availability of Multiple Measurements to Classify Agricultural Soil Compaction: A Case-Study in The Netherlands. Agronomy. 2022; 12(7):1669. https://doi.org/10.3390/agronomy12071669
Chicago/Turabian StyleVan Orsouw, Tijn L., Vera L. Mulder, Jeroen M. Schoorl, Gera J. Van Os, Everhard A. Van Essen, Karin H. J. Pepers, and Gerard B. M. Heuvelink. 2022. "Practical Implications of the Availability of Multiple Measurements to Classify Agricultural Soil Compaction: A Case-Study in The Netherlands" Agronomy 12, no. 7: 1669. https://doi.org/10.3390/agronomy12071669






