Relationship between the Dynamic Characteristics of Tomato Plant Height and Leaf Area Index with Yield, under Aerated Drip Irrigation and Nitrogen Application in Greenhouses
Abstract
:1. Introduction
2. Materials and Methods
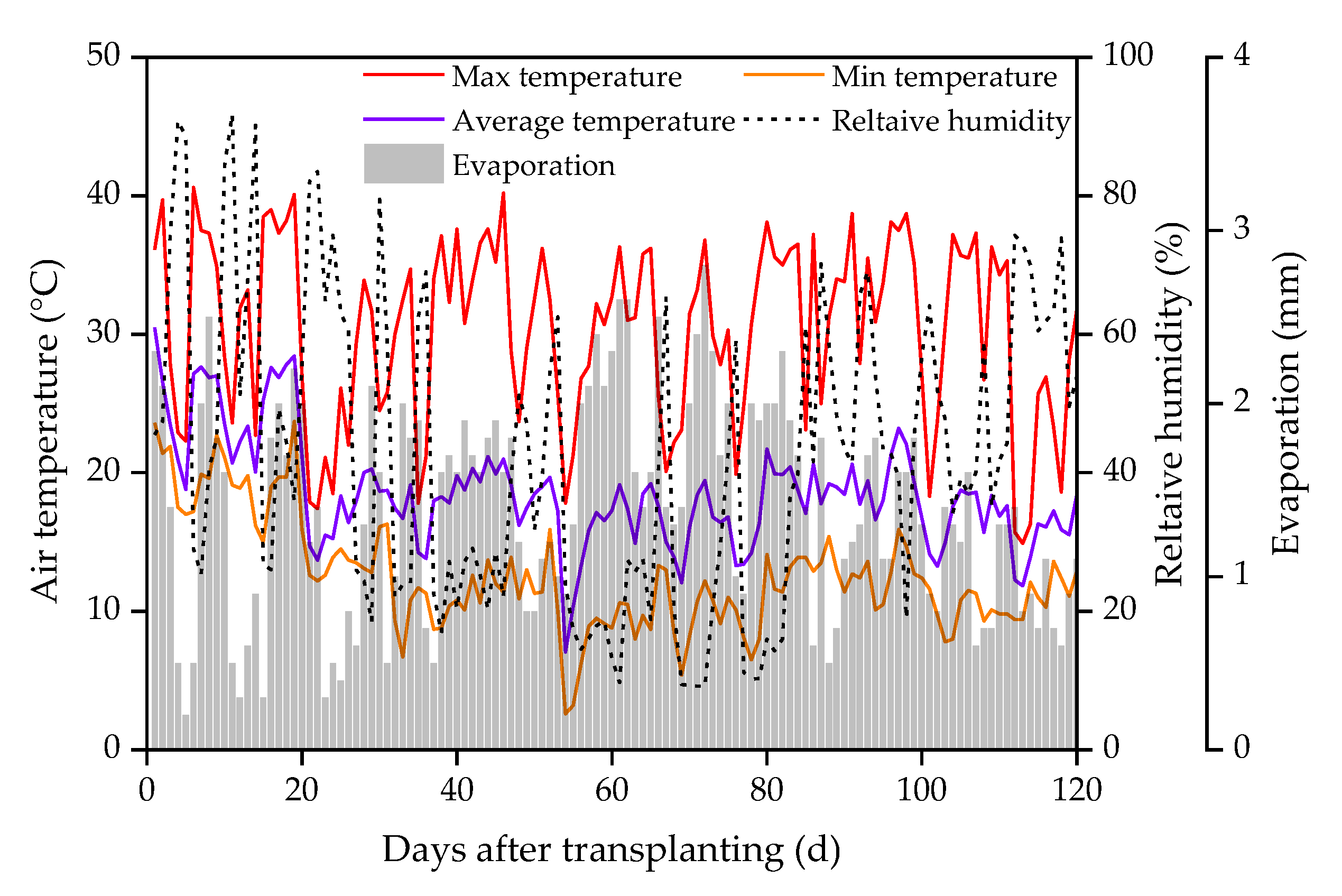
2.1. Experimental Site
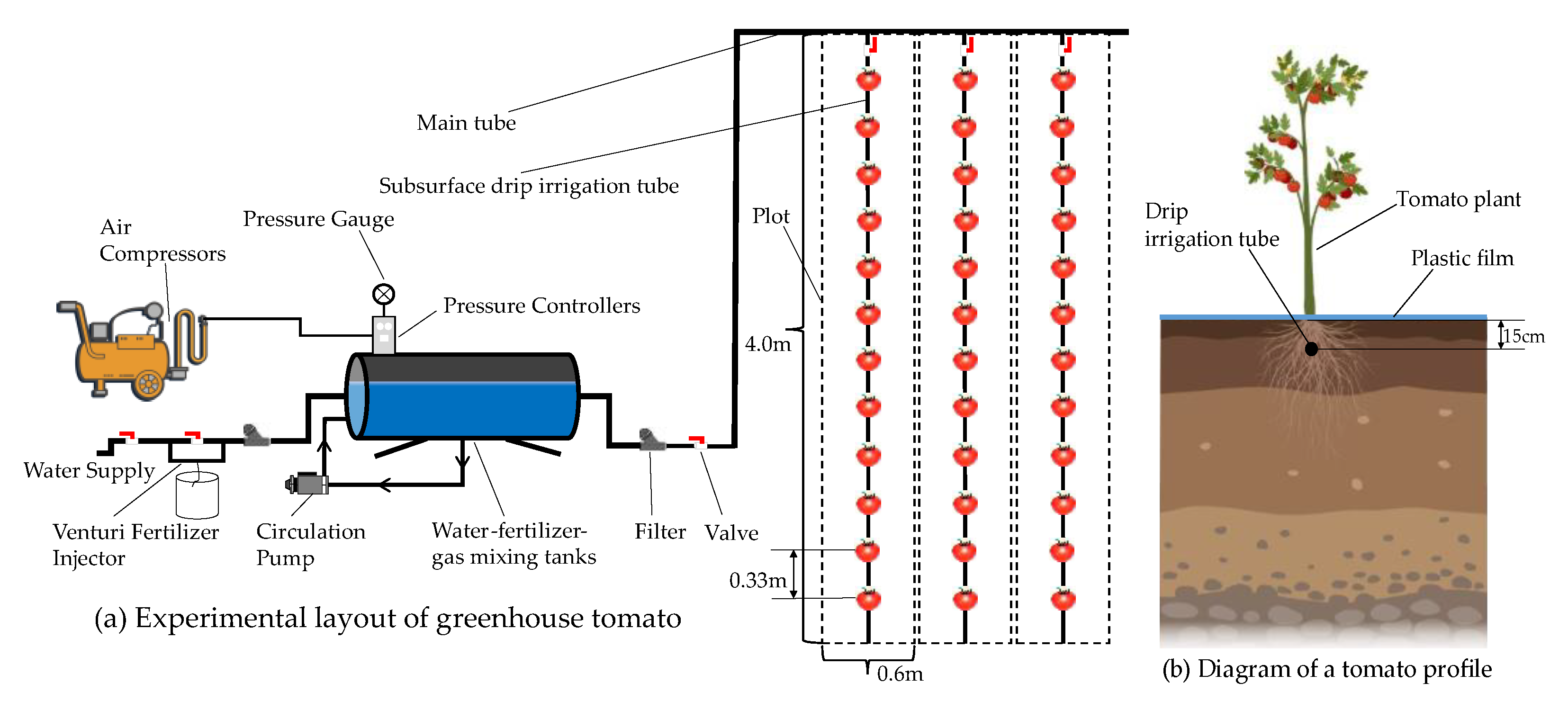
2.2. Experimental Design
2.3. Plant Height and Leaf Area Index (LAI)
2.4. Shoot Biomass and Yield of Tomato
2.5. Model Description and Application
2.5.1. Effective Cumulative Temperature
2.5.2. Logistic Model
2.5.3. Richards Model
2.6. Grey Correlation Analysis
2.7. Statistical Analysis
3. Results
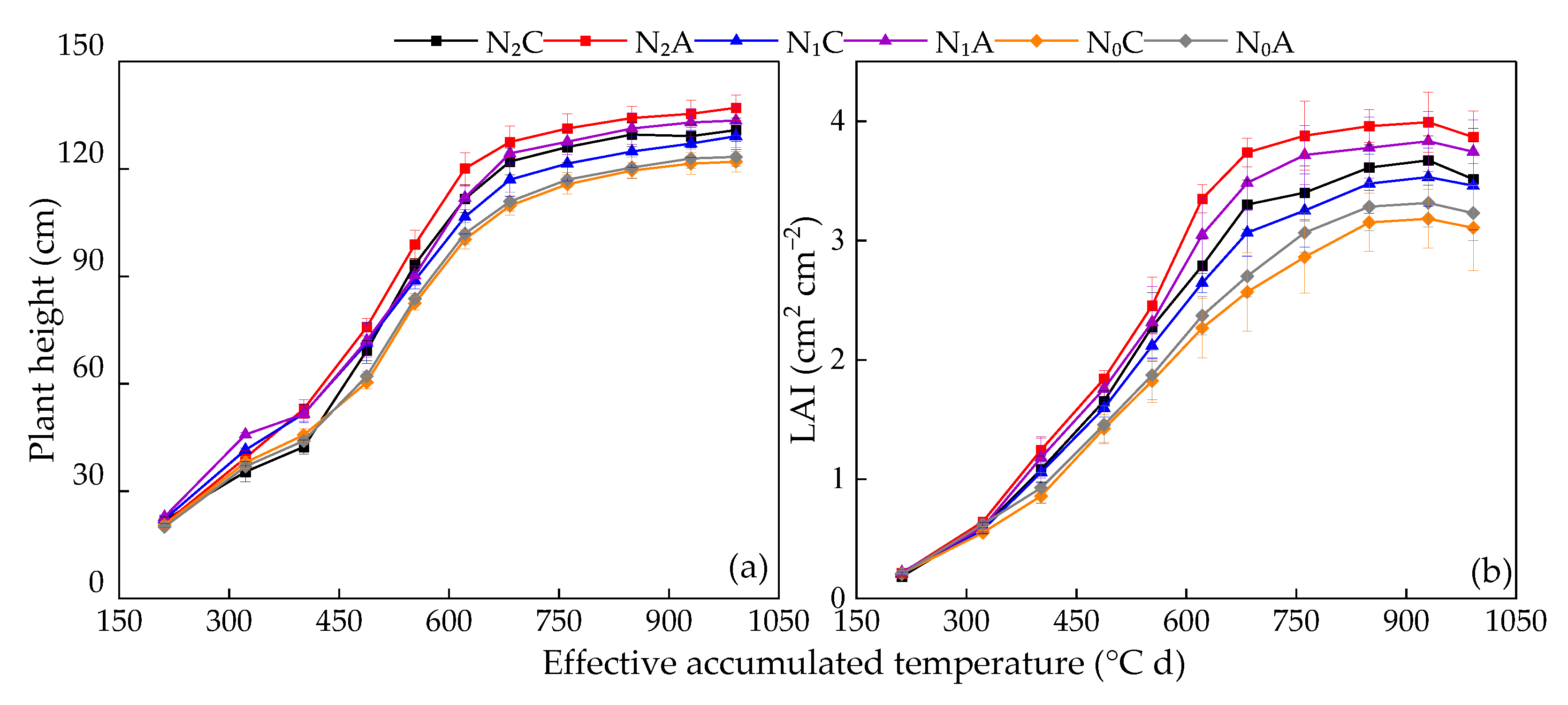
3.1. Plant Height and LAI
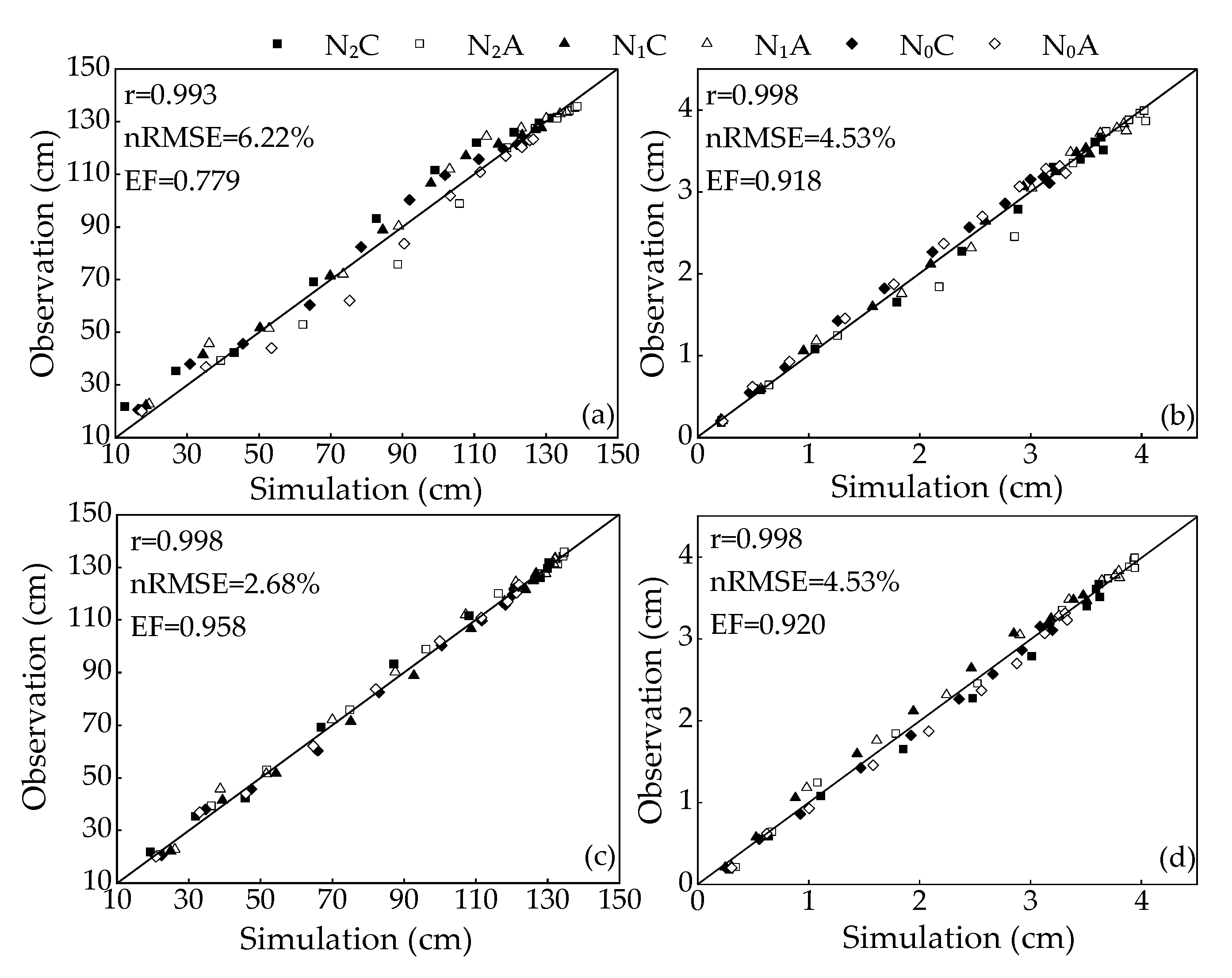
3.2. Fitting of Equation Based on Logistic and Richards Models
3.3. Characteristic Parameters Plant Height of Tomato
3.4. Characteristic Parameters of LAI
3.5. Dry Matter Accumulation and Yield of Tomato
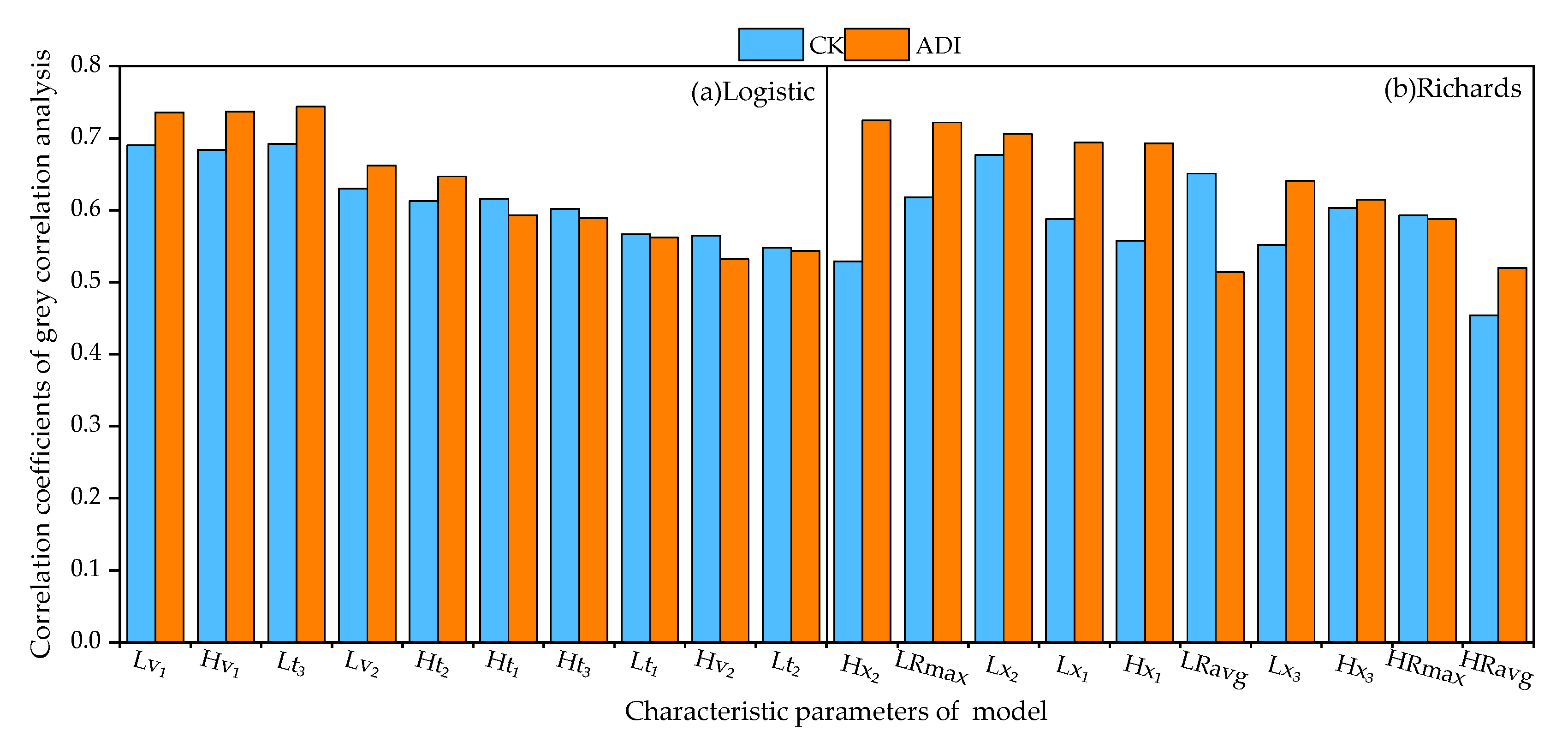
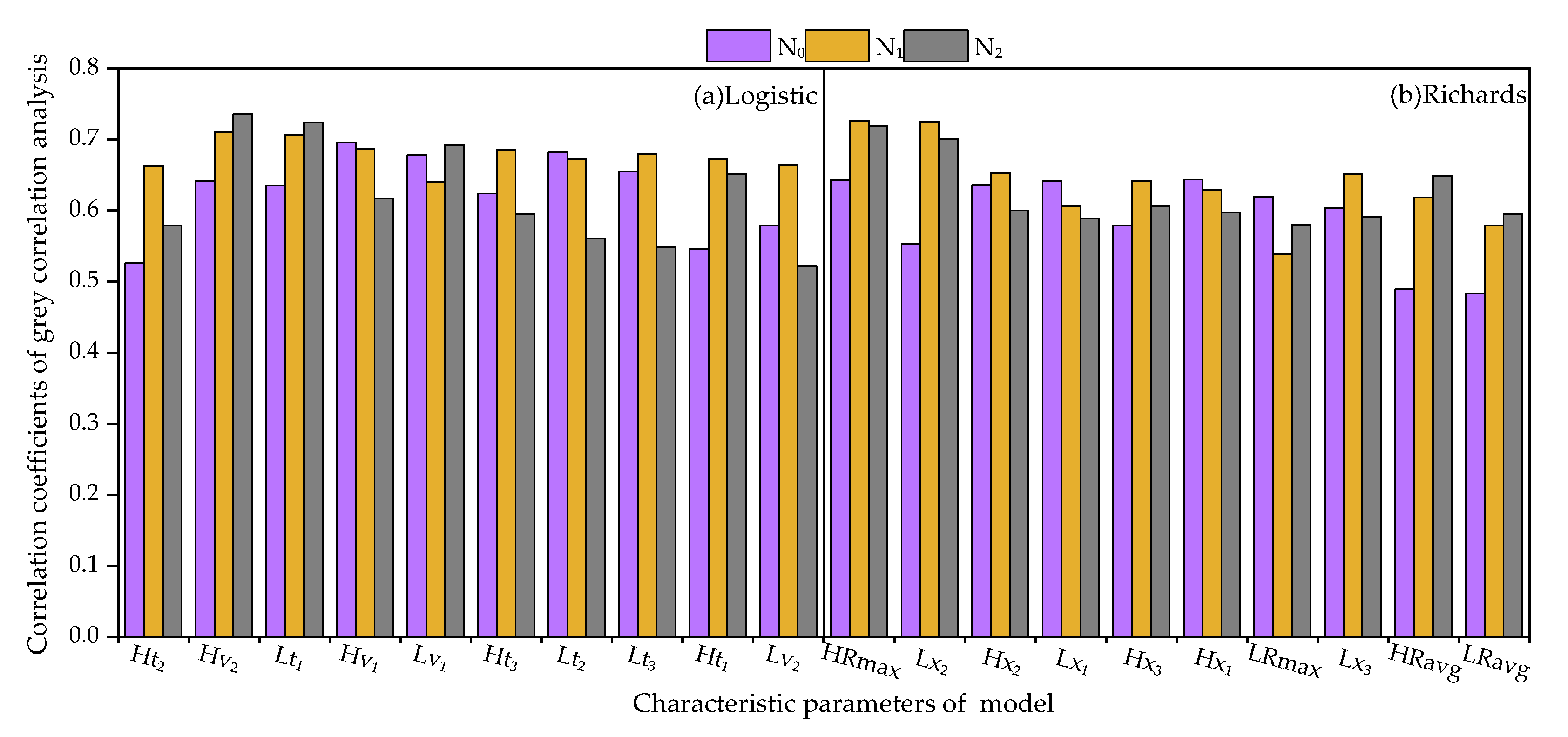
3.6. Grey Correlation Analysis
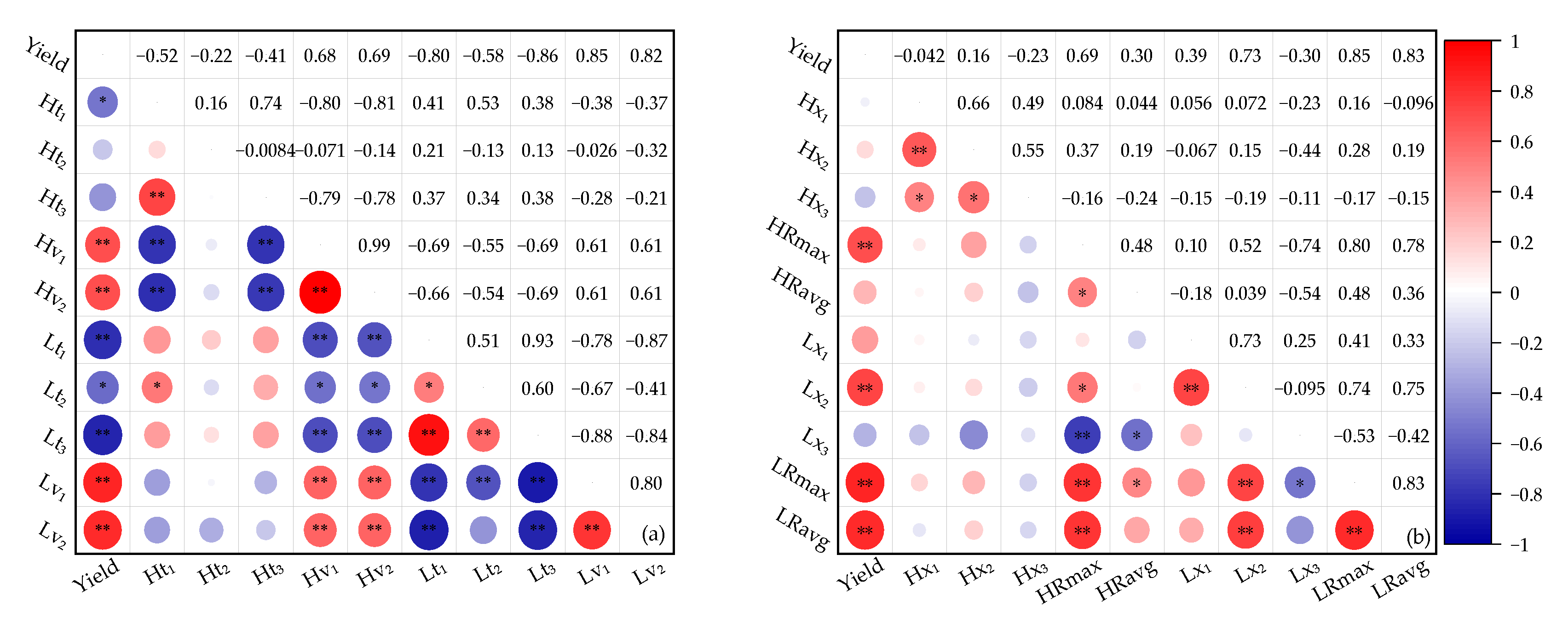
3.7. Relationship between Growth Characteristic Parameters and Yield of Tomato
4. Discussion
4.1. Model Construction and Analysis of Tomato Plant Height and LAI
4.2. Relationship of Model Characteristic Parameters of Plant Height and LAI of Tomato with Yield
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ma, Y.; Liu, Z.H.; Xi, B.D.; He, X.S.; Li, Q.L.; Qi, Y.J.; Jin, M.Y.; Guo, Y. Characteristics of groundwater pollution in a vegetable cultivation area of typical facility agriculture in a developed city. Ecol. Indic. 2019, 105, 709–716. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, P.J.; Wang, L.; Sun, G.Q.; Zhao, J.Y.; Zhang, H.; Du, N. The influence of facility agriculture production on phthalate esters distribution in black soils of northeast China. Sci. Total Environ. 2015, 506, 118–125. [Google Scholar] [CrossRef] [PubMed]
- Niu, W.Q.; Jia, Z.X.; Zhang, X.; Shao, H.B. Effects of soil rhizosphere aeration on the root growth and water absorption of tomato. Clean-Soil Air Water 2012, 40, 1364–1371. [Google Scholar] [CrossRef]
- Niu, W.Q.; Guo, Q.; Zhou, X.B.; Helmers, M.J. Effect of Aeration and Soil Water Redistribution on the Air Permeability under Subsurface Drip Irrigation. Soil Sci. Soc. Am. J. 2012, 76, 815–820. [Google Scholar] [CrossRef]
- Zhu, J.J.; Niu, W.Q.; Zhang, Z.H.; Siddique, K.H.; Sun, D.; Yang, R. Distinct roles for soil bacterial and fungal communities associated with the availability of carbon and phosphorus under aerated drip irrigation. Agr. Water Manag. 2022, 274, 107925. [Google Scholar] [CrossRef]
- Jiang, S.Q.; Yu, Y.N.; Gao, R.W.; Wang, H.; Zhang, J.; Li, R.; Long, X.H.; Shen, Q.R.; Chen, W.; Cai, F. High-throughput absolute quantification sequencing reveals the effect of different fertilizer applications on bacterial community in a tomato cultivated coastal saline soil. Sci. Total Environ. 2019, 687, 601–609. [Google Scholar] [CrossRef]
- Du, Y.D.; Zhang, Q.; Cui, B.J.; Sun, J.; Wang, Z.; Ma, L.H.; Niu, W.Q. Aerated irrigation improves tomato yield and nitrogen use efficiency while reducing nitrogen application rate. Agr. Water Manag. 2020, 235, 106152. [Google Scholar] [CrossRef]
- Niu, W.Q.; Zhang, E.X.; Lv, C.; Sun, J.; Dong, A.H.; Wu, M.L. Clogging characteristics of muddy drip irrigation dripper under different aeration and particle size conditions. Trans. Chin. Soc. Agric. Mach. 2021, 52, 144–152. (In Chinese) [Google Scholar]
- Gu, X.B.; Li, Y.N.; Du, Y.D.; Yin, M.H. Ridge-furrow rainwater harvesting with supplemental irrigation to improve seed yield and water use efficiency of winter oilseed rape (Brassica napus L.). J. Interg. Agr. 2017, 16, 1162–1172. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Y.P.; Bastida, F.; Zhou, B.; Sun, Y.F.; Gu, T.; Li, S.Q.; Li, Y.K. Soil fertility and crop production are fostered by micro-nano bubble irrigation with associated changes in soil bacterial community. Soil Biol. Biochem. 2020, 141, 107663. [Google Scholar] [CrossRef]
- Lei, H.J.; Xiao, Z.Y.; Zhang, Z.H.; Jin, C.C.; Pan, H.W.; Sun, K.P.; Xi, H.P. Effects of oxygen and nitrogen coupled irrigation on soil fertility and bacterial community under greenhouse pepper cropping system. Trans. Chin. Soc. Agric. Eng. 2021, 37, 158–166. (In Chinese) [Google Scholar]
- Wang, R.; Sun, Z.; Yang, D.; Ma, L. Simulating cucumber plant heights using optimized growth functions driven by water and accumulated temperature in a solar greenhouse. Agr. Water Manag. 2022, 259, 107170. [Google Scholar] [CrossRef]
- Jo, W.J.; Shin, J.H. Effect of leaf-area management on tomato plant growth in greenhouses. Hortic. Environ. Biotechnol. 2020, 61, 981–988. [Google Scholar] [CrossRef]
- Shabani, A.; Sepaskhah, A.; Kamgar-Haghighi, A.A. Estimation of yield and dry matter of rapeseed using Logistic model under water, salinity and deficit irrigation. Arch. Agron. Soil Sci. 2014, 60, 951–969. [Google Scholar] [CrossRef]
- Ding, D.Y.; Feng, H.; Zhao, Y.; Robert, L.H.; Yan, H.M.; Chen, H.X.; Hou, H.J.; Chu, X.S.; Liu, J.C.; Wang, N.J.; et al. Effects of continuous plastic mulching on crop growth in a winter wheat-summer maize rotation system on the Loess Plateau of China. Agric. For. Meteorol. 2019, 271, 385–397. [Google Scholar] [CrossRef]
- Li, G.Q.; Tang, L.; Zhang, W.Y.; Cao, W.X.; Zhu, Y. Dynamic analysis on response of dry matter accumulation and partitioning to nitrogen fertilizer in wheat cultivars with different plant types. Acta Agron. Sin. 2009, 35, 2258–2265. (In Chinese) [Google Scholar] [CrossRef]
- Fang, S.L.; Kuo, Y.H.; Kang, L.; Chen, C.C.; Hsieh, C.Y.; Yao, M.H.; Kuo, B.J. Article using sigmoid growth models to simulate greenhouse tomato growth and development. Horticulturae 2022, 8, 1021. [Google Scholar] [CrossRef]
- Archontoulis, S.A.; Miguez, F.E. Nonlinear regression models and applications in agricultural research. Agron. J. 2015, 107, 786–798. [Google Scholar] [CrossRef] [Green Version]
- Miguez, F.E.; Zhu, X.; Humphries, S.; Bollero, G.A.; Long, S.P. A semimechanistic model predicting growth and production of the bioenergy crop Miscanthus × giganteus: Description, parameterization and validation. GCB Bioenergy 2009, 1, 282–296. [Google Scholar] [CrossRef]
- Mahbod, M.; Sepaskhah, A.R.; Zand-Parsa, S. Estimation of yield and dry matter of winter wheat using logistic model under different irrigation water regimes and nitrogen application rates. Arch. Agron. Soil Sci. 2014, 60, 1661–1676. [Google Scholar] [CrossRef]
- Royo, C.; Blanco, R. Growth analysis of five spring and five winter triticale genotypes. Agron. J. 1999, 91, 305–311. [Google Scholar] [CrossRef]
- Richards, F. A flexible growth function for empirical use. J. Exp. Bot. 1959, 10, 290–301. [Google Scholar] [CrossRef]
- Wu, Y.; Yan, S.; Fan, J.; Zhang, F.; Xiang, Y.; Zheng, J.; Guo, J. Responses of growth, fruit yield, quality and water productivity of greenhouse tomato to deficit drip irrigation. Sci. Hortic. 2021, 275, 109710. [Google Scholar] [CrossRef]
- Hsieh, C.Y.; Fang, S.L.; Wu, Y.F.; Chu, Y.C.; Kuo, B.J. Using Sigmoid Growth Curves to Establish Growth Models of Tomato and Eggplant Stems Suitable for Grafting in Subtropical Countries. Horticulturae 2021, 7, 537. [Google Scholar] [CrossRef]
- Diel, M.I.; Lúcio, A.D.C.; Valera, O.V.S.; Sari, B.G.; Olivoto, T.; Pinheiro, M.V.M.; Melo, P.J.d.; Tartaglia, F.d.L.; Schmidt, D. Production of biquinho pepper in different growing seasons characterized by the logistic model and its critical points. Cienc. Rural. 2020, 50. [Google Scholar] [CrossRef] [Green Version]
- Lucio, A.D.; Nunes, L.F.; Rego, F. Nonlinear models to describe production of fruit in Cucurbita pepo and Capiscum annuum. Sci. Hortic. 2015, 193, 286–293. [Google Scholar] [CrossRef]
- Gong, X.W.; Qiu, R.J.; Sun, J.S.; Ge, J.K.; Li, Y.B.; Wang, S.S. Evapotranspiration and crop coefficient of tomato grown in a solar greenhouse under full and deficit irrigation. Agric. Water Manag. 2020, 235, 106154. [Google Scholar] [CrossRef]
- Gu, X.B.; Li, Y.N.; Du, Y.D. Effects of ridge-furrow film mulching and nitrogen fertilization on growth, seed yield and water productivity of winter oilseed rape (Brassica napus L.) in Northwestern China. Agric. Water Manag. 2018, 200, 60–70. [Google Scholar] [CrossRef]
- Adams, S.; Cockshull, K.; Cave, C. Effect of temperature on the growth and development of tomato fruits. Ann. Bot. 2001, 88, 869–877. [Google Scholar] [CrossRef] [Green Version]
- Jia, H.; Wang, Z.; Zhang, J.; Li, W.; Ren, Z.; Jia, Z.; Wang, Q. Effects of biodegradable mulch on soil water and heat conditions, yield and quality of processing tomatoes by drip irrigation. J. Arid Land. 2020, 12, 819–836. [Google Scholar] [CrossRef]
- Rosa, R.D.; Paredes, P.; Rodrigues, G.C.; Alves, I.; Fernando, R.M.; Pereira, L.S.; Allen, R.G. Implementing the dual crop coefficient approach in interactive software. 1. Background and computational strategy. Agric. Water Manag. 2012, 103, 8–24. [Google Scholar] [CrossRef]
- Bannayan, M.; Hoogenboom, G. Using pattern recognition for estimating cultivar coefficients of a crop simulation model. Field Crop. Res. 2009, 111, 290–302. [Google Scholar] [CrossRef]
- Qiu, R.J.; Du, T.S.; Kang, S.Z.; Chen, R.Q.; Wu, L.S. Assessing the SIMDualKc model for estimating evapotranspiration of hot pepper grown in a solar greenhouse in Northwest China. Agr. Syst. 2015, 138, 1–9. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, L.; Bai, Y.L.; Lu, Y.L.; Ni, L.; Wang, Y.H.; Xu, M.Z. Quantitative relationship between effective accumulated temperature and plant height & leaf area index of summer maize under different nitrogen, phosphorus and potassium levels. Sci. Agric. Sin. 2021, 54, 4761–4777. (In Chinese) [Google Scholar]
- Ben-Noah, I.; Nitsan, I.; Cohen, B.; Kaplan, G.; Friedman, S.P. Soil aeration using air injection in a citrus orchard with shallow groundwater. Agr. Water Manag. 2021, 245, 106664. [Google Scholar] [CrossRef]
- Ouyang, Z.; Tian, J.; Yan, X.; Shen, H. Effects of different concentrations of dissolved oxygen or temperatures on the growth, photosynthesis, yield and quality of lettuce. Agr. Water Manag. 2020, 228, 105896. [Google Scholar] [CrossRef]
- Wei, C.L.; Zhu, Y.; Zhang, J.Z.; Wang, Z.H. Evaluation of suitable mixture of water and air for processing tomato in drip irrigation in Xinjiang Oasis. Sustainability 2021, 13, 7845. [Google Scholar] [CrossRef]
- Li, Y.; Niu, W.Q.; Dyck, M.; Wang, J.W.; Zou, X.Y. Yields and nutritional of greenhouse tomato in response to different soil aeration volume at two depths of subsurface drip irrigation. Sci. Rep. 2016, 6, 39307. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Guo, J.P.; Song, Y.L. Optimizing parameters of a non-linear accumulated temperature model and method to calculate linear accumulated temperature for spring maize in Northeast China. Theor. Appl. Climatol. 2020, 141, 1629–1644. [Google Scholar] [CrossRef]
- Jiao, X.; Zhang, H.C.; Zheng, J.Q.; Yin, Y.; Wang, G.S.; Chen, Y.; Yu, J.; Ge, Y.F. Comparative analysis of nonlinear growth curve models for Arabidopsis thaliana rosette leaves. Acta Physiol. Plant. 2018, 40, 114. [Google Scholar] [CrossRef]
- Liu, Y.; Su, L.; Wang, Q.; Zhang, J.; Shan, Y.; Deng, M. Comprehensive and quantitative analysis of growth characteristics of winter wheat in China based on growing degree days. Adv. Agron. 2020, 159, 237–273. [Google Scholar]
- Hu, L.Y.; Ding, Y.F. Crop Cultivation; Higher Education Press: Beijing, China, 2008; pp. 23–26. (In Chinese) [Google Scholar]
- Li, Z.P.; Song, M.D.; Feng, H. Dynamic characteristics of leaf area index and plant height of winter wheat influenced by irrigation and nitrogen coupling and their relationships with yield. Trans. Chin. Soc. Agric. Eng. 2017, 33, 195–202. (In Chinese) [Google Scholar]
- Xiao, Z.Y.; Lei, H.J.; Zhang, Z.H.; Zhang, Q.; Jin, C.C.; Sun, K.P. Modelling Growth and Yield of Aerated Pepper by the Logistic Model. J. Irrig. Drain. 2022, 41, 16–23. (In Chinese) [Google Scholar]
- Huang, J.X.; Tian, L.Y.; Liang, S.L.; Ma, H.Y.; Becker-Reshef, I.; Huang, Y.B.; Su, W.; Zhang, X.D.; Zhu, D.H.; Wu, W.B. Improving winter wheat yield estimation by assimilation of the leaf area index from Landsat TM and MODIS data into the WOFOST model. Agric. For. Meteorol. 2015, 204, 106–121. [Google Scholar] [CrossRef]
- Song, M.D.; Li, Z.P.; Feng, H. Effects of irrigation and nitrogen regimes on dry matter dynamic accumulation and yield of winter wheat. Trans. Chin. Soc. Agric. Eng. 2016, 32, 119–126. (In Chinese) [Google Scholar]
- Wang, X.X.; Wang, Q.J.; Fan, J.; Su, L.J.; Shen, X.L. Logistic model analysis of winter wheat growth on China’s Loess Plateau. Can. J. Plant Sci. 2014, 94, 1471–1479. [Google Scholar]
- Chen, Y.; Xu, M.Z.; Wang, Y.H.; Bai, Y.L.; Lu, Y.L.; Wang, L. Quantitative Study on Effective Accumulated Temperature and Dry Matter and Nitrogen Accumulation of Summer Maize Under Different Nitrogen Supply Levels. Sci. Agric. Sin. 2022, 55, 2973–2987. (In Chinese) [Google Scholar]

| Index | Treatments | Parameters of Logistic Model | R2 | Parameters of Richards Model | R2 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| a | b | k | A | B | C | D | ||||
| Plant height | N0C | 127.37 ± 2.77 | 29.89 ± 2.28 | 0.007 ± 0.001 | 0.989 ** | 120.86 ± 2.74 | 11.46 ± 1.70 | 0.018 ± 0.001 | 4.54 ± 0.15 | 0.997 ** |
| N0A | 128.00 ± 2.62 | 34.62 ± 2.09 | 0.008 ± 0.001 | 0.990 ** | 122.08 ± 1.98 | 10.80 ± 1.16 | 0.017 ± 0.001 | 4.08 ± 0.14 | 0.997 ** | |
| N1C | 132.11 ± 3.59 | 27.05 ± 2.20 | 0.007 ± 0.001 | 0.994 ** | 126.90 ± 1.68 | 9.04 ± 1.34 | 0.015 ± 0.001 | 3.61 ± 0.12 | 0.998 ** | |
| N1A | 139.31 ± 3.22 | 27.21 ± 2.79 | 0.007 ± 0.001 | 0.987 ** | 132.14 ± 2.10 | 13.93 ± 1.48 | 0.021 ± 0.001 | 5.85 ± 0.17 | 0.996 ** | |
| N2C | 135.67 ± 2.25 | 53.49 ± 2.11 | 0.009 ± 0.001 | 0.988 ** | 130.35 ± 2.51 | 11.98 ± 1.37 | 0.019 ± 0.001 | 4.16 ± 0.16 | 0.997 ** | |
| N2A | 139.51 ± 2.45 | 46.11 ± 2.88 | 0.009 ± 0.001 | 0.992 ** | 134.67 ± 2.06 | 11.66 ± 1.25 | 0.019 ± 0.001 | 4.23 ± 0.16 | 0.999 ** | |
| Coefficient of variation, CV | 0.04 | 0.30 | 0.13 | 0.04 | 0.14 | 0.11 | 0.17 | |||
| LAI | N0C | 3.26 ± 0.18 | 78.26 ± 2.01 | 0.008 ± 0.001 | 0.998 ** | 3.24 ± 0.11 | 4.77 ± 0.15 | 0.009 ± 0.001 | 1.14 ± 0.17 | 0.998 ** |
| N0A | 3.41 ± 0.12 | 77.73 ± 2.08 | 0.008 ± 0.001 | 0.997 ** | 3.35 ± 0.13 | 6.26 ± 0.17 | 0.011 ± 0.001 | 1.65 ± 0.09 | 0.998 ** | |
| N1C | 3.58 ± 0.19 | 102.44 ± 1.75 | 0.009 ± 0.001 | 0.998 ** | 3.55 ± 0.11 | 5.80 ± 0.14 | 0.010 ± 0.001 | 1.39 ± 0.10 | 0.999 ** | |
| N1A | 3.89 ± 0.21 | 146.26 ± 1.56 | 0.010 ± 0.001 | 0.996 ** | 3.81 ± 0.10 | 9.24 ± 0.15 | 0.015 ± 0.001 | 2.40 ± 0.11 | 0.998 ** | |
| N2C | 3.68 ± 0.19 | 138.11 ± 2.01 | 0.010 ± 0.001 | 0.996 ** | 3.63 ± 0.08 | 7.11 ± 0.15 | 0.013 ± 0.001 | 1.71 ± 0.13 | 0.997 ** | |
| N2A | 4.05 ± 0.21 | 183.77 ± 3.59 | 0.011 ± 0.001 | 0.993 ** | 3.94 ± 0.14 | 12.93 ± 0.68 | 0.021 ± 0.001 | 3.48 ± 0.12 | 0.997 ** | |
| Coefficient of variation, CV | 0.08 | 0.35 | 0.13 | 0.07 | 0.39 | 0.33 | 0.44 | |||
| Treatments | Characteristic Parameters of Logistic Model | Characteristic Parameters of Richards Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Ht1 | Ht2 | Ht3 | Hv1 | Hv2 | Hx1 | Hx2 | Hx3 | HRmax | HRavg | |
| (°C d) | (cm (°C d)−1) | (°C d) | (cm (°C d)−1) | |||||||
| N0C | 485.4 ± 12.0 a | 297.2 ± 21.2 a | 637.5 ± 11.5 ab | 0.223 ± 0.01 d | 0.195 ± 0.01 d | 552.6 ± 12.6 ab | 441.4 ± 11.7 b | 663.9 ± 13.4 ab | 0.269 ± 0.01 c | 0.166 ± 0.02 c |
| N0A | 443.1 ± 14.5 bc | 278.4 ± 11.7 a | 607.7 ± 21.7 bc | 0.256 ± 0.01 b | 0.225 ± 0.01 b | 542.3 ± 10.6 ab | 438.7 ± 7.4 b | 666.5 ± 10.7 ab | 0.274 ± 0.01 c | 0.171 ± 0.02 bc |
| N1C | 471.1 ± 21.1 ab | 283.0 ± 12.3 a | 659.2 ± 14.9 a | 0.231 ± 0.01 cd | 0.203 ± 0.01 cd | 517.1 ± 10.9 c | 392.8 ± 8.0 b | 641.4 ± 17.1 b | 0.270 ± 0.01 c | 0.170 ± 0.02 bc |
| N1A | 471.9 ± 20.9 ab | 283.8 ± 9.6 a | 660.1 ± 18.2 a | 0.244 ± 0.01 bc | 0.214 ± 0.01 bc | 579.2 ± 14.5 a | 476.0 ± 9.2 a | 682.4 ± 14.3 a | 0.292 ± 0.01 b | 0.177 ± 0.02 abc |
| N2C | 442.2 ± 17.1 bc | 295.8 ± 16.2 a | 588.5 ± 17.2 cd | 0.305 ± 0.02 a | 0.268 ± 0.01 a | 555.5 ± 9.4 ab | 453.0 ± 13.4 b | 658.1 ± 14.5 ab | 0.324 ± 0.01 a | 0.201 ± 0.02 ab |
| N2A | 425.7 ± 16.4 c | 279.3 ± 14.1 a | 572.0 ± 17.0 d | 0.314 ± 0.01 a | 0.275 ± 0.01 a | 537.8 ± 12.1 bc | 434.7 ± 12.0 b | 640.9 ± 14.8 b | 0.331 ± 0.01 a | 0.205 ± 0.02 a |
| N | * | ns | ** | ** | ** | ** | ns | ns | ns | ** |
| I | * | ns | ns | * | * | * | ns | ns | ** | ns |
| N × I | ns | ns | ns | ns | ns | ns | ** | * | ** | ns |
| Treatments | Characteristic Parameters of Logistic Model | Characteristic Parameters of Richards Model | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Lt1 | Lt2 | Lt3 | Lv1 | Lv2 | Lx1 | Lx2 | Lx3 | LRmax | LRavg | |
| (°C d) | (cm2 cm−2 °C −1 d−1) | (°C d) | (cm2 cm−2 °C −1 d−1) | |||||||
| N0C | 545.0 ± 14.0 a | 380.4 ± 8.4 a | 709.6 ± 10.6 a | 0.007 ± 0.001 c | 0.006 ± 0.001 d | 515.4 ± 15.3 c | 364.7 ± 13.8 c | 666.2 ± 11.0 ab | 0.007 ± 0.001 c | 0.005 ± 0.001 c |
| N0A | 544.2 ± 14.6 a | 379.5 ± 14.8 a | 708.8 ± 15.3 a | 0.007 ± 0.001 c | 0.006 ± 0.001 d | 523.6 ± 13.9 bc | 388.4 ± 11.8 bc | 658.8 ± 13.0 b | 0.008 ± 0.001 c | 0.005 ± 0.001 c |
| N1C | 514.4 ± 14.9 b | 368.0 ± 14.1 ab | 660.7 ± 16.3 b | 0.008 ± 0.001 c | 0.007 ± 0.001 cd | 547.1 ± 13.4 ab | 404.8 ± 12.2 b | 689.4 ± 13.5 a | 0.008 ± 0.001 c | 0.005 ± 0.001 c |
| N1A | 498.5 ± 15.0 bc | 366.8 ± 12.0 ab | 630.2 ± 13.4 c | 0.010 ± 0.001 b | 0.009 ± 0.001 ab | 557.6 ± 13.7 a | 447.6 ± 8.7 a | 667.7 ± 11.7 ab | 0.010 ± 0.001 b | 0.006 ± 0.001 b |
| N2C | 492.8 ± 15.7 bc | 361.1 ± 11.0 ab | 624.5 ± 12.2 c | 0.009 ± 0.001 b | 0.008 ± 0.001 bc | 505.7 ± 15.0 c | 390.2 ± 12.5 bc | 621.1 ± 13.4 c | 0.010 ± 0.001 b | 0.006 ± 0.001 b |
| N2A | 474.0 ± 13.6 c | 354.3 ± 10.8 b | 593.7 ± 8.8 d | 0.011 ± 0.001 a | 0.010 ± 0.001 a | 556.3 ± 10.3 a | 468.5 ± 12.8 a | 644.1 ± 9.0 bc | 0.012 ± 0.001 a | 0.008 ± 0.001 a |
| N | ** | * | ** | ** | ** | ** | ** | ** | ** | ** |
| I | ns | ns | ** | ** | ** | ** | ** | ns | ** | ** |
| N × I | ns | ns | ns | ns | ns | * | * | * | ns | ** |
| Model | Factors | R2 | Unstandardized Coefficients, B | Standardized Coefficients, Beta | Sig. |
|---|---|---|---|---|---|
| Logistic | Constant | 0.722 | 198.77 | 0.004 | |
| Lt3 | −0.195 | −0.859 | 0.002 | ||
| Richards | Constant | 0.702 | 29.02 | 0.001 | |
| LRmax | 4610.64 | 0.848 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Z.; Lei, H.; Jin, C.; Pan, H.; Lian, Y. Relationship between the Dynamic Characteristics of Tomato Plant Height and Leaf Area Index with Yield, under Aerated Drip Irrigation and Nitrogen Application in Greenhouses. Agronomy 2023, 13, 116. https://doi.org/10.3390/agronomy13010116
Xiao Z, Lei H, Jin C, Pan H, Lian Y. Relationship between the Dynamic Characteristics of Tomato Plant Height and Leaf Area Index with Yield, under Aerated Drip Irrigation and Nitrogen Application in Greenhouses. Agronomy. 2023; 13(1):116. https://doi.org/10.3390/agronomy13010116
Chicago/Turabian StyleXiao, Zheyuan, Hongjun Lei, Cuicui Jin, Hongwei Pan, and Yingji Lian. 2023. "Relationship between the Dynamic Characteristics of Tomato Plant Height and Leaf Area Index with Yield, under Aerated Drip Irrigation and Nitrogen Application in Greenhouses" Agronomy 13, no. 1: 116. https://doi.org/10.3390/agronomy13010116
APA StyleXiao, Z., Lei, H., Jin, C., Pan, H., & Lian, Y. (2023). Relationship between the Dynamic Characteristics of Tomato Plant Height and Leaf Area Index with Yield, under Aerated Drip Irrigation and Nitrogen Application in Greenhouses. Agronomy, 13(1), 116. https://doi.org/10.3390/agronomy13010116





