The Study of Structural Optimization on Hydraulic Performance and Anti-Clogging Performance of Labyrinth Drip Irrigation Emitters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Physical Model
2.2. Mesh Classification and Numerical Simulation Methods
2.3. Hydraulic Performance and Anti-Clogging Performance
2.4. Model Test of Drip Irrigation Emitter
2.5. Statistical Analysis of Flow Channel
3. Results
3.1. Optimization of Structure Parameters of Drip Irrigation Emitter
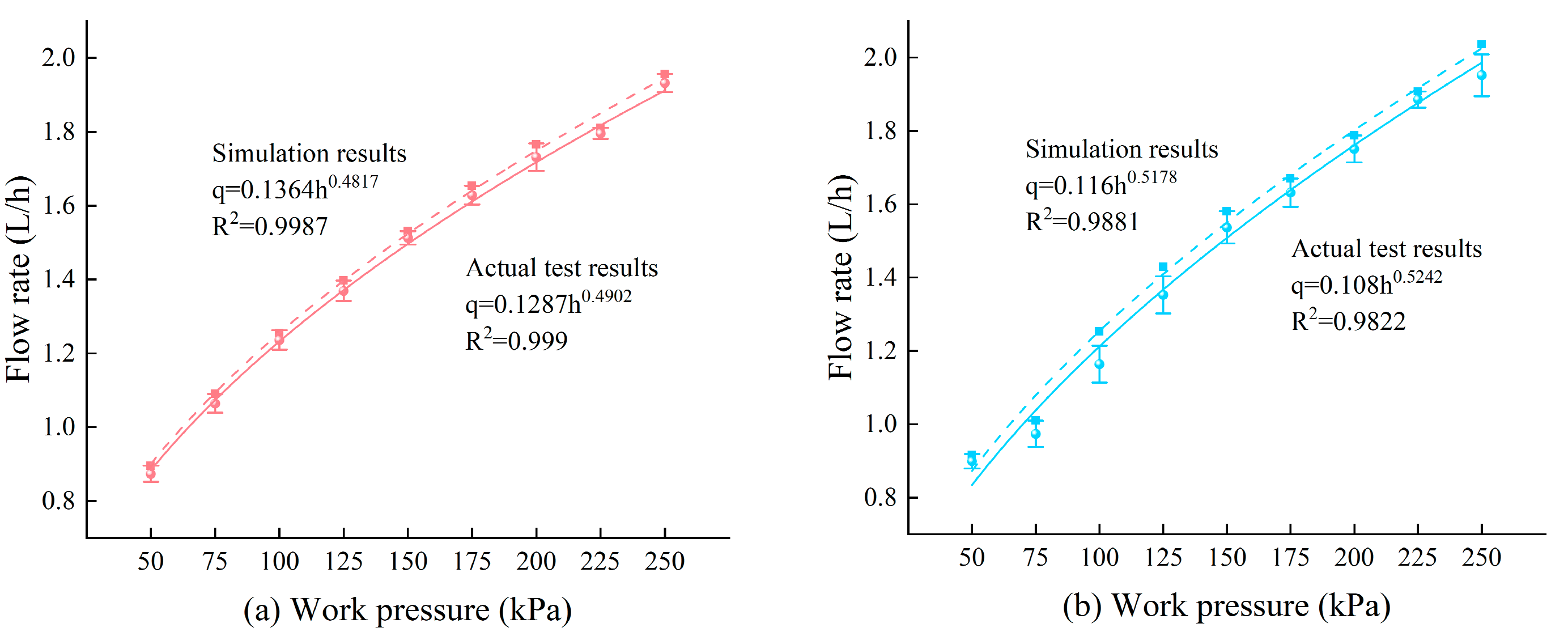
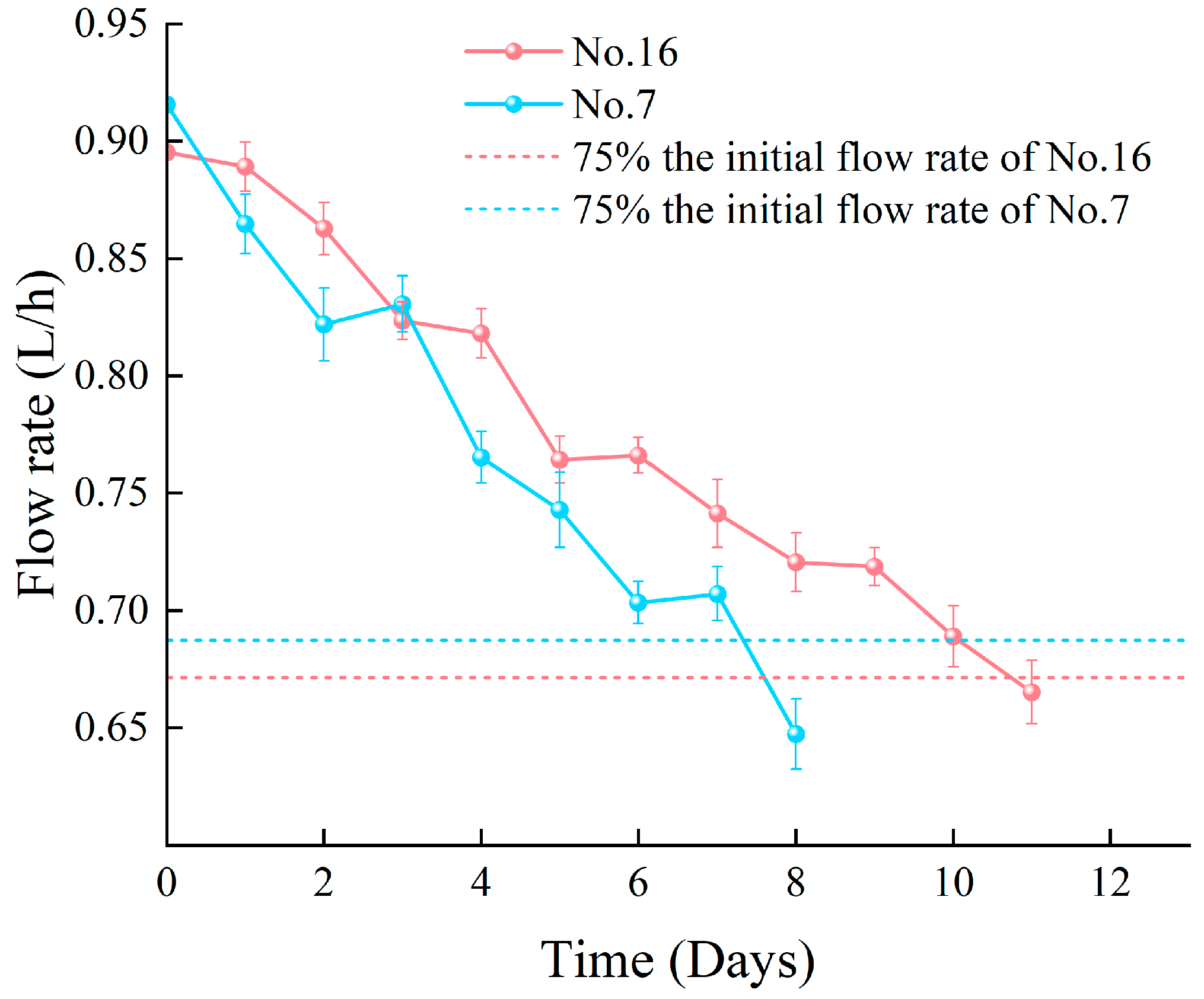
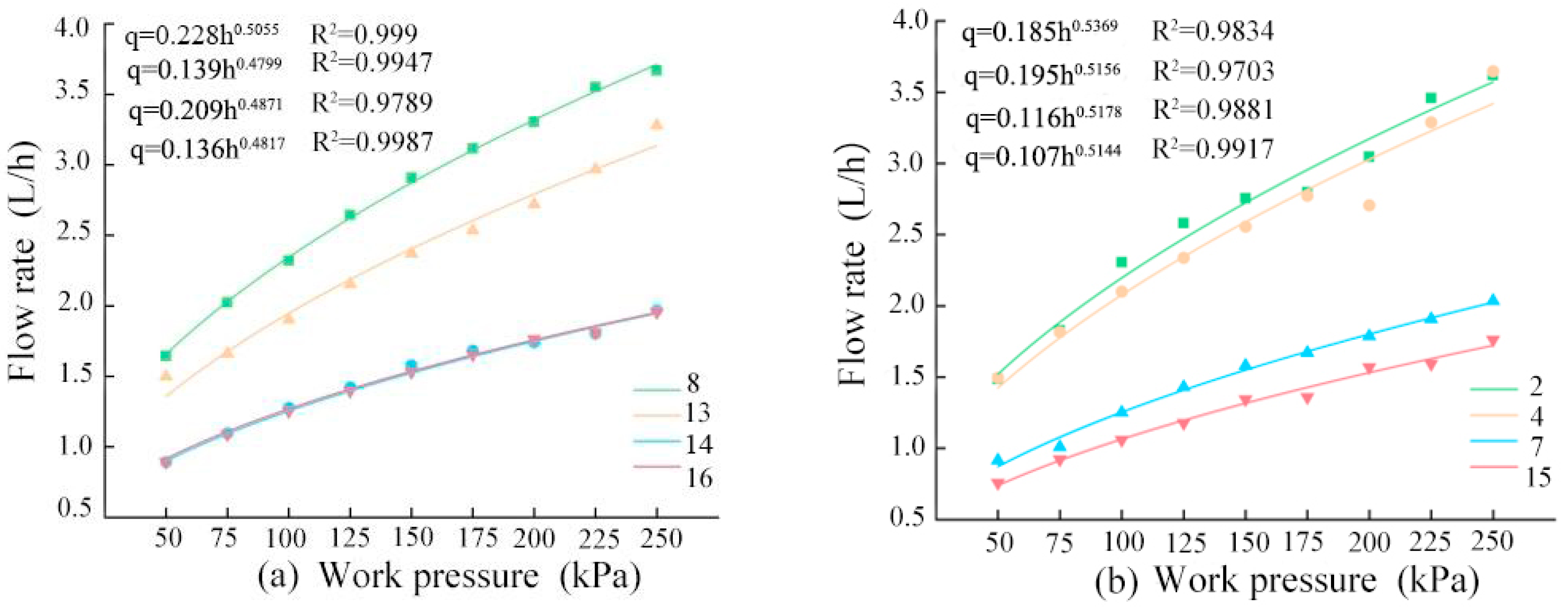
3.2. Verification of Hydraulic Performance and Anti-Clogging Performance
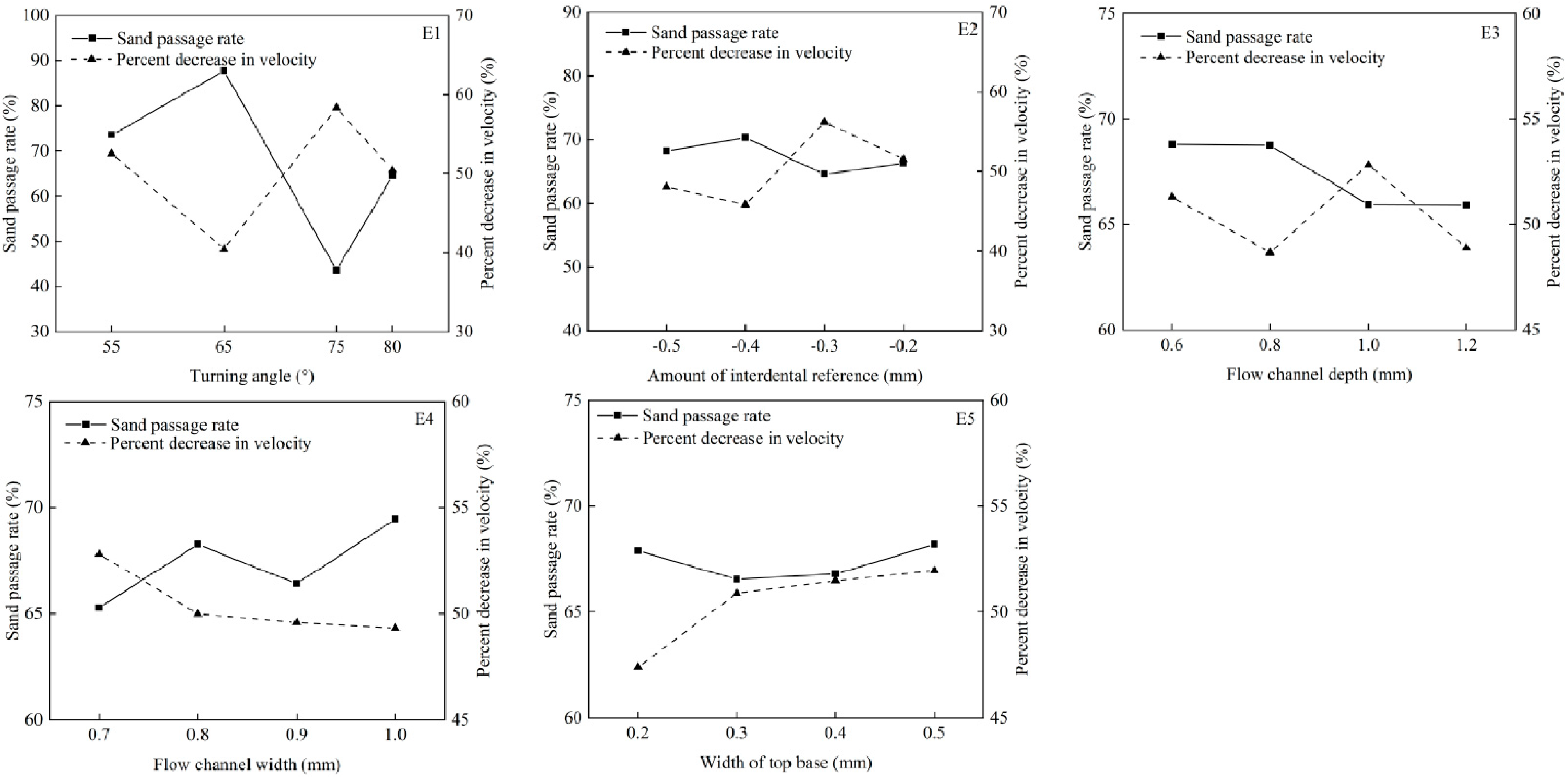
3.3. Influence of Flow Channel Structure Parameters on Sand Passage Rate and Percentage Decrease in Velocity
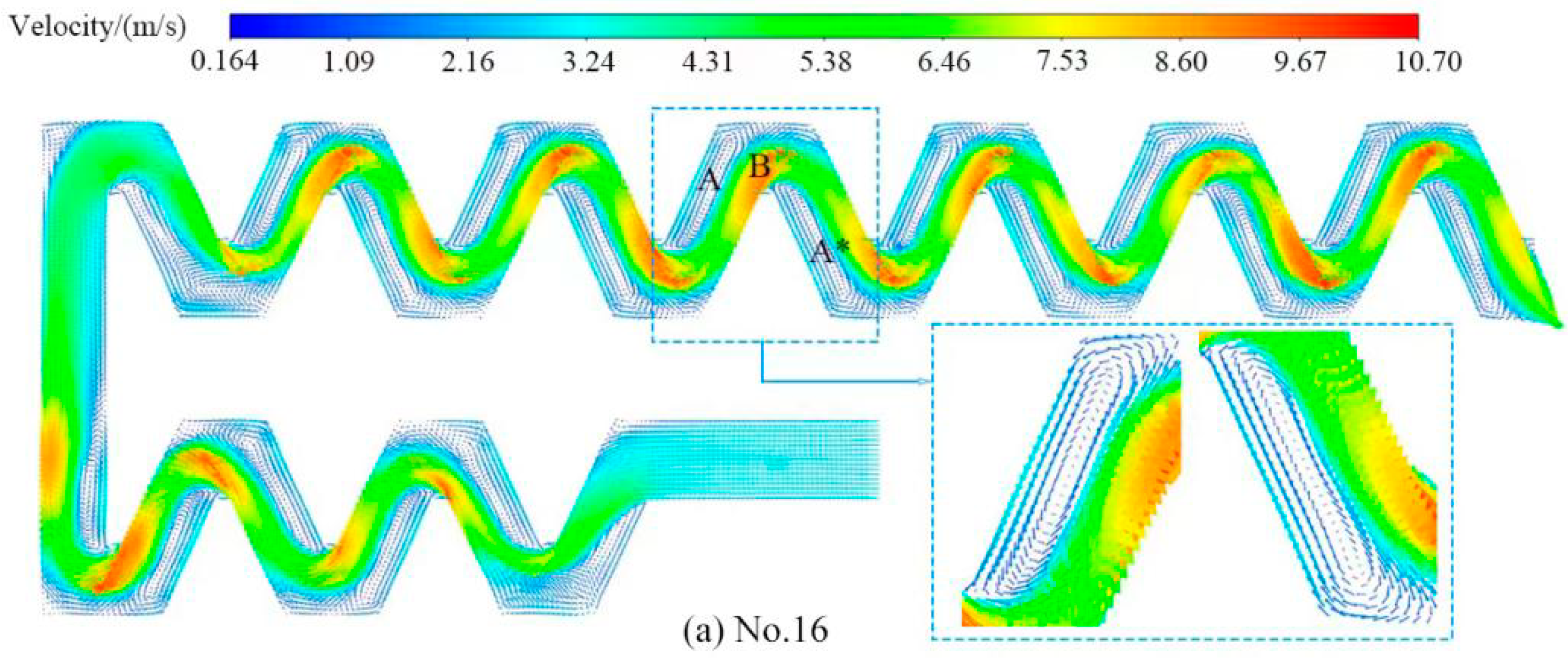
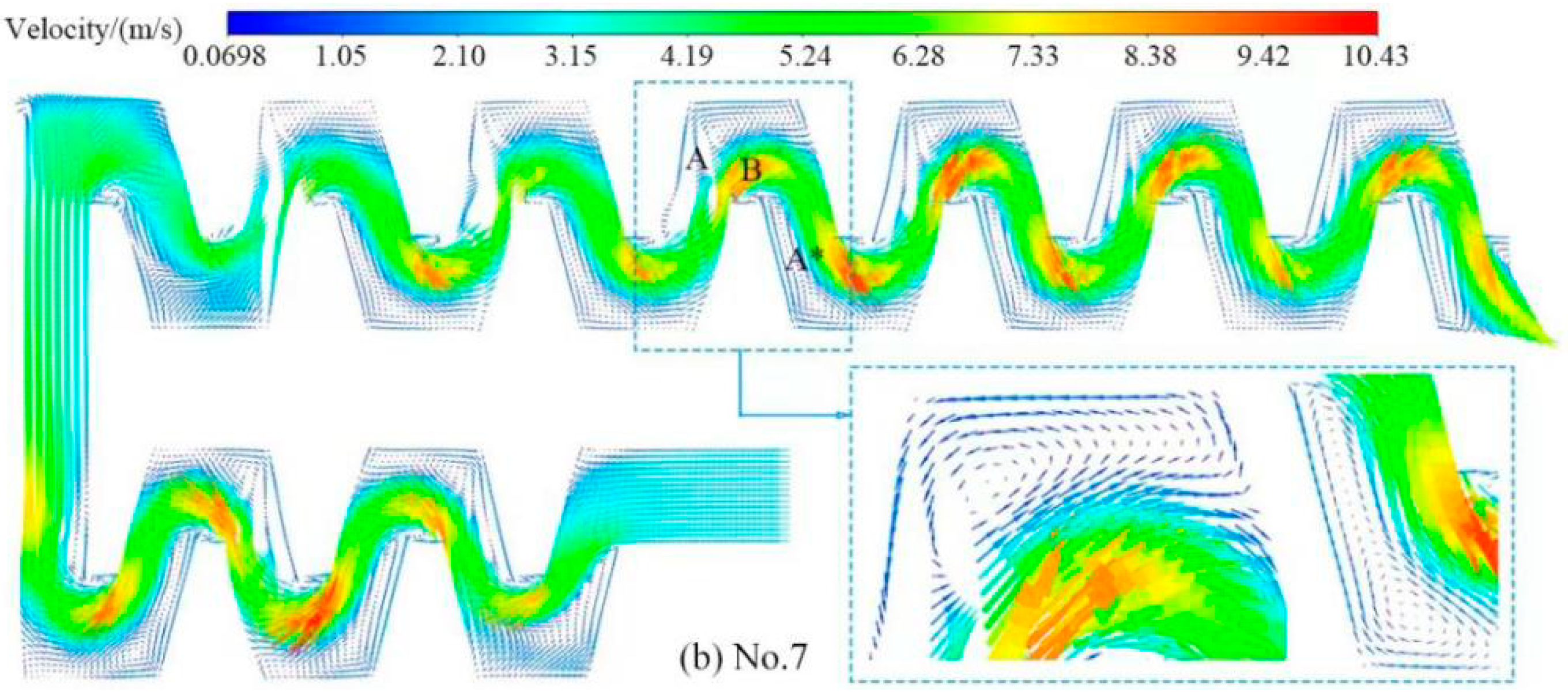
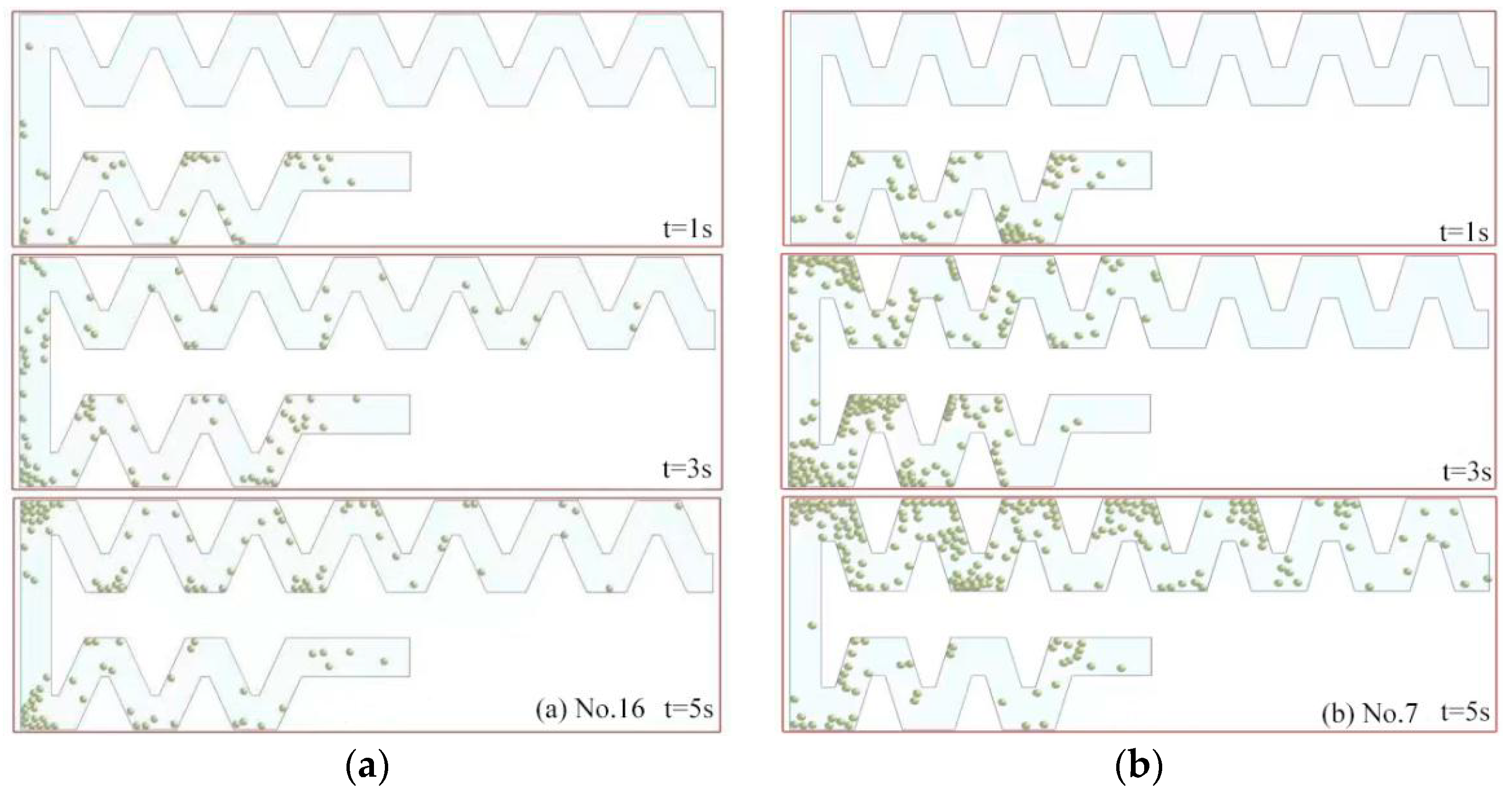
3.4. Flow Field Variations and Sand Distribution in the Flow Channel
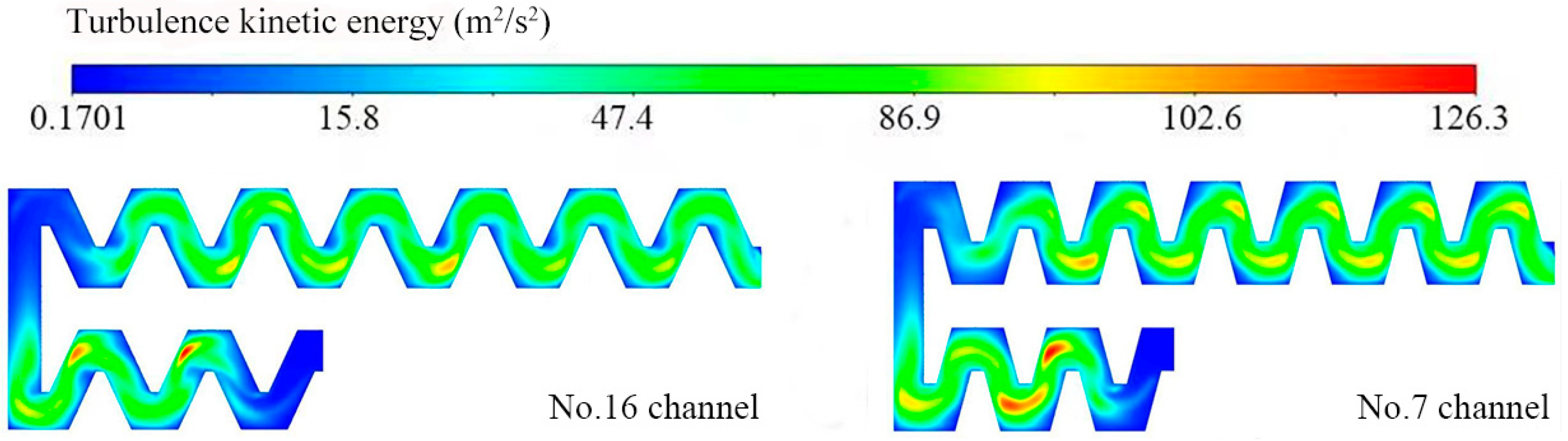
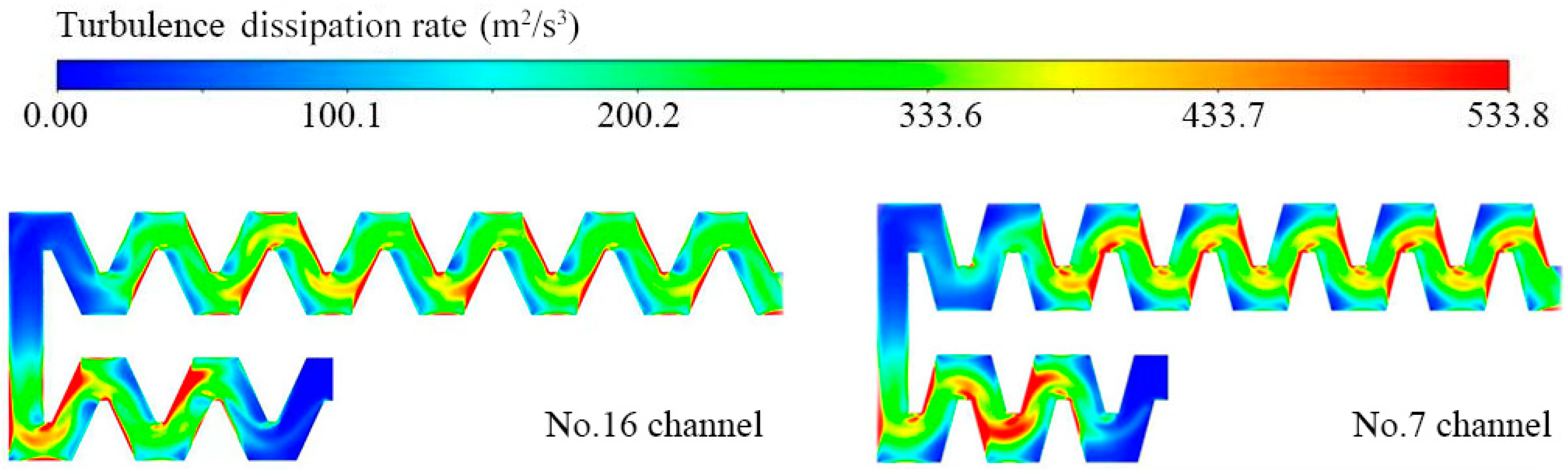
3.5. Turbulence Kinetic Energy and Turbulence Dissipation Rate in a Flow Channel
3.6. Influence of Flow Index on Sand Passage Rate
4. Discussion
5. Conclusions
- (1)
- The structural parameters of the labyrinth-type flow channel had an influence on the sand passage rate, and the order from large to small was as follows: turning angle, amount of interdental reference, flow channel depth, flow channel width, and width of the top base. The turning angle had the most significant effect on the sand passage rate and flow index, the drip irrigation emitter at a 65° turning angle had the highest sand passage rate.
- (2)
- The percentage decrease in velocity had a good negative correlation with the sand passage rate, and it can be a sideways indication of the anti-clogging performance of the drip irrigation emitter. The flow velocity, turbulence kinetic energy, and turbulence dissipation rate in the flow field had a significant impact on the movement of sand particles.
- (3)
- The hydraulic performance had a good linear relationship with the sand passage rate at the turning angle was 65°~75°. The equation for the relationship between flow index and sand passage rate was a negative correlation for drip irrigation emitter, which had better hydraulic performance and anti-clogging performance with a 65° turning angle.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, Y.K.; Zhou, B.; Yang, P. Research advances in drip irrigation emitter clogging mechanism and controlling methods. J. Hydraul. Eng. 2018, 49, 103–114. [Google Scholar] [CrossRef]
- Shi, K.; Lu, T.; Zheng, W.; Zhang, X.; Zhangzhong, L. A review of the category, mechanism, and controlling methods of chemical clogging in drip irrigation system. Agriculture 2022, 12, 202. [Google Scholar] [CrossRef]
- Yuan, W.; Wei, Z.; Chu, H.; Ma, S. Optimal design and experiment for divided-flow emitter in drip irrigation. Trans. Chin. Soc. Agric. Eng. 2014, 30, 117–124. [Google Scholar]
- Pei, Y.; Li, Y.; Liu, Y.; Zhou, B.; Shi, Z.; Jiang, Y. Eight emitters clogging characteristics and its suitability under on-site reclaimed water drip irrigation. Irrig. Sci. 2014, 32, 141–157. [Google Scholar] [CrossRef]
- Xu, T.; Zhang, L. Influence and analysis of structure design and optimization on the performance of a pit drip irrigation emitter. Irrig. Drain. 2020, 69, 633–645. [Google Scholar] [CrossRef]
- Qin, C.; Zhang, J.; Wang, Z.; Lyu, D.; Liu, N.; Xing, S.; Wang, F. Anti-Clogging Performance Optimization for Shunt-Hedging Drip Irrigation Emitters Based on Water–Sand Motion Characteristics. Water 2022, 14, 3901. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Ma, J. Influence of emitter structure on its hydraulic performance based on the vortex. Agriculture 2021, 11, 508. [Google Scholar] [CrossRef]
- Baghel, Y.K.; Kumar, J.; Patel, V.K. CFD analysis of the flow characteristics of in-line drip emitter with different labyrinth channels. J. Inst. Eng. India Ser. A 2021, 102, 111–119. [Google Scholar] [CrossRef]
- Li, G.Y.; Wang, J.D.; Alam, M.; Zhao, Y.F. Influence of geometrical parameters of labyrinth flow path of drip emitters on hydraulic and anti-clogging performance. Trans. ASABE 2006, 49, 637–643. [Google Scholar] [CrossRef]
- Zhangzhong, L.; Yang, P.; Li, Y.; Ren, S. Effects of flow path geometrical parameters on flow characteristics and hydraulic performance of drip irrigation emitters. Irrig. Drain. 2016, 65, 426–438. [Google Scholar] [CrossRef]
- Wu, D.; Li, Y.K.; Liu, H.S.; Yang, P.L.; Sun, H.S.; Liu, Y.Z. Simulation of the flow characteristics of a drip irrigation emitter with large eddy methods. Math. Comput. Model. 2013, 58, 497–506. [Google Scholar] [CrossRef]
- Zhou, B.; Li, Y.; Song, P.; Zhou, Y.; Yu, Y.; Bralts, V. Anti-clogging evaluation for drip irrigation emitters using reclaimed water. Irrig. Sci. 2017, 35, 181–192. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, W.; Tang, Y.; Lu, B. Anti-clogging performance evaluation and parameterized design of emitters with labyrinth channels. Comput. Electron. Agric. 2010, 74, 59–65. [Google Scholar] [CrossRef]
- Yu, L.; Li, N.; Liu, X.; Yang, Q.; Li, Z.; Long, J. Influence of Dentation Angle of Labyrinth Channel of Drip Emitters on Hydraulic and Anti-Clogging Performance. Irrig. Drain. 2019, 68, 256–267. [Google Scholar] [CrossRef]
- Xu, T.; Su, Y.; Su, Z.; Zhi, S.; Zheng, E.; Yan, C. Simulation of the hydraulic behavior of a bionic-structure drip irrigation emitter. Water Sav. Irrig. 2022, 10, 11. [Google Scholar] [CrossRef]
- Ma, Y.; Li, Z.; Jin, L.; Wang, C. Numerical analysis of hydraulic performance of single-tooth rectangular labyrinth emitter. Water Sav. Irrig. 2017, 20–24. [Google Scholar] [CrossRef]
- Wei, Q.; Shi, Y.; Dong, W.; Lu, G.; Huang, S. Study on hydraulic performance of drip emitters by computational fluid dynamics. Agric. Water Manag. 2006, 84, 130–136. [Google Scholar] [CrossRef]
- Li, Y.; Feng, X.; Liu, Y.; Han, X.; Liu, H.; Sun, Y.; Li, H.; Xie, Y. Research on hydraulic properties and energy dissipation mechanism of the novel water-retaining labyrinth channel emitters. Agronomy 2022, 12, 1708. [Google Scholar] [CrossRef]
- Nishimura, T.; Bian, Y.; Matsumoto, Y.; Kunitsugu, K. Fluid flow and mass transfer characteristics in a sinusoidal wavy-walled tube at moderate Reynolds numbers for steady flow. Heat Mass Transf. 2003, 39, 239–248. [Google Scholar] [CrossRef]
- Deng, J.; Han, D. Influence of Stress Relaxation on the Elastic Properties of Unconsolidated Sands. J. Jilin Univ. Earth Sci. Ed. 2011, 41, 283–291. [Google Scholar]
- Asakura, K.; Asari, T.; Nakajima, I. Simulation of solid—Liquid flows in a vertical pipe by a collision model. Powder Technol. 1977, 94, 201–206. [Google Scholar] [CrossRef]
- Tang, X.; Yu, X.; Ren, S. Solid-Liquid Two Phase Fluid Dynamics and Its Application in Hydraulic Machinery; The Yellow River Water Conservancy Press: Zhengzhou, China, 2006. [Google Scholar]
- Wang, G.; Hao, W.; Wang, J. Discrete Unit Method and Its Practice on EDEM; Northwestern Polytechnical University Press: Xi’an, China, 2010. [Google Scholar]
- Wang, F. Computational Fluid Dynamics Analysis CFD Software Principles and Applications; Tsinghua University Press: Beijing, China, 2004. [Google Scholar]
- Peng, H.; Shuqin, L.; Zeyuan, L.; Hongxu, Z.; Muhammd, T.; Ruonan, W.; Wenchao, L.; Yunkai, L. Water temperature effects on hydraulic performance of pressure-compensating emitter in a drip irrigation system. Irrig. Drain. 2021, 70, 332–341. [Google Scholar] [CrossRef]
- Xing, S.; Wang, Z.; Zhang, J.; Liu, N.; Zhou, B. Simulation and verification of hydraulic performance and energy dissipation mechanism of perforated drip irrigation emitters. Water 2021, 13, 171. [Google Scholar] [CrossRef]
- Quinino, R.C.; Reis, E.A.; Bessegato, L.F. Using the coefficient of determination R2 to test the significance of multiple linear regression. Teach. Stat. 2013, 35, 84–88. [Google Scholar] [CrossRef]
- Han, X.; Chang, L.; Wang, N.; Kong, W.; Wang, C. Effects of Meteorological Factors on Apple Yield Based on Multilinear Regression Analysis: A Case Study of Yantai Area, China. Atmosphere 2023, 14, 183. [Google Scholar] [CrossRef]
- Wei, Z.; Tang, Y.; Zhao, W.; Lu, B. Experimental study on the structure and hydraulic performance of maze runner of drip irrigation irrigator. Trans. Chin. Soc. Agric. Mach. 2005, 36, 51–55. [Google Scholar]
- Zhang, A.; Zhang, G.; Guo, H.; Chu, Y.; Han, X.; He, Q. Research advances in drip irrigation emitter clogging and anti-clogging measures. Agric. Eng. 2021, 11, 59–64. [Google Scholar]
- Sun, H.; Li, Y.; Feng, J.; Liu, H.; Liu, Y. Effects of flow path boundary optimizations on particle transport in drip irrigation emitters. Irrig. Drain. 2016, 65, 417–425. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, W.; Tang, Y.; Lu, B. Structural optimization of labyrinth-channel emitters based on hydraulic and anti-clogging performances. Irrig. Sci. 2011, 29, 351–357. [Google Scholar] [CrossRef]
- Yu, L.; Xu, X.; Yang, Q.; Wu, Y.; Bai, X. Influence of geometrical parameters of labyrinth passage of drip irrigation emitter on sand movement. Trans. CSAM 2017, 48, 255–261. [Google Scholar] [CrossRef]
- Cheng, C.; Fu, L. A scale-based study of the Reynolds number scaling for the near-wall streamwise turbulence intensity in wall turbulence. Int. J. Heat Fluid Flow 2023, 101, 109136. [Google Scholar] [CrossRef]
- Yang, B.; Wang, J.; Zhang, Y.; Wang, H.; Ma, X.; Mo, Y. Anti-clogging performance optimization for dentiform labyrinth emitters. Irrig. Sci. 2020, 38, 275–285. [Google Scholar] [CrossRef]
- Feng, J.; Li, Y.; Wang, W.; Xue, S. Effect of optimization forms of flow path on emitter hydraulic and anti-clogging performance in drip irrigation system. Irrig. Sci. 2018, 36, 37–47. [Google Scholar] [CrossRef]
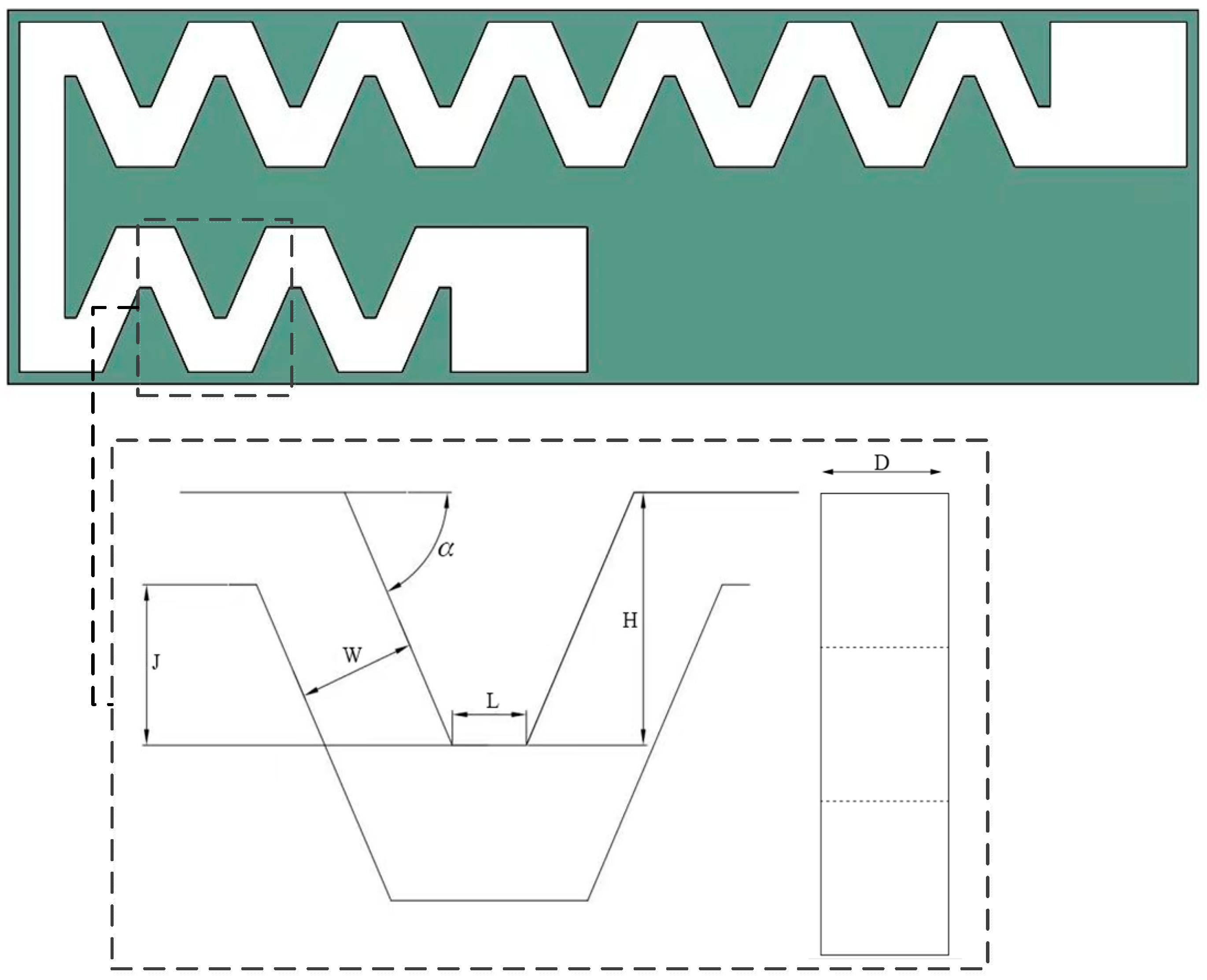

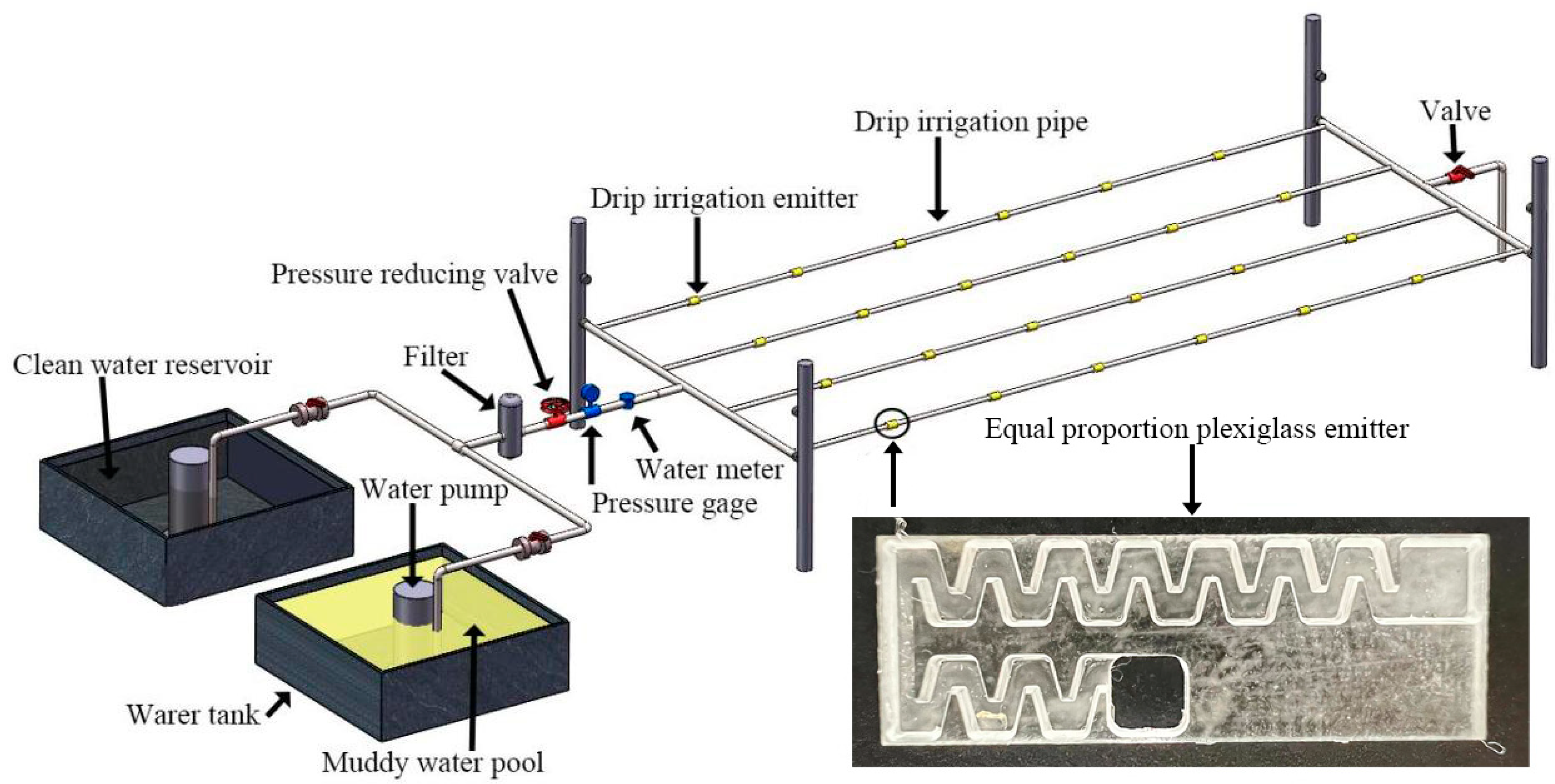
| Level | Turning Angle α/(°) | Flow Channel Width W/(mm) | Flow Channel Depth D/(mm) | Width of Top Base L/(mm) | Amount of Interdental Reference J/(mm) |
|---|---|---|---|---|---|
| 1 | 80 | 0.7 | 0.6 | 0.2 | −0.2 |
| 2 | 75 | 0.8 | 0.8 | 0.3 | −0.3 |
| 3 | 65 | 0.9 | 1.0 | 0.4 | −0.4 |
| 4 | 55 | 1.0 | 1.2 | 0.5 | −0.5 |
| Research Subjects | Parameters | Symbol | Unit | Numerical Value |
|---|---|---|---|---|
| sand particles | Density of sand particles | ρ | kg/m3 | 2500 |
| Diameter | di | μm | 100 | |
| Poisson’s ratio | V | – | 0.4 | |
| Shear modulus | E | N/m2 | 7.143 × 106 | |
| Young’s modulus | E | N/m2 | 2 × | |
| Recovery coefficient | c | – | 0.5 | |
| Rolling friction coefficient | – | 0.3 | ||
| Sliding frictioncoefficient | – | 0.01 | ||
| Initial velocity of the sand | – | m/s | 0.2 (80°, 75°), 0.3 (65°, 55°) | |
| Water | Density | ρ | kg/m3 | 998.20 |
| Viscosity | m | kg/m/s | 0.001 | |
| Inlet pressure | – | Pa | 50,000 | |
| outlet pressure | – | Pa | 0 |
| Designation | Formula | Instruction |
|---|---|---|
| Water phase continuity equation | ||
| Phase continuity equation of sand particles | ||
| Normal force between sand particles | ||
| Normal nylon resistance between sand grains | ||
| Tangential force between sand particles | ||
| Tangential nylon resistance between sand grains | ||
| Sliding friction |
| Test Serial Number | Turning Angle | Flow Channel Width | Flow Channel Depth | Width of Top Base | Amount of Interdental Reference | Average Speed of Sand Particles/(m/s) | Initial Velocity of Sand Particles/(m/s) | Percentage Decrease in Sand Velocity/% | Sand Passage Rate/% | Flow Index |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 80 | 0.9 | 0.8 | 0.5 | −0.4 | 0.04474 | 0.08104 | 44.79% | 68.79% | 0.5044 |
| 2 | 75 | 0.8 | 1.0 | 0.5 | −0.2 | 0.04055 | 0.1094 | 62.93% | 42.84% | 0.5369 |
| 3 | 80 | 0.7 | 0.6 | 0.2 | −0.2 | 0.0266 | 0.0759 | 51.78% | 63.43% | 0.5061 |
| 4 | 75 | 1.0 | 1.2 | 0.2 | −0.4 | 0.04661 | 0.08972 | 48.05% | 47.77% | 0.5156 |
| 5 | 55 | 0.9 | 1.0 | 0.2 | −0.3 | 0.06478 | 0.1501 | 56.84% | 68.92% | 0.5011 |
| 6 | 80 | 0.8 | 1.2 | 0.4 | −0.3 | 0.04353 | 0.09738 | 55.30% | 60.72% | 0.5047 |
| 7 | 75 | 0.7 | 0.8 | 0.3 | −0.3 | 0.0299 | 0.08597 | 65.22% | 39.26% | 0.5178 |
| 8 | 65 | 0.9 | 1.2 | 0.3 | −0.2 | 0.073 | 0.121 | 39.67% | 83.53% | 0.5055 |
| 9 | 55 | 0.7 | 1.2 | 0.5 | −0.5 | 0.05442 | 0.1147 | 52.55% | 71.76% | 0.4958 |
| 10 | 80 | 1.0 | 1.0 | 0.3 | −0.5 | 0.04931 | 0.09827 | 49.82% | 65.31% | 0.4941 |
| 11 | 55 | 1.0 | 0.8 | 0.4 | −0.2 | 0.028 | 0.059 | 51.84% | 75.45% | 0.4917 |
| 12 | 55 | 0.8 | 0.6 | 0.3 | −0.4 | 0.04884 | 0.09548 | 48.85% | 78.04% | 0.4924 |
| 13 | 65 | 1.0 | 0.6 | 0.5 | −0.3 | 0.054 | 0.09334 | 47.58% | 89.35% | 0.4799 |
| 14 | 65 | 0.7 | 1.0 | 0.4 | −0.4 | 0.03287 | 0.05643 | 41.73% | 86.65% | 0.4871 |
| 15 | 75 | 0.9 | 0.6 | 0.4 | −0.5 | 0.0564 | 0.1312 | 57.02% | 44.38% | 0.5144 |
| 16 | 65 | 0.8 | 0.8 | 0.2 | −0.5 | 0.03632 | 0.0541 | 32.87% | 91.48% | 0.4817 |
| Structure Parameters | Sum of Squares of Partial Variances | Degree of Freedom | F | Significance (Sand Passage Rate) | Significance (Flow Index) |
|---|---|---|---|---|---|
| turning angle | 1266.444 | 4 | 5.906 | 0.064 * | 0.074 * |
| Flow channel width | 22.984 | 4 | 0.76 | 0.785 | 0.603 |
| Flow channel depth | 25.901 | 4 | 0.085 | 0.772 | 0.398 |
| Width of top base | 0.251 | 4 | 0.01 | 0.977 | 0.841 |
| Amount of interdental reference | 26.496 | 4 | 0.087 | 0.770 | 0.210 |
| Structure Parameters | Non-Standardized Coefficient | Standardization Coefficient | Significance | Variance Expansion Coefficient |
|---|---|---|---|---|
| Constant term | 593.418 | — | 0.002 | — |
| Flow index | −1046.029 | −0.883 | 0.004 ** | 1.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, T.; Bao, S.; Li, Z.; Yu, Q.; Zheng, E. The Study of Structural Optimization on Hydraulic Performance and Anti-Clogging Performance of Labyrinth Drip Irrigation Emitters. Agronomy 2023, 13, 2496. https://doi.org/10.3390/agronomy13102496
Xu T, Bao S, Li Z, Yu Q, Zheng E. The Study of Structural Optimization on Hydraulic Performance and Anti-Clogging Performance of Labyrinth Drip Irrigation Emitters. Agronomy. 2023; 13(10):2496. https://doi.org/10.3390/agronomy13102496
Chicago/Turabian StyleXu, Tianyu, Sanlin Bao, Zonglei Li, Qiuyue Yu, and Ennan Zheng. 2023. "The Study of Structural Optimization on Hydraulic Performance and Anti-Clogging Performance of Labyrinth Drip Irrigation Emitters" Agronomy 13, no. 10: 2496. https://doi.org/10.3390/agronomy13102496
APA StyleXu, T., Bao, S., Li, Z., Yu, Q., & Zheng, E. (2023). The Study of Structural Optimization on Hydraulic Performance and Anti-Clogging Performance of Labyrinth Drip Irrigation Emitters. Agronomy, 13(10), 2496. https://doi.org/10.3390/agronomy13102496






