Estimating Chlorophyll Content, Production, and Quality of Sugar Beet under Various Nitrogen Levels Using Machine Learning Models and Novel Spectral Indices
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Site and Experimental Design
2.2. Plant Traits Measurements
2.3. Canopy Spectral Reflectance Measurements and Selection of Spectral Reflectance Indices
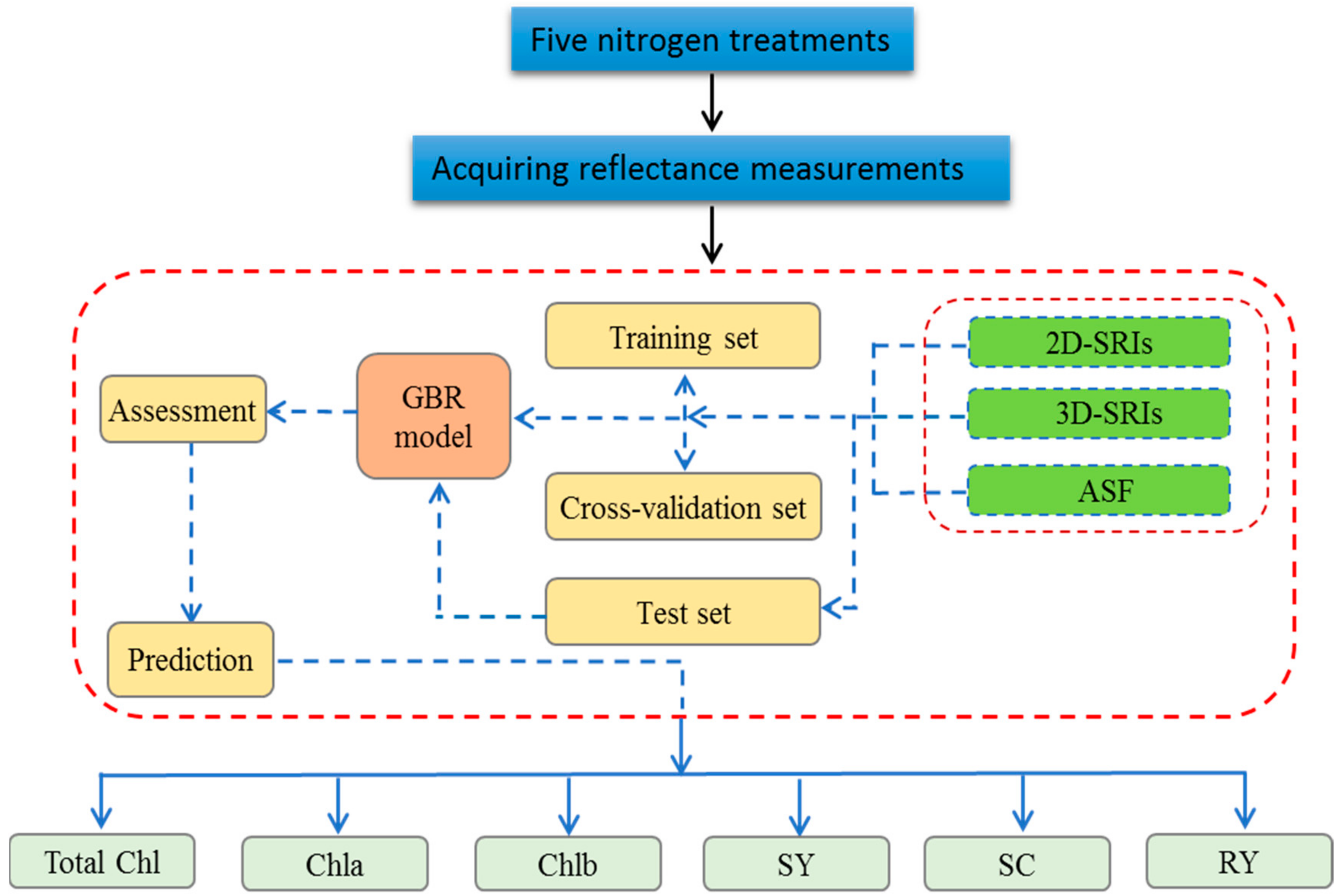
2.4. Gradient Boosting Regression (GBR)
2.5. Data Analysis Software and Datasets
2.6. Model Evaluation
2.7. Statistical Analysis
3. Results and Discussion
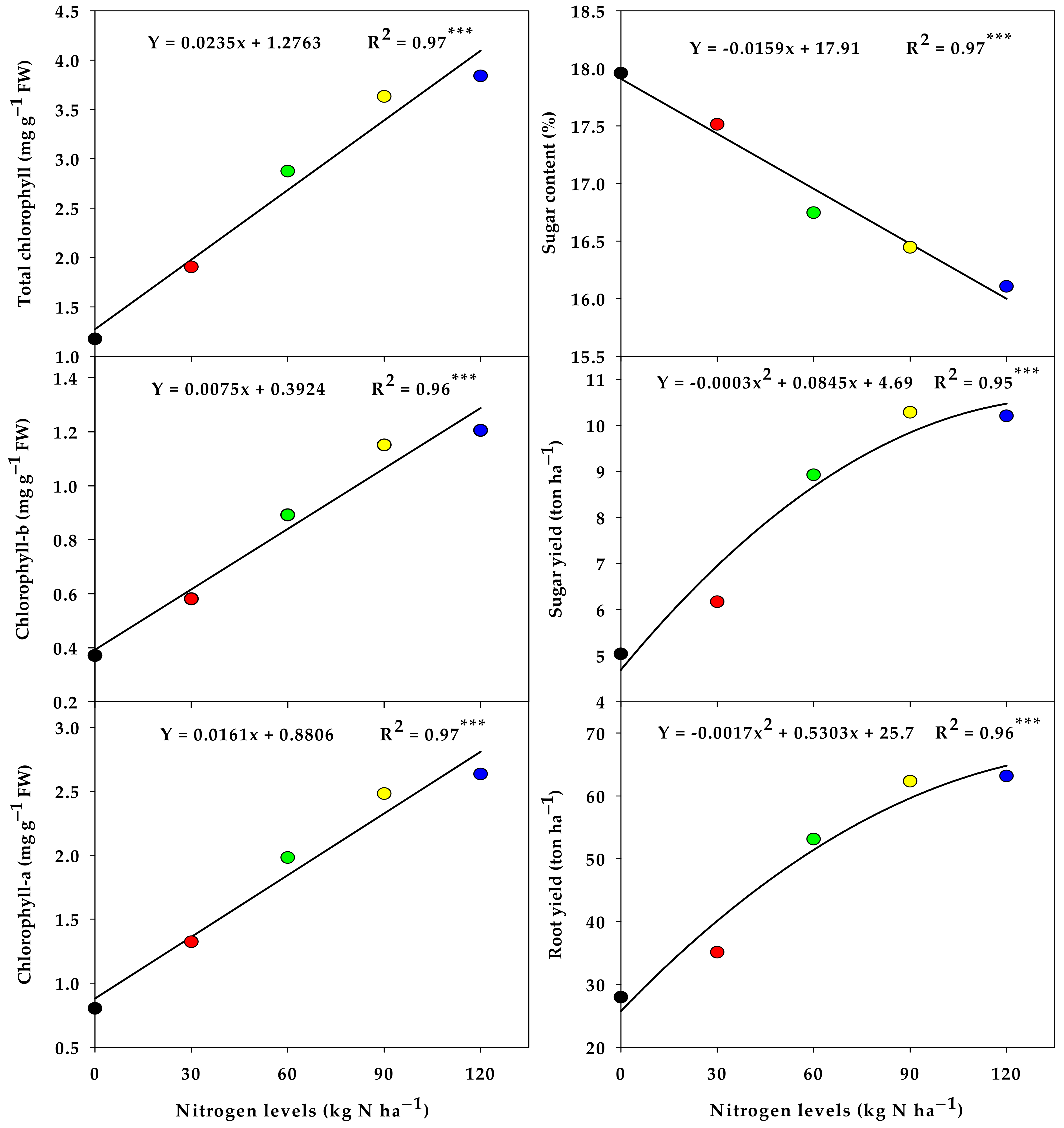
3.1. Response of Chlorophyll Content, Production, and Quality of Sugar Beet to Nitorgen Levels
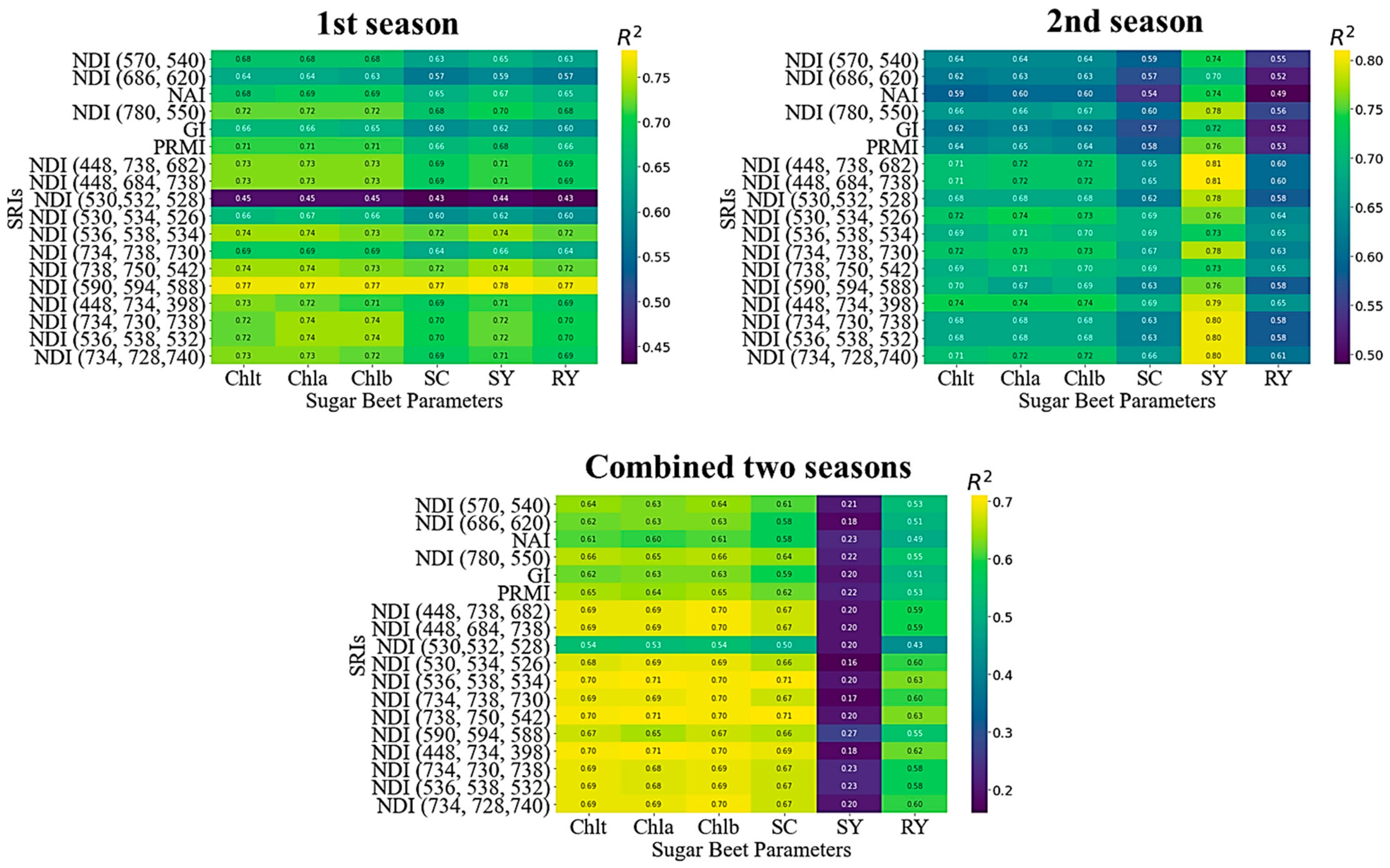
3.2. Response of Published and Newly Spectral Reflectance Indices of Sugar Beet to Different Nitrogen Levels
3.3. Potential of the Published and Newly Developed 3D-SRIs to Estimate the Sugar Beet Parameters
3.4. Performance of Gradient Boosting Regression Model for Predicting Sugar Beet Parameters
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Jaggard, K.W.; Qi, A.; Milford, G.; Clark, C.; Ober, E.; Walters, C.; Burks, E. Determining the optimal population density of sugar beet crops in England. Int. Sugar J. 2011, 113, 114–119. [Google Scholar]
- Draycott, A.P.; Christenson, D.R. Nutrients for Sugar Beet Production: Soil–Plant Relationships; CABI Publishing: Wallingford, UK, 2003; 242p. [Google Scholar]
- Steduto, P.; Hsiao, T.C.; Fereres, E.; Raes, D. Crop Yield Response to Water; FAO: Rome, Italy, 2012. [Google Scholar]
- Malnou, C.S.; Jaggard, K.W.; Sparkes, D.L. A canopy approach to nitrogen fertilizer recommendation for the sugar beet crop. Eur. J. Agron. 2006, 25, 254–263. [Google Scholar] [CrossRef]
- Malnou, C.; Jaggard, K.; Sparkes, D. Nitrogen fertilizer and the efficiency of the sugar beet crop in late summer. Eur. J. Agron. 2008, 28, 47–56. [Google Scholar] [CrossRef]
- Abd El-Lateef, E.M.; Abd El-Salam, M.S.; Elewa, T.A.; Farrag, A.A. Effect of organic manure and nitrogen level on sugar beet (Beta vulgaris Var. Saccharifera L.) yield and root nitrate content. Am. Eurasian J. Agron. 2019, 12, 1–5. [Google Scholar]
- Leilah, A.A.A.; Khan, N. Interactive Effects of Gibberellic Acid and Nitrogen Fertilization on the Growth, Yield, and Quality of Sugar Beet. Agronomy 2021, 11, 137. [Google Scholar] [CrossRef]
- Varga, I.; Lončarić, Z.; Kristek, S.; Kulundžić, A.M.; Rebekić, A.; Antunović, M. Sugar Beet Root Yield and Quality with Leaf Seasonal Dynamics in Relation to Planting Densities and Nitrogen Fertilization. Agriculture 2021, 11, 407. [Google Scholar] [CrossRef]
- Varga, I.; Jović, J.; Rastija, M.; Markulj Kulundžić, A.; Zebec, V.; Lončarić, Z.; Iljkić, D.; Antunović, M. Efficiency and Management of Nitrogen Fertilization in Sugar Beet as Spring Crop: A Review. Nitrogen 2022, 3, 170–185. [Google Scholar] [CrossRef]
- Franzen, D.W. Delineating nitrogen management zones in a sugarbeet rotation using remote sensing—A review. J. Sugar Beet Res. 2004, 41, 47–60. [Google Scholar] [CrossRef]
- Varga, I.; Lončarić, Z.; Pospišil, M.; Rastija, M.; Antunović, M. Changes of nitrate nitrogen in sugar beet petioles fresh tissue during season with regard to nitrogen fertilization and plant population. Listy Cukrov. Reparské 2020, 136, 198–204. [Google Scholar]
- Milford, G.F.J.; Pocock, T.O.; Jaggard, K.W.; Biscoe, P.V.; Armstrong, M.J.; Last, P.J.; Goodman, P.J. An analysis of leaf growth in sugar-beet. 4. The expansion of the leaf canopy in relation to temperature and nitrogen. Ann. Appl. Biol. 1985, 107, 335–347. [Google Scholar] [CrossRef]
- Jaggard, K.W.; Qi, A. Crop physiology and agronomy. In Sugar Beet; Draycott, A.P., Ed.; Blackwell Publishing: Oxford, UK, 2006; pp. 134–168. [Google Scholar]
- Elsayed, S.; Barmeier, G.; Schmidhalter, U. Passive reflectance sensing and digital image analysis allows for assessing the biomass and nitrogen status of wheat in early and late tillering stages. Front. Plant Sci. 2018, 9, 1478. [Google Scholar] [CrossRef] [PubMed]
- Milford, G.F.J.; Travis, K.Z.; Pocock, T.O.; Jaggard, K.W.; Day, W. Growth and dry matter partitioning in sugar-beet. J. Agric. Sci. 1988, 110, 301–308. [Google Scholar] [CrossRef]
- Salami, M.; Saadat, S. Study of potassium and nitrogen fertilizer levels on the yield of sugar beet in Jolge cultivar. J. Novel Appl. Sci. 2013, 2, 94–100. [Google Scholar]
- Li, D.; Li, F.; Hu, Y.; Mistele, B.; Schmidhalter, U. Study on the estimation of nitrogen content in wheat and maize canopy based on band optimization of spectral parameters. Spectrosc. Spect. Anal. 2016, 36, 1150–1157. [Google Scholar] [CrossRef]
- Moran, J.A.; Mitchell, A.K.; Goodmanson, G.; Stockburger, K.A. Differentiation among effects of nitrogen fertilization plant stress responses to gas leaks. Remote Sens. Environ. 2000, 92, 207–217. [Google Scholar]
- Kaushal, S.S.; Groffman, P.M.; Band, L.E.; Elliott, E.M.; Shields, C.A.; Kendall, C. Tracking nonpoint source nitrogen pollution in human-impacted watersheds. Environ. Sci. Technol. 2011, 45, 8225–8232. [Google Scholar] [CrossRef]
- Jaggard, K.W.; Qi, A.; Armstrong, M.J. A meta-analysis of sugar beet yield responses to nitrogen fertilizer measured in England since 1980. J. Agric. Sci. 2009, 147, 287–301. [Google Scholar] [CrossRef]
- Koch, H.; Laufer, D.; Nielsen, O.; Wilting, P. Nitrogen requirement of fodder and sugar beet (Beta vulgaris L.) cultivars under high-yielding conditions of northwestern Europe. Arch. Agron. Soil Sci. 2016, 62, 1222–1235. [Google Scholar] [CrossRef]
- Tsialtas, J.T.; Maslaris, N. Nitrogen effects on yield, quality and K/Na selectivity of sugar beets grown on clays under semi-arid, irrigated conditions. Int. J. Plant Prod. 2013, 7, 355–372. [Google Scholar]
- Mekdad, A.A.A.; Rady, M.M. Response of Beta vulgaris L. to nitrogen and micronutrients in dry environment. Plant Soil Environ. 2016, 62, 23–29. [Google Scholar] [CrossRef]
- Carter, G.A. Reflectance wavebands and indices for remote estimation of photosynthesis and stomatal conductance in pine canopies. Remote Sens. Environ. 1998, 63, 61–72. [Google Scholar] [CrossRef]
- Clevers, J.G.P.W.; Gitelson, A.A. Remote estimation of crop and grass chlorophyll and nitrogen content using red-edge bands on Sentinel-2 and -3. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 344–351. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, D.J.; Shi, P.H.; Omass, K. Estimating rice chlorophyll content and leaf nitrogen concentration with a digital still color camera under natural light. Plant Methods 2014, 10, 36. [Google Scholar] [CrossRef] [PubMed]
- Meskinivishkaee, F.; Mohammadi, M.H.; Neyshabouri, M.R.; Shekari, F. Evaluation of canola chlorophyll index and leaf nitrogen under wide range of soil moisture. Int. Agrophys. 2015, 29, 83–90. [Google Scholar] [CrossRef]
- Manderscheid, R.; Pacholski, A.; Weigel, H.J. Effect of free air carbon dioxide enrichment combined with two nitrogen levels on growth, yield and yield quality of sugar beet: Evidence for a sink limitation of beet growth under elevated CO2. Eur. J. Agron. 2010, 32, 228–239. [Google Scholar] [CrossRef]
- Richardson, A.D.; Duigan, S.; Berlyn, G. An evaluation of noninvasive methods to estimate foliar chlorophyll content. New Phytol. 2002, 153, 185–194. [Google Scholar] [CrossRef]
- Jin, S.; Wang, P.; Zhao, K.; Yang, Y.; Yao, S.; Jiang, D. Characteristics of gas exchange and chlorophyll fluorescence in different position leaves at booting stage in rice plants. Rice Sci. 2004, 11, 283–289. [Google Scholar]
- Marenco, R.A.; Antezana-Vera, S.A.; Nascimento, H.C.S. Relationship between specific leaf area, leaf thickness, leaf water content and SPAD—502 readings in six Amazonian tree species. Photosynthetica 2009, 47, 184–190. [Google Scholar] [CrossRef]
- El-Hendawy, S.; Elsayed, S.; Al-Suhaibani, N.; Alotaibi, M.; Tahir, M.U.; Mubushar, M.; Attia, A.; Hassan, W.M. Use of Hyperspectral Reflectance Sensing for Assessing Growth and Chlorophyll Content of Spring Wheat Grown under Simulated Saline Field Conditions. Plants 2021, 10, 101. [Google Scholar] [CrossRef]
- Chen, X.W.; Dong, Z.Y.; Liu, J.B.; Wang, H.Y.; Zhang, Y.; Chen, T.Q.; Du, Y.C.; Shao, L.; Xie, J.C. Hyperspectral characteristics and quantitative analysis of leaf chlorophyll by reflectance spectroscopy based on a genetic algorithm in combination with partial least squares regression. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 243, 118786. [Google Scholar] [CrossRef]
- Marang, I.J.; Filippi, P.; Weaver, T.B.; Evans, B.J.; Whelan, B.M.; Bishop, T.F.A.; Murad, O.F.M.; Al-Shammari, D.; Roth, G. Machine Learning Optimised Hyperspectral Remote Sensing Retrieves Cotton Nitrogen Status. Remote Sens. 2021, 13, 1428. [Google Scholar] [CrossRef]
- Tao, H.; Feng, H.; Xu, L.; Miao, M.; Long, H.; Yue, J.; Li, Z.; Yang, G.; Yang, X.; Fan, L. Estimation of Crop Growth Parameters Using UAV-Based Hyperspectral Remote Sensing Data. Sensors 2020, 20, 1296. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Li, F.; Hu, Y.; Yu, K. Hyperspectral indices optimization algorithms for estimating canopy nitrogen concentration in potato (Solanum tuberosum L.). Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102416. [Google Scholar] [CrossRef]
- Zhang, J.; Tian, H.; Wang, D.; Li, H.; Mouazen, A.M. A novel spectral index for estimation of relative chlorophyll content of sugar beet. Comput. Electron. Agric. 2021, 184, 106088. [Google Scholar] [CrossRef]
- Geipel, J.; Link, J.; Claupein, W. Combined spectral and spatial modeling of corn yield based on aerial images and crop surface models acquired with an unmanned aircraft system. Remote Sens. 2014, 6, 10335–10355. [Google Scholar] [CrossRef]
- Hamblin, J.; Knight, R.; Atkinson, M.J. The influence of systematic micro-environmental variation on individual plant yield within selection plots. Euphytica 1978, 27, 497–503. [Google Scholar] [CrossRef]
- Köksal, E.S.; Güngör, Y.; Yildirim, Y.E. Spectral reflectance characteristics of sugar beet under different levels of irrigation water and relationships between growth parameters and spectral indexes. Irrig. Drain. 2011, 60, 187–195. [Google Scholar] [CrossRef]
- Kira, O.; Linker, R.; Gitelson, A.A. Non-destructive estimation of foliar chlorophyll and carotenoid contents: Focus on informative spectral bands. J. Appl. Earth Observ. Geoinf. 2015, 38, 251–260. [Google Scholar] [CrossRef]
- Zhao, Y.X.; Yan, C.H.; Lu, S.; Wang, P.; Qiu, G.Y.; Li, R.L. Estimation of chlorophyll content in intertidal mangrove leaves with different thicknesses using hyperspectral data. Ecol. Ind. 2019, 106, 105511. [Google Scholar] [CrossRef]
- Romero, A.P.; Alarcón, A.; Valbuena, R.I.; Galeano, C.H. Physiological assessment of water stress in potato using spectral information. Front. Plant Sci. 2017, 8, 1608. [Google Scholar] [CrossRef]
- Miloš, B.; Josef, H.; Jana, M.; Kateřina, S.; Alica, K. Dehydration-induced changes in spectral reflectance indices and chlorophyllfluorescence of Antarctic lichens with different thalluscolor, and intrathallinephotobiont. Acta Physiol. Plant. 2018, 40, 177. [Google Scholar] [CrossRef]
- Jay, S.; Gorretta, N.; Morel, J.; Maupas, F.; Bendoula, R.; Rabatel, G.; Dutartre, D.; Comar, A.; Baret, F. Estimating leaf chlorophyll content in sugar beet canopies using millimeter- to centimeter-scale reflectance imagery. Remote Sens. Environ. 2017, 198, 173–186. [Google Scholar] [CrossRef]
- Datt, B. A new reflectance index for remote sensing of chlorophyll content in higher plants: Tests using Eucalyptus leaves. J. Plant Physiol. 1999, 154, 30–36. [Google Scholar] [CrossRef]
- Amirruddin, A.D.; Muharam, F.M.; Ismail, M.H.; Ismail, M.F.; Tan, N.P.; Karam, D.S. Hyperspectral remote sensing for assessment of chlorophyll sufficiency levels in mature oil palm (Elaeis guineensis) based on frond numbers: Analysis of decision tree and random forest. Comput. Electron. Agric. 2020, 169, 105–221. [Google Scholar] [CrossRef]
- Gitelson, A.A. Nondestructive estimation of foliar pigment (chlorophylls, carotenoids, and anthocyanins) contents. In Hyperspectral Remote Sensing of Vegetation; Thenkabail, P.S., Lyon, J.G., Huete, A., Eds.; CRC Press: London, UK; New York, NY, USA, 2011; pp. 141–166. [Google Scholar]
- Lu, S.; Lu, F.; You, W.; Wang, Z.; Liu, Y.; Omasa, K. A robust vegetation index for remotely assessing chlorophyll content of dorsiventral leaves across several species in different seasons. Plant Methods 2018, 14, 15. [Google Scholar] [CrossRef]
- Dong, T.F.; Liu, J.G.; Shang, J.L.; Qian, B.D.; Ma, B.L.; Kovacs, M.J.; Walters, D.; Jiao, X.F.; Geng, X.Y.; Shi, Y.C. Assessment of red-edge vegetation indices for crop leaf area index estimation. Remote Sens. Environ. 2019, 222, 133–143. [Google Scholar] [CrossRef]
- Mistele, B.; Schmidhalter, U. Spectral measurements of the total aerial N and biomass dry weight in maize using a quadrilateral-view optic. Field Crops Res. 2008, 106, 94–103. [Google Scholar] [CrossRef]
- Dray, F.A., Jr.; Center, T.D.; Mattison, E.D. In situ estimates of waterhyacinth leaf tissue nitrogen using a SPAD-502 chlorophyll meter. Aquat. Bot. 2012, 100, 72–75. [Google Scholar] [CrossRef]
- Adelabu, S.; Mutanga, O.; Adam, E. Evaluating the impact of red-edge band from rapideye image for classifying insect defoliation levels. ISPRS J. Photogramm. Remote Sens. 2014, 95, 34–41. [Google Scholar] [CrossRef]
- Evangelides, C.; Nobajas, A. Red-edge normalised difference vegetation index (NDVI 705) from sentinel-2 imagery to assess post-fire regeneration. Remote Sens. Appl. Soc. Environ. 2020, 17, 100283. [Google Scholar]
- Ray, S.S.; Das, G.; Singh, J.P.; Panigrahy, S. Evaluation of hyperspectral indices for LAI estimation anddiscrimination of potato crop under different irrigationtreatments. Int. J. Remote Sens. 2006, 27, 5373–5387. [Google Scholar] [CrossRef]
- Hasituya; Li, F.; Elsayed, S.; Hu, Y.; Schmidhalter, U. Passive reflectance sensing using optimized two- and three-band spectral indices for quantifying the total nitrogen yield of maize. Comput. Electron. Agric. 2021, 173, 105403. [Google Scholar] [CrossRef]
- Li, F.; Li, D.; Elsayed, S.; Hu, Y.; Schmidhalter, U. Using optimized three-band spectral indices to assess canopy N uptake incorn and wheat. Eur. J. Agron. 2021, 127, 126286. [Google Scholar] [CrossRef]
- El-Hendawy, S.; Dewir, Y.H.; Elsayed, S.; Schmidhalter, U.; Al-Gaadi, K.; Tola, E.; Refay, Y.; Tahir, M.U.; Hassan, W.M. CombiningHyperspectral Reflectance Indicesand Multivariate Analysis to Estimate Different Units of Chlorophyll Content of Spring Wheat under Salinity Conditions. Plants 2022, 11, 456. [Google Scholar] [CrossRef] [PubMed]
- Beltrán, N.H.; Duarte-Mermoud, M.A.; Salah, S.A.; Bustos, M.A.; Peña-Neira, A.I.; Loyola, E.A.; Jalocha, J.W. Feature selection algorithms using Chilean wine chromatograms as examples. J. Food Eng. 2005, 67, 483–490. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar]
- Schuize, F.H.; Wolf, H.; Jansen, H.; Vander, V.P. Applications of artificial neural networks in integrated water management: Fiction or future? Water Sci. Technol. 2005, 52, 21–31. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.-L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Glorfeld, L.W. A methodology for simplification and interpretation of backpropagation-based neural network models. Expert Syst. Appl. 1996, 10, 37–54. [Google Scholar] [CrossRef]
- Melis, G.; Dyer, C.; Blunsom, P. On the state of the art of evaluation in neural language models. arXiv 2017, arXiv:1707.05589. [Google Scholar]
- Bergstra, J.; Yamins, D.; Cox, D. Making a science of model search: Hyperparameter optimization in hundreds of dimensions for vision architectures. In Proceedings of the 30th International Conference on Machine Learning (ICML), Atlanta, GA, USA, 16–21 June 2013; pp. 115–123. [Google Scholar]
- Wu, J.; Chen, X.-Y.; Zhang, H.; Xiong, L.-D.; Lei, H.; Deng, S.-H. Hyperparameter optimization for machine learning models based on Bayesian optimization. J. Electron. Sci. Technol. 2019, 17, 26–40. [Google Scholar]
- Doorenbos, I.; Kassam, A. Yield Response to Water; F.A.O Irrigation and Drainage Paper No. 33; FAO: Rome, Italy, 1979. [Google Scholar]
- Lichtenthaler, H.K.; Wellburn, A.R. Determinations of total carotenoids and chlorophylls a and b of leaf extracts in differentsolvents. Biochem. Soc. Trans. 1983, 603, 591–592. [Google Scholar] [CrossRef]
- Carruthers, A.; Oldfield, J.F.T. Methods for the assessment of beet quality. Int. Sugar J. 1960, 63, 72–74. [Google Scholar]
- Elsayed, S.; El-Gozayer, K.; Allam, A.; Schmidhalter, U. Passive reflectance sensing using regression and multivariate analysis to estimate biochemical parameters of different fruits kinds. Sci. Hortic. 2019, 243, 21–33. [Google Scholar] [CrossRef]
- Elsayed, S.; Galal, H.; Allam, A.P.; Schmidhalter, U. Passive reflectance sensing anddigital image analysis for assessing quality parameters of mango fruits. Sci. Hortic. 2016, 212, 136–147. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement of Retro Gradation of Natural Vegetation; NASA/GSFC, Type lll, Final Report; NASA/GSFC: Greenbelt, MD, USA, 1974. [Google Scholar]
- Gutierrez, M.; Reynolds, M.P.; Raun, W.R.; Stone, M.L.; Klatt, A.R. Spectral water indices for assessing yield in elite bread wheat genotypes in well irrigated, water stressed, and high temperature conditions. Crop Sci. 2010, 50, 197–214. [Google Scholar] [CrossRef]
- Acharya, U.K.; Subedi, P.P.; Walsh, K.B.; McGlasson, W.B. Estimation of fruit maturation and ripening using spectral indices. Acta Hortic. 2016, 1119, 265–272. [Google Scholar] [CrossRef]
- Nagy, A.; Riczu, P.; Tamás, J. Spectral evaluation of apple fruit ripening and pigment content alteration. Sci. Hortic. 2016, 201, 256–264. [Google Scholar] [CrossRef]
- Gilbert, C.; Browell, J.; McMillan, D. Leveraging Turbine-Level Data for Improved ProbabilisticWind Power Forecasting. IEEE Trans. Sustain. Energy 2019, 11, 1152–1160. [Google Scholar]
- Elith, J.; Leathwick, J.R.; Hastie, T. A Working Guide to Boosted Regression Trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Zhu, J.; Huang, Z.H.; Sun, H.; Wang, G.X. Mapping forest ecosystem biomass density for Xiangjiang river basin by combining plot and remote sensing data and comparing spatial extrapolation methods. Remote Sens. 2017, 9, 241. [Google Scholar] [CrossRef]
- Malone, B.P.; Styc, Q.; Minasny, B.; McBratney, A.B. Digital soil mapping of soil carbon at the farm scale: A spatial downscaling approach in consideration of measured and uncertain data. Geoderma 2017, 290, 91–99. [Google Scholar] [CrossRef]
- Saggi, M.K.; Jain, S. Reference evapotranspiration estimation and modeling of the Punjab Northern India using deep learning. Comput. Electron. Agric. 2019, 156, 387–398. [Google Scholar] [CrossRef]
- Kristek, S.; Kristek, A.; Evačić, M. Influence of nitrogen fertilization on sugar beet root yield and quality. Cereal Res. Commun. 2008, 36, 371–374. [Google Scholar]
- Wang, Z.; Skidmore, A.K.; Darvishzadeh, R.; Wang, T. Mapping forest canopy nitrogen content by inversion of coupled leaf-canopy radiative transfer models from airborne hyperspectral imagery. Agric. For. Meteorol. 2018, 253–254, 247–260. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Hornero, A.; Beck, P.S.A.; Kattenborn, T.; Kempeneers, P.; Hernández-Clemente, R. Chlorophyll content estimation in an open-canopy conifer forest with Sentinel-2A and hyperspectral imagery in the context of forest decline. Remote Sens. Environ. 2019, 223, 320–335. [Google Scholar] [CrossRef]
- Zhang, G.; Liu, Q.; Zhang, Z.; Ci, D.; Zhang, J.; Xu, Y.; Guo, Q.; Xu, M.; He, K. Effect of reducing nitrogen fertilization and adding organic fertilizer on net photosynthetic rate, root nodules and yield in peanut. Plants 2023, 12, 2902. [Google Scholar] [CrossRef]
- Wang, B.F.; Yu, Z.Y.; Cheng, J.P.; Li, Y.; Zhang, Z.S.; Yang, X.L. Research progress on the effect of nitrogen on rice yield and quality formation. J. Huazhong Agric. Univ. 2022, 41, 76–83. [Google Scholar]
- Yin, H.; Li, B.; Wang, X.; Xi, Z. Effect of ammonium and nitrate supplies on nitrogen and sucrose metabolism of cabernet sauvignon (Vitis vinifera cv.). J. Sci. Food Agric. 2020, 100, 5239–5250. [Google Scholar] [CrossRef]
- Li, J.; Liu, X.; Yao, Q.; Xu, L.; Li, W.; Tan, W.; Wang, Q.; Xing, W.; Liu, D. Tolerance and adaptation characteristics of sugar beet (Beta vulgaris L.) to low nitrogen supply. Plant Signal. Behav. 2023, 18, 2159155. [Google Scholar] [CrossRef]
- Li, F.; Mistele, B.; Hu, Y.; Chen, X.; Schmidhalter, U. Comparing hyperspectral index optimization algorithms to estimate aerial N uptake using multi-temporal winter wheat datasets. Agric. For. Meteorol. 2013, 180, 44–57. [Google Scholar] [CrossRef]
- Li, F.; Mistele, B.; Hu, Y.; Chen, X.; Schmidhalter, U. Optimising three-band spectral indices to assess aerial N concentration, N uptake and aboveground biomass of winter wheat remotely in China and Germany. ISPRS J. Photogramm. Remote Sens. 2014, 92, 112–123. [Google Scholar] [CrossRef]
- Barmeier, G.; Schmidhalter, U. High-throughput field phenotyping of leaves, leaf sheaths, culms and ears of spring barley cultivars at anthesis and dough Ripeness. Front. Plant Sci. 2017, 8, 1920. [Google Scholar] [CrossRef] [PubMed]
- Elsherbiny, O.; Fan, Y.; Zhou, L.; Qiu, Z. Fusion of feature selection methods and regression algorithms for predicting the canopy water content of rice based on hyperspectral data. Agriculture 2021, 11, 51. [Google Scholar] [CrossRef]


| Season | Month | Temperature, °C | Relative Humidity, % | Wind Speed, m/s | Direct Normal Irradiance (MJ/m2/day) | Precipitation, mm | |
|---|---|---|---|---|---|---|---|
| Max | Min | ||||||
| Season 2020/2021 | Sep. | 40.34 | 20.14 | 60.31 | 0.84 | 26.03 | 0 |
| Oct. | 37.87 | 16.68 | 63.00 | 0.15 | 24.27 | 0 | |
| Nov. | 27.00 | 9.57 | 67.88 | 0.17 | 18.16 | 0 | |
| Dec. | 25.09 | 9.01 | 66.75 | 0.18 | 18.03 | 0 | |
| Jan. | 25.94 | 4.60 | 66.94 | 0.14 | 16.39 | 0.17 | |
| Feb. | 26.26 | 5.97 | 67.19 | 0.22 | 19.18 | 0.94 | |
| Mar. | 30.81 | 5.84 | 64.62 | 0.16 | 19.9 | 4.25 | |
| Apr. | 39.15 | 6.84 | 57.00 | 0.22 | 25.38 | 0.02 | |
| May. | 41.50 | 13.65 | 49.56 | 0.25 | 30.27 | 0 | |
| Season 2021/2022 | Sep. | 40.18 | 18.59 | 58.19 | 7.00 | 27.09 | 0 |
| Oct. | 34.25 | 15.87 | 60.06 | 6.20 | 23.98 | 0.06 | |
| Nov. | 31.42 | 12.20 | 65.88 | 6.85 | 19.50 | 1.48 | |
| Dec. | 22.59 | 6.37 | 70.44 | 9.97 | 13.59 | 1.03 | |
| Jan. | 20.73 | 2.47 | 70.31 | 0.06 | 15.51 | 1.38 | |
| Feb. | 23.23 | 4.73 | 69.38 | 0.18 | 18.79 | 0.35 | |
| Mar. | 28.82 | 4.26 | 65.19 | 0.41 | 19.39 | 0.92 | |
| Apr. | 39.44 | 8.48 | 55.94 | 0.61 | 21.50 | 0 | |
| May. | 40.68 | 12.56 | 53.88 | 0.19 | 25.60 | 0 | |
| SRIs | Formula | Ref. |
|---|---|---|
| Published SRIs | ||
| Normalized difference index (NDI570, 540) | (R570 − R540)/(R570 + R540) | [71] |
| Normalized difference index (NDI686, 620) | (R686 − R620)/(R686 + R620) | [71] |
| Anthocyanin index (NAI) | (R760 − R720)/(R760 + R720) | [72] |
| NDI780, 550 | (R780 − R550)/(R780 + R550) | [73] |
| Greenness index (GI) | R554/R677 | [74] |
| Pigment-Sensitive Ripening Monitoring Index (PRMI) | (R750 − R678)/R550 | [75] |
| Newly 3D-SRIs as normalized difference indices (NDI) | ||
| NDI448, 738, 682 | (R448 − R738 − R682)/(R448 + R738 + R682) | |
| NDI448, 684, 738 | (R448 − R684 − R738)/(R448 + R684 + R738) | |
| NDI530, 532, 528 | (R530 − R532 − R528)/(R530 + R532 + R528) | |
| NDI530, 534, 526 | (R530 − R534 − R526)/(R530 + R534 + R526) | |
| NDI536, 538, 534 | (R536 − R538 − R534)/(R536 + R538 + R534) | |
| NDI734, 738, 730 | (R734 − R738 − R730)/(R734 + R738 + R730) | |
| NDI738, 750, 542 | (R738 − R750 − R542)/(R738 + R750 + R542) | |
| NDI590, 594, 588 | (R590 − R594 − R588)/(R590 + R594 + R588) | |
| NDI448, 734, 398 | (R448 − R734 − R398)/(R448 + R734 + R398) | |
| NDI734, 730, 738 | (R734 − R730 − R738)/(R734 + R730 + R738) | |
| NDI536, 538, 534 | (R536 − R538 − R532)/(R536 + R538 + R532) | |
| NDI734, 728, 740 | (R734 − R728 − R740)/(R734 + R728 + R740) | |
| Source of Variation | df | Chla | Chlb | Chlt | SC | SY | RY |
|---|---|---|---|---|---|---|---|
| Sum of Squares (%) | |||||||
| Blocks | 4 | 0.15 ns | 0.17 ns | 0.14 ns | 0.32 ns | 0.64 ns | 0.51 ns |
| Year (Y) | 1 | 1.90 * | 2.70 *** | 2.15 ** | 59.88 *** | 14.70 *** | 3.92 ** |
| Error-1 | 4 | 0.42 | 0.14 | 0.31 | 0.13 | 0.43 | 0.30 |
| N | 4 | 92.39 *** | 92.20 *** | 92.90 *** | 37.24 *** | 80.44 *** | 92.67 *** |
| N × Y | 4 | 1.80 ** | 2.45 *** | 1.78 ** | 0.02 ns | 0.72 ns | 0.17 ns |
| Error-2 | 32 | 3.34 | 2.46 | 2.70 | 2.40 | 3.08 | 2.43 |
| Total | 49 | 99.85 | 99.95 | 99.85 | 99.68 | 99.37 | 99.49 |
| Treatment | Statis. | NDI570, 540 | NDI686, 620 | NAI | NDI780, 550 | GI | PRMI | NDI448, 738, 682 | NDI448, 684, 738 | NDI530, 532, 528 |
|---|---|---|---|---|---|---|---|---|---|---|
| N0 | Min | 0.0371 | −0.0204 | 0.1283 | 0.4380 | 1.0174 | 1.4088 | −0.7806 | −0.7484 | −0.3330 |
| Max | 0.0599 | 0.0047 | 0.2044 | 0.5334 | 1.2390 | 2.2516 | −0.7354 | −0.4612 | −0.3329 | |
| SD | 0.0075 | 0.0088 | 0.0290 | 0.0348 | 0.0762 | 0.2985 | 0.0142 | 0.0799 | 0.0001 | |
| Mean | 0.0482 a | −0.0081 a | 0.1664 c | 0.4865 d | 1.1234 d | 1.8215 e | −0.7637 a | −0.5513 a | −0.3329 d | |
| N30 | Min | 0.0384 | −0.0185 | 0.1458 | 0.4665 | 1.0794 | 1.6443 | −0.7883 | −0.5809 | −0.3330 |
| Max | 0.0545 | −0.0062 | 0.2117 | 0.5381 | 1.2105 | 2.2577 | −0.7582 | −0.4961 | −0.3328 | |
| SD | 0.0053 | 0.0039 | 0.0214 | 0.0228 | 0.0434 | 0.2008 | 0.0096 | 0.0275 | 0.0001 | |
| Mean | 0.0445 a | −0.0126 a | 0.1839 c | 0.5122 c | 1.1657 d | 2.0380 d | −0.7762 b | −0.5522 a | −0.3329 d | |
| N60 | Min | 0.0209 | −0.0420 | 0.1731 | 0.4951 | 1.1298 | 1.8766 | −0.8118 | −0.6726 | −0.3329 |
| Max | 0.0478 | −0.0094 | 0.2553 | 0.6015 | 1.4419 | 3.0213 | −0.7674 | −0.5311 | −0.3327 c | |
| SD | 0.0087 | 0.0125 | 0.0247 | 0.0320 | 0.1082 | 0.3525 | 0.0128 | 0.0455 | 0.0001 | |
| Mean | 0.0334 b | −0.0248 b | 0.2188 b | 0.5555 b | 1.2918 c | 2.4884 c | −0.7934 c | −0.6109 b | −0.3328 | |
| N90 | Min | 0.0117 | −0.0578 | 0.2040 | 0.5443 | 1.2142 | 2.3261 | −0.8241 | −0.7148 | −0.3329 |
| Max | 0.0405 | −0.0143 | 0.2775 | 0.6236 | 1.6175 | 3.3633 | −0.7915 | −0.5862 | −0.3326 | |
| SD | 0.0090 | 0.0147 | 0.0256 | 0.0283 | 0.1284 | 0.3500 | 0.0104 | 0.0421 | 0.0001 | |
| Mean | 0.0267 b | −0.0352 c | 0.2315 b | 0.5763 b | 1.3910 b | 2.7466 b | −0.8042 d | −0.6452 b | −0.3328 b | |
| N120 | Min | −0.0009 | −0.0739 | 0.2512 | 0.6102 | 1.5129 | 3.1723 | −0.8441 | −0.7645 | −0.3327 |
| Max | 0.0176 | −0.0453 | 0.3020 | 0.6652 | 1.8305 | 4.0204 | −0.8181 | −0.6912 | −0.3325 | |
| SD | 0.0066 | 0.0097 | 0.0185 | 0.0188 | 0.1058 | 0.2855 | 0.0083 | 0.0248 | 0.0000 | |
| Mean | 0.0102 c | −0.0577 d | 0.2763 a | 0.6319 a | 1.6342 a | 3.4850 a | −0.8279 e | −0.7206 c | −0.3326 a | |
| Treatment | Statis. | NDI530, 534, 526 | NDI536, 538, 534 | NDI734, 738, 730 | NDI738, 750, 542 | NDI590, 588, 594 | NDI448, 734, 398 | NDI734, 730, 738 | NDI536, 538, 532 | NDI734, 728, 740 |
| N0 | Min | −0.3322 | −0.3331 | −0.3321 | −0.1927 | −0.3336 | −0.7367 | −0.3321 | −0.3332 | −0.3309 |
| Max | −0.3315 | −0.3330 | −0.3315 | −0.1760 | −0.3332 | −0.6725 | −0.3315 | −0.3331 | −0.3292 | |
| SD | 0.0002 | 0.0001 | 0.0002 | 0.0056 | 0.0001 | 0.0213 | 0.0002 | 0.0001 | 0.0005 | |
| Mean | −0.3318 d | −0.3331 d | −0.3318 e | −0.1831 e | −0.3334 d | −0.7099 a | −0.3318 e | −0.3331 d | −0.3299 d | |
| N30 | Min | −0.3319 | −0.3331 | −0.3319 | −0.1848 | −0.3335 | −0.7438 | −0.3319 | −0.3331 | −0.3301 |
| Max | −0.3314 | −0.3330 | −0.3314 | −0.1744 | −0.3332 | −0.7008 | −0.3314 | −0.3330 | −0.3291 | |
| SD | 0.0002 | 0.0000 | 0.0002 | 0.0033 | 0.0001 | 0.0136 | 0.0002 | 0.0000 | 0.0003 | |
| Mean | −0.3316 d | −0.3330 c | −0.3316 d | −0.1782 d | −0.3333 d | −0.7275 b | −0.3316 d | −0.3330 c | −0.3295 c | |
| N60 | Min | −0.3317 | −0.3330 | −0.3316 | −0.1817 | −0.3334 | −0.7790 | −0.3316 | −0.3330 | −0.3296 |
| Max | −0.3310 | −0.3328 | −0.3312 | −0.1662 | −0.3328 | −0.7155 | −0.3312 | −0.3328 | −0.3285 | |
| SD | 0.0002 | 0.0001 | 0.0001 | 0.0049 | 0.0002 | 0.0188 | 0.0001 | 0.0001 | 0.0003 | |
| Mean | −0.3313 c | −0.3329 b | −0.3314 c | −0.1722 c | −0.3331 c | −0.7530 c | −0.3314 c | −0.3329 b | −0.3289 b | |
| N90 | Min | −0.3316 | −0.3330 | −0.3314 | −0.1726 | −0.3332 | −0.7968 | −0.3314 | −0.3330 | −0.3291 |
| Max | −0.3306 | −0.3328 | −0.3310 | −0.1619 | −0.3327 | −0.7485 | −0.3310 | −0.3327 | −0.3281 | |
| SD | 0.0003 | 0.0001 | 0.0001 | 0.0034 | 0.0002 | 0.0154 | 0.0001 | 0.0001 | 0.0003 | |
| Mean | −0.3310 b | −0.3329 b | −0.3312 b | −0.1681 b | −0.3330 b | −0.7685 d | −0.3312 b | −0.3329 b | −0.3287 b | |
| N120 | Min | −0.3308 | −0.3329 | −0.3311 | −0.1639 | −0.3328 | −0.8220 | −0.3311 | −0.3329 | −0.3283 |
| Max | −0.3302 | −0.3327 | −0.3307 | −0.1576 | −0.3325 | −0.7883 | −0.3307 | −0.3327 | −0.3278 | |
| SD | 0.0002 | 0.0000 | 0.0001 | 0.0023 | 0.0001 | 0.0108 | 0.0001 | 0.0000 | 0.0002 | |
| Mean | −0.3305 a | −0.3328 a | −0.3310 a | −0.1615 a | −0.3327 a | −0.8011 e | −0.3310 a | −0.3328 a | −0.3281 a |
| Variable | VIs | Optimal Features | Hyperparameters | Training | Cross-Validation | Testing | |||
|---|---|---|---|---|---|---|---|---|---|
| R2 | RMSE | R2 | RMSE | R2 | RMSE | ||||
| Chlt (mg g−1 FW) | 2D | NDI570, 540, NDI686, 620, GI, PRMI, NDI780, 550 | (Ns = 300, Mf = log2) | 0.990 | 0.072 | 0.655 | 0.345 | 0.648 | 0.356 |
| 3D | NDI590, 594, 588, NDI536, 538, 534 | (Ns = 100, Mf = sqrt) | 0.988 | 0.080 | 0.618 | 0.344 | 0.732 | 0.311 | |
| ASRIs | NDI686, 620, NDI590, 588, 594, NDI734, 730, 738, NDI530, 534, 526, NDI536, 534, 538, NDI590, 594, 588 | (Ns = 100, Mf = sqrt) | 0.989 | 0.073 | 0.748 | 0.304 | 0.652 | 0.354 | |
| Chla (mg g−1 FW) | 2D | PRMI, NDI780, 550, GI | (Ns = 300, Mf = sqrt) | 0.989 | 0.035 | 0.677 | 0.152 | 0.651 | 0.162 |
| 3D | NDI734, 738, 730, NDI590, 588, 594, NDI536, 538, 534, NDI590, 594, 588, NDI536, 534, 538, NDI536, 538, 534 | (Ns = 100, Mf = sqrt) | 0.988 | 0.037 | 0.655 | 0.156 | 0.641 | 0.148 | |
| ASRIs | NDI536, 538, 534, NDI590, 588, 594, NDI734, 738, 730 | (Ns = 200, Mf = log2) | 0.989 | 0.036 | 0.667 | 0.159 | 0.611 | 0.123 | |
| Chlb (mg g−1 FW) | 2D | NAI, GI, NDI780, 550, NDI686, 620, NDI570, 540, PRMI | (Ns = 500, Mf = sqrt) | 0.989 | 0.108 | 0.669 | 0.493 | 0.634 | 0.517 |
| 3D | NDI590, 588, 594, NDI590, 594, 588 | (Ns = 100, Mf = auto) | 0.985 | 0.132 | 0.636 | 0.479 | 0.596 | 0.544 | |
| ASRIs | NDI686, 620, NDI530, 532, 528, NDI734, 738, 730, NDI536, 534, 538, NDI590, 588, 594, NDI448, 738, 682, NDI734, 730, 738, NDI530, 534, 526, NDI590, 594, 588, NDI536, 538, 534 | (Ns = 200, Mf = log2) | 0.989 | 0.108 | 0.691 | 0.492 | 0.557 | 0.569 | |
| SC (%) | 2D | NDI570, 540, PRMI, NDI780, 550 | (Ns = 100, Mf = auto) | 0.987 | 1.721 | 0.682 | 6.458 | 0.667 | 2.427 |
| 3D | NDI734, 730, 738, NDI734, 738, 730, NDI590, 594, 588, NDI536, 534, 538, NDI536, 538, 534, NDI536, 538, 534 | (Ns = 200, Mf = sqrt) | 0.989 | 1.524 | 0.661 | 6.637 | 0.651 | 7.916 | |
| ASRIs | GI, NDI686, 620, NDI734, 738, 730, NDI590, 588, 594, NDI734, 730, 738, NDI536, 538, 534, NDI536, 534, 538, NDI536, 538, 534 | (Ns = 100, Mf = sqrt) | 0.989 | 1.568 | 0.692 | 6.120 | 0.779 | 6.294 | |
| SY (ton ha−1) | 2D | NDI686, 620, NDI780, 550, PRMI, NAI | (Ns = 200, Mf = sqrt) | 0.998 | 0.054 | 0.601 | 0.523 | 0.611 | 0.511 |
| 3D | NDI448, 738, 682, NDI530, 532, 528, NDI448, 682, 738, NDI536, 538, 534, NDI448, 684, 738, NDI530, 534, 526, NDI738, 750, 542 | (Ns = 400, Mf = log2) | 0.998 | 0.053 | 0.503 | 0.657 | 0.501 | 0.649 | |
| ASF | NDI530, 532, 528, NDI 536, 538, 534, NDI686, 620, GI, NDI 734, 738, 730, NDI536, 538, 534, NDI448, 682, 738, NDI734, 728, 740, NDI 448, 684, 738, NDI448, 734, 398, NDI738, 750, 542 | (Ns = 100, Mf = sqrt) | 0.997 | 0.062 | 0.533 | 0.618 | 0.518 | 0.634 | |
| RY (ton ha−1) | 2D | NDI570, 540, NDI686, 620, NAI, PRMI, NDI780, 550 | (Ns = 100, Mf = log2) | 0.988 | 0.264 | 0.824 | 0.931 | 0.815 | 0.958 |
| 3D | NDI448, 684, 738, NDI734, 730, 738, NDI734, 738, 730, NDI590, 588, 594, NDI590, 594, 588, NDI530, 534, 526, NDI530, 532, 528, NDI536, 538, 534, NDI536, 534, 538, NDI536, 538, 534 | (Ns = 500, Mf = log2) | 0.990 | 0.236 | 0.501 | 1.341 | 0.743 | 1.128 | |
| ASRIs | NAI, NDI780, 550, NDI686, 620, GI, NDI590, 588, 594, NDI734, 738, 730, NDI590, 594, 588, NDI530, 532, 528, NDI734, 730, 738, NDI536, 538, 534, NDI536, 538, 534, NDI530, 534, 526, NDI536, 534, 538 | (Ns = 100, Mf = log2) | 0.989 | 0.247 | 0.522 | 1.345 | 0.725 | 1.167 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elsayed, S.; El-Hendawy, S.; Elsherbiny, O.; Okasha, A.M.; Elmetwalli, A.H.; Elwakeel, A.E.; Memon, M.S.; Ibrahim, M.E.M.; Ibrahim, H.H. Estimating Chlorophyll Content, Production, and Quality of Sugar Beet under Various Nitrogen Levels Using Machine Learning Models and Novel Spectral Indices. Agronomy 2023, 13, 2743. https://doi.org/10.3390/agronomy13112743
Elsayed S, El-Hendawy S, Elsherbiny O, Okasha AM, Elmetwalli AH, Elwakeel AE, Memon MS, Ibrahim MEM, Ibrahim HH. Estimating Chlorophyll Content, Production, and Quality of Sugar Beet under Various Nitrogen Levels Using Machine Learning Models and Novel Spectral Indices. Agronomy. 2023; 13(11):2743. https://doi.org/10.3390/agronomy13112743
Chicago/Turabian StyleElsayed, Salah, Salah El-Hendawy, Osama Elsherbiny, Abdelaziz M. Okasha, Adel H. Elmetwalli, Abdallah E. Elwakeel, Muhammad Sohail Memon, Mohamed E. M. Ibrahim, and Hazem H. Ibrahim. 2023. "Estimating Chlorophyll Content, Production, and Quality of Sugar Beet under Various Nitrogen Levels Using Machine Learning Models and Novel Spectral Indices" Agronomy 13, no. 11: 2743. https://doi.org/10.3390/agronomy13112743












