Economic Evaluation and Risk Premium Estimation of Rainfed Soybean under Various Planting Practices in a Semi-Humid Drought-Prone Region of Northwest China
Abstract
:1. Introduction
2. Materials and Methods
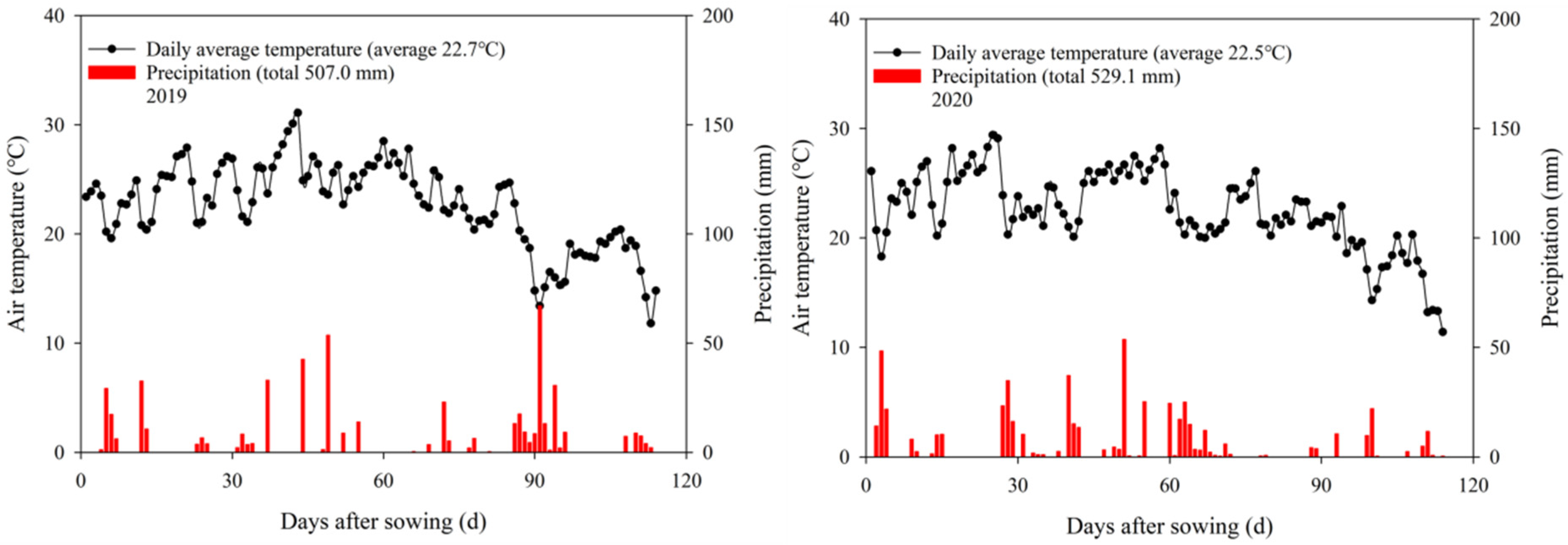
2.1. Experimental Site Description
2.2. Experimental Design and Field Management
3. Economic Evaluation and Risk Premium Estimation
3.1. Economic Return and Production-to-Investment Ratio
3.2. Economic Analysis
3.3. Economic Risk Analysis
4. Results and Discussion
4.1. Data and Simulation
4.1.1. Fluctuating Prices of Soybean
4.1.2. Soybean Yield Analysis
4.1.3. Input Costs of Soybean
4.1.4. Net Income of Soybean
4.2. Economic Feasibility Analysis
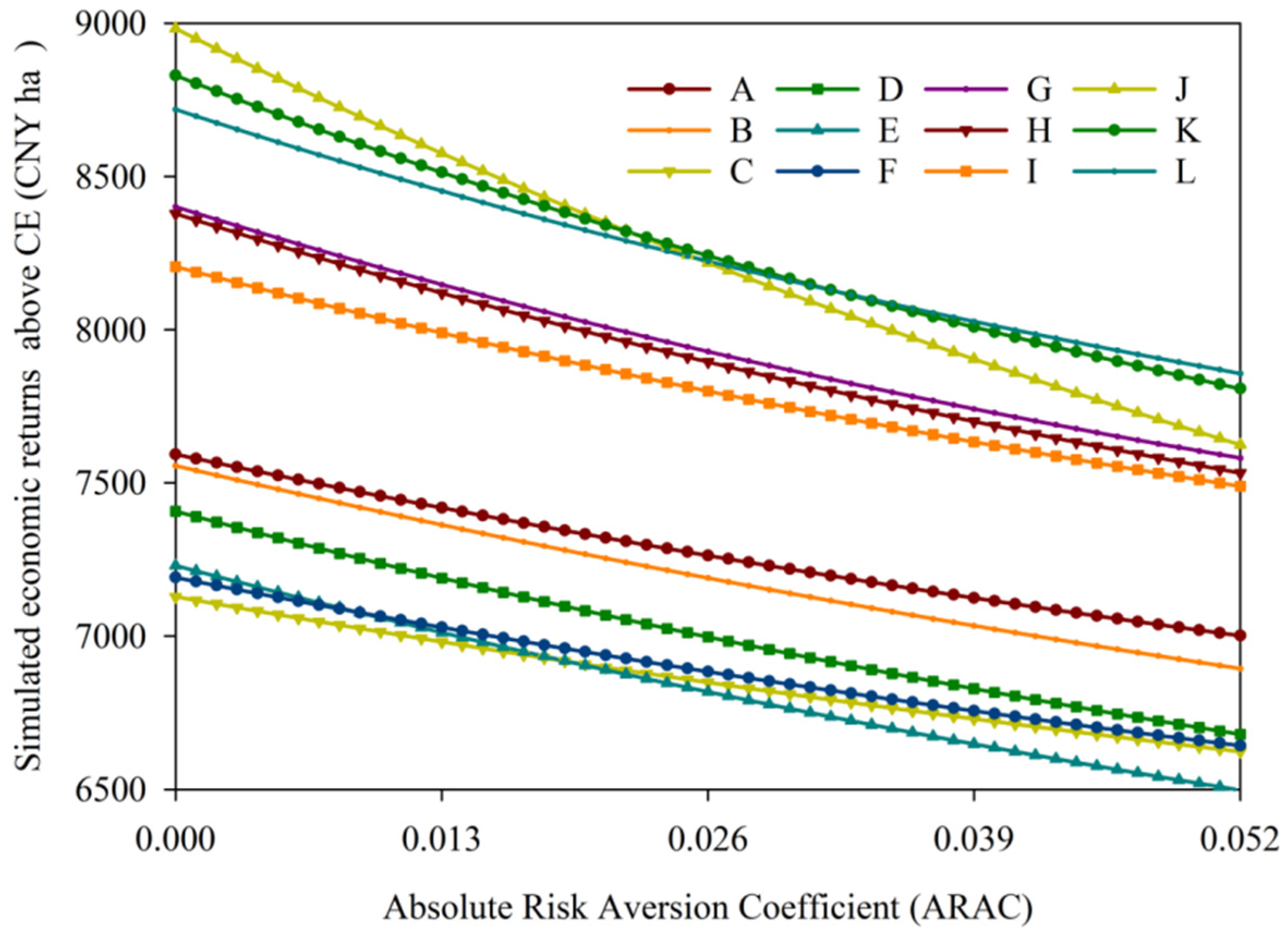
4.3. Risk Premium Estimation
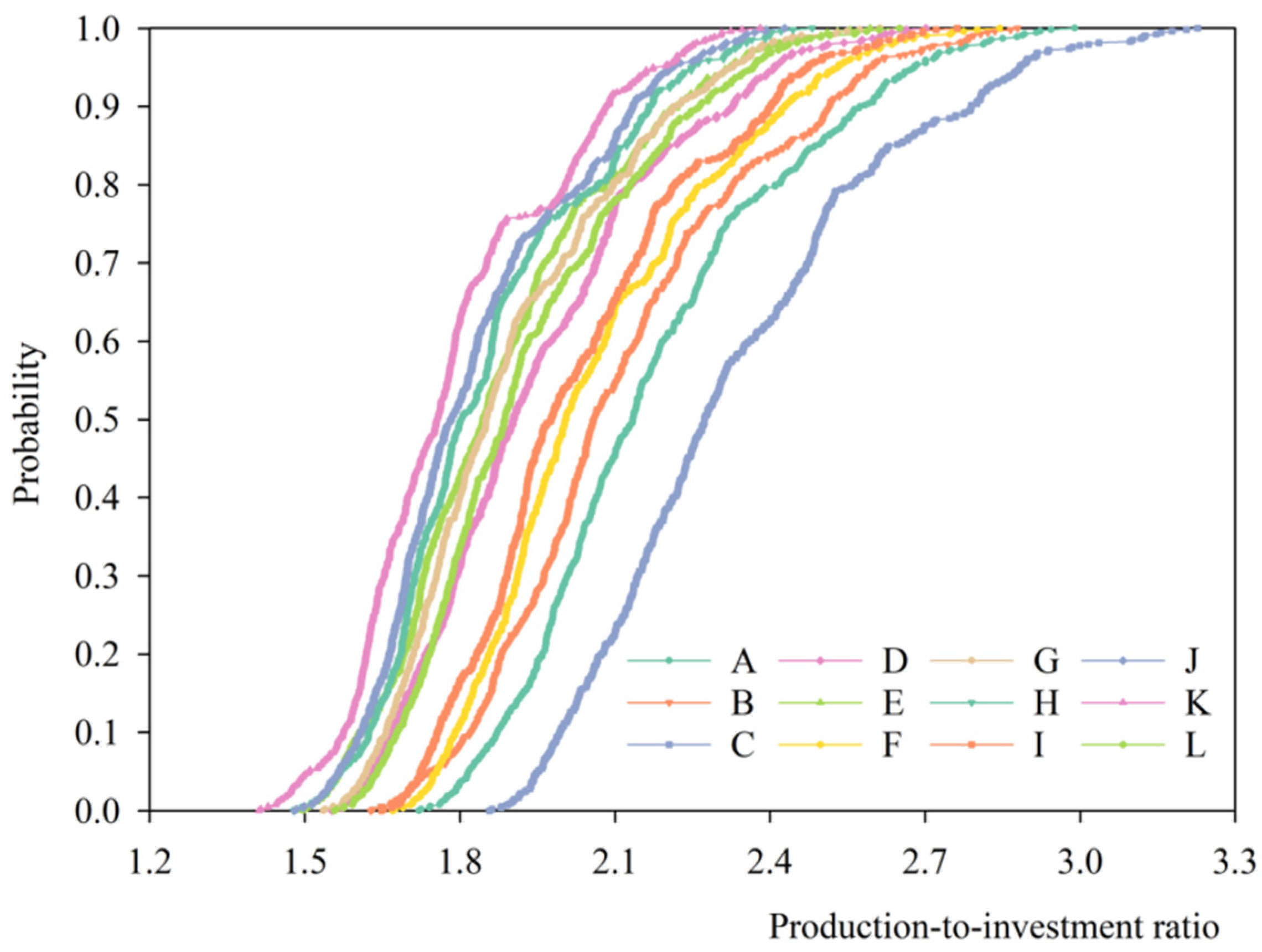
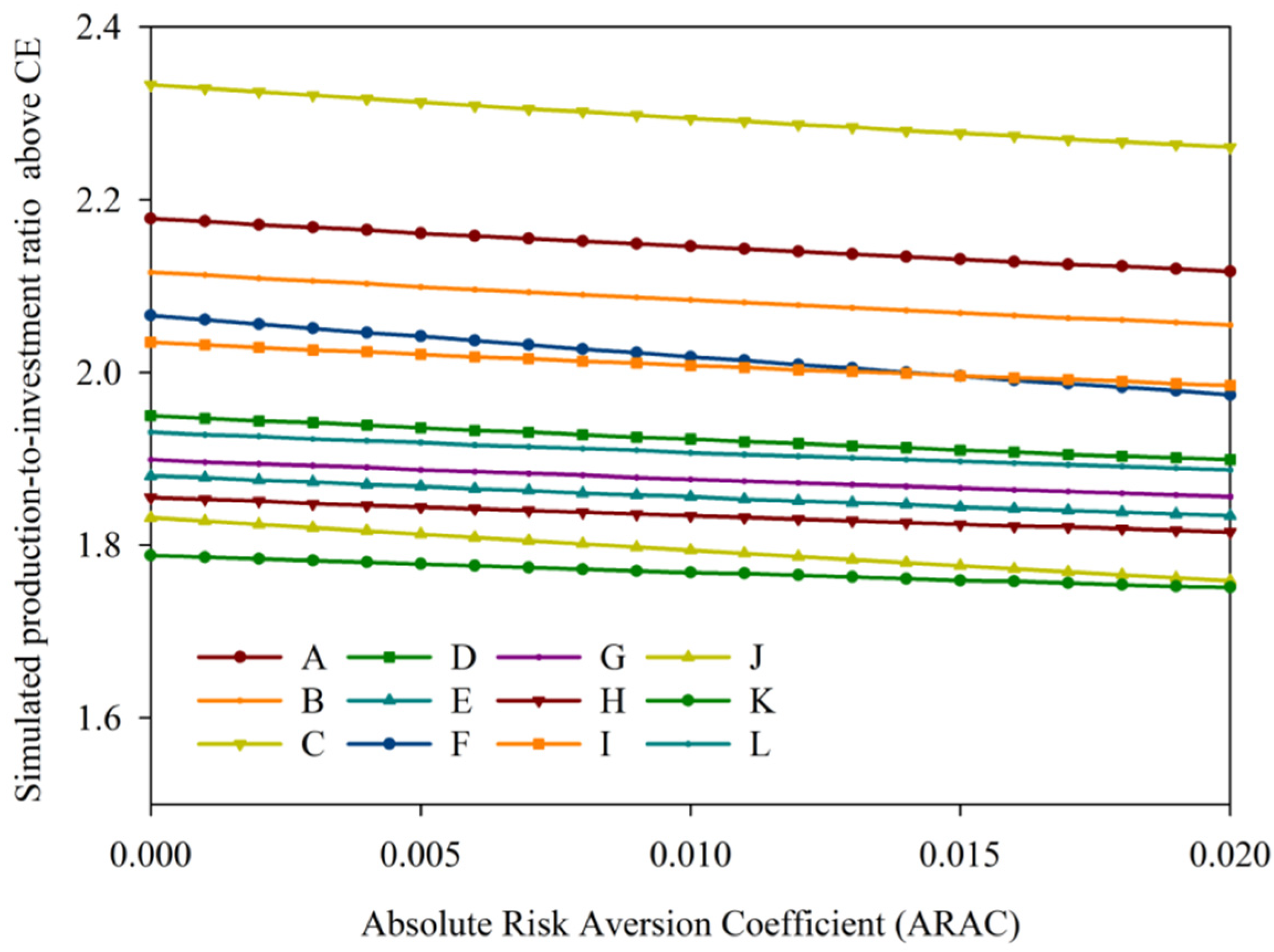
4.4. Estimation of Production-to-Investment Ratio
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- FAOSTAT. ProdStat. Core Production Data Base, Electronic Resource. 2020. Available online: http://faostat.fao.org/ (accessed on 23 January 2020).
- World Bank. Weather Index Insurance for Agriculture: Guidance for Development Practitioners; World Bank: Washington, DC, USA, 2011. [Google Scholar]
- Júnior RS, N.; Sentelhas, P.C. Soybean-maize succession in Brazil: Impacts of sowing dates on climate variability, yields and economic profitability. Eur. J. Agron. 2019, 103, 140–151. [Google Scholar] [CrossRef]
- Liao, Z.Q.; Zeng, H.L.; Fan, J.L.; Lai, Z.; Zhang, C.; Zhang, F.; Wang, H.; Cheng, M.; Guo, J.; Li, Z.; et al. Effects of plant density, nitrogen rate and supplemental irrigation on photosynthesis, root growth, seed yield and water-nitrogen use efficiency of soybean under ridge-furrow plastic mulching. Agric. Water Manag. 2022, 268, 107688. [Google Scholar] [CrossRef]
- Chen, S.; Chen, X.; Xu, J. Impacts of climate change on agriculture: Evidence from China. J. Environ. Econ. Manag. 2016, 76, 105–124. [Google Scholar] [CrossRef]
- Elahi, E.; Khalid, Z.; Tauni, M.Z.; Zhang, H.; Lirong, X. Extreme weather events risk to crop-production and the adaptation of innovative management strategies to mitigate the risk: A retrospective survey of rural Punjab, Pakistan. Technovation 2021, 117, 102255. [Google Scholar] [CrossRef]
- Li, R.; Hou, X.; Jia, Z.; Han, Q. Soil environment and maize productivity in semi-humid regions prone to drought of Weibei Highland are improved by ridge-and-furrow tillage with mulching. Soil Tillage Res. 2020, 196, 104476. [Google Scholar] [CrossRef]
- Akhtar, S.; Li, G.C.; Ullah, R.; Nazir, A.; Amjed, M.; Haseeb, M.; Iqbal, N.; Faisal, M. Factors influencing hybrid maize farmers’ risk attitudes and their perceptions in Punjab Province, Pakistan. J. Integr. Agric. 2018, 17, 1454–1462. [Google Scholar] [CrossRef]
- Anderson, J.R.; Dillon, J.L. Risk Analysis in Dryland Farming Systems (No. 2); Food and Agriculture Organization: Rome, Italy, 1992. [Google Scholar]
- Groom, B.; Koundouri, P.; Nauges, C.; Thomas, A. The story of the moment: Risk averse cypriot farmers respond to drought management. Appl. Econ. 2008, 40, 315–326. [Google Scholar] [CrossRef]
- Gaspar, A.P.; Mitchell, P.D.; Conley, S.P. Economic risk and profitability of soybean fungicide and insecticide seed treatments at reduced seeding rates. Crop Sci. 2015, 55, 924–933. [Google Scholar] [CrossRef]
- Gaspar, A.P.; Mueller, D.S.; Wise, K.A.; Chilvers, M.I.; Tenuta, A.U.; Conley, S.P. Response of Broad-Spectrum and Target-Specific Seed Treatments and Seeding Rate on Soybean Seed Yield, Profitability, and Economic Risk. Crop Sci. 2017, 57, 2251–2262. [Google Scholar] [CrossRef]
- Babcock, B.A.; Choi, E.K.; Feinerman, E. Risk and probability premiums for CARA utility functions. J. Agric. Resour. Econ. 1993, 18, 17–24. [Google Scholar]
- Boyer, C.N.; Stefanini, M.; Larson, J.A.; Smith, S.A.; Mengistu, A.; Bellaloui, N. Profitability and risk analysis of soybean planting date by maturity group. Agron. J. 2015, 107, 2253–2262. [Google Scholar] [CrossRef]
- Valvekar, M.; Chavas, J.P.; Gould, B.W.; Cabrera, V.E. Revenue risk management, risk aversion and the use of livestock gross margin for dairy cattle insurance. Agric. Syst. 2011, 104, 671–678. [Google Scholar] [CrossRef]
- Cormos, A.M.; Cormos, C.C. Techno-economic evaluations of post-combustion CO2 capture from sub-and super-critical circulated fluidised bed combustion (CFBC) power plants. Appl. Therm. Eng. 2017, 127, 106–115. [Google Scholar] [CrossRef]
- Gwak, Y.R.; Kim, Y.B.; Gwak, I.S.; Lee, S.H. Economic evaluation of synthetic ethanol production by using domestic biowastes and coal mixture. Fuel 2018, 213, 115–122. [Google Scholar] [CrossRef]
- Purola, T.; Lehtonen, H. Evaluating profitability of soil-renovation investments under crop rotation constraints in Finland. Agric. Syst. 2020, 180, 102762. [Google Scholar] [CrossRef]
- Cavalett, O.; Ortega, E. Emergy, nutrients balance, and economic assessment of soybean production and industrialization in Brazil. J. Clean. Prod. 2009, 17, 762–771. [Google Scholar] [CrossRef]
- Adler, P.R.; Hums, M.E.; McNeal, F.M.; Spatari, S. Evaluation of environmental and cost tradeoffs of producing energy from soybeans for on-farm use. J. Clean. Prod. 2019, 210, 1635–1649. [Google Scholar] [CrossRef]
- Kamali, F.P.; Borges, J.A.R.; Meuwissen, M.P.M.; De Boer, I.J.M.; Oude Lansink, A.G.J.M. Sustainability assessment of agricultural systems: The validity of expert opinion and robustness of a multi-criteria analysis. Agric. Syst. 2017, 157, 118–128. [Google Scholar] [CrossRef]
- Adusumilli, N.; Wang, H. Analysis of soil management and water conservation practices adoption among crop and pasture farmers in humid-south of the United States. Int. Soil Water Conserv. Res. 2018, 6, 79–86. [Google Scholar] [CrossRef]
- Adusumilli, N.; Wang, H. Conservation adoption among owners and tenant farmers in the Southern United States. Agriculture 2019, 9, 53. [Google Scholar] [CrossRef]
- Wang, H.; Adusumilli, N.; Gentry, D.; Fultz, L. Economic and stochastic efficiency analysis of alternative cover crop systems in Louisiana. Exp. Agric. 2020, 56, 651–661. [Google Scholar] [CrossRef]
- Gang, X.; Huabing, L.; Yufu, P.; Tiezhao, Y.; Xi, Y.; Shixiao, X. Plastic film mulching combined with nutrient management to improve water use efficiency, production of rain-fed maize and economic returns in semi-arid regions. Field Crops Res. 2019, 231, 30–39. [Google Scholar] [CrossRef]
- Lee, S.H.; Lee, T.H.; Jeong, S.M.; Lee, J.M. Economic analysis of a 600 mwe ultra supercritical circulating fluidized bed power plant based on coal tax and biomass co-combustion plans. Renew. Energy 2019, 138, 121–127. [Google Scholar] [CrossRef]
- Adusumilli, N.; Davis, S.; Fromme, D. Economic evaluation of using surge valves in furrow irrigation of row crops in Louisiana: A net present value approach. Agric. Water Manag. 2016, 174, 61–65. [Google Scholar] [CrossRef]
- Hernandez-Torres, D.; Bridier, L.; David, M.; Lauret, P.; Ardiale, T. Technico-economical analysis of a hybrid wave power-air compression storage system. Renew. Energy 2015, 74, 708–717. [Google Scholar] [CrossRef]
- Gwak, I.S.; Hwang, J.H.; Sohn, J.M.; Lee, S.H. Economic evaluation of domestic biowaste to ethanol via a fluidized bed gasifier. J. Ind. Eng. Chem. 2017, 47, 391–398. [Google Scholar] [CrossRef]
- Hardaker, J.B.; Richardson, J.W.; Lien, G.; Schumann, K.D. Stochastic efficiency analysis with risk aversion bounds: A simplified approach. Aust. J. Agric. Resour. Econ. 2004, 48, 253–270. [Google Scholar] [CrossRef]
- Adusumilli, N.; Wang, H.; Dodla, S.; Deliberto, M. Estimating risk premiums for adopting no-till and cover crops production systems in soybean production system using stochastic efficiency approach. Agric. Syst. 2020, 178, 102744. [Google Scholar] [CrossRef]
- Meyer, J. Expected utility as a paradigm for decision making in agriculture. In A Comprehensive Assessment of the Role of Risk in US Agriculture; Springer: Boston, MA, USA, 2002; pp. 3–19. [Google Scholar]
- Schumann, K.D.; Richardson, J.W.; Lien, G.D.; Hardaker, J.B. Stochastic Efficiency Analysis Using Multiple Utility Functions. In Proceedings of the Association Annual Meeting, Denver, CO, USA, 1–4 August 2004. [Google Scholar]
- Abdulkadri, A.O. Estimating risk aversion coefficients for dry land wheat, irrigated corn and dairy producers in Kansas. Appl. Econ. 2003, 35, 825–834. [Google Scholar] [CrossRef]
- Saha, A. Expo-power utility: A ‘flexible’form for absolute and relative risk aversion. Am. J. Agric. Econ. 1993, 75, 905–913. [Google Scholar] [CrossRef]
- Sulewski, P.; Wąs, A.; Kobus, P.; Pogodzińska, K.; Szymańska, M.; Sosulski, T. Farmers’ Attitudes towards Risk—An Empirical Study from Poland. Agronomy 2020, 10, 1555. [Google Scholar] [CrossRef]
- Watkins, K.B.; Hill, J.L.; Anders, M.M. An economic risk analysis of no-till management and rental arrangements in Arkansas rice production. J. Soil Water Conserv. 2008, 63, 242–250. [Google Scholar] [CrossRef]
- Williams, J.R.; Llewelyn, R.V.; Pendell, D.L.; Schlegel, A.; Dumler, T. A Risk Analysis of Converting Conservation Reserve Program Acres to a Wheat-Sorghum-Fallow Rotation. Agron. J. 2010, 102, 612–622. [Google Scholar] [CrossRef]
- Van der Werf, H.M.G.; Knudsen, M.T.; Cederberg, C. Towards better representation of organic agriculture in life cycle assessment. Nat. Sustain. 2020, 3, 419–425. [Google Scholar] [CrossRef]
- Greer, K.; Martins, C.; White, M.; Pittelkow, C.M. Assessment of high-input soybean management in the US Midwest: Balancing crop production with environmental performance. Agric. Ecosyst. Environ. 2020, 292, 106811. [Google Scholar] [CrossRef]
- Boyer, C.N.; Lambert, D.M.; Larson, J.A.; Tyler, D.D. Investment analysis of cover crop and no-tillage systems on Tennessee cotton. Agron. J. 2018, 110, 331–338. [Google Scholar] [CrossRef]
- Razzaq, A.; Xiao, M.; Zhou, Y.; Liu, H.; Abbas, A.; Liang, W.; Naseer, M.A.U.R. Impact of Participation in Groundwater Market on Farmland, Income and Water Access: Evidence from Pakistan. Water 2022, 14, 1832. [Google Scholar] [CrossRef]
- Shi, Y.; Huang, G.; An, C.; Zhou, Y.; Yin, J. Assessment of regional greenhouse gas emissions from spring wheat cropping system: A case study of Saskatchewan in Canada. J. Clean. Prod. 2021, 301, 126917. [Google Scholar] [CrossRef]
- Battisti, R.; Ferreira MD, P.; Tavares, É.B.; Knapp, F.M.; Bender, F.D.; Casaroli, D.; Júnior, J.A. Rules for grown soybean-maize cropping system in midwestern Brazil: Food production and economic profits. Agric. Syst. 2020, 182, 102850. [Google Scholar] [CrossRef]
- Yang, G.T.; Li, J.; Liu, Z.; Zhang, Y.; Xu, X.; Zhang, H.; Xu, Y. Research trends in crop-livestock systems: A bibliometric review. Int. J. Environ. Res. Public Health 2022, 19, 8563. [Google Scholar] [CrossRef]


| Soil Properties | 2019–2020 | 2020–2021 |
|---|---|---|
| Organic matter (g kg−1) | 12.50 | 14.30 |
| Total nitrogen (g kg−1) | 0.87 | 0.90 |
| Nitrate nitrogen (mg kg−1) | 76.30 | 82.30 |
| Available phosphorus (mg kg−1) | 23.30 | 25.30 |
| Available potassium (mg kg−1) | 133.80 | 145.70 |
| pH (water) | 8.10 | 8.00 |
| Dry bulk density (g cm−3) | 1.40 | 1.41 |
| Field capacity (%) | 24.00 | 23.90 |
| Permanent wilting point (%) | 8.50 | 8.50 |
| Management Practice | Main Plot | Split Plot | Re-Split Plot |
|---|---|---|---|
| A | D1 (160,000 plants ha−1) | F1: 20 kg ha−1 N, 30 kg ha−1 P, 30 kg ha−1 K | R+W0 |
| B | R+W1 | ||
| C | F+W0 | ||
| D | F2: 40 kg ha−1 N, 60 kg ha−1 P, 60 kg ha−1 K | R+W0 | |
| E | R+W1 | ||
| F | F+W0 | ||
| G | D2 (320,000 plants ha−1) | F1: 20 kg ha−1 N, 30 kg ha−1 P, 30 kg ha−1 K | R+W0 |
| H | R+W1 | ||
| I | F+W0 | ||
| J | F2: 40 kg ha−1 N, 60 kg ha−1 P, 60 kg ha−1 K | R+W0 | |
| K | R+W1 | ||
| L | F+W0 |
| Production Systems | Mean | St. Dev. | CV | Minimum | Maximum |
|---|---|---|---|---|---|
| A | 3150.5 | 206.9 | 6.57% | 2906.0 | 3439.2 |
| B | 3206.0 | 222.2 | 6.93% | 2886.6 | 3458.7 |
| C | 2853.4 | 219.1 | 7.68% | 2614.1 | 3085.6 |
| D | 3415.7 | 279.7 | 8.19% | 3150.3 | 3742.6 |
| E | 3454.0 | 263.5 | 7.63% | 3183.2 | 3791.8 |
| F | 3135.2 | 190.1 | 6.06% | 2945.6 | 3414.8 |
| G | 3950.8 | 214.6 | 5.43% | 3691.1 | 4307.2 |
| H | 3989.4 | 180.9 | 4.53% | 3706.4 | 4124.1 |
| I | 3551.8 | 228.7 | 6.44% | 3335.5 | 3845.6 |
| J | 4338.9 | 201.1 | 4.63% | 4066.5 | 4590.1 |
| K | 4423.0 | 246.9 | 5.58% | 4022.4 | 4695.9 |
| L | 3904.4 | 164.7 | 4.22% | 3687.9 | 4103.2 |
| Expense Item (CNY ha−1) | FHPC (CNY ha−1) | SC (CNY ha−1) | PFC (CNY ha−1) | IWC (CNY ha−1) | MFC (CNY ha−1) | LC (CNY ha−1) | IV (CNY ha−1) | |
|---|---|---|---|---|---|---|---|---|
| Production Systems | ||||||||
| A | 1431.35 | 1732.50 | 803.92 | 0.00 | 2029.67 | 450.00 | 6447.44 | |
| B | 1431.35 | 1732.50 | 803.92 | 120.00 | 2083.66 | 600.00 | 6771.43 | |
| C | 1431.35 | 1732.50 | 0.00 | 0.00 | 1733.90 | 450.00 | 5347.75 | |
| D | 2459.67 | 1732.50 | 803.92 | 0.00 | 2122.74 | 675.00 | 7793.83 | |
| E | 2459.67 | 1732.50 | 803.92 | 120.00 | 2268.05 | 825.00 | 8209.14 | |
| F | 2459.67 | 1732.50 | 0.00 | 0.00 | 1879.48 | 675.00 | 6746.65 | |
| G | 1528.85 | 3465.00 | 1089.74 | 0.00 | 2511.77 | 750.00 | 9345.36 | |
| H | 1528.85 | 3465.00 | 1089.74 | 120.00 | 2695.10 | 900.00 | 9798.69 | |
| I | 1528.85 | 3465.00 | 0.00 | 0.00 | 2186.12 | 750.00 | 7929.96 | |
| J | 2600.19 | 3465.00 | 1089.74 | 0.00 | 2667.34 | 975.00 | 10,797.27 | |
| K | 2600.19 | 3465.00 | 1089.74 | 120.00 | 2802.24 | 1125.00 | 11,202.18 | |
| L | 2600.19 | 3465.00 | 0.00 | 0.00 | 2324.94 | 975.00 | 9365.13 | |
| Production Systems | Mean | St. Dev. | CV | Minimum | Maximum |
|---|---|---|---|---|---|
| A | 7592.88 | 1684.32 | 22.18% | 4705.64 | 12,783.04 |
| B | 7555.69 | 1767.98 | 23.40% | 4266.70 | 12,774.65 |
| C | 7128.37 | 1544.33 | 21.66% | 4556.73 | 11,899.56 |
| D | 7407.10 | 1888.32 | 25.49% | 4284.87 | 13,270.30 |
| E | 7230.09 | 1889.81 | 26.14% | 4074.28 | 13,229.71 |
| F | 7190.93 | 1627.47 | 22.63% | 4498.81 | 12,426.98 |
| G | 8401.32 | 2048.71 | 24.39% | 4985.11 | 15,117.28 |
| H | 8378.72 | 2065.40 | 24.65% | 4666.09 | 14,594.08 |
| I | 8206.07 | 1882.86 | 22.94% | 5141.01 | 13,999.36 |
| J | 8982.53 | 2208.50 | 24.59% | 5170.27 | 15,537.08 |
| K | 8829.51 | 2287.72 | 25.91% | 4621.10 | 15,690.02 |
| L | 8718.78 | 2095.96 | 24.04% | 5214.48 | 15,539.96 |
| Production Systems | IV | NIa | NImin | NImax | NPV1 at the Beginning of the First Year | NPV2 at the End of the First Year | NPV3 at the Beginning of the Second Year | NPV4 at the End of the Second Year (CNY) |
|---|---|---|---|---|---|---|---|---|
| A | 6447.44 | 7592.88 | 4705.64 | 12,783.04 | −IV | NI − i × IV | NI − (1 + i) × IV | (1) 2 × NI − i × IV, (CNY3 ≥ 0); (2) (2 + i) × NI − (2i + i2) × IV, (CNY3 < 0) |
| B | 6771.43 | 7555.69 | 4266.7 | 12,774.65 | ||||
| C | 5347.75 | 7128.37 | 4556.73 | 11,899.56 | ||||
| D | 7793.83 | 7407.10 | 4284.87 | 13,270.3 | ||||
| E | 8209.14 | 7230.09 | 4074.28 | 13,229.71 | ||||
| F | 6746.65 | 7190.93 | 4498.81 | 12,426.98 | ||||
| G | 9345.36 | 8401.32 | 4985.11 | 15,117.28 | ||||
| H | 9798.69 | 8378.72 | 4666.09 | 14,594.08 | ||||
| I | 7929.96 | 8206.07 | 5141.01 | 13,999.36 | ||||
| J | 10,797.27 | 8982.53 | 5170.27 | 15,537.08 | ||||
| K | 11,202.18 | 8829.51 | 4621.1 | 15,690.02 | ||||
| L | 9365.13 | 8718.78 | 5214.48 | 15,539.96 |
| Absolute Risk Aversion Coefficient (ARAC) | |||||
|---|---|---|---|---|---|
| 0.000 | 0.013 | 0.026 | 0.039 | 0.052 | |
| Production systems | Certainty Equivalents (CNY ha−1) | ||||
| A | 7592.88 | 7418.43 | 7262.73 | 7124.30 | 7001.13 |
| B | 7555.69 | 7362.83 | 7189.39 | 7033.80 | 6893.91 |
| C | 7128.37 | 6981.18 | 6848.66 | 6729.79 | 6623.19 |
| D | 7407.10 | 7189.15 | 6997.01 | 6828.21 | 6679.74 |
| E | 7230.09 | 7011.46 | 6818.13 | 6647.73 | 6497.26 |
| F | 7190.93 | 7028.32 | 6883.72 | 6755.74 | 6642.47 |
| G | 8401.32 | 8147.49 | 7929.05 | 7741.86 | 7580.91 |
| H | 8378.72 | 8119.70 | 7895.01 | 7700.80 | 7532.06 |
| I | 8206.07 | 7989.72 | 7799.87 | 7634.04 | 7488.99 |
| J | 8982.53 | 8575.59 | 8218.44 | 7904.20 | 7624.95 |
| K | 8829.51 | 8513.23 | 8241.66 | 8008.86 | 7807.52 |
| L | 8718.78 | 8452.97 | 8223.86 | 8027.08 | 7857.44 |
| Risk premiums (CNY ha−1) | |||||
| A | 401.95 | 390.11 | 379.01 | 368.56 | 358.65 |
| B | 364.76 | 334.51 | 305.67 | 278.06 | 251.44 |
| C | −62.55 | −47.14 | −35.06 | −25.95 | −19.29 |
| D | 216.17 | 160.83 | 113.28 | 72.47 | 37.26 |
| E | 39.17 | −16.86 | −65.59 | −108.02 | −145.21 |
| F | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 |
| G | 1210.39 | 1119.17 | 1045.32 | 986.12 | 938.43 |
| H | 1187.80 | 1091.37 | 1011.28 | 945.06 | 889.59 |
| I | 1015.14 | 961.40 | 916.15 | 878.30 | 846.51 |
| J | 1791.61 | 1547.27 | 1334.71 | 1148.46 | 982.48 |
| K | 1638.58 | 1484.91 | 1357.94 | 1253.12 | 1165.04 |
| L | 1527.86 | 1424.65 | 1340.13 | 1271.34 | 1214.96 |
| Production Systems | Mean | St. Dev. | CV | Minimum | Maximum |
|---|---|---|---|---|---|
| A | 2.178 | 0.264 | 12.11% | 1.721 | 2.990 |
| B | 2.116 | 0.262 | 12.37% | 1.628 | 2.879 |
| C | 2.333 | 0.290 | 12.41% | 1.857 | 3.227 |
| D | 1.950 | 0.241 | 12.38% | 1.552 | 2.702 |
| E | 1.880 | 0.228 | 12.14% | 1.496 | 2.594 |
| F | 2.066 | 0.242 | 11.70% | 1.670 | 2.845 |
| G | 1.899 | 0.219 | 11.52% | 1.536 | 2.613 |
| H | 1.855 | 0.210 | 11.34% | 1.478 | 2.482 |
| I | 2.035 | 0.236 | 11.62% | 1.648 | 2.763 |
| J | 1.832 | 0.204 | 11.12% | 1.480 | 2.429 |
| K | 1.788 | 0.203 | 11.34% | 1.411 | 2.382 |
| L | 1.931 | 0.222 | 11.52% | 1.557 | 2.651 |
| Absolute Risk Aversion Coefficient (ARAC) | |||||
|---|---|---|---|---|---|
| 0.000 | 0.005 | 0.010 | 0.015 | 0.020 | |
| Production Systems | Certainty Equivalents | ||||
| A | 2.178 | 2.161 | 2.146 | 2.131 | 2.117 |
| B | 2.116 | 2.099 | 2.084 | 2.069 | 2.055 |
| C | 2.333 | 2.313 | 2.294 | 2.277 | 2.261 |
| D | 1.950 | 1.936 | 1.923 | 1.910 | 1.899 |
| E | 1.880 | 1.868 | 1.856 | 1.844 | 1.834 |
| F | 2.066 | 2.042 | 2.018 | 1.996 | 1.974 |
| G | 1.899 | 1.887 | 1.876 | 1.866 | 1.856 |
| H | 1.855 | 1.844 | 1.834 | 1.824 | 1.815 |
| I | 2.035 | 2.021 | 2.008 | 1.996 | 1.985 |
| J | 1.832 | 1.813 | 1.794 | 1.776 | 1.759 |
| K | 1.788 | 1.778 | 1.768 | 1.759 | 1.751 |
| L | 1.931 | 1.919 | 1.907 | 1.897 | 1.887 |
| Production-to-investment ratio spillover | |||||
| A | 0.112 | 0.120 | 0.127 | 0.135 | 0.143 |
| B | 0.050 | 0.058 | 0.065 | 0.073 | 0.081 |
| C | 0.267 | 0.271 | 0.276 | 0.281 | 0.286 |
| D | −0.116 | −0.106 | −0.095 | −0.086 | −0.076 |
| E | −0.186 | −0.174 | −0.163 | −0.151 | −0.141 |
| F | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
| G | −0.167 | −0.154 | −0.142 | −0.130 | −0.118 |
| H | −0.211 | −0.197 | −0.184 | −0.171 | −0.159 |
| I | −0.031 | −0.021 | −0.010 | 0.001 | 0.011 |
| J | −0.234 | −0.229 | −0.224 | −0.220 | −0.216 |
| K | −0.278 | −0.264 | −0.250 | −0.236 | −0.224 |
| L | −0.135 | −0.123 | −0.111 | −0.099 | −0.088 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liao, Z.; Pei, S.; Bai, Z.; Lai, Z.; Wen, L.; Zhang, F.; Li, Z.; Fan, J. Economic Evaluation and Risk Premium Estimation of Rainfed Soybean under Various Planting Practices in a Semi-Humid Drought-Prone Region of Northwest China. Agronomy 2023, 13, 2840. https://doi.org/10.3390/agronomy13112840
Liao Z, Pei S, Bai Z, Lai Z, Wen L, Zhang F, Li Z, Fan J. Economic Evaluation and Risk Premium Estimation of Rainfed Soybean under Various Planting Practices in a Semi-Humid Drought-Prone Region of Northwest China. Agronomy. 2023; 13(11):2840. https://doi.org/10.3390/agronomy13112840
Chicago/Turabian StyleLiao, Zhenqi, Shengzhao Pei, Zhentao Bai, Zhenlin Lai, Lei Wen, Fucang Zhang, Zhijun Li, and Junliang Fan. 2023. "Economic Evaluation and Risk Premium Estimation of Rainfed Soybean under Various Planting Practices in a Semi-Humid Drought-Prone Region of Northwest China" Agronomy 13, no. 11: 2840. https://doi.org/10.3390/agronomy13112840
APA StyleLiao, Z., Pei, S., Bai, Z., Lai, Z., Wen, L., Zhang, F., Li, Z., & Fan, J. (2023). Economic Evaluation and Risk Premium Estimation of Rainfed Soybean under Various Planting Practices in a Semi-Humid Drought-Prone Region of Northwest China. Agronomy, 13(11), 2840. https://doi.org/10.3390/agronomy13112840








