Root Location and Root Diameter Estimation of Trees Based on Deep Learning and Ground-Penetrating Radar
Abstract
:1. Introduction
2. Materials and Methods
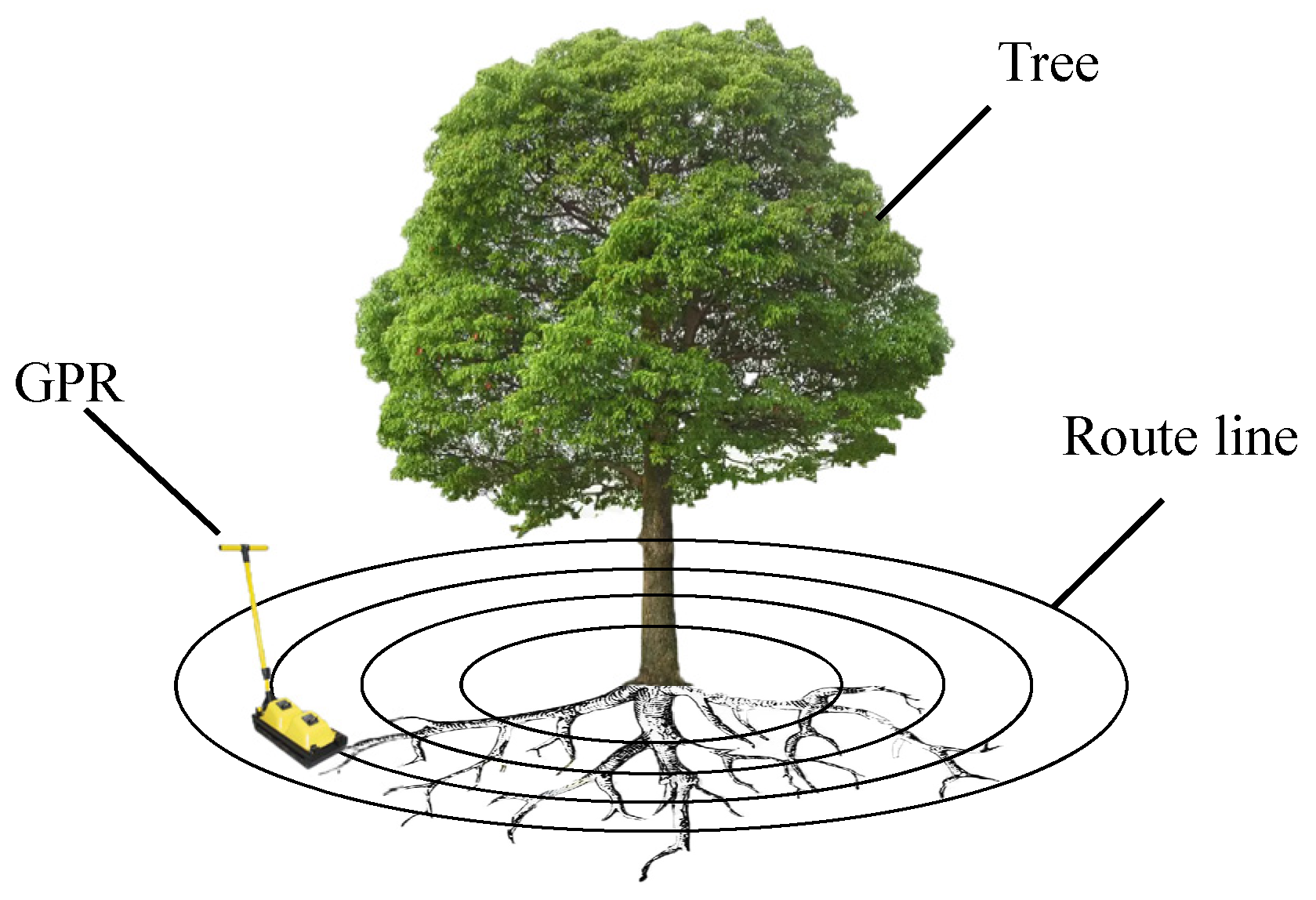
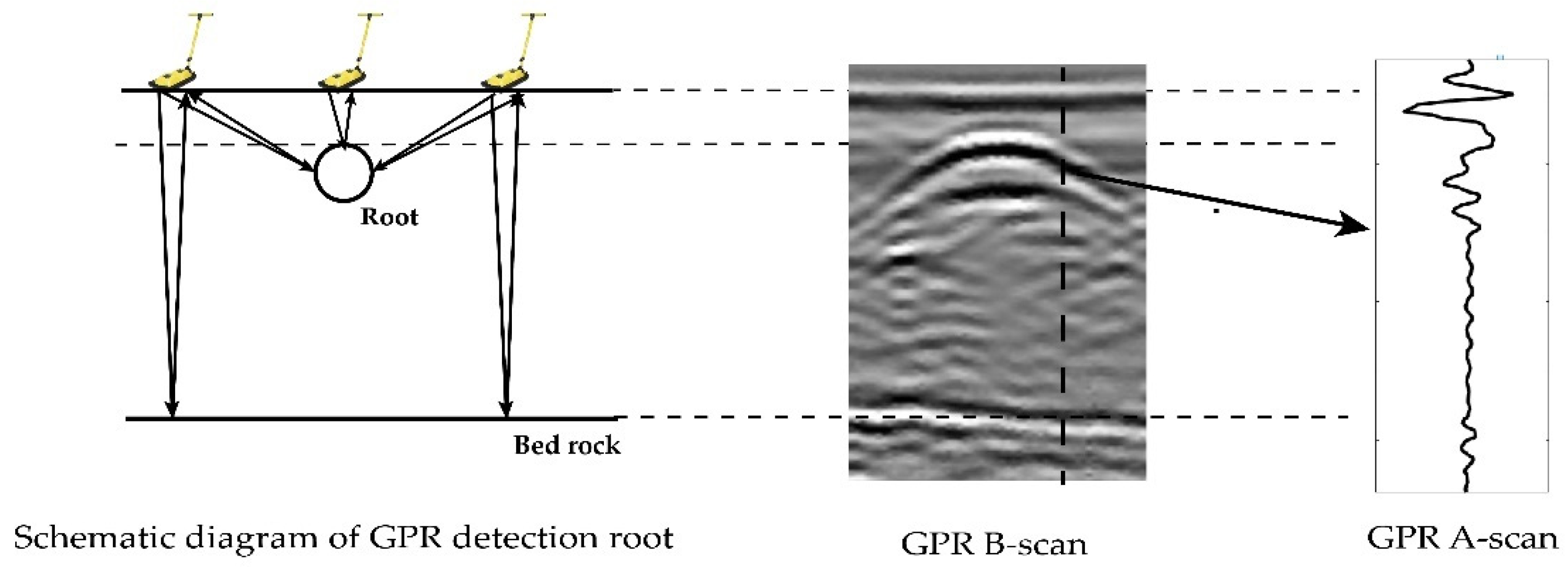
2.1. GPR Detection Methods and Imaging Principles
2.2. Model Training
2.2.1. Data Pre-Processing
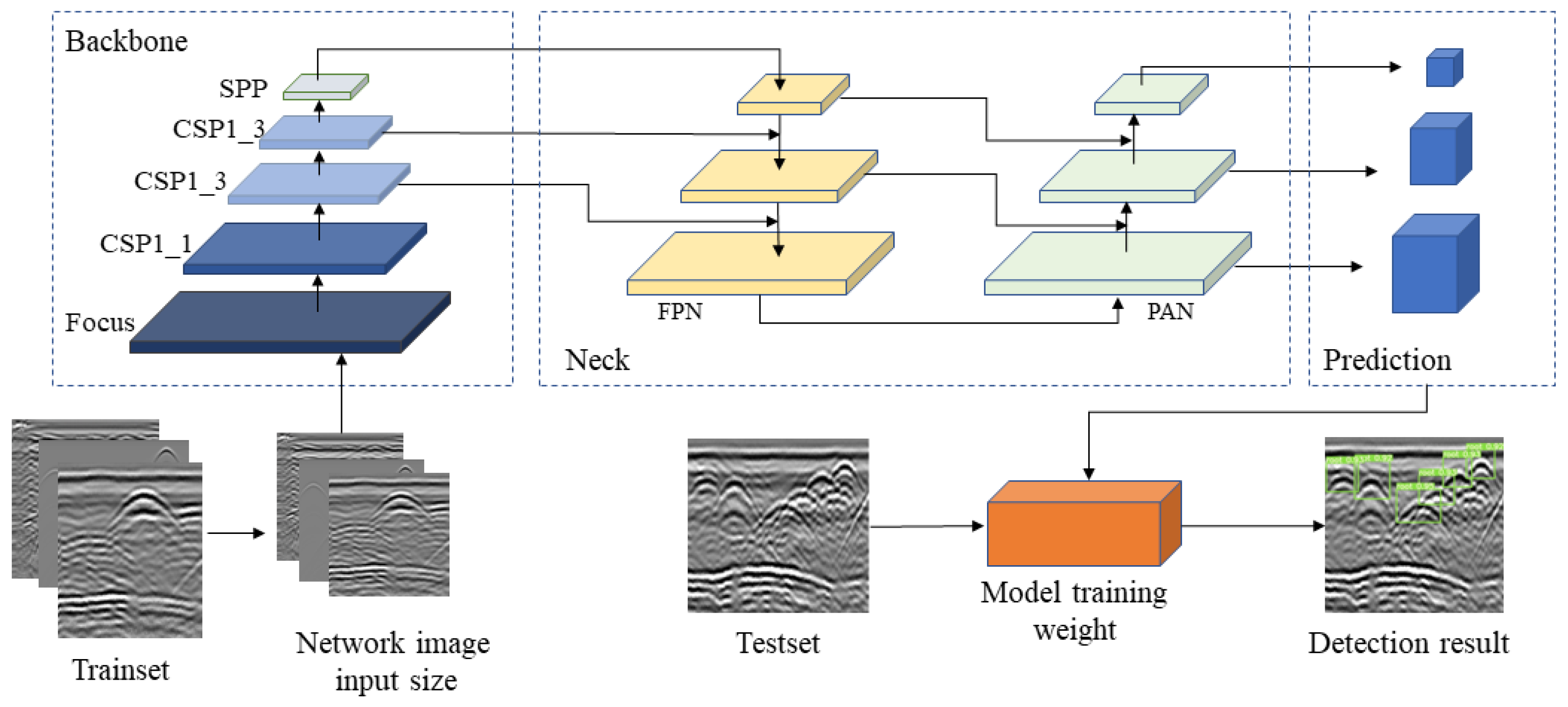
2.2.2. YOLOv5s Network Model
2.2.3. Model Evaluation Indicators
2.2.4. Experimental Environment and Parameter Settings
2.3. Root System Localization and Root Diameter Estimation Using the TPFC Method
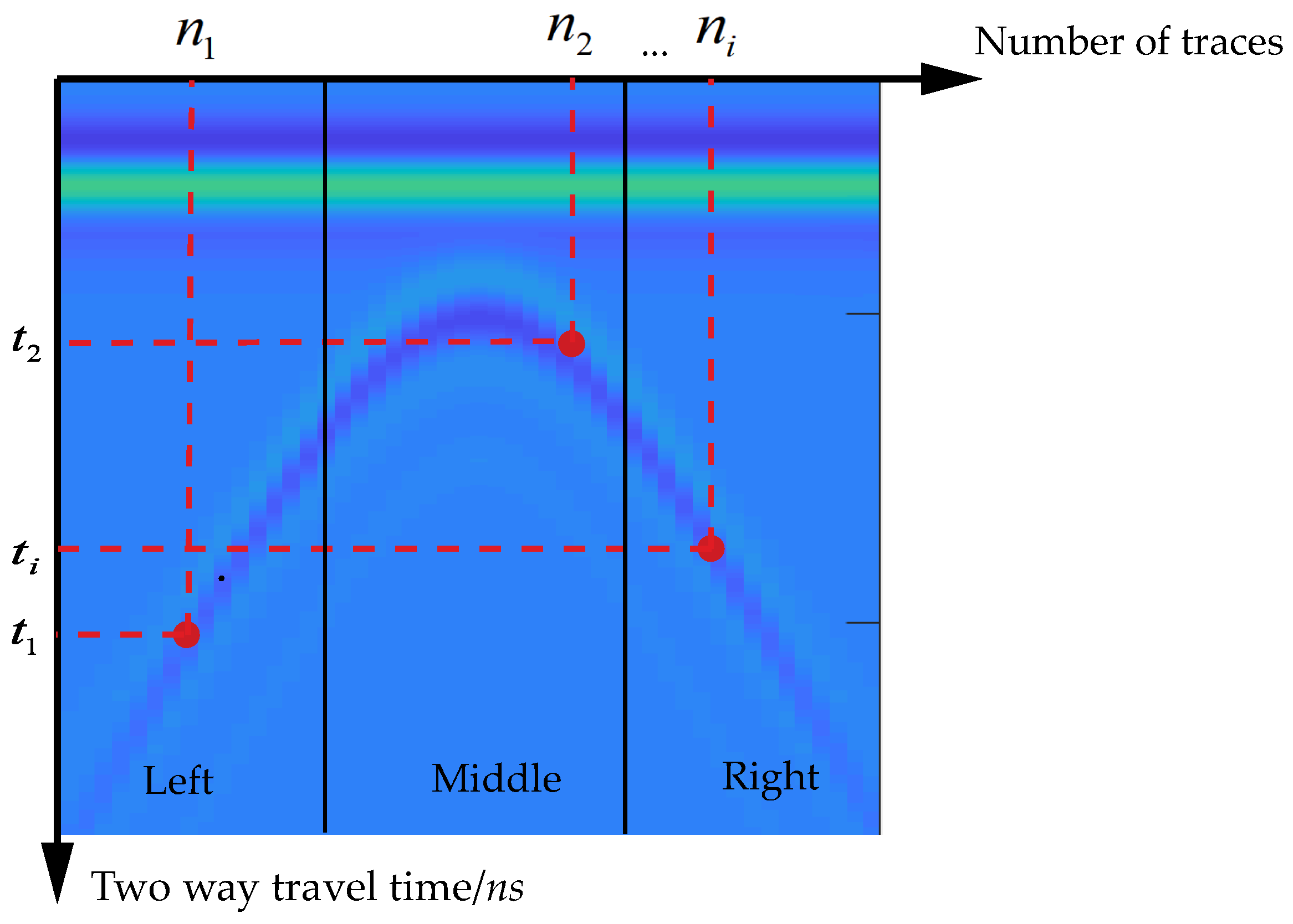
2.3.1. Principle of TPFC Method
2.3.2. Experimental Design
- Simulation test
- 2.
- Pre-buried root test
- 3.
- Field test
2.4. Root System Localization and Root Diameter Estimation Method for Trees Using Ground-Penetrating Radar
- Acquisition of B-scan image data collected by ground-penetrating radar, whose specific steps are shown in Section 2.1.
- Image pre-processing. Its main purpose is to reduce the noise related information in the ground-penetrating radar data, and its main operations include zero correction, background removal, and image gain and filtering [27,28], with the related operations mainly completed on EKKO_Project4 software and MATLAB. In the zero correction, the time point was calibrated when the electromagnetic wave emitted from the radar antenna reached the ground; in the background removal, the mean reference value was gained by subtracting the background noise date from all B-scan trace data. The image gain mainly adopted automatic gain and spherical wave index compensation, and the image filtering mainly refers to Gaussian filtering, etc.
- The trained YOLOv5s were used to detect the target hyperbolas in the B-scan images, which generated the region of interest (ROI) containing only one root target hyperbola, and sent back the coordinate information of the target borders. The specific training method is shown in Section 2.2.
- The image was processed within the region of interest to extract the feature information of the hyperbolas. Its main operations include image clustering, image segmentation, and edge detection [29]. Image clustering was to cluster independent hyperbolas and separate the intersecting hyperbolas using the column connection clustering (C3) algorithm [30] proposed by Dou et al. Image segmentation refers to the binarized image segmentation using the OSTU algorithm, and after the segmented image was obtained, the Canny operator or Sobel operator was used to perform edge detection on the segmented image.
- After three or more coordinate points on the hyperbola were selected, the center point (x, y) of the root was located and the root diameter was estimated using the TPFC method, as shown in Section 2.3.
3. Results
3.1. Experimental Analysis of Root Detection Based on YOLOv5s
3.2. Root System Localization and Root Diameter Estimation Results
3.2.1. Simulation Test Results
3.2.2. Pre-Buried Root Test Results
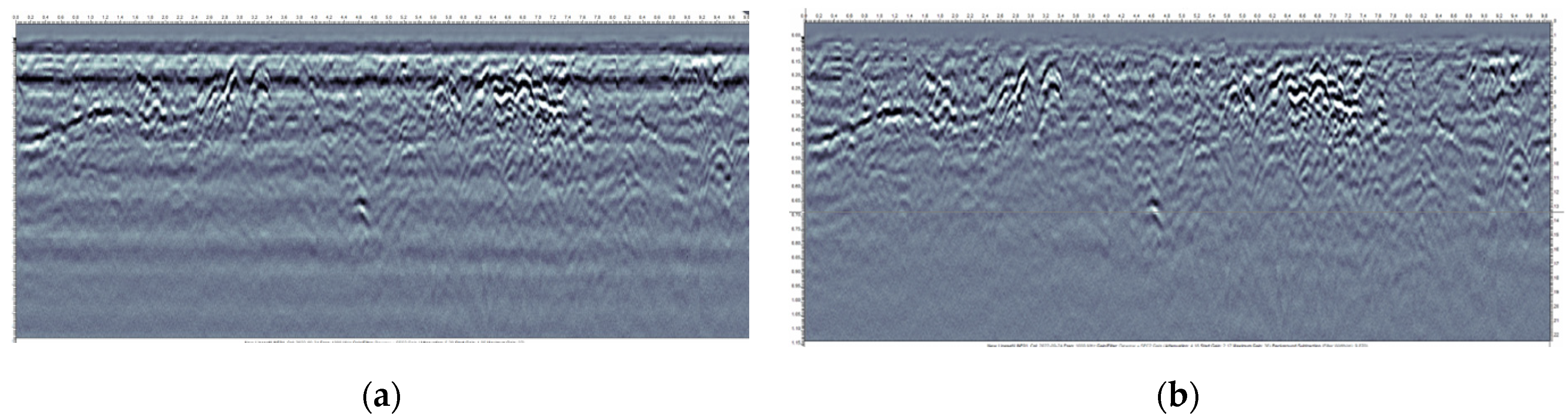
3.2.3. Field Test Results
4. Discussion
4.1. Discussion on Root Detection Test Results Based on YOLOv5s
4.2. Discussion on Root Positioning and Root Diameter Estimation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lynch, J.P. Root Phenotypes for Improved Nutrient Capture: An Underexploited Opportunity for Global Agriculture. New Phytol. 2019, 223, 548–564. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, L.; Cui, X.; Quan, Z. Availability of ground penetrating radar in recognizing plant roots in field. Prog. Geophys. 2021, 36, 2764–2774. [Google Scholar]
- Cabal, C.; De Deurwaerder, H.P.T.; Matesanz, S. Field Methods to Study the Spatial Root Density Distribution of Individual Plants. Plant Soil 2021, 462, 25–43. [Google Scholar] [CrossRef]
- Zhang, X.; Derival, M.; Albrecht, U.; Ampatzidis, Y. Evaluation of a Ground Penetrating Radar to Map the Root Architecture of HLB-Infected Citrus Trees. Agronomy 2019, 9, 354. [Google Scholar] [CrossRef] [Green Version]
- Molon, M.; Boyce, J.I.; Arain, M.A. Quantitative, Nondestructive Estimates of Coarse Root Biomass in a Temperate Pine Forest Using 3-D Ground-Penetrating Radar (GPR). J. Geophys. Res.-Biogeosci. 2017, 122, 80–102. [Google Scholar] [CrossRef]
- Alani, A.M.; Lantini, L. Recent Advances in Tree Root Mapping and Assessment Using Non-Destructive Testing Methods: A Focus on Ground Penetrating Radar. Surv. Geophys. 2020, 41, 605–646. [Google Scholar] [CrossRef]
- Weigand, M.; Kemna, A. Multi-Frequency Electrical Impedance Tomography as a Non-Invasive Tool to Characterize and Monitor Crop Root Systems. Biogeosciences 2017, 14, 921–939. [Google Scholar] [CrossRef] [Green Version]
- Shamir, O.; Goldshleger, N.; Basson, U.; Reshef, M. Laboratory Measurements of Subsurface Spatial Moisture Content by Ground-Penetrating Radar (GPR) Diffraction and Reflection Imaging of Agricultural Soils. Remote Sens. 2018, 10, 1667. [Google Scholar] [CrossRef] [Green Version]
- Streda, T.; Haberle, J.; Klimesova, J.; Klimek-Kopyra, A.; Stredova, H.; Bodner, G.; Chloupek, O. Field Phenotyping of Plant Roots by Electrical Capacitance—A Standardized Methodological Protocol for Application in Plant Breeding: A Review. Int. Agrophysics 2020, 34, 173–184. [Google Scholar] [CrossRef]
- Liu, X.; Cui, X.; Guo, L.; Chen, J.; Li, W.; Yang, D.; Cao, X.; Chen, X.; Liu, Q.; Lin, H. Non-Invasive Estimation of Root Zone Soil Moisture from Coarse Root Reflections in Ground-Penetrating Radar Images. Plant Soil 2019, 436, 623–639. [Google Scholar] [CrossRef]
- Liu, X.; Dong, X.; Leskovar, D.I. Ground Penetrating Radar for Underground Sensing in Agriculture: A Review. Int. Agrophysics 2016, 30, 533–543. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Wen, J.; Li, W. Qualitative Research: The Impact of Root Orientation on Coarse Roots Detection Using Ground-Penetrating Radar (GPR). Bioresources 2020, 15, 2237–2257. [Google Scholar] [CrossRef]
- Yamase, K.; Tanikawa, T.; Dannoura, M.; Ohashi, M.; Todo, C.; Ikeno, H.; Aono, K.; Hirano, Y. Ground-Penetrating Radar Estimates of Tree Root Diameter and Distribution under Field Conditions. Trees-Struct. Funct. 2018, 32, 1657–1668. [Google Scholar] [CrossRef]
- Hou, F.; Shi, R.; Lei, W.; Dong, J.; Xu, M.; Xi, J. A Review of Target Detection Algorithm for GPR B-scan Processing. Ournal Electron. Inf. Technol. 2020, 42, 191–200. [Google Scholar]
- Zhang, X.; Xue, F.; Wang, Z.; Wen, J.; Guan, C.; Wang, F.; Han, L.; Ying, N. A Novel Method of Hyperbola Recognition in Ground Penetrating Radar (GPR) B-Scan Image for Tree Roots Detection. Forests 2021, 12, 1019. [Google Scholar] [CrossRef]
- Li, W.; Cui, X.; Guo, L.; Chen, J.; Chen, X.; Cao, X. Tree Root Automatic Recognition in Ground Penetrating Radar Profiles Based on Randomized Hough Transform. Remote Sens. 2016, 8, 430. [Google Scholar] [CrossRef] [Green Version]
- Maas, C.; Schmalzl, J. Using Pattern Recognition to Automatically Localize Reflection Hyperbolas in Data from Ground Penetrating Radar. Comput. Geosci. 2013, 58, 116–125. [Google Scholar] [CrossRef]
- Wang, Y.; Cui, G.; Xu, J. Semi-Automatic Detection of Buried Rebar in GPR Data Using a Genetic Algorithm. Autom. Constr. 2020, 114, 103186. [Google Scholar] [CrossRef]
- Li, S.; Cui, X.; Guo, L.; Zhang, L.; Chen, X.; Cao, X. Enhanced Automatic Root Recognition and Localization in GPR Images Through a YOLOv4-Based Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5114314. [Google Scholar] [CrossRef]
- Liu, H.; Lin, C.; Cui, J.; Fan, L.; Xie, X.; Spencer, B.F. Detection and Localization of Rebar in Concrete by Deep Learning Using Ground Penetrating Radar. Autom. Constr. 2020, 118, 103279. [Google Scholar] [CrossRef]
- Sun, H.-H.; Lee, Y.H.; Dai, Q.; Li, C.; Ow, G.; Yusof, M.L.M.; Yucel, A.C. Estimating Parameters of the Tree Root in Heterogeneous Soil Environments via Mask-Guided Multi-Polarimetric Integration Neural Network. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5108716. [Google Scholar] [CrossRef]
- Pham, M.-T.; Lefèvre, S. Buried Object Detection from B-Scan Ground Penetrating Radar Data Using Faster-RCNN. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 6804–6807. [Google Scholar]
- Hou, F.; Lei, W.; Li, S.; Xi, J. Deep Learning-Based Subsurface Target Detection From GPR Scans. IEEE Sens. J. 2021, 21, 8161–8171. [Google Scholar] [CrossRef]
- Qiu, Z.; Zhao, Z.; Chen, S.; Zeng, J.; Huang, Y.; Xiang, B. Application of an Improved YOLOv5 Algorithm in Real-Time Detection of Foreign Objects by Ground Penetrating Radar. Remote Sens. 2022, 14, 1895. [Google Scholar] [CrossRef]
- Zhang, P.; Dong, T.; Ma, B.; Wang, X. Research on Interpreting the Information of Underground Pipeline’s Diameter Detected by GPR. Chin. J. Undergr. Space Eng. 2015, 11, 1023–1032. [Google Scholar]
- Zhou, L.; Yu, D.; Wang, X.; Wang, X.; Zhang, H. Determination of Top Soil Water Content Based on High-frequency Ground Penetrating Radar. Acta Pedol. Sin. 2016, 53, 621–626. [Google Scholar]
- Wang, Z.; Zhang, X.; Xue, F.; Wen, J.; Han, H.; Huang, Y. Estimating the location and diameter of tree roots using ground penetrating radar. Trans. Chin. Soc. Agric. Eng. 2021, 37, 160–168. [Google Scholar]
- Srimuk, P.; Boonpoonga, A.; Kaemarungsi, K.; Athikulwongse, K.; Dentri, S. Implementation of and Experimentation with Ground-Penetrating Radar for Real-Time Automatic Detection of Buried Improvised Explosive Devices. Sensors 2022, 22, 8710. [Google Scholar] [CrossRef] [PubMed]
- Lan, X.; Lai, B.; Zhou, D.; Wu, Y.; Sun, X.; Ye, H. GPR B-Scan hyperbola extraction based on multi-layer fusion processing. Electron. Meas. Technol. 2021, 44, 97–103. [Google Scholar] [CrossRef]
- Dou, Q.; Wei, L.; Magee, D.R.; Cohn, A.G. Real-Time Hyperbola Recognition and Fitting in GPR Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Zhao, Z.; Luo, Y.; Qiu, Z. Real-Time Pattern-Recognition of GPR Images with YOLO v3 Implemented by Tensorflow. Sensors 2020, 20, 6476. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Li, N.; Wu, R.; Wang, H.; Gui, Z.; Song, D. GPR-RCNN: An Algorithm of Subsurface Defect Detection for Airport Runway Based on GPR. IEEE Robot. Autom. Lett. 2021, 6, 3001–3008. [Google Scholar] [CrossRef]
- Li, S.; Gu, X.; Xu, X.; Xu, D.; Zhang, T.; Liu, Z.; Dong, Q. Detection of Concealed Cracks from Ground Penetrating Radar Images Based on Deep Learning Algorithm. Constr. Build. Mater. 2021, 273, 121949. [Google Scholar] [CrossRef]
- Tanikawa, T.; Hirano, Y.; Dannoura, M.; Yamase, K.; Aono, K.; Ishii, M.; Igarashi, T.; Ikeno, H.; Kanazawa, Y. Root Orientation Can Affect Detection Accuracy of Ground-Penetrating Radar. Plant Soil 2013, 373, 317–327. [Google Scholar] [CrossRef]







| True Location/(x, y) | Antenna Frequency: 500 MHz | Antenna Frequency: 750 MHz | Antenna Frequency: 1000 MHz | |||
|---|---|---|---|---|---|---|
| Estimated Location/(x, y) | Distance Error/cm | Estimated Location/(x, y) | Distance Error/cm | Estimated Location/(x, y) | Distance Error/cm | |
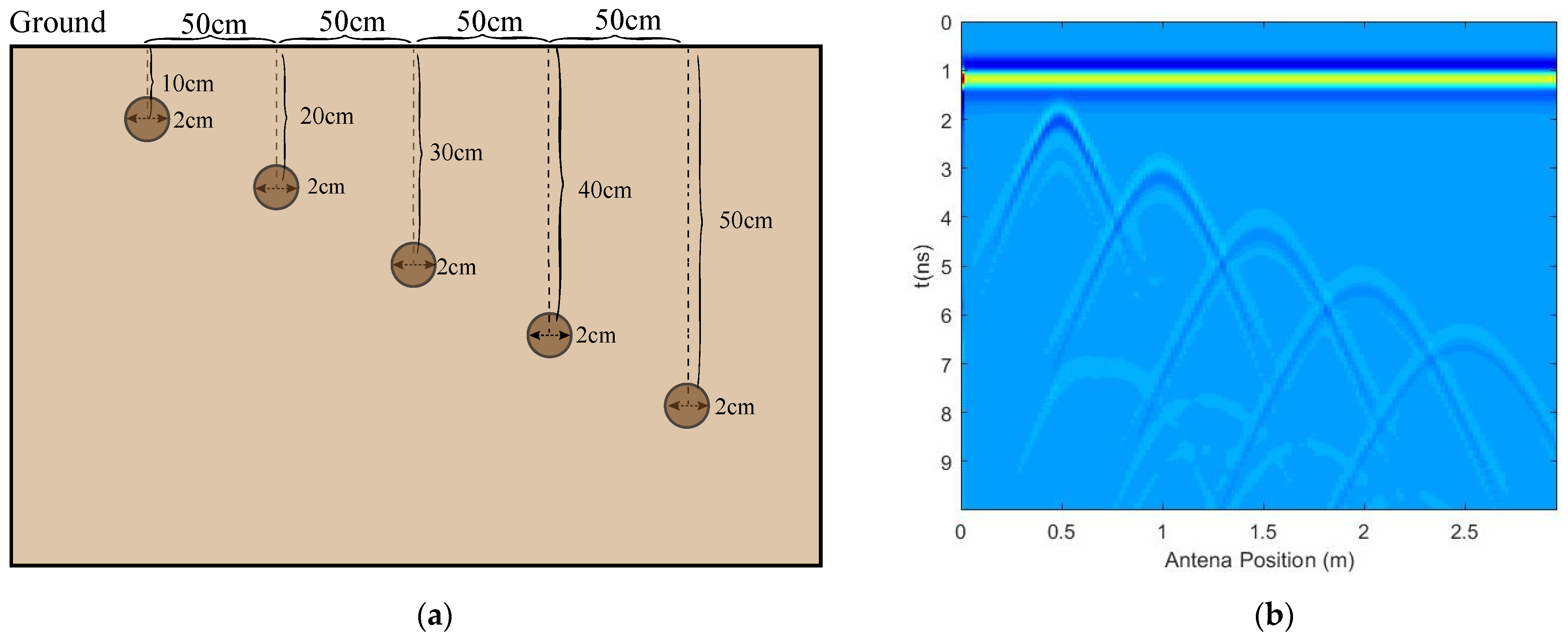
| (0.5, 0.10) | (0.526, 0.119) | 3.22 | (0.476, 0.118) | 3.00 | (0.478, 0.107) | 2.26 |
| (1.0, 0.20) | (1.029, 0.219) | 3.45 | (0.978, 0.114) | 3.26 | (0.970, 0.198) | 3.02 |
| (1.5, 0.30) | (1.524, 0.322) | 3.25 | (1.469, 0.312) | 3.34 | (1.489, 0.324) | 2.64 |
| (2.0, 0.40) | (2.036, 0.416) | 3.94 | (1.980, 0.381) | 2.79 | (1.978, 0.430) | 3.72 |
| (2.5, 0.50) | (2.520, 0.539) | 4.38 | (2.469, 0.467) | 4.51 | (2.492, 0.535) | 3.61 |
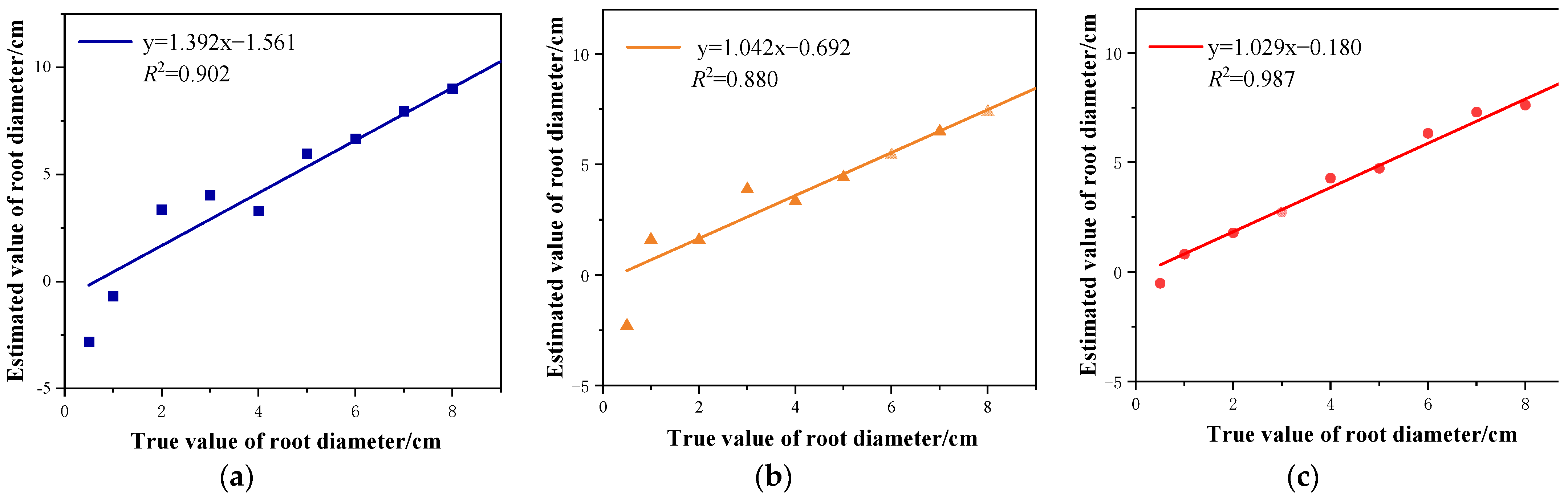
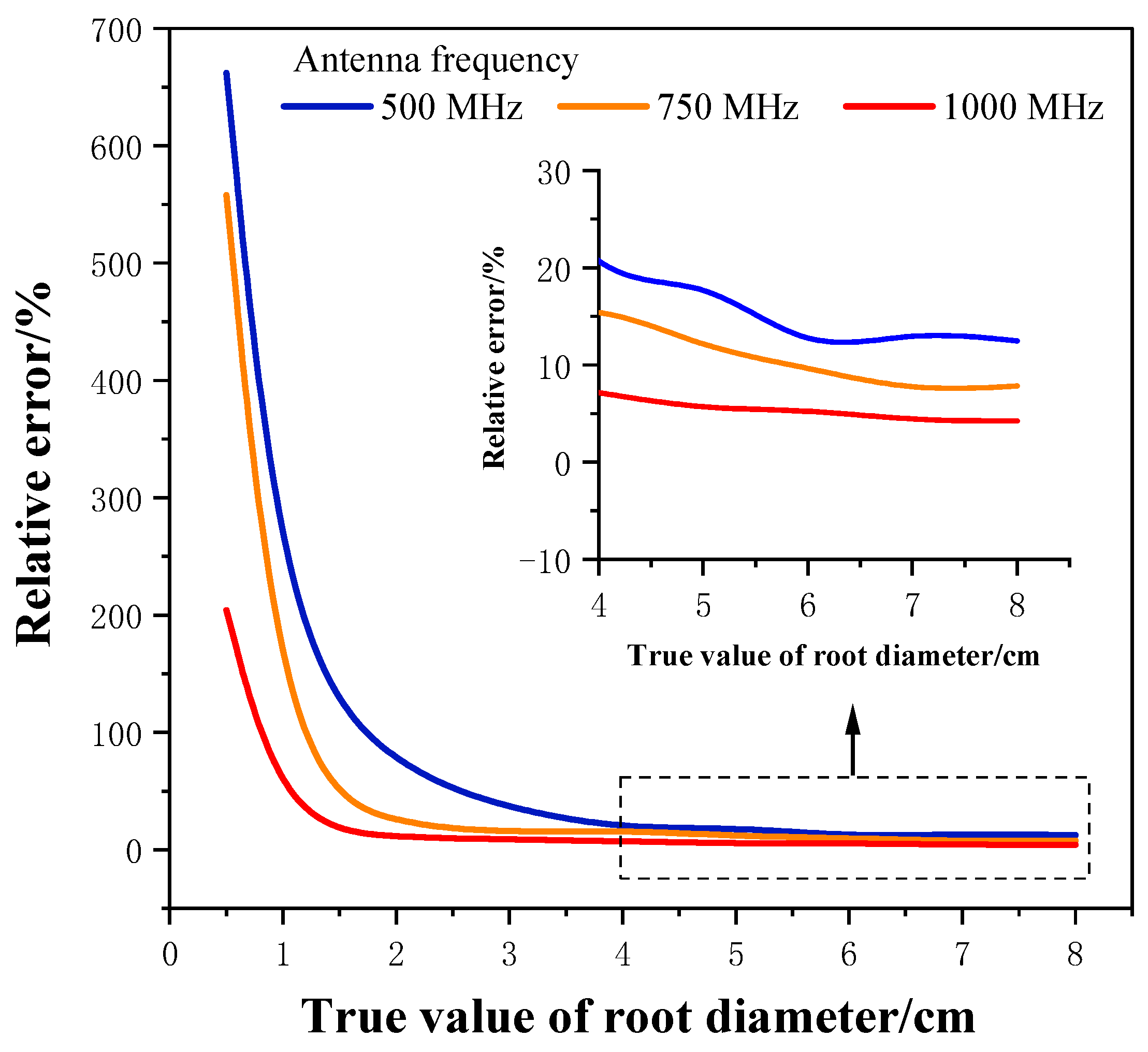
| True Value of Root Diameter/cm | Antenna Frequency: 500 MHz | Antenna Frequency: 750 MHz | Antenna Frequency: 1000 MHz | |||
|---|---|---|---|---|---|---|
| Estimated Value/cm | Relative Error/% | Estimated Value/cm | Relative Error/% | Estimated Value/cm | Relative Error/% | |
| 0.5 | −2.809 | 661.8 | −2.809 | 558 | −2.809 | 204.2 |
| 1 | −0.69 | 169 | 1.597 | 59.7 | 0.81 | 19 |
| 2 | 3.349 | 67.45 | 1.594 | 20.3 | 1.792 | 10.4 |
| 3 | 4.033 | 34.43 | 3.882 | 14.7 | 2.735 | 8.83 |
| 4 | 3.295 | 17.63 | 3.341 | 16.48 | 4.286 | 7.15 |
| 5 | 5.968 | 19.36 | 4.415 | 11.7 | 4.73 | 5.4 |
| 6 | 6.656 | 10.93 | 5.416 | 9.73 | 6.325 | 5.42 |
| 7 | 7.949 | 13.56 | 6.692 | 4.4 | 7.318 | 4.54 |
| 8 | 8.996 | 12.45 | 7.373 | 7.84 | 7.622 | 4.23 |
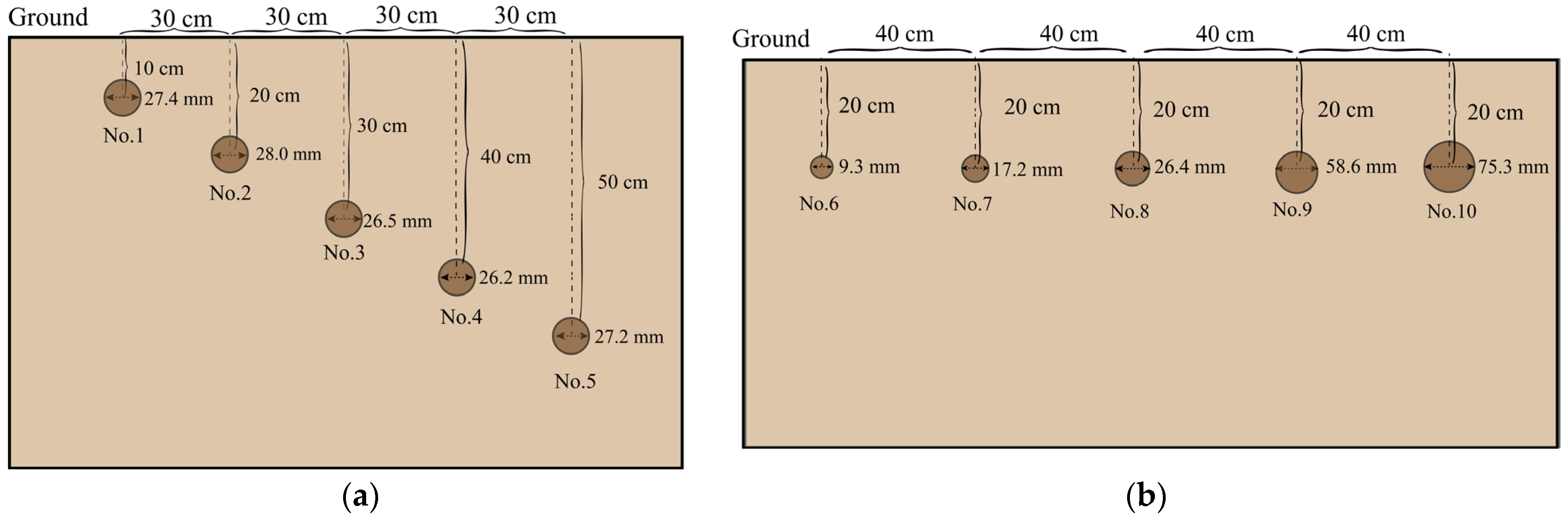
| Root | Actual Position (x, y) | Actual Diameter/mm | Predicted Position (x, y) | Predicted Diameter/mm | Distance Error/cm | Diameter Prediction Error |
|---|---|---|---|---|---|---|
| 1 | (0.282, 0.11) | 27.4 | (0.303, 0.136) | 22.64 | 3.45 | 17.37 |
| 2 | (0.558, 0.21) | 28.0 | (0.570, 0.245) | 24.12 | 3.70 | 13.86 |
| 3 | (0.870, 0.30) | 26.5 | (0.861, 0.325) | 23.32 | 2.66 | 12 |
| 4 | (1.170, 0.39) | 26.2 | (1.195, 0.361) | 22.80 | 3.83 | 12.98 |
| 5 | (1.405, 0.49) | 27.2 | (1.418, 0.542) | 23.44 | 5.36 | 13.82 |
| 6 | (0.503, 0.207) | 9.3 | (0.524, 0.210) | 18.58 | 3.11 | 106.4 |
| 7 | (0.933, 0.199) | 17.2 | (0.929, 0.169) | 10.83 | 3.03 | 36.2 |
| 8 | (1.345, 0.192) | 26.4 | (1.329, 0.177) | 23.2 | 2.19 | 10.77 |
| 9 | (1.410, 0.182) | 58.6 | (1.422, 0.193) | 65.72 | 1.62 | 13.31 |
| 10 | (1.833, 0.185) | 75.3 | (1.804, 0.214) | 67.44 | 4.10 | 10.08 |
| Root Node | Route Number | Predicted Position (x, y) | Predicted Diameter/cm | Actual Position (x, y) | Actual Diameter/cm | Distance Error/cm | Diameter Prediction Error |
|---|---|---|---|---|---|---|---|
| 1 | L-1 | (86.4, 17.2) | 10.97 | (85.4, 18.5) | 15 | 1.58 | 25.88 |
| 2 | L-1 | (105.4, 9.5) | 4.48 | (105.7, 6.0) | 6.8 | 3.51 | 34.18 |
| 3 | L-2 | (149.3, 17.8) | 1.75 | (157.5, 15.8) | 2.1 | 8.73 | 16.48 |
| 4 | L-2 | (178.3, 9.3) | 1.70 | (183.7, 6.8) | 2.0 | 5.97 | 15.05 |
| 5 | L-3 | (168.1, 15.6) | 3.73 | (167.6, 8.5) | 4.0 | 7.11 | 6.83 |
| 6 | L-3 | (175.5, 12.7) | 6.23 | (175.8, 9.0) | 5.5 | 3.72 | 13.24 |
| 7 | L-4 | (193.0, 17.9) | 5.29 | (184.9, 15.0) | 4.5 | 8.56 | 17.53 |
| 8 | L-5 | (218.0, 17.5) | 4.87 | (218.4, 18.0) | 4.2 | 0.67 | 15.86 |
| 9 | L-5 | (341.2, 20.8) | 1.40 | (345.1, 16.0) | 1.1 | 6.16 | 27.54 |
| 10 | L-6 | (392.8, 20.7) | 1.02 | (386.1, 19.0) | 0.8 | 6.91 | 27.50 |
| 11 | L-7 | (266.3, 15.5) | 2.03 | (267.8, 10.5) | 2.6 | 5.26 | 21.92 |
| 12 | L-7 | (296.0, 14.1) | 2.79 | (291.7, 14.0) | 3.4 | 4.24 | 17.94 |
| 13 | L-8 | (365.9, 9.2) | 2.67 | (360.1, 6.5) | 3.0 | 6.40 | 11.10 |
| 14 | L-8 | (381.7, 10.1) | 2.91 | (376.7, 8.5) | 3.2 | 5.20 | 9.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, D.; Jiang, F.; Wu, H.; Liu, S.; Luo, P.; Zhao, Z. Root Location and Root Diameter Estimation of Trees Based on Deep Learning and Ground-Penetrating Radar. Agronomy 2023, 13, 344. https://doi.org/10.3390/agronomy13020344
Sun D, Jiang F, Wu H, Liu S, Luo P, Zhao Z. Root Location and Root Diameter Estimation of Trees Based on Deep Learning and Ground-Penetrating Radar. Agronomy. 2023; 13(2):344. https://doi.org/10.3390/agronomy13020344
Chicago/Turabian StyleSun, Daozong, Fangyong Jiang, Haohou Wu, Shuoling Liu, Peiwen Luo, and Zuoxi Zhao. 2023. "Root Location and Root Diameter Estimation of Trees Based on Deep Learning and Ground-Penetrating Radar" Agronomy 13, no. 2: 344. https://doi.org/10.3390/agronomy13020344
APA StyleSun, D., Jiang, F., Wu, H., Liu, S., Luo, P., & Zhao, Z. (2023). Root Location and Root Diameter Estimation of Trees Based on Deep Learning and Ground-Penetrating Radar. Agronomy, 13(2), 344. https://doi.org/10.3390/agronomy13020344





