The Dynamic Response of Runoff to Human Activities and Climate Change Based on a Combined Hierarchical Structure Hydrological Model and Vector Autoregressive Model
Abstract
:1. Introduction
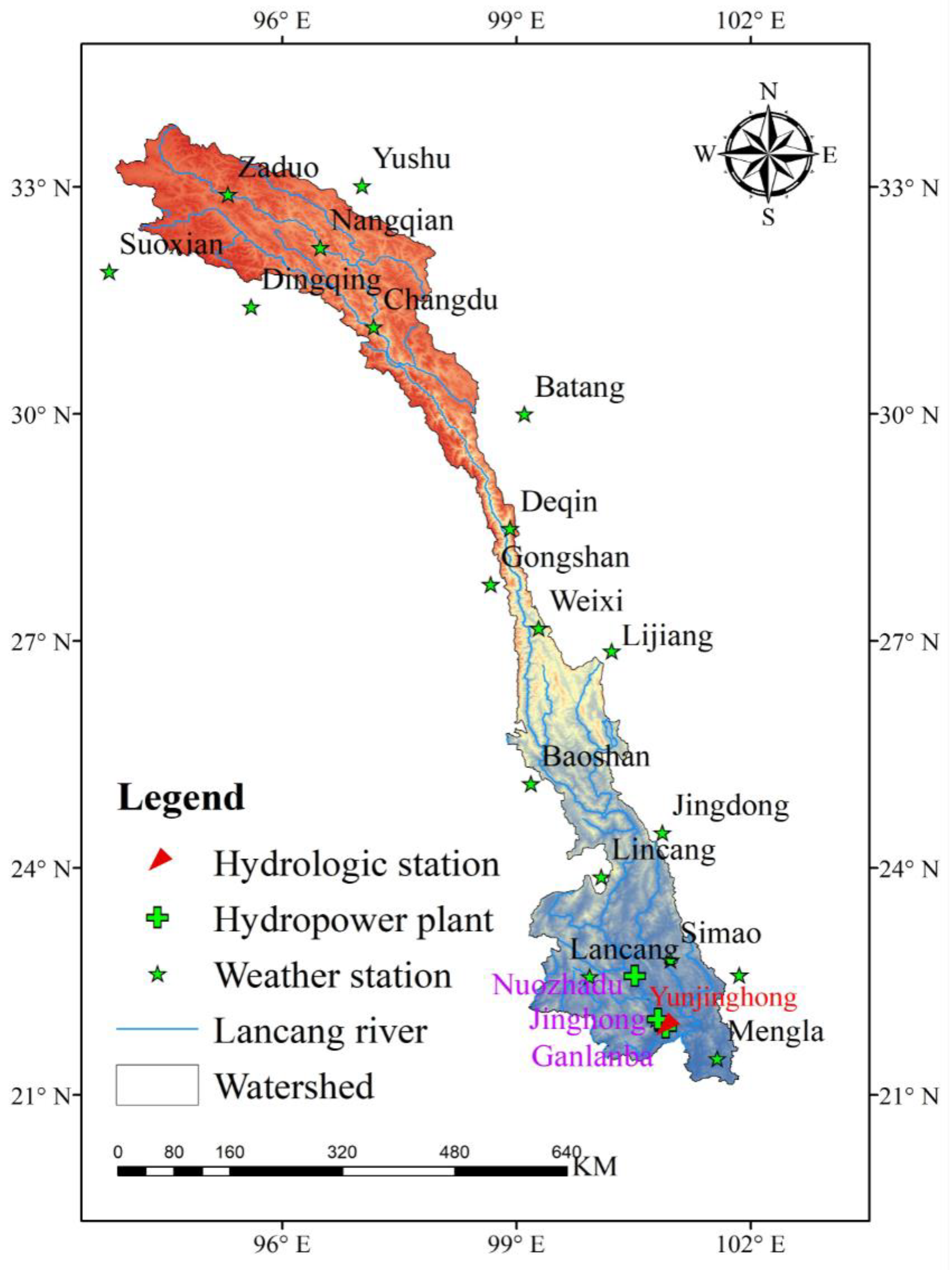
2. Study Area and Data
3. Methods
3.1. CHSH Model
3.1.1. Model Evaluation
- (1)
- Simulated accuracy
- (2)
- Simulated stability
3.1.2. Model Construction
- (1)
- Determination of the weight of a single model under simulation accuracy
- (2)
- Determination of the weight of a single model under simulation stability
- (3)
- Determination of the weights of the evaluation indexes
- (1)
- Due to the inconsistent dimension of each selected index, the original data index matrix needs to be standardized. The indexes for simulated accuracy and simulated stability selected in this study were all positive with an attribute of large and excellent, and the standardized equation is . The matrix after standardizing is , where and .
- (2)
- The proportion for the index values of the i-th simulated method are calculated under the j-th index in the sum of all methods .
- (3)
- Taking , using Equations (7)–(11), the j-th index entropy value is calculated, with .
- (4)
- The j-th index difference coefficient is calculated, .
- (5)
- A value is assigned to each index, and the weight of the j-th index is as follows:
3.2. VAR Model
- (1)
- The Augmented Dickey–Fuller (ADF) method is used to test the unit roots in the sequence to eliminate the phenomenon of spurious regression.
- (2)
- The lag intervals for the endogenous variables are determined.
- (3)
- The model coefficient is estimated and the VAR model is constructed.
- (4)
- The root estimate method is used for stationarity test.
- (5)
- The impact of a variable or several variables, after considering the impact on the numerical results of other variables in the present and future, is determined by the impulse response function.
- (6)
- The variance decomposition method is used to conduct dynamic research on the VAR model and analyze the reaction for each variable after being impacted. Concurrently, this is compared with the analysis results of the impulse response so as to test the stability and scientific validity of the model.
4. Results and Discussion
4.1. Impacts of Human Activities and Climate Change
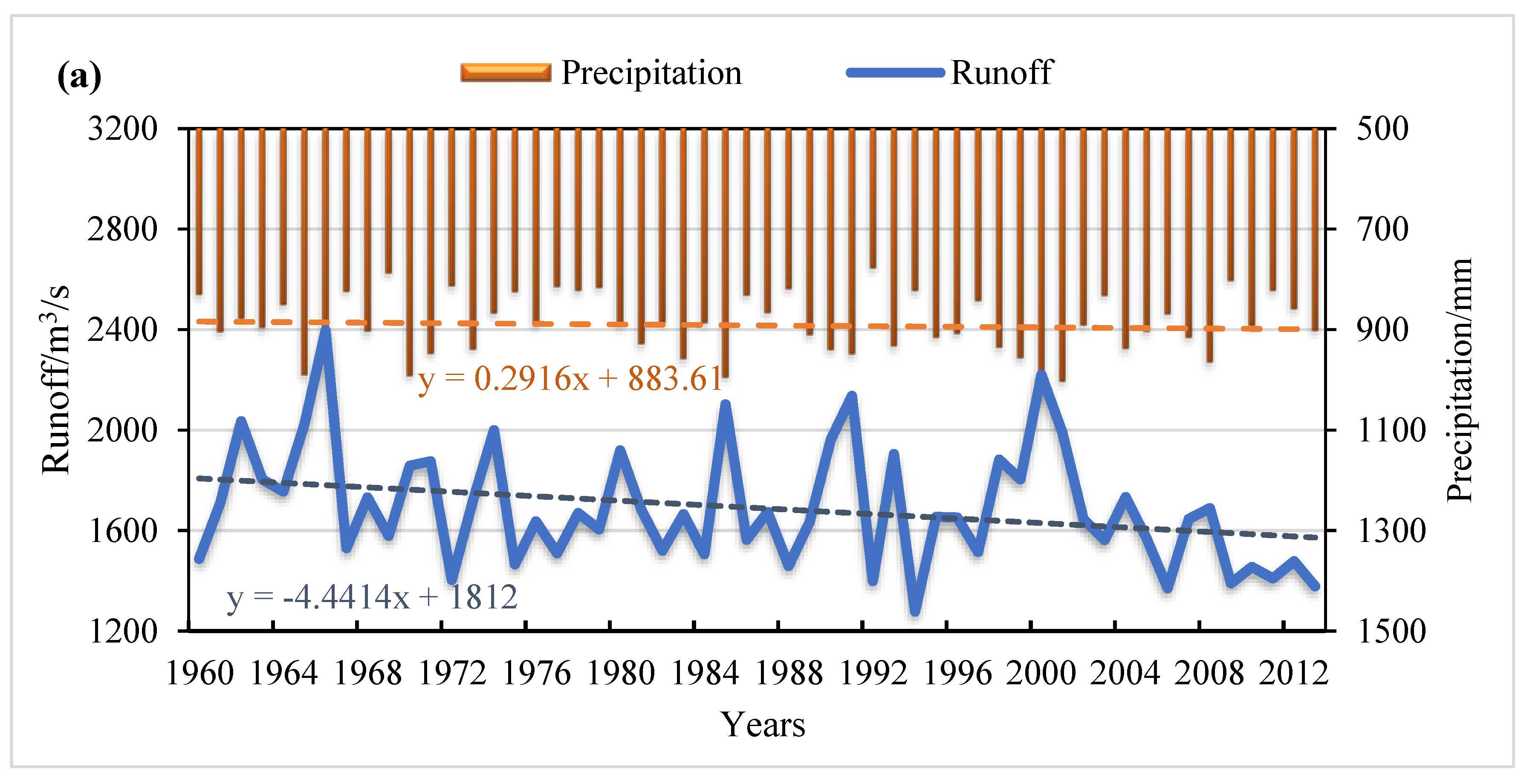
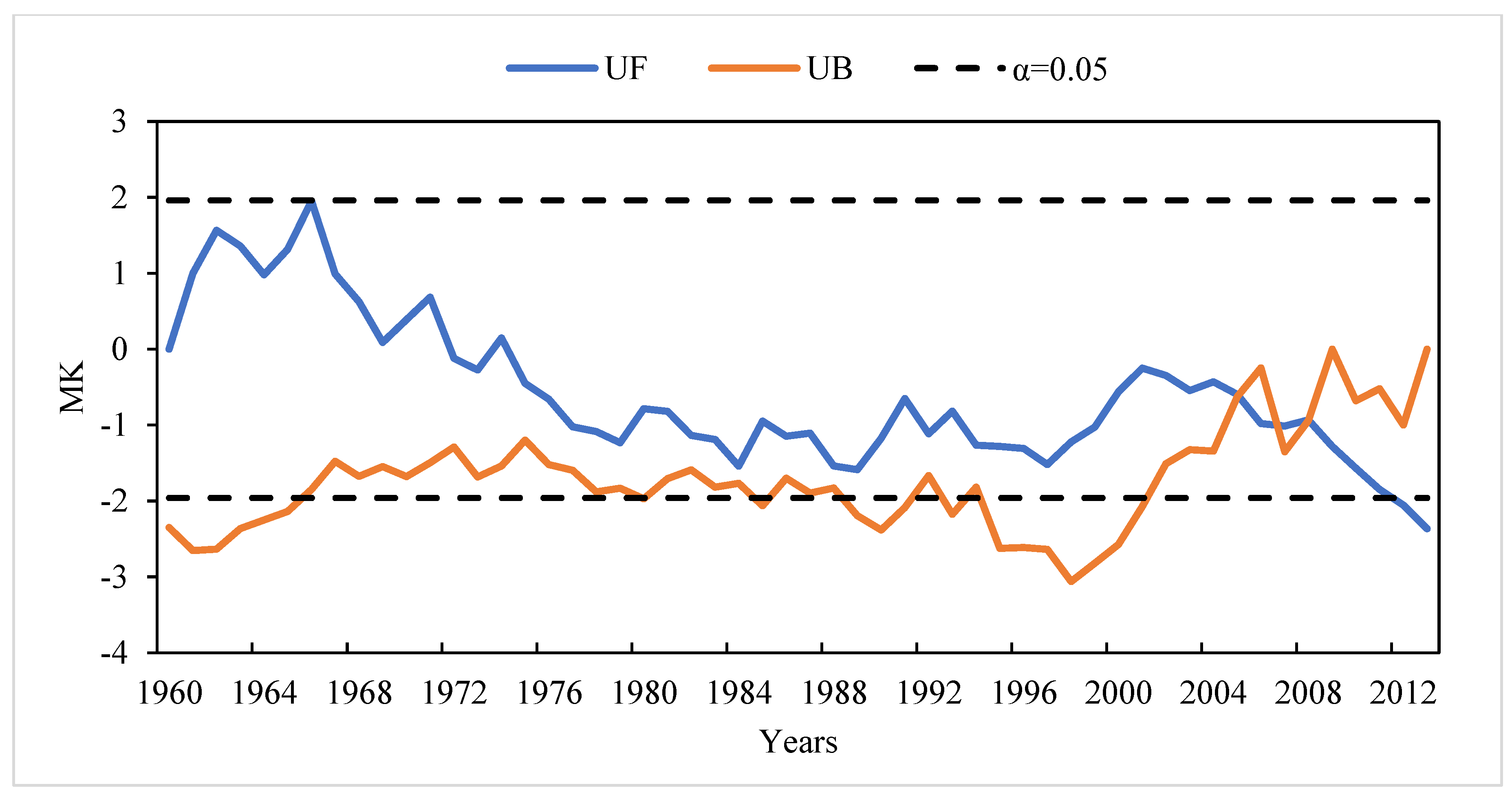
4.1.1. Analysis of Measured Hydro-Meteorological Data
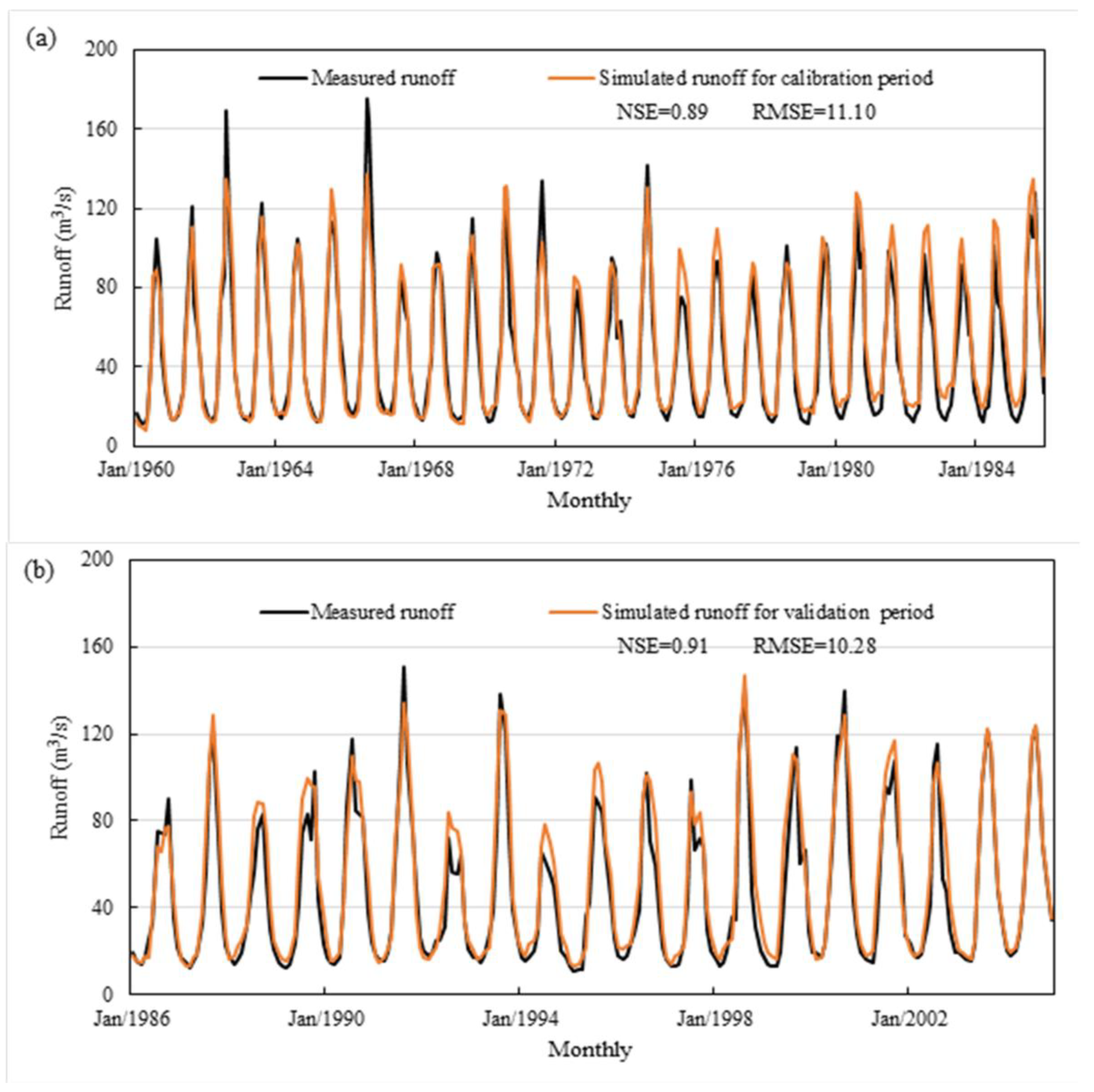
4.1.2. Simulating Natural Runoff by a CHSH Model
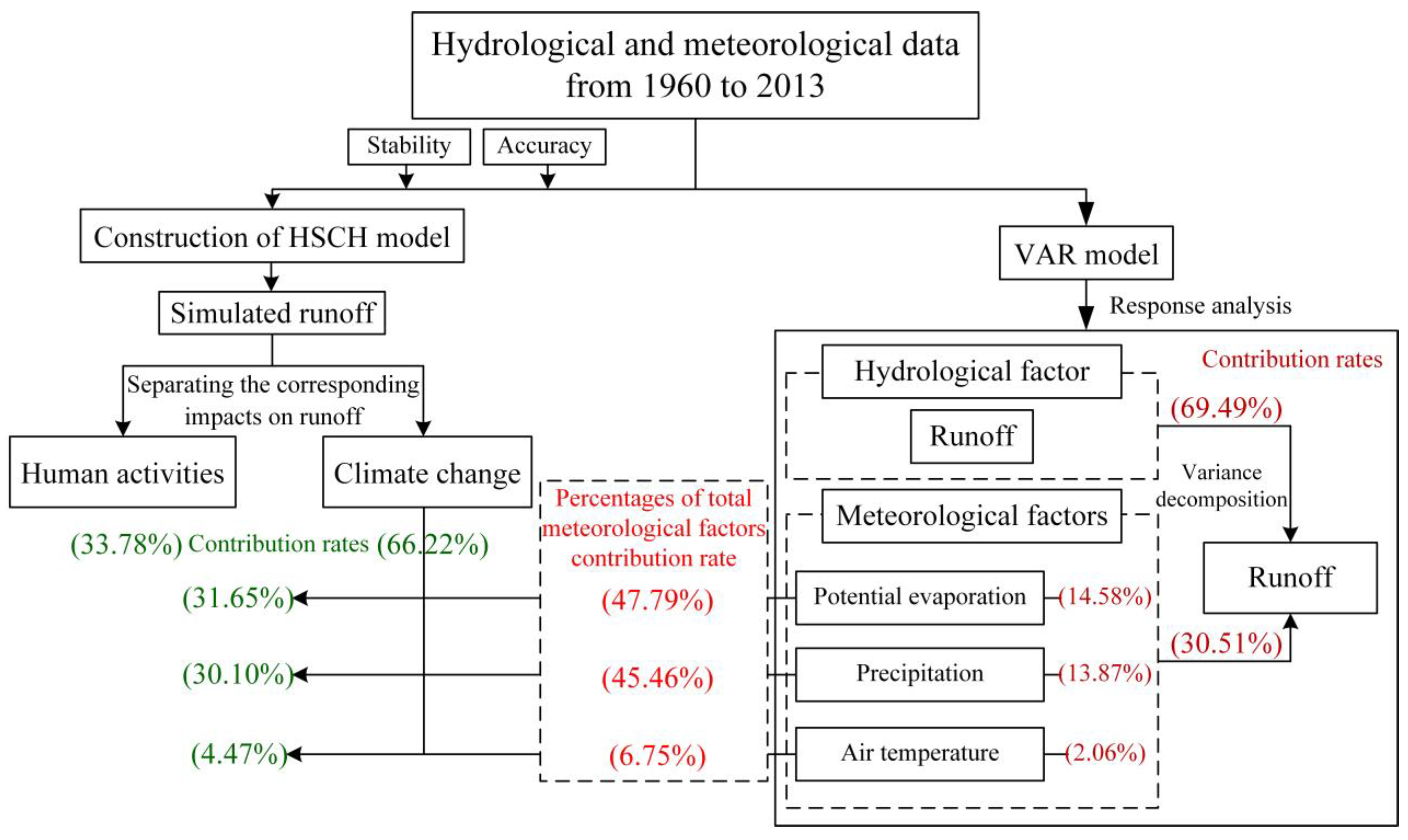
4.1.3. Quantification of the Impact of Human Activities and Climate Change on Runoff
4.2. Separating the Impact of Each Meteorological Factor on Runoff
4.2.1. Construction of the VAR Model
4.2.2. Stationarity Test of the VAR Model
4.2.3. Impulse Response of Runoff to the Meteorological Factors
4.2.4. Analysis of the Contribution Rates of the Meteorological Factors to Runoff
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sivapalan, M. Debates-Perspectives on socio-hydrology: Changing water systems and the “tyranny of small problems”-Sociohydrology. Water Resour. Res. 2015, 51, 4795–4805. [Google Scholar] [CrossRef]
- Liu, D.; Tian, F.; Lin, M.; Sivapalan, M. A conceptual socio-hydrological model of the co-evolution of humans and water: Case study of the Tarim River basin, western China. Hydrol. Earth Syst. Sci. 2015, 19, 1035–1054. [Google Scholar] [CrossRef]
- Lu, Y.; Tian, F.; Guo, L.; Borzi, I.; Patil, R.; Wei, J.; Liu, D.; Wei, Y.; Yu, D.; Sivapalan, M. Socio-hydrologic modeling of the dynamics of cooperation in the transboundary Lancang-Mekong River. Hydrol. Earth Syst. Sci. 2021, 25, 1883–1903. [Google Scholar] [CrossRef]
- Alinezhad, A.; Gohari, A.; Eslamian, S.; Saberi, Z. A probabilistic Bayesian framework to deal with the uncertainty in hydro-climate projection of Zayandeh-Rud River Basin. Theor. Appl. Climatol. 2021, 144, 1–14. [Google Scholar] [CrossRef]
- Meles, M.B.; Goodrich, D.C.; Gupta, H.V.; Burns, I.S.; Unkrich, C.L.; Razavi, S.; Guertin, D.P. Multi-criteria, time dependent sensitivity analysis of an event-oriented, physically-based, distributed sediment and runoff model. J. Hydrol. 2021, 598, 126268. [Google Scholar] [CrossRef]
- Cheng, C.-T.; Xie, J.-X.; Chau, K.-W.; Layeghifard, M. A new indirect multi-step-ahead prediction model for a long-term hydrologic prediction. J. Hydrol. 2008, 361, 118–130. [Google Scholar] [CrossRef]
- Kennedy, A.M.; Garen, D.C.; Koch, R.W. The association between climate teleconnection indices and Upper Klamath seasonal streamflow: Trans-Niño Index. Hydrol. Process. 2009, 23, 973–984. [Google Scholar] [CrossRef]
- Mutlu, E.; Chaubey, I.; Hexmoor, H.; Bajwa, S.G. Comparison of artificial neural network models for hydrologic predictions at multiple gauging stations in an agricultural watershed. Hydrol. Process. 2008, 22, 5097–5106. [Google Scholar] [CrossRef]
- Sibtain, M.; Li, X.; Azam, M.I.; Bashir, H. Applicability of a Three-Stage Hybrid Model byEmploying a Two-Stage Signal DecompositionApproach and a Deep Learning Methodologyfor Runoff Forecasting at Swat River Catchment,Pakistan. Pol. J. Environ. Stud. 2020, 30, 369–384. [Google Scholar] [CrossRef]
- Rajesh, R.; Rajendran, C. Grey- and rough-set-based seasonal disaster predictions: An analysis of flood data in India. Nat. Hazards 2019, 97, 395–435. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Lian, J. Applicability Study of Hydrological Period Identification Methods: Application to Huayuankou and Lijin in the Yellow River Basin, China. Water 2021, 13, 1265. [Google Scholar] [CrossRef]
- Han, H.; Morrison, R.R. Data-driven approaches for runoff prediction using distributed data. Stoch. Environ. Res. Risk A 2021, 36, 2153–2171. [Google Scholar] [CrossRef]
- Emerton, R.E.; Stephens, E.M.; Cloke, H.L. What is the most useful approach for forecasting hydrological extremes during El Niño. Environ. Res. Commun. 2019, 1, 31002. [Google Scholar] [CrossRef]
- Wei, B.; Xie, N. Parameter estimation for grey system models: A nonlinear least squares perspective. Commun. Nonlinear Sci. 2021, 95, 105653. [Google Scholar] [CrossRef]
- Ma, C.; Xu, R.; He, W.; Xia, J. Determining the limiting water level of early flood season by combining multiobjective optimization scheduling and copula joint distribution function: A case study of three gorges reservoir. Sci. Total Environ. 2020, 737, 139789. [Google Scholar] [CrossRef] [PubMed]
- Xie, M.; Zhou, J.; Li, C.; Zhu, S. Long-term generation scheduling of Xiluodu and Xiangjiaba cascade hydro plants considering monthly streamflow forecasting error. Energ. Convers. Manag. 2015, 105, 368–376. [Google Scholar] [CrossRef]
- Regonda, S.K.; Rajagopalan, B.; Clark, M.; Zagona, E. A multimodel ensemble forecast framework: Application to spring seasonal flows in the Gunnison River Basin. Water Resour. Res. 2006, 42, 764–777. [Google Scholar] [CrossRef]
- Shamseldin, A.Y.; O’Connor, K.M.; Liang, G.C. Methods for combining the outputs of different rainfall–runoff models. J. Hydrol. 1997, 197, 203–229. [Google Scholar] [CrossRef]
- Georgakakos, K.P.; Seo, D.J.; Gupta, H.; Schaake, J.; Butts, M.B. Towards the characterization of streamflow simulation uncertainty through multimodel ensembles. J. Hydrol. 2004, 298, 222–241. [Google Scholar] [CrossRef]
- Xie, T.; Zhang, G.; Hou, J.; Xie, J.; Lv, M.; Liu, F. Hybrid forecasting model for non-stationary daily runoff series: A case study in the Han River Basin, China. J. Hydrol. 2019, 577, 123915. [Google Scholar] [CrossRef]
- Zhang, J.; Li, H.; Sun, B.; Fang, H. Multi-time scale co-integration forecast of annual runoff in the source area of the Yellow River. J. Water Clim. Chang. 2021, 12, 101–115. [Google Scholar] [CrossRef]
- Zhang, L.; Huang, Q.; Liu, D.; Deng, M.; Zhang, H.; Pan, B.; Zhang, H. Long-term and mid-term ecological operation of cascade hydropower plants considering ecological water demands in arid region. J. Clean. Prod. 2021, 279, 123599. [Google Scholar] [CrossRef]
- Mo, C.; Ruan, Y.; Xiao, X.; Lan, H.; Jin, J. Impact of climate change and human activities on the baseflow in a typical karst basin, Southwest China. Ecol. Indic. 2021, 126, 107628. [Google Scholar] [CrossRef]
- Su, X.; Li, X.; Niu, Z.; Wang, N.; Liang, X. A new complexity-based three-stage method to comprehensively quantify positive/negative contribution rates of climate change and human activities to changes in runoff in the upper Yellow River. J. Clean. Prod. 2021, 287, 125017. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Z. Derivation of the relative contributions of the climate change and human activities to mean annual streamflow change. J. Hydrol. 2021, 595, 125740. [Google Scholar] [CrossRef]
- Alifujiang, Y.; Abuduwaili, J.; Groll, M.; Issanova, G.; Maihemuti, B. Changes in intra-annual runoff and its response to climate variability and anthropogenic activity in the Lake Issyk-Kul Basin, Kyrgyzstan. Catena 2021, 198, 104974. [Google Scholar] [CrossRef]
- Yang, G.; Guo, S.; Liu, P.; Block, P. Integration and Evaluation of Forecast-Informed Multiobjective Reservoir Operations. J. Water Res. Plan. Manag. 2020, 146, 4020038. [Google Scholar] [CrossRef]
- Athar, H.; Nabeel, A.; Nadeem, I.; Saeed, F. Projected changes in the climate of Pakistan using IPCC AR5-based climate models. Theor. Appl. Climatol. 2021, 145, 567–584. [Google Scholar] [CrossRef]
- Iturbide, M.; Gutiérrez, J.M.; Alves, L.M.; Bedia, J.; Cerezo-Mota, R.; Cimadevilla, E.; Cofiño, A.S.; Luca, A.D.; Faria, S.H.; Gorodetskaya, I.V.; et al. An update of IPCC climate reference regions for subcontinental analysis of climate model data: Definition and aggregated datasets. Earth Syst. Sci. Data 2020, 12, 2959–2970. [Google Scholar] [CrossRef]
- Makarigakis, A.K.; Jimenez-Cisneros, B.E. UNESCO’s Contribution to Face Global Water Challenges. Water 2019, 11, 388. [Google Scholar] [CrossRef] [Green Version]
- Saurral, R.I. The hydrologic cycle of the La Plata Basin in the WCRP-CMIP3 multimodel dataset. J. Hydrometeorol. 2010, 11, 1083–1102. [Google Scholar] [CrossRef]
- de Jong, P.; Barreto, T.B.; Tanajura, C.A.; Oliveira-Esquerre, K.P.; Kiperstok, A.; Torres, E.A. The Impact of Regional Climate Change on Hydroelectric Resources in South America. Renew. Energ. 2021, 173, 76–91. [Google Scholar] [CrossRef]
- Huq, E.; Abdul-Aziz, O.I. Climate and land cover change impacts on stormwater runoff in large-scale coastal-urban environments. Sci. Total Environ. 2021, 778, 146017. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Zhou, Z.; Yan, Z.; Gong, J.; Jia, Y.; Xu, C.-Y.; Wang, H. A new approach to separating the impacts of climate change and multiple human activities on water cycle processes based on a distributed hydrological model. J. Hydrol. 2019, 578, 124096. [Google Scholar] [CrossRef]
- Chang, J.; Zhang, H.; Wang, Y.; Zhu, Y. Assessing the impact of climate variability and human activities on streamflow variation. Hydrol. Earth Syst. Sci. 2016, 20, 1547–1560. [Google Scholar] [CrossRef]
- Chang, J.; Zhang, H.; Wang, Y.; Zhang, L. Impact of climate change on runoff and uncertainty analysis. Nat. Hazards 2017, 88, 1113–1131. [Google Scholar] [CrossRef]
- Chaudhari, S.; Felfelani, F.; Shin, S.; Pokhrel, Y. Climate and anthropogenic contributions to the desiccation of the second largest saline lake in the twentieth century. J. Hydrol. 2018, 560, 342–353. [Google Scholar] [CrossRef]
- Silva, A.T.; Portela, M.M. Using Climate-Flood Links and CMIP5 Projections to Assess Flood Design Levels Under Climate Change Scenarios: A Case Study in Southern Brazil. Water Resour. Manag. 2018, 32, 4879–4893. [Google Scholar] [CrossRef]
- Wu, H.; Liu, D.; Hao, M.; Li, R.; Yang, Q.; Ming, G.; Liu, H. Identification of Time-Varying Parameters of Distributed Hydrological Model in Wei River Basin on Loess Plateau in the Changing Environment. Water 2022, 14, 4021. [Google Scholar] [CrossRef]
- Sims, C.A. Macroeconomics and reality. Econometrica 1980, 48, 1–48. [Google Scholar] [CrossRef] [Green Version]
- Sims, C.A.; Stock, J.H.; Watson, M.W. Inference in Linear Time Series Models with Same Unit Roots. Econometrica 1990, 58, 113–144. [Google Scholar] [CrossRef]
- Fathian, F.; Fakheri-Fard, A.; Modarres, R.; Van Gelder, P.H. Regional scale rainfall-runoff modeling using varx-mgarch approach. Stoch. Environ. Res. Risk A 2018, 33, 407–425. [Google Scholar] [CrossRef]
- Zeng, W.; Song, S.; Kang, Y.; Gao, X.; Ma, R. Response of runoff to meteorological factors based on time-varying parameter vector autoregressive model with stochastic volatility in arid and semi-arid area of weihe river basin. Sustainability 2022, 14, 6989. [Google Scholar] [CrossRef]
- Li, G.; Lei, Y.; Ge, J.; Wu, S. The Empirical Relationship between Mining Industry Development and Environmental Pollution in China. Int. J. Environ. Res. Public Health 2017, 14, 254. [Google Scholar] [CrossRef]
- Wu, S.; Li, J.; Zhou, W.; Lewis, B.J.; Yu, D.; Zhou, L.; Jiang, L.; Dai, L. A statistical analysis of spatiotemporal variations and determinant factors of forest carbon storage under China’s Natural Forest Protection Program. J. Forestry Res. 2018, 29, 415–424. [Google Scholar] [CrossRef]
- Zhao, J.; Mu, X.; Gao, P. Dynamic response of runoff to soil and water conservation measures and precipitation based on VAR model. Hydrol. Res. 2019, 50, 837–848. [Google Scholar] [CrossRef]
- Deng, J.; Li, Y.; Xu, B.; Ding, W.; Zhou, H.; Schmidt, A. Ecological Optimal Operation of Hydropower Stations to Maximize Total Phosphorus Export. J. Water Res. Plan. Manag. 2020, 146, 4020075. [Google Scholar] [CrossRef]
- Zhang, H.; Chang, J.; Gao, C.; Wu, H.; Wang, Y.; Lei, K.; Long, R.; Zhang, L. Cascade hydropower plants operation considering comprehensive ecological water demands. Energ. Convers. Manag. 2019, 180, 119–133. [Google Scholar] [CrossRef]
- Zhong, R.; Zhao, T.; He, Y.; Chen, X. Hydropower change of the water tower of Asia in 21st century: A case of the Lancang River hydropower base, upper Mekong. Energy 2019, 179, 685–696. [Google Scholar] [CrossRef]
- Shi, W.; Yu, X.; Liao, W.; Wang, Y.; Jia, B. Spatial and temporal variability of daily precipitation concentration in the Lancang River basin, China. J. Hydrol. 2013, 495, 197–207. [Google Scholar] [CrossRef]
- Kirkby, M.; Beven, K. A physically based, variable contributing area model of basin hydrology. Hydrol. Sci. J. 1979, 24, 43–69. [Google Scholar]
- Karimi, M. Order selection criteria for vector autoregressive models. Signal Process. 2011, 91, 955–969. [Google Scholar] [CrossRef]
- Santosa, B.J. Differential evolution adaptive metropolis sampling method to provide model uncertainty and model selection criteria to determine optimal model for Rayleigh wave dispersion. Arab. J. Geosci. 2015, 8, 7003–7023. [Google Scholar]
- Ahking, F.W. Model mis-specification and Johansen’s co-integration analysis: An application to the US money demand. J. Macroecon. 2002, 24, 51–66. [Google Scholar] [CrossRef]
- Lütkepohl, H. A note on the asymptotic distribution of impulse response functions of estimated var models with orthogonal residuals. J. Econom. 1989, 42, 371–376. [Google Scholar] [CrossRef]





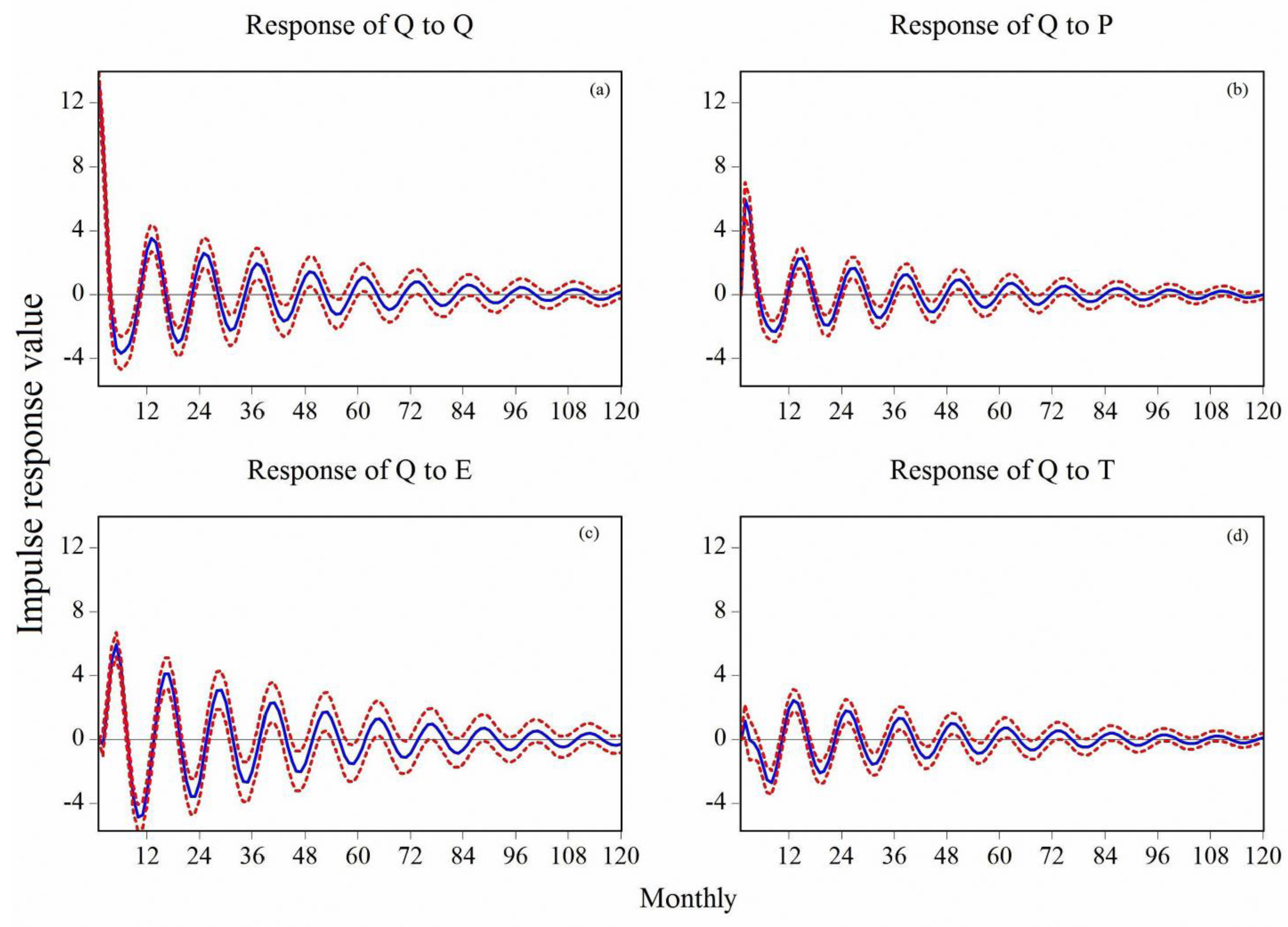
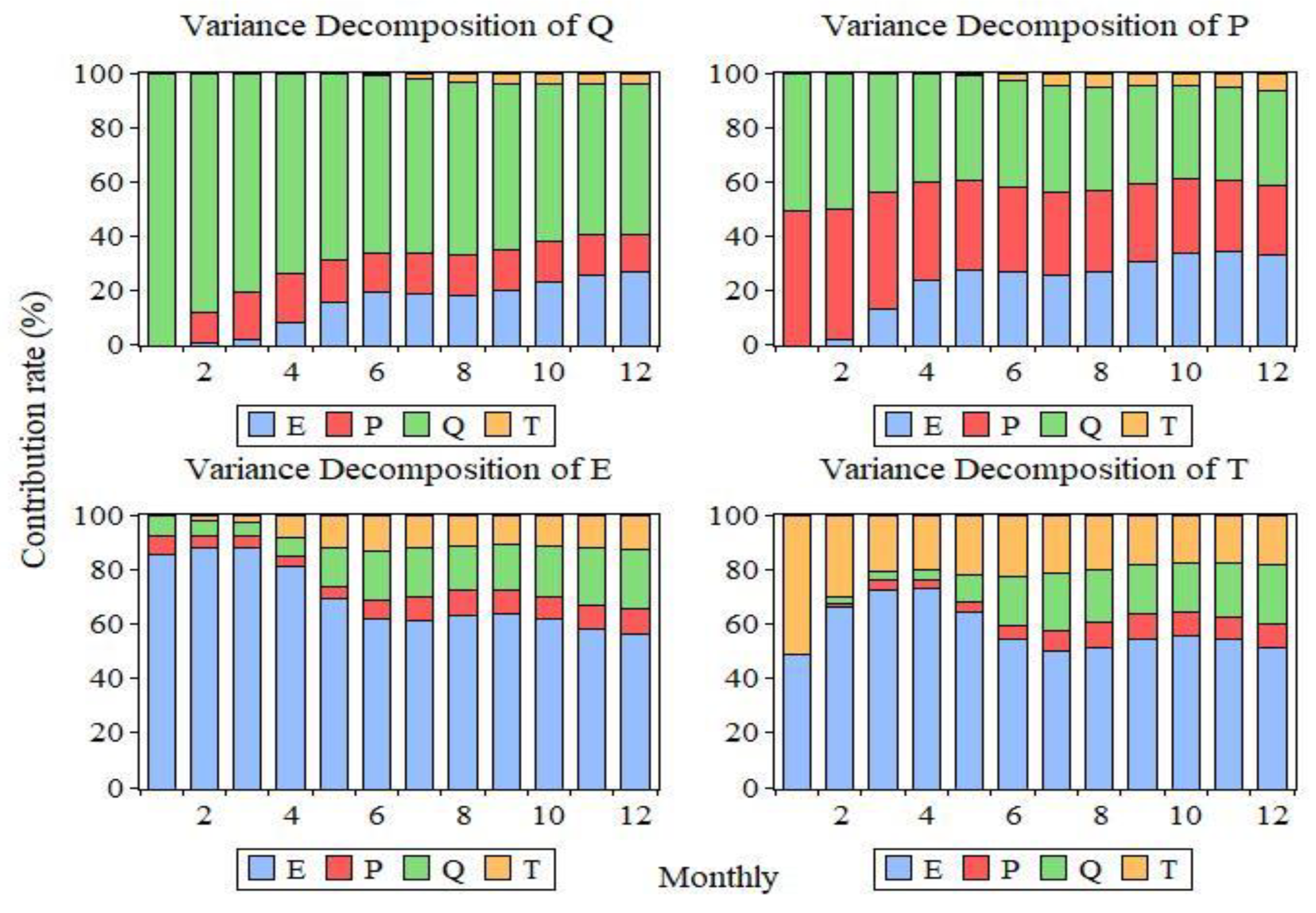
| Indexes | BP | NAR | RBF | SVM | Topmodel | |
|---|---|---|---|---|---|---|
| Calibration Period | Validation Period | |||||
| RE (%) | 16 | 17 | 17 | 14 | 20 | 19 |
| RMSE (108 m3) | 12 | 11 | 12 | 12 | 11 | 10 |
| NSE | 0.87 | 0.89 | 0.88 | 0.87 | 0.89 | 0.91 |
| Indexes | BP | NAR | RBF | SVM | Topmodel |
|---|---|---|---|---|---|
| Variance–Covariance | 16 | 17 | 15 | 18 | 34 |
| Weight | 20 | 20 | 20 | 20 | 20 |
| Determined Weigh | 16 | 17 | 15 | 18 | 34 |
| Period | /108 m3 | /108 m3 | /108 m3 | /% | Human Activities | Climate Change | ||
|---|---|---|---|---|---|---|---|---|
/108 m3 | /% | /108 m3 | /% | |||||
| 1960–2004 | 545 | - | - | - | - | - | - | - |
| 2005–2013 | 469 | 495 | −77 | −14 | −26 | 34 | −50 | 66 |
| Variable | ADF Test | Critical Value (α = 5%) | Result | ||
|---|---|---|---|---|---|
| t-Statistic | p-Value | t-Statistic | p-Value | ||
| Q | −4.5 * | 0.0002 | −2.9 | 0.05 | Stationary |
| P | −5.8 * | 0 | −2.9 | 0.05 | Stationary |
| T | −3.1 * | 0.029 | −2.9 | 0.05 | Stationary |
| E | −3.2 * | 0.022 | −2.9 | 0.05 | Stationary |
| Lag | LogL | LR | FPE | AIC | SC | HQ |
|---|---|---|---|---|---|---|
| 0 | −611 | NA | 7.9 × 10−5 | 1.9 | 1.9 | 1.9 |
| 1 | −3. 3 | 1207 | 1.3 × 10−5 | 0.072 | 0.21 | 0.13 |
| 2 | 302 | 601* | 5.2 × 10−6 * | −0.83 * | −0.58 * | −0.73 * |
| 3 | 514 | 416 | 2.8 × 10−6 | −1.4 | −1.1 | −1.3 |
| Statistics | Q | P | E | T |
|---|---|---|---|---|
| Q (-1) | 0.27 | −0.015 | 0.078 | 0.0075 |
| Q (-2) | −0.20 | −0.77 | −0.14 | −0.018 |
| P (-1) | 0.27 | 0.38 | 0.068 | 0.016 |
| P (-2) | 0.094 | 0.23 | −0.0094 | 0.0012 |
| E (-1) | −0.21 | 0.37 | 0.67 | 0.082 |
| E (-2) | 0.29 | 1.2 | 0.15 | 0.012 |
| T (-1) | 1.8 | 1.6 | 2.0 | 0.63 |
| T (-2) | −1.7 | −2.9 | −4.7 | −0.54 |
| C | 6.7 | −47 | 43 | 2.2 |
| R2 | 0.84 | 0.81 | 0.90 | 0.99 |
| Lag | Q | P | E | T |
|---|---|---|---|---|
| 1 | 100 | 0 | 0 | 0 |
| 2 | 88 | 12 | 0.030 | 0.45 |
| 3 | 80 | 18 | 1.6 | 0.40 |
| 4 | 74 | 18 | 8.1 | 0.37 |
| 5 | 68 | 17 | 16 | 0.44 |
| 6 | 65 | 15 | 19 | 0.96 |
| 7 | 65 | 15 | 18 | 2.2 |
| 8 | 63 | 15 | 18 | 3.5 |
| 9 | 61 | 15 | 20 | 4.1 |
| 10 | 58 | 15 | 23 | 4.0 |
| 11 | 56 | 15 | 26 | 3.9 |
| 12 | 55 | 14 | 27 | 4.4 |
| Average | 69 | 14 | 15 | 2.1 |
| Response for Runoff | Human Activities | |||
|---|---|---|---|---|
| Variation/108 m3 | −26 | −24 | −23 | −3.4 |
| Contribution rate/% | 34 | 32 | 30 | 4.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, L.; Zhang, H.; Liu, D.; Huang, Q.; Chang, J.; Liu, S. The Dynamic Response of Runoff to Human Activities and Climate Change Based on a Combined Hierarchical Structure Hydrological Model and Vector Autoregressive Model. Agronomy 2023, 13, 510. https://doi.org/10.3390/agronomy13020510
Zhang L, Zhang H, Liu D, Huang Q, Chang J, Liu S. The Dynamic Response of Runoff to Human Activities and Climate Change Based on a Combined Hierarchical Structure Hydrological Model and Vector Autoregressive Model. Agronomy. 2023; 13(2):510. https://doi.org/10.3390/agronomy13020510
Chicago/Turabian StyleZhang, Lianpeng, Hongxue Zhang, Dengfeng Liu, Qiang Huang, Jianxia Chang, and Siyuan Liu. 2023. "The Dynamic Response of Runoff to Human Activities and Climate Change Based on a Combined Hierarchical Structure Hydrological Model and Vector Autoregressive Model" Agronomy 13, no. 2: 510. https://doi.org/10.3390/agronomy13020510
APA StyleZhang, L., Zhang, H., Liu, D., Huang, Q., Chang, J., & Liu, S. (2023). The Dynamic Response of Runoff to Human Activities and Climate Change Based on a Combined Hierarchical Structure Hydrological Model and Vector Autoregressive Model. Agronomy, 13(2), 510. https://doi.org/10.3390/agronomy13020510








