A Fast Path Planning Method of Seedling Tray Replanting Based on Improved Particle Swarm Optimization
Abstract
:1. Introduction
2. Materials and Methods
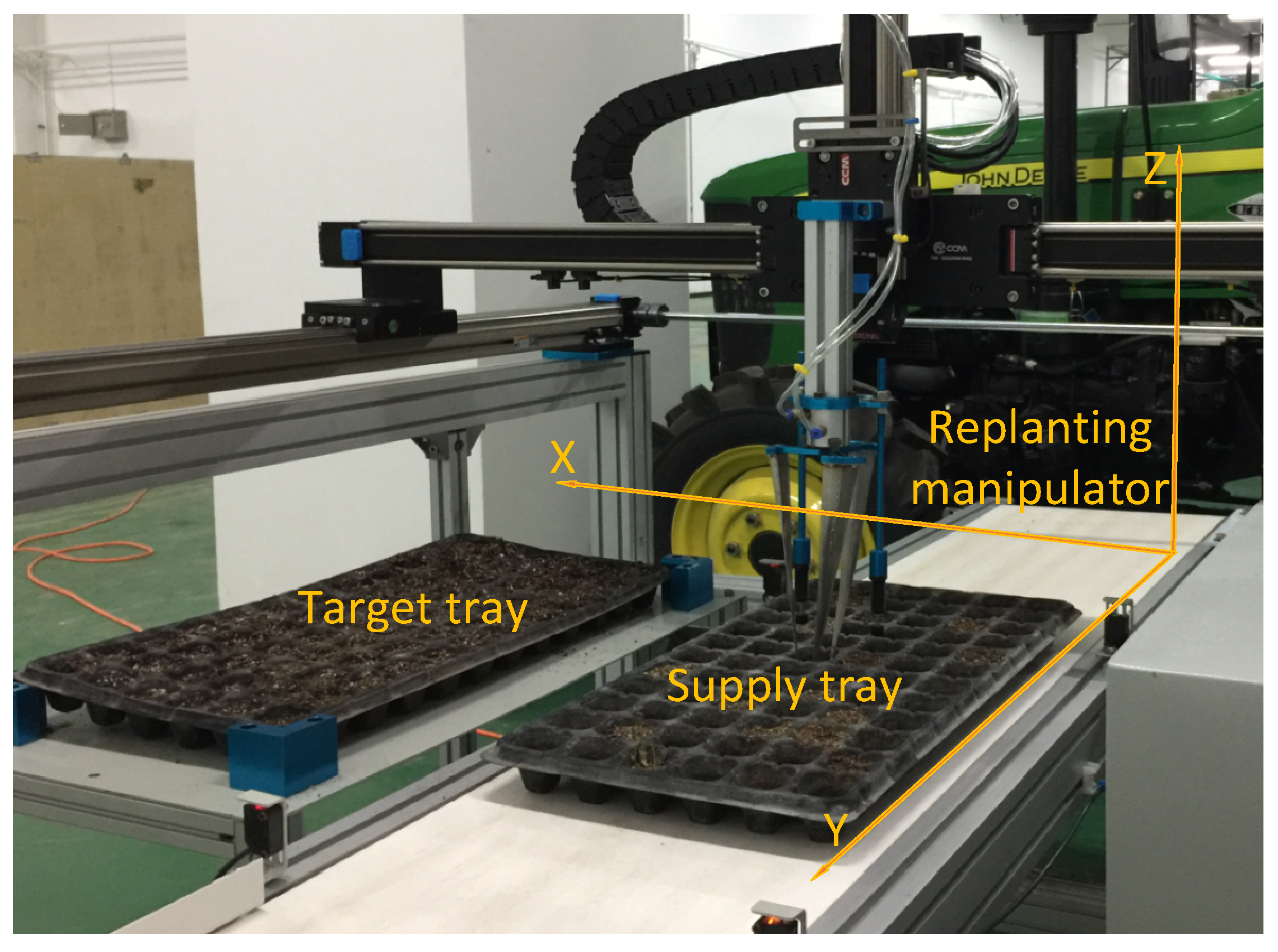
2.1. Materials and Equipment
2.2. Path Planning Algorithm
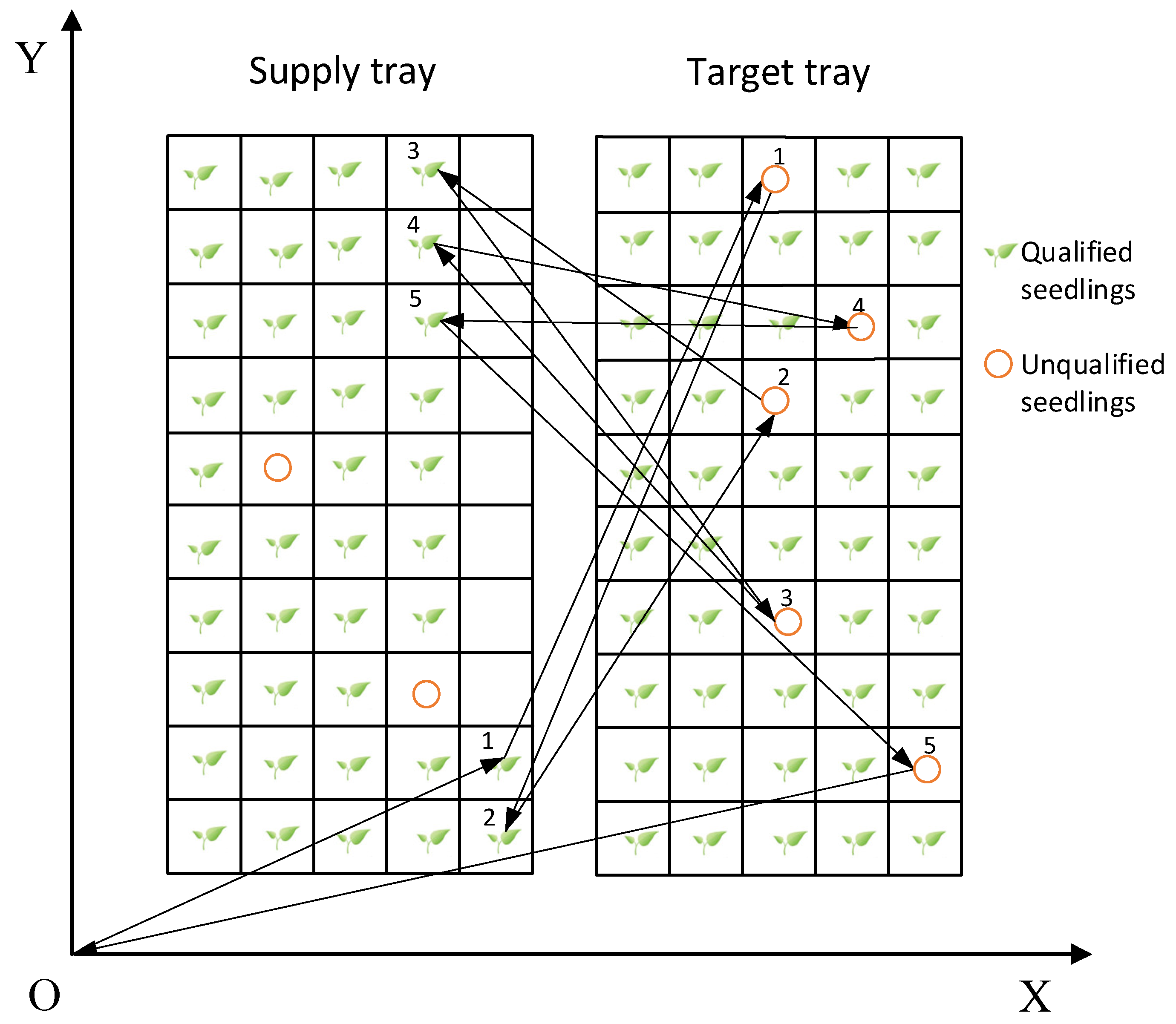
2.2.1. Fixed-Order Path Planning Method
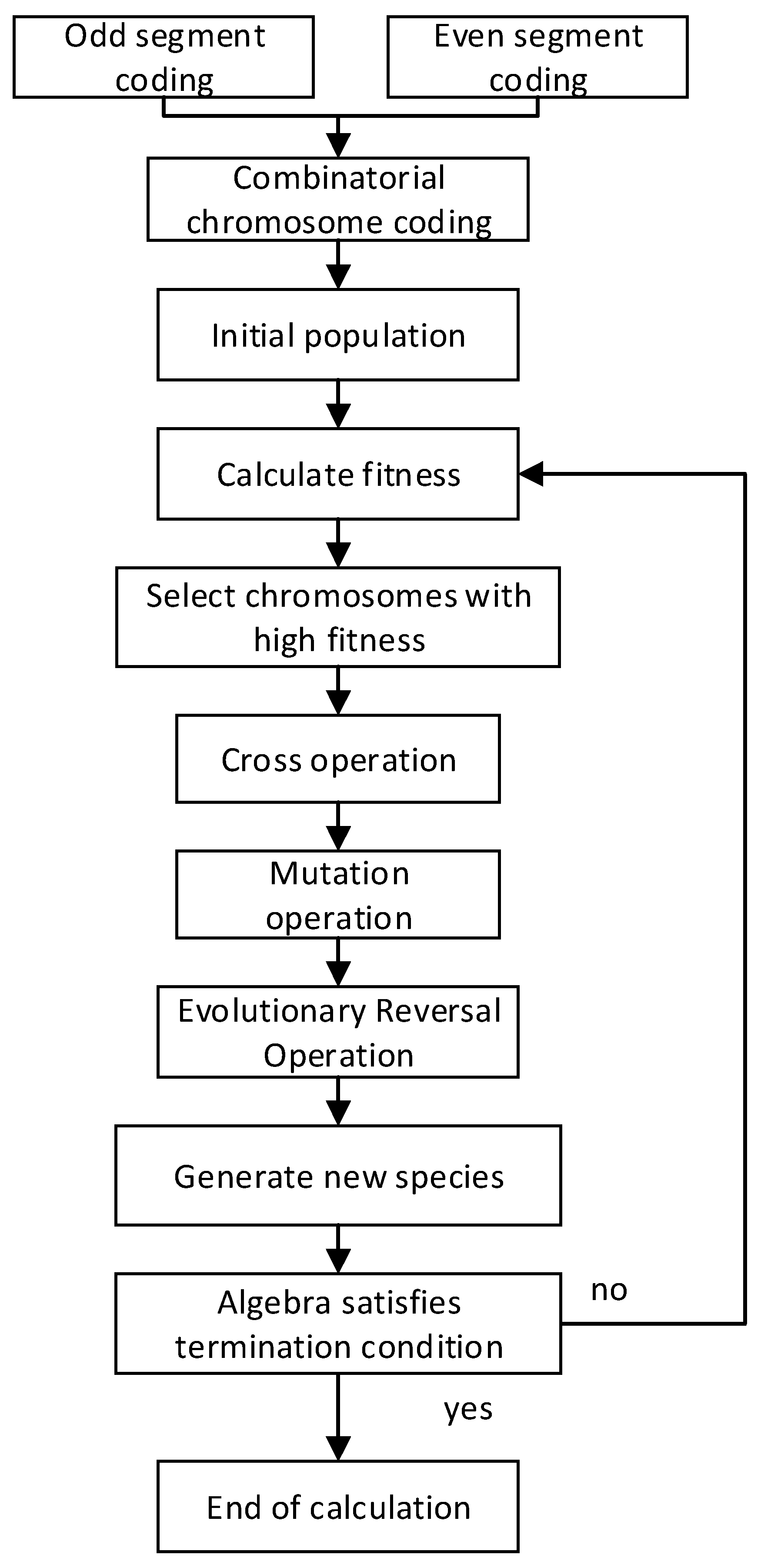
2.2.2. Genetic Algorithm-Based Path Planning Method
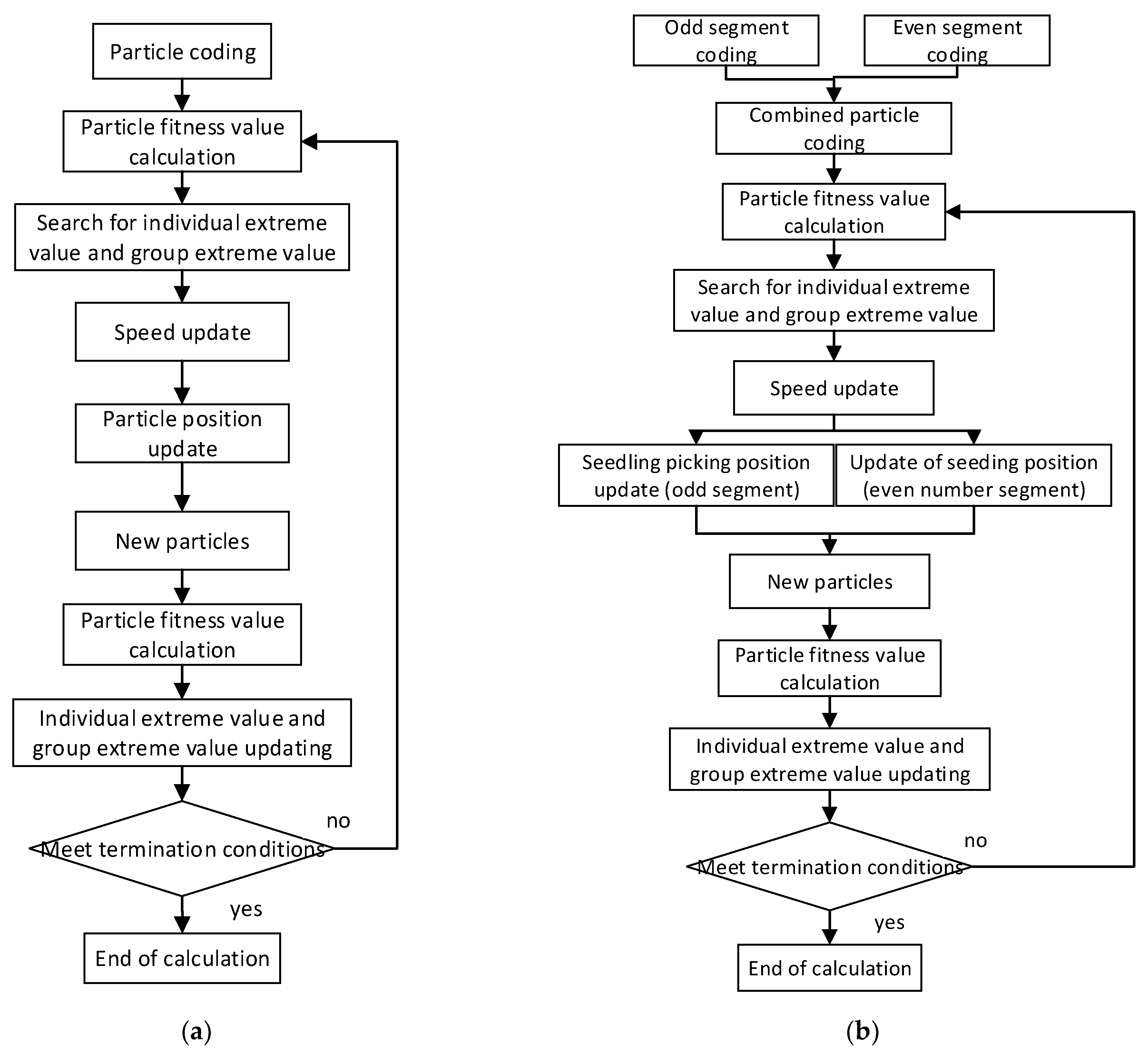
2.2.3. Path Planning Method Based on Improved Particle Swarm Optimization
- (1)
- Combined particle coding
- (2)
- Particle fitness calculation
- (3)
- Velocity update calculation
- (4)
- Seedling position update operator (odd segment)
2.3. Optimization of Algorithm Parameters
2.3.1. Particle Swarm Optimization Is Parameter Setting
2.3.2. Genetic Algorithm Parameter Setting
3. Results and Discussion
3.1. Replanting Path Planning Test for 50-Hole Seedling Trays
3.1.1. Replanting Path Planning Test for 50-Hole Seedling Trays with 5–20% Replanting Quantity
3.1.2. Replanting Path Planning Test for 50-Hole Seedling Trays with 10% Replanting
3.2. Replanting Path Planning Test with 72-Hole Seedling Trays
3.2.1. Replanting Path Planning Test for 72-Hole Seedling Trays with 5–20% Replanting Quantity
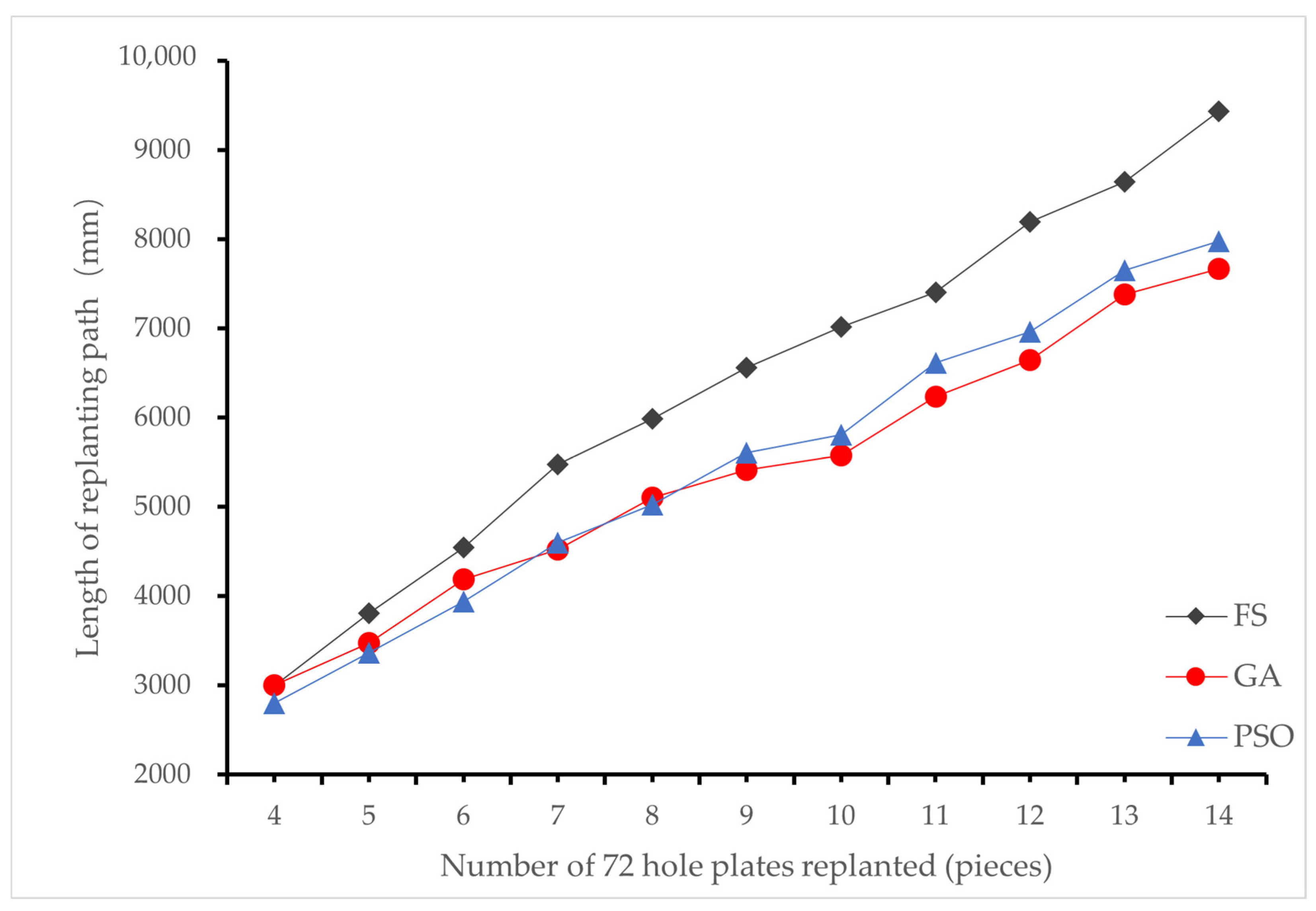
3.2.2. Replanting Path Planning Test for a 72-Hole Seedling Tray with 10% Replanting
3.3. Replanting Path Planning Test for 105-Hole Seedling Trays
3.3.1. Path Planning Test for Replanting 105-Hole Seedling Trays 5–20% Replanting
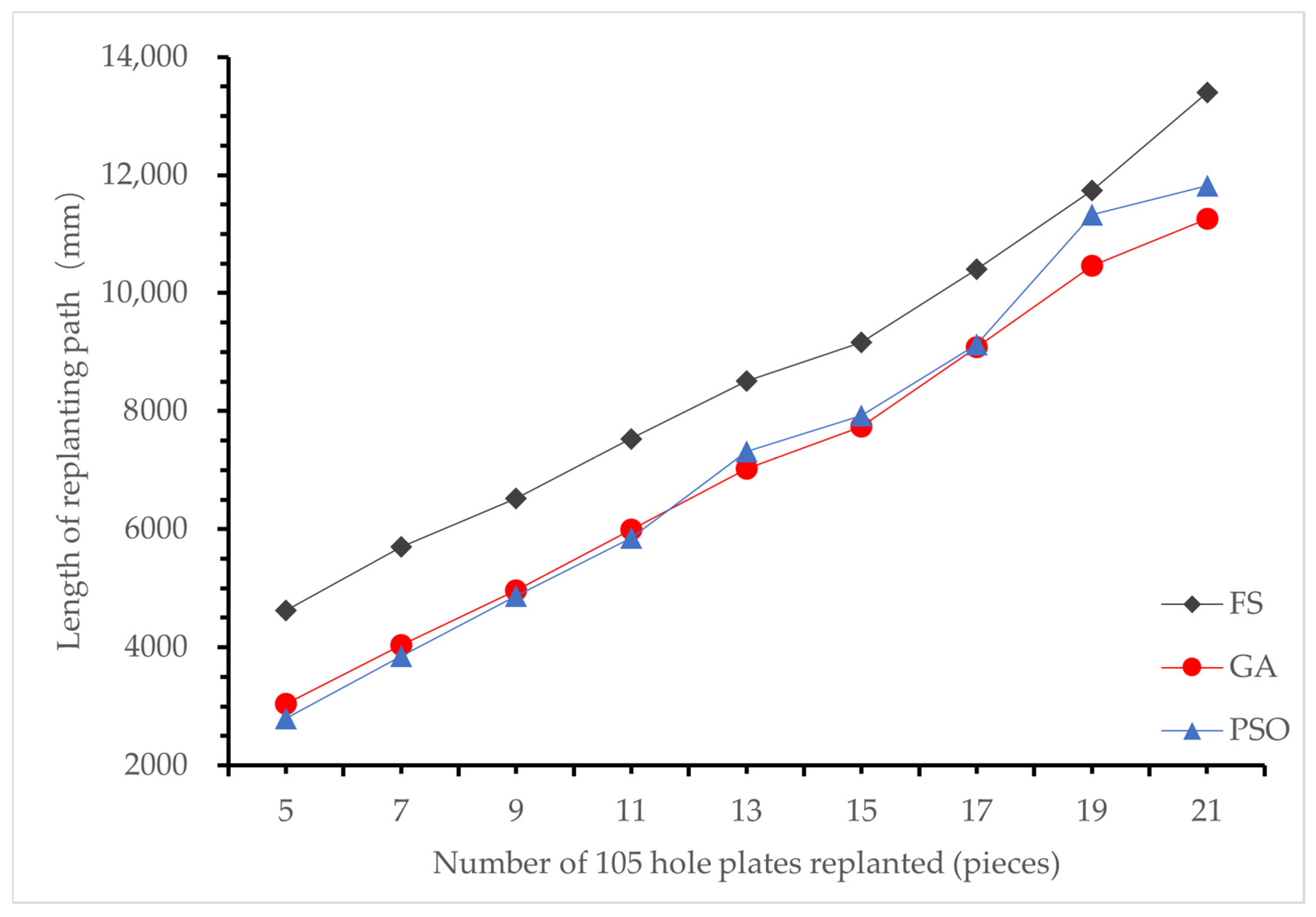
3.3.2. Replanting Path Planning Test for 105-Hole Seedling Trays with 10% Replanting Number
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mingchi, L.; Yanhai, J.; Zhanhui, W.; Weiming, H. Current situation and development trend of vegetable seedling industry in China. China Veg. 2018, 11, 1–7. [Google Scholar] [CrossRef]
- Chunyan, Z.; Dongjie, Y. Current Situation and Technical Trend of Vegetable Seedling Production in China. Agric. Eng. Technol. 2019, 39, 34–38. [Google Scholar] [CrossRef]
- Mengbao, G.; Mingjin, Y.; Bin, L.; Po, N.; Ling, Y. Current situation and development trend of vegetable seedling industry in China. J. Agric. Mech. Res. 2015, 37, 250–253. [Google Scholar] [CrossRef]
- National Development and Reform Commission. National Vegetable Industry Development Plan (2011–2020). China Veg. 2012, 5, 1–12. [Google Scholar] [CrossRef]
- Zhenhe, Z.; Zhaohong, M. Overview of China’s protected vegetable industry and the development priorities of the “13th Five Year Plan”—Interview with Zhang Zhenhe, Vice President of China Vegetable Association. China Veg. 2017, 5, 1–5. [Google Scholar] [CrossRef]
- Diankui, C. Current Situation, Problems and Development Trend of Vegetable Seedling Cultivation in China. China Veg. 2000, 6, 4–6. [Google Scholar]
- Junjie, Z.; Xiqun, Z.; Fazhi, P.; Jingzhe, C. The Vegetable Industralized Sowing Seedling Technology and Its Application Prospect. J. Hebei Agric. Sci. 2013, 17, 20–23. [Google Scholar] [CrossRef]
- Honghui, Y.; Chunshan, G.; Shun, Z. Discussion on the present situation and development trend of vegetable seedling in China. South China Agric. 2019, 13, 19+22. [Google Scholar] [CrossRef]
- Ying, Z. Design and simulation analysis of pot seedling transplanter in greenhouse. Agric. Technol. 2012, 32, 46. [Google Scholar]
- Yin, B.; Kai, P.; Lin, S. Application and development trend of plug substrate seedling technology. North. Hortic. 2008, 9, 60–62. [Google Scholar]
- Jinkui, H.; Xiqun, Z.; Xin, Q.; Guochang, F.; Zheng, L.; Fazhi, P. Current Situation and Development Countermeasures of Industrialized Seedling Raising Technology. Jiangsu Agric. Sci. 2012, 40, 349–351. [Google Scholar] [CrossRef]
- Wang, C.-N.; Yang, F.-C.; Nguyen, V.T.T.; Vo, N.T.J.M. CFD analysis and optimum design for a centrifugal pump using an effectively artificial intelligent algorithm. Micromachines 2022, 13, 1208. [Google Scholar] [CrossRef] [PubMed]
- Huynh, N.T.; Nguyen, T.V.; Nguyen, Q.M.; Continua, J.C.-C.M. Optimum Design for the Magnification Mechanisms Employing Fuzzy Logic-ANFIS. CMC-Comput. Mater. Contin. 2022, 73, 5961–5983. [Google Scholar]
- Lühua, H.; Hanping, M.; Xiaohua, M.; Jianping, H.; Xuejun, Y. Design of Automatic Picking Up Seedling End-effector Based on Mechanical Properties of Plug Seedlings. Trans. Chin. Soc. Agric. Mach. 2013, 44, 260–265. [Google Scholar]
- Lühua, H.; Hanping, M.; Lei, Y.; Jianping, H.; Wenyue, H.; Lili, D. Pincette-Type End-Effector Using Two Fingers and Four Pins for Picking Up Seedlings. Trans. Chin. Soc. Agric. Mach. 2015, 46, 23–30. [Google Scholar]
- Xin, J.; Xinwu, D.; Chuanhua, Y.; Jiangtao, J.; Zhe, D.; Hua, Y. Design and Experiment on Automatic Transporting Mechanism for Vegetable Potted Seedlings. Trans. Chin. Soc. Agric. Mach. 2016, 47, 103–111. [Google Scholar]
- Yongshuang, W.; Junxiong, Z.; Ting, Y.; Yuzhi, T. Current situation and analysis of automatic pick-up technology for vegetable plug seedlings. J. China Agric. Univ. 2021, 26, 128–142. [Google Scholar]
- Kutz, L.J.; Miles, G.E.; Hammer, P.A.; Krutz, G.W. Robotic transplanting of bedding plants. Trans. ASABE 1987, 30, 586–590. [Google Scholar] [CrossRef]
- Ryu, K.H.; Kim, G.; Han, J.S. AE—Automation and emerging technologies: Development of a robotic transplanter for bedding plants. J. Agric. Eng. Res. 2001, 78, 141–146. [Google Scholar] [CrossRef]
- Ting, Z.; Xiaopeng, W.; Chaoqun, W.; Liang, Z.; Xiaobo, L.; Xiaojun, Q.; Cheng, W. Design and Simulation Analysis of Transplanter for Potted Tray Seedlings in Greenhouse. Mach. Des. Res. 2009, 25, 121–124. [Google Scholar] [CrossRef]
- Guoxiang, S.; Xiaopeng, W.; Guomin, H.; Ting, Z.; Cheng, W.; Xiaojun, Q. Design of the End Actuator for Plug Seedling Transplanter and Virtual Prototype Analysis. Trans. Chin. Soc. Agric. Mach. 2010, 41, 48–53+47. [Google Scholar] [CrossRef]
- Feng, Q.; Zhao, C.; Jiang, K.; Fan, P.; Wang, X. Design and test of tray-seedling sorting transplanter. Int. J. Agric. Biol. Eng. 2015, 8, 14–20. [Google Scholar] [CrossRef]
- Lühua, H.; Hanping, M.; Jianping, H.; Jingyun, X.; Zhengrong, Z.; Guoxin, M. Design and Test of Automatic Transplanter for Greenhouse Plug Seedlings. Trans. Chin. Soc. Agric. Mach. 2016, 47, 59–67. [Google Scholar] [CrossRef]
- Jianping, H.; Heqi, J.; Yanchao, C.; Wei, L.; Lühua, H.; Qizhi, Y. Dimensional Synthesis and Trajectory Planning of Plug Seedling Transplanting Robot Based on Delta Parallel Mechanism. Trans. Chin. Soc. Agric. Mach. 2017, 48, 28–35. [Google Scholar] [CrossRef]
- Han, L.; Mao, H.; Kumi, F.; Hu, J. Development of A Multi-Task Robotic Transplanting Workcell for Greenhouse Seedlings. Appl. Eng. Agric. 2018, 34, 335–342. [Google Scholar] [CrossRef]
- Junhua, T.; Huanyu, J.; Mingchuan, Z. Optimization of Seedling Transplanting Path Based on Genetic Algorithm. Trans. Chin. Soc. Agric. Mach. 2013, 44, 45–49+26. [Google Scholar] [CrossRef]
- Jiang, Z.; Zhou, M.; Tong, J.; Jiang, H.; Yang, Y.; Wang, A.; You, Z. Comparing an ant colony algorithm with a genetic algorithm for replugging tour planning of seedling transplanter. Comput. Electron. Agric. 2015, 113, 225–233. [Google Scholar] [CrossRef]
- Junhua, T.; Huanyu, J.; Chuanyu, W. Optimization of Seedlings Lower Density Transplanting Path Based on Greedy Algorithm. Trans. Chin. Soc. Agric. Mach. 2016, 47, 8–13. [Google Scholar] [CrossRef]
- Leiying, H.; Taiwei, Y.; Chuanyu, W.; Yaxin, Y.; Junhua, T.; Chengjin, C. Optimization of Replugging Tour Planning Based on Greedy Genetic Algorithm. Trans. Chin. Soc. Agric. Mach. 2017, 48, 36–43. [Google Scholar] [CrossRef]
- Shoujiang, X.; Zhuqing, L. Frog Leaping Algorithm for Path Optimization of Pot Moving of Plug Seedlings Based on Neighborhood Search. J. Agric. Mech. Res. 2018, 40, 208–212. [Google Scholar] [CrossRef]
- Ronghua, J.; Guowei, Z.; Hongtao, Y.; Lihua, Z. Research on Segmental Optimization Algorithm of Pot Seedling Automatic Transplantation Path Based on Greed Ant Colony. J. Chin. Agric. Mech. 2019, 40, 165–170. [Google Scholar] [CrossRef]
- Taiwei, Y. Study on Health Identification and Transplanting Path Optimization of Greenhouse Leafy Seedling. Master’s Thesis, Zhejiang Sci-Tech University, Hangzhou, China, 2018. [Google Scholar]
- Xiaojun, L.; Weibing, W.; Ganghui, L.; Runze, L.; Fei, L. Optimizing the Path of Plug Tray Seedling Transplanting by Using the Improved A* Algorithm. Agriculture 2022, 12, 1302. [Google Scholar]
- Lina, Z.; Yu, T.; Haotun, L.; Baosheng, L.; Yiyu, J.; Shuo, W. Optimization of automatic transplanting path for plug seedlings in greenhouse. Trans. Chin. Soc. Agric. Eng. 2020, 36, 65–72. [Google Scholar]
- Lei, Y. Analysis of 30 Cases of MATLAB Intelligent Algorithm; Beihang University Press: Beijing, China, 2015. [Google Scholar]
- Bhatt, P.; Sarangi, S.; Pappula, S. Comparison of CNN models for application in crop health assessment with participatory sensing. In Proceedings of the 2017 IEEE Global Humanitarian Technology Conference (GHTC), San Jose, CA, USA, 19–22 October 2017; pp. 1–7. [Google Scholar]
- Shoujiang, X. Optimization of Automatic Bowl Moving Path of Pot Seedlings Based on Ant Colony Algorithm. Jiangsu Agric. Sci. 2015, 43, 475–477. [Google Scholar] [CrossRef]




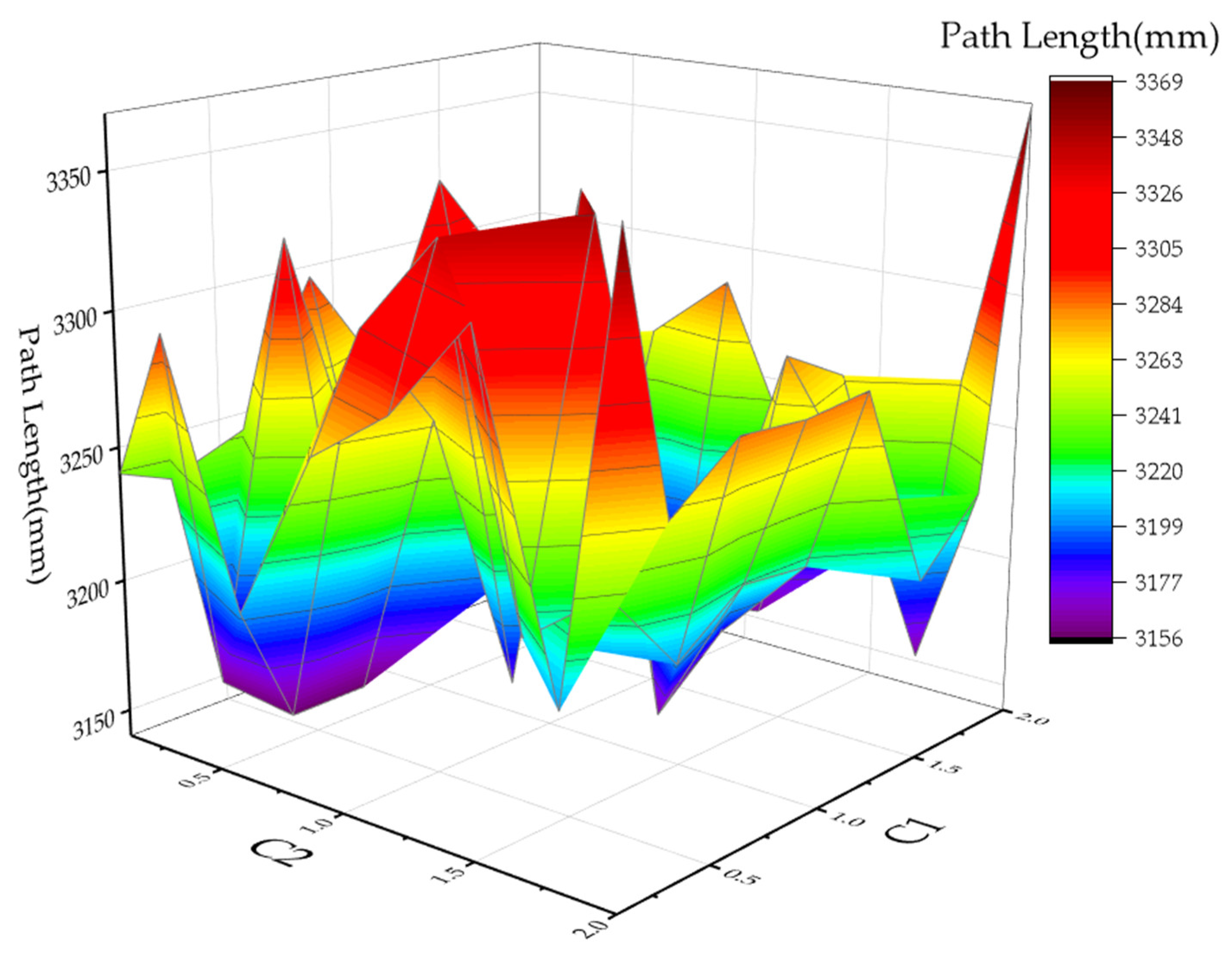
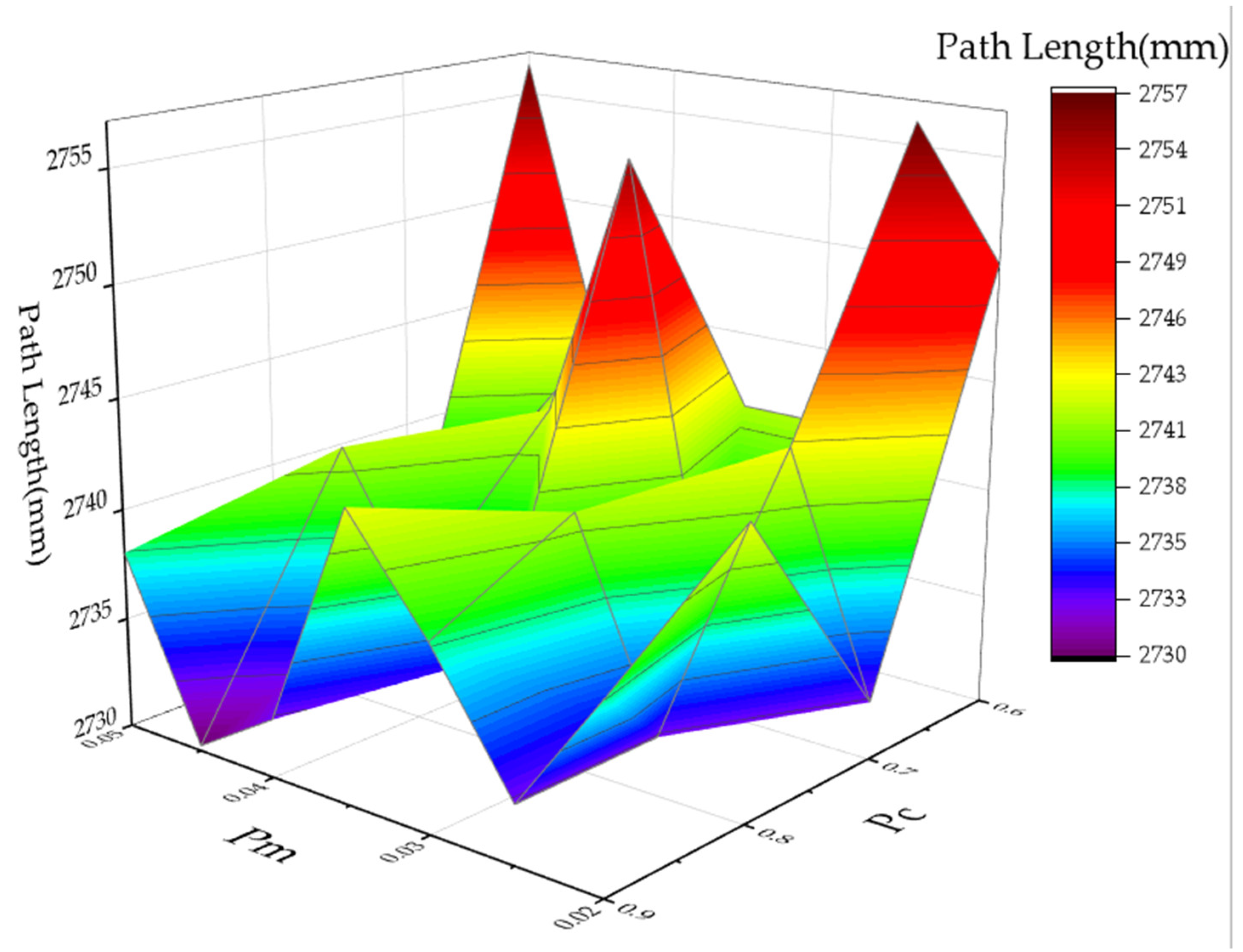

| Parameter | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | Level 6 | Level 7 | Level 8 |
|---|---|---|---|---|---|---|---|---|
| C1 | 0.1 | 0.3 | 0.6 | 0.9 | 1.2 | 1.5 | 1.8 | 2 |
| C2 | 0.1 | 0.3 | 0.6 | 0.9 | 1.2 | 1.5 | 1.8 | 2 |
| Parameter | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 | Level 6 | Level 7 |
|---|---|---|---|---|---|---|---|
| Pc | 0.6 | 0.7 | 0.8 | 0.9 | |||
| Pm | 0.02 | 0.025 | 0.03 | 0.035 | 0.04 | 0.045 | 0.05 |
| Number of Replanting | FS (mm) | GA (mm) | PSO (mm) | e (mm) | r1 (%) | r2 (%) |
|---|---|---|---|---|---|---|
| 3 | 2991.60 | 2665.46 | 2472.62 | 192.84 | 10.90 | 17.35 |
| 4 | 3778.80 | 3217.96 | 2979.74 | 238.22 | 14.84 | 21.15 |
| 5 | 4444.94 | 3675.56 | 3362.29 | 313.27 | 17.31 | 24.36 |
| 6 | 5221.43 | 4201.96 | 4132.41 | 69.55 | 19.52 | 20.86 |
| 7 | 5914.42 | 4673.76 | 4692.54 | −18.78 | 20.98 | 20.66 |
| 8 | 6772.81 | 5279.33 | 5378.80 | −99.47 | 22.05 | 20.58 |
| 9 | 7251.32 | 5521.23 | 5787.34 | −266.11 | 23.86 | 20.19 |
| 10 | 8080.09 | 5989.18 | 6219.95 | −230.77 | 25.88 | 23.02 |
| Average | / | / | / | / | 19.41 | 21.02 |
| Serial No | FS (mm) | GA (mm) | PSO (mm) | e (mm) | r1 (%) | r2 (%) | Time (GA) | Time (PSO) | r3 (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2248.78 | 1971.69 | 1981.01 | −9.32 | 12.32 | 11.91 | 2.2666 | 0.9732 | 57.06 |
| 2 | 3524.64 | 3127.93 | 3159.80 | −31.87 | 11.26 | 10.35 | 2.3633 | 0.9747 | 58.76 |
| 3 | 3138.54 | 2848.13 | 2887.64 | −39.51 | 9.25 | 7.99 | 2.2891 | 0.9542 | 58.32 |
| 4 | 2786.05 | 2619.12 | 2666.41 | −47.29 | 5.99 | 4.29 | 2.3567 | 0.9714 | 58.78 |
| 5 | 3151.32 | 2801.87 | 2857.01 | −55.14 | 11.09 | 9.34 | 2.2274 | 0.9587 | 56.96 |
| 6 | 3378.62 | 2997.29 | 2993.13 | 4.16 | 11.29 | 11.41 | 2.2796 | 0.9924 | 56.47 |
| 7 | 3382.79 | 2869.45 | 2896.22 | −26.77 | 15.18 | 14.38 | 2.2969 | 0.9717 | 57.70 |
| 8 | 3337.79 | 3122.95 | 3164.44 | −41.49 | 6.44 | 5.19 | 2.3604 | 0.9790 | 58.52 |
| 9 | 3395.63 | 2748.84 | 2761.31 | −12.47 | 19.05 | 18.68 | 2.3619 | 0.9619 | 59.27 |
| 10 | 3367.58 | 2925.95 | 2950.97 | −25.02 | 13.11 | 12.37 | 2.3800 | 0.9849 | 58.62 |
| Average | 3171.17 | 2803.32 | 2831.79 | −28.47 | 11.50 | 10.59 | 2.3182 | 0.9722 | 58.05 |
| Number of Replanting | FS (mm) | GA (mm) | PSO (mm) | e (mm) | r1 (%) | r2 (%) |
|---|---|---|---|---|---|---|
| 4 | 2994.56 | 3001.71 | 2801.03 | 200.68 | −0.24 | 6.46 |
| 5 | 3806.63 | 3474.84 | 3361.52 | 113.32 | 8.72 | 11.69 |
| 6 | 4544.81 | 4183.64 | 3938.27 | 245.37 | 7.95 | 13.35 |
| 7 | 5473.38 | 4520.61 | 4596.34 | −75.73 | 17.40 | 16.02 |
| 8 | 5986.81 | 5104.67 | 5023.12 | 81.55 | 14.73 | 16.10 |
| 9 | 6558.08 | 5407.68 | 5605.23 | −197.55 | 17.54 | 14.53 |
| 10 | 7019.04 | 5574.34 | 5807.53 | −233.19 | 20.58 | 17.26 |
| 11 | 7400.95 | 6235.31 | 6609.03 | −373.72 | 15.75 | 10.70 |
| 12 | 8194.72 | 6645.94 | 6963.80 | −317.86 | 18.90 | 15.02 |
| 13 | 8645.39 | 7377.96 | 7649.34 | −271.38 | 14.66 | 11.52 |
| 14 | 9437.74 | 7669.57 | 7976.82 | −307.25 | 18.74 | 15.48 |
| Average | / | / | / | / | 14.07 | 13.47 |
| Serial No | FS (mm) | GA (mm) | PSO (mm) | e (mm) | r1 (%) | r2 (%) | Time (GA) | Time (PSO) | r3 (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 5471.16 | 3603.59 | 3500.36 | 103.23 | 34.13 | 36.02 | 2.5199 | 1.0086 | 59.97 |
| 2 | 5819.32 | 4469.41 | 4375.92 | 93.49 | 23.19 | 24.80 | 2.5299 | 1.0132 | 59.95 |
| 3 | 4553.5 | 3514.09 | 3640.5 | −126.41 | 22.82 | 20.05 | 2.5255 | 1.0565 | 58.16 |
| 4 | 4962.23 | 3315.24 | 3360.4 | −45.16 | 33.19 | 32.28 | 2.5199 | 1.0078 | 60.01 |
| 5 | 5871.38 | 4655.48 | 4554.62 | 100.86 | 20.70 | 22.42 | 2.6034 | 0.9972 | 61.69 |
| 6 | 5555.82 | 3914.09 | 3725.73 | 188.36 | 29.54 | 32.94 | 2.5133 | 1.0157 | 59.58 |
| 7 | 4753.39 | 3390.91 | 3398.12 | −7.21 | 28.66 | 28.51 | 2.5260 | 1.0091 | 60.05 |
| 8 | 5497.17 | 3971.93 | 4148.8 | −176.87 | 27.74 | 24.52 | 2.5355 | 1.1002 | 56.60 |
| 9 | 5699.25 | 3884.64 | 3750.24 | 134.4 | 31.83 | 34.19 | 2.6302 | 0.9933 | 62.23 |
| 10 | 5251.65 | 3728.98 | 3550.61 | 178.37 | 28.99 | 32.39 | 2.4866 | 1.0018 | 59.71 |
| Average | 5343.48 | 3844.83 | 3800.53 | 44.31 | 28.08 | 28.81 | 2.5390 | 1.0203 | 59.79 |
| Number of Replanting | FS (mm) | GA (mm) | PSO (mm) | e (mm) | r1 (%) | r2 (%) |
|---|---|---|---|---|---|---|
| 5 | 4626.83 | 3045.83 | 2801.28 | 244.55 | 34.17 | 39.46 |
| 7 | 5700.16 | 4031.08 | 3846.21 | 184.87 | 29.28 | 32.52 |
| 9 | 6521.69 | 4963.72 | 4872.71 | 91.01 | 23.89 | 25.28 |
| 11 | 7530.11 | 5991.30 | 5845.45 | 145.85 | 20.44 | 22.37 |
| 13 | 8506.13 | 7024.97 | 7317.80 | −292.83 | 17.41 | 13.97 |
| 15 | 9159.77 | 7730.32 | 7917.21 | −186.89 | 15.61 | 13.57 |
| 17 | 10,398.79 | 9078.10 | 9130.27 | −52.17 | 12.70 | 12.20 |
| 19 | 11,736.63 | 10,463.17 | 11,326.85 | −863.68 | 10.85 | 3.49 |
| 21 | 13,404.15 | 11,259.28 | 11,817.37 | −558.09 | 16.00 | 11.84 |
| Average | / | / | / | / | 14.07 | 13.47 |
| Serial No | FS (mm) | GA (mm) | PSO (mm) | e (mm) | r1 (%) | r2 (%) | Time (GA) | Time (PSO) | r3 (%) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 8160.27 | 5550.51 | 5704.15 | −153.64 | 31.98 | 30.10 | 3.5157 | 1.4819 | 57.85 |
| 2 | 8786.58 | 5844.80 | 6420.66 | −575.86 | 33.48 | 26.93 | 3.2936 | 1.4771 | 55.15 |
| 3 | 8112.86 | 5533.13 | 5784.15 | −251.02 | 31.80 | 28.70 | 3.5098 | 1.5160 | 56.81 |
| 4 | 8522.22 | 5792.78 | 5739.12 | 53.66 | 32.03 | 32.66 | 3.3608 | 1.5012 | 55.33 |
| 5 | 8281.36 | 5905.31 | 5712.46 | 192.85 | 28.69 | 31.02 | 3.3197 | 1.5317 | 53.86 |
| 6 | 7968.31 | 5199.72 | 5287.27 | −87.55 | 34.75 | 33.65 | 3.3598 | 1.4911 | 55.62 |
| 7 | 7732.35 | 5587.81 | 5562.36 | 25.45 | 27.73 | 28.06 | 3.2863 | 1.5124 | 53.98 |
| 8 | 7754.31 | 5246.52 | 5398.02 | −151.5 | 32.34 | 30.39 | 3.3029 | 1.5276 | 53.75 |
| 9 | 7761.83 | 5243.84 | 5600.69 | −356.85 | 32.44 | 27.84 | 3.3093 | 1.5400 | 53.46 |
| 10 | 8058.54 | 5987.40 | 6107.55 | −120.15 | 25.70 | 24.21 | 3.3113 | 1.4964 | 54.81 |
| Average | 8113.86 | 5589.18 | 5731.64 | −142.46 | 31.09 | 29.36 | 3.35692 | 1.50754 | 55.06 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, E.; Xiao, Z.; Tan, Y. A Fast Path Planning Method of Seedling Tray Replanting Based on Improved Particle Swarm Optimization. Agronomy 2023, 13, 853. https://doi.org/10.3390/agronomy13030853
Sun E, Xiao Z, Tan Y. A Fast Path Planning Method of Seedling Tray Replanting Based on Improved Particle Swarm Optimization. Agronomy. 2023; 13(3):853. https://doi.org/10.3390/agronomy13030853
Chicago/Turabian StyleSun, Erjie, Zhang Xiao, and Yu Tan. 2023. "A Fast Path Planning Method of Seedling Tray Replanting Based on Improved Particle Swarm Optimization" Agronomy 13, no. 3: 853. https://doi.org/10.3390/agronomy13030853
APA StyleSun, E., Xiao, Z., & Tan, Y. (2023). A Fast Path Planning Method of Seedling Tray Replanting Based on Improved Particle Swarm Optimization. Agronomy, 13(3), 853. https://doi.org/10.3390/agronomy13030853





