Design and Testing of an End-Effector for Tomato Picking
Abstract
1. Introduction
2. Materials and Methods
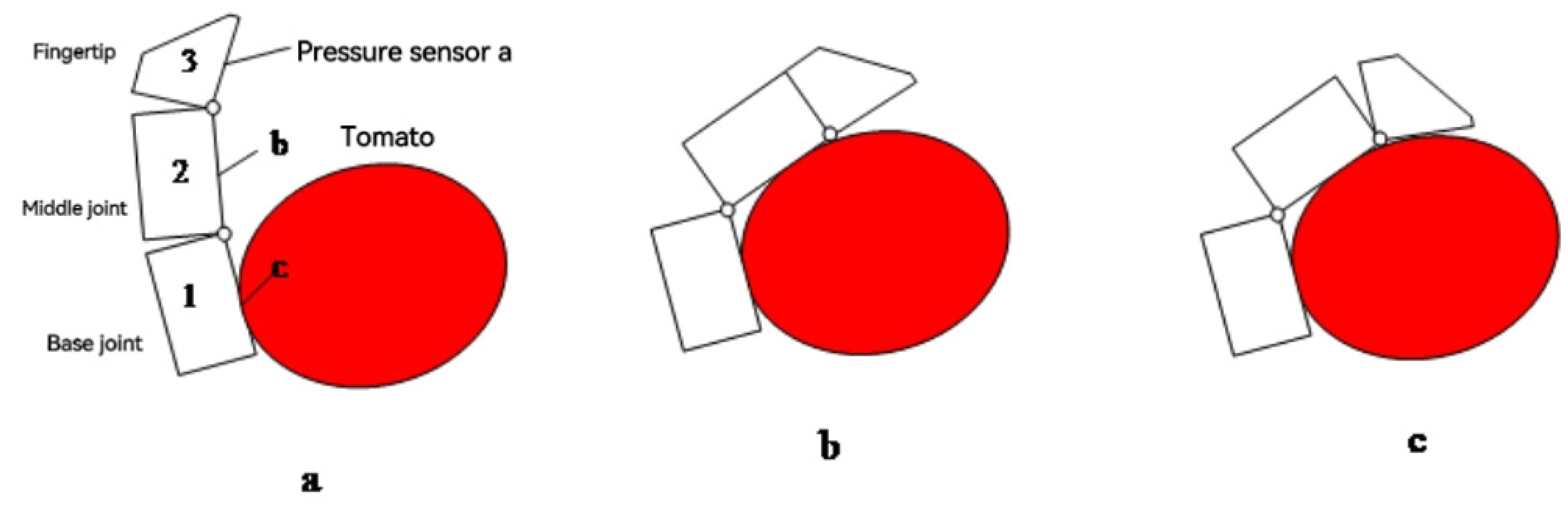
2.1. Mechanistic Analysis of the Motion Characteristics of Tomato Picking End-Effectors
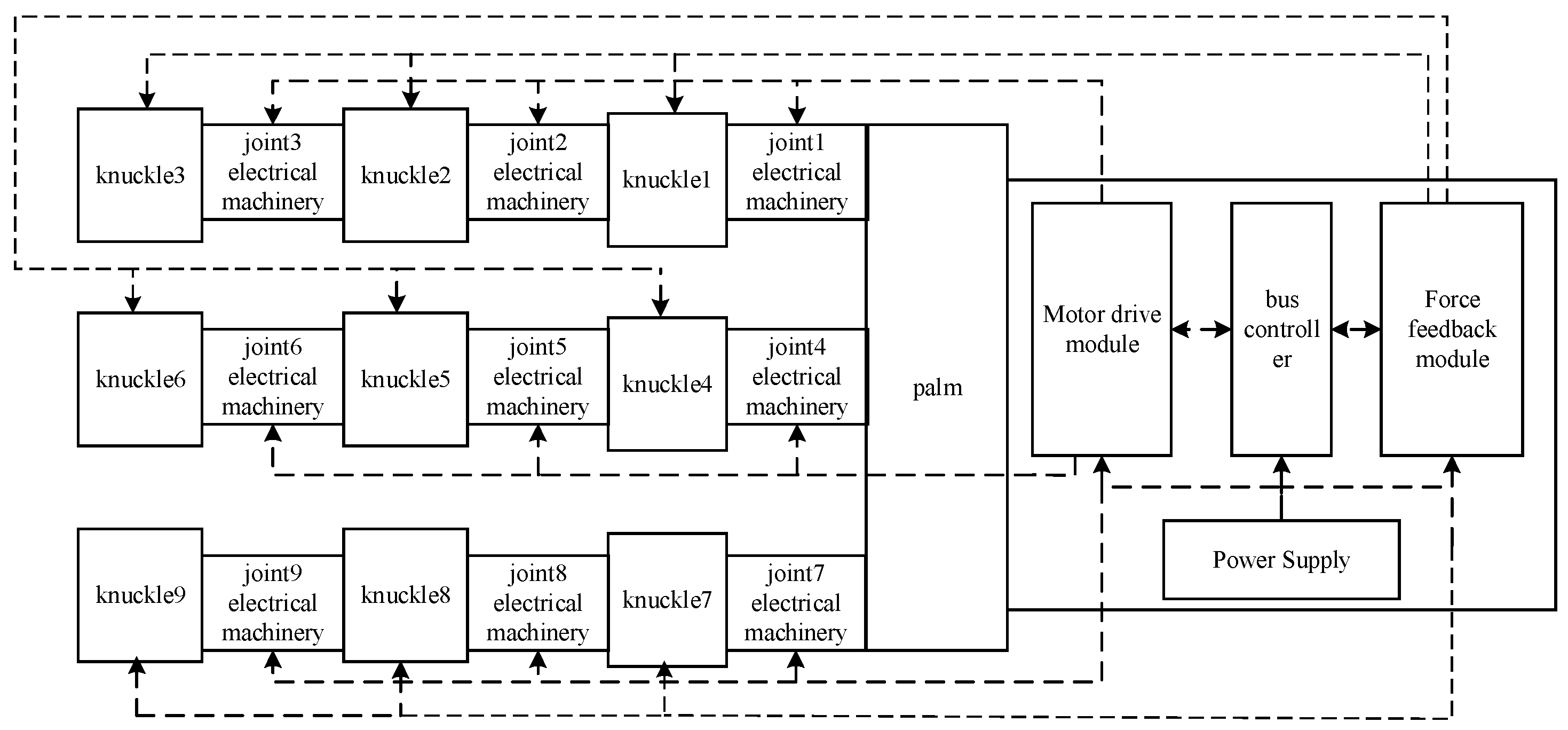
2.2. Tomato Picking End-Effector Mechanical Structure Design and Calibration
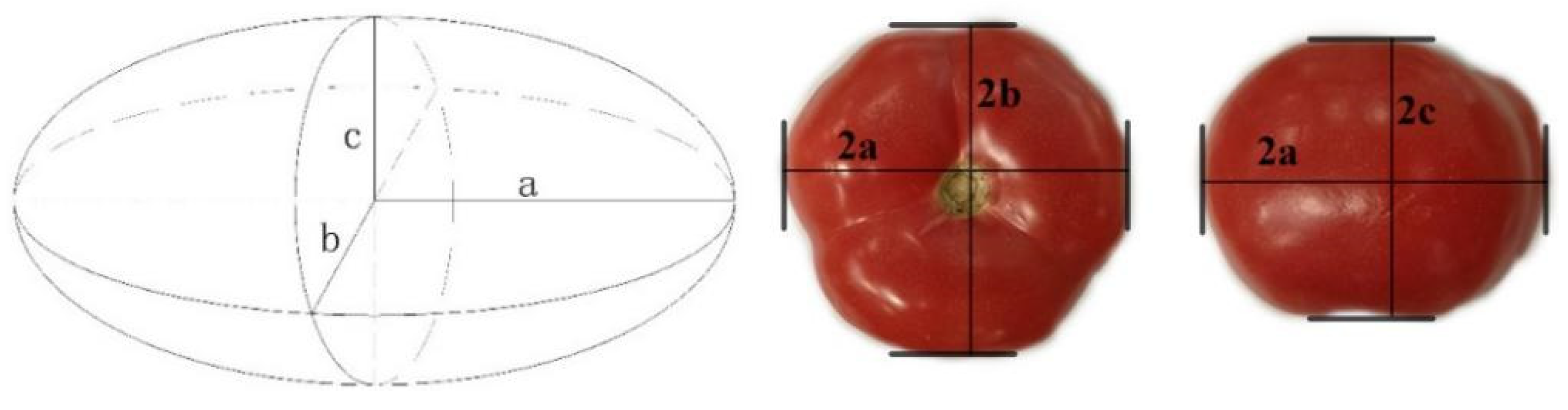
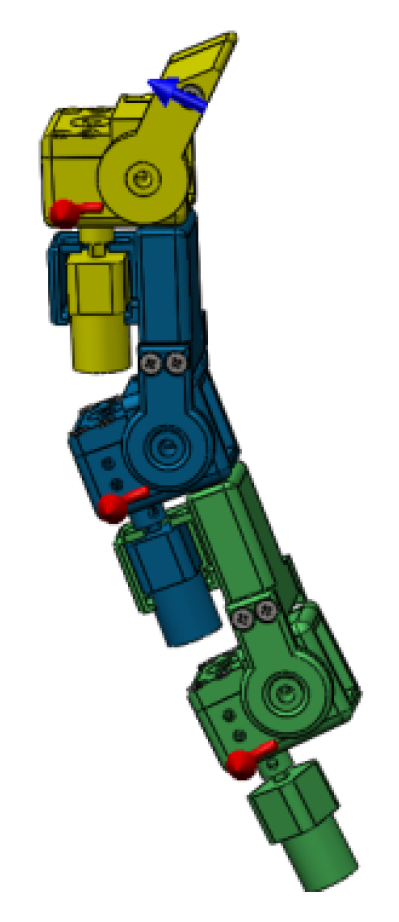
2.2.1. Determining the Size of the Tomato Picking End-Effector
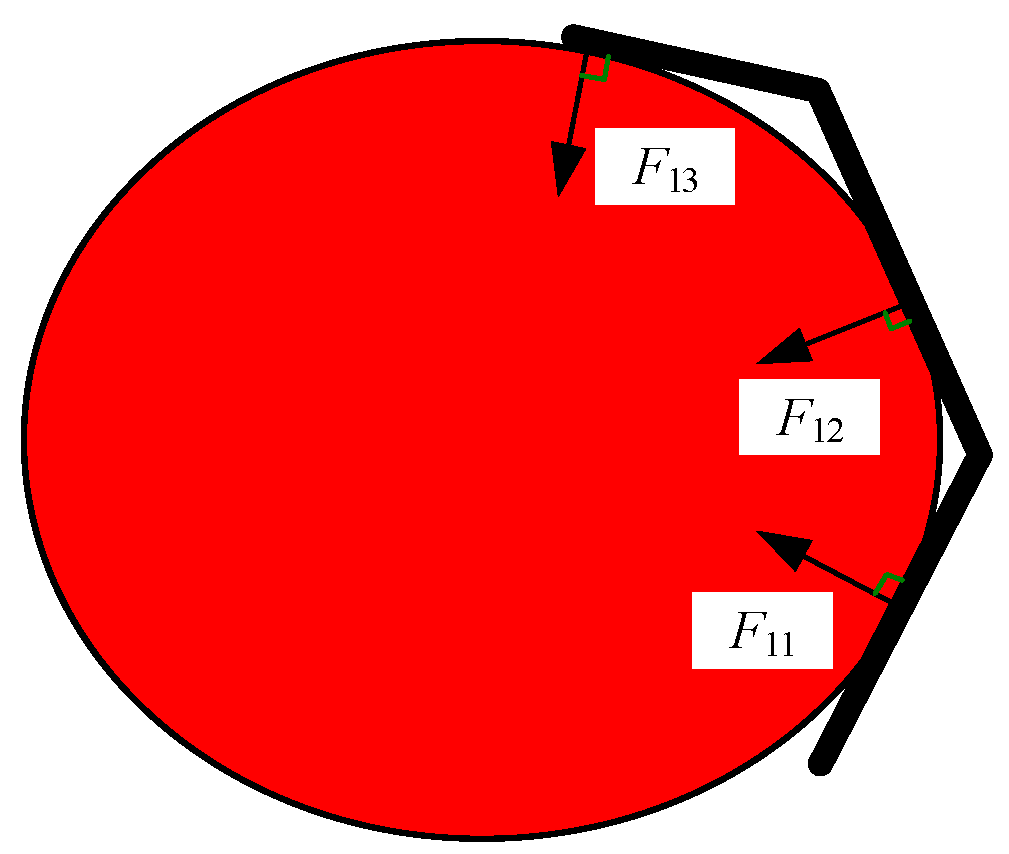
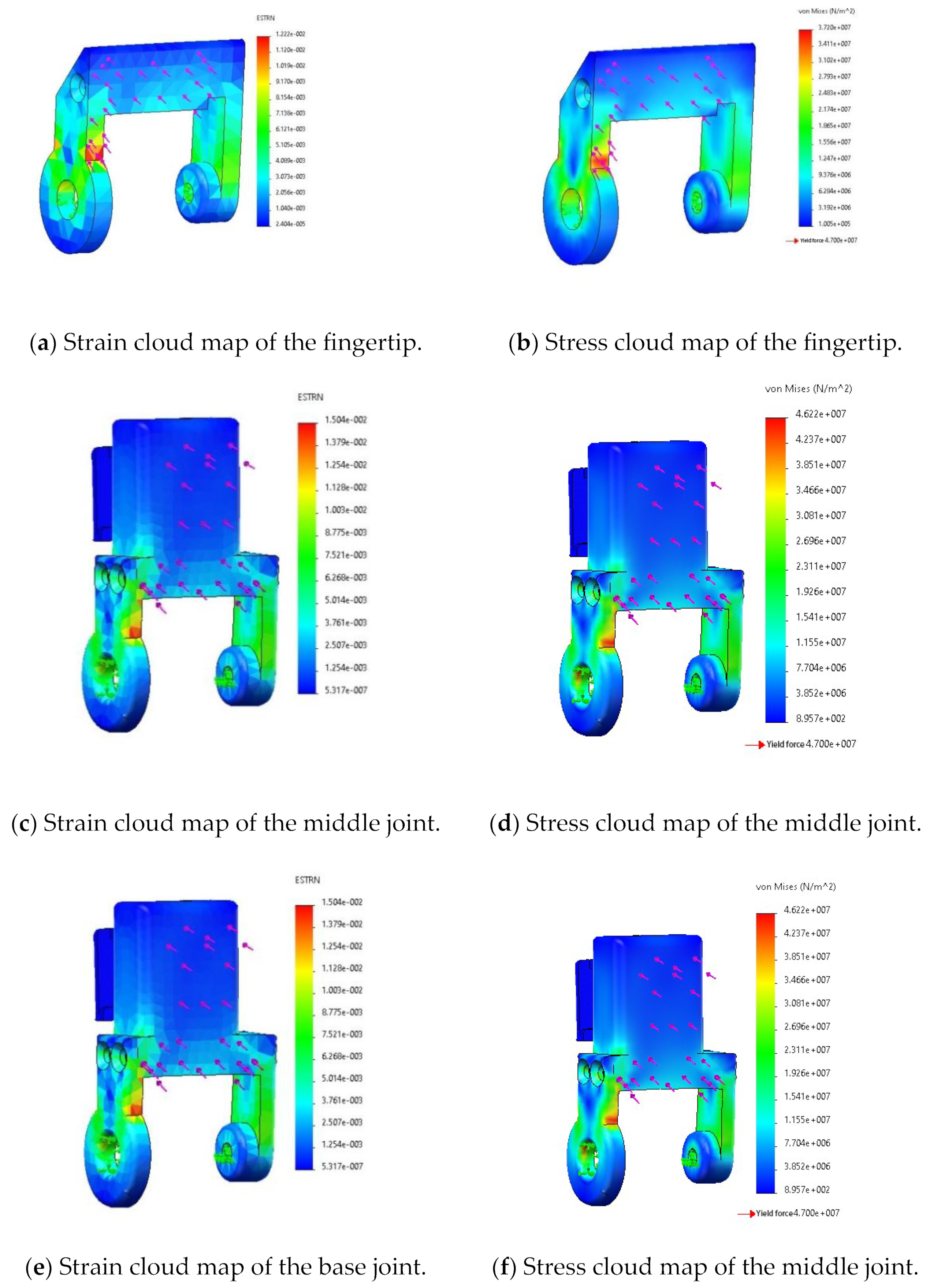
2.2.2. Strength Checking of the Key Parts
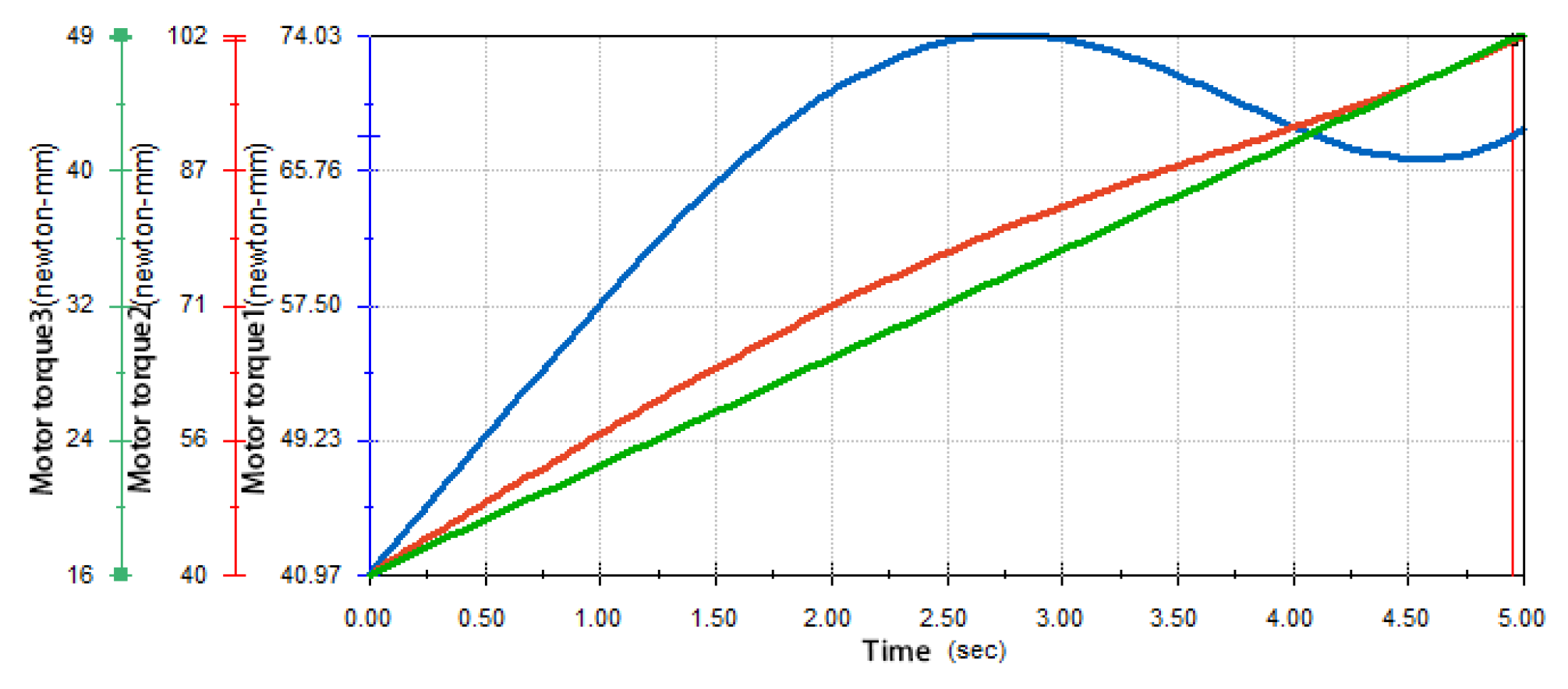
2.2.3. Motor Performance Checking
2.3. Kinematic Simulation Analysis of Tomato Picking End-Effector
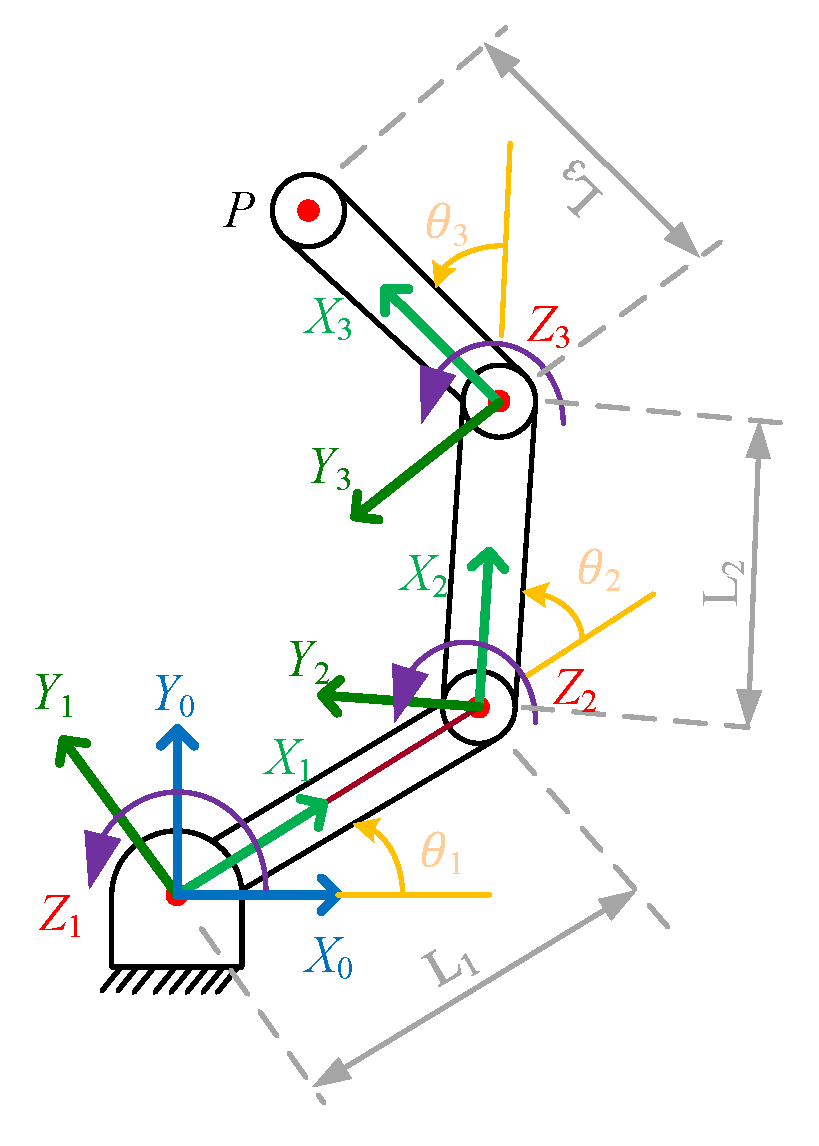
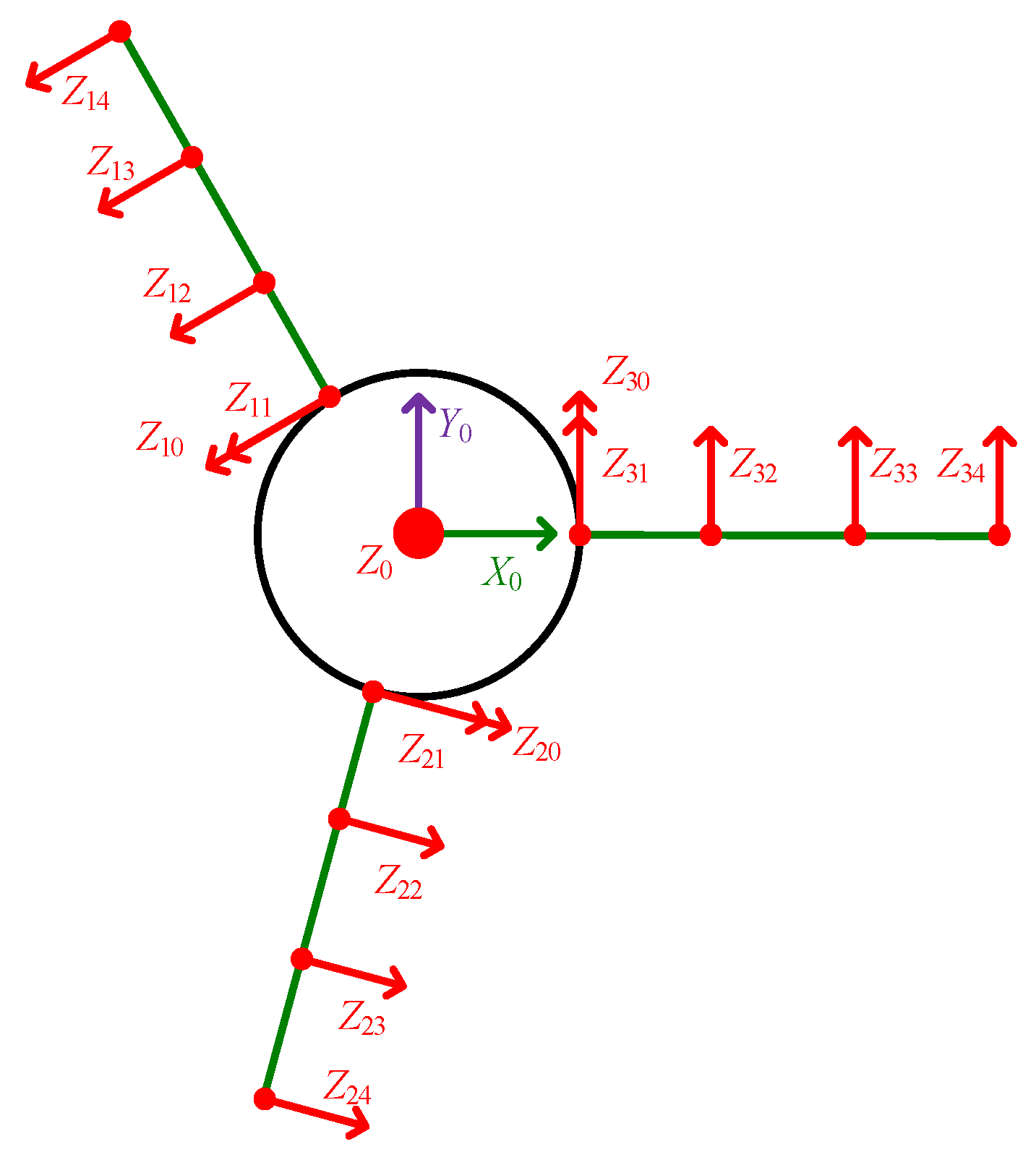
2.3.1. Kinematic Analysis
2.3.2. Forward Kinematic Analysis
- Rotation of angles around the axis;
- Translation along the axis by lengths;
- Rotation of angles around the axis;
- Translation along the axis by lengths.
2.3.3. Inverse Kinematic Analysis
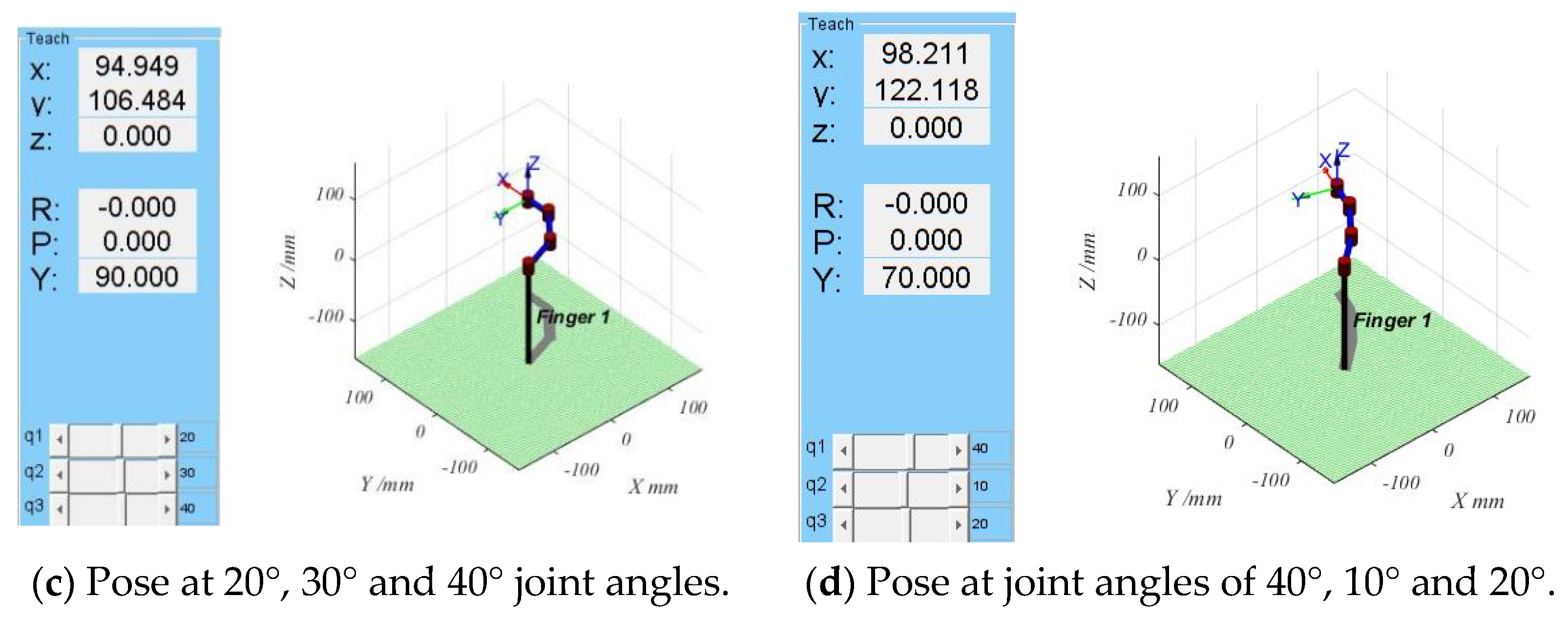
2.3.4. Kinematic Simulation Verification
2.4. Tomato Picking End-Effector Trajectory Planning and Workspace Simulation Verification
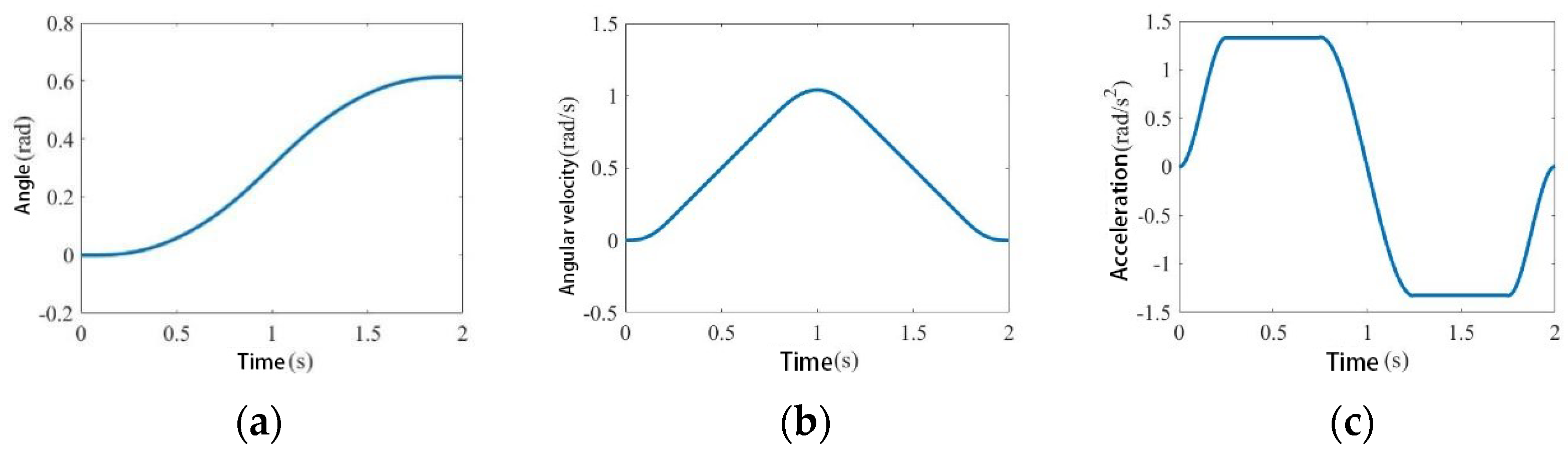
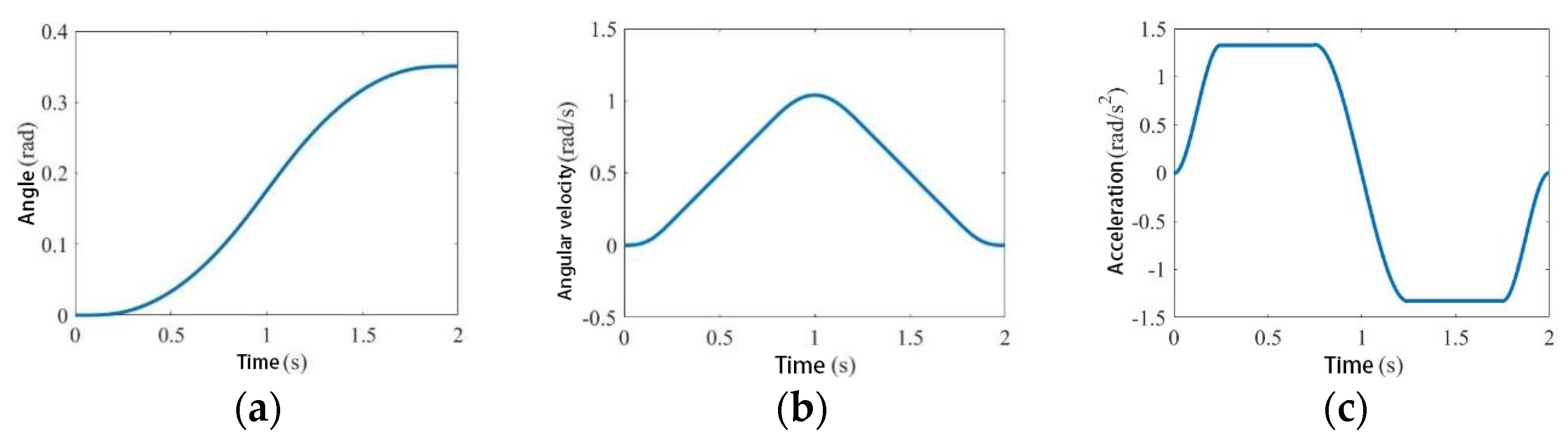
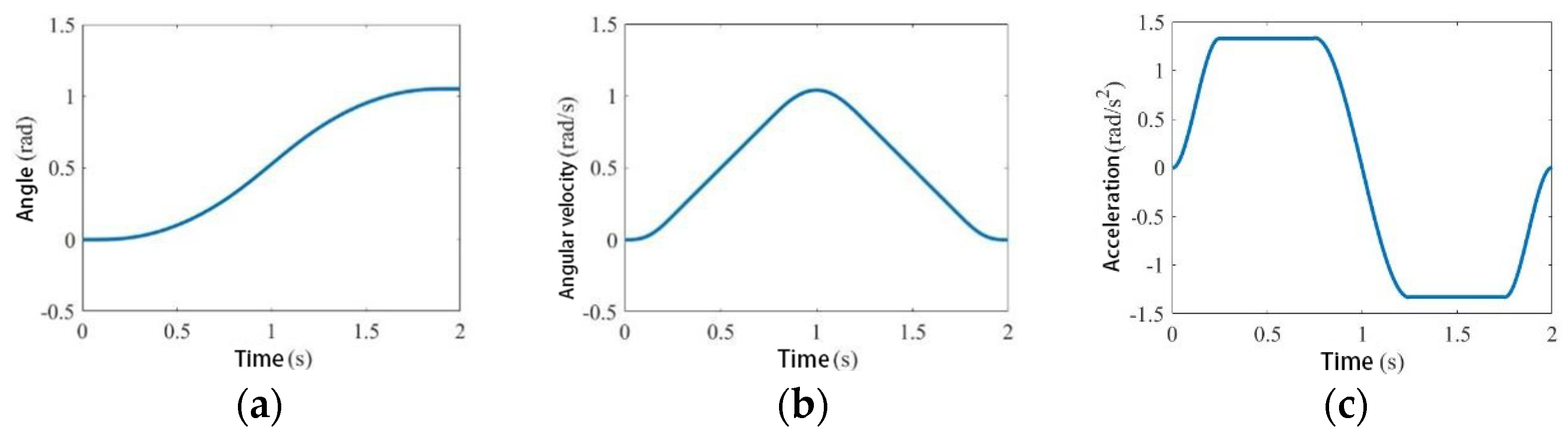
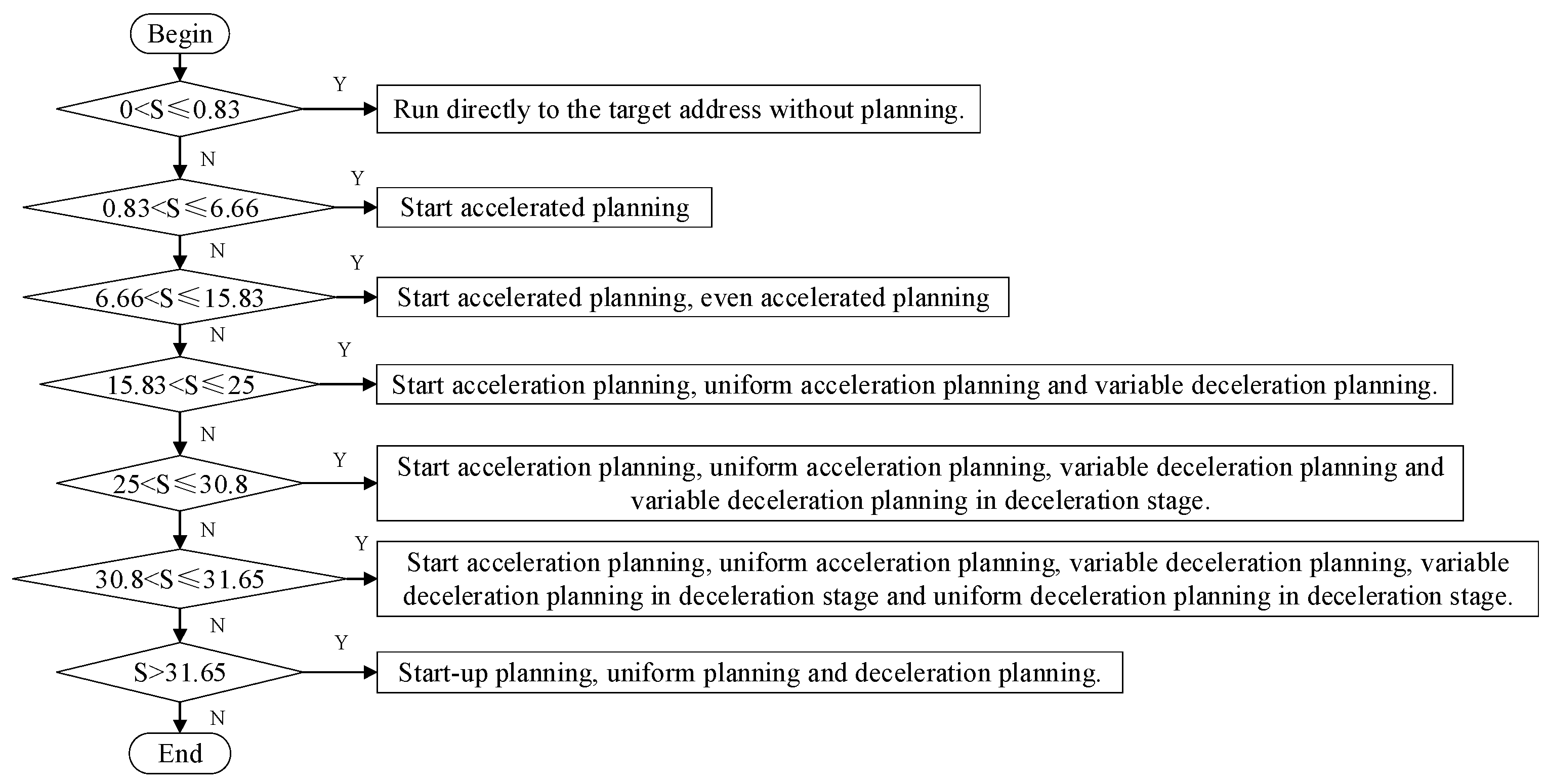
2.4.1. Trajectory Planning
2.4.2. Workspace Simulation Verification
3. Results
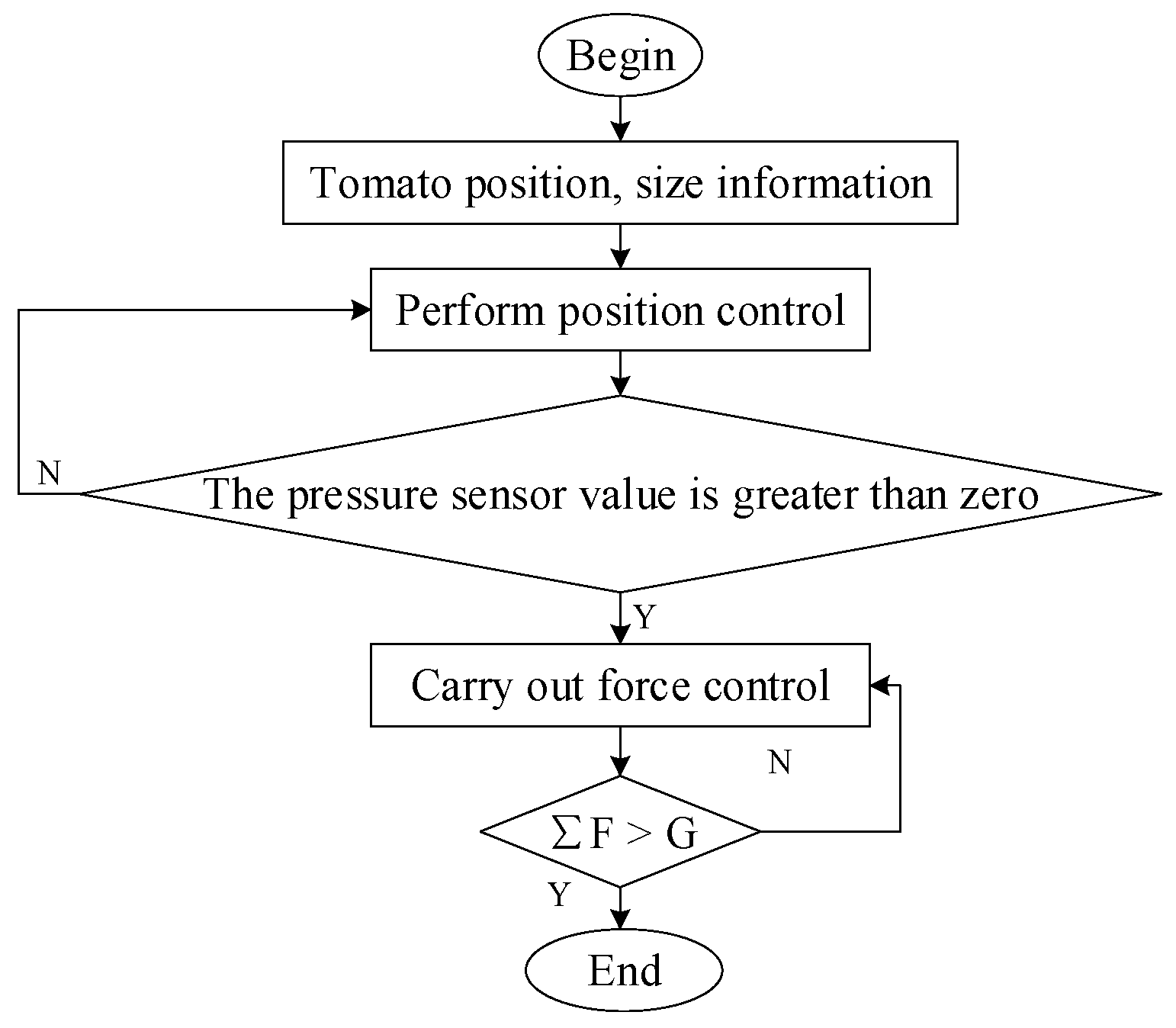
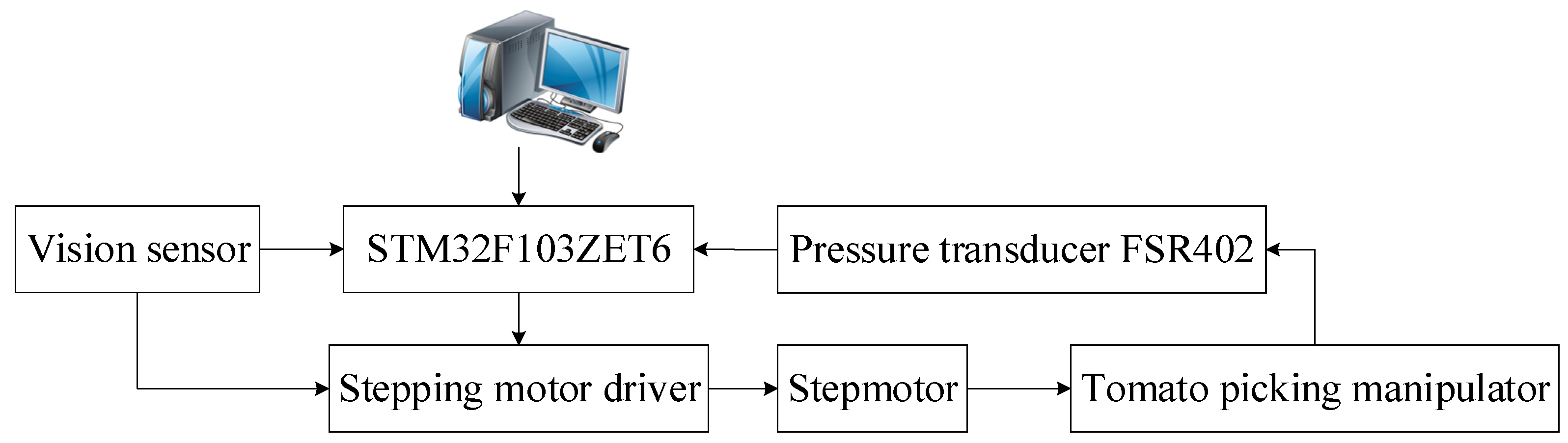
3.1. Test Platform Construction
3.2. Test and Result Analysis
4. Discussion
- Flexible joints could be added for the finger structure of the tomato picking end-effector. A suitable integrated driven joint motor could be selected to improve the compactness of the end-effector structure, yielding more of a bionic shape, size and movement.
- More accurate pressure sensors for contact force collection and more sensors on the end-effector, such as tactile sensors, joint displacement sensors, joint torque sensors, etc., could render the end-effector capable of humanoid picking in the greenhouse environment.
- The control algorithm of the end-effector could be optimized to equip the end-effector with multiple picking modes while also improving the picking efficiency and enhancing the flexibility and stability of the end-effector when grasping. The control system could also be optimized by adding the human–computer interaction interface for the convenience of user debugging.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, H.; He, Y.; Zou, J.; Wu, Q. Analysis of spatiotemporal differences of cultivated land use intensity in Poyang Lake eco-economic zone based on emergy. J. Geogr. Sci. 2016, 26, 1412–1430. [Google Scholar] [CrossRef]
- Liu, X.-J.; Yin, B.-Z.; Hu, Z.-H.; Bao, X.-Y.; Wang, Y.-D.; Zhen, W.-C. Physiological response of flag leaf and yield formation of winter wheat under different spring restrictive irrigation regimes in the Haihe Plain, China. J. Integr. Agric. 2021, 20, 2343–2359. [Google Scholar] [CrossRef]
- Li, W.; Wu, W.; Wang, H.; Cheng, X.; Chen, H.; Zhou, Z.; Ding, R. Crowd intelligence in AI 2.0 era. Front. Inf. Technol. Electron. Eng. 2017, 18, 15–43. [Google Scholar] [CrossRef]
- Su, L.; Liu, R.; Liu, K.; Li, K.; Liu, L.; Shi, Y. Greenhouse Tomato Picking Robot Chassis. Agriculture 2023, 13, 532. [Google Scholar] [CrossRef]
- Du, T.; Kang, S.; Yan, B.; Zhang, J. Alternate Furrow Irrigation: A Practical Way to Improve Grape Quality and Water Use Efficiency in Arid Northwest China. J. Integr. Agric. 2013, 12, 509–519. [Google Scholar] [CrossRef]
- Wu, C.; Zhang, T. Intelligent Unmanned System: Important Achievements and Applications of the New Generation of Artificial Intelligence. Front. Inf. Technol. Electron. Eng. 2020, 21, 649–654. [Google Scholar] [CrossRef]
- Ma, J.; Sun, S.; Rui, H.; Zhang, J. Summary of Academic Research on China Road Building Machinery 2018. J. China Highw. Eng. 2018, 31, 509–519. [Google Scholar]
- Bu, L.; Hu, G.; Chen, J. Assessment of Grasp Ability for An End-effecter with Fin-ray Structure. J. Phys. Conf. Ser. 2021, 1865, 032030. [Google Scholar] [CrossRef]
- Cao, P.; Wang, T.; Zhai, L.; Niu, S.; Liu, L.; Shi, Y. Design of 6-DOF Tomato Picking Lifting Platform. Agriculture 2022, 12, 1945. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, X.; Wang, C. A review on structural development and recognition–localization methods for end-effector of fruit–vegetable picking robots. Int. J. Adv. Robot. Syst. 2022, 19, 17298806221104906. [Google Scholar] [CrossRef]
- Gao, J.; Zhang, F.; Zhang, J.; Yuan, T.; Yin, J.; Guo, H.; Yang, C. Development and evaluation of a pneumatic finger-like end-effector for cherry tomato harvesting robot in greenhouse. Comput. Electron. Agric. 2022, 197, 106879. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, Q.; Tian, Q.; Huo, L.; Feng, X. Research status of underwater multi-fingered hand. Robotics 2020, 42, 749–768. [Google Scholar] [CrossRef]
- Zhou, Y.; Tang, Y.; Zou, X.; Wu, M.; Tang, W.; Meng, F.; Zhang, Y.; Kang, H. Adaptive Active Positioning of Camellia oleifera Fruit Picking Points: Classical Image Processing and YOLOv7 Fusion Algorithm. Appl. Sci. 2022, 12, 12959. [Google Scholar] [CrossRef]
- Carreon, A.; Baltazar, A.; Treesatayapun, C. Development of a model-free force controller for soft contact of an ultrasonic test probe. Int. J. Adv. Manuf. Technol. 2017, 90, 2839–2847. [Google Scholar] [CrossRef]
- Das, P.S.; Chhetry, A.; Maharjan, P.; Rasel, M.S.; Park, J.Y. A laser ablated graphene-based flexible self-powered pressure sensor for human gestures and finger pulse monitoring. Nano Res. 2019, 12, 1789–1795. [Google Scholar] [CrossRef]
- Ji, W.; Tang, C.; Xu, B.; He, G. Contact force modeling and variable damping impedance control of apple harvesting robot. Comput. Electron. Agric. 2022, 198, 107026. [Google Scholar] [CrossRef]
- Zhang, K.; Lammers, K.; Chu, P.; Li, Z.; Lu, R. System design and control of an apple harvesting robot. Mechatronics 2021, 79, 102644. [Google Scholar] [CrossRef]
- Yozo, F.; Siringoringo, D.M.; Yoshiki, I.; Nagayama, T.; Mizutani, T. Summary of research and implementation of monitoring of bridges and building structures in Japan. Engineering 2019, 5, 1093–1119. [Google Scholar]
- Zhang, Y.; Chen, Y.; Song, Y.; Zhang, R.; Wang, X. Finding the lowest damage picking mode for tomatoes based on finite element analysis. Comput. Electron. Agric. 2023, 204, 107536. [Google Scholar] [CrossRef]
- Lu, W.; Wang, X.; Wang, F. Design and implementation of micro root morphology in situ collection system for tomato and pepper. J. Agric. Eng. 2018, 34, 12–18. [Google Scholar]
- Chen, B.; Hu, G.; Liu, W.; Sun, S.; Sun, C.; Xiao, M. Study on the mechanism of automatic vegetable transplanter to alternately pick and drop seedlings from the opposite trays. J. Agric. Mach. 2022, 53, 131–139+151. [Google Scholar]
- Zhang, B.; Guo, W.; Wang, Y.; Liu, X. Children’s mouse shape design based on key points. J. Mech. Eng. 2012, 48, 158–163. [Google Scholar] [CrossRef]
- Huang, Y.; Lu, R.; Qi, C.; Chen, K. Study on tomato maturity discrimination method based on spatial resolution spectrum. Spectrosc. Spectr. Anal. 2018, 38, 2183–2188. [Google Scholar]
- Huang, J.; Lian, F.; Wang, Z.; Sun, S.; Li, M.; Zhang, D.; Cai, X.; Ma, G.; Mai, Z.; Shen, A.; et al. Superconductivity research and performance regulation of two-dimensional van der Waals materials. J. Phys. 2022, 71, 299–317. [Google Scholar]
- Sun, Q.; Li, N.; Duan, Y.; Li, H.; Tang, H. Interpretation method of formation dip while drilling based on short-term and short-term memory neural network. Pet. Explor. Dev. 2021, 48, 843–850. [Google Scholar] [CrossRef]
- Zhang, Z.; Yao, Y.; Shi, Z.; Wang, H.; Qiao, Z.; Wang, S.; Qin, L.; Du, S.; Luo, F.; Liu, W. Potential field boundary recognition method based on deep learning. J. Geophys. 2022, 65, 1785–1801. [Google Scholar]
- Li, G.; Tan, X.; Xiao, F.; Yi, J.; Xue, C.; Yu, Q. Robot inverse kinematics solution based on improved fitness function combination method. J. Agric. Mach. 2022, 53, 436–445. [Google Scholar]
- Xiao, Y.; Zhu, C.; Li, W.; Han, K. A new high-order continuous point-to-point motion trajectory planning algorithm. J. Harbin Inst. Technol. 2021, 53, 135–143. [Google Scholar]
- Zhang, L.; Ma, Y.; Shan, J.; Xie, A. Dynamic optimization design of a 4-DOF local closed-chain palletizing robot. J. Agric. Mach. 2013, 44, 336–341. [Google Scholar]









| Serial Number | x | y | z | |||
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 160.000 | 0 | 0 |
| 2 | 35 | 20 | 60 | 66.6590 | 119.8160 | 0 |
| 3 | 20 | 30 | 40 | 94.9488 | 106.4839 | 0 |
| 4 | 40 | 10 | 20 | 98.2107 | 122.1176 | 0 |
| Given Angle | Forward Kinematics/mm | Inverse Kinematics/° | Inverse Kinematics/mm | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| x | y | z | x | y | z | ||||||
| 0 | 0 | 0 | 160.00 | 0 | 0 | 0 | 0 | 0 | 160.00 | 0 | 0 |
| 35 | 20 | 60 | 66.659 | 119.816 | 0 | 35.000 | 20.000 | 60.000 | 66.659 | 119.8160 | 0 |
| 20 | 30 | 40 | 94.949 | 106.484 | 0 | 20.000 | 30.000 | 40.000 | 94.949 | 106.484 | 0 |
| 40 | 10 | 20 | 98.211 | 122.117 | 0 | 39.999 | 10.000 | 19.999 | 98.211 | 122.118 | 0 |
| Parameter | ||||
|---|---|---|---|---|
| Z10 | 0 | −120° | 90° | 40 |
| Z20 | 0 | 120° | 90° | 40 |
| Z30 | 0 | 0° | 90° | 40 |
| Number | Large Diameter/mm | Small Diameter/mm | Height/mm | Weight/g |
|---|---|---|---|---|
| 1 | 82.4 | 75.2 | 66.7 | 230 |
| 2 | 68.2 | 65.4 | 56.5 | 189 |
| 3 | 58.9 | 56.1 | 52.6 | 128 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, T.; Du, W.; Zeng, L.; Su, L.; Zhao, Y.; Gu, F.; Liu, L.; Chi, Q. Design and Testing of an End-Effector for Tomato Picking. Agronomy 2023, 13, 947. https://doi.org/10.3390/agronomy13030947
Wang T, Du W, Zeng L, Su L, Zhao Y, Gu F, Liu L, Chi Q. Design and Testing of an End-Effector for Tomato Picking. Agronomy. 2023; 13(3):947. https://doi.org/10.3390/agronomy13030947
Chicago/Turabian StyleWang, Tianchi, Weiwei Du, Lingshen Zeng, Long Su, Yiming Zhao, Fang Gu, Li Liu, and Qian Chi. 2023. "Design and Testing of an End-Effector for Tomato Picking" Agronomy 13, no. 3: 947. https://doi.org/10.3390/agronomy13030947
APA StyleWang, T., Du, W., Zeng, L., Su, L., Zhao, Y., Gu, F., Liu, L., & Chi, Q. (2023). Design and Testing of an End-Effector for Tomato Picking. Agronomy, 13(3), 947. https://doi.org/10.3390/agronomy13030947






