An Improved Craig–Gordon Isotopic Model: Accounting for Transpiration Effects on the Isotopic Composition of Residual Water during Evapotranspiration
Abstract
:1. Introduction
2. Materials and Methods
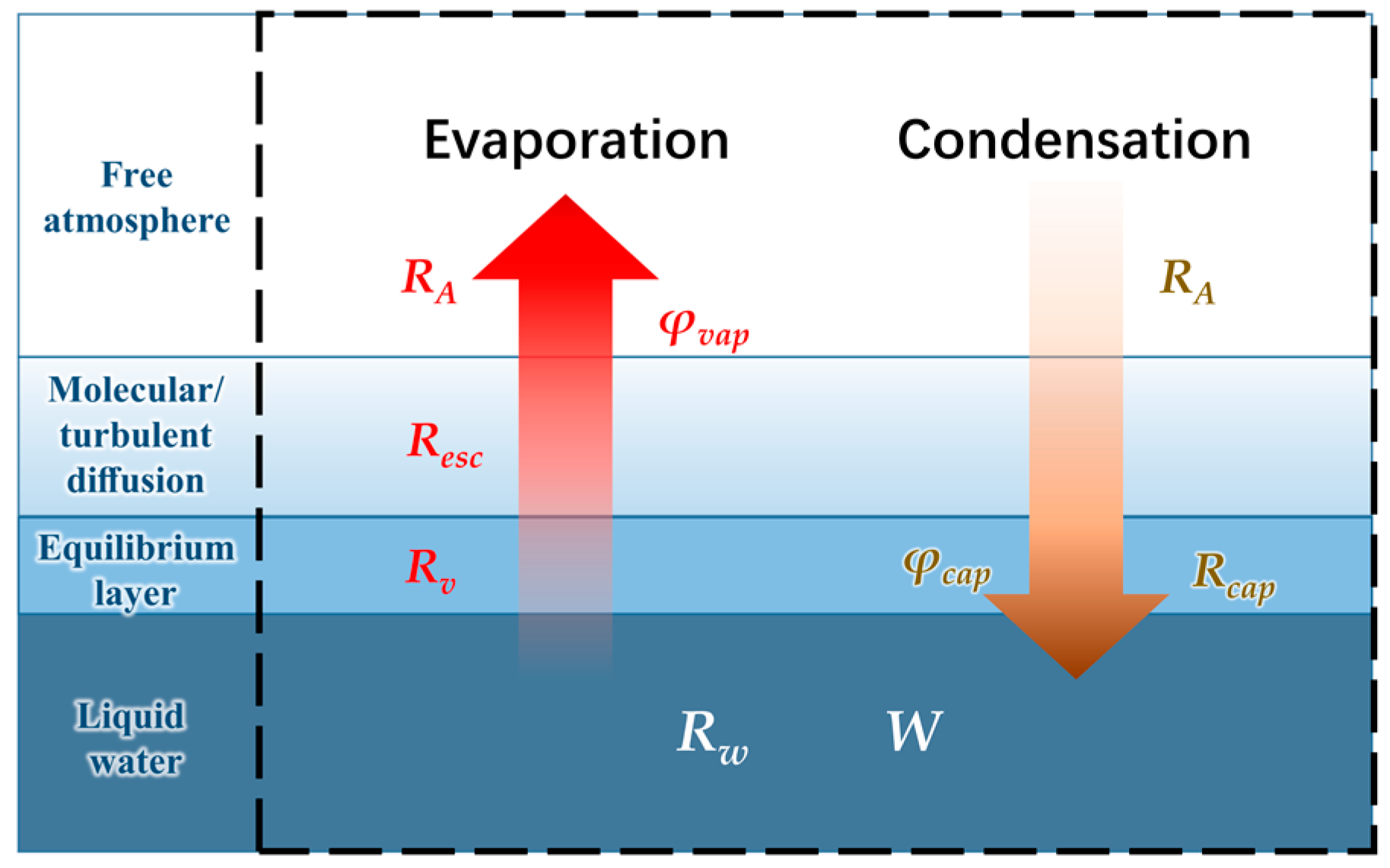
2.1. Theoretical Background of the C-G Model
2.2. An Improved C-G Model Accounting for the Effects of Both Transpiration and Evaporation
2.3. Numerical Experiments
3. Results
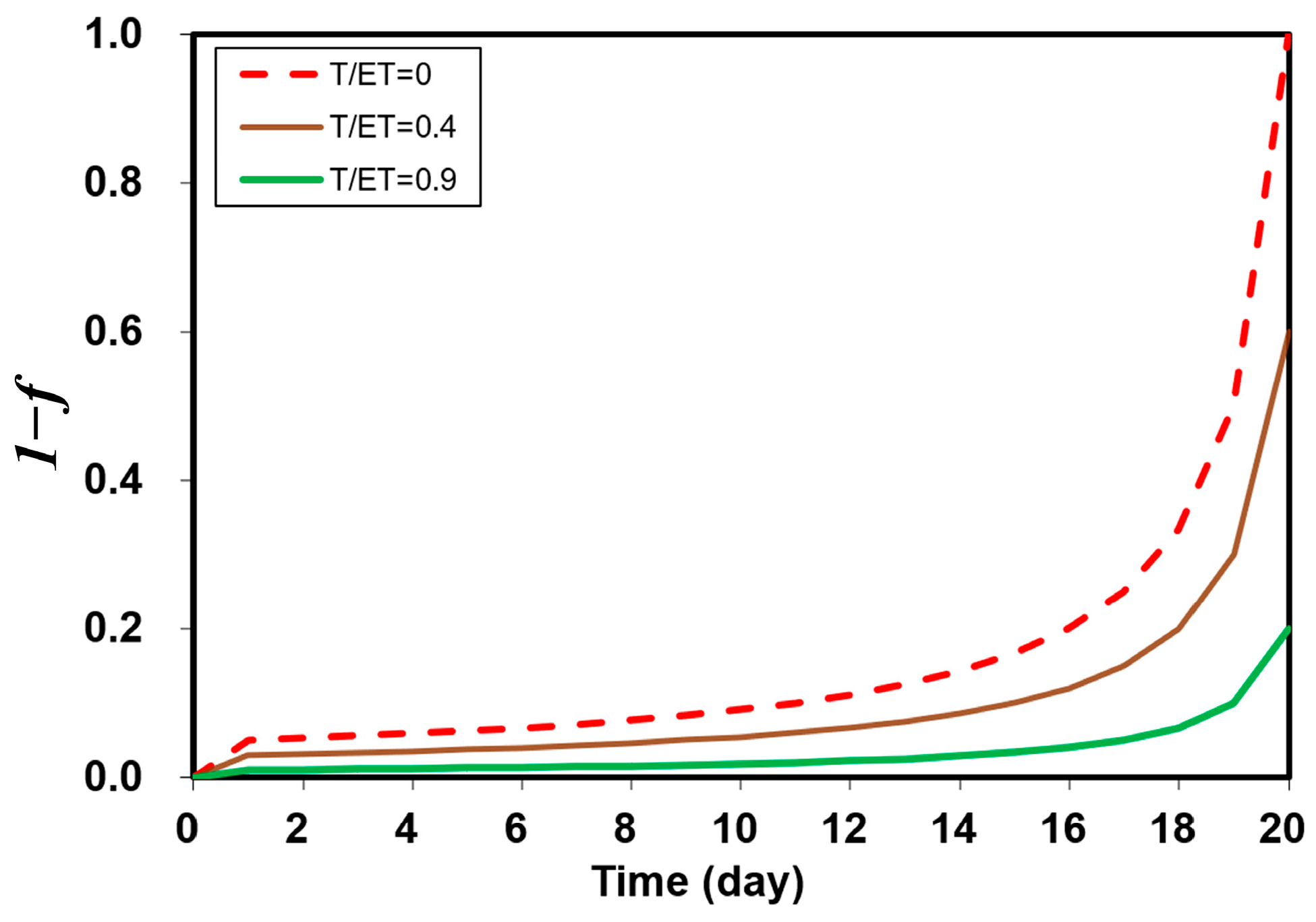
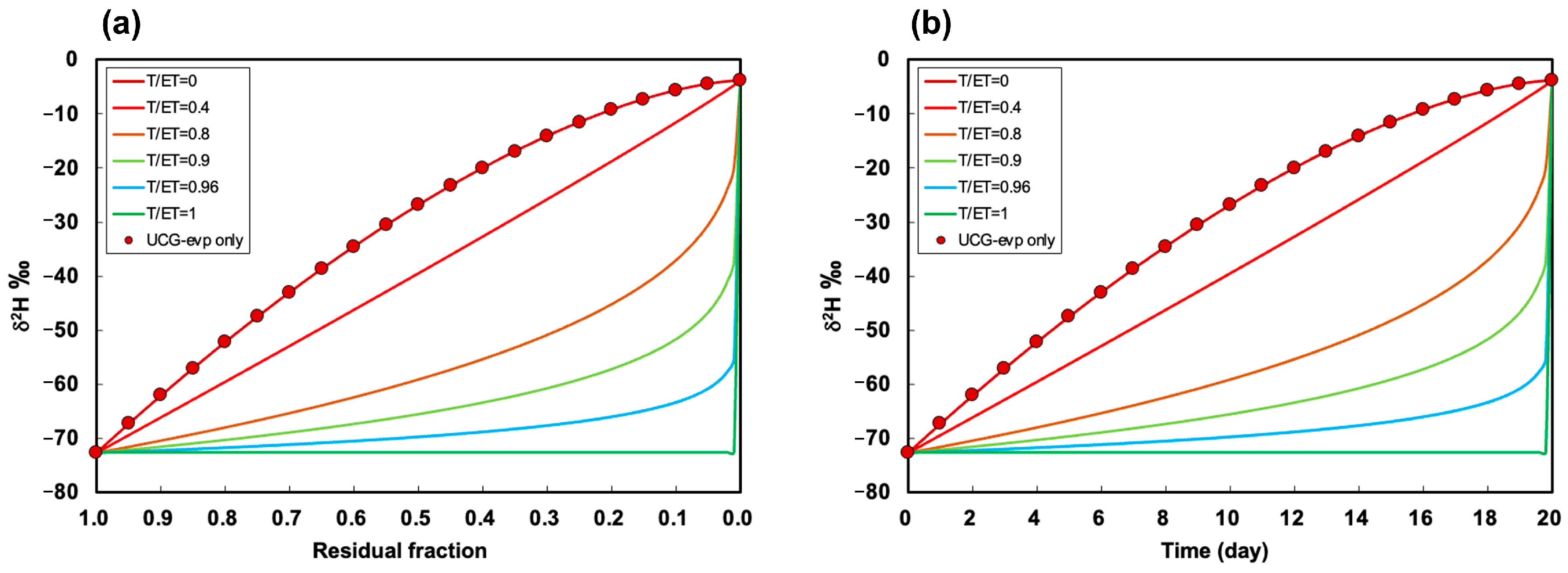
3.1. Validation of the ET-UCG Model by Theoretical Tests
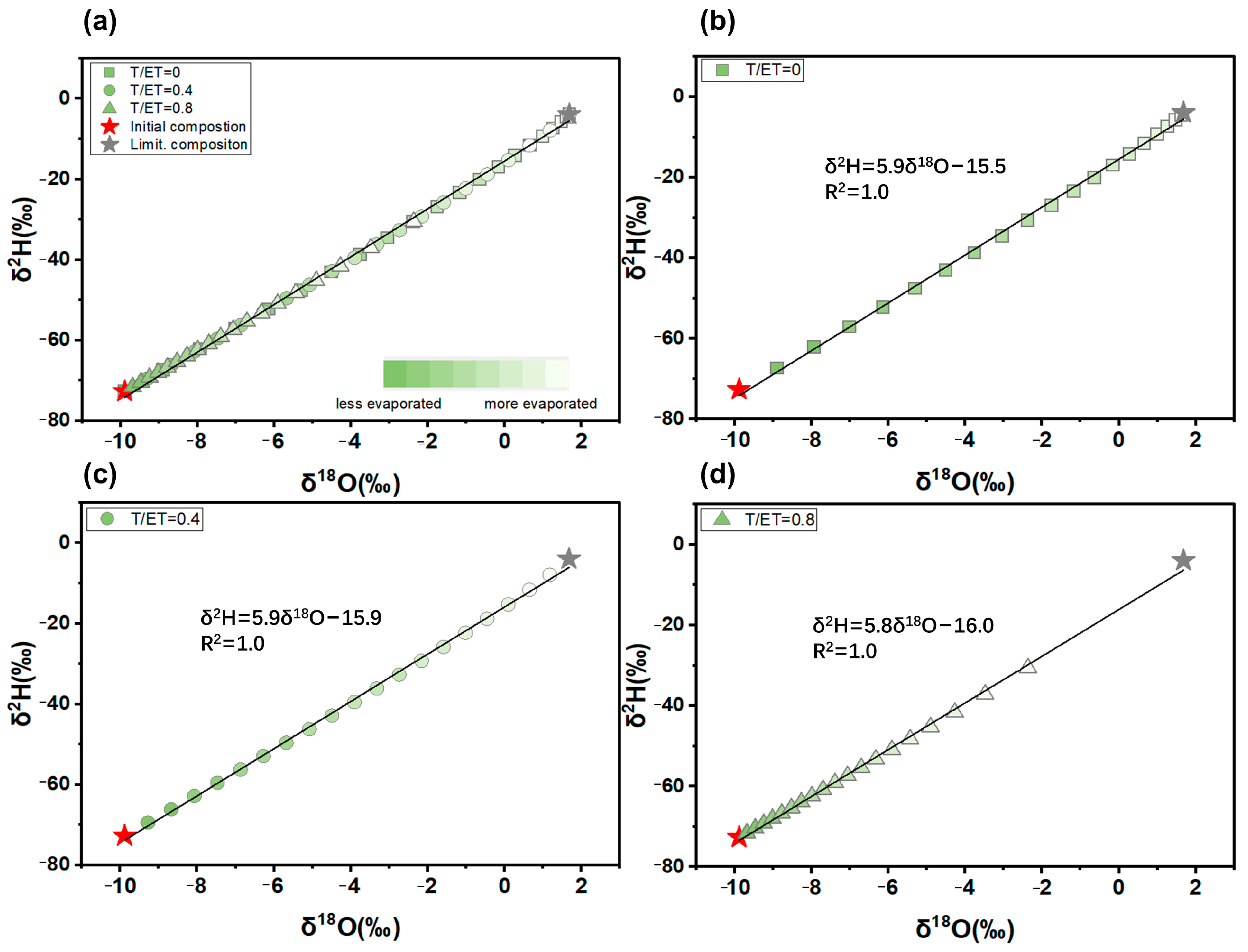
3.2. Isotopic Patterns in Water Body Undergoing Evapotranspiration
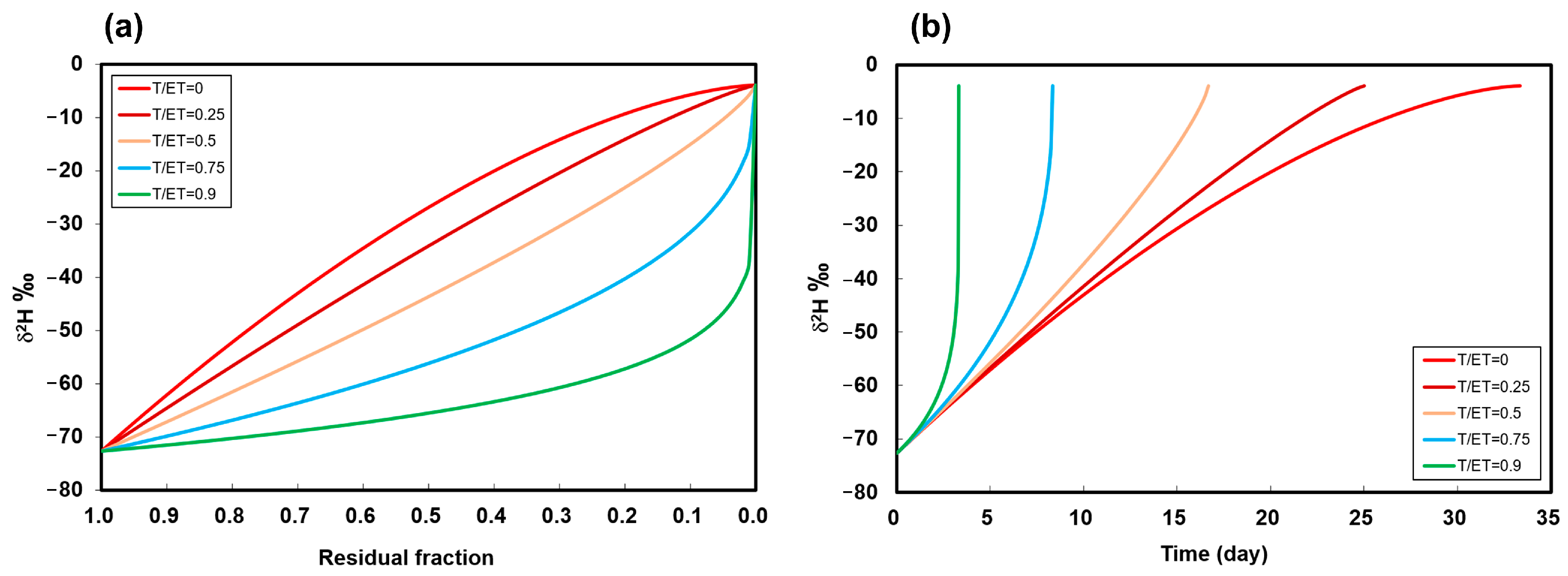
3.2.1. Scenario 1: Constant ET and Varying T/ET
3.2.2. Scenario 2: Constant E and Varying T/ET
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Brooks, J.R. Water, Bound and Mobile. Science 2015, 349, 138–139. [Google Scholar] [CrossRef]
- Evaristo, J.; Jasechko, S.; McDonnell, J.J. Global Separation of Plant Transpiration from Groundwater and Streamflow. Nature 2015, 525, 91–94. [Google Scholar] [CrossRef] [PubMed]
- Or, D.; Lehmann, P. Surface Evaporative Capacitance: How Soil Type and Rainfall Characteristics Affect Global-Scale Surface Evaporation. Water Resour. Res. 2019, 55, 519–539. [Google Scholar] [CrossRef]
- Sprenger, M.; Leistert, H.; Gimbel, K.; Weiler, M. Illuminating Hydrological Processes at the Soil-Vegetation-Atmosphere Interface with Water Stable Isotopes. Rev. Geophys. 2016, 54, 674–704. [Google Scholar] [CrossRef]
- Sprenger, M.; Tetzlaff, D.; Soulsby, C. Soil Water Stable Isotopes Reveal Evaporation Dynamics at the Soil–Plant–Atmosphere Interface of the Critical Zone. Hydrol. Earth Syst. Sci. 2017, 21, 3839–3858. [Google Scholar] [CrossRef]
- Braud, I.; Biron, P.; Bariac, T.; Richard, P.; Canale, L.; Gaudet, J.P.; Vauclin, M. Isotopic Composition of Bare Soil Evaporated Water Vapor. Part I: RUBIC IV Experimental Setup and Results. J. Hydrol. 2009, 369, 1–16. [Google Scholar] [CrossRef]
- Mahindawansha, A.; Külls, C.; Kraft, P.; Breuer, L. Investigating Unproductive Water Losses from Irrigated Agricultural Crops in the Humid Tropics through Analyses of Stable Isotopes of Water. Hydrol. Earth Syst. Sci. 2020, 24, 3627–3642. [Google Scholar] [CrossRef]
- Skrzypek, G.; Mydłowski, A.; Dogramaci, S.; Hedley, P.; Gibson, J.J.; Grierson, P.F. Estimation of Evaporative Loss Based on the Stable Isotope Composition of Water Using Hydrocalculator. J. Hydrol. 2015, 523, 781–789. [Google Scholar] [CrossRef]
- Dubbert, M.; Cuntz, M.; Piayda, A.; Maguás, C.; Werner, C. Partitioning Evapotranspiration—Testing the Craig and Gordon Model with Field Measurements of Oxygen Isotope Ratios of Evaporative Fluxes. J. Hydrol. 2013, 496, 142–153. [Google Scholar] [CrossRef]
- Rothfuss, Y.; Biron, P.; Braud, I.; Canale, L.; Durand, J.-L.; Gaudet, J.-P.; Richard, P.; Vauclin, M.; Bariac, T. Partitioning Evapotranspiration Fluxes into Soil Evaporation and Plant Transpiration Using Water Stable Isotopes under Controlled Conditions. Hydrol. Process. 2010, 24, 3177–3194. [Google Scholar] [CrossRef]
- Al-Oqaili, F.; Good, S.P.; Peters, R.T.; Finkenbiner, C.; Sarwar, A. Using Stable Water Isotopes to Assess the Influence of Irrigation Structural Configurations on Evaporation Losses in Semiarid Agricultural Systems. Agric. For. Meteorol. 2020, 291, 108083. [Google Scholar] [CrossRef]
- Allison, G.B.; Barnes, C.J. Estimation of Evaporation from Non-Vegetated Surfaces Using Natural Deuterium. Nature 1983, 301, 143–145. [Google Scholar] [CrossRef]
- Zimmermann, U.; Münnich, K.O.; Roether, W.; Kreutz, W.; Schubach, K.; Siegel, O. Tracers Determine Movement of Soil Moisture and Evapotranspiration. Science 1966, 152, 346–347. [Google Scholar] [CrossRef] [PubMed]
- Jasechko, S.; Sharp, Z.D.; Gibson, J.J.; Birks, S.J.; Yi, Y.; Fawcett, P.J. Terrestrial Water Fluxes Dominated by Transpiration. Nature 2013, 496, 347–350. [Google Scholar] [CrossRef] [PubMed]
- Craig, H.; Gordon, L.I. Deuterium and Oxygen 18 Variations in the Ocean and Marine Atmosphere; Consiglio Nationale delle Ricerche Laboratorio di Geologia Nucleare: Pisa, Italy, 1965. [Google Scholar]
- Gibson, J.J.; Birks, S.J.; Yi, Y. Stable Isotope Mass Balance of Lakes: A Contemporary Perspective. Quat. Sci. Rev. 2016, 131, 316–328. [Google Scholar] [CrossRef]
- Gonfiantini, R.; Wassenaar, L.I.; Araguas-Araguas, L.; Aggarwal, P.K. A Unified Craig-Gordon Isotope Model of Stable Hydrogen and Oxygen Isotope Fractionation during Fresh or Saltwater Evaporation. Geochim. Cosmochim. Acta 2018, 235, 224–236. [Google Scholar] [CrossRef]
- Horita, J.; Rozanski, K.; Cohen, S. Isotope Effects in the Evaporation of Water: A Status Report of the Craig–Gordon Model. Isotopes Environ. Health Stud. 2008, 44, 23–49. [Google Scholar] [CrossRef]
- Dar, S.S.; Ghosh, P.; Swaraj, A.; Kumar, A. Craig-Gordon Model Validation Using Observed Meteorological Parameters and Measured Stable Isotope Ratios in Water Vapor over the Southern Ocean. Atmos. Chem. Phys. 2019, 1–19. [Google Scholar] [CrossRef]
- Benettin, P.; Volkmann, T.H.M.; von Freyberg, J.; Frentress, J.; Penna, D.; Dawson, T.E.; Kirchner, J.W. Effects of Climatic Seasonality on the Isotopic Composition of Evaporating Soil Waters. Hydrol. Earth Syst. Sci. 2018, 22, 2881–2890. [Google Scholar] [CrossRef]
- Mahindawansha, A.; Kulls, C.; Kraft, P.; Breuer, L.J.H.; Discussions, E.S.S. Estimating Water Flux and Evaporation Losses Using Stable Isotopes of Soil Water from Irrigated Agricultural Crops in Tropical Humid Regions. Hydrol. Earth Syst. Sci. 2019, 213, 1–28. [Google Scholar] [CrossRef]
- Barnes, C.J.; Allison, G.B. Tracing of Water Movement in the Unsaturated Zone Using Stable Isotopes of Hydrogen and Oxygen. J. Hydrol. 1988, 100, 143–176. [Google Scholar] [CrossRef]
- Majoube, M. Oxygen-18 and Deuterium Fractionation between Water and Steam. J. Chim. Phys. Phys.-Chim. Biol. 1971, 68, 1423–1436. [Google Scholar] [CrossRef]
- Merlivat, L. Molecular Diffusivities of H2 16O, HD16O, and H2 18O in Gases. J. Chem. Phys. 1978, 69, 2864. [Google Scholar] [CrossRef]
- Barkan, E.; Luz, B. Diffusivity Fractionations of H216O/H217O and H216O/H218O in Air and Their Implications for Isotope Hydrology. Rapid Commun. Mass Spectrom. 2007, 21, 2999–3005. [Google Scholar] [CrossRef]
- Clark, I.D.; Fritz, P. Environmental Isotopes in Hydrology; Lewis Publisher: Boca Raton, FL, USA, 1997. [Google Scholar]
- Xie, C.; Xiao, W.; Zhang, M.; Liu, S.; Qian, Y.; Zhu, H.; Zhang, Z.; Liu, Q.; Hu, Y.; Wang, J.; et al. Isotopic Kinetic Fractionation of Evaporation from Small Water Bodies. J. Hydrol. 2021, 603, 126974. [Google Scholar] [CrossRef]
- Tanny, J.; Cohen, J. Revisiting the Boundary Layer Structure Used in Craig and Gordon’s Model of Isotope Fractionation in Evaporation. Isot. Environ. Health Stud. 2008, 44, 11–21. [Google Scholar] [CrossRef]
- Good, S.P.; Soderberg, K.; Guan, K.; King, E.G.; Scanlon, T.M.; Caylor, K.K. δ 2 H Isotopic Flux Partitioning of Evapotranspiration over a Grass Field Following a Water Pulse and Subsequent Dry Down. Water Resour. Res. 2014, 50, 1410–1432. [Google Scholar] [CrossRef]
- Xiang, W.; Si, B.; Li, M.; Li, H.; Lu, Y.; Zhao, M.; Feng, H. Stable Isotopes of Deep Soil Water Retain Long-Term Evaporation Loss on China’s Loess Plateau. Sci. Total Environ. 2021, 784, 147153. [Google Scholar] [CrossRef]
- Schlesinger, W.H.; Jasechko, S. Transpiration in the Global Water Cycle. Agric. For. Meteorol. 2014, 189–190, 115–117. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Y.; Wen, M.; Li, P.; Liang, J.; Wei, H.; Li, M. An Improved Craig–Gordon Isotopic Model: Accounting for Transpiration Effects on the Isotopic Composition of Residual Water during Evapotranspiration. Agronomy 2023, 13, 1531. https://doi.org/10.3390/agronomy13061531
Lu Y, Wen M, Li P, Liang J, Wei H, Li M. An Improved Craig–Gordon Isotopic Model: Accounting for Transpiration Effects on the Isotopic Composition of Residual Water during Evapotranspiration. Agronomy. 2023; 13(6):1531. https://doi.org/10.3390/agronomy13061531
Chicago/Turabian StyleLu, Yanwei, Mingyi Wen, Peiyue Li, Jiaping Liang, Haoyan Wei, and Min Li. 2023. "An Improved Craig–Gordon Isotopic Model: Accounting for Transpiration Effects on the Isotopic Composition of Residual Water during Evapotranspiration" Agronomy 13, no. 6: 1531. https://doi.org/10.3390/agronomy13061531
APA StyleLu, Y., Wen, M., Li, P., Liang, J., Wei, H., & Li, M. (2023). An Improved Craig–Gordon Isotopic Model: Accounting for Transpiration Effects on the Isotopic Composition of Residual Water during Evapotranspiration. Agronomy, 13(6), 1531. https://doi.org/10.3390/agronomy13061531







