Estimation of the Total Soil Nitrogen Based on a Differential Evolution Algorithm from ZY1-02D Hyperspectral Satellite Imagery
Abstract
:1. Introduction
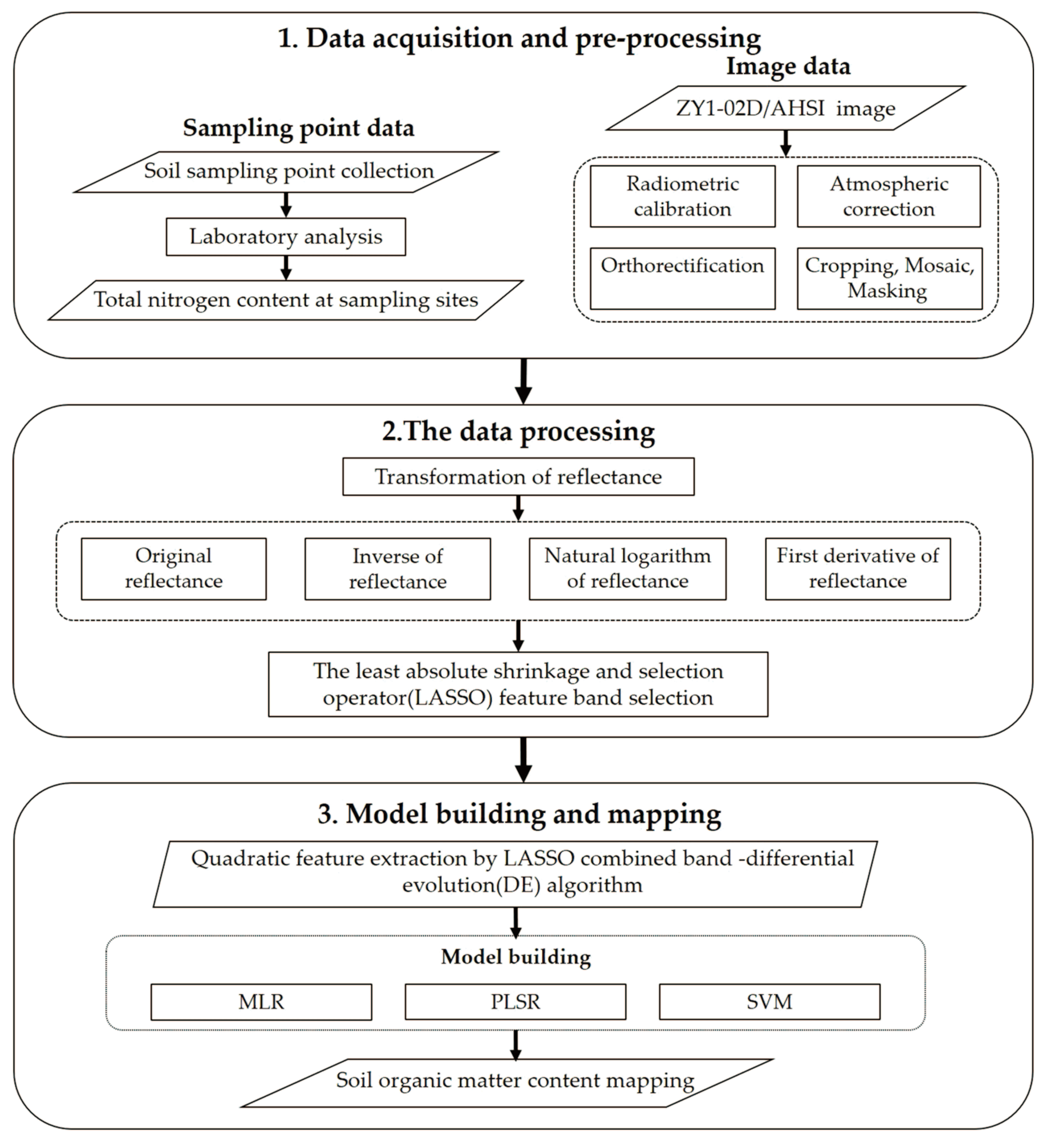
2. Materials and Methods
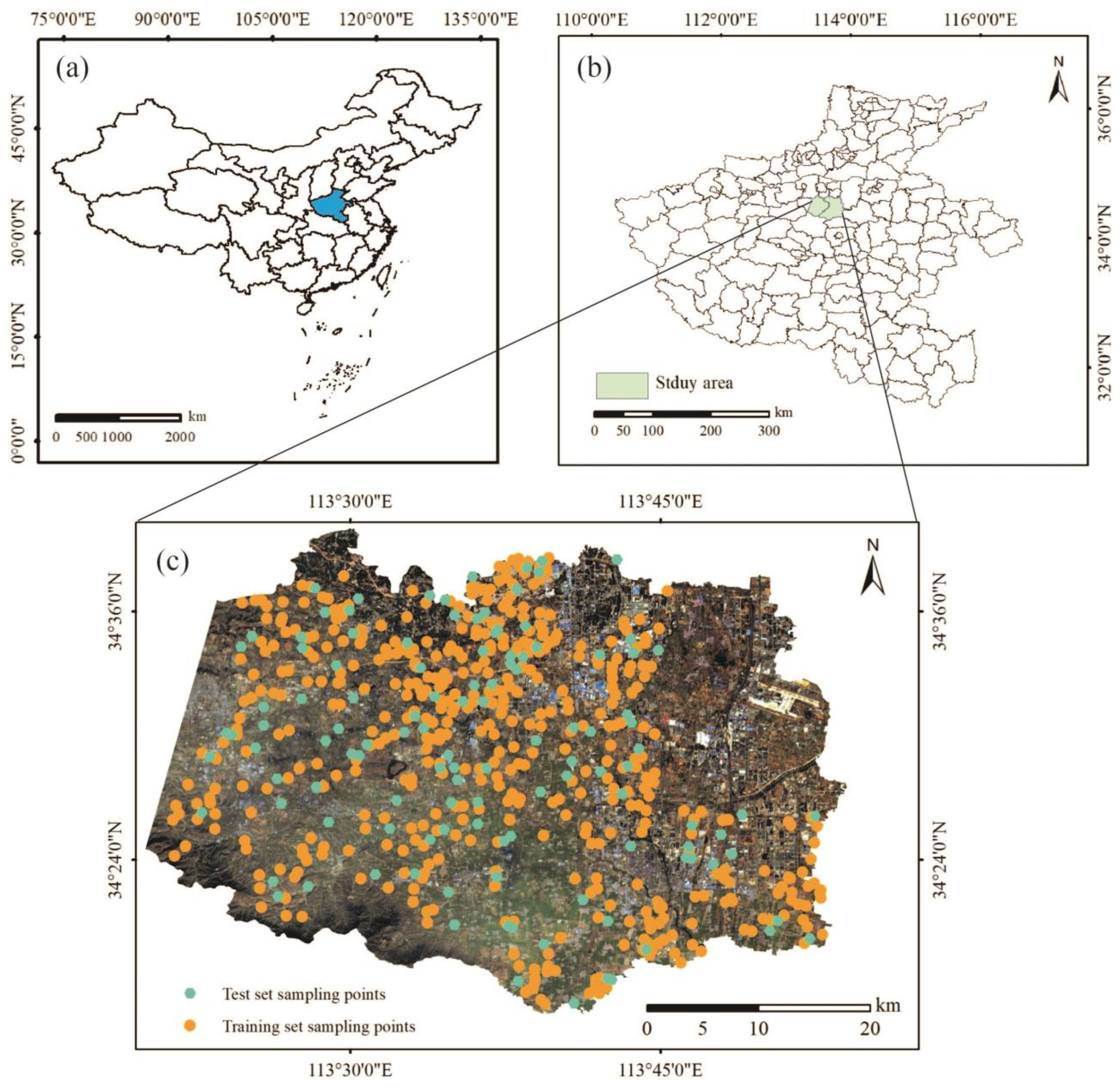
2.1. Study Area
2.2. Soil Sample Acquisition and TN Content Determination
2.3. ZY1-02D/AHSI Remote Sensing Image Collection and Pre-Processing
2.4. Methodology
2.4.1. Spectral Reflectance Transformation
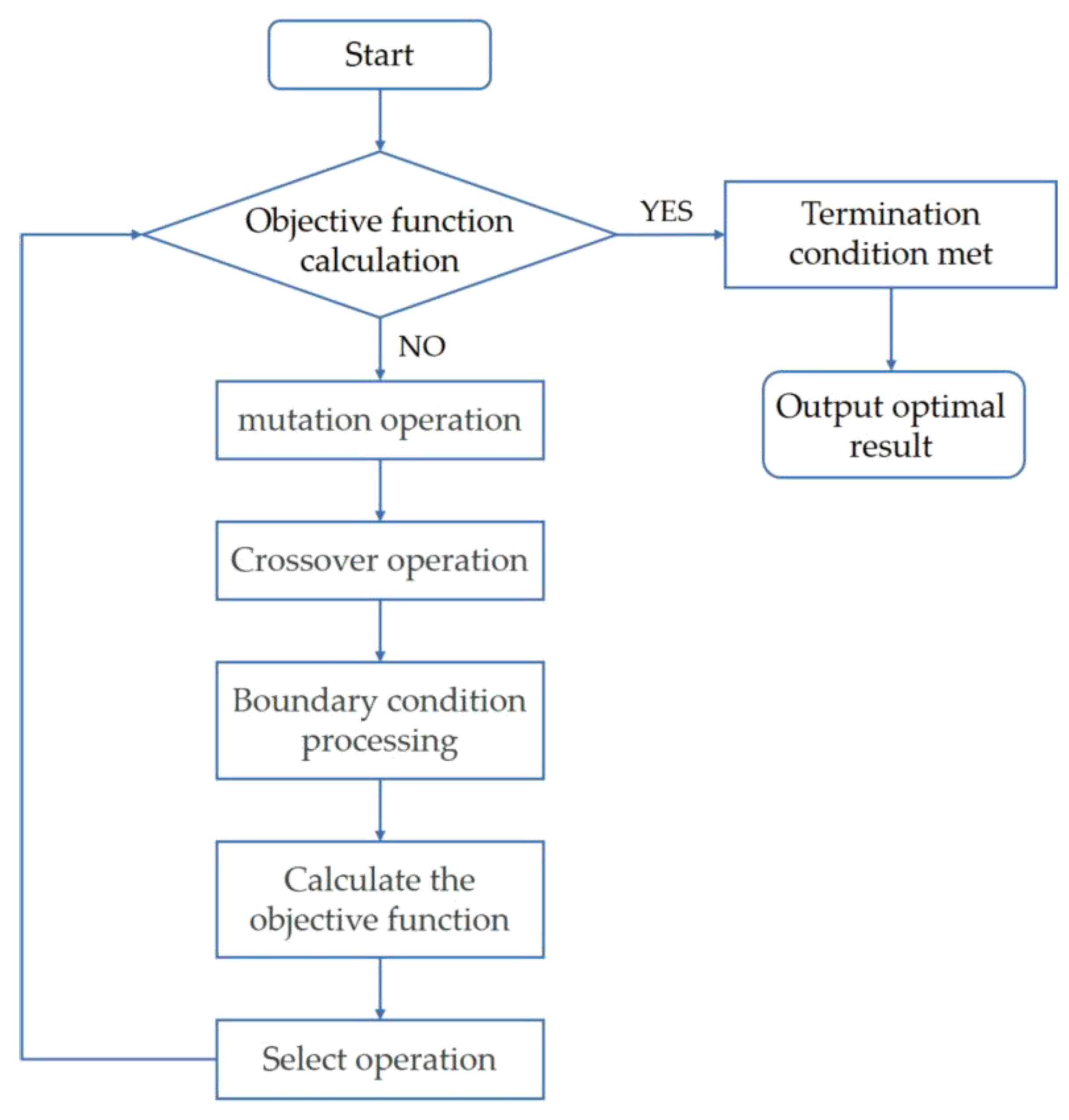
2.4.2. Selection of Spectral Feature Variables
- (a)
- Initializing the population: M individuals, each made up of an n-dimensional vector, are created uniformly and randomly in the solution space. The vector and the j-th dimensional value assigned to the i-th individual, respectively, are given in Equations (5) and (6):where is the i-th individual; j denotes the j-th dimension; M denotes the population size parameter; n denotes the optimization dimension; and are the lower and upper bounds of the j-th dimension, respectively; and denotes a random number on the interval [0, 1].
- (b)
- Mutation operation: The DE algorithm implements an individual mutation operation through a difference strategy. Equation (7) shows the vector mutation operation for each individual:where c1, c2, and c3 are random numbers; Z is a scaling factor; and G is the index of individual mutation generations.
- (c)
- Crossover operation: the mutated individuals are subject to the crossover operation shown in formula eight:where CR is the crossover probability.
- (d)
- The operation for selecting the next generation of individuals is shown in Equation (9):where f is the objective function.
2.4.3. Construction and Evaluation of the TN Content Estimation Model
3. Results
3.1. Statistical Description of the TN Content of the Sampling Points
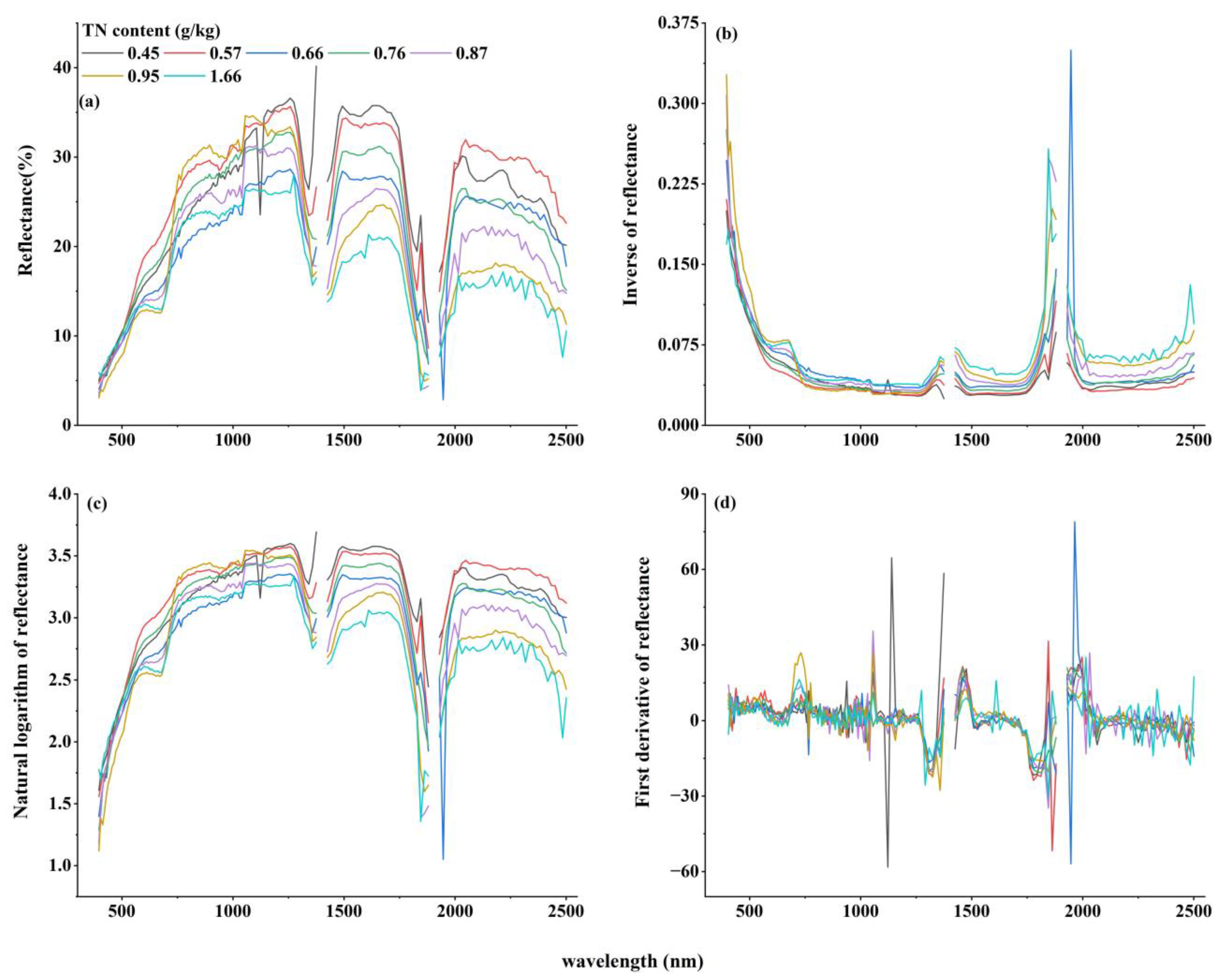
3.2. TN Content Spectral Features Analysis and Spectral Transformation Processing
3.2.1. Spectral Features Analysis of TN Content
3.2.2. Spectral Transformation Processing
3.3. Selection of TN Spectral Characteristics
3.4. TN Content Model Estimation Results
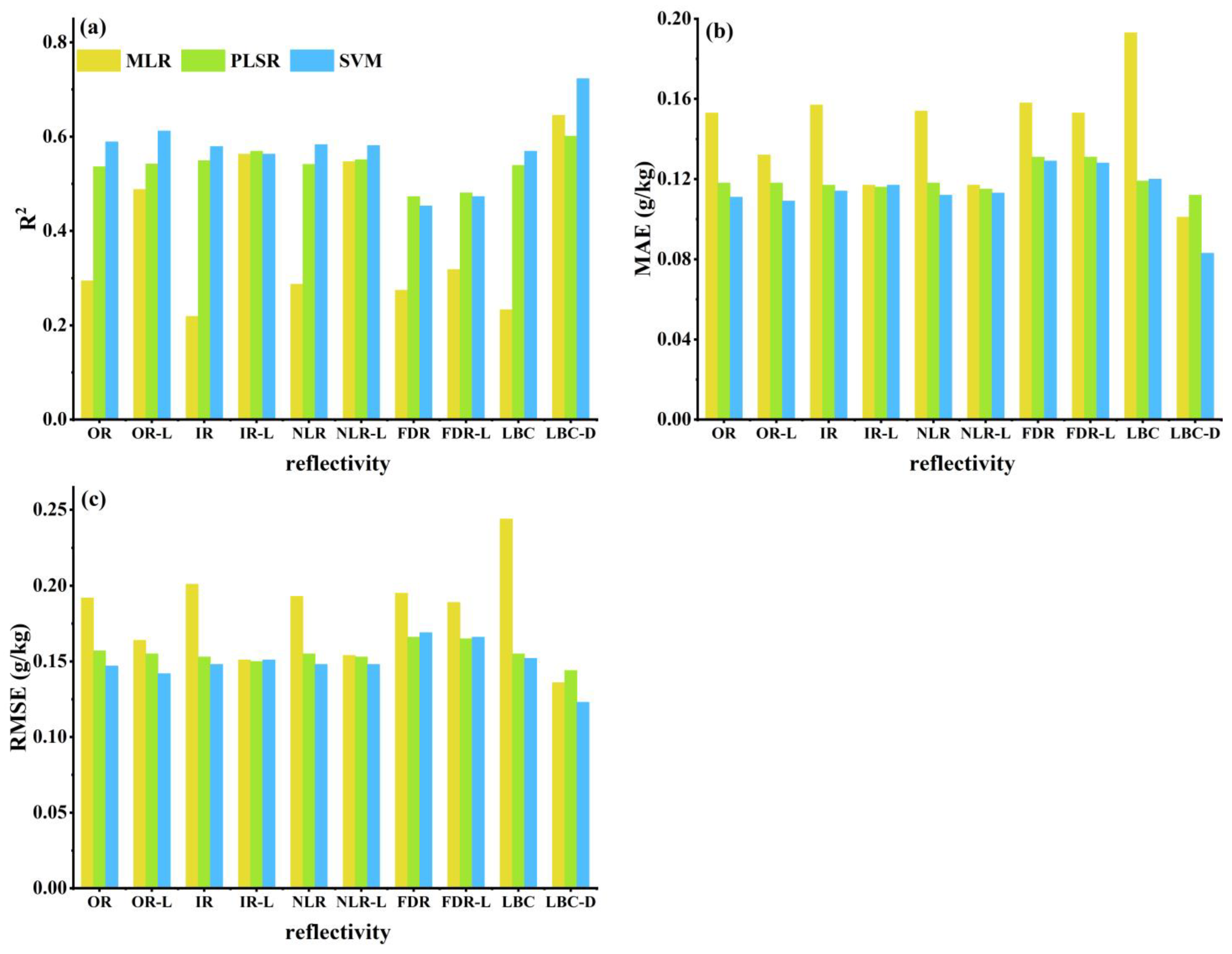
3.4.1. Results of All Bands Based on the Individual Spectral Reflectance Transformation
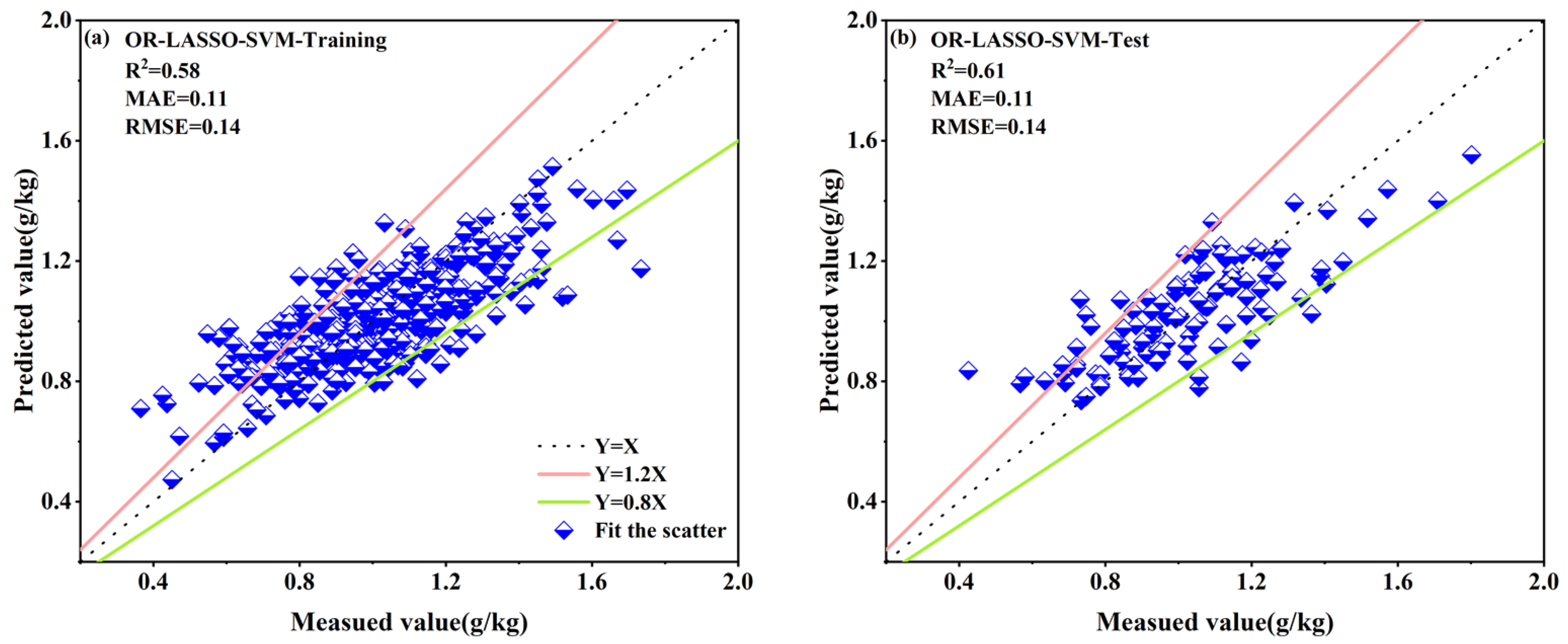
3.4.2. Results of the LASSO Feature Selection Based on the Individual Spectral Reflectance Transformations
3.4.3. LASSO-Selected Spectral Band Combinations for the Four Spectral Reflectance Transformations
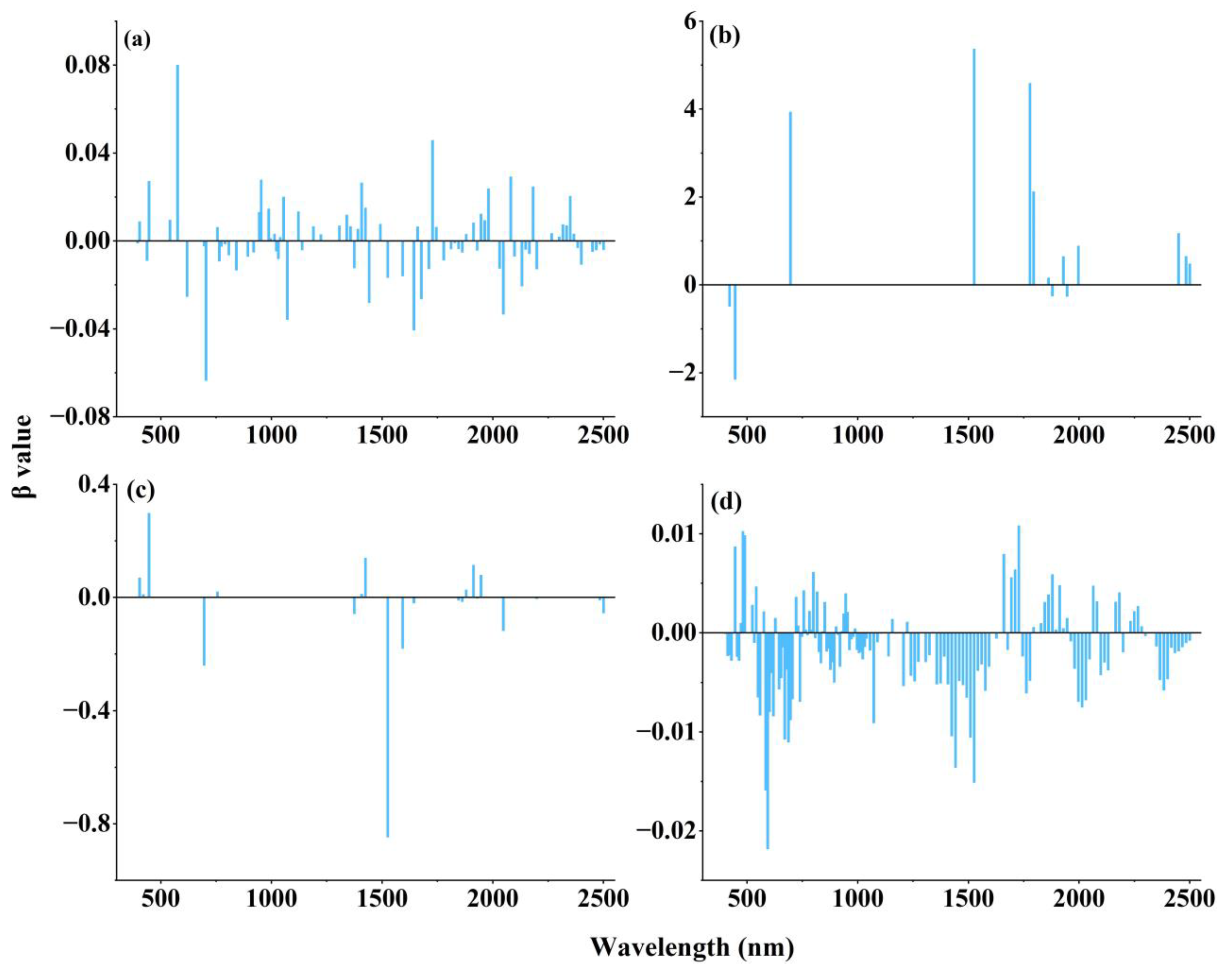
3.4.4. DE Secondary Feature Selection from LASSO-Selected Spectral Band Combinations Based on Four Spectral Reflectance Transformations
4. Discussion
4.1. Role of Spectral Reflectance Transformation Processing
4.2. The Role of Spectral Feature Extraction
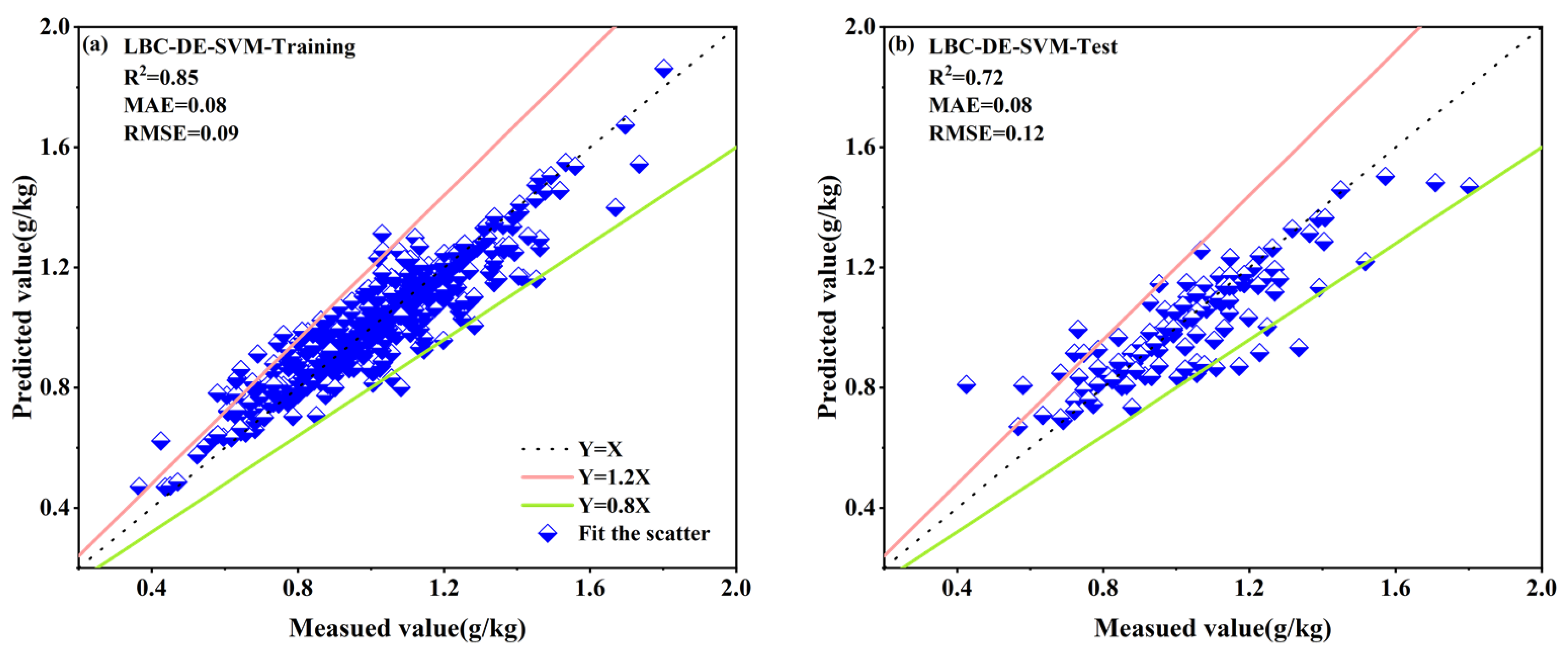
4.3. Estimated Model Comparison and Best Model TN Content Mapping
5. Conclusions
- (1)
- The transformation of the spectral reflectance data can highlight some of the enhanced spectral information. However, the best spectral data pre-processing methods for different estimation models differ, where even the optimal spectral transformation methods for the training and test sets of the same model are different. Suitable spectral reflectance transformation methods can be selected for different prediction models in the TN content estimation studies in other regions to improve the estimation accuracy.
- (2)
- Using the LASSO method for feature variable selection for full-band data not only reduced the spectral data redundancy and simplified the model but also improved the estimation accuracy of the model. Compared with individual spectral reflectance data, the LBC contained more valid spectral information and concentrated a large amount of noise information. This study used a combination of the DE algorithm and the prediction model to extract feature variables from the LBC, which can achieve the purpose of retaining valid information in the LBC and eliminating invalid information and can provide a reference for future research in making full use of the spectral reflectance transform and feature data for TN content estimation.
- (3)
- Compared with ground-based hyperspectral data and airborne hyperspectral data, ZY1-02D/AHSI hyperspectral satellite image data have the advantages of wide image coverage, the automatic acquisition of hyperspectral remote sensing image data, and a short return cycle, and thus, it can enable the dynamic, rapid, and large area estimation of TN content.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Wang, J.; Zhang, J.; Liu, T.; Acquah, G.E.; Yuan, H. Combining Variable Selection and Multiple Linear Regression for Soil Organic Matter and Total Nitrogen Estimation by DRIFT-MIR Spectroscopy. Agronomy 2022, 12, 638. [Google Scholar] [CrossRef]
- Otto, R.; Castro, S.A.Q.; Mariano, E.; Castro, S.G.Q.; Franco, H.C.J.; Trivelin, P.C.O. Nitrogen Use Efficiency for Sugarcane-Biofuel Production: What Is Next? BioEnergy Res. 2016, 9, 1272–1289. [Google Scholar] [CrossRef]
- Kaushal, S.S.; Lewis, W.M., Jr.; McCutchan, J.H., Jr. Land Use Change and Nitrogen Enrichment of A Rocky Mountain Watershed. Ecol. Appl. 2006, 16, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Wang, L.; Zhao, L.; Liu, Z.; Lin, C.; Hu, Y.; Liu, L. Estimation of Soil Nutrient Content Using Hyperspectral Data. Agriculture 2021, 11, 1129. [Google Scholar] [CrossRef]
- Bao, Y.; Meng, X.; Ustin, S.; Wang, X.; Zhang, X.; Liu, H.; Tang, H. Vis-SWIR spectral prediction model for soil organic matter with different grouping strategies. CATENA 2020, 195, 104703. [Google Scholar] [CrossRef]
- Kuang, B.; Mouazen, A.M. Non-biased prediction of soil organic carbon and total nitrogen with vis–NIR spectroscopy, as affected by soil moisture content and texture. Biosyst. Eng. 2013, 114, 249–258. [Google Scholar] [CrossRef] [Green Version]
- Sun, H.; Zhao, Z.; Zhao, J.; Chen, W. Inversion of Topsoil Organic Matter Content by Hyperspectral Remote Sensing of Zhuhai-1. Remote Sens. Inf. 2020, 35, 40–46. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, X.; Sun, W.; Wang, J.; Ding, S.; Liu, S. Effects of hyperspectral data with different spectral resolutions on the estimation of soil heavy metal content: From ground-based and airborne data to satellite-simulated data. Sci. Total Environ. 2022, 838, 156129. [Google Scholar] [CrossRef]
- Yin, F.; Wu, M.; Liu, L.; Zhu, Y.; Feng, J.; Yin, D.; Yin, C.; Yin, C. Predicting the abundance of copper in soil using reflectance spectroscopy and GF5 hyperspectral imagery. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102420. [Google Scholar] [CrossRef]
- Liu, Y.; Sun, D.; Han, B.; Zhu, H.; Liu, S.; Yuan, J. Development of Advanced Visible and Short-wave Infrared Hyperspectral Imager Onboard ZY-1-02D Satellite. Spacecr. Eng. 2020, 29, 85–92. [Google Scholar] [CrossRef]
- Shang, K.; Gu, H.; Yang, Y. Inversion of Total Copper Content in Mining Soils with Different Spectral Pretreatment Techniques Using AHSI/ZY1-02D Data. In Proceedings of the 2021 IEEE International Geoscience and Remote Sensing Symposium IGARSS 2021, Brussels, Belgium, 11–16 July 2021; pp. 6461–6464. [Google Scholar] [CrossRef]
- Yang, Y.; Shang, K.; Xiao, C.; Wang, C.; Tang, H. Spectral Index for Mapping Topsoil Organic Matter Content Based on ZY1-02D Satellite Hyperspectral Data in Jiangsu Province, China. ISPRS Int. J. Geo-Inf. 2022, 11, 111. [Google Scholar] [CrossRef]
- Meng, X.; Bao, Y.; Liu, J.; Liu, H.; Zhang, X.; Zhang, Y.; Wang, P.; Tang, H.; Kong, F. Regional soil organic carbon prediction model based on a discrete wavelet analysis of hyperspectral satellite data. Int. J. Appl. Earth Obs. Geoinf. 2020, 89, 102111. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, M.; Zheng, L.; Qin, Q.; Lee, W.S. Spectral features extraction for estimation of soil total nitrogen content based on modified ant colony optimization algorithm. Geoderma 2019, 333, 23–34. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Cattle, S.R.; Ortega, A.; Fouad, Y. In situ measurements of soil colour, mineral composition and clay content by vis–NIR spectroscopy. Geoderma 2009, 150, 253–266. [Google Scholar] [CrossRef]
- Xie, S.; Ding, F.; Chen, S.; Wang, X.; Li, Y.; Ma, K. Prediction of soil organic matter content based on characteristic band selection method. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2022, 273, 120949. [Google Scholar] [CrossRef]
- Shen, L.; Gao, M.; Yan, J.; Li, Z.; Leng, P.; Yang, Q.; Duan, S. Hyperspectral Estimation of Soil Organic Matter Content using Different Spectral Preprocessing Techniques and PLSR Method. Remote Sens. 2020, 12, 1206. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Dong, Z.; Xia, J.; Wang, H.; Meng, T.; Zhang, R.; Han, J.; Wang, N.; Xie, J. Estimation of soil organic matter content based on CARS algorithm coupled with random forest. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2021, 258, 119823. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Yao, T.; Lu, H.; Feng, W.; Xue, Y.; Liu, B. Improving estimation of soil organic matter content by combining Landsat 8 OLI images and environmental data: A case study in the river valley of the southern Qinghai-Tibet Plateau. Comput. Electron. Agric. 2021, 185, 106144. [Google Scholar] [CrossRef]
- Vašát, R.; Kodešová, R.; Klement, A.; Borůvka, L. Simple but efficient signal pre-processing in soil organic carbon spectroscopic estimation. Geoderma 2017, 298, 46–53. [Google Scholar] [CrossRef]
- Zhang, Z.; Ding, J.; Zhu, C.; Wang, J. Combination of efficient signal pre-processing and optimal band combination algorithm to predict soil organic matter through visible and near-infrared spectra. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2020, 240, 118553. [Google Scholar] [CrossRef]
- Gao, L.; Zhu, X.; Han, Z.; Wang, L.; Zhao, G.; Jiang, Y. Spectroscopy-Based Soil Organic Matter Estimation in Brown Forest Soil Areas of the Shandong Peninsula, China. Pedosphere 2019, 29, 810–818. [Google Scholar] [CrossRef]
- Leardi, R. Application of genetic algorithm-PLS for feature selection in spectral data sets. J. Chemom. 2000, 14, 643–655. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, W.; Tang, Z.; Gu, J.; Mo, L.; Chen, H. Application of Interval Partial Least Squares with Differential Evolution Algorithm in Wavelength Selection of Near Infrared Spectroscopy for Fishmeal. FENXI CESHI XUEBAO J. Instrum. Anal. 2020, 39, 1392–1397. [Google Scholar] [CrossRef]
- Cao, F.; Yang, Z.; Ren, J.; Jiang, M.; Ling, W. Linear vs. Nonlinear Extreme Learning Machine for Spectral-Spatial Classification of Hyperspectral Images. Sensors 2017, 17, 2603. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kooistra, L.; Wehrens, R.; Leuven, R.S.E.W.; Buydens, L.M.C. Possibilities of visible–near-infrared spectroscopy for the assessment of soil contamination in river floodplains. Anal. Chim. Acta 2001, 446, 97–105. [Google Scholar] [CrossRef]
- Zhang, S.; Shen, Q.; Nie, C.; Huang, Y.; Wang, J.; Hu, Q.; Ding, X.; Zhou, Y.; Chen, Y. Hyperspectral inversion of heavy metal content in reclaimed soil from a mining wasteland based on different spectral transformation and modeling methods. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2019, 211, 393–400. [Google Scholar] [CrossRef]
- Zhao, H.; Liu, P.; Qiao, B.; Wu, K. The Spatial Distribution and Prediction of Soil Heavy Metals Based on Measured Samples and Multi-Spectral Images in Tai Lake of China. Land 2021, 10, 1227. [Google Scholar] [CrossRef]
- Kinoshita, R.; Roupsard, O.; Chevallier, T.; Albrecht, A.; Taugourdeau, S.; Ahmed, Z.; van Es, H.M. Large topsoil organic carbon variability is controlled by Andisol properties and effectively assessed by VNIR spectroscopy in a coffee agroforestry system of Costa Rica. Geoderma 2016, 262, 254–265. [Google Scholar] [CrossRef]
- Mouazen, A.M.; Kuang, B.; De Baerdemaeker, J.; Ramon, H. Comparison among principal component, partial least squares and back propagation neural network analyses for accuracy of measurement of selected soil properties with visible and near infrared spectroscopy. Geoderma 2010, 158, 23–31. [Google Scholar] [CrossRef]
- Xu, S.; Zhao, Y.; Wang, M.; Shi, X. Comparison of multivariate methods for estimating selected soil properties from intact soil cores of paddy fields by Vis–NIR spectroscopy. Geoderma 2018, 310, 29–43. [Google Scholar] [CrossRef]
- Rossel, R.A.V.; Behrens, T. Using data mining to model and interpret soil diffuse reflectance spectra. Geoderma 2010, 158, 46–54. [Google Scholar] [CrossRef]
- Xu, Z.; Chen, S.; Zhu, B.; Chen, L.; Ye, Y.; Lu, P. Evaluating the Capability of Satellite Hyperspectral Imager, the ZY1–02D, for Topsoil Nitrogen Content Estimation and Mapping of Farmlands in Black Soil Area, China. Remote Sens. 2022, 14, 1008. [Google Scholar] [CrossRef]
- Gao, F.; Chen, S.; Du, X.; Zhou, X.; Wang, X. FOSS Kjeltec 8400 Automatic Kjeldahl Nitrogen Determinator for Determination of Total Nitrogen in Soil. Tianjin Agric. Sci. 2022, 28, 76–80. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, H.; Liu, W.; Zhao, S. Inversion of heavy metals content with hyperspectral reflectance in soil of well-facilitied capital farmland construction areas. Trans. Chin. Soc. Agric. Eng. 2017, 33, 230–239. [Google Scholar] [CrossRef]
- Petropoulos, G.P.; Arvanitis, K.; Sigrimis, N. Hyperion hyperspectral imagery analysis combined with machine learning classifiers for land use/cover mapping. Expert Syst. Appl. 2012, 39, 3800–3809. [Google Scholar] [CrossRef]
- Sorol, N.; Arancibia, E.; Bortolato, S.A.; Olivieri, A.C. Visible/near infrared-partial least-squares analysis of Brix in sugar cane juice. Chemom. Intell. Lab. Syst. 2010, 102, 100–109. [Google Scholar] [CrossRef]
- Tibshirani, R. Regression Shrinkage and Selection via the Lasso. J. R. Stat. Soc. Ser. B 1996, 58, 267–288. [Google Scholar] [CrossRef]
- Storn, R. On the usage of differential evolution for function optimization. In Proceedings of the North American Fuzzy Information Processing, Berkeley, CA, USA, 19–22 June 1996. [Google Scholar] [CrossRef]
- Chattopadhyay, S.; Mishra, S.; Goswami, S. Feature Selection Using Differential Evolution with Binary Mutation Scheme; IEEE: Durgapur, India, 2016. [Google Scholar] [CrossRef]
- Minhoni, R.T.D.A.; Scudiero, E.; Zaccaria, D.; Saad, J.C.C. Multitemporal satellite imagery analysis for soil organic carbon assessment in an agricultural farm in southeastern Brazil. Sci. Total Environ. 2021, 784, 147216. [Google Scholar] [CrossRef] [PubMed]
- Wang, F.; Shi, Z.; Biswas, A.; Yang, S.; Ding, J. Multi-algorithm comparison for predicting soil salinity. Geoderma 2020, 365, 114211. [Google Scholar] [CrossRef]
- Demattê, J.A.M.; Ramirez-Lopez, L.; Marques, K.P.P.; Rodella, A.A. Chemometric soil analysis on the determination of specific bands for the detection of magnesium and potassium by spectroscopy. Geoderma 2017, 288, 8–22. [Google Scholar] [CrossRef]
- Jakab, G.; Rieder, Á.; Vancsik, A.V.; Szalai, Z. Soil organic matter characterisation by photometric indices or photon correlation spectroscopy: Are they comparable? Hung. Geogr. Bull. 2018, 67, 109–120. [Google Scholar] [CrossRef] [Green Version]
- Smola, A.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef] [Green Version]
- Peng, X.; Shi, T.; Song, A.; Chen, Y.; Gao, W. Estimating Soil Organic Carbon Using VIS/NIR Spectroscopy with SVMR and SPA Methods. Remote Sens. 2014, 6, 2699–2717. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Zhang, F.; Kung, H.; Johnson, V.C. New methods for improving the remote sensing estimation of soil organic matter content (SOMC) in the Ebinur Lake Wetland National Nature Reserve (ELWNNR) in northwest China. Remote Sens. Environ. 2018, 218, 104–118. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, R.; Dai, W.; Zhou, X.; Zhang, D.; Yang, Y.; Cui, J. Mapping Soil Organic Matter Content Based on Feature Band Selection with ZY1-02D Hyperspectral Satellite Data in the Agricultural Region. Agronomy 2022, 12, 2111. [Google Scholar] [CrossRef]
- Zornoza, R.; Guerrero, C.; Mataix-Solera, J.; Scow, K.M.; Arcenegui, V.; Mataix-Beneyto, J. Near infrared spectroscopy for determination of various physical, chemical and biochemical properties in Mediterranean soils. Soil Biol. Biochem. 2008, 40, 1923–1930. [Google Scholar] [CrossRef] [Green Version]
- Buddenbaum, H.; Steffens, M. The Effects of Spectral Pretreatments on Chemometric Analyses of Soil Profiles Using Laboratory Imaging Spectroscopy. Appl. Environ. Soil Sci. 2012, 2012, 274903. [Google Scholar] [CrossRef] [Green Version]
- Li, B.; Xie, W. Adaptive fractional differential approach and its application to medical image enhancement. Comput. Electr. Eng. 2015, 45, 324–335. [Google Scholar] [CrossRef]
- Mehmood, T.; Liland, K.H.; Snipen, L.; Sæbø, S. A review of variable selection methods in Partial Least Squares Regression. Chemom. Intell. Lab. Syst. 2012, 118, 62–69. [Google Scholar] [CrossRef]
- Vohland, M.; Ludwig, M.; Thiele-Bruhn, S.; Ludwig, B. Quantification of Soil Properties with Hyperspectral Data: Selecting Spectral Variables with Different Methods to Improve Accuracies and Analyze Prediction Mechanisms. Remote Sens. 2017, 9, 1103. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Ju, J.; Guo, H.; Qiao, B.; Nie, B.; Zhu, L. Bathymetric Inversion and Mapping of Two Shallow Lakes Using Sentinel-2 Imagery and Bathymetry Data in the Central Tibetan Plateau. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4279–4296. [Google Scholar] [CrossRef]
- Yang, H.; Guo, H.; Dai, W.; Nie, B.; Qiao, B.; Zhu, L. Bathymetric mapping and estimation of water storage in a shallow lake using a remote sensing inversion method based on machine learning. Int. J. Digit. Earth 2022, 15, 789–812. [Google Scholar] [CrossRef]
- Guo, H.; Dai, W.; Zhang, R.; Zhang, D.; Qiao, B.; Zhang, G.; Zhao, S.; Shang, J. Mineral content estimation for salt lakes on the Tibetan plateau based on the genetic algorithm-based feature selection method using Sentinel-2 imagery: A case study of the Bieruoze Co and Guopu Co lakes. Front. Earth Sci. 2023, 11, 1118118. [Google Scholar] [CrossRef]



| Items | Parameters |
|---|---|
| Date of launch | 12 September 2019 |
| Spectral bands | 76 (VNIR), 90 (SWIR) |
| Spectral range (nm) | 400–2500 |
| Spectral resolution (nm) | 10 (VNIR), 20 (SWIR) |
| Spatial resolution (m) | 30 |
| Swath width (km) | 60 |
| Revisit cycle (d) | 3 |
| Set | N | Max (g/kg) | Min (g/kg) | Mean (g/kg) | SD (g/kg) | CV |
|---|---|---|---|---|---|---|
| Whole set | 595 | 1.80 | 0.37 | 1.01 | 0.22 | 0.22 |
| Training set | 476 | 1.80 | 0.37 | 1.01 | 0.22 | 0.22 |
| Test set | 119 | 1.71 | 0.43 | 1.02 | 0.24 | 0.23 |
| Reflectance Representation | n | Wavelengths (nm) |
|---|---|---|
| OR | 77 | 396–405, 439–227, 542, 577, 619, 696–705, 756–774, 791, 808, |
| 842, 894, 920, 945–954, 988–997, 1014–1073, 1123–1139, 1190, | ||
| 1224, 1308, 1341–1442, 1493, 1526, 1594, 1644–1678, 1711–1745, | ||
| 1779, 1812–1880, 1930–1981, 2014–2048, 2081–2098, | ||
| 2132–2199, 2267, 2300–2401, 2450–2501 | ||
| IR | 17 | 395–404, 422, 447, 697, 1526, 1778–1795, 1845–1880, 1929–1947, |
| 1998, 2451, 2484–2501 | ||
| NLR | 19 | 404, 422, 447, 697, 757, 1375, 1425, 1526, 1594, 1644, |
| 1845–1880, 1930–1947, 2048, 2199, 2484–2501 | ||
| FDR | 141 | 404–430, 447–490, 524–559, 576–628, 645–705, 722–1106, |
| 1139–1173, 1207–1274, 1307–1324, 1357–1594, 1627, 1660–1795, | ||
| 1828–2132, 2165–2199, 2233–2317, 2350–2501 | ||
| Total | 254 |
| Model | Reflectance | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|---|
| R2 | MAE (g/kg) | RMSE (g/kg) | R2 | MAE (g/kg) | RMSE (g/kg) | ||
| MLR | OR | 0.68 | 0.10 | 0.13 | 0.29 | 0.15 | 0.19 |
| IR | 0.69 | 0.10 | 0.12 | 0.22 | 0.16 | 0.20 | |
| NLR | 0.69 | 0.10 | 0.12 | 0.28 | 0.15 | 0.19 | |
| FDR | 0.68 | 0.10 | 0.13 | 0.27 | 0.16 | 0.20 | |
| PLSR | OR | 0.51 | 0.12 | 0.16 | 0.54 | 0.12 | 0.16 |
| IR | 0.54 | 0.12 | 0.15 | 0.55 | 0.12 | 0.15 | |
| NLR | 0.53 | 0.12 | 0.15 | 0.54 | 0.12 | 0.16 | |
| FDR | 0.50 | 0.12 | 0.16 | 0.47 | 0.13 | 0.17 | |
| SVM | OR | 0.60 | 0.10 | 0.14 | 0.59 | 0.11 | 0.15 |
| IR | 0.61 | 0.10 | 0.14 | 0.58 | 0.11 | 0.15 | |
| NLR | 0.61 | 0.10 | 0.14 | 0.58 | 0.11 | 0.15 | |
| FDR | 0.58 | 0.10 | 0.14 | 0.45 | 0.13 | 0.17 | |
| Model | Reflectance | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|---|
| R2 | MAE (g/kg) | RMSE (g/kg) | R2 | MAE (g/kg) | RMSE (g/kg) | ||
| LASSO–MLR | OR | 0.62 | 0.11 | 0.14 | 0.49 | 0.13 | 0.16 |
| IR | 0.53 | 0.12 | 0.15 | 0.56 | 0.12 | 0.15 | |
| NLR | 0.54 | 0.12 | 0.15 | 0.55 | 0.12 | 0.15 | |
| FDR | 0.67 | 0.10 | 0.13 | 0.32 | 0.15 | 0.19 | |
| LASSO–PLSR | OR | 0.55 | 0.12 | 0.15 | 0.54 | 0.12 | 0.16 |
| IR | 0.52 | 0.12 | 0.15 | 0.57 | 0.12 | 0.15 | |
| NLR | 0.53 | 0.12 | 0.15 | 0.55 | 0.12 | 0.15 | |
| FDR | 0.51 | 0.12 | 0.16 | 0.48 | 0.13 | 0.17 | |
| LASSO–SVM | OR | 0.58 | 0.11 | 0.14 | 0.61 | 0.11 | 0.14 |
| IR | 0.54 | 0.12 | 0.15 | 0.56 | 0.12 | 0.15 | |
| NLR | 0.62 | 0.10 | 0.14 | 0.58 | 0.11 | 0.15 | |
| FDR | 0.57 | 0.11 | 0.15 | 0.47 | 0.13 | 0.17 | |
| Model | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|
| R2 | MAE (g/kg) | RMSE (g/kg) | R2 | MAE (g/kg) | RMSE (g/kg) | |
| LBC–MLR | 0.80 | 0.08 | 0.10 | 0.23 | 0.19 | 0.24 |
| LBC–PLSR | 0.52 | 0.12 | 0.15 | 0.54 | 0.12 | 0.16 |
| LBC–SVM | 0.65 | 0.10 | 0.13 | 0.57 | 0.12 | 0.15 |
| Reflectance | MLR | N | PLSR | N | SVM | N |
|---|---|---|---|---|---|---|
| Representation | Wavelengths (nm) | Wavelengths (nm) | Wavelengths (nm) | |||
| OR | 404, 542, 576, 619, 765–774, | 33 | 705, 757, 1880, 2132 | 4 | 447, 954, 1139, 1308, 1341, | 11 |
| 791, 954, 1023, 1056, 1139, | 1375, 1425, 1812, 2317, | |||||
| 1190, 1308, 1442, 1526, 1644, | 2451 | |||||
| 1745, 1812–1845, 1880, 1930- | ||||||
| 1947, 1981, 2031–2048, 2082- | ||||||
| 2098, 2183–2199, 2267, 2301, | ||||||
| 2451 | ||||||
| IR | 396, 697, 1526, 1795, 1880, | 7 | 1526, 1880, 1930–1947, 2451, | 7 | 404, 422, 1795, 1862, 2484, | 6 |
| 1998, 2501 | 2484–2501 | 2501 | ||||
| NLR | 697, 757, 1425, 1526, 1880, | 9 | 422, 1526, 1593, 1880, 1947 | 5 | 404, 4222, 1644, 1880, 1947 | 5 |
| 1930, 2199, 2484–2501 | ||||||
| FDR | 413, 490, 551–559, 594–628, | 49 | 413, 447–456, 551–559, 576- | 45 | 482, 525, 594–602, 619, 622, | 28 |
| 654–662, 679–688, 722–731, | 602, 619, 757, 808–842, 877, | 679–688, 705, 748, 834, | ||||
| 757, 834, 851, 868–877, 894, | 894, 928, 946, 980, 1073, | 877–885, 1073, 1089, 1224, | ||||
| 1073–1089, 1156–1173, 1257, | 1139, 1173, 1277, 1241, 1375, | 1526, 1745, 1778–1795, 1880, | ||||
| 1375, 1442–1476, 1526, 1678- | 1442, 1510–1526, 1678, 1728, | 1930, 2098, 2183, 2233, | ||||
| 1728, 1762, 1795, 1947–1981, | 1829–1846, 1880, 1930–1947, | 2301, 2501 | ||||
| 2048, 2081, 2199, 2267, | 1981, 2048–2098, 2132, 2183, | |||||
| 2367–2417, 2451 | 2367 | |||||
| Total | 98 | 61 | 50 |
| Model | Training Set | Test Set | ||||
|---|---|---|---|---|---|---|
| R2 | MAE (g/kg) | RMSE (g/kg) | R2 | MAE (g/kg) | RMSE (g/kg) | |
| LBC–DE–MLR | 0.64 | 0.10 | 0.13 | 0.65 | 0.10 | 0.14 |
| LBC–DE–PLSR | 0.57 | 0.11 | 0.15 | 0.60 | 0.11 | 0.14 |
| LBC–DE–SVM | 0.85 | 0.08 | 0.09 | 0.72 | 0.08 | 0.12 |
| Model | Training Set | Test Set | Model | Training Set | Test Set |
|---|---|---|---|---|---|
| OR–MLR | 0.014 | 0.032 | FDR–LASSO–MLR | 0.014 | 0.033 |
| IR–MLR | 0.014 | 0.034 | OR–LASSO–PLSR | 0.013 | 0.029 |
| NLR–MLR | 0.014 | 0.033 | IR–LASSO–PLSR | 0.012 | 0.028 |
| FDR–MLR | 0.014 | 0.033 | NLR–LASSO–PLSR | 0.012 | 0.028 |
| OR–PLSR | 0.012 | 0.027 | FDR–LASSO–PLSR | 0.012 | 0.025 |
| IR–PLSR | 0.012 | 0.028 | OR–LASSO–SVM | 0.012 | 0.027 |
| NLR–PLSR | 0.012 | 0.028 | IR–LASSO–SVM | 0.012 | 0.027 |
| FDR–PLSR | 0.012 | 0.025 | NLR–LASSO–SVM | 0.013 | 0.028 |
| OR–SVM | 0.012 | 0.028 | FDR–LASSO–SVM | 0.010 | 0.021 |
| IR–SVM | 0.012 | 0.028 | LBC–MLR | 0.015 | 0.041 |
| NLR–SVM | 0.012 | 0.028 | LBC–PLSR | 0.012 | 0.028 |
| FDR–SVM | 0.010 | 0.021 | LBC–SVM | 0.012 | 0.025 |
| OR–LASSO–MLR | 0.013 | 0.031 | LBC–DE–MLR | 0.014 | 0.031 |
| IR–LASSO–MLR | 0.012 | 0.027 | LBC–DE–PLSR | 0.013 | 0.028 |
| NLR–LASSO–MLR | 0.013 | 0.028 | LBC–DE–SVM | 0.015 | 0.030 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, R.; Cui, J.; Zhou, W.; Zhang, D.; Dai, W.; Guo, H.; Zhao, S. Estimation of the Total Soil Nitrogen Based on a Differential Evolution Algorithm from ZY1-02D Hyperspectral Satellite Imagery. Agronomy 2023, 13, 1842. https://doi.org/10.3390/agronomy13071842
Zhang R, Cui J, Zhou W, Zhang D, Dai W, Guo H, Zhao S. Estimation of the Total Soil Nitrogen Based on a Differential Evolution Algorithm from ZY1-02D Hyperspectral Satellite Imagery. Agronomy. 2023; 13(7):1842. https://doi.org/10.3390/agronomy13071842
Chicago/Turabian StyleZhang, Rongrong, Jian Cui, Wenge Zhou, Dujuan Zhang, Wenhao Dai, Hengliang Guo, and Shan Zhao. 2023. "Estimation of the Total Soil Nitrogen Based on a Differential Evolution Algorithm from ZY1-02D Hyperspectral Satellite Imagery" Agronomy 13, no. 7: 1842. https://doi.org/10.3390/agronomy13071842
APA StyleZhang, R., Cui, J., Zhou, W., Zhang, D., Dai, W., Guo, H., & Zhao, S. (2023). Estimation of the Total Soil Nitrogen Based on a Differential Evolution Algorithm from ZY1-02D Hyperspectral Satellite Imagery. Agronomy, 13(7), 1842. https://doi.org/10.3390/agronomy13071842






