Hyperspectral Estimation of Chlorophyll Content in Apple Tree Leaf Based on Feature Band Selection and the CatBoost Model

Abstract

Leaf chlorophyll content (LCC) is a crucial indicator of nutrition in apple trees and can be applied to assess their growth status. Hyperspectral data can provide an important means for detecting the LCC in apple trees. In this study, hyperspectral data and the measured LCC were obtained. The original spectrum (OR) was pretreated using some spectral transformations. Feature bands were selected based on the competitive adaptive reweighted sampling (CARS) algorithm, random frog (RF) algorithm, elastic net (EN) algorithm, and the EN-RF and EN-CARS algorithms. Partial least squares regression (PLSR), random forest regression (RFR), and the CatBoost algorithm were used before and after grid search parameter optimization to estimate the LCC. The results revealed the following: (1) The spectrum after second derivative (SD) transformation had the highest correlation with LCC (–0.929); moreover, the SD-based model produced the highest accuracy, making SD an effective spectrum pretreatment method for apple tree LCC estimation. (2) Compared with the single band selection algorithm, the EN-RF algorithm had a better dimension reduction effect, and the modeling accuracy was generally higher. (3) CatBoost after grid search optimization had the best estimation effect, and the validation set of the SD-EN-CARS-CatBoost model after parameter optimization had the highest estimation accuracy, with the determination coefficient (R²), root mean square error (RMSE), and relative prediction deviation (RPD) reaching 0.923, 2.472, and 3.64, respectively. As such, the optimized SD-EN-CARS-CatBoost model, with its high accuracy and reliability, can be used to monitor the growth of apple trees, support the intelligent management of apple orchards, and facilitate the economic development of the fruit industry.

1. Introduction

Chlorophyll is one of the most essential plant pigments, and is responsible for plant photosynthesis. Chlorophyll content is a vital index for evaluating plant aging, environmental stress, and nitrogen status. Accordingly, the nutrient and growth status of plants can be evaluated by measuring the chlorophyll content [1,2,3]. However, traditional chemical leaf chlorophyll content (LCC) measurement methods damage the plant structure and are time consuming and laborious [4]. Therefore, they cannot meet the needs of real-time and non-destructive monitoring. By contrast, hyperspectral remote sensing (HRS) technology possesses advantages such as a high spectral resolution and continuous narrow bands that can be used to identify bands sensitive to specific crop parameters [5]; consequently, HRS can be employed for the non-destructive, immediate, and accurate monitoring and diagnosis of crop parameters [6,7]. Owing to these attributes, HRS has been widely applied in the estimation of crop chlorophyll content [8,9], biomass [10,11], nitrogen content [12,13], leaf area index [14,15], and other physiological and biochemical parameters.

For LCC estimation, HRS is increasingly being used to monitor the LCC of vegetation [16,17]. HRS can be utilized to obtain the spectral curves of vegetation. In recent years, with the development of computer technology and continuous innovation in analysis and processing methods, numerous scholars have used preprocessing methods to denoise the original spectral data to highlight spectral features and improve the accuracy of estimation. Currently, commonly used spectral transformation methods include spectral smoothing, derivative transformation, continuum removal transformation, and wavelet transform [18,19,20]. Fu et al. [21] performed a wavelet transform of hyperspectral data and monitored crop nitrogen based on artificial neural networks (ANNs). Cui et al. [22] found that hyperspectral data after the first derivative transformation were better able to fit the measured chlorophyll-a concentration than the original spectrum (OR), achieving a maximum correlation coefficient of 0.8588. Spectral transformation plays a crucial role in plant HRS monitoring, and there are different optimal spectral preprocessing methods for different plants.

A serious multicollinearity problem exists because of the strong correlation between spectral reflectance at different wavelengths [23,24]. This issue can cause model deviation and overfitting, resulting in models established from hyperspectral data having low accuracy or poor universality. To address this problem, researchers have developed various methods, such as using a vegetation index at specified wavelengths, building a spectral index of any band, and selecting feature bands [25,26,27]. Some researchers have used the index method to invert crop biochemical parameters. Luo et al. [28] found that the combining of feature bands, common vegetation indices, and any two-band vegetation index improved the accuracy of the plant anthocyanin content estimation. Wang et al. [29] reported that the accuracy of the model constructed using the spectral data after dimensionality reduction was 0.1 higher than that of the full-band model. Wen et al. [30] estimated the nitrogen content of maize leaves using HRS and the red-edge absorption area index. In addition, the band selection methods were used to estimate plant biochemical parameters. Sun et al. [31] used the random frog (RF) algorithm to select feature bands, which were then combined with hyperspectral images to visualize potato leaf water content. Gao et al. [32] proposed a new image segmentation method using correlation analysis (CA) and an RF algorithm combined with the partial least squares regression (PLSR) model, improving the R² of LCC estimation by 0.09 and 0.03, respectively. Most current studies adopt a single dimension reduction method; nevertheless, some studies have demonstrated that estimation models established by combining different band dimensionality-reduction algorithms have higher accuracy [33,34]. However, reports on the hyperspectral estimation of LCC by combining multiple dimension reduction methods are scarce. Additionally, there are some deficiencies in the universality of models established using these algorithms; in other words, the optimal models for estimating the physiological and biochemical parameters of different crops are different.

In terms of modeling, the rise of machine learning methods has improved the accuracy of estimations. Wang et al. [35] used Sentinel-2A images to predict soil organic carbon content in the western Guanzhong Plain, showing that the prediction model established using random forest regression (RFR) had the highest accuracy (R² = 0.8581). Yang et al. [36] used unmanned aerial vehicle (UAV) hyperspectral data to estimate wheat chlorophyll content and found that the XGBoost model established by K-means clustering performed better than the RFR model. This indicates that, under certain conditions, the modeling accuracy of Boosting algorithms such as the XGBoost and CatBoost algorithms was higher than that of Bagging algorithms such as the RFR algorithm for estimating LCC. Ta et al. [37] used HRS to estimate apple tree LCC and proposed that the LCC modeling accuracy of the RFR algorithm surpassed the MLR and SVR algorithms. The input variable types, spectral transformation methods, and the number of feature bands selected can all affect the accuracy of machine learning algorithms [38]. Therefore, it is necessary to build different estimation models, fully utilize hyperspectral information, and further improve the applicability and scientificity of estimation models.

Apple (Malus pumila Mill.) orchards occupy the largest planting area and produce the highest output among all fruit plantations in China, contributing significantly to the local economy [39]. The LCC of apple trees varies under different growing conditions, resulting in different photosynthetic rates and different accumulations of organic matter content [37]. This variation significantly impacts the final apple yield. Real-time monitoring of apple LCC is critical for ensuring high apple yields. However, few studies have been conducted on the application of hyperspectral processing for apple tree leaf pigment estimation. Accurate methods for estimating apple LCC enable appropriate orchard management measures for optimizing the planting structure and fertilization regimen of apple orchards to be developed. Therefore, applying HRS to apple tree LCC estimation has practical significance for apple tree growth and scientific management [40].

In conclusion, the limitations of previous research are as follows. First, there is a scarcity of reports concerning the estimation of chlorophyll content in cash crops such as apples. Second, most previous studies estimating crop content utilize vegetation indices, with fewer studies employing band selection algorithms. Lastly, most band dimension reduction algorithms previously used are primarily single-band dimension reduction algorithms, with only a few researchers having investigated the impact of combined dimension reduction algorithms on the accuracy of the estimation model. Consequently, this study used the hyperspectral information on apple tree leaves and multiple feature selection methods and established three inversion models (PLSR, RFR, CatBoost) to estimate apple tree LCC, enabling the nutrient and growth status of apple trees to be accurately monitored. The specific research objectives are as follows: (1) determine the best spectral preprocessing method; (2) identify the advantages of the improved feature band selection algorithm; and (3) evaluate the accuracy of different apple tree LCC estimation models.

2. Materials and Methods

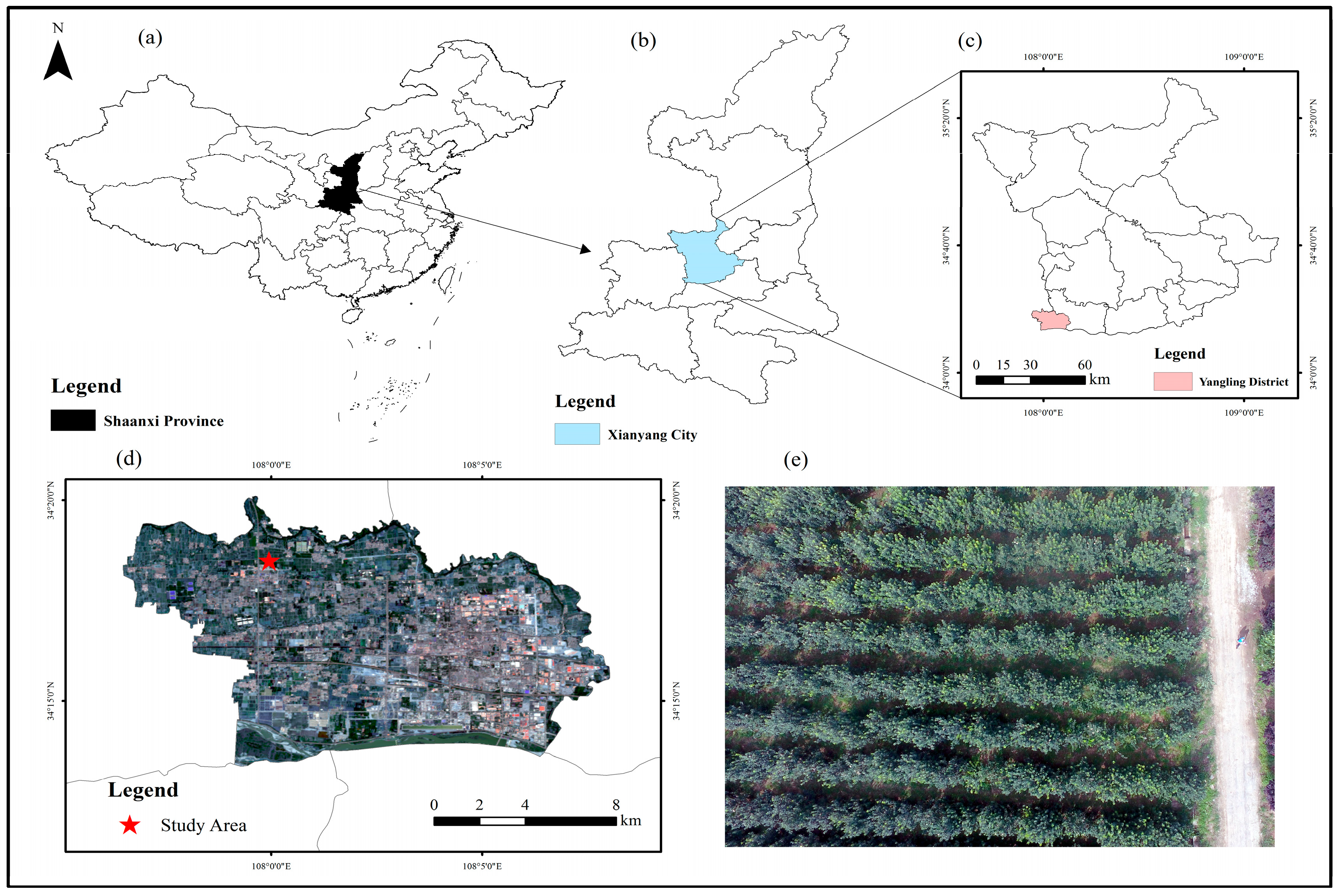
2.1. Study Area

The apple industry contributes significantly to the economic development of Shaanxi Province. Thus, a representative, extensive orchard was chosen as the research area within this province. This study was conducted in a ten-year-old apple orchard located in Yangling District, Xianyang City, Shaanxi Province (Figure 1). The satellite imagery data in Figure 1 were obtained from Landsat-8 OLI data, acquired in August 2021, with a spatial resolution of 30 m, covering the band information of 9 bands. This orchard is not only conveniently located and representative of the region, but also offers an accessible environment for experiments because of its long-lasting cultivation period. The area of the orchard is about 3.75 hm², and the soil type is Lou soil. The climate is warm, with four distinct seasons; the average temperature and rainfall are 14.1 °C and 635 nm, respectively.

2.2. Data Measurement

In August 2021, we selected 40 apple trees, relatively evenly distributed, from the apple orchard. For example, we would randomly select an apple tree from one of the plots we drew in the orchard, resulting in 40 such plots and the selection of 40 apple trees. Chlorophyll synthesis is influenced by illumination intensity and duration [41,42]. Hence, six leaves were randomly picked from the east, north, west, and south directions of the sample tree (Figure 2), providing a total of 960 apple tree leaves for analysis. Taking different trees and directions as a single sample group resulted in a total of 160 samples.

Dualex Scientific+ (Force-A, Orsay, France) is a commonly used portable plant leaf-measuring instrument that uses plant fluorescence technology to achieve real-time and non-destructive measurements of LCC and obtain the dimensionless relative value of LCC [43] (Figure 2). The measured LCCs were the dependent variables for establishing the regression model. We selected three areas (leaf tip, leaf middle, and leaf base) on each apple tree leaf, and the LCC of each area was measured by Dualex. Then, the mean value of the measured areas value was taken as the LCC value of that leaf, providing a total of 960 chlorophyll values. Finally, we calculated the average LCC of the six leaves from each sample as the LCC of that sample group, yielding a total of 160 measured LCC samples. We set a fixed random state value in Python to divide the 160 samples into a modeling set and a verification set using a ratio of 7:3. The statistical characteristics of the LCC of the samples are listed in

Table 1. Descriptive statistics of the LCC of all sets of variables.

Sample Sets	No. of Samples	Max.	Min.	Mean	Standard Deviation
All Samples	160	51.44	15.00	33.93	10.10
Modeling set	112	51.44	15.00	33.86	10.57
Validation set	48	48.05	18.34	34.10	9.01

.

2.3. Hyperspectral Data Acquisition and Preprocessing

2.3.1. Hyperspectral Data Acquisition

SVC HR-1024i (Spectra Vista Crop., Poughkeepsie, NY, USA), a portable non-imaging all-band ground object spectrometer, was used to collect hyperspectral data (Figure 2). This instrument, employing a built-in tungsten lamp as its light source, has spectral resolutions of 3.5, 9.5, and 6.5 nm, corresponding to the spectral ranges of 350–1000 nm, 1000–1850 nm, and 1850–2500 nm, respectively. Prior to any spectral measurements, the instrument underwent calibration. Whiteboard calibration was required, in order to obtain the spectral curve in the whiteboard state, and then measure the spectrum of apple tree leaves. Whiteboard calibration refers to the probe of the SVC HR-1024i leaf clamp emitting vertical rays towards the whiteboard, ultimately obtaining the spectrum of the whiteboard. The final obtained spectral curve of apple tree leaves was the spectral curve after whiteboard calibration. In addition, for every measurement of the spectrum of an apple tree leaf, it is necessary to calibrate the whiteboard once. Once the correction curve stabilized, an apple leaf was secured in the instrument’s leaf clamp for measurement. The probe of the leaf clamp tightly adheres to the apple leaf, emitting vertical rays onto the leaf in order to ultimately derive the leaf’s spectral curve. To ensure the collected hyperspectral data remain consistent, the SVC HR-1024i was programmed to automatically measure two spectral curves each time, with the average value being recorded as the spectral curve for that particular point. Moreover, during the SVC HR-1024i measurement process, blackboard correction was performed after each set of apple leaf spectra was measured in order to achieve more accurate results. A spectral curve was obtained from the tip, middle, and base of each apple tree leaf. Then, the average value was taken as the average spectral curve of the leaf. Finally, the average value of the spectral curves of six leaves in each sample was taken to represent the spectral curve of this sample. This process yielded a total of 160 spectral curves.

2.3.2. Hyperspectral Data Preprocessing

Previous research [44] revealed that the bands affecting the LCC of healthy plants are concentrated at 400–1000 nm; therefore, bands in this range were captured and resampled at 1 nm intervals. One of the primary objectives of this manuscript is to identify the most effective spectral transformation method for estimating the apple tree LCC among various methodologies. In this study, to partially mitigate the effects of light scattering and noise, the second derivative (SD) following Savitzky–Golay (SG) smoothing, continuum removal (CR), and multiplicative scatter correction (MSC) were used to pretreat the original spectrum (OR). CR can be utilized to compare the absorption characteristics of spectral reflectance from a common baseline. SD was used to eliminate linear background migration, and MSC eliminated the impact of spectral scattering, reduce baseline shifts or translation between samples and maximize the retention of spectral absorption information related to the chemical composition of the samples [19,45].

2.4. Feature Band Selection Method

2.4.1. Competitive Adaptive Reweighted Sampling Algorithm

The competitive adaptive reweighted sampling (CARS) algorithm uses Monte Carlo [7] to perform a cyclic analysis of each band of the spectrum and cross validation (CV) to evaluate the dimensionality-reduction effect of the subsets. Finally, spectral bands with large errors are eliminated, and the feature bands are selected after several sampling cycles. With a ‘survival of the fittest’ characteristic, CARS effectively removes non-informative variables, and minimizes the influence of collinear variables on the model [46,47]. The steps can be briefly described as follows [48]:

Using the Monte Carlo sampling method, 80% of the samples are randomly selected each time, and the remaining samples are used as the validation set for constructing the PLS model. The number of sampling times (N) for Monte Carlo must be preset. During the Nth sampling process, the absolute weight of the regression coefficients in the PLS model needs to be recorded sequentially, as defined using Equation (1).

$$w_i=\left|b_i\right|/{\sum }_{i=1}^m\left|b_i\right|$$

(1)

where m is the number of remaining variables in a single sampling; $b_i$ is the absolute value of the regression coefficient of the ith variable; $w_i$ is the absolute weight of the regression coefficient for the ith variable.

The exponential decay function (EDF) is used to remove the value with the smallest absolute value for the regression coefficient, and at the ith sampling, the ratio of the retained wavelength points obtained according to the EDF is denoted as $R_i$. $R_i$ can be formulated using Equation (2):

$$R_i={\mu e}^{-\mathit{ki}}$$

(2)

where µ and k are constants. When the Nth sampling is completed, the ratio of the remaining wavelength points becomes 2/n, where n is the number of original wavelength points; then, µ and k can be formulated using Equations (3) and (4):

$${\mu =\left(\frac{n}{2}\right)}^{\frac{1}{N-1}}$$

(3)

$$k=\frac{\ln \left(\frac{n}{2}\right)}{N-1}$$

(4)

In each sampling round, adaptive weighted sampling is used to select a corresponding number of wavelength variables from the number of variables in the previous sampling. PLS modeling is then performed to calculate the CV mean square error. After N sampling, the wavelength variable corresponding to the minimum value of root mean squared error of cross validation (RMSECV) is selected as the feature variable [49].

2.4.2. Random Frog Algorithm

The random frog (RF) algorithm [50] establishes a Markov chain with a stationary distribution in the characteristic space and produces a one-dimensional probability matrix, where each probability value represents the likelihood of each band being selected. Compared with the classical dimensionality-reduction algorithm, RF features a random search and uses fewer variables in the CV process [51]. Consequently, the number of model iterations and the computational complexity are reduced [52]. The main operational steps of the RF algorithm are as follows:

(1)

Enter an initial band variable subset F₀, which includes K random bands during initialization, and set the number of iterations N.

(2)

Select a candidate band variable subset F* based on F₀, including K* bands. Establish a PLS model for F₀, and calculate and rank the absolute regression coefficients of each band in descending order. If K* = K, then F* = F₀; if K* < K, generate K* bands form a candidate band variable subset F*; if K* > K, the first Q bands form a candidate subset F*.

(3)

Select F* to replace the initial band variable subset F₀, iterate N times, and complete the calculation.

(4)

Calculate the probability value of each band being selected after N iterations. The magnitude of this probability value is used as the criterion for whether the variable is selected. The higher the probability value, the more likely it is that the selected band is prioritized.

2.4.3. Elastic Net Algorithm

Zou and Hastie proposed the elastic net (EN) algorithm [53], which synthesizes L1 and L2 norms and uses their convex combination as a new penalty term to optimize the Least Absolute Shrinkage and Selection Operator (LASSO) algorithm [54]. It combines the benefits of both the Ridge and LASSO algorithms [55]. It offers high estimation accuracy and solves the group effect problem by eliminating redundant and similar band variables [56]; moreover, it can be employed to select feature bands in hyperspectral data. The EN algorithm overcomes the disadvantage of using a small number of samples and realizes the precise selection of bands.

Letting $y=\left[\begin{array}{c}\begin{array}{c}{y}_1\\ y_2\\ ⋮\end{array}\\ y_n\end{array}\right]$, $\beta =\left[\begin{array}{c}{\beta }_0\\ \begin{array}{c}{\beta }_1\\ ⋮\end{array}\\ {\beta }_p\end{array}\right]$, $X=\left[\begin{array}{cc}\begin{array}{c}\begin{array}{ccc}1& x_{11}& x_{12}\\ 1& x_{21}& x_{22}\\ ⋮& ⋮& ⋮\end{array}\\ \begin{array}{ccc}1& x_{n1}& x_{n2}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\begin{array}{c}\dots \\ \dots \end{array}\\ \ddots \\ \dots \end{array}& \begin{array}{c}\begin{array}{c}{x}_{1p}\\ x_{2p}\end{array}\\ ⋮\\ x_{np}\end{array}\end{array}\end{array}\right]$, the EN algorithm can be formulated using Equation (5) [57,58]:

$$\mathrm{J}\left(\beta \right)=\sum {\left(y-X\beta \right)}^2+\alpha \lambda {‖\beta ‖}_1+\left(1-\alpha \right)/2·\lambda {‖\beta ‖}_2^2=\sum {\left(y-X\beta \right)}^2+\lambda \sum \left(\alpha \left|\beta \right|+\left(1-\alpha p\right){\beta }^2\right)$$

(5)

where X is a matrix of n × p, containing p spectral bands of n samples; β is the regression vector of p × 1; y is the measured LCC of the samples; α is the penalty item, and is selected based on the minimum mean square error (MSE) of the training set and the prediction deviation; and λ is the coefficient of the penalty term and is selected based on generalized CV minimization.

2.4.4. Improved Feature Band Selection Algorithm

The CARS, RF, and EN algorithms also have limitations. CARS assigns the regions with high reflectance fluctuation as variables with high weightings when selecting the characteristic band [59]. When selecting the feature bands, the RF algorithm sets a probability threshold value and selects variables whose probability values are greater than the threshold value as the feature bands. However, there is no theoretical basis for setting the probability threshold value, and since the generation of the initial variable set is random, it is difficult to guarantee the availability of the initial variable set [60]. The EN algorithm screens feature bands based on the minimum MSE of the training sample; thus, there may be hundreds of variables screened by the EN algorithm [58].

To establish a more effective regression model, in this study, the three algorithms were combined in pairs to fully leverage their respective advantages, compensate for their limitations, and ultimately improve the hyperspectral estimation accuracy for LCC [33,34,61]. Therefore, in this study, first, the EN algorithm, which screened more feature bands, was employed to preliminarily select the spectrum and eliminate irrelevant information. Then, the CARS and RF algorithms were applied to optimize the selected bands to obtain two improved methods, EN-CARS and EN-RF, further reducing the multicollinearity between variables.

2.5. Estimation Algorithm and Model Evaluation

2.5.1. Estimation Algorithm

The CatBoost algorithm is a gradient-boosted algorithm proposed by Yandex in 2017. CatBoost optimizes the gradient boosting decision tree (GBDT) and integrates multiple base learners using a sequential method. There is a dependency between different base learners generated by training, and the final result is obtained by weighting the regression values of all the base learners [62]. Compared to previous gradient-boosted algorithms such as XGBoost and LightGBM, CatBoost possesses enhancements in terms of both classification and regression. It uses a greedy strategy to effectively improve prediction accuracy, ordered boosting to optimize gradient migration, and oblivious trees as the predictor to reduce the possibility of overfitting; therefore, the model has superior generalization performance and robustness [63,64].

In the modeling process of CatBoost, the important parameters are as follows: the number of iterations refers to the maximum number of decision trees, set to a maximum of 1000. The learning rate controls the model’s convergence rate, and depth indicates the maximum depth of the tree. The loss function calculates the error of one sample; the root mean square error (RMSE) was selected as the loss function in this study. The grid search method with CV was used to optimize the model’s hyperparameters. To prevent overfitting, the iterations were set to a value of 100 at every interval in the range of 100 to 1000. The learning rate was set to any value in the range of 0.01–0.1. The depth was set in the integer range of 6–12. The other parameters in the model were set to their default values.

Partial least squares regression (PLSR) and random forest regression (RFR) were also employed to estimate the LCC. PLSR is the most commonly used multiple regression method in regression analysis and produces good results in practical applications. The PLSR model has the advantages of canonical correlation analysis, principal component analysis, and least-squares regression [65,66]. RFR is an ensemble machine learning algorithm proposed by Breiman [67] that randomly selects a portion of the training samples and variable subsets to generate multiple decision trees using the bootstrap sampling method with placement. In the regression problem, the final prediction result is the average of the prediction results of each decision tree in the RFR, which is a popular machine-learning algorithm with high accuracy, good generalization, and robustness to noise points and outliers [7,68].

Combining the above three estimation algorithms with spectral transformations and feature band selection algorithms, a total of 52 estimation models were constructed, as illustrated in Figure 3.

2.5.2. Model Evaluation

In this study, the determination coefficient (R²), RMSE, and relative prediction deviation (RPD) were used to evaluate the model accuracy. As shown in Equations (6)–(8), the closer R² is to 1, the better the fit of the model to the measured variables. RMSE reflects the deviation between the predicted and measured values. RPD values greater than 2 indicate that the model has an excellent prediction ability for the measured set, while RPD values between 1.4 and 2 indicate that the model can only roughly predict the variables in the measured set. If the RPD is less than 1.4, the model lacks predictive ability for the measured set [69].

$$R^2=\frac{{\sum }_{i=1}^n{\left({\widehat{y}}_i-{\overline{y}}_i\right)}^2}{{\sum }_{i=1}^n{\left(y_i-{\overline{y}}_i\right)}^2}$$

(6)

$$\mathrm{RMSE}=\sqrt{\frac{{\sum }_{i=1}^n{\left({\widehat{y}}_i-{\overline{y}}_i\right)}^2}{n}}$$

(7)

$$\mathrm{RPD}=\sqrt{\frac{{\sum }_{i=1}^n{\left(y_i-{\overline{y}}_i\right)}^2}{\frac{1}{n}{\sum }_{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2}}$$

(8)

where $n$ is the number of samples, $y_i,{\widehat{y}}_i,$ and ${\overline{y}}_i$ represent the measured values, the predicted values of the samples, and the average values of the measured values of the modeling and validation sets, respectively.

3. Results

3.1. Original Spectral Characteristics of Apple Tree Leaves

Figure 4 shows the original spectral reflection curves of apple tree leaves with different LCCs. The trend of the spectral reflectance curves is similar across different LCCs. The overall trend reveals that the original band reflectance is low in the visible light band (400–780 nm), whereas the reflectance of the near-infrared band (780–1000 nm) is high. In the visible light band, the spectral reflectance decreases with increasing LCC, particularly in the green light band (530–555 nm). In the near-infrared band, the spectral reflectance increases with increasing LCC. In addition, there is an obvious reflection peak near 550 nm and an absorption valley near 670 nm. The spectral reflectance increases rapidly in the range of 670–760 nm, then forms a high reflection platform in the near-infrared band that is typical for plant spectra.

3.2. Correlation Analysis between Different Spectral Transformations and LCC

Three spectral transformations (CR, MSC, and SD) were used to process the original spectrum (Figure 5). Additionally, through correlation analysis of the LCC and reflectance of each band after different spectral transformations, correlation results were obtained (Figure 6). Statistical analysis based on 160 samples showed that the absolute value of the 0.01 significance level correlation was 0.202. The LCC exhibited a significant correlation (p = 0.01) with the reflectance of the bands after different spectral transformations in most bands. The OR had the highest correlation at 716 nm (r = −0.895). Below 750 nm, the correlation between LCC and reflectance of each OR band was significant (p = 0.01). However, there was almost no significant correlation between them from 750 nm to 900 nm.

The correlation was improved after the application of different spectral transformations. Among them, the SD transformation significantly improved the correlation in the range between 520 and 720 nm, with the best correlation being observed at 579 nm (r = −0.929). The correlation coefficient curve of the CR was consistent with that of OR before 720 nm, but exhibited better correlation, particularly at 731 nm (r = −0.918). The MSC showed very high correlation for most bands, with the highest correlation being observed at 650 nm, reaching 0.912. In summary, compared with the correlation coefficients of the OR and spectral transformations, the SD and MSC methods may be better preprocessing methods.

3.3. Feature Band Selection

3.3.1. Feature Band Selection Based on the CARS Algorithm

The feature bands were selected under the OR and different spectral transformations based on the CARS algorithm combined with the LCC of the apple tree leaves. Taking SD as an example (Figure 7), with increasing number of CARS iterations, the number of feature bands selected gradually decreased. The RMSECV showed a slow decrease and reached its minimum when the number of sampling runs reached 22; subsequently, it increased significantly. Thus, a total of 52 bands were selected. The selected feature bands are listed in

Table 2. Specific band selection based on the CARS algorithm and different spectral transformations.

Spectral Transformation	Feature Band Selection/nm	Number
OR	402, 417, 418, 419, 420, 437, 438, 458, 463, 532, 659, 732, 836, 914, 926, 936, 953, 956, 963, 969, 970, 980, 987	23
CR	425, 435, 558, 594, 652, 696, 709, 710, 711, 712, 728, 729, 730, 731, 732, 743, 744, 745, 968, 969, 970	21
MSC	418, 419, 556, 603, 660, 849, 925, 926, 953, 961, 962, 980, 987	13
SD	416, 420, 426, 433, 439, 444, 448, 457, 458, 459, 463, 486, 488, 501, 503, 506, 542, 545, 554, 575, 577, 611, 644, 655, 671, 705, 708, 710, 718, 767, 770, 775, 779, 833, 852, 854, 882, 887, 890, 897, 898, 903, 906, 908, 915, 927, 934, 947, 951, 955, 964, 968	52

. Among them, 23 feature bands were selected from the OR curve, 21 bands were optimized from the CR curve, and 13 bands were optimized from the MSC curve. Overall, the feature bands selected by the CARS algorithm were distributed evenly, and bands were selected in each band interval.

3.3.2. Feature Band Selection Based on the RF Algorithm

The RF algorithm was used in combination with LCC to select the feature bands. In this study, the possibility threshold of RF was set to 0.3 for all transformations. For instance, the spectrum obtained from the SD curve (Figure 8) indicated the possibility of each band being selected. Twelve bands were selected using the RF algorithm from the SD and they were evenly distributed. In addition, the 11 bands selected from the CR curve were also relatively evenly distributed (

Table 3. Specific band selection based on the RF algorithm and different spectral transformations.

Spectral Transformation	Feature Band Selection/nm	Number
OR	447, 899, 914, 920, 926, 951, 974, 988	8
CR	588, 592, 654, 655, 710, 728, 744, 745, 755, 968, 969	11
MSC	898, 914, 921, 926, 941, 987	6
SD	444, 575, 611, 625, 763, 767, 770, 779, 808, 816, 823, 908	12

). However, only eight bands were selected using the RF algorithm from the OR, and the band distribution was uneven; the six bands selected from the MSC curve had the same problem. All the bands selected from MSC were distributed after 850 nm (Table 3). Overall, the modeling effects of SD-RF and CR-RF may be better than those of OR-RF and MSC-RF because of their more uniform distribution of feature bands.

3.3.3. Selection of Feature Bands Using the EN Algorithm

The EN algorithm used in this study selected α based on the minimum MSE of the training set. Since α ranged from 0 to 1, the (0,1) range was divided into 20 parts, and the values of MSE at different α values are shown in Figure 9. Higher values of α correspond to a greater weight of L1 regularization and the selection of fewer variables. Taking the SD spectrum as an example (Figure 10), the left log λ selected the feature bands based on the minimum standard error [57], while the right log λ selected the feature bands based on the minimum MSE in Figure 10a. When the MSE was minimized, the EN algorithm had a higher accuracy and better performance. Therefore, the feature bands were selected based on the minimum MSE, which was obtained at α = 0.95, resulting in the screening of 16 feature bands. The bands selected by the EN algorithm from the four transformation methods are shown in

Table 4. Number of specific bands selected on the basis of the optimal alpha values and fixed alpha values under different spectral transformations.

Different Alpha Values	Spectrum Transform	Value	Number
Optimal value	OR	0.55	43
	CR	0.60	38
	MSC	0.10	133
	SD	0.95	16
Fixed value	OR	0.10	123
	CR	0.10	87
	MSC	0.10	133
	SD	0.10	116

. The EN algorithm selected 43, 38, and 133 bands from the OR, CR, and MSC, respectively (the optimal values of α were 0.55, 0.6 and 0.1, respectively). The bands screened from OR and SD were distributed evenly in each band interval. However, the distribution of bands selected from CR and MSC were highly concentrated, with the feature bands of CR all being distributed in 500–550 nm and 700–750 nm ranges, while the feature bands of MSC were concentrated in the 650–850 nm range.

3.4. Estimation Results of LCC Based on a Single Band Selection Algorithm and Three Models

The feature bands of apple tree LCCs extracted under different spectral transformations were distinctive, but it was not known how accurate the LCC prediction was when using these feature bands; therefore, three models, namely PLSR, RFR, and CatBoost were constructed with the aim of achieving accurate LCC estimates using hyperspectral data (Figure 11).

For OR, different modeling methods showed different accuracies of the verification set using bands extracted with different feature band selection algorithms as independent variables. Among them, the accuracy of the EN-RFR model was the highest, with the R², RMSE, and RPD values reaching 0.862, 3.693, and 2.440, respectively, followed by the CARS-PLSR model and the EN-CatBoost model (R² values of 0.859 and 0.843, respectively).

The accuracies of the different model verification sets established after spectral transformations were better than that of the OR model. Among them, the SD-RF-Catboost model demonstrated the highest accuracy, with R², RMSE, and RPD values of 0.905, 2.774, and 3.249, respectively. The accuracies of all models established using SD were higher than those of models established using OR. In addition, there was an inconspicuous improvement in accuracy for the CR model and the MSC model, while the CR-CARS-RFR model (R² = 0.875) and the MSC-EN-CatBoost model (R² = 0.865) performed the best.

The scatter distributions of the measured and predicted values of the LCC verification set obtained by the OR and three spectral transformations based on their respective optimal estimation models are shown in Figure 12. Although the scatter points of the CR-CARS-RF model were closer to the 1:1 line, some points were outside the 95% prediction band, with a large deviation. The scatter distribution of the SD-RF-CatBoost model was more reasonable and accurate; all points were distributed within the 95% prediction band, and the R² value was also the highest. Therefore, it was the optimal estimation model for apple tree LCC that was established using a single feature band selection algorithm. However, fewer scatter points of this model were distributed within the 95% confidence interval.

The CatBoost model had more prominent advantages compared to the other two models. Except for the ordinary performance of the OR, the models incorporating the use of spectral transformations had high accuracy. The performance of RFR was stable, and although the accuracy of any transformations was not low, the modeling effect was not prominent. The performance of the PLSR model was generally stable, and the modeling accuracy by SD was relatively high, with the highest R² value of 0.902.

3.5. CatBoost Estimation Results of LCC Based on Improved Band Selection Algorithm and Grid Search Optimization

3.5.1. Band Selection Based on Improved Feature Selection Algorithm

To establish a more effective regression model, this study used the EN-CARS and EN-RF algorithms to improve the estimation accuracy of LCC.

To obtain more feature bands in the initial selection, α in the EN algorithm was fixed at 0.1 (Table 4). Taking the SD as an example (Figure 13), log λ was set to select the feature band according to the minimum MSE, which corresponded to the position of the green line, and 116 feature bands were screened. OR, CR, and MSC initially screened out 123, 87, and 133 bands, respectively. Subsequently, the CARS and RF algorithms were adopted for the second screening (

Table 5. Number of sensitive bands selected based on the different improved feature band selection algorithms and different spectral transformations.

Selection Method	Spectrum Transform	Sensitive Band Selection/nm	Number
EN-CARS	OR	401, 402, 404, 423, 424, 437, 447, 535, 663, 670, 705, 706, 710, 711, 713, 727, 729, 778, 955, 983	20
	CR	522, 530, 531, 536, 735, 745, 748, 756, 926, 956	10
	MSC	641, 642, 650, 684, 686, 705, 712, 713, 727, 728, 729, 779, 785, 801, 839, 847, 848, 849, 963	19
	SD	444, 556, 575, 577, 705, 710, 718, 734, 753, 756, 779, 816, 905, 908, 909, 957	16
EN-RF	OR	401, 402, 403, 404, 423, 425, 428, 433, 434, 437, 438, 439, 447, 662, 663, 664, 672, 705, 706, 711, 712, 713, 714, 726, 727, 728, 729, 955, 963, 983	30
	CR	530, 531, 535, 536, 537, 744, 745, 756, 757, 771, 866, 867, 926	13
	MSC	642, 644, 705, 728, 783, 808, 847, 963	8
	SD	444, 552, 560, 575, 590, 705, 706, 710, 712, 717, 718, 734, 756, 779, 816	15

), and the selection threshold of the RF algorithm was set at 0.3. In Table 5, the EN-CARS algorithm based on OR, CR, MSC, and SD selected 20, 10, 19, and 16 bands, respectively while the EN-RF algorithm based on OR, CR, MSC, and SD selected 30, 13, 8, and 15 bands, respectively. The number of selected feature bands was lower than with the single band selection algorithm, but the dimensionality-reduction effect should be further verified by LCC modeling estimation.

3.5.2. CatBoost Estimation Results Based on Grid Search Parameter Optimization

The CatBoost model and the parameter-optimized CatBoost model were established for apple tree LCC estimation based on the bands selected by the improved feature selection algorithms (

Table 6. Comparison of the CatBoost model estimation results before and after parameter optimization based on different improved feature band selection algorithms and different spectral transformations.

Selection Method	Spectrum Transform	Default CatBoost			CatBoost Based on Grid Search Optimization
					Optimal Parameter			Optimized CatBoost
		R2	RMSE	RPD	Iterations	Learning Rate	Depth	R2	RMSE	RPD
EN-RF	OR	0.823	3.754	2.401	400	0.010	9	0.832	3.650	2.469
	CR	0.814	4.100	2.198	200	0.030	10	0.840	3.565	2.528
	MSC	0.868	3.288	2.740	300	0.013	9	0.900	2.814	3.202
	SD	0.871	3.575	2.521	100	0.029	9	0.892	2.936	3.069
EN-CARS	OR	0.837	3.824	2.356	100	0.100	11	0.846	3.505	2.571
	CR	0.828	3.976	2.266	200	0.051	9	0.856	3.379	2.666
	MSC	0.873	3.483	2.587	200	0.015	9	0.885	3.027	2.977
	SD	0.909	2.623	3.435	100	0.079	10	0.923	2.472	3.646

). It was found that the optimal parameters selected by different spectral transformations and feature band selection algorithms through grid search varied, and the accuracy of the verification set was significantly improved by optimization using the grid search algorithm.

Compared with the CatBoost model with default parameters, the accuracy of the optimized CatBoost model based on the EN-RF algorithm showed a significant improvement. The R² values of the models established based on the OR, CR, MSC, and SD were 0.832, 0.840, 0.900, and 0.892, respectively. The R² values of CR and MSC were 3.19% and 3.69%, respectively, which were higher than that of the optimal model established by the single band selection algorithm. However, the accuracy of the models established using OR and CR was lower than that of the single band selection algorithm.

The validation set R² values for the optimized CatBoost model based on the EN-CARS algorithm after OR, CR, MSC, and SD increased by 1.08%, 3.38%, 1.37%, and 1.54%, respectively, compared with the R² value of the original CatBoost. Moreover, the estimation accuracy of the two CatBoost models based on SD transformation was the highest, and was higher than that of the models derived using the single band selection algorithm. The SD-EN-CARS-CatBoost model performed best with the number of iterations, learning rate, and depth set as 100, 0.079, and 10, respectively, with R², RMSE, and RPD values of 0.923, 2.472, and 3.64, respectively. The modeling accuracy based on MSC was also improved, but the modeling accuracy optimized by OR or CR was even lower than that of the optimal model established by the single band selection algorithm.

Based on the EN-RF and EN-CARS algorithms, the MSC-EN-RF-CatBoost model and the SD-EN-CARS-CatBoost model, respectively, performed the best after parameter optimization, and the scatter distribution of the predicted and measured values of the LCC validation set were established based on these two models (Figure 14). The slopes of the scatter plots were close to 1, but there were two scattered points of the optimized MSC-EN-RF-CatBoost model that were outside the 95% prediction band. The R² and RMSE values of the optimized SD-EN-CARS-CatBoost model were higher and lower, respectively, than those of the MSC-EN-RF-CatBoost model. All of the points of the SD-EN-CARS-CatBoost model were located within the 95% prediction band, and more than 50% of the scattered points were within the 95% confidence interval. Therefore, the fitting effect of the SD-EN-CARS-CatBoost model was more accurate and reasonable.

4. Discussion

4.1. Selected Optimized Spectral Transformation Method

In this study, the SG-SD transformation produced the highest correlation with the chlorophyll content of apple tree leaves, reaching −0.929. The bands with high correlation were mostly distributed between 500 and 750 nm (Figure 6), which is consistent with previous studies [28,37,44]. SD also performed the best in terms of estimation modeling accuracy and was the best spectral preprocessing method for LCC estimation. The spectral curves after CR and MSC transformations showed similar trends to the original spectral curve. Although the bands with a high correlation between MSC transform spectra and LCC were distributed over the entire range, the selected feature bands were mostly after 700 nm, potentially resulting in lower modeling accuracy. The same issue was the case for CR. The correlation between the original spectra and LCC was lower compared to the CR transformation, and the spectral features were not prominent. Therefore, it was necessary to perform spectral transformation on the original spectrum.

4.2. Advantages of Combining Dimensionality-Reduction Algorithms

In this study, three dimensionality-reduction algorithms were selected: CARS, RF, and EN. The sensitive bands selected by the CARS algorithm were distributed more evenly compared to the RF algorithm (Table 2 and Table 3), and they were distributed in each interval. Although the RF algorithm was able to select a small number of bands, the accuracy of the LCC estimation model was uncertain because of the randomness of the selected feature bands [70]. The number of bands selected by the EN algorithm was determined by the α value. However, compared with the CARS and RF algorithms, if the α value was selected according to the minimum MSE value, the EN algorithm could select more feature bands [58]. In combination with the modeling method, excellent prediction results could be obtained. However, there is still room for improvement, and the dimensionality-reduction effect can be further improved.

To date, most hyperspectral estimation research has employed a single dimensionality-reduction method [51,71,72]. To achieve the most accurate estimation of apple tree LCC, this study fully exploited the advantages of the CARS, RF and EN algorithms to maximize the mining of the sensitive bands of apple tree leaf spectra. The algorithms were improved using the combination algorithms EN-CARS and EN-RF, and the number of sensitive bands selected by different spectral transformations and machine learning methods was mostly less than 20 (Table 5). Owing to the uneven distribution of the bands selected by the CARS and RF algorithms in the MSC transformation, the bands selected by the EN-CARS and EN-RF algorithms in the MSC transformation were mostly below 600 nm, while the feature bands selected using the other spectral transformations were evenly distributed. Table 6 shows that the combined feature band selection algorithm performed better than using a single feature band selection algorithm.

Compared to the EN-RF algorithm, the CatBoost model established by the EN-CARS algorithm exhibited higher accuracy. Therefore, the algorithms combining EN and CARS outperformed the algorithms combining EN and RF. However, the accuracy of the EN-CARS algorithm for the hyperspectral estimation of other biochemical parameters in different crops remains unknown. Further research is needed to explore the universality and accuracy of EN-CARS. In addition, vegetation indices are increasingly being used in research to evaluate crop parameters [73,74], so feature band selection and vegetation indices can be combined to obtain more band information and improve the accuracy of estimation models.

4.3. Competitiveness of the CatBoost Algorithm for Performing Hyperspectral Estimation

Machine learning algorithms can be used to analyze datasets with rich information and high-dimensional observation data, and have been widely applied in the analysis of remote sensing data and the estimation of the physiological and biochemical parameters of vegetation [75]. However, different vegetation and different physical and chemical parameters require careful selection of the appropriate machine learning algorithm for estimation. While the CatBoost algorithm has been widely applied in various fields [76,77,78], it has a potential use in the estimation of crop biochemical parameters. This study also demonstrated the effectiveness of the CatBoost algorithm in crop hyperspectral estimation.

The CatBoost model optimized with grid search parameters performed the best (Figure 11). CatBoost employs a greedy strategy to effectively improve prediction accuracy and uses oblivious trees as base learners to reduce the possibility of overfitting [63]. Compared to the two traditionally used estimation modeling algorithms, RFR and PLSR, the CatBoost algorithm exhibited superior robustness and generalization performance.

Grid search is one of the most popular parameter optimization methods in machine learning algorithms, and is computationally fast, making it suitable for parallel computing. When applied to the CatBoost algorithm, grid search enables the determination of optimal parameters for the LCC prediction model. The SD-EN-CARS-CatBoost model, optimized through grid search, demonstrated excellent LCC estimation capabilities with a validation set R² = 0.923 (Table 6), making it an outstanding method for LCC estimation. These results confirmed the high accuracy and predictive ability of the CatBoost algorithm in crop biochemical parameter estimation. Therefore, the CatBoost algorithm can be used to accurately predict apple LCC, facilitating real-time monitoring of dynamic apple tree growth information. This study provided an accurate LCC estimation model that can serve as a reference for future estimation of other vegetation parameters for the rapid and non-destructive monitoring of plant growth, thus enabling efficient orchard management and fruit production strategies to be developed.

4.4. Challenges and Future Research

In this study, we confirmed the high accuracy of using ground hyperspectral data, feature band selection, and the CatBoost model to estimate chlorophyll content in apple leaves. However, the spatial distribution of chlorophyll content within the apple leaf canopy at a larger scale remains unknown. In future research, we will use advanced technologies such as UAV and satellite remote sensing images, combined with radiation transfer models, to obtain the canopy reflectance of apple trees and achieve spatial inversion mapping of the physiological parameters of apple trees, further expanding the baseline data for the intelligent management of apple orchards. Moreover, in this study, we only selected spectra within the commonly used 400–1000 nm range for estimating LCC. The correlation and estimation accuracy between spectra and LCC in other bands still need further investigation. In future work, we aim to include information from all bands in the estimation model, and compare the accuracy of this model with that of the current model.

5. Conclusions

After performing correlation analysis, spectral feature band selection, and modeling estimation, it was determined that SD is the most effective spectral preprocessing method for apple tree LCC estimation. The data obtained after the selection of the feature bands exhibited reduced multicollinearity, and the characterization ability of apple tree LCC increased. The combined algorithm based on EN-CARS demonstrated higher accuracy compared to the use of a single band selection algorithm. Among all the models, the CatBoost model optimized through grid search achieved the highest prediction accuracy. Specifically, the R² and RPD values of the SD-EN-CARS-CatBoost model after parameter optimization reached as high as 0.923 and 3.646, respectively, and the RMSE was 2.472. In the future, to validate the accuracy and applicability of the model for LCC estimation, it is recommended to expand the sample size to include the leaf spectra of apple trees from different apple orchards. In conclusion, the improved algorithm combining multiple band selection algorithms has more advantages in crop parameter estimation than a single band selection algorithm. This provides inspiration for future crop parameter estimation and even other remote sensing fields, and provides a certain basis and reference for further research and innovation. Additionally, the SD-EN-CARS-CatBoost model optimized by grid search demonstrated exceptional performance in accurately estimating apple tree LCC using HRS. It provides a reliable and efficient method to predict the nutrient status and growth information of apple trees, which is vital for effective crop management and the development of the fruit industry, and also provides a certain theoretical basis for the estimation of future fruit industry production.