Estimation of Spring Maize Planting Dates in China Using the Environmental Similarity Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Datasets
2.2. Method
- (1)
- Characterizing the geographic environment associated with spring maize planting dates
- (2)
- Calculating environmental similarities
- (3)
- Calculating the reliability of each sample
- (4)
- Predicting planting date values and determining uncertainty
2.3. Evaluation and Validation
3. Results and Discussion
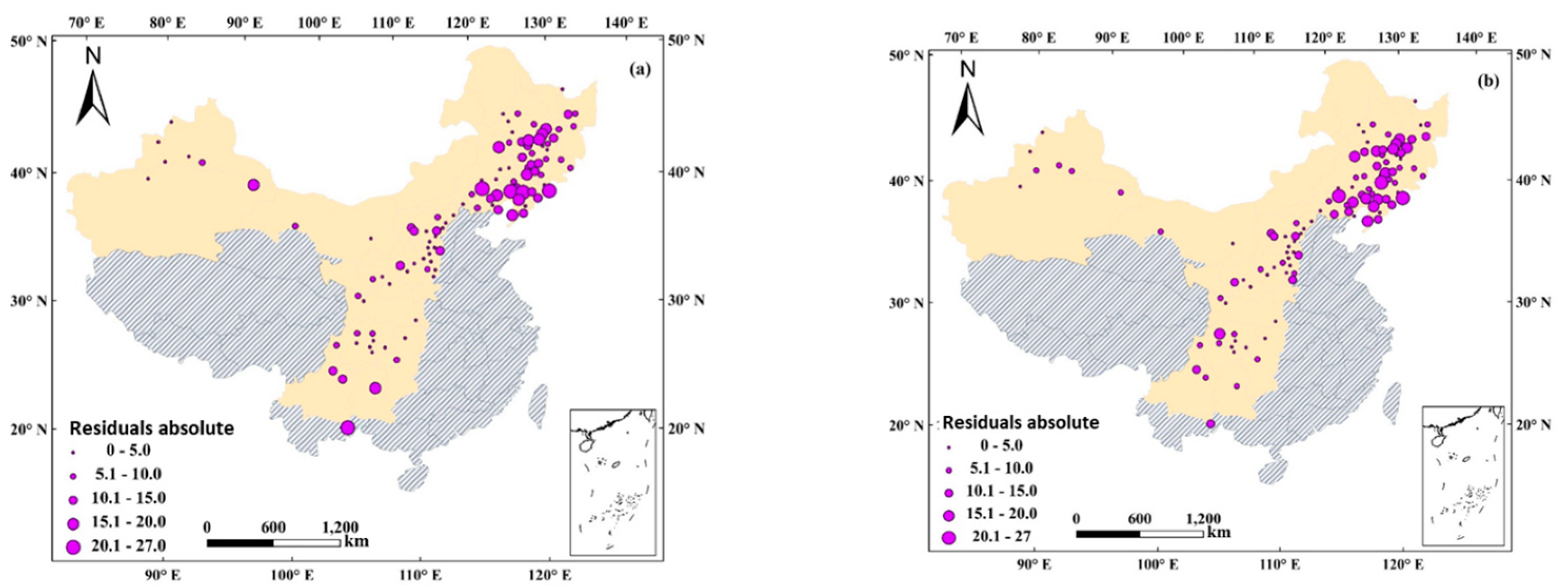
3.1. Independent Validation Results
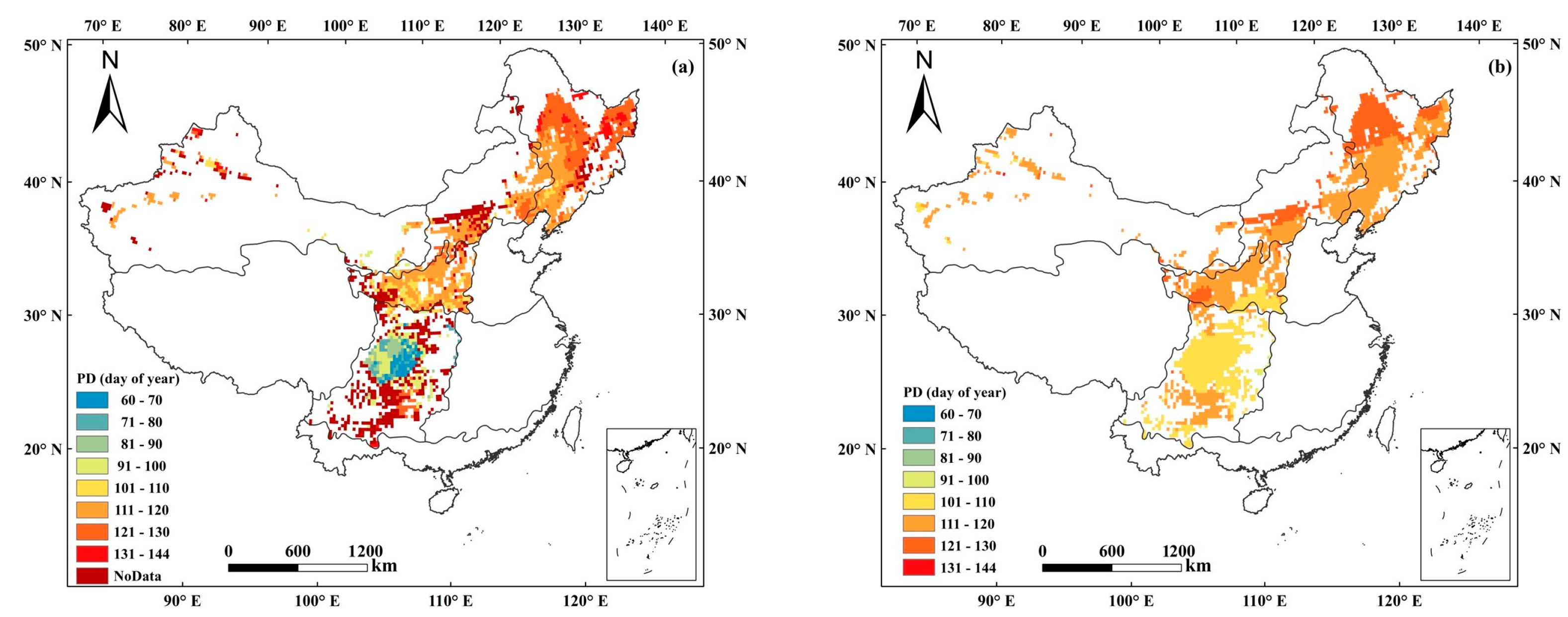
3.2. Predicting Spatial Distribution of Planting Dates
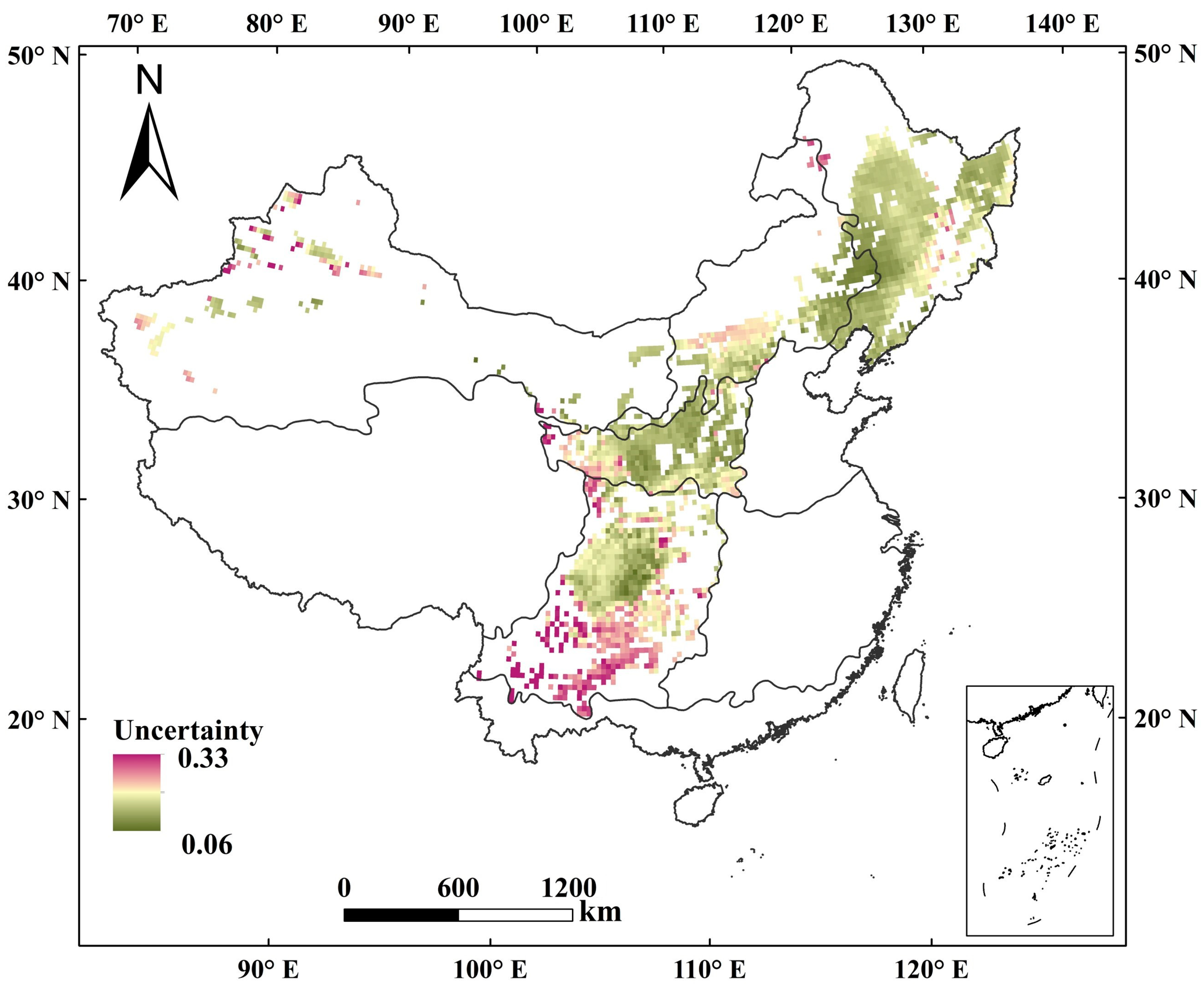
3.3. Uncertainty Analysis of Environmental Similarity-Based Predictions
3.4. Comparison of National-Scale and Regional-Scale Prediction
3.5. Advantages and Limitations of the Environmental Similarity Method
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PD | Planting date |
| NE | Northeast China |
| IMA | Inner Mongolia Autonomous Region north of the Great Wall |
| NW | Northwest China |
| LP | Loess Plateau China |
| SW | Southwest China |
| CMA | Chinese Meteorological Administration |
| Ti | Monthly average temperature, the i is the month number |
| Tmini | Monthly average minimum temperature, the i is the month number |
| Pi | Monthly precipitation, the i is the month number |
| GDD8 | Growing degree days above 8 ℃ |
| GDD10 | Growing degree days above 10 ℃ |
| RA | Relief amplitude |
| DEM | Digital elevation model |
| RMSE | Root mean square error |
| MAE | Mean absolute error |
| R2 | Coefficient of determination |
| Lon | Longitude |
| Lat | Latitude |
| PCA | Principal component analysis |
References
- Foley, J.A.; Ramankutty, N.; Brauman, K.A.; Cassidy, E.S.; Gerber, J.S.; Johnston, M.; Mueller, N.D.; O’Connell, C.; Ray, D.K.; West, P.C.; et al. Solutions for a cultivated planet. Nature 2011, 478, 337–342. [Google Scholar] [CrossRef] [PubMed]
- Godfray, H.C.J.; Beddington, J.R.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Pretty, J.; Robinson, S.; Thomas, S.M.; Toulmin, C. Food Security: The Challenge of Feeding 9 Billion People. Science 2010, 327, 812–818. [Google Scholar] [CrossRef] [PubMed]
- Rosenzweig, C.; Elliott, J.; Deryng, D.; Ruane, A.C.; Müller, C.; Arneth, A.; Boote, K.J.; Folberth, C.; Glotter, M.; Khabarov, N.; et al. Assessing agricultural risks of climate change in the 21st century in a global gridded crop model inter-comparison. Proc. Natl. Acad. Sci. USA 2014, 111, 3268–3273. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Guan, K.; Chen, M.; Lawrence, D.M.; Pokhrel, Y.; Suyker, A.; Arkebauer, T.; Lu, Y. Improving maize growth processes in the community land model: Implementation and evaluation. Agric. For. Meteorol. 2018, 250–251, 64–89. [Google Scholar] [CrossRef]
- FAO. Food and Agriculture Organization of the United Nations (FAO), FAO Statistical Databases. 2022. Available online: http://faostat.fao.org (accessed on 1 December 2023).
- National Bureau of Statistics. National Data Bank (In Chinese). 2023. Available online: http://www.stats.gov.cn/ (accessed on 1 December 2023).
- Estes, L.D.; Beukes, H.; Bradley, B.A.; Debats, S.R.; Oppenheimer, M.; Ruane, A.C.; Schulze, R.; Tadross, M. Projected climate impacts to South African maize and wheat production in 2055: A comparison of empirical and mechanistic modeling approaches. Glob. Chang. Biol. 2013, 19, 3762–3774. [Google Scholar] [CrossRef]
- Lobell, D.B.; Asseng, S. Comparing estimates of climate change impacts from process-based and statistical crop models. Environ. Res. Lett. 2017, 12, 015001. [Google Scholar] [CrossRef]
- Craufurd, P.Q.; Wheeler, T.R. Climate change and the flowering time of annual crops. J. Exp. Bot. 2009, 60, 2529–2539. [Google Scholar] [CrossRef] [PubMed]
- Siebert, S.; Ewert, F. Spatio-temporal patterns of phenological development in Germany in relation to temperature and day length. Agric. For. Meteorol. 2012, 152, 44–57. [Google Scholar] [CrossRef]
- He, L.; Asseng, S.; Zhao, G.; Wu, D.R.; Yang, X.Y.; Zhuang, W.; Jin, N.; Yu, Q. Impacts of recent climate warming, cultivar changes, and crop management on winter wheat phenology across the Loess Plateau of China. Agric. For. Meteorol. 2015, 200, 135–143. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, S.; Zhang, Z.; Rötter, R.P. Maize growing duration was prolonged across China in the past three decades under the combined effects of temperature, agronomic management, and cultivar shift. Glob. Chang. Biol. 2014, 20, 3686–3699. [Google Scholar] [CrossRef]
- Tao, F.; Zhang, Z.; Xiao, D.; Zhang, S.; Rötter, R.P.; Shi, W.; Liu, Y.; Wang, M.; Liu, F.; Zhang, H. Responses of wheat growth and yield to climate change in different climate zones of China, 1981–2009. Agric. For. Meteorol. 2014, 189–190, 91–104. [Google Scholar] [CrossRef]
- van Bussel, L.G.J.; Stehfest, E.; Siebert, S.; Müller, C.; Ewert, F. Simulation of the phenological development of wheat and maize at the global scale. Glob. Ecol. Biogeogr. 2015, 24, 1018–1029. [Google Scholar] [CrossRef]
- Koimbori, J.K.; Wang, S.; Pan, J.; Guo, L.; Li, K. Yield Response of Spring Maize under Future Climate and the Effects of Ad-aptation Measures in Northeast China. Plants 2022, 11, 1634. [Google Scholar] [CrossRef] [PubMed]
- Kucharik, C.J. Contribution of Planting Date Trends to Increased Maize Yields in the Central United States. Agron. J. 2008, 100, 328. [Google Scholar] [CrossRef]
- Twine, T.E.; Kucharik, C.J.; Foley, J.A. Effects of Land Cover Change on the Energy and Water Balance of the Mississippi River Basin. J. Hydrometeorol. 2004, 5, 640–655. [Google Scholar] [CrossRef]
- Xu, F.; Wang, B.; He, C.; Liu, D.L.; Feng, P.; Yao, N.; Zhang, R.; Xu, S.; Xue, J.; Feng, H.; et al. Optimizing Sowing Date and Planting Density Can Mitigate the Impacts of Future Climate on Maize Yield: A Case Study in the Guanzhong Plain of China. Agronomy 2021, 11, 1452. [Google Scholar] [CrossRef]
- Dobor, L.; Barcza, Z.; Hlásny, T.; Árendás, T.; Spitkó, T.; Fodor, N. Crop planting date matters: Estimation methods and effect on future yields. Agric. For. Meteorol. 2016, 223, 103–115. [Google Scholar] [CrossRef]
- Rosenzweig, C.; Parry, M.L. Potential impact of climate change on world food supply. Nature 1994, 367, 133–138. [Google Scholar] [CrossRef]
- Tubiello, F.N.; Donatelli, M.; Rosenzweig, C.; O Stockle, C. Effects of climate change and elevated CO2 on cropping systems: Model predictions at two Italian locations. Eur. J. Agron. 2000, 13, 179–189. [Google Scholar] [CrossRef]
- Waha, K.; van Bussel, L.G.J.; Müller, C.; Bondeau, A. Climate-driven simulation of global crop sowing dates. Glob. Ecol. Biogeogr. 2011, 21, 247–259. [Google Scholar] [CrossRef]
- Deryng, D.; Sacks, W.J.; Barford, C.C.; Ramankutty, N. Simulating the effects of climate and agricultural management practices on global crop yield. Glob. Biogeochem. Cycles 2011, 25. [Google Scholar] [CrossRef]
- Sacks, W.J.; Deryng, D.; Foley, J.A.; Ramankutty, N. Crop planting dates: An analysis of global patterns. Glob. Ecol. Biogeogr. 2010, 19, 607–620. [Google Scholar] [CrossRef]
- Elliott, J.; Müller, C.; Deryng, D.; Chryssanthacopoulos, J.; Boote, K.J.; Büchner, M.; Foster, I.; Glotter, M.; Heinke, J.; Iizumi, T.; et al. The Global Gridded Crop Model Intercomparison: Data and modeling protocols for Phase 1 (v1.0). Geosci. Model Dev. 2015, 8, 261–277. [Google Scholar] [CrossRef]
- Frieler, K.; Lange, S.; Piontek, F.; Reyer, C.P.O.; Schewe, J.; Warszawski, L.; Zhao, F.; Chini, L.; Denvil, S.; Emanuel, K.; et al. Assessing the impacts of 1.5 °C global warming–simulation protocol of the Inter-Sectoral Impact Model Intercomparison Project (ISIMIP2b). Geosci. Model Dev. 2017, 10, 4321–4345. [Google Scholar] [CrossRef]
- Ma, Y.P.; Wang, S.L.; Zhang, L. A Preliminary Study on a Regional Growth Simulation Model of Winter Wheat in North China Based on Scaling-up Approach I. Potential Production Level. ACTA Agron. Sin. 2005, 31, 697–705. [Google Scholar]
- Liu, Z.; Zan, X.L.; Liu, W.; Li, S.; Zhang, X.; Zhu, D. Filling and comparison of the growth period data of agricultural meteorological stations. Resour. Sci. 2019, 41, 176–184. [Google Scholar]
- Yang, Y.; Yang, J.Y.; Li, S.M.; Zhang, X.; Zhu, D. Comparison of spatial interpolation methods for maize growth period. Trans. CSAE 2009, 25, 163–167. [Google Scholar]
- Gerstmann, H.; Doktor, D.; Glaser, C.; Möller, M. PHASE: A geostatistical model for the Kriging-based spatial prediction of crop phe-nology using public phenological and climatological observations. Comput. Electron. Agric. 2016, 127, 726–738. [Google Scholar] [CrossRef]
- Iizumi, T.; Kim, W.; Nishimori, M. Modeling the Global Sowing and Harvesting Windows of Major Crops Around the Year. Geosci. Model Dev. 2019, 11, 99–112. [Google Scholar] [CrossRef]
- Mathison, C.; Deva, C.; Falloon, P.; Challinor, A.J. Estimating sowing and harvest dates based on the Asian summer monsoon. Earth Syst. Dyn. 2018, 9, 563–592. [Google Scholar] [CrossRef]
- Parker, P.S.; Shonkwiler, J.S.; Aurbacher, J. Cause and Consequence in Maize Planting Dates in Germany. J. Agron. Crop. Sci. 2016, 203, 227–240. [Google Scholar] [CrossRef]
- Sheng, M.; Zhu, A.-X.; Rossiter, D.G.; Liu, J. How Much Are Planting Dates for Maize Affected by the Climate Trend? Lessons for Scenario Analysis Using Land Surface Models. Agronomy 2019, 9, 316. [Google Scholar] [CrossRef]
- Gümüşçü, A.; Tenekeci, M.E.; Bilgili, A.V. Estimation of wheat planting date using machine learning algorithms based on available climate data. Sustain. Comput. Inform. Syst. 2019, 28, 100308. [Google Scholar] [CrossRef]
- Sheng, M.; Liu, J.; Zhu, A.-X.; Rossiter, D.G.; Zhu, L.; Peng, G. Evaluation of CLM-Crop for maize growth simulation over Northeast China. Ecol. Model. 2018, 377, 26–34. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Turner, M. How is the Third Law of Geography different? Ann. GIS 2022, 28, 57–67. [Google Scholar] [CrossRef]
- Zhu, A.-X.; Liu, J.; Du, F.; Zhang, S.J.; Qin, C.Z.; Burt, J.; Behrens, T. Scholten. Predictive soil mapping with limited sample data. Eur. J. Soil Sci. 2015, 66, 535–547. [Google Scholar] [CrossRef]
- Liu, F.; Rossiter, D.G.; Song, X.-D.; Zhang, G.-L.; Yang, R.-M.; Zhao, Y.-G.; Li, D.-C.; Ju, B. A similarity-based method for three-dimensional prediction of soil organic matter concentration. Geoderma 2016, 263, 254–263. [Google Scholar] [CrossRef]
- Zhang, X.-J.; Tang, Q.; Pan, M.; Tang, Y. A Long-Term Land Surface Hydrologic Fluxes and States Dataset for China. J. Hydrometeorol. 2014, 15, 2067–2084. [Google Scholar] [CrossRef]
- Gower, J.C. A General Coefficient of Similarity and Some of Its Properties. Biometrics 1971, 27, 857. [Google Scholar] [CrossRef]
- Sarbu, C.; Pop, H.F. Principal component analysis versus fuzzy principal component analysis A case study: The quality of daube water (1985–1996). Talanta 2005, 65, 1215–1220. [Google Scholar] [CrossRef]
- Shrestha, S.; Kazama, F. Assessment of surface water quality using multivariate statistical techniques: A case study of the Fuji river basin, Japan. Environ. Model. Softw. 2007, 22, 464–475. [Google Scholar] [CrossRef]
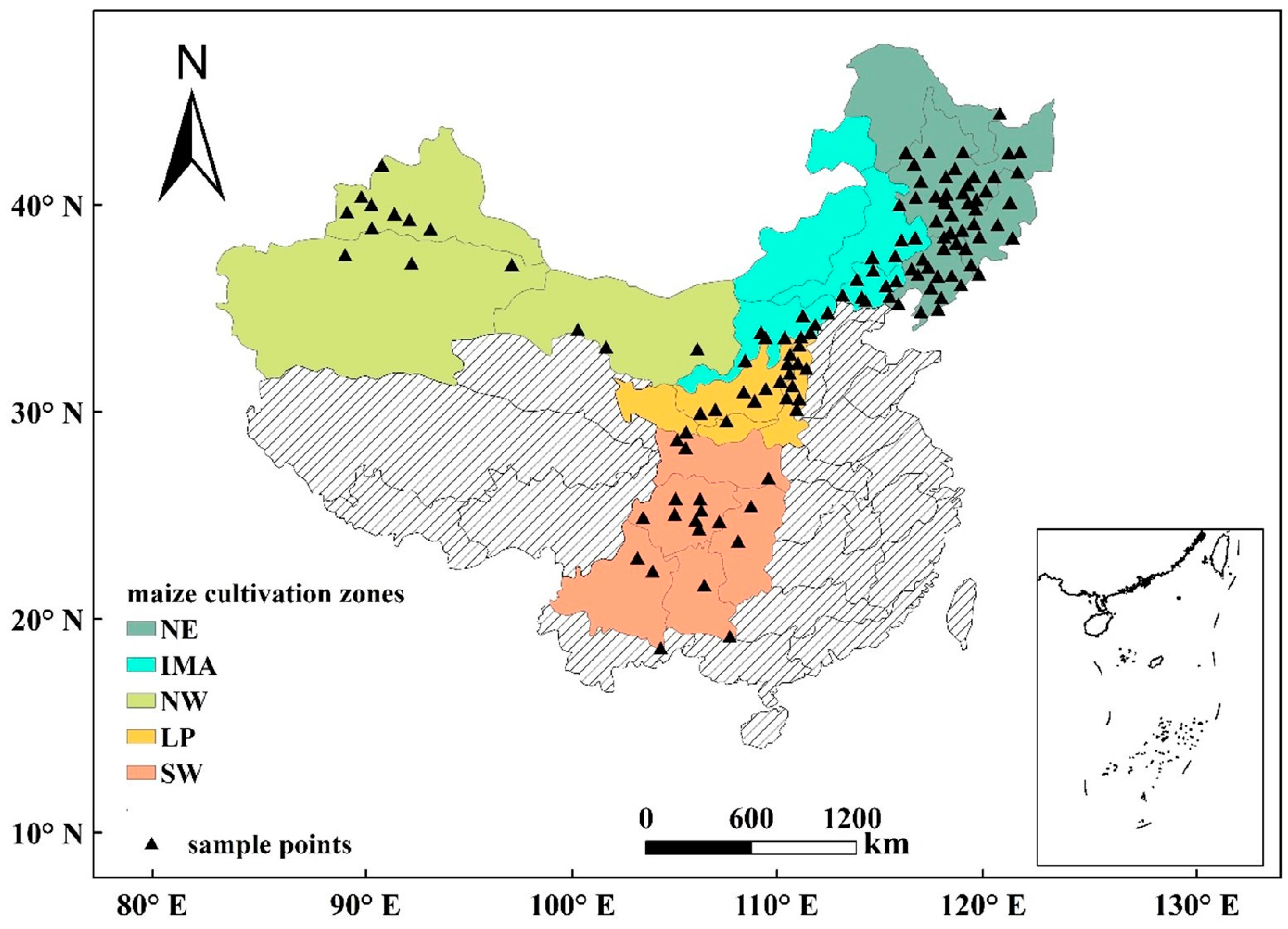
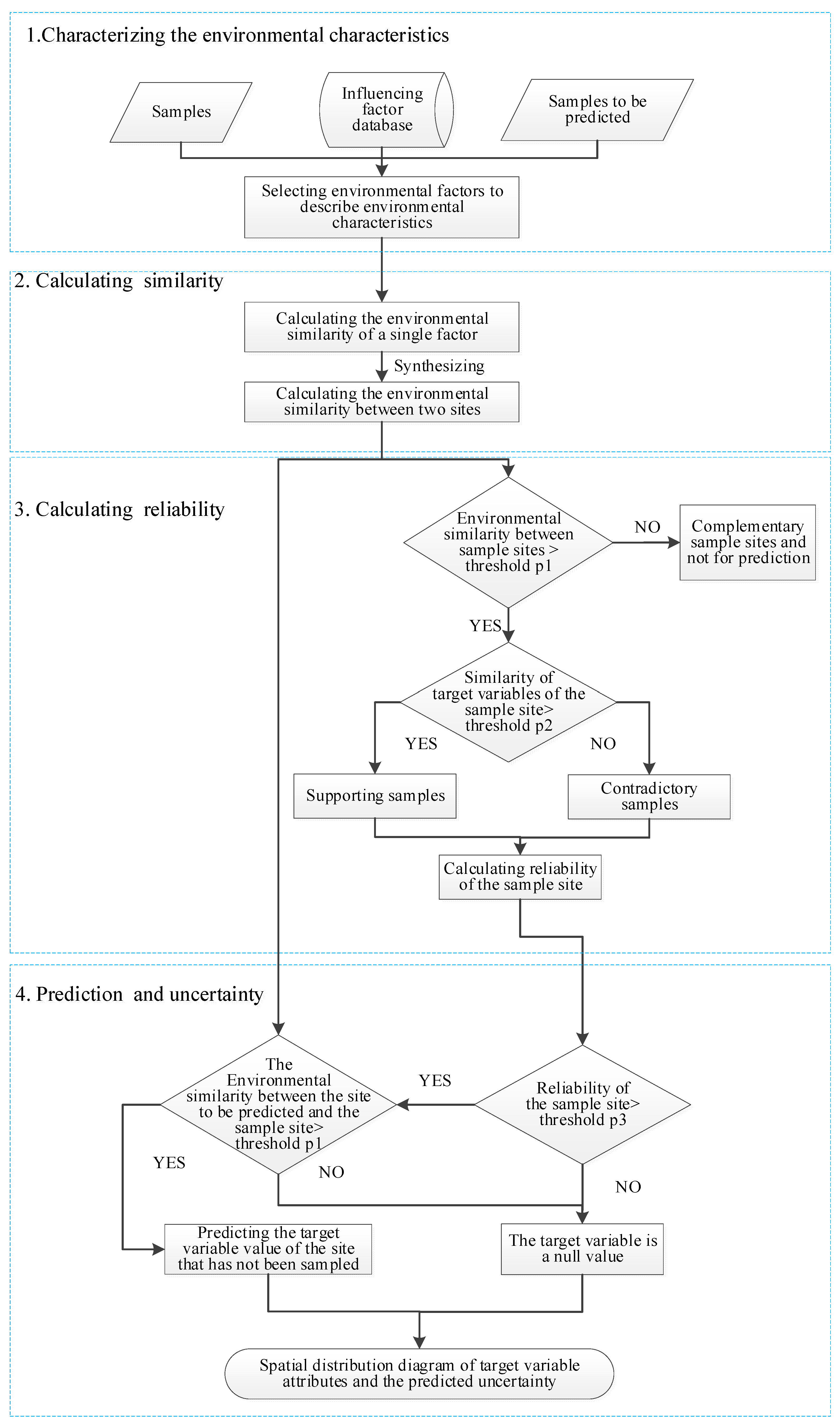
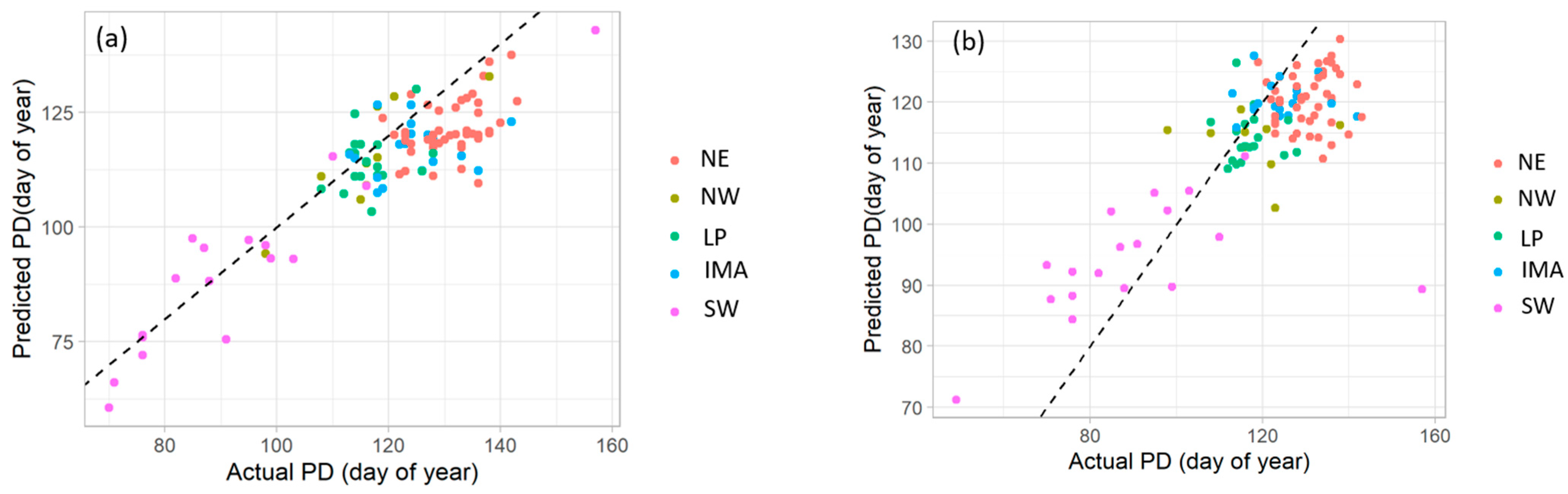
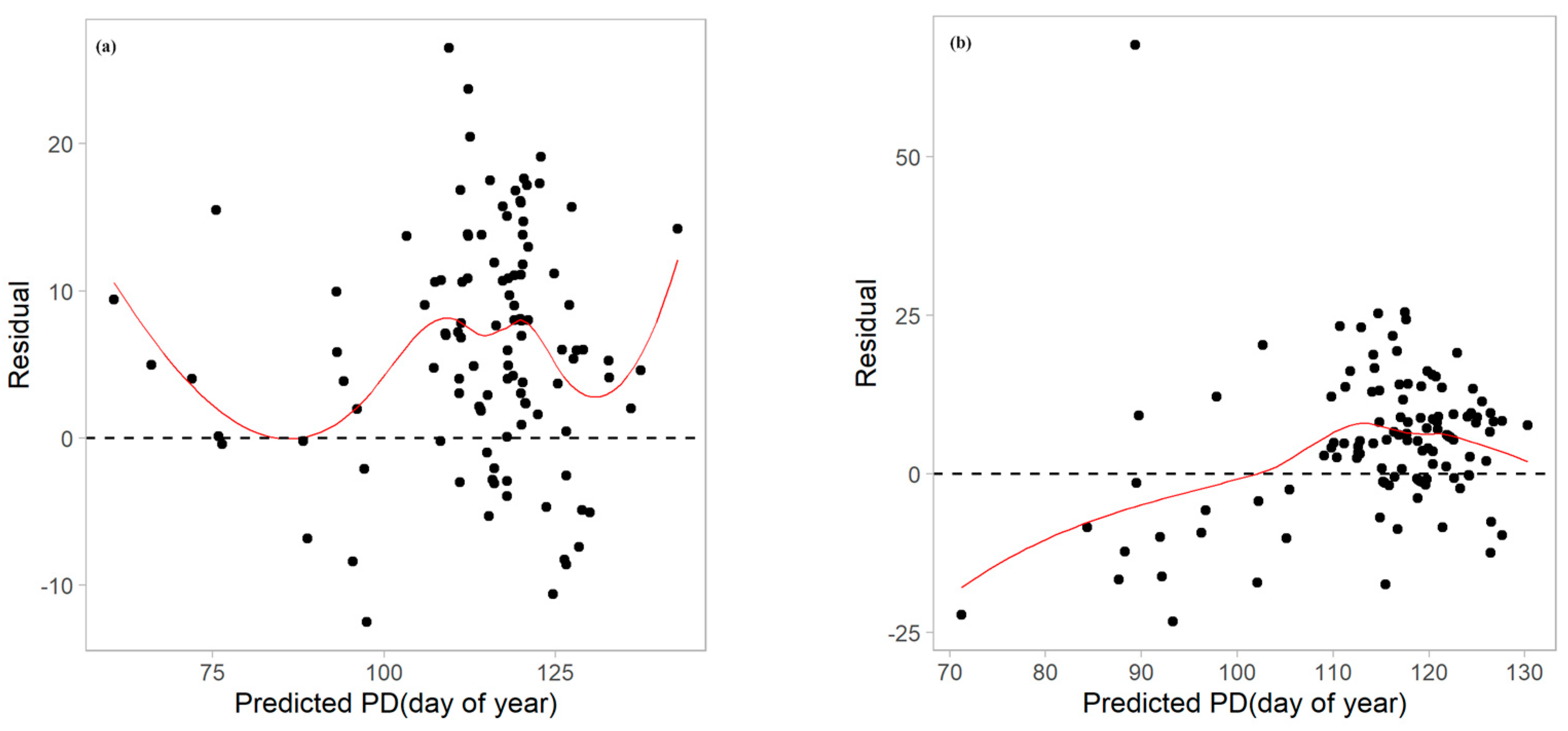
| Min | Med | Mean | Max | SD | |
|---|---|---|---|---|---|
| Training (n = 1404) | 39 | 117 | 115 | 167 | 15.4 |
| Validation (n = 116) | 49 | 123 | 120 | 157 | 17.5 |
| Variables | PC1 | PC2 | PC3 | PC4 | PC5 |
|---|---|---|---|---|---|
| T2 | 0.89 | −0.21 | −0.12 | −0.09 | 0.19 |
| Tmin2 | 0.91 | −0.20 | −0.09 | −0.09 | 0.15 |
| P2 | 0.55 | 0.18 | 0.34 | −0.08 | −0.50 |
| T3 | 0.92 | −0.14 | −0.20 | −0.09 | 0.11 |
| Tmin3 | 0.95 | −0.12 | −0.12 | −0.10 | 0.06 |
| P3 | 0.57 | −0.12 | 0.41 | −0.10 | −0.30 |
| T4 | 0.91 | 0.05 | −0.21 | −0.04 | 0.05 |
| Tmin4 | 0.96 | 0.04 | −0.07 | −0.08 | 0.04 |
| P4 | 0.59 | −0.15 | 0.47 | −0.12 | −0.12 |
| T5 | 0.79 | 0.33 | −0.26 | 0.06 | 0.06 |
| Tmin5 | 0.92 | 0.28 | −0.05 | −0.01 | 0.05 |
| P5 | 0.62 | −0.09 | 0.53 | −0.11 | −0.14 |
| T6 | 0.57 | 0.62 | −0.23 | 0.29 | −0.19 |
| Tmin6 | 0.75 | 0.56 | 0.11 | 0.14 | 0.01 |
| P6 | 0.43 | −0.08 | 0.64 | −0.26 | 0.29 |
| GDD8 | 0.92 | 0.34 | 0.03 | 0.04 | 0.00 |
| GDD10 | 0.90 | 0.39 | 0.03 | 0.06 | −0.01 |
| Lon | −0.44 | 0.21 | 0.58 | 0.15 | 0.48 |
| Lat | −0.87 | 0.35 | 0.04 | 0.12 | −0.16 |
| Elevation | 0.27 | −0.72 | −0.51 | −0.17 | −0.02 |
| RA | 0.47 | −0.53 | 0.18 | 0.62 | 0.00 |
| Slop | 0.51 | −0.47 | 0.09 | 0.66 | 0.03 |
| Eigenvalue | 12.19 | 2.55 | 2.09 | 1.15 | 0.84 |
| % of Variance | 55 | 12 | 10 | 5 | 4 |
| Cumulative % | 55 | 67 | 77 | 82 | 86 |
| Indictors | Methodology for Spatial Prediction of Planting Dates | |
|---|---|---|
| Environmental Similarity Method | Multiple Line Regression Method | |
| RMSE (days) | 10 | 13 |
| MAE (days) | 8 | 9 |
| R2 | 0.64 | 0.48 |
| L5(%) | 37.5 | 31.9 |
| Cultivation Zones | Type of Samples | Number of Samples | Min | Med | Mean | Max | SD |
|---|---|---|---|---|---|---|---|
| NE | training | 651 | 104 | 121 | 122 | 146 | 7.6 |
| validation | 49 | 119 | 131 | 131 | 143 | 5.9 | |
| IAM | training | 211 | 102 | 118 | 119 | 167 | 9.6 |
| validation | 19 | 113 | 124 | 125 | 142 | 7.3 | |
| LP | training | 216 | 98 | 115 | 114 | 140 | 7.0 |
| validation | 19 | 108 | 116 | 117 | 128 | 4.9 | |
| SW | training | 179 | 39 | 90 | 87 | 157 | 21.9 |
| validation | 18 | 49 | 88 | 91 | 157 | 23 | |
| NW | training | 147 | 88 | 113 | 114 | 138 | 9.8 |
| validation | 11 | 98 | 118 | 118 | 138 | 9.8 |
| Zones | Indictors | Regional Scale | National Scale |
|---|---|---|---|
| NE | RMSE (days) | 11 | 11 |
| MAE (days) | 10 | 10 | |
| R2 | 0.16 | 0.16 | |
| L5 (%) | 20.8 | 25 | |
| IAM | RMSE (days) | 10 | 11 |
| MAE (days) | 8 | 9 | |
| R2 | 0.04 | 0.04 | |
| L5 (%) | 52.6 | 36.8 | |
| LP | RMSE (days) | 6 | 7 |
| MAE (days) | 4 | 5 | |
| R2 | 0.02 | 0.09 | |
| L5 (%) | 73.6 | 63.2 | |
| SW | RMSE (days) | 10 | 8 |
| MAE (days) | 7 | 6 | |
| R2 | 0.82 | 0.85 | |
| L5 (%) | 44.4 | 41.2 | |
| NW | RMSE (days) | 8 | 6 |
| MAE (days) | 6 | 5 | |
| R2 | 0.58 | 0.65 | |
| L5 (%) | 63.6 | 44.4 | |
| Mean | RMSE (days) | 10 | 10 |
| MAE (days) | 8 | 8 | |
| R2 | 0.68 | 0.64 | |
| L5 (%) | 42.6 | 37.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sheng, M.; Zhu, A.-X.; Ma, T.; Fei, X.; Ren, Z.; Deng, X. Estimation of Spring Maize Planting Dates in China Using the Environmental Similarity Method. Agronomy 2024, 14, 97. https://doi.org/10.3390/agronomy14010097
Sheng M, Zhu A-X, Ma T, Fei X, Ren Z, Deng X. Estimation of Spring Maize Planting Dates in China Using the Environmental Similarity Method. Agronomy. 2024; 14(1):97. https://doi.org/10.3390/agronomy14010097
Chicago/Turabian StyleSheng, Meiling, A-Xing Zhu, Tianwu Ma, Xufeng Fei, Zhouqiao Ren, and Xunfei Deng. 2024. "Estimation of Spring Maize Planting Dates in China Using the Environmental Similarity Method" Agronomy 14, no. 1: 97. https://doi.org/10.3390/agronomy14010097
APA StyleSheng, M., Zhu, A.-X., Ma, T., Fei, X., Ren, Z., & Deng, X. (2024). Estimation of Spring Maize Planting Dates in China Using the Environmental Similarity Method. Agronomy, 14(1), 97. https://doi.org/10.3390/agronomy14010097








