Estimation of Canopy Water Content by Integrating Hyperspectral and Thermal Imagery in Winter Wheat Fields
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Conditions and Field Design
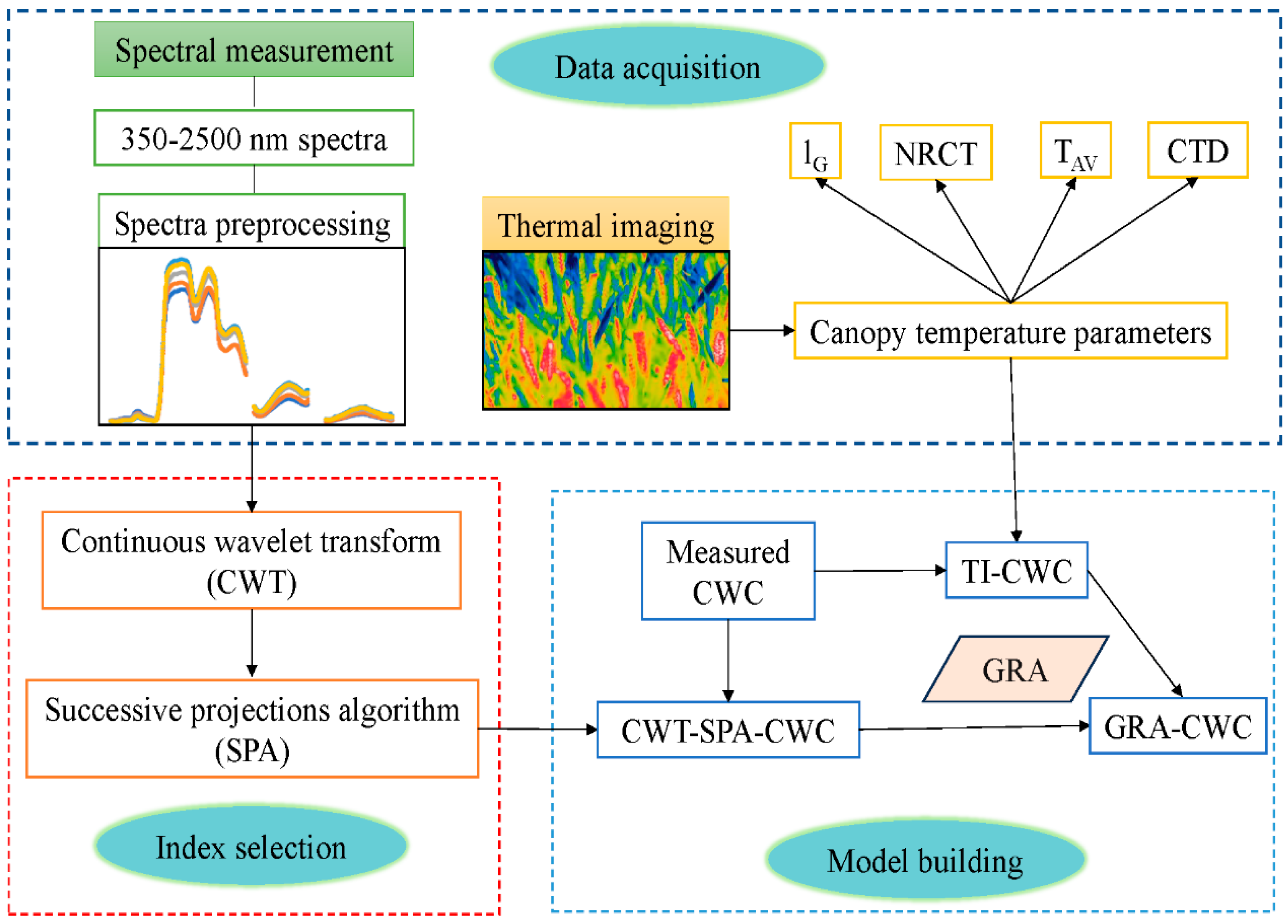
2.2. Data Measurements
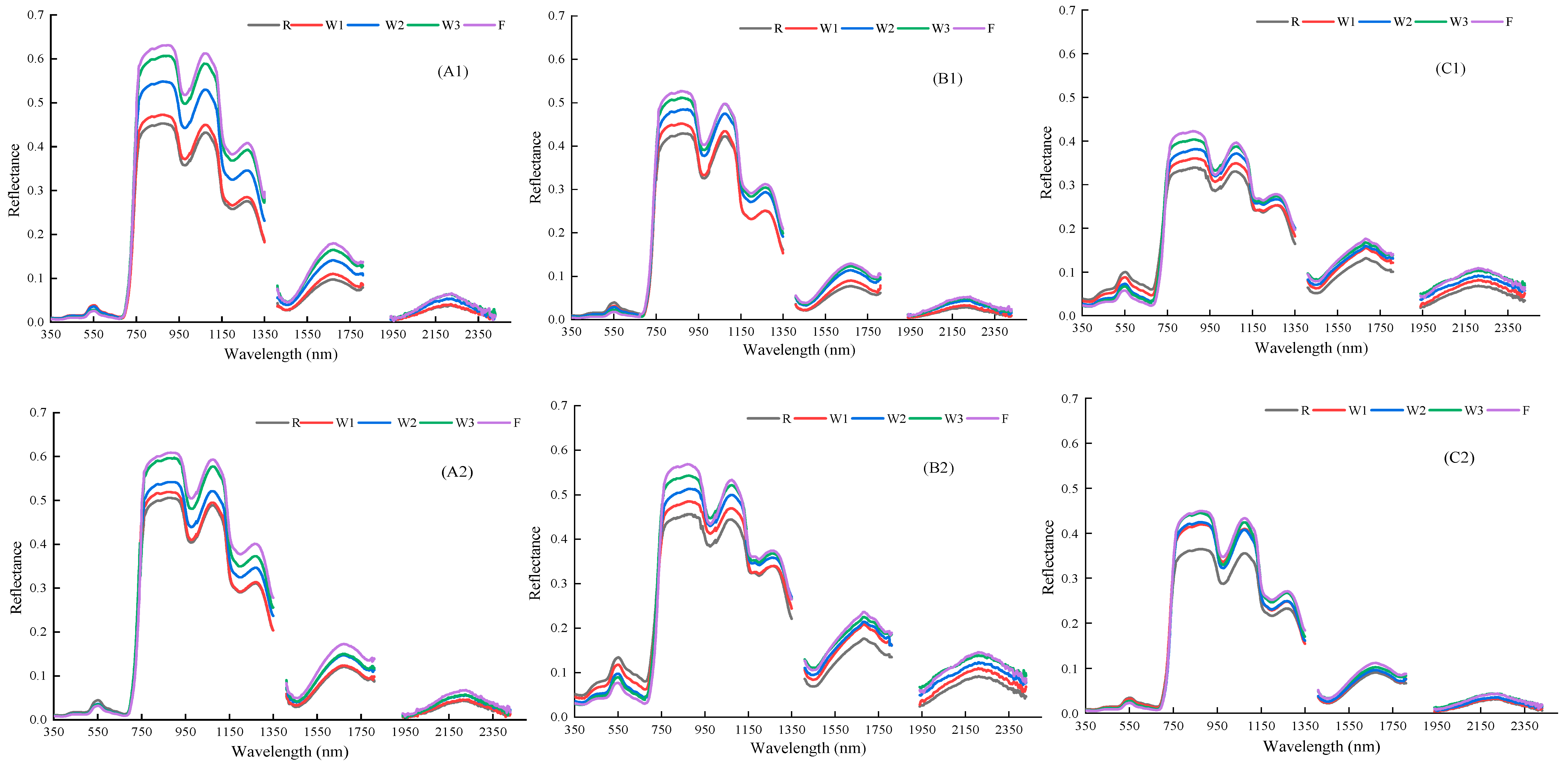
2.2.1. Measurement of Canopy Hyperspectral Data
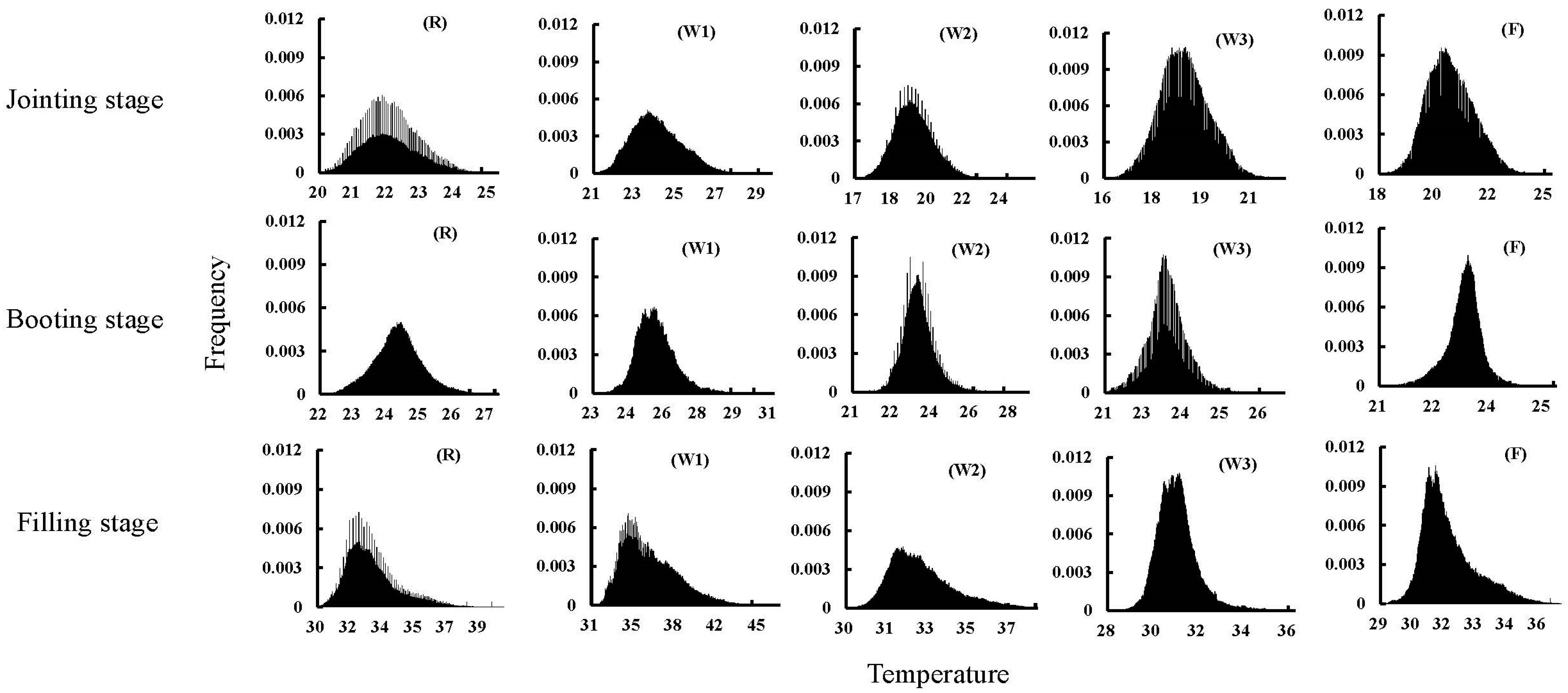
2.2.2. Acquisition of Canopy Temperature Parameters
2.2.3. Determination of Canopy Water Content
2.2.4. Continuous Wavelet Transform
2.2.5. Successive Projection Algorithm
2.2.6. GRA Data Fusion Algorithm
2.3. Data Analysis
3. Results
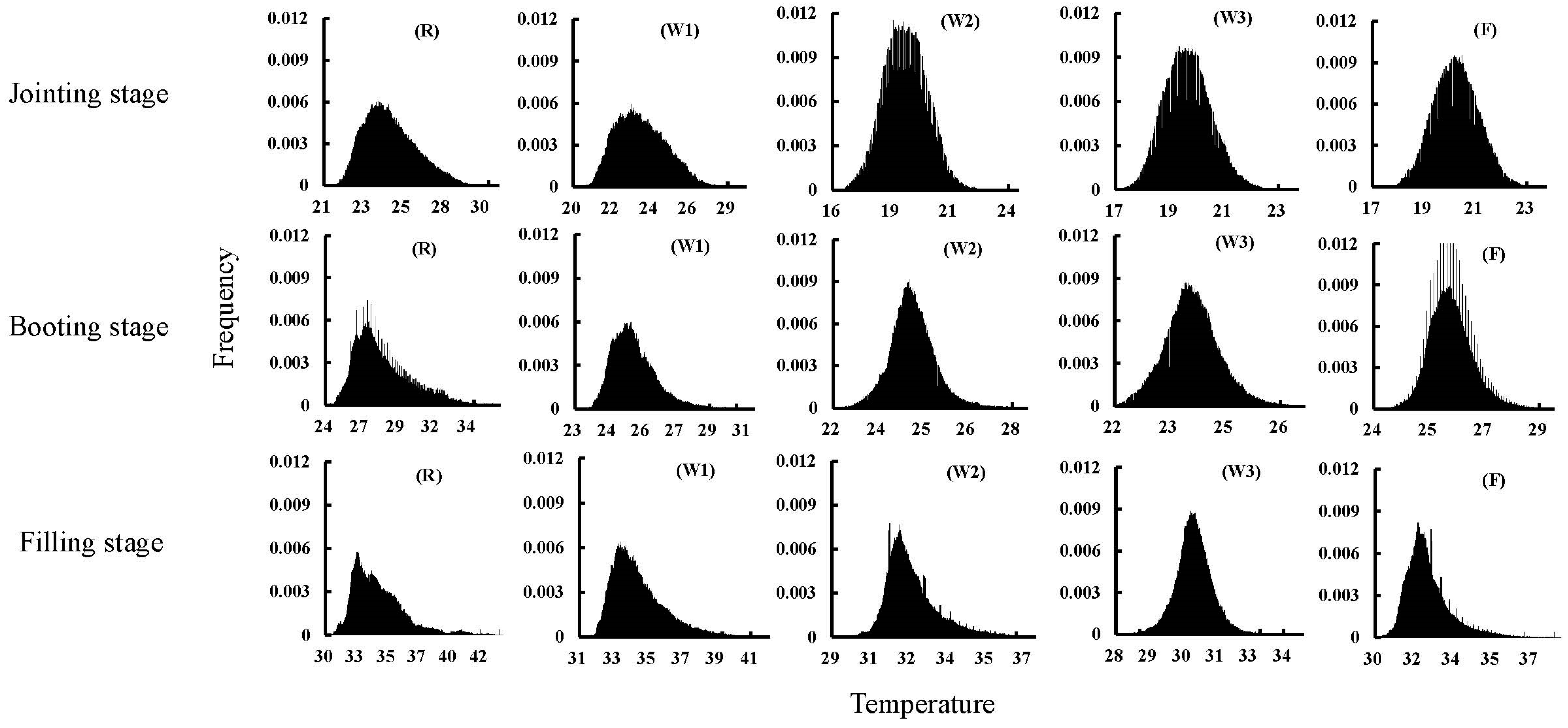
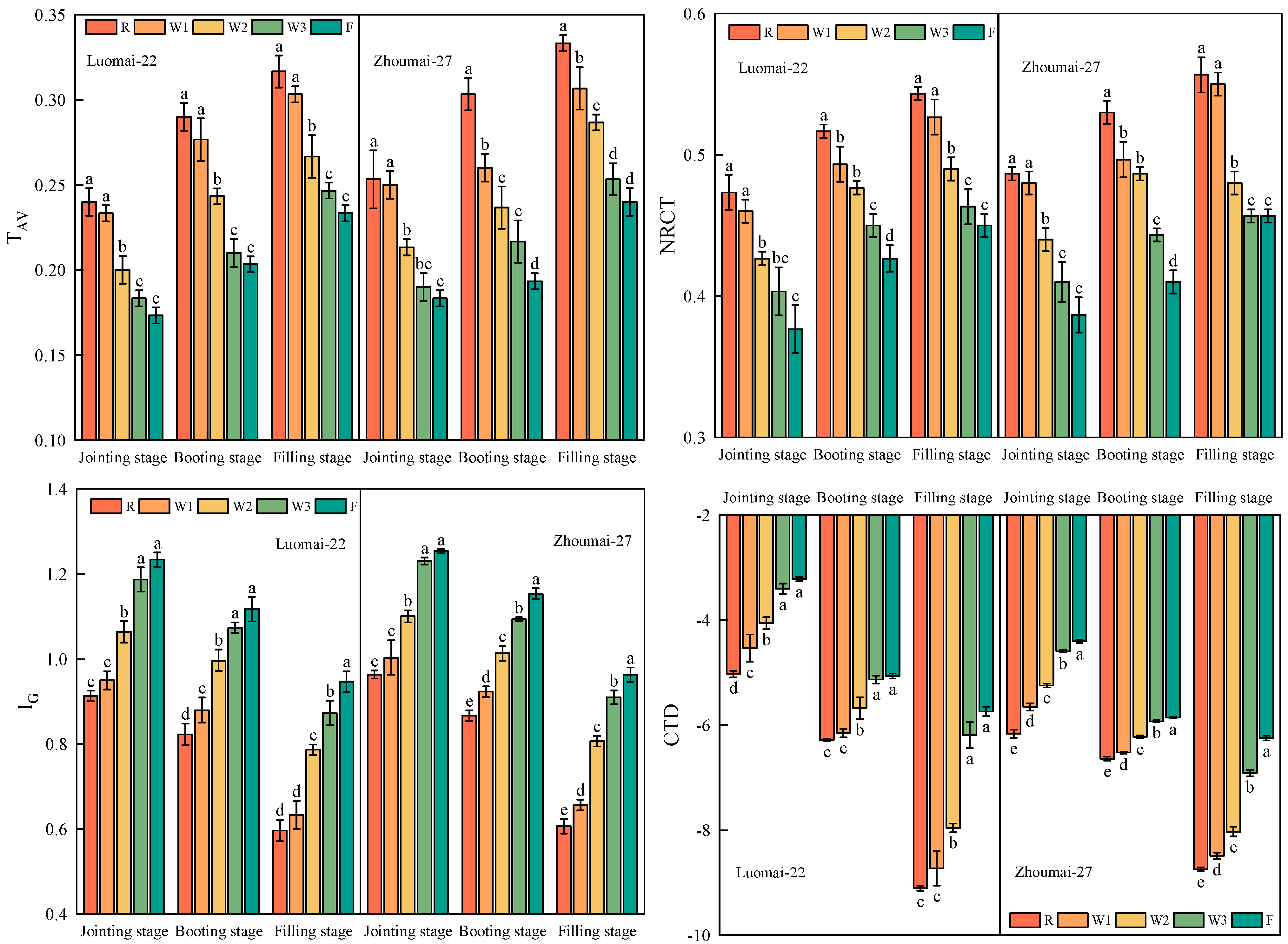
3.1. Effect of Different Water Treatments on Canopy Temperature Parameters in Winter Wheat
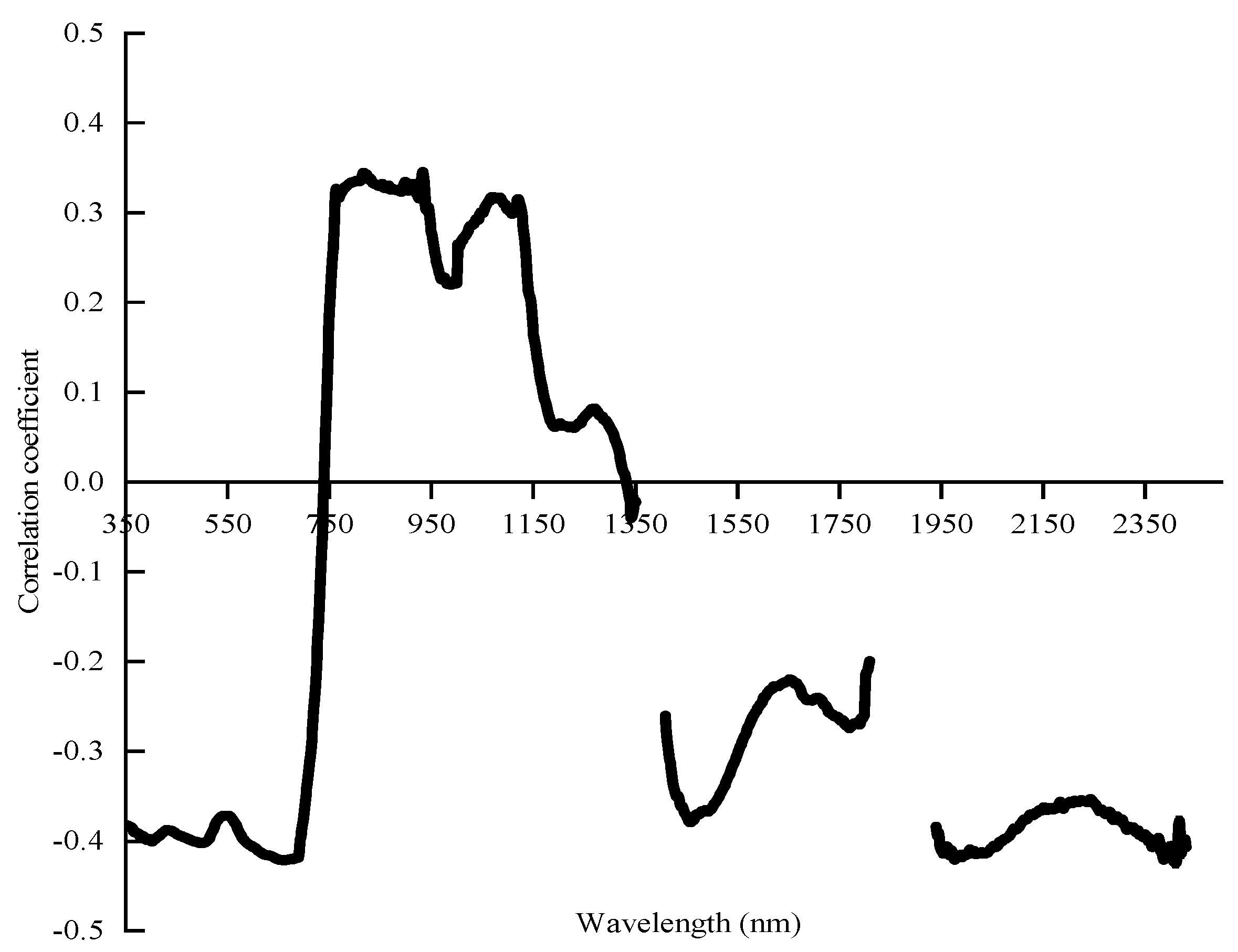
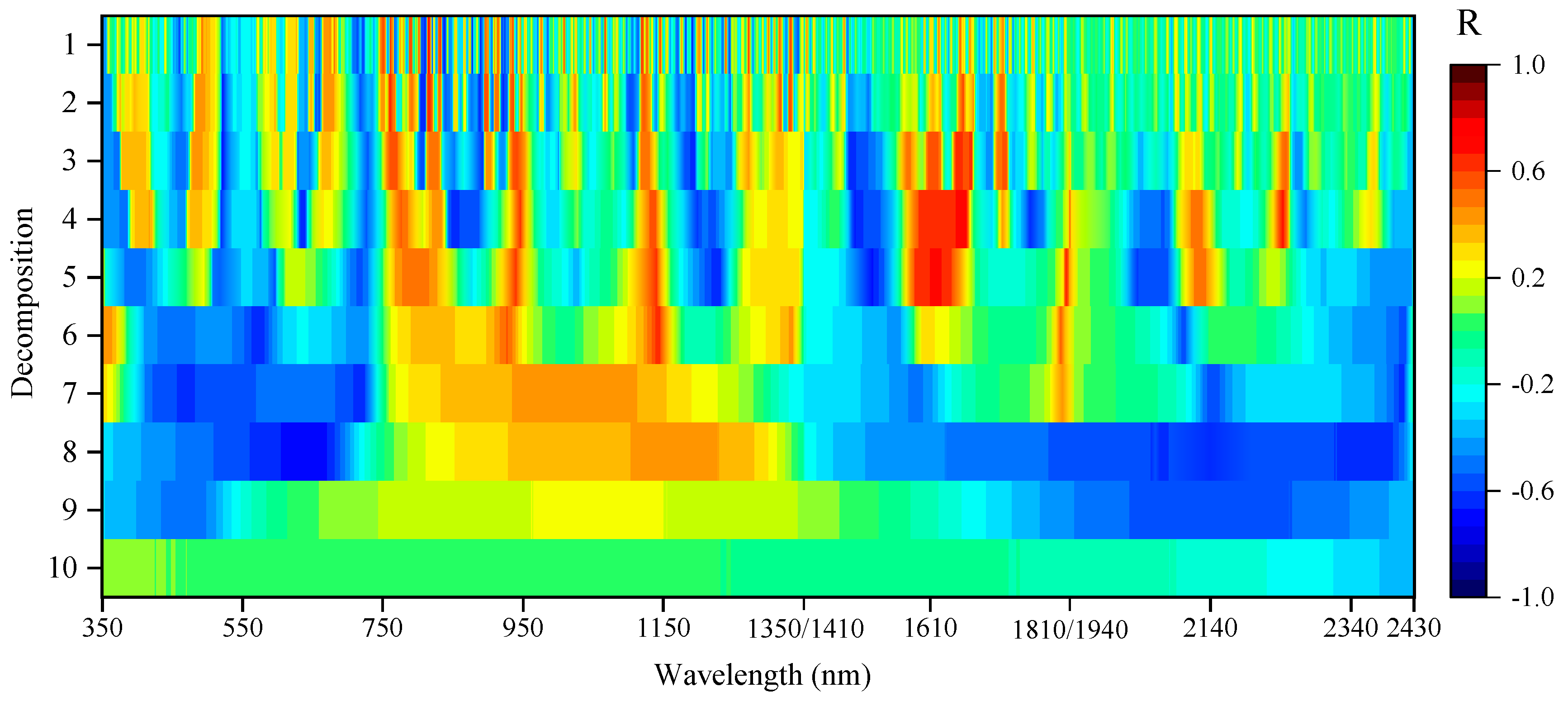
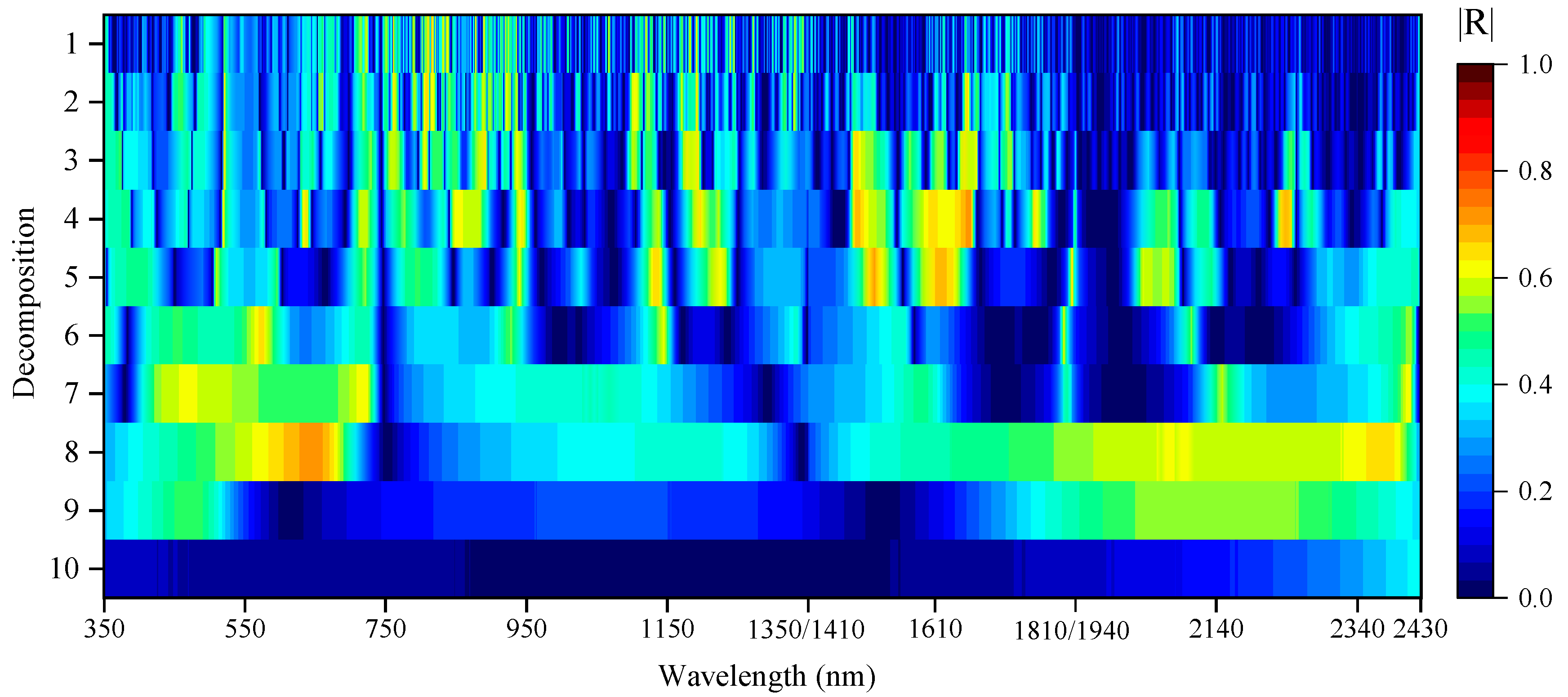
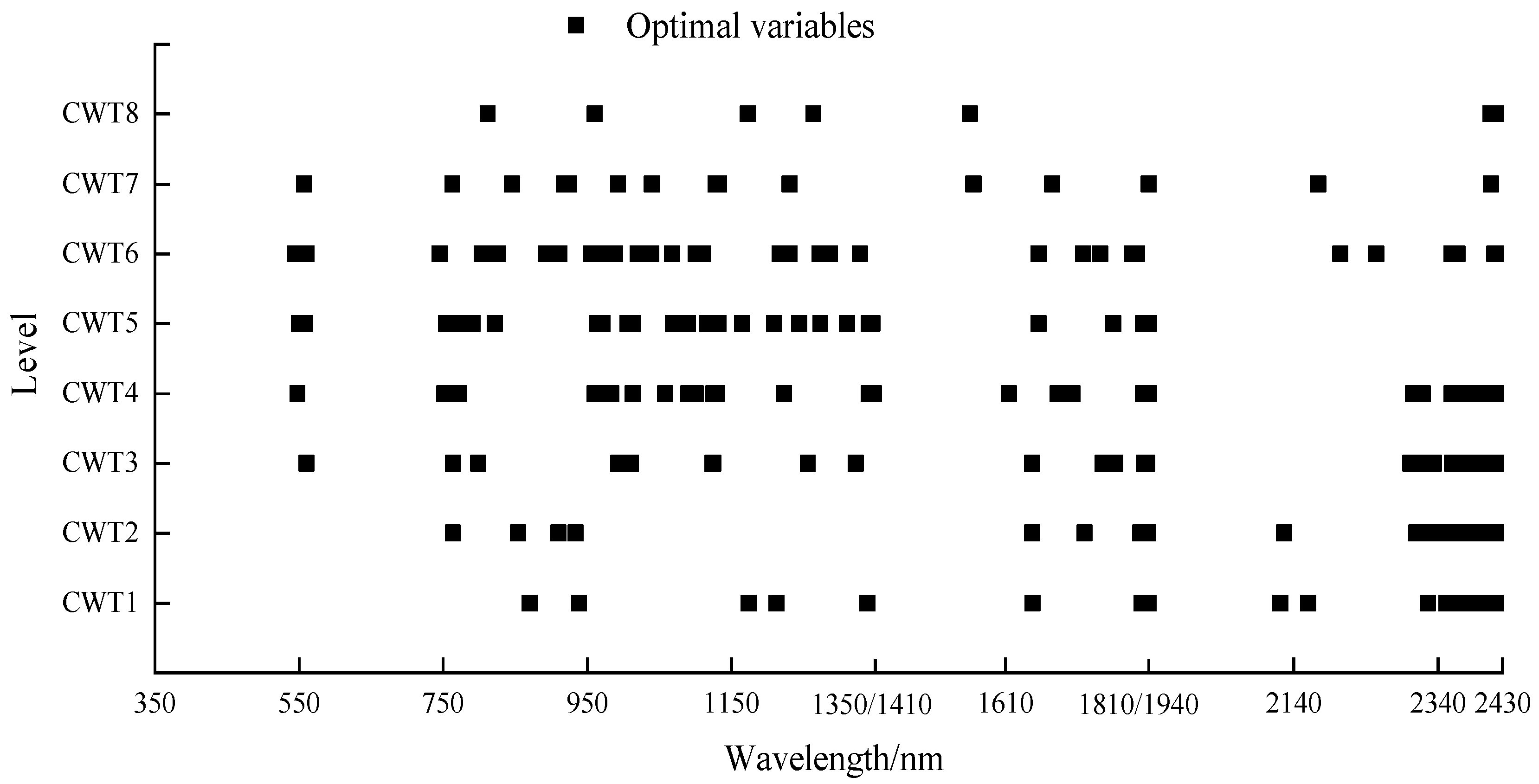
3.2. Sensitive Band Screening of CWC Based on CWT and SPA
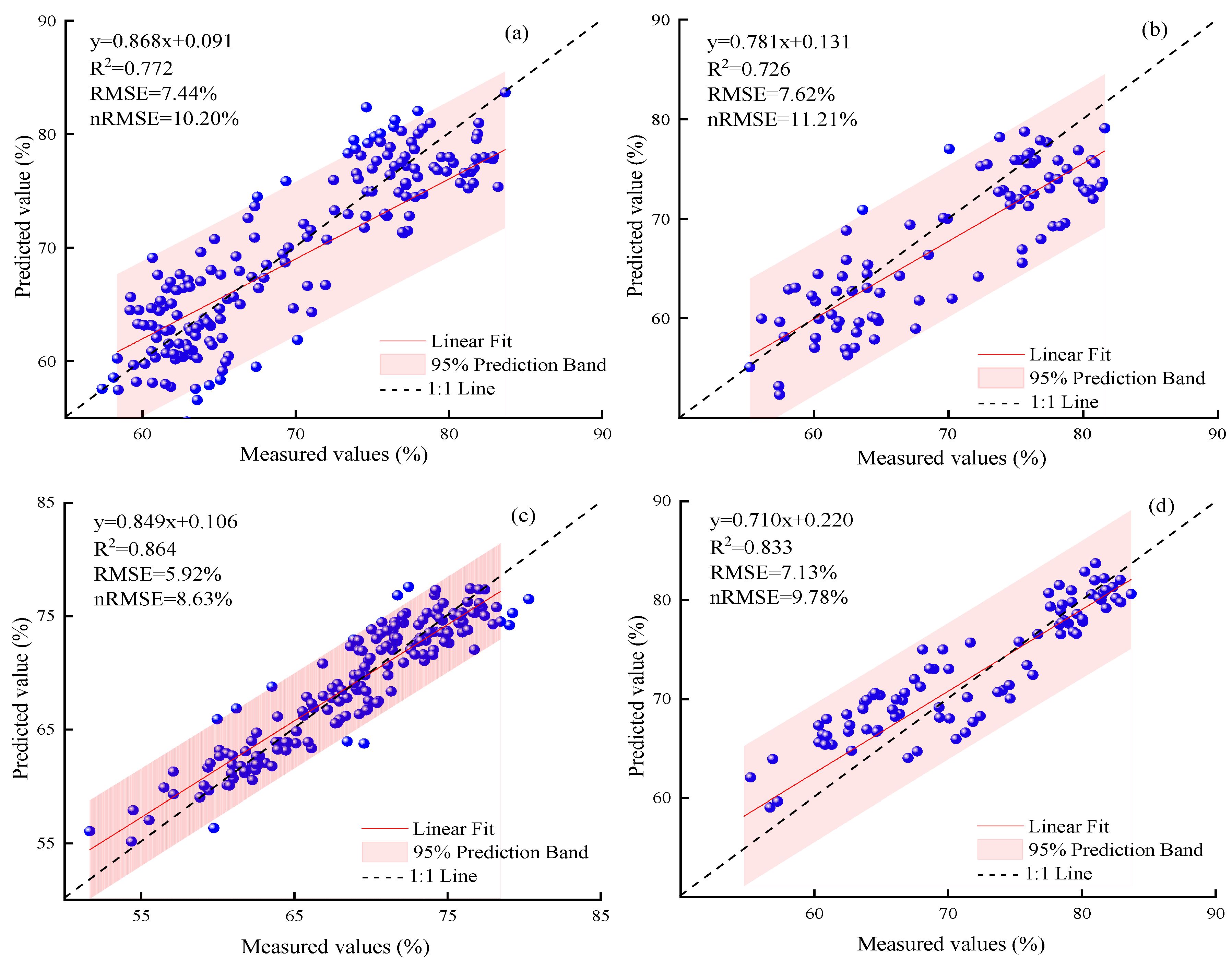
3.3. Construction of a Fusion Model Based on Hyperspectral and Thermal Imaging Data
4. Discussion
4.1. Effect of Different Water Treatments on Canopy Temperature and Spectral Reflectance in Winter Wheat
4.2. Combining CWT and SPA to Screen Hyperspectral Water-Sensitive Bands
4.3. The GRA Improves the Accuracy of the CWC Prediction Model
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fang, Y.J.; Xiong, L.Z. General mechanisms of drought response and their application in drought resistance improvement in plants. Cell. Mol. Life Sci. 2015, 72, 673–689. [Google Scholar] [CrossRef] [PubMed]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal Drought Prediction: Advances, Challenges, and Future Prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef]
- He, B.; Lü, A.F.; Wu, J.J.; Zhao, L.; Liu, M. Drought hazard assessment and spatial characteristics analysis in China. J. Geogr. Sci. 2011, 21, 235–249. [Google Scholar] [CrossRef]
- Sun, H.Y.; Liu, C.M.; Zhang, X.Y.; Shen, Y.J.; Zhang, Y.Q. Effects of irrigation on water balance, yield and WUE of winter wheat in the North China Plain. Agric. Water Manag. 2006, 85, 211–218. [Google Scholar] [CrossRef]
- Jha, S.K.; Gao, Y.; Liu, H.; Huang, Z.D.; Wang, G.S.; Liang, Y.P.; Duan, A.W. Root development and water uptake in winter wheat under different irrigation methods and scheduling for North China. Agric. Water Manag. 2017, 182, 139–150. [Google Scholar] [CrossRef]
- Liu, X.F.; Pan, Y.Z.; Zhu, X.F.; Yang, T.T.; Bai, J.J.; Sun, Z.L. Drought evolution and its impact on the crop yield in the North China Plain. J. Hydrol. 2018, 564, 984–996. [Google Scholar] [CrossRef]
- Sallam, A.; Alqudah, A.M.; Dawood, M.F.A.; Baenziger, P.S.; Börner, A. Drought Stress Tolerance in Wheat and Barley: Advances in Physiology, Breeding and Genetics Research. Int. J. Mol. Sci. 2019, 20, 3137. [Google Scholar] [CrossRef]
- Jones, H.G.; Serraj, R.; Loveys, B.R.; Xiong, L.Z.; Wheaton, A.; Price, A.H. Thermal infrared imaging of crop canopies for the remote diagnosis and quantification of plant responses to water stress in the field. Funct. Plant Biol. 2009, 36, 978–989. [Google Scholar] [CrossRef]
- Wedeking, R.; Mahlein, A.-K.; Steiner, U.; Oerke, E.-C.; Goldbach, H.E.; Wimmer, M.A. Osmotic adjustment of young sugar beets (Beta vulgaris) under progressive drought stress and subsequent rewatering assessed by metabolite analysis and infrared thermography. Funct. Plant Biol. 2017, 44, 119–133. [Google Scholar] [CrossRef]
- DeJonge, K.C.; Taghvaeian, S.; Trout, T.J.; Comas, L.H. Comparison of canopy temperature-based water stress indices for maize. Agric. Water Manag. 2015, 156, 51–62. [Google Scholar] [CrossRef]
- Qi, Z.; Ma, L.; Bausch, W.C.; Trout, T.J.; Ahuja, L.R.; Flerchinger, G.N.; Fang, Q.X. Simulating Maize Production, Water and Surface Energy Balance, Canopy Temperature, and Water Stress under Full and Deficit Irrigation. Trans. Asabe 2016, 59, 623–633. [Google Scholar]
- Grant, O.M.; Tronina, L.; Jones, H.G.; Chaves, M.M. Exploring thermal imaging variables for the detection of stress responses in grapevine under different irrigation regimes. J. Exp. Bot. 2007, 58, 815–825. [Google Scholar] [CrossRef]
- Mangus, D.L.; Sharda, A.; Zhang, N.Q. Development and evaluation of thermal infrared imaging system for high spatial and temporal resolution crop water stress monitoring of corn within a greenhouse. Comput. Electron. Agric. 2016, 121, 149–159. [Google Scholar] [CrossRef]
- Kurunc, A.; Tezcan, N.Y.; Bimurzayev, N. Determination of Water Stress in Wheat Crops by Thermal Images Under Mediterranean Conditions. Commun. Soil Sci. Plant Anal. 2023, 54, 1713–1726. [Google Scholar] [CrossRef]
- Banerjee, K.; Krishnan, P.; Das, B. Thermal imaging and multivariate techniques for characterizing and screening wheat genotypes under water stress condition. Ecol. Indic. 2020, 119, 106829. [Google Scholar] [CrossRef]
- Tavares, T.R.; Molin, J.P.; Javadi, S.H.; de Carvalho, H.W.P.; Mouazen, A.M. Combined Use of Vis-NIR and XRF Sensors for Tropical Soil Fertility Analysis: Assessing Different Data Fusion Approaches. Sensors 2021, 21, 148. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; González-Dugo, V.; Berni, J.A.J. Fluorescence, temperature and narrow-band indices acquired from a UAV platform for water stress detection using a micro-hyperspectral imager and a thermal camera. Remote Sens. Environ. 2012, 117, 322–337. [Google Scholar] [CrossRef]
- Sims, D.A.; Gamon, J.A. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance: A comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Wang, Q.Y.; Zhao, Y.L.; Yang, F.F.; Liu, T.; Xiao, W.; Sun, H.Y. Simulating Heat Stress of Coal Gangue Spontaneous Combustion on Vegetation Using Alfalfa Leaf Water Content Spectral Features as Indicators. Remote Sens. 2021, 13, 2634. [Google Scholar] [CrossRef]
- Galvao, R.K.H.; Araújo, M.C.U.; Fragoso, W.D.; Silva, E.C.; José, G.E.; Soares, S.F.C.; Paiva, H.M. A variable elimination method to improve the parsimony of MLR models using the successive projections algorithm. Chemom. Intell. Lab. Syst. 2008, 92, 83–91. [Google Scholar] [CrossRef]
- Huang, L.S.; Zhang, H.S.; Ruan, C.; Huang, W.J.; Hu, T.G.; Zhao, J.L. Detection of scab in wheat ears using in situ hyperspectral data and support vector machine optimized by genetic algorithm. Int. J. Agric. Biol. Eng. 2020, 13, 182–188. [Google Scholar] [CrossRef]
- Shi, B.; Yuan, Y.F.; Zhuang, T.X.; Xu, X.; Schmidhalter, U.; Ata-Ui-Karim, S.T.; Zhao, B.; Liu, X.J.; Tian, Y.C.; Zhu, Y.; et al. Improving water status prediction of winter wheat using multi-source data with machine learning. Eur. J. Agron. 2022, 139, 126548. [Google Scholar] [CrossRef]
- Sudu, B.; Rong, G.Z.; Guga, S.; Li, K.W.; Zhi, F.; Guo, Y.; Zhang, J.Q.; Bao, Y.L. Retrieving SPAD Values of Summer Maize Using UAV Hyperspectral Data Based on Multiple Machine Learning Algorithm. Remote Sens. 2022, 14, 5407. [Google Scholar] [CrossRef]
- Wang, L.S.; Wang, R.J.; Lu, C.P.; Wang, J.; Huang, W. Rapid determination of moisture content in compound fertilizer using visible and near infrared spectroscopy combined with chemometrics. Infrared Phys. Technol. 2019, 102, 6–20. [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, G.A.; Feng, J.; Calvo-Polanco, M. Continuous wavelet analysis for the detection of green attack damage due to mountain pine beetle infestation. Remote Sens. Environ. 2010, 114, 899–910. [Google Scholar] [CrossRef]
- Peng, J.; Shen, H.; He, S.W.; Wu, J.S. Soil moisture retrieving using hyperspectral data with the application of wavelet analysis. Environ. Earth Sci. 2013, 69, 279–288. [Google Scholar] [CrossRef]
- Gu, X.H.; Wang, Y.C.; Sun, Q.; Yang, G.J.; Zhang, C. Hyperspectral inversion of soil organic matter content in cultivated land based on wavelet transform. Comput. Electron. Agric. 2019, 167, 105053. [Google Scholar] [CrossRef]
- Cheng, T.; Riaño, D.; Ustin, S.L. Detecting diurnal and seasonal variation in canopy water content of nut tree orchards from airborne imaging spectroscopy data using continuous wavelet analysis. Remote Sens. Environ. 2014, 143, 39–53. [Google Scholar] [CrossRef]
- Cheng, T.; Rivard, B.; Sánchez-Azofeifa, A. Spectroscopic determination of leaf water content using continuous wavelet analysis. Remote Sens. Environ. 2011, 115, 659–670. [Google Scholar] [CrossRef]
- Li, J.B.; Huang, W.Q.; Chen, L.P.; Fan, S.X.; Zhang, B.H.; Guo, Z.M.; Zhao, C.J. Variable Selection in Visible and Near-Infrared Spectral Analysis for Noninvasive Determination of Soluble Solids Content of ‘Ya’ Pear. Food Anal. Methods 2014, 7, 1891–1902. [Google Scholar] [CrossRef]
- Huang, X.Y.; Wang, X.M.; Baishan, K.; An, B.S. Hyperspectral Estimation of Soil Organic Carbon Content Based on Continuous Wavelet Transform and Successive Projection Algorithm in Arid Area of Xinjiang, China. Sustainability 2023, 15, 2587. [Google Scholar] [CrossRef]
- Nawar, S.; Corstanje, R.; Halcro, G.; Mulla, D.; Mouazen, A.M. Delineation of Soil Management Zones for Variable-Rate Fertilization: A Review. Adv. Agron. 2017, 143, 175–245. [Google Scholar]
- Elsayed, S.; Elhoweity, M.; Ibrahim, H.H.; Dewir, Y.H.; Migdadi, H.M.; Schmidhalter, U. Thermal imaging and passive reflectance sensing to estimate the water status and grain yield of wheat under different irrigation regimes. Agric. Water Manag. 2017, 189, 98–110. [Google Scholar] [CrossRef]
- Wang, J.J.; Lou, Y.; Wang, W.T.; Liu, S.Y.; Zhang, H.H.; Hui, X.; Wang, Y.L.; Yan, H.J.; Maes, W.H. A robust model for diagnosing water stress of winter wheat by combining UAV multispectral and thermal remote sensing. Agric. Water Manag. 2024, 291, 108616. [Google Scholar] [CrossRef]
- Castanedo, F. A Review of Data Fusion Techniques. Sci. World J. 2013, 2013, 704504. [Google Scholar] [CrossRef]
- Xu, D.Y.; Chen, S.C.; Rossel, R.A.V.; Biswas, A.; Li, S.; Zhou, Y.; Shi, Z. X-ray fluorescence and visible near infrared sensor fusion for predicting soil chromium content. Geoderma 2019, 352, 61–69. [Google Scholar] [CrossRef]
- Granger, C.W.J.; Ramanathan, R.J.J.o.F. Improved Methods of Combining Forecasts. J. Forecast. 1984, 3, 197–204. [Google Scholar] [CrossRef]
- O’Rourke, S.M.; Stockmann, U.; Holden, N.M.; McBratney, A.B.; Minasny, B. An assessment of model averaging to improve predictive power of portable vis-NIR and XRF for the determination of agronomic soil properties. Geoderma 2016, 279, 31–44. [Google Scholar] [CrossRef]
- Shi, X.Y.; Song, J.H.; Wang, H.J.; Lv, X.; Zhu, Y.Q.; Zhang, W.X.; Bu, W.Q.; Zeng, L.Y. Improving soil organic matter estimation accuracy by combining optimal spectral preprocessing and feature selection methods based on pXRF and vis-NIR data fusion. Geoderma 2023, 430, 116301. [Google Scholar] [CrossRef]
- Pancorbo, J.L.; Camino, C.; Alonso-Ayuso, M.; Sereno, R.; Gonzalez-Fernandez, I.; Gabriel, J.; Zarco-Tejada, P.; Quemada, M. Simultaneous assessment of nitrogen and water status in winter wheat using hyperspectral and thermal sensors. Eur. J. Agron. 2021, 127, 126287. [Google Scholar] [CrossRef]
- Purushothaman, R.; Thudi, M.; Krishnamurthy, L.; Upadhyaya, H.D.; Kashiwagi, J.; Gowda, C.L.L.; Varshney, R.K. Association of mid-reproductive stage canopy temperature depression with the molecular markers and grain yields of chickpea (Cicer arietinum L.) germplasm under terminal drought. Field Crops Res. 2015, 174, 1–11. [Google Scholar] [CrossRef]
- Elsayed, S.; Rischbeck, P.; Schmidhalter, U. Comparing the performance of active and passive reflectance sensors to assess the normalized relative canopy temperature and grain yield of drought-stressed barley cultivars. Field Crops Res. 2015, 177, 148–160. [Google Scholar] [CrossRef]
- Jones, H.G. Use of infrared thermometry for estimation of stomatal conductance as a possible aid to irrigation scheduling. Agric. For. Meteorol. 1999, 95, 139–149. [Google Scholar] [CrossRef]
- Zhao, J.; Li, H.; Chen, C.; Pang, Y.Y.; Zhu, X.Q. Detection of Water Content in Lettuce Canopies Based on Hyperspectral Imaging Technology under Outdoor Conditions. Agriculture 2022, 12, 1796. [Google Scholar] [CrossRef]
- Lakshmanan, M.K.; Boelt, B.; Gislum, R. A chemometric method for the viability analysis of spinach seeds by near infrared spectroscopy with variable selection using successive projections algorithm. J. Near Infrared Spectrosc. 2023, 31, 24–32. [Google Scholar] [CrossRef]
- Elvanidi, A.; Katsoulas, N.; Ferentinos, K.P.; Bartzanas, T.; Kittas, C. Hyperspectral machine vision as a tool for water stress severity assessment in soilless tomato crop. Biosyst. Eng. 2018, 165, 25–35. [Google Scholar] [CrossRef]
- Krishna, G.; Rabi, N.; Singh, P.; Bajpai, V.; Patra, H.; Kumar, S.; Dandapani, R.; Gupta, V.K.; Viswanathan, C.; Ahmad, T.; et al. Comparison of various modelling approaches for water deficit stress monitoring in rice crop through hyperspectral remote sensing. Agric. Water Manag. 2019, 213, 231–244. [Google Scholar] [CrossRef]
- Yi, Q.X.; Bao, A.M.; Wang, Q.; Zhao, J. Estimation of leaf water content in cotton by means of hyperspectral indices. Comput. Electron. Agric. 2013, 90, 144–151. [Google Scholar] [CrossRef]
- Chandel, A.K.; Khot, L.R.; Yu, L.X. Alfalfa (Medicago sativa L.) crop vigor and yield characterization using high-resolution aerial multispectral and thermal infrared imaging technique. Comput. Electron. Agric. 2021, 182, 105999. [Google Scholar] [CrossRef]
- Yu, M.H.; Ding, G.D.; Gao, G.L.; Zhao, Y.Y.; Yan, L.; Sai, K. Using Plant Temperature to Evaluate the Response of Stomatal Conductance to Soil Moisture Deficit. Forests 2015, 6, 3748–3762. [Google Scholar] [CrossRef]
- Feng, Z.H.; Song, L.; Duan, J.Z.; He, L.; Zhang, Y.Y.; Wei, Y.K.; Feng, W. Monitoring Wheat Powdery Mildew Based on Hyperspectral, Thermal Infrared, and RGB Image Data Fusion. Sensors 2022, 22, 31. [Google Scholar] [CrossRef] [PubMed]
- Pandey, B.R.; Burton, W.A.; Salisbury, P.A.; Nicolas, M.E. Comparison of osmotic adjustment, leaf proline concentration, canopy temperature and root depth for yield of juncea canola under terminal drought. J. Agron. Crop Sci. 2017, 203, 397–405. [Google Scholar] [CrossRef]
- Ray, S.S.; Das, G.; Singh, J.P.; Panigrahy, S. Evaluation of hyperspectral indices for LAI estimation and discrimination of potato crop under different irrigation treatments. Int. J. Remote Sens. 2006, 27, 5373–5387. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Rajaee, T. Simulation of groundwater level variations using wavelet combined with neural network, linear regression and support vector machine. Glob. Planet Change 2017, 148, 181–191. [Google Scholar] [CrossRef]
- Dou, S.Q.; Zhang, W.J.; Deng, Y.X.; Zhang, C.H.; Mei, Z.M.; Yan, J.C.; Li, M.L. Comparison of Citrus Leaf Water Content Estimations Based on the Continuous Wavelet Transform and Fractional Derivative Methods. Horticulturae 2024, 10, 177. [Google Scholar] [CrossRef]
- Zhao, X.H.; Zhang, J.C.; Pu, R.L.; Shu, Z.F.; He, W.Z.; Wu, K.H. The continuous wavelet projections algorithm: A practical spectral-feature-mining approach for crop detection. Crop J. 2022, 10, 1264–1273. [Google Scholar] [CrossRef]
- Zygielbaum, A.I.; Gitelson, A.A.; Arkebauer, T.J.; Rundquist, D.C. Non-destructive detection of water stress and estimation of relative water content in maize. Geophys. Res. Lett. 2009, 36, 1–4. [Google Scholar] [CrossRef]
- Liu, S.B.; Jin, X.L.; Nie, C.W.; Wang, S.Y.; Yu, X.; Cheng, M.H.; Shao, M.C.; Wang, Z.X.; Tuohuti, N.; Bai, Y.; et al. Estimating leaf area index using unmanned aerial vehicle data: Shallow vs. deep machine learning algorithms. Plant Physiol. 2021, 187, 1551–1576. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Hartling, S.; Esposito, F.; Fritschi, F.B. Soybean yield prediction from UAV using multimodal data fusion and deep learning. Remote Sens. Environ. 2020, 237, 111599. [Google Scholar] [CrossRef]
- Wang, S.; Wang, C.Z.; Zhang, C.L.; Xue, J.Y.; Wang, P.; Wang, X.W.; Wang, W.S.; Zhang, X.; Li, W.C.; Huang, G.H.; et al. A classification-based spatiotemporal adaptive fusion model for the evaluation of remotely sensed evapotranspiration in heterogeneous irrigated agricultural area. Remote Sens. Environ. 2022, 273, 112962. [Google Scholar] [CrossRef]
- Tian, M.Y.; Ma, X.B.; Liang, M.Y.; Zang, H.C. Application of Rapid Identification and Determination of Moisture Content of Coptidis Rhizoma from Different Species Based on Data Fusion. J. AOAC Int. 2023, 106, 1389–1401. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, G.; Calvelo-Pereira, R.; Roudier, P.; Martin, A.P.; Turnbull, R.E.; Kereszturi, G.; Jeyakumar, P.; Anderson, C.W.N. Quantification of multiple soil trace elements by combining portable X-ray fluorescence and reflectance spectroscopy. Geoderma 2022, 409, 115649. [Google Scholar] [CrossRef]

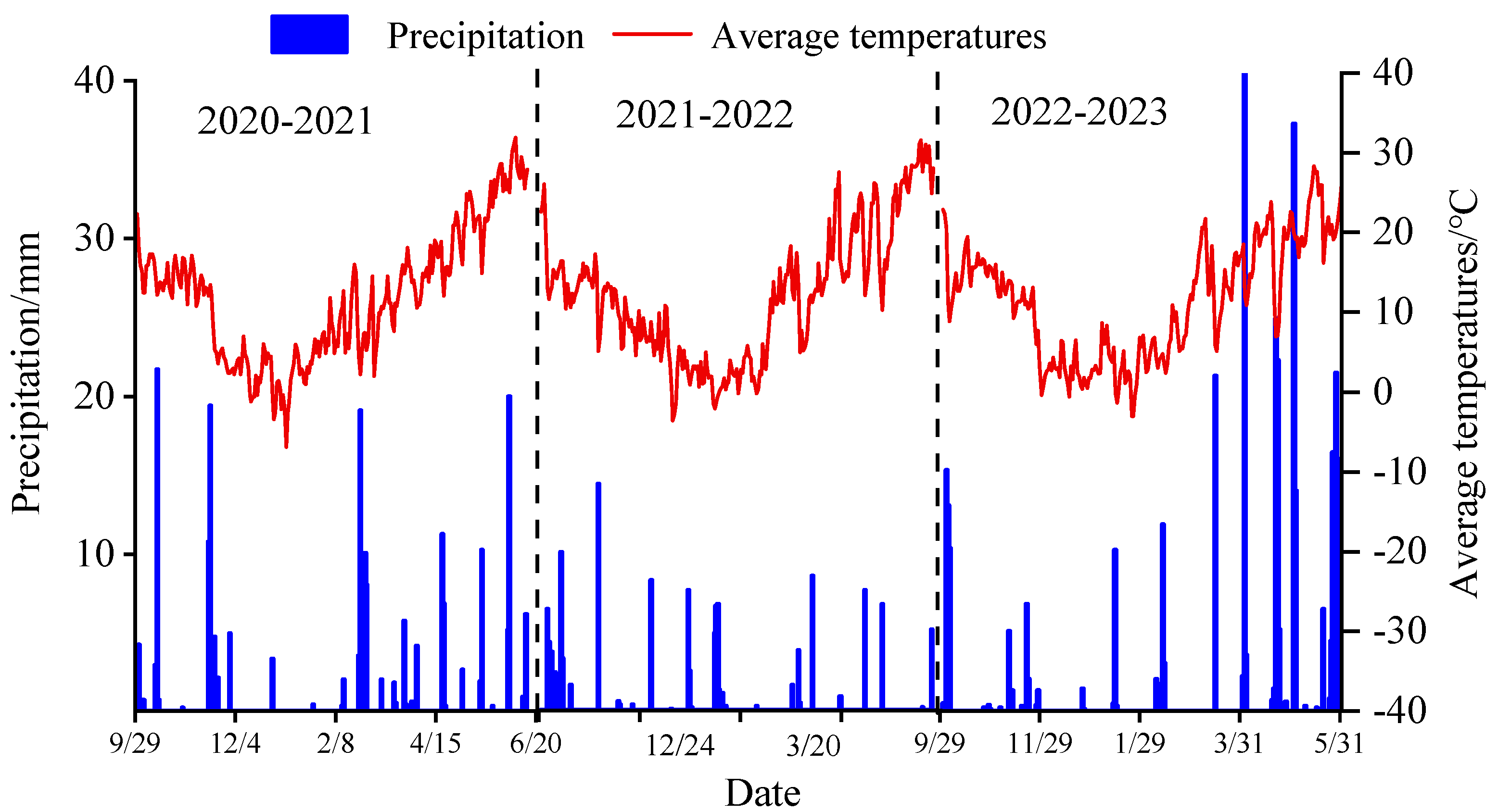
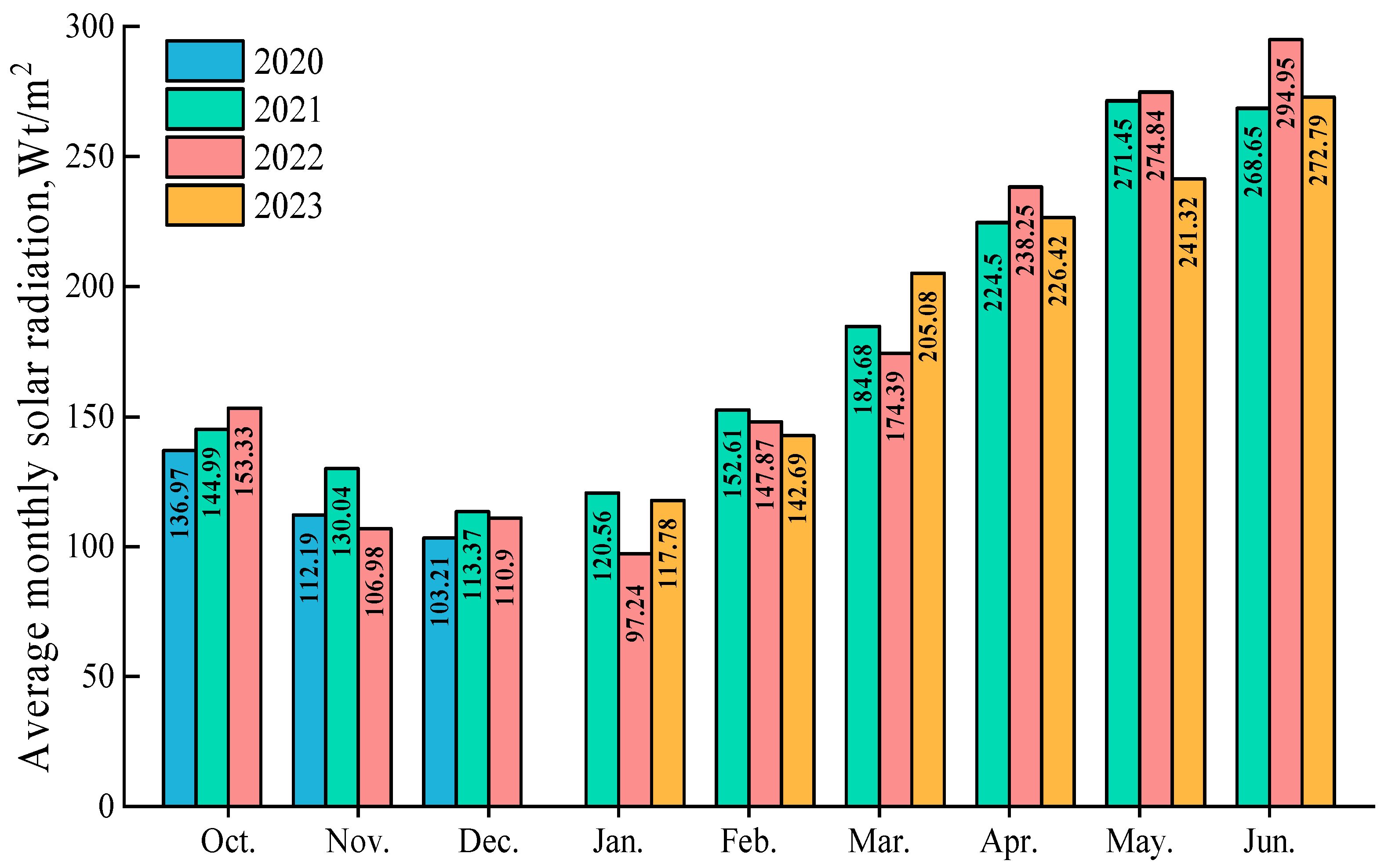
| Year | Variety | Sowing Date | Harvest Date | Water Treatment Date | Maturity | Drought Resistance | Seeding Rate (kg/hm2) | Plant Height (cm) | Number of Grains per Ear |
|---|---|---|---|---|---|---|---|---|---|
| 2020–2021 | Luomai-22 | 11 October 2020 | 26 May 2021 | 21 March 2021 | Mid late maturing | Drought tolerance | 110–125 | 76–83 | 35–37 |
| Zhoumai-27 | Mid maturing | Mid drought tolerance | 115–130 | 74–78 | 36–38 | ||||
| 2021–2022 | Luomai-22 | 13 October 2021 | 26 May 2022 | 23 March 2022 | Mid late maturing | Drought tolerance | 110–125 | 75–81 | 35–37 |
| Zhoumai-27 | Mid maturing | Mid drought tolerance | 115–130 | 76–79 | 36–38 | ||||
| 2022–2023 | Xinmai-26 | 10 October 2022 | 28 May 2023 | 20 March 2023 | Mid maturing | Mid drought tolerance | 115–130 | 78–82 | 34–36 |
| Yunong-804 | Mid late maturing | Drought tolerance | 120–135 | 77–82 | 36–38 |
| Canopy Temperature Parameter | Calculation Formula | References |
|---|---|---|
| Canopy temperature depression (CTD) | CTD = Ta − Tc | [41] |
| Normalized relative canopy temperature (NRCT) | [42] | |
| Stomatal conductance index (IG) | [43] | |
| Average canopy temperature (TAV) | [12] |
| Factor | Variance Inflation Factor |
|---|---|
| CTD | 2.933 |
| IG | 5.554 |
| NRCT | 3.563 |
| TAV | 5.606 |
| Calibration Datasets | Validation Datasets | |||||
|---|---|---|---|---|---|---|
| R2 | RMSE | nRMSE | R2 | RMSE | nRMSE | |
| HS-CWC | 0.864 | 5.92% | 8.63% | 0.833 | 7.13% | 9.78% |
| TI-CWC | 0.813 | 7.22% | 10.49% | 0.783 | 8.84% | 12.40% |
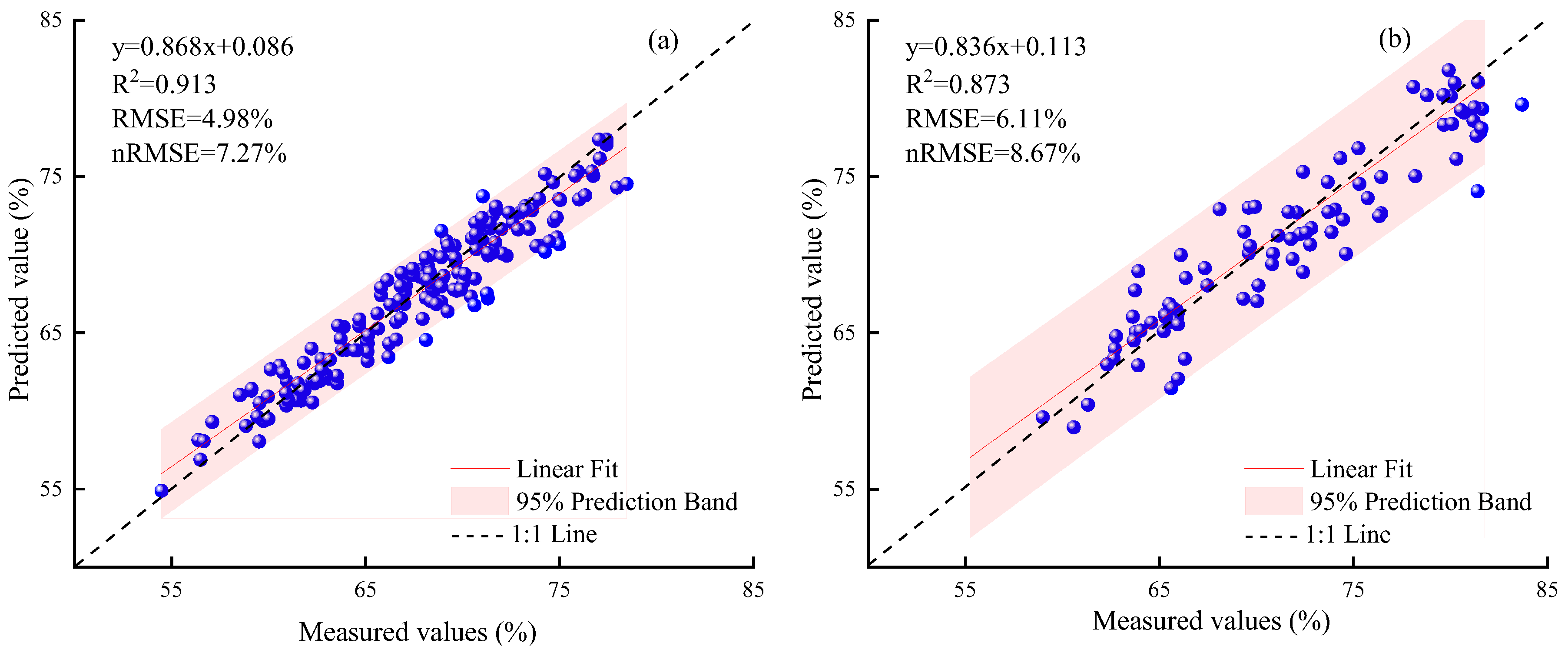
| GRA-CWC | 0.913 | 4.98% | 7.27% | 0.873 | 6.11% | 8.67% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, C.; Liu, S.; Wu, P.; Wang, Y.; Wu, K.; Li, L.; Wang, J.; Liu, S.; Gao, P.; Zhao, Z.; et al. Estimation of Canopy Water Content by Integrating Hyperspectral and Thermal Imagery in Winter Wheat Fields. Agronomy 2024, 14, 2569. https://doi.org/10.3390/agronomy14112569
Gao C, Liu S, Wu P, Wang Y, Wu K, Li L, Wang J, Liu S, Gao P, Zhao Z, et al. Estimation of Canopy Water Content by Integrating Hyperspectral and Thermal Imagery in Winter Wheat Fields. Agronomy. 2024; 14(11):2569. https://doi.org/10.3390/agronomy14112569
Chicago/Turabian StyleGao, Chenkai, Shuimiao Liu, Pengnian Wu, Yanli Wang, Ke Wu, Lingyun Li, Jinghui Wang, Shilong Liu, Peimeng Gao, Zhiheng Zhao, and et al. 2024. "Estimation of Canopy Water Content by Integrating Hyperspectral and Thermal Imagery in Winter Wheat Fields" Agronomy 14, no. 11: 2569. https://doi.org/10.3390/agronomy14112569
APA StyleGao, C., Liu, S., Wu, P., Wang, Y., Wu, K., Li, L., Wang, J., Liu, S., Gao, P., Zhao, Z., Shao, J., Yu, H., Guan, X., Wang, T., & Wen, P. (2024). Estimation of Canopy Water Content by Integrating Hyperspectral and Thermal Imagery in Winter Wheat Fields. Agronomy, 14(11), 2569. https://doi.org/10.3390/agronomy14112569






