Abstract
This study applies the Multilayer Perceptron (MLP) and Random Forest (RF) models, utilizing remote sensing and ground-based net primary productivity (NPP) data from 1992 to 2020, along with meteorological data and soil properties, to model the NPP in the alpine grassland and alpine meadow ecosystems of the Qinghai-Tibetan Plateau (TP) and assess their sensitivity to climate change. As a vital ecological barrier, the TP’s grassland ecosystems are critical for understanding the impacts of climate change. However, sensitivity analysis of the NPP in the TP grasslands has been limited, which this study aims to address by focusing on the effects of maximum temperature, solar radiation, and wind speed on the NPP. The results show that the MLP model outperforms the RF model in prediction accuracy (R2 = 0.98, RMSE = 16.24 g C·m−2·a−1, MAE = 9.04 g C·m−2·a−1). NPP responses to climate factors are diverse: linear with temperature and nonlinear with solar radiation and wind speed. Under multi-factor scenarios, the NPP in both alpine meadow and alpine grassland exhibit nonlinear trends, with a higher sensitivity to changes in all three factors than to single- or two-factor changes. Spatial distribution analysis revealed that the NPP in alpine meadows was more sensitive to climate change in the southern regions, while alpine grassland showed greater sensitivity in the central regions. This study, using machine learning models and sensitivity analysis, sheds light on the complex response of the NPP in the TP grasslands to climate change, offering valuable insights for carbon cycle research in cold ecosystems and regional climate adaptation management.
1. Introduction
Grassland ecosystems, as one of the most widespread terrestrial ecosystems on Earth, play a crucial role in the global carbon cycle [1]. Net primary productivity (NPP) is a key indicator for assessing the productivity and carbon sequestration capacity of grassland ecosystems. It represents the amount of organic carbon fixed by plants through photosynthesis per unit of time, after accounting for the carbon consumed by autotrophic respiration [2]. NPP is not only a critical indicator for evaluating ecosystem health but also an essential parameter in global carbon balance studies [3,4,5,6]. As climate change intensifies, the spatial distribution and temporal trends of the NPP have become increasingly important for ecosystem management and carbon emission control, particularly in high-altitude and high-latitude regions, which typically store substantial amounts of carbon and are highly sensitive to climate change [7].
The Qinghai-Tibet Plateau (TP), as the highest plateau in the world, possesses unique geographical and climatic features, with an average elevation exceeding 4000 m, earning it the title “Roof of the World” [8]. The TP has experienced a more pronounced warming trend than the global average, with the rate of temperature increase being twice as fast as the global mean [9]. The alpine meadows and alpine grasslands of the TP are the dominant vegetation types in the region, are highly sensitive to climate change, and play a key role in the terrestrial carbon cycle [10]. However, due to the region’s complex topography and variable climate, estimating the NPP on the Tibetan Plateau presents significant challenges. Existing studies largely rely on traditional process-based or empirical models, which lack sufficient spatial resolution and fail to fully account for the complex interactions between climate factors [11,12].
In recent years, machine learning (ML) methods, particularly Random Forest (RF) and Multilayer Perceptron (MLP) models, have been widely applied in ecological research. Compared to traditional methods, machine learning approaches handle nonlinear, complex multidimensional data without relying on fixed assumptions, with clear advantages in large-scale spatial analysis [13]. In ecological research, machine learning methods have been shown to improve prediction accuracy, particularly in large and complex ecosystem models [14]. Song et al. [15] employed RF to estimate the global NPP, highlighting its ability to handle complex interactions between meteorological factors and vegetation productivity. Bulut et al. [16] assessed the performance of multiple ML algorithms, including linear regression, support vector machines, and deep learning, for NPP estimation, highlighting the advantage of ML in integrating diverse data sources. Similarly, Tramontana et al. [17] applied RF to analyze the uncertainty in GPP predictions, demonstrating the importance of incorporating meteorological and remote sensing variables at a continental scale.
As an ensemble learning method, RF was shown to be an effective tool for scaling biomass observations to the regional level and generating continuous biomass estimates for the TP [18]. Similarly, Yu et al. [19] evaluated the performance of RF in NPP estimation, demonstrating its clear advantages over other machine learning models. They highlighted RF’s superior ability to integrate multiple remote sensing variables and its robustness in handling missing data, which often challenges other models such as support vector machines. The MLP, on the other hand, is a deep neural network model particularly well-suited for modeling highly complex nonlinear relationships, as highlighted by Park and Lek [20], who demonstrated its effectiveness in capturing intricate ecological interactions, and Abbasi et al. [21], who showcased its ability to model carbon dynamics under crop rotations. However, despite MLP’s success in many fields [22], its application in NPP estimation remains relatively limited. Specifically, MLP processes high-dimensional data through multiple hidden layers, capturing more complex nonlinear relationships between variables, which is especially important for regions like the TP where the interactions between climate factors are particularly complex.
Therefore, this study uses meteorological data and soil properties to compare the performance of RF and MLP models in predicting the NPP. Additionally, although previous studies have mainly focused on NPP estimation in grassland ecosystems, the responses of alpine grasslands and alpine meadows, located on the TP, to climate change exhibit significant differences. Given this, we specifically selected alpine grasslands and alpine meadows as two representative types of grasslands, conducting detailed sensitivity analyses for each to explore their distinct responses to climate change.
2. Materials and Methods
2.1. Overview of the Study Area
The Qinghai-Tibetan Plateau (73° E–105° E, 25° N–40° N) is located in the western part of China (Figure 1), covering an area of approximately 2.5 × 106 km2, with an average elevation of 4500 m [23]. Grasslands dominate the vegetation of the plateau, covering over 60% of the total area, while forests and trees are sparsely distributed in the southern regions. The TP lies within an arid and semi-arid climate zone, characterized by a harsh climate. The average annual temperature is below 0 °C, with the annual precipitation averaging around 500 mm [11]. The region is ecologically fragile, exhibiting significant geographical variation and distinct wet and dry seasons.
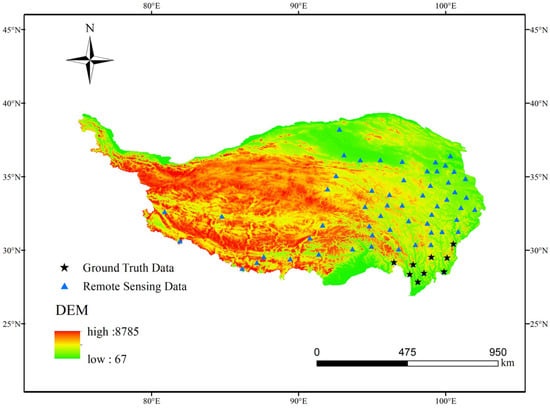
Figure 1.
Geographical location map of the Qinghai-Tibet Plateau.
Under the influence of global climate change, the vegetation types of the TP are gradually shifting. However, natural grasslands remain the predominant vegetation type, with alpine grasslands and alpine meadows being the most widely distributed. Alpine grasslands are primarily located in the northwestern and some northeastern regions, while alpine meadows are predominantly found in the central, southeastern, and some southwestern regions (Figure 2). In addition to alpine grasslands and alpine meadows, other vegetation types, including scrublands, deserts, and grasses, are present on the plateau, though their overall coverage is minimal [11].
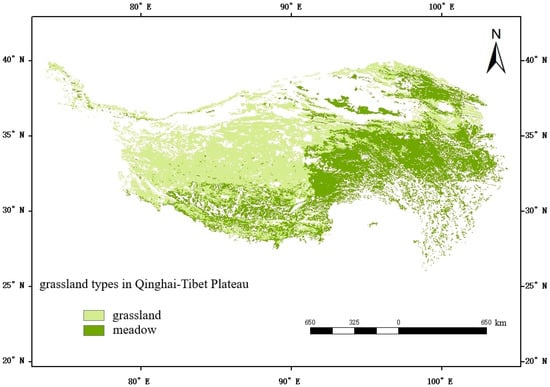
Figure 2.
Grassland types on the Qinghai-Tibet Plateau.
2.2. Data and Processing
2.2.1. Meteorological Data
In this study, the meteorological data were obtained from the National Meteorological Science Data Center website (http://data.cma.cn/, accessed on 10 November 2023), including the daily maximum temperature, minimum temperature, average precipitation, solar radiation, relative humidity, and wind speed data of the meteorological stations in the Tibetan Plateau region from 1992 to 2020. The monthly CO2 concentration data from 1992–2020 were obtained from the global tropospheric CO2 concentration satellite remote sensing product (AIRS, AIR×3C2M005), sourced from NASA, Greenbelt, MD, USA. the data of each station on the Qinghai-Tibet Plateau were extracted in ArcGIS10.8 software.
2.2.2. Vegetation Type Data and Soil Data
The vegetation type data for both alpine grassland and alpine meadow were selected from the 1 km vegetation type raster data of the Resource and Environment Science and Data Center of the Chinese Academy of Sciences (https://www.resdc.cn/, accessed on 10 November 2023). Soil data were obtained from the World Soil Database V1.2 (http://www.fao.org/, accessed on 12 November 2023), produced by ISRIC-World Soil Information. Among the data within the World Soil Database V1.2, predicted variables relevant to this work were soil thickness, soil gravel content, soil clay content, soil chalk content, pH, soil organic matter, wilting point, field capacity, saturated hydraulic conductivity, and bulk density.
2.2.3. NPP Data
The remote sensing data from 1992–2000 were provided by the University of Maryland’s Global Land Cover Facility (GLCF) website (http://glcf.umd.edu/data/glopem/, accessed on 8 November 2023), and the data from 2001–2020 were provided by the National Aeronautics and Space Administration (NASA)’s Earth Observing System (https://www.nasa.gov/, accessed on 8 November 2023). The downloaded remote sensing data were formatted and stitched using Modi’s reprojection tools (MRT), and the mask extraction of the stitched NPP remote sensing data was carried out in ArcGIS10.8 software using the Tibetan Plateau vector boundary to obtain the NPP values of each station on the Tibetan Plateau. The measured NPP data were extracted from the National Tibetan Plateau Science Data Center (https://data.tpdc.ac.cn/zh-hans/, accessed on 8 November 2023), specifically for assessing the carbon storage of grassland vegetation on the TP. The details of these variables are summarized in Table 1.

Table 1.
Data sources and types for training, validation, and testing of machine learning models.
2.3. Research Methods
2.3.1. Data Preprocessing and Evaluation Metrics
All input variables were normalized to ensure consistency and to improve model performance. Random grid search was used to optimize key hyperparameters for both RF and MLP models. Model performance was evaluated using R2, RMSE, and MAE, with independent validation assessing the accuracy on unseen data and five-fold cross-validation testing model stability. Cross-validation helped reveal model overfitting and assessed the model’s performance on unseen data. Residual analysis was also conducted.
2.3.2. Random Forest
Random Forest (RF) is an ensemble learning method that improves prediction accuracy by combining multiple decision trees [24]. Key hyperparameters include “Max_depth”, specifying the maximum depth of individual trees, and “Max_features”, determining the number of variables considered at each split. Additionally, “Min_sample_leaf” and “Min_sample_split” define the stopping criteria for tree branching. The algorithm recursively optimizes tree branching from the root, based on a set optimality criterion, and stops when no further splitting is justified [25,26].
In this study, we used RF to predict remotely sensed NPP values, influenced by various climate and soil factors. The input variables included monthly variations in temperature, precipitation, solar radiation, relative humidity, wind speed, CO2 levels, and soil properties such as organic matter content, pH, wilting point, field capacity, and hydraulic conductivity.
2.3.3. Multilayer Perceptron Neural Network
The Multilayer Perceptron (MLP) is a feedforward artificial neural network, ideal for classifying large datasets and establishing complex nonlinear mappings [27]. Utilizing hidden neurons, MLP models simulate interactions between limited input and output variables effectively.
The MLP model in this study processed the same eight categories of input variables as the RF model: maximum and minimum temperatures, precipitation, solar radiation, relative humidity, wind speed, CO2 concentration, and soil properties.
The architecture consisted of four hidden layers with neuron configurations of 8, 8, 4, and 1, trained using the ReLU activation function. The model was further optimized through random grid search, with a maximum of 1000 iterations to ensure convergence.
2.3.4. Sensitivity Analysis Design
To assess the sensitivity of the NPP in different grassland types on the TP to climate change, this study designed a series of simulation scenarios (Table 2 and Table 3). These scenarios focus on three key climatic variables: maximum temperature, solar radiation, and wind speed, using the best-performing trained models for sensitivity analysis while altering the selected variables and keeping others constant.

Table 2.
Single factor sensitivity analysis design.

Table 3.
Multi-factor sensitivity analysis design.
The ranges of these climatic variables were defined based on reported values from prior studies [28,29]. Specifically, the maximum temperature was varied within a range of ±1–4 °C, in line with the temperature increases observed in global climate change projections, particularly for high-altitude and high-latitude regions [28]. The wind speed was adjusted by ±0–40%, reflecting commonly observed changes in the wind speed from climate models, which account for potential alterations in wind patterns and extreme weather events due to climate change [29]. Additionally, the range of solar radiation was set to ±0–40%, based on estimates of the fluctuations in solar radiation intensity from international climate change research [29].
A multi-factor sensitivity analysis was employed to systematically evaluate the interactions between these climatic variables and their cumulative effects on the NPP. By incrementally adjusting the values of the climatic variables and analyzing the corresponding model outputs, this approach allowed for a comprehensive understanding of how these factors influence the productivity of grassland ecosystems on the TP under various climate scenarios.
3. Results
3.1. The Performance of Estimation of the NPP Using the RF and MLP
The quantitative evaluation clearly demonstrated that the MLP model outperformed the RF model (Table 4). The optimal parameters for both models were determined through grid search, as detailed in Table 4. For independent validation, the MLP achieved an R2 of 0.98, significantly higher than the RF’s 0.95, indicating a stronger explanatory ability for predicting the NPP. Furthermore, the MLP yielded lower RMSE and MAE values (16.24 and 9.04, respectively) compared to the RF’s 39.99 and 27.60, reflecting its superior ability to minimize prediction errors. Similarly, in cross-validation, the MLP achieved an R2 of 0.98, whereas the RF reached only 0.90. The RMSE and MAE for the MLP were 24.11 and 13.59, respectively, much lower than the RF’s 46.73 and 27.89. These results indicate that the MLP model consistently delivered higher accuracy and robustness across both validation approaches.

Table 4.
Comparison of optimal parameters and performance between RF and MLP.
Residual analysis further supported these findings (Figure 3). The residuals of the MLP model (Figure 3b) were tightly clustered around zero, with a range limited to ±100, indicating more consistent predictions and lower errors. In contrast, the residuals of the RF model (Figure 3a) exhibited a broader range, extending up to ±200, with more scattered distribution, suggesting larger prediction errors in some regions. This distinct difference underscored the superior predictive performance of the MLP model in estimating grassland productivity.
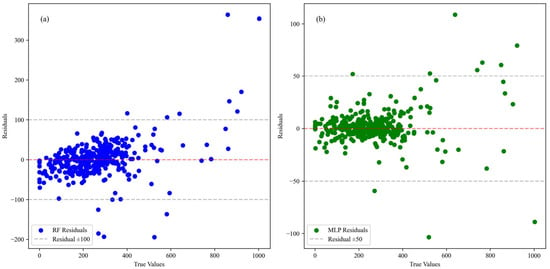
Figure 3.
Residuals comparison between RF and MLP. (a) Residual plot for RF, (b) Residual plot for MLP.
3.2. Single-Factor Sensitivity Analysis of the NPP in Different Grassland Types
3.2.1. Trend Analysis of the NPP of Different Grassland Types Under Changes in Single Climate Factors
In this study, the three climate factors of maximum temperature, solar radiation and wind speed were selected to perform trend analysis on the NPP of different grassland types, and these results are shown in Figure 4. From Figure 4a, it can be seen that the NPP of both grassland types continued to increase (or decrease) when the maximum temperature increased (or decreased) by 1–4 °C, and the magnitude of the change was linearly related to the NPP. At different magnitudes of change, the NPP of alpine meadow and the rate of change was always higher than that of alpine grassland. The NPP of alpine meadow was much higher than that of alpine grassland when the maximum temperature was changed by the same magnitude, because the vegetation had sufficient conditions for photosynthesis due to the lower latitude and elevation of the area where alpine meadows grow, and thus produced more NPP than alpine grasslands.
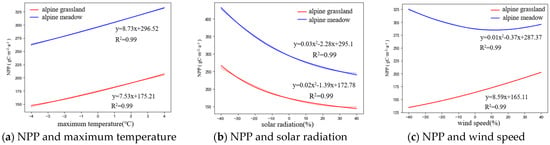
Figure 4.
Variation trends of NPP under individual climatic factors: (a) Linear relationship for both grassland types; (b) Quadratic relationship for both grassland types; (c) Linear relationship for alpine grassland, quadratic relationship for alpine meadow.
As illustrated in Figure 4b, in contrast to the effect of maximum temperature, both grassland types exhibited a declining trend in the NPP under the influence of solar radiation. The magnitude of change demonstrated a non-linear relationship with the NPP, characterized by a quadratic function. However, it is noteworthy that despite this decline, the NPP of alpine meadow consistently surpassed that of alpine grassland at different magnitudes of change. This suggested that excessive solar radiation has a detrimental impact. Stronger solar radiation tends to dry the topsoil, which hinders vegetation growth and consequently leads to a reduction in the NPP.
Furthermore, the response threshold was reached at a 40% reduction in solar radiation for both grassland types within various magnitudes of variation. As shown in Figure 4c, the NPP of the two grassland types showed different responses under the influence of different magnitudes of wind speed variation. Although the NPP of alpine meadow was still higher than alpine grassland in the overall value, the difference was that the alpine meadow value showed a nonlinear relationship with the magnitude of change, and the relationship between the two was approximately quadratic, while the alpine grassland value showed a linear relationship with the magnitude of change. The linear trend was stronger than that shown in Figure 4a. Besides, unlike the maximum temperature and solar radiation, the NPP of alpine meadow reached the response threshold at a 40% reduction in wind speed, while that of the alpine grassland reached the response threshold at a 40% increase in wind speed for different magnitudes of variation.
3.2.2. Spatial Analysis of the NPP of Different Grassland Types with Climate Factors
The spatial distribution of the NPP change in alpine grassland with different magnitudes in the maximum temperature from 1992 to 2020 (Figure 5) showed that when the maximum temperature increased to 3 °C, the NPP values in the central as well as the northwestern regions increased significantly; until 4 °C, the NPP values in the central and western regions increased to the maximum value, and though there was a weak increase in the northeastern regions, the values still mainly decreased (Figure 5a–d), indicating that the sensitivity of the central and western regions to increases in the maximum temperature was higher. Compared to the increase in maximum temperature, the trend of the NPP in the alpine grassland was not obvious after the decrease in maximum temperature, and when the maximum temperature decreased to −4 °C, the NPP values decreased in most of the northeast and only slightly increased in a small part of the central and western regions (Figure 5e–h). This is because an increase in the maximum temperature promotes photosynthesis in plants, which in turn leads to a larger amount of change in the NPP.
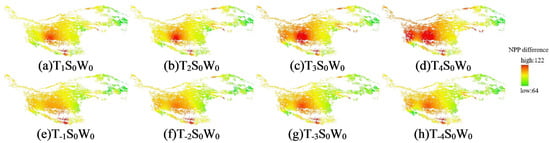
Figure 5.
Spatial distribution of NPP in alpine grassland under maximum temperature variation.
Figure 6 shows the spatial distribution of the NPP of alpine meadows under the highest temperature variation. Overall, the amount of NPP variation in alpine meadows was higher in the central and southeastern part of the country and lower in the southwestern and northeastern parts. Since alpine meadows grow in a region with low latitude and more abundant water and heat conditions, its NPP variation is larger than that of alpine grasslands. As shown in Figure 6a–d, the alpine meadow NPP increased substantially as the maximum temperature increased until 4 °C for the entire region. With the decrease in the maximum temperature, only the NPP in the southeastern region decreased at first, and the areas with larger decreases were concentrated in the east and the south (Figure 6e–h), which was likely because the continuous decrease in the maximum temperature would inhibit the vegetation to carry out photosynthesis, which then reduces the carbon accumulation. The above results indicate that the NPP in the southeastern region responds more strongly to the change in maximum temperature, and the alpine meadow NPP is more sensitive to the change in maximum temperature than the alpine grassland NPP.
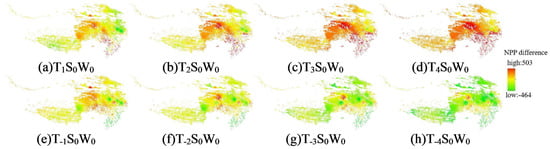
Figure 6.
Spatial distribution of NPP in alpine meadows under maximum temperature variation.
The spatial distribution of the alpine grassland NPP under the change in solar radiation is shown in Figure S1. As a whole, the alpine grassland NPP responded more strongly to the decrease in solar radiation. From Figure S1a–d, it can be seen that when the solar radiation increased by 10%, the NPP in the west showed a slightly increasing distribution, but most of the northeast was decreasing; until the solar radiation increased to 40%, the area of the decreasing NPP expanded from the northeast to the center, indicating that the sensitivity of the northeast to the increase in solar radiation is higher. In contrast, when solar radiation decreased by 10%, the increase in the NPP in the alpine grassland was mainly concentrated in the central region, but when the decrease was 20%, the NPP value basically increased in the whole region, and this trend continued until the change reached 40% (Figure S1e–h), indicating that the decrease in solar radiation has a greater effect on the NPP in the alpine grassland than the increase in solar radiation.
In the same trend of the alpine grassland, the amount of change in the NPP of alpine meadows was negatively correlated with the change in solar radiation (Figure S2). The difference was that the alpine meadow NPP responded more strongly to the increase in solar radiation, and the area of NPP decrease expanded from the southeast to the central and southern parts of the country as the magnitude increased, until most of the area showed a decreasing trend in the NPP (Figure S2a–d). The effect of reduced solar radiation on the NPP of alpine meadows was even greater: the area of the increased NPP expanded from the central part to the surrounding area as the solar radiation decreased, and eventually, the NPP values were increased in basically all areas (Figure S2e–h). The alpine meadow NPP was more sensitive to changes in solar radiation than the alpine grassland NPP.
Figure S3 showed the spatial distribution of the alpine grassland NPP under wind speed variation. When the increase in wind speed was between 10% and 30%, the NPP of the central region increased and the western and northeastern regions decreased. Until the wind speed increased to 40%, the area of the NPP increase expanded to the central as well as the northeastern region and the NPP decreased only in the western region (Figure S3a–d). Under the influence of a decreasing wind speed, the change trend of the NPP in the alpine grassland was more obvious, from increasing the NPP in the central and most of the western region to decreasing the NPP in the central and northeastern regions. This indicated that increases in wind speed favored the accumulation of NPP in the alpine grassland, and the response to wind speed changes was stronger in the central and northeastern regions.
The spatial distribution of the alpine meadow NPP under wind speed variation was different from that of alpine grassland (Figure S4). The NPP of alpine meadows gradually increased, regardless of whether the wind speed increased or decreased. With the gradual increase in wind speed, the values of the NPP in the central and northeastern parts of the country became larger and larger, and finally only a small part of the NPP in the southeast decreased (Figure S4a–d). Besides, it can be seen from Figure S4e,h that the alpine meadow NPP changed from decreasing in the northeast and southwest and increasing in the central and southeast to increasing in almost all areas as the wind speed decreased, and this effect of wind speed decrease on the alpine meadow NPP was stronger. In summary, the sensitivity of the alpine meadow NPP to changes in wind speed was greater than that of the alpine grassland. Additionally, the central region of alpine meadows exhibited higher sensitivity to changes in wind speed.
3.3. Sensitivity Analysis of the NPP in Different Grassland Types
3.3.1. Two-Factor Sensitivity Analysis of the NPP in Different Grassland Types
To analyze the NPP responses in the alpine grasslands and meadows to climate change, a sensitivity analysis was conducted, assessing the impacts of concurrent climate factors with the alpine grassland NPP depicted in green and the alpine meadow NPP in blue (Figure 7a,d). This analysis found that both grassland types experienced NPP increases with higher maximum temperatures and lower solar radiation, though alpine meadows were notably more responsive.
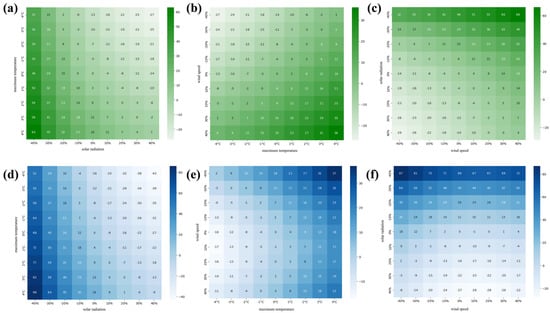
Figure 7.
Sensitivity analysis of NPP values in alpine grasslands and alpine meadows. (a,d) NPP response to maximum temperature and solar radiation. (b,e) NPP response to wind speed. (c,f) NPP response to wind speed and solar radiation. Green represents alpine grassland and blue represents alpine meadow.
This analysis also revealed a significant negative correlation between solar radiation and the NPP, which was particularly pronounced in alpine meadows, suggesting a dominant influence of solar radiation on vegetation dynamics (Figure 7a,d).
Figure 7b,e examined NPP responses to variations in maximum temperature and wind speed. The alpine grassland NPP was positively correlated with increased wind speeds, whereas the alpine meadow NPP decreased under reduced wind speeds, highlighting the critical influence of wind on NPP changes.
In Figure 7c,f, both grassland types showed increased NPP values with rising wind speeds and declining solar radiation, indicating a combined effect greater than either factor alone. Alpine meadows, in particular, showed an increased sensitivity to decreasing wind speed and increasing solar radiation, identifying solar radiation as a pivotal factor in NPP variability.
These findings demonstrate a complex interaction between climate factors and the NPP, with alpine meadows showing a higher sensitivity to solar radiation and wind speed changes than alpine grasslands, underscoring the importance of these factors in vegetation response to climate change.
3.3.2. Multi-Factor Sensitivity Analysis of the NPP in Different Grassland Types
By conducting sensitivity analysis on two factors of the NPP of different grassland types on the Tibetan Plateau, the effects of different factor combinations on the NPP of different grassland types were studied. To further analyze the differences in the response of the NPP of different grassland types to the changes of three factors, given the positive correlation of the NPP in the alpine grassland with maximum temperature and wind speed, and its negative correlation with solar radiation, the simulation allowed for an increase (or decrease) in both maximum temperature and wind speed of 1–4 °C and 10–40%, respectively, while the solar radiation decreased (or increased) 10–40%, which was used to analyze the trend of the alpine meadow NPP. Since the alpine meadow NPP was positively correlated with the maximum temperature, negatively correlated with solar radiation, positively and negatively correlated with wind speed increases and decreases, respectively, and that wind speed decreases had a greater impact on the alpine meadow NPP, the maximum temperature was increased (or decreased) 1–4 °C, while solar radiation and wind speed were decreased (or increased) by 10–40% to analyze the trend of the NPP in alpine meadows. The trends of the NPP for different grassland types under multi-factor changes are shown in Figure 8. Both grassland types showed a quadratic non-linear relationship between the magnitude of NPP and climate factors, where both the alpine meadow NPP and the rate of change were always higher than the values for the alpine grassland, and both were greater than the rate of change in the NPP under single-factor changes. In addition, the maximum value of the NPP in the alpine meadow was 491.82 g C·m−2·a−1 and the minimum value was 209.42 g C·m−2·a−1, while the maximum value of the NPP in the alpine grasslands was 261.3 g C·m−2·a−1 and the minimum value was 158.9 g C·m−2·a−1. The above results indicated that the sensitivity of the NPP of both grassland types to changes in the three climatic factors was higher than their sensitivity to single and two-factor changes.
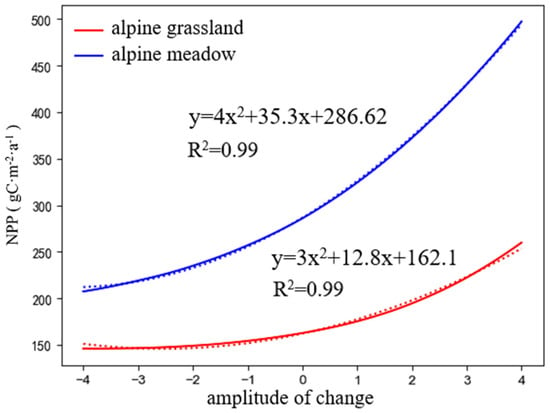
Figure 8.
Variation trends of the NPP in different grassland types under multi-factor changes.
After the trend analysis of the change in the NPP of different grassland types under multi-factor variation, a spatial analysis was conducted. Figure 9 shows the spatial distribution of the amount of NPP variation in alpine grassland under multi-factor variation. It can be seen from the figure that when the maximum temperature and wind speed were increased by a certain magnitude and the solar radiation decreased by a corresponding magnitude, the change in the NPP of the alpine grassland was more obvious, from a weak increase in the NPP only in the central region to an increase in the NPP in the central and most of the eastern regions (Figure 9a,d), indicating that the sensitivity of the NPP to changes in climate factors was greater in the central region. In contrast, when the maximum temperature and wind speed were decreased by 1 °C and 10%, respectively, and solar radiation increased by 10%, only a small part of the northeastern region had a decreasing NPP. As the magnitude of change increased, the area of the NPP decrease expanded from the northeast to the central part, but the overall expansion was smaller, indicating that the increases in maximum temperature and wind speed and the decrease in solar radiation had a greater effect on the NPP in the alpine grassland.
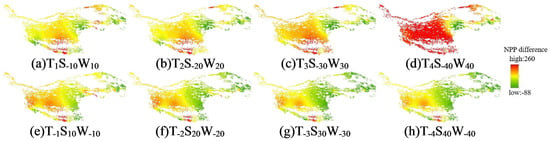
Figure 9.
Spatial distribution of NPP in alpine grassland with multiple factors.
Figure S5 shows the spatial distribution of the amount of NPP changes in alpine meadows under multi-factor changes. Unlike alpine grasslands, the change in the alpine meadow NPP was more obvious when the climate factor increased or decreased by a certain magnitude. It can be seen from the figure that when the maximum temperature increased to 2 °C and the solar radiation and wind speed decreased to 20%, the NPP in the southern region started to increase gradually, and as the magnitude of change increased, the area of the NPP increase gradually expanded from the south to the central region as well as to the north, where finally the NPP value in the vast majority of the region was increased (Figure S5b–d). When the magnitude of change decreased, it was also the NPP values in the southern region that were decreasing, indicating that the southern region was more sensitive to changes in climate factors. The above results indicated that the response of the alpine meadow NPP to different magnitudes of changes in maximum temperature, solar radiation, and wind speed was stronger than that of alpine grasslands, and the sensitivity to these factors was greater in the southern region.
4. Discussion
4.1. Model Performance and Limitations in Data Processing
The results of this study demonstrate that the MLP outperformed the RF model in predicting the NPP. This finding is consistent with previous studies, where the MLP exhibited superior performance due to its robust nonlinear modeling capabilities. These capabilities enable it to capture complex interactions among ecological variables while maintaining higher resistance to noise and data incompleteness [22,30,31]. In contrast, although the RF model performed well in handling high-dimensional data, it demonstrated higher sensitivity to input noise and a tendency to overfit, as evidenced in this study by its better performance in independent validation compared to cross-validation [32].
Despite the promising results achieved by the MLP and RF models in predicting the NPP, there are limitations in data processing that warrant attention. The normalization and imputation of missing or infinite values using mean values may have introduced errors, especially in cases where data distribution is highly heterogeneous or extreme. Additionally, inconsistencies in the spatial resolution of the climate, vegetation, and soil datasets used in this study may limit the broader applicability of the model outputs.
4.2. Diverse Responses of the NPP to Climatic Factors
This study revealed distinct patterns of NPP responses to maximum temperature, solar radiation, and wind speed on the TP. An increase in maximum temperature exhibited a linear relationship with the NPP, indicating that higher temperatures promote plant photosynthesis and carbon sequestration. This conclusion is in agreement with findings by Li et al. [33] and Zheng et al. [34], reported that temperature increases enhance primary productivity in alpine grasslands. Alpine meadows were found to be more sensitive to temperature changes, likely due to their higher vegetation density and productivity.
The relationship between solar radiation and NPP exhibited a quadratic declining trend. When solar radiation was reduced by 40% from the baseline, NPP values were higher than the baseline level. However, when solar radiation remained at the baseline or increased, the NPP decreased. This finding suggests that reducing solar radiation may alleviate photoinhibition and excessive soil water evaporation, thereby improving water use efficiency [33,34]. These results contradict the conventional view that increased solar radiation enhances photosynthesis. This inconsistency may reflect the heightened water stress and photoinhibitory effects experienced by alpine grassland ecosystems under high radiation conditions.
The effects of wind speed on the NPP demonstrated significant regional variation. In alpine meadows, the NPP exhibited a nonlinear response to wind speed, where moderate wind speeds promoted gas exchange, while high wind speeds negatively impacted water use efficiency by increasing evapotranspiration. Conversely, the NPP in alpine grasslands displayed a stable linear response, reflecting their sparse vegetation coverage and lower sensitivity to climatic variations [35,36].
4.3. Spatial Variability and Multi-Factor Interactions
Spatial analysis highlighted significant regional differences in the effects of climatic factors on the NPP. In the central and southeastern regions of the plateau, temperature variations had a more pronounced impact on the NPP, supported by favorable conditions such as large diurnal temperature ranges and higher precipitation, which facilitated plant carbon fixation [37]. In contrast, solar radiation-sensitive areas, such as the northeastern alpine grasslands, exhibited stronger responses to radiation changes, underscoring the critical role of solar radiation as a limiting factor for productivity under drought conditions [38].
Bivariate sensitivity analysis further revealed that the combined effects of temperature and solar radiation on the NPP were significantly greater than the impacts of either factor alone. Temperature increases enhanced photosynthesis, while reductions in solar radiation mitigated evapotranspiration, alleviating water stress [33,34]. These findings align with Hao et al. [39], who noted that the synergistic effects of precipitation and radiation were particularly significant during the summer on the TP.
5. Conclusions
This study evaluated the accuracy of RF and MLP models in simulating grassland NPP on the Tibetan Plateau from 1992 to 2020, with the following specific conclusions:
(1) The MLP model outperformed the RF model with higher accuracy and lower errors in both independent and cross-validation evaluations, demonstrating its robustness for simulating grassland NPP.
(2) NPP responses to climatic factors exhibited linear correlations with temperature and non-linear correlations with other factors. Alpine meadows showed an approximately quadratic response to wind speed variations, whereas alpine grasslands responded linearly.
(3) Analysis of the NPP’s spatial sensitivity to climatic changes indicated stronger responses to temperature increases in the central and western regions, particularly for alpine grasslands, whereas northeastern regions exhibited higher sensitivity to increased solar radiation.
(4) Sensitivity analysis matrices indicated that solar radiation significantly influenced NPP responses to combined climatic changes, while wind speed had a more pronounced impact in alpine meadows.
(5) Exploring multifactorial changes, this study found that the NPP’s response to combined climatic factors was more intense than to individual or dual factors, with the alpine grasslands showing greater sensitivity in central regions and the alpine meadows showing greater sensitivity in southern regions under variable climatic conditions.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/agronomy14122997/s1, Figure S1: Spatial distribution of NPP in alpine grassland under solar radiation variation; Figure S2: Spatial distribution of NPP in alpine meadow under solar radiation variation; Figure S3: Spatial distribution of NPP in alpine grassland under wind speed variation; Figure S4: Spatial distribution of NPP in alpine meadow under wind speed variation; Figure S5: Spatial distribution of NPP in alpine meadow under multi-factor changes.
Author Contributions
Conceptualization, X.L.; methodology, X.L.; software, X.L.; validation, M.Z. and X.L.; investigation, Y.Z.; resources, M.Z.; data curation, M.Z.; writing—original draft preparation, X.L.; writing—review and editing, M.S.; visualization, M.S.; supervision, Y.Z.; project administration, M.Z.; funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China under the grant 32260353; the Natural Science Foundation of Gansu province, China, grants 1606RJZA077 and 1308RJZA262; and the Ministry of Science and Technology of China high-end foreign expert introduction program, grant 2022042009L.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
We acknowledge the support of the National Natural Science Foundation of China (32260353), and Ministry of Science and Technology of China high-end foreign expert introduction Program (2022042009L). We thank the National Glacier Frozen Soil Desert Science Data Center, the European Space Agency, and the World Resources Institute for their open data policies.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Scurlock, J.M.O.; Hall, D.O. The Global Carbon Sink: A Grassland Perspective. Glob. Change Biol. 1998, 4, 229–233. [Google Scholar] [CrossRef]
- Sun, J.; Wang, Y.; Lee, T.M.; Nie, X.; Wang, T.; Liang, E.; Wang, Y.; Zhang, L.; Wang, J.; Piao, S.; et al. Nature-Based Solutions Can Help Restore Degraded Grasslands and Increase Carbon Sequestration in the Tibetan Plateau. Commun. Earth Environ. 2024, 5, 1–12. [Google Scholar] [CrossRef]
- Luo, Z.; Wu, W.; Yu, X.; Song, Q.; Yang, J.; Wu, J.; Zhang, H. Variation of Net Primary Production and Its Correlation with Climate Change and Anthropogenic Activities over the Tibetan Plateau. Remote Sens. 2018, 10, 1352. [Google Scholar] [CrossRef]
- Zhou, W.; Li, J.; Yue, T. Grassland Degradation Remote Sensing Monitoring and Driving Factors Quantitative Assessment in China from 1982 to 2010. In Remote Sensing Monitoring and Evaluation of Degraded Grassland in China: Accounting of Grassland Carbon Source and Carbon Sink; Zhou, W., Li, J., Yue, T., Eds.; Springer: Singapore, 2020; pp. 105–123. ISBN 978-981-329-382-3. [Google Scholar]
- Montibeller, B.; Marshall, M.; Mander, Ü.; Uuemaa, E. Increased Carbon Assimilation and Efficient Water Usage May Not Compensate for Carbon Loss in European Forests. Commun. Earth Environ. 2022, 3, 1–11. [Google Scholar] [CrossRef]
- Perolo, P.; Escoffier, N.; Chmiel, H.E.; Many, G.; Bouffard, D.; Perga, M.-E. Alkalinity Contributes at Least a Third of Annual Gross Primary Production in a Deep Stratified Hardwater Lake. Limnol. Oceanogr. Lett. 2023, 8, 359–367. [Google Scholar] [CrossRef]
- Bhattarai, P.; Timilsina, B.; Parajuli, R.; Chen, Y.; Gao, J.; Zhang, Y. Distinct Response of High-Latitude Ecosystem and High-Altitude Alpine Ecosystem to Temperature and Precipitation Dynamics: A Meta-Analysis of Experimental Manipulation Studies. Prog. Phys. Geogr. Earth Environ. 2022, 46, 909–921. [Google Scholar] [CrossRef]
- Jiang, Y.; Wang, P.; Xu, X.; Zhang, J. Dynamics of Carbon Fluxes with Responses to Vegetation, Meteorological and Terrain Factors in the South-Eastern Tibetan Plateau. Environ. Earth Sci. 2014, 72, 4551–4565. [Google Scholar] [CrossRef]
- Chen, H.; Zhu, Q.; Peng, C.; Wu, N.; Wang, Y.; Fang, X.; Gao, Y.; Zhu, D.; Yang, G.; Tian, J.; et al. The Impacts of Climate Change and Human Activities on Biogeochemical Cycles on the Qinghai-Tibetan Plateau. Glob. Change Biol. 2013, 19, 2940–2955. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, T.; Xiao, J.; Wang, K.; Yu, W.; Du, Z.; Huang, L.; Yue, T. Grassland Productivity Increase Was Dominated by Climate in Qinghai-Tibet Plateau from 1982 to 2020. J. Clean. Prod. 2024, 434, 140144. [Google Scholar] [CrossRef]
- Guo, B.; Zang, W.; Yang, F.; Han, B.; Chen, S.; Liu, Y.; Yang, X.; He, T.; Chen, X.; Liu, C.; et al. Spatial and Temporal Change Patterns of Net Primary Productivity and Its Response to Climate Change in the Qinghai-Tibet Plateau of China from 2000 to 2015. J. Arid Land 2020, 12, 1–17. [Google Scholar] [CrossRef]
- Wang, Y.; Yue, H.; Peng, Q.; He, C.; Hong, S.; Bryan, B.A. Recent Responses of Grassland Net Primary Productivity to Climatic and Anthropogenic Factors in Kyrgyzstan. Land Degrad. Dev. 2020, 31, 2490–2506. [Google Scholar] [CrossRef]
- Pichler, M.; Hartig, F. Machine Learning and Deep Learning—A Review for Ecologists. Methods Ecol. Evol. 2023, 14, 994–1016. [Google Scholar] [CrossRef]
- Cai, J.; Xu, K.; Zhu, Y.; Hu, F.; Li, L. Prediction and Analysis of Net Ecosystem Carbon Exchange Based on Gradient Boosting Regression and Random Forest. Appl. Energy 2020, 262, 114566. [Google Scholar] [CrossRef]
- Song, L.; Li, M.; Xu, H.; Guo, Y.; Wang, Z.; Li, Y.; Wu, X.; Feng, L.; Chen, J.; Lu, X.; et al. Spatiotemporal Variation and Driving Factors of Vegetation Net Primary Productivity in a Typical Karst Area in China from 2000 to 2010. Ecol. Indic. 2021, 132, 108280. [Google Scholar] [CrossRef]
- Bulut, S.; Günlü, A.; Şatır, O. Estimating Net Primary Productivity of Semi-Arid Crimean Pine Stands Using Biogeochemical Modelling, Remote Sensing, and Machine Learning. Ecol. Inform. 2023, 76, 102137. [Google Scholar] [CrossRef]
- Tramontana, G.; Ichii, K.; Camps-Valls, G.; Tomelleri, E.; Papale, D. Uncertainty Analysis of Gross Primary Production Upscaling Using Random Forests, Remote Sensing and Eddy Covariance Data. Remote Sens. Environ. 2015, 168, 360–373. [Google Scholar] [CrossRef]
- Xia, J.; Ma, M.; Liang, T.; Wu, C.; Yang, Y.; Zhang, L.; Zhang, Y.; Yuan, W. Estimates of Grassland Biomass and Turnover Time on the Tibetan Plateau. Environ. Res. Lett. 2018, 13, 014020. [Google Scholar] [CrossRef]
- Yu, B.; Chen, F.; Chen, H. NPP Estimation Using Random Forest and Impact Feature Variable Importance Analysis. J. Spat. Sci. 2019, 64, 173–192. [Google Scholar] [CrossRef]
- Park, Y.-S.; Lek, S. Chapter 7—Artificial Neural Networks: Multilayer Perceptron for Ecological Modeling. In Developments in Environmental Modelling; Jørgensen, S.E., Ed.; Ecological Model Types; Elsevier: Amsterdam, The Netherlands, 2016; Volume 28, pp. 123–140. [Google Scholar]
- Abbasi, N.A.; Hamrani, A.; Madramootoo, C.A.; Zhang, T.; Tan, C.S.; Goyal, M.K. Modelling Carbon Dioxide Emissions under a Maize-Soy Rotation Using Machine Learning. Biosyst. Eng. 2021, 212, 1–18. [Google Scholar] [CrossRef]
- Chen, S.; Xu, D.; Li, S.; Ji, W.; Yang, M.; Zhou, Y.; Hu, B.; Xu, H.; Shi, Z. Monitoring Soil Organic Carbon in Alpine Soils Using in Situ vis-NIR Spectroscopy and a Multilayer Perceptron. Land Degrad. Dev. 2020, 31, 1026–1038. [Google Scholar] [CrossRef]
- Liu, J.; Ji, Y.-H.; Zhou, G.-S.; Zhou, L.; Lyu, X.-M.; Zhou, M.-Z. Temporal and Spatial Variations of Net Primary Productivity (NPP) and Its Climate Driving Effect in the Qinghai-Tibet Plateau, China from 2000 to 2020. Ying Yong Sheng Tai Xue Bao = J. Appl. Ecol./Zhongguo Sheng Tai Xue Xue Hui Zhongguo Ke Xue Yuan Shenyang Ying Yong Sheng Tai Yan Jiu Suo Zhu Ban 2022, 33, 1533–1538. [Google Scholar] [CrossRef]
- Cutler, D.R.; Edwards, T.C., Jr.; Beard, K.H.; Cutler, A.; Hess, K.T.; Gibson, J.; Lawler, J.J. Random Forests for Classification in Ecology. Ecology 2007, 88, 2783–2792. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Nicholson, D.; Huang, B.; Cassar, N. Global Estimates of Marine Gross Primary Production Based on Machine Learning Upscaling of Field Observations. Glob. Biogeochem. Cycles 2021, 35, e2020GB006718. [Google Scholar] [CrossRef]
- Zeng, J.; Matsunaga, T.; Tan, Z.-H.; Saigusa, N.; Shirai, T.; Tang, Y.; Peng, S.; Fukuda, Y. Global Terrestrial Carbon Fluxes of 1999–2019 Estimated by Upscaling Eddy Covariance Data with a Random Forest. Sci. Data 2020, 7, 313. [Google Scholar] [CrossRef]
- Guliyev, N.J.; Ismailov, V.E. On the Approximation by Single Hidden Layer Feedforward Neural Networks with Fixed Weights. Neural Netw. 2018, 98, 296–304. [Google Scholar] [CrossRef]
- Chen, B. The Impact of Climate Change and Anthropogenic Activities on Alpine Grassland over the Qinghai-Tibet Plateau. Agric. For. Meteorol. 2014, 189–190, 11–18. [Google Scholar] [CrossRef]
- Zhang, X. Spatial-Temporal Changes in NPP and Its Relationship with Climate Factors Based on Sensitivity Analysis in the Shiyang River Basin. J. Earth Syst. Sci. 2020, 129, 24. [Google Scholar] [CrossRef]
- Cheshmberah, F.; Fathizad, H.; Parad, G.A.; Shojaeifar, S. Comparison of RBF and MLP Neural Network Performance and Regression Analysis to Estimate Carbon Sequestration. Int. J. Environ. Sci. Technol. 2020, 17, 3891–3900. [Google Scholar] [CrossRef]
- Mirici, M.E. Land use/cover change modelling in a mediterranean rural landscape using multi-layer perceptron and markov chain (MLP-MC). Appl. Ecol. Environ. Res. 2018, 16, 467–486. [Google Scholar] [CrossRef]
- Guo, Y.; Li, Y.; Xu, Y. Study on the Application of LSTM-LightGBM Model in Stock Rise and Fall Prediction. MATEC Web Conf. 2021, 336, 05011. [Google Scholar] [CrossRef]
- Li, M.; Li, Q.; Xue, M. Spatio-Temporal Changes of Vegetation Net Primary Productivity and Its Driving Factors on the Tibetan Plateau from 1979 to 2018. Atmosphere 2024, 15, 579. [Google Scholar] [CrossRef]
- Zheng, Z.; Zhu, W.; Zhang, Y. Seasonally and Spatially Varied Controls of Climatic Factors on Net Primary Productivity in Alpine Grasslands on the Tibetan Plateau. Glob. Ecol. Conserv. 2020, 21, e00814. [Google Scholar] [CrossRef]
- Yan, W.; Sun, G.; Zhang, C.; He, J.; Zhang, N. Impacts of Experimental Warming and Moderate Grazing on Ecosystem Carbon Exchange and Its Compositions in an Alpine Meadow on the Eastern Qinghai-Tibetan Plateau. Chin. J. Appl. Environ. Biol. 2018, 24, 132–139. [Google Scholar] [CrossRef]
- Ren, Y.; Yang, K.; Wang, H.; Zhao, L.; Chen, Y.; Zhou, X.; La, Z. The South Asia Monsoon Break Promotes Grass Growth on the Tibetan Plateau. J. Geophys. Res. (Biogeosciences) 2021, 126, e2020JG005951. [Google Scholar] [CrossRef]
- Wang, S.; Liu, F.; Zhou, Q.; Chen, Q.; Liu, F. Simulation and Estimation of Future Ecological Risk on the Qinghai-Tibet Plateau. Sci. Rep. 2021, 11, 17603. [Google Scholar] [CrossRef]
- Jin, H.; Wang, S.; Yan, P.; Qiao, L.; Sun, L.; Zhang, L. Spatial and Temporal Characteristics of Surface Solar Radiation in China and Its Influencing Factors. Front. Environ. Sci. 2022, 10, 916748. [Google Scholar] [CrossRef]
- Hao, A.; Xue, X.; Duan, H.; Peng, F.; You, Q. Different Spatiotemporal Variations in Seasonal NDVI and Their Climatic Driving Forces of a Typical Grassland on the Qinghai-Tibetan Plateau. Acta Ecol. Sin. 2022, 43, 352–363. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).