Prediction of Specific Fuel Consumption of a Tractor during the Tillage Process Using an Artificial Neural Network Method
Abstract
:1. Introduction
2. Materials and Methods
2.1. The Information Needed to Model Tractor-Specific Fuel Consumption
2.2. The Validity of Fuel Consumption and Draft Measurements in the Collected Dataset
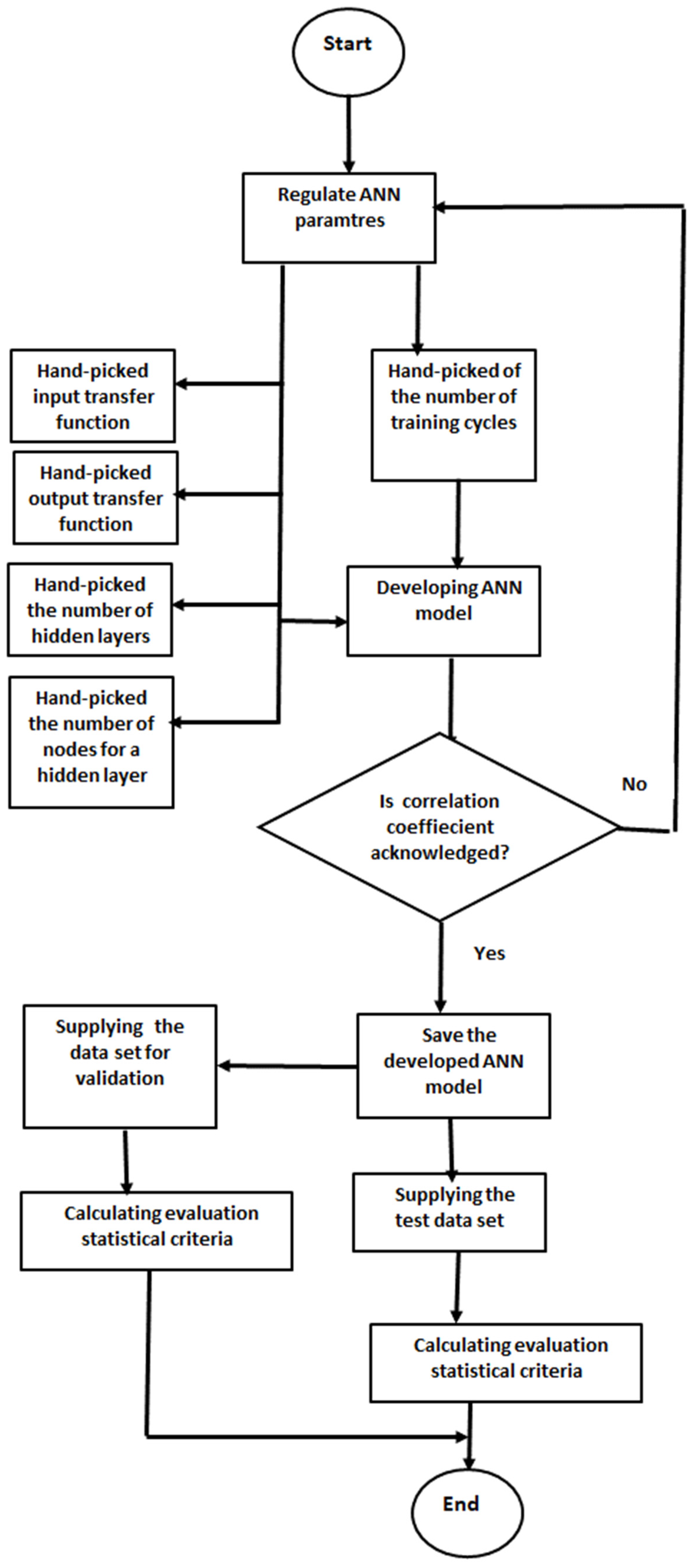
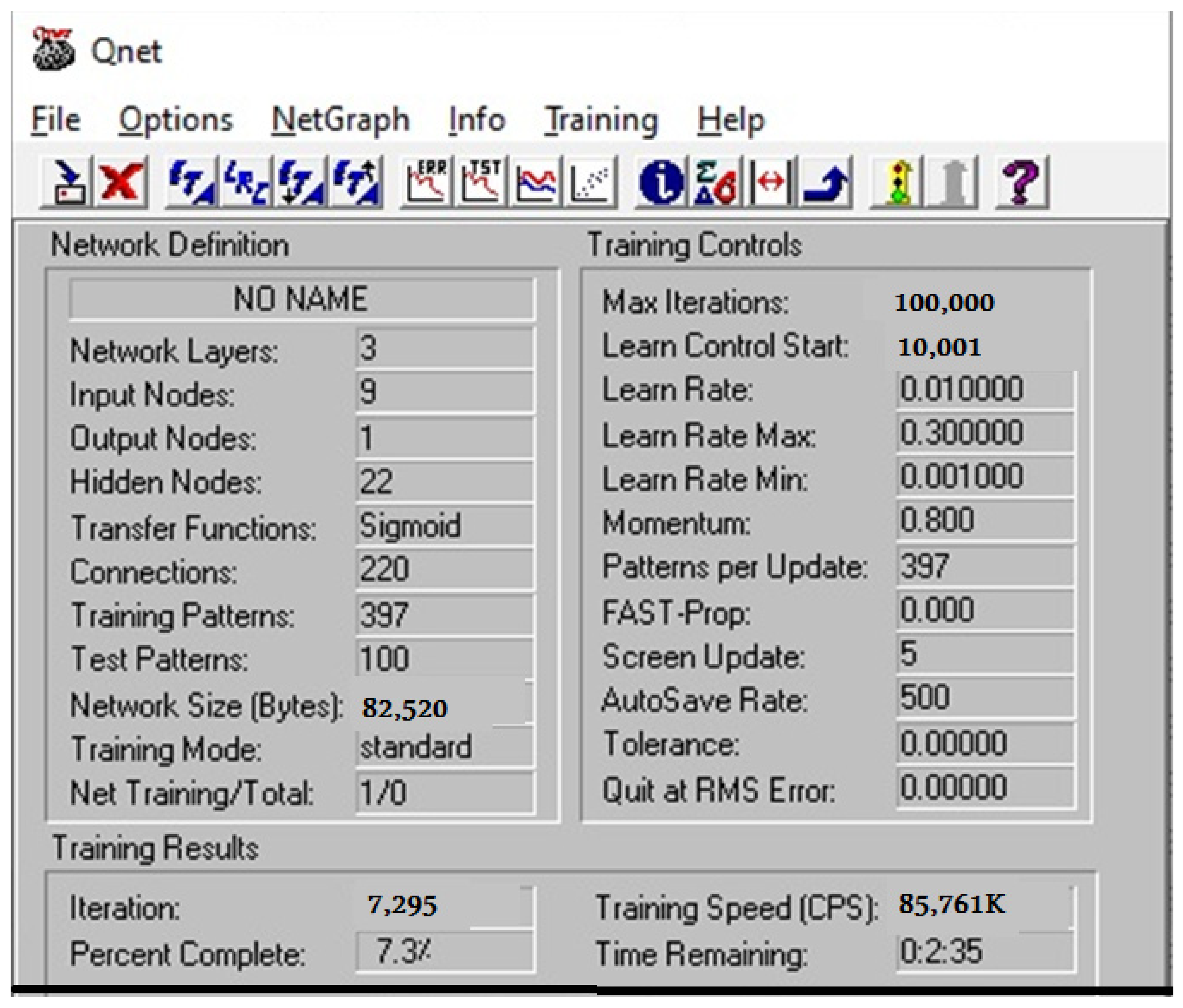
2.3. Structure of Tractor-Specific Fuel Consumption Prediction ANN Model
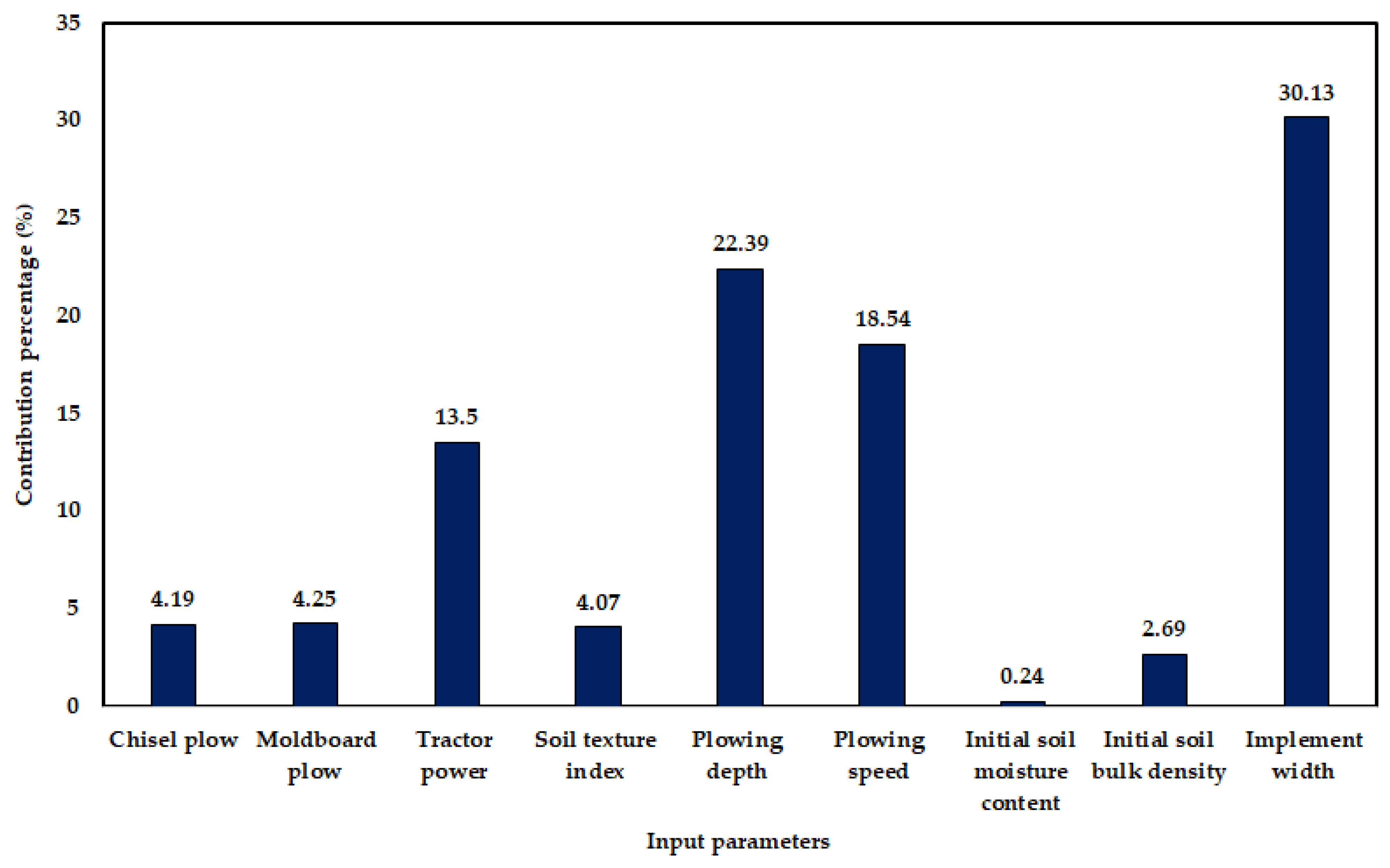
2.4. Calculating the Importance of Variable Contributions
2.5. Field Experiments for Verifying the Developed ANN Model
2.6. Evaluation of the Developed ANN Model’s Performance
3. Results and Discussion
3.1. Statistical Data Analysis
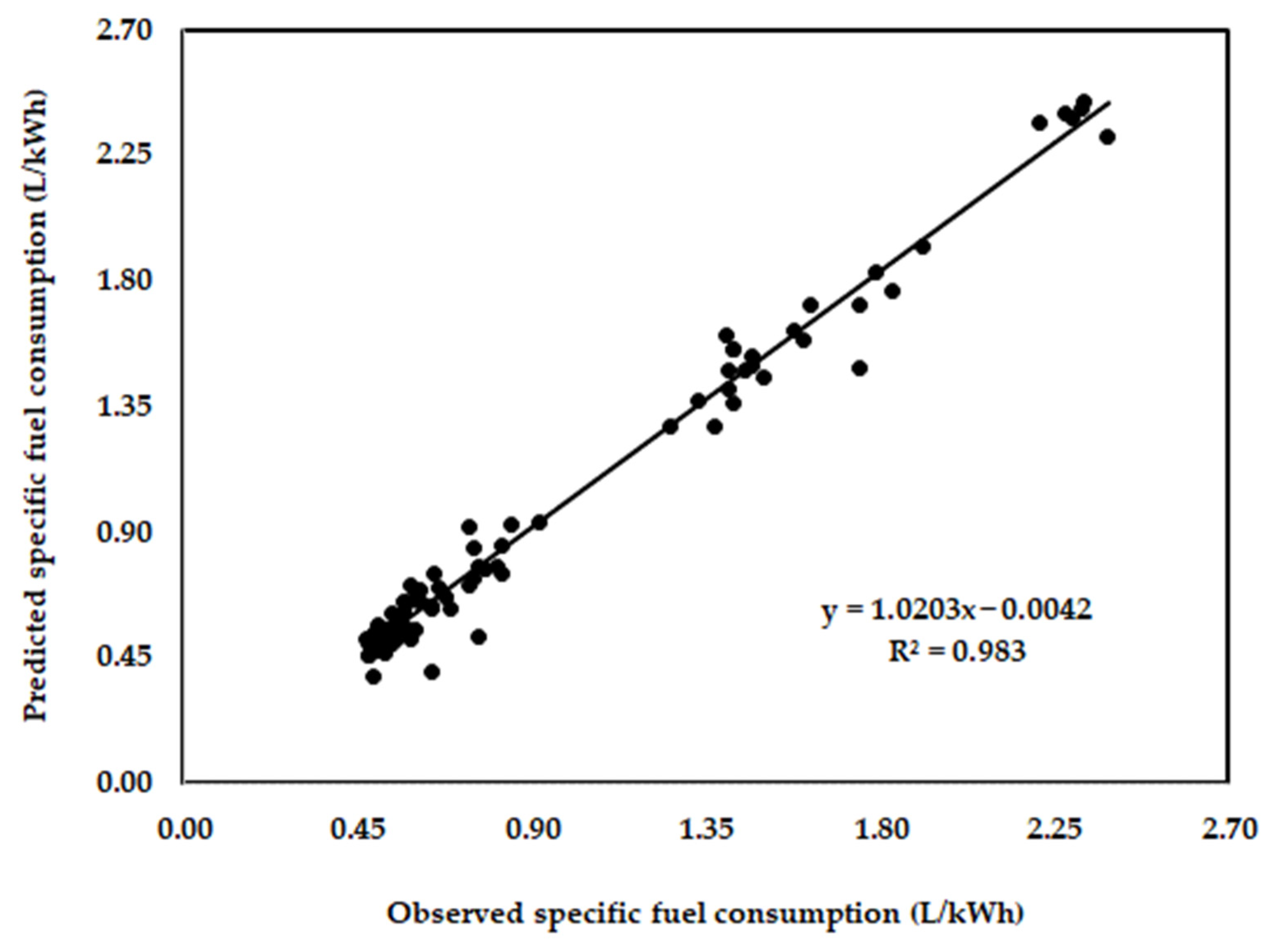
3.2. Analysis of the Developed ANN Model Using Training and Testing Datasets
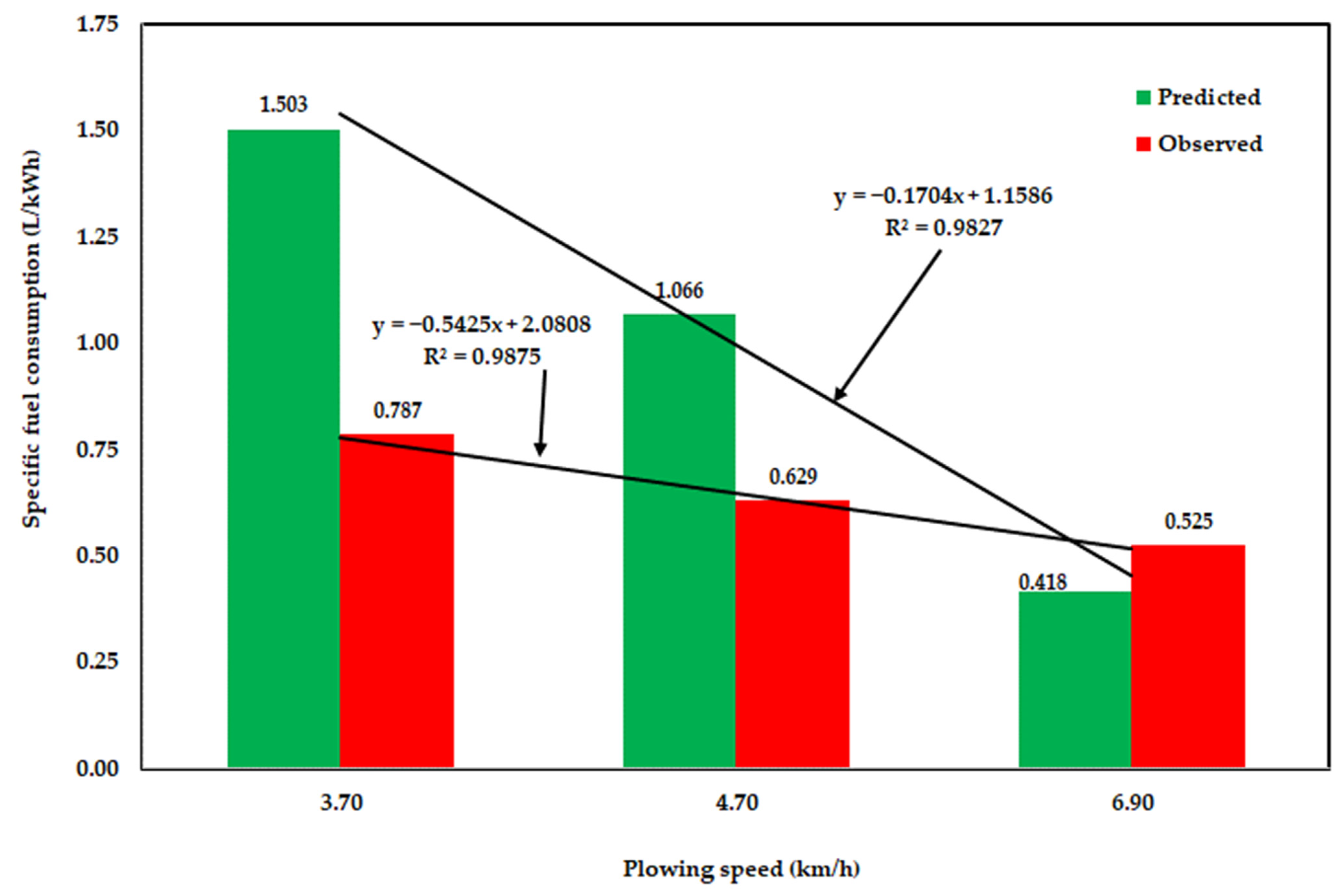
3.3. Analysis of the Developed ANN Model Using Validation Dataset
3.4. Contribution Analysis of the Affecting Parameters on Predicted Specific Fuel Consumption
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Adewoyin, A.O.; Ajav, E. Fuel consumption of some tractor models for ploughing operations in the sandy-loam soil of Nigeria at various speeds and ploughing depths. Agric. Eng. Int. CIGR J. 2013, 15, 67–74. [Google Scholar]
- Kolator, B.A. Modeling of tractor fuel consumption. Energies 2021, 14, 2300. [Google Scholar] [CrossRef]
- Alhassan, E.A.; Asaleye, J.A.; Biniyat, J.K.; Alhassan, T.R.; Olaoy, J.O. Tractor acquisition and agricultural performance among Nigerian farmers: Evidence from co-integration modeling technique. Heliyon 2024, 10, e24485. [Google Scholar] [CrossRef]
- Janulevičius, A.; Šarauskis, E.; Čiplienė, A.; Juostas, A. Estimation of farm tractor performance as a function of time efficiency during ploughing in fields of different sizes. Biosyst. Eng. 2019, 179, 80–93. [Google Scholar] [CrossRef]
- Dahab, M.H.; Kheiry, A.N.O.; Talha, T.H.A. A computer model of fuel consumption estimation for different agricultural farm operations. Int. J. Environ. Agric. Res. 2016, 2, 77–85. [Google Scholar]
- Kim, W.S.; Kim, Y.J.; Chung, S.O.; Lee, D.H.; Choi, C.H.; Yoon, Y.H. Development of simulation model for fuel efficiency of agricultural tractor. Korean J. Agric. Sci. 2016, 43, 116–126. [Google Scholar] [CrossRef]
- Kareem, K.I.; Peets, S. Effect of ploughing depth, tractor forward speed, and plough types on the fuel consumption and tractor performance. Polytech. J. 2019, 9, 43–49. [Google Scholar] [CrossRef]
- Moitzi, G.; Wagentristl, H.; Refenner, K.; Reinhardtian, H.; Piringer, G.; Boxberger, J.; Gronauer, A. Effects of working depth and wheel slip on fuel consumption of selected tillage implements. Agric. Eng. Int. CIGR J. 2014, 16, 184–190. [Google Scholar]
- Tayel, M.Y.; Shaaban, S.M.; Mansour, H.A. Effect of plowing conditions on the tractor wheel slippage and fuel consumption in sandy soil. Int. J. ChemTech Res. CODEN 2015, 8, 151–159. [Google Scholar]
- Ekemube, R.A.; Nkakini, S.O.; Igoni, A.H.; Akpa, J.G. Evaluation of tractor fuel efficiency parameters variability during ploughing operations. In Proceedings of the International Conference on New Views in Engineering and Technology (Icnet) Maiden Edition, Port Harcourt, Nigeria, 27 October 2021; pp. 111–122. [Google Scholar]
- Ekemube, R.A.; Atta, A.T.; Ndirika, V.I.O. Optimization of fuel consumption for tractor-tilled land area during harrowing operation using full factorial experimental design. Covenant J. Eng. Technol. 2023, 7, 21–31. [Google Scholar]
- Tihanov, G.; Ivanov, N. Fuel consumption of a machine-tractor unit in direct sowing of wheat. Agric. Sci. Technol. 2021, 13, 40–42. [Google Scholar] [CrossRef]
- Lee, J.W.; Kim, J.S.; Kim, K.U. Computer simulations to maximise fuel efficiency and work performance of agricultural tractors in rotovating and ploughing operations. Biosyst. Eng. 2016, 142, 1–11. [Google Scholar] [CrossRef]
- Oyelade, O.A.; Oni, K.C. Modelling of tractor fuel consumption for harrowing operation in a sandy loam soil. Arid. Zone J. Eng. Technol. Environ. 2018, 14, 8–19. [Google Scholar]
- Almaliki, S.; Alimardani, R.; Omid, M. Fuel consumption models of MF285 tractor under various field conditions. Agric. Eng. Int. CIGR J. 2016, 18, 147–152. [Google Scholar]
- Shafaei, S.M.; Loghavi, M.; Kamgar, S. A comparative study between mathematical models and the ANN data mining technique in draft force prediction of disk plow implement in clay loam soil. Agric. Eng. Int. CIGR J. 2018, 20, 71–79. [Google Scholar]
- Jalilnezhad, H.; Abbaspour-Gilandeh, Y.; Rasooli-Sharabiani, V.; Mardani, A.; Hernández-Hernández, J.L.; Montero-Valverde, J.A.; Hernández-Hernández, M. Use of a convolutional neural network for predicting fuel consumption of an agricultural tractor. Resources 2023, 12, 46. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A.; Karim-Maslak, H.; Kalbkhan, H. Artificial neural network estimation of wheel rolling resistance in clay loam soil. Appl. Soft Comput. 2013, 13, 3544–3551. [Google Scholar] [CrossRef]
- Taghavifar, H.; Mardani, A.; Hosseinloo, A.H. Appraisal of artificial neural network-genetic algorithm-based model for prediction of the power provided by the agricultural tractors. Energy 2015, 93, 1704–1717. [Google Scholar] [CrossRef]
- Çarman, K.; Çitil, E.; Taner, A. Artificial neural network model for predicting specific draft force and fuel consumption requirement of a mouldboard plough. Selcuk. J. Agric. Food Sci. 2019, 33, 241–247. [Google Scholar] [CrossRef]
- Küçüksarıyıldız, H.; Çarman, K.; Sabancı, K. Prediction of specific fuel consumption of 60 HP 2WD tractor using artificial neural networks. Int. J. Automot. Sci. Technol. 2021, 5, 436–444. [Google Scholar] [CrossRef]
- Dahham, G.A.; Al-Irhayim, M.N.; Al-Mistawi, K.E.; Khessro, M.K. Performance evaluation of artificial neural network modelling to a ploughing unit in various soil conditions. Acta Technol. Agric. 2023, 26, 194–200. [Google Scholar] [CrossRef]
- Kazemi, N.; Almassi, M.; Bahrami, H.; Shaykhdavoodi, M.; Mesgarbashi, M. Analysis of factors affecting the management of overall energy efficiency of tractor-implement by real-time performance monitoring. J. Agric. Mach. 2015, 4, 214–225. [Google Scholar]
- Far, A.S.; Kazemi, N.; Rahnama, M.; Nejad, M.G. Simultaneous comparison of the effects of shaft load and shaft positions on tractor OEE in two soil conditions (cultivated and uncultivated). Int. J. Farming Allied Sci. 2015, 4, 215–221. [Google Scholar]
- Pitla, S.K.; Luck, J.D.; Werner, J.; Lin, N.; Shearer, S.A. In-field fuel use and load states of agricultural field machinery. Comput. Electron. Agric. 2016, 121, 290–300. [Google Scholar] [CrossRef]
- López-Vázquez, A.; Cadena-Zapata, M.; Campos-Magaña, S.; Zermeño-Gonzalez, A.; Mendez-Dorado, M. Comparison of energy used and effects on bulk density and yield by tillage systems in a semiarid condition of Mexico. Agronomy 2019, 9, 189. [Google Scholar] [CrossRef]
- Askari, M.; Abbaspour-Gilandeh, Y.; Taghinezhad, E.; Hegazy, R.; Okasha, M. Prediction and optimizing the multiple responses of the overall energy efficiency (OEE) of a tractor-implement system using response surface methodology. J. Terramech. 2022, 103, 11–17. [Google Scholar] [CrossRef]
- Ranjbarian, S.; Askari, M.; Jannatkhah, J. Performance of tractor and tillage implements in clay soil. J. Saudi Soc. Agric. Sci. 2017, 16, 154–162. [Google Scholar] [CrossRef]
- Uddin, S.M.A.; Ahamed, J.U.; Alam, M.M.; Azad, A.K. Performance comparison of di diesel engine by using esterified mustard oil and pure musatrd oil blending with diesel. Mech. Eng. Res. J. 2013, 9, 104–109. [Google Scholar]
- Schaschke, C.; Fletcher, I.; Glen, N. Density and viscosity measurement of diesel fuels at combined high pressure and elevated temperature. Processes 2013, 1, 30–48. [Google Scholar] [CrossRef]
- Osman, S.; Stefaniu, A. Density, viscosity, and distillation temperatures of binary blends of diesel fuel mixed with oxygenated components at different temperatures. Sustainability 2023, 15, 15460. [Google Scholar] [CrossRef]
- Klanfar, M.; Korman, T.; Kujundžić, T. Fuel consumption and engine load factors of equipment in quarrying of crushed stone. Teh. Vjesn. 2016, 23, 163–169. [Google Scholar] [CrossRef]
- Damanauskas, V.; Janulevicius, A. Validation of criteria for predicting tractor fuel consumption and CO2 emissions when ploughing fields of different shapes and dimensions. AgriEngineering 2023, 5, 2408–2422. [Google Scholar] [CrossRef]
- Niazian, M.; Niedbała, G. Machine learning for plant breeding and biotechnology. Agriculture 2020, 10, 436. [Google Scholar] [CrossRef]
- Zhang, Q.; Deng, D.; Dai, W.; Li, J.; Jin, X. Optimization of culture conditions for differentiation of melon based on artificial neural network and genetic algorithm. Sci. Rep. 2020, 10, 3524. [Google Scholar] [CrossRef]
- Sharma, P.; Said, Z.; Kumar, A.; Nižetić, S.; Pandey, A.; Hoang, A.T.; Huang, Z.; Afzal, A.; Li, C.; Le, A.T.; et al. Recent advances in machine learning research for nanofluid-based heat transfer in renewable energy system. Energy Fuels 2022, 36, 6626–6658. [Google Scholar] [CrossRef]
- Gosukonda, R.; Mahapatra, A.K.; Ekefre, D.; Latimore, M., Jr. Prediction of thermal properties of sweet sorghum bagasse as a function of moisture content using artificial neural networks and regression models. Acta Technol. Agric. 2017, 2, 29–35. [Google Scholar] [CrossRef]
- Montesinos López, O.A.; Montesinos López, A.; Crossa, J. Fundamentals of Artificial Neural Networks and Deep Learning. In Multivariate Statistical Machine Learning Methods for Genomic Prediction; Springer: Cham, Switzerland, 2022. [Google Scholar] [CrossRef]
- Sheela, K.G.; Deepa, S.N. Review on methods to fix number of hidden neurons in neural networks. Math. Probl. Eng. 2013, 2013, 425740. [Google Scholar] [CrossRef]
- Abdipour, M.; Younessi-Hmazekhanlu, M.; Ramazani, M.Y.H.; Omidi, A.H. Artificial neural networks and multiple linear regression as potential methods for modeling seed yield of safflower (Carthamus tinctorius L.). Ind. Crops Prod. 2019, 27, 185–194. [Google Scholar] [CrossRef]
- Zheng, A.; Casari, A. Feature Engineering for Machine Learning: Principles and Techniques for Data Scientists; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2018. [Google Scholar]
- Silva, F.A.N.; Delgado, J.M.P.Q.; Cavalcanti, R.S.; Azevedo, A.C.; Guimarães, A.S.; Lima, A.G.B. Use of nondestructive testing of ultrasound and artificial neural networks to estimate compressive strength of concrete. Buildings 2021, 11, 44. [Google Scholar] [CrossRef]
- Brandic, I.; Pezo, L.; Bilandžija, N.; Peter, A.; Šuri’c, J.; Vo´ca, N. Artificial neural network as a tool for estimation of the higher heating value of miscanthus based on ultimate analysis. Mathematics 2022, 10, 3732. [Google Scholar] [CrossRef]
- Hensh, S.; Chattopadhyay, P.S.; Das, K. Drawbar performance of a power tiller on a sandy loam soil of the Nadia district of West Bengal. Res. Agric. Eng. 2022, 68, 41–46. [Google Scholar] [CrossRef]
- Tsae, N.B.; Adachi, T.; Kawamura, Y. Application of artificial neural network for the prediction of copper ore grade. Minerals 2023, 13, 658. [Google Scholar] [CrossRef]
- Sammen, S.S.; Kisi, O.; Ehteram, M.; El-Shafie, A.; Al-Ansari, N.; Ghorbani, M.A.; Bhat, S.A.; Ahmed, A.N.; Shahid, S. Rainfall modeling using two different neural networks improved by metaheuristic algorithms. Environ. Sci. Eur. 2023, 35, 112. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Lee, S.-D.; Baek, S.-M.; Baek, S.-Y.; Jeon, H.-H.; Lee, J.-H.; Kim, W.-S.; Shim, J.-Y.; Kim, Y.-J. Analysis of the Effect of Tillage Depth on the Working Performance of Tractor-Moldboard Plow System under Various Field Environments. Sensors 2022, 22, 2750. [Google Scholar] [CrossRef] [PubMed]
- Chenarbon, H.A. Effect of moldboard plow share age and tillage depth on slippage and fuel consumption of Tractor (MF399) in Varamin region. Idesia 2022, 40, 113–122. [Google Scholar] [CrossRef]
- Moitzi, G.; Haas, M.; Wagentristl, H.; Boxberger, J.; Gronauer, A. Energy consumption in cultivating and ploughing with traction improvement system and consideration of the rear furrow wheel-load in ploughing. Soil Tillage Res. 2013, 134, 56–60. [Google Scholar] [CrossRef]
- Askari, M.; Abbaspour-Gilandeh, Y.; Taghinezhad, E.; El Shal, A.M.; Hegazy, R.; Okasha, M. Applying the response surface methodology (rsm) approach to predict the tractive performance of an agricultural tractor during semi-deep tillage. Agriculture 2021, 11, 1043. [Google Scholar] [CrossRef]
- Said, Z.; Sharma, P.; Elavarasan, R.M.; Tiwari, A.K.; Rathod, M.K. Exploring the specific heat capacity of water-based hybrid nanofluids for solar energy applications: A comparative evaluation of modern ensemble machine learning techniques. J. Energy Storage 2022, 54, 105230. [Google Scholar] [CrossRef]
- Chen, H.; Bu, Y.; Zong, K.; Huang, L.; Hao, W. The Effect of Data Skewness on the LSTM-Based Mooring Load Prediction Model. J. Mar. Sci. Eng. 2022, 10, 1931. [Google Scholar] [CrossRef]
- Ahmadi, I. A draught force estimator for disc harrow using the laws of classical soil mechanics. Biosyst. Eng. 2018, 171, 52–62. [Google Scholar] [CrossRef]
- Oduma, O.; Ehiomogue, P.; Okeke, C.G.; Orji, N.F.; Ugwu, E.C.; Umunna, M.F.; Nwosu-Obieogu, K. Modeling and optimization of energy requirements of disc plough operation on loamy-sand soil in South-East Nigeria using response surface methodology. Sci. Afr. 2022, 17, e01325. [Google Scholar] [CrossRef]
- Gebre, T.; Abdi, Z.; Wako, A.; Yitbarek, T. Development of a mathematical model for determining the draft force of ard plow in silt clay soil. J. Terramech. 2023, 106, 13–19. [Google Scholar] [CrossRef]
- Fawzi, H.; Mostafa, S.A.; Ahmed, D.; Alduais, N.; Mohammed, M.A.; Elhoseny, M. TOQO: A new tillage operations quality optimization model based on parallel and dynamic decision support system. J. Clean. Prod. 2021, 316, 128263. [Google Scholar] [CrossRef]
- He, C.; Guo, Y.; Guo, X.; Sang, H. A mathematical model for predicting the draft force of shank-type tillage tine in a compacted sandy loam. Soil Tillage Res. 2023, 228, 105642. [Google Scholar] [CrossRef]
- Badgujar, C.; Das, S.; Figueroa, D.M.; Flippo, D. Application of computational intelligence methods in agricultural soil-machine interaction: A review. Agriculture 2022, 13, 357. [Google Scholar] [CrossRef]
- Cviklovič, V.; Srnánek, R.; Hrubý, D.; Harničárová, M. The control reversing algorithm for autonomous vehicles with PSD controlled trailers. Acta Technol. Agric. 2021, 24, 187–194. [Google Scholar] [CrossRef]
- Almaliki, S.; Alimardani, R.; Omid, M. Artificial neural network-based modeling of tractor performance at different field conditions. Agric. Eng. Int. CIGR J. 2016, 18, 262–273. [Google Scholar]
- Algezi, A.; Almaliki, S. Prediction of fuel consumption criteria of tractor using neural networks and mathematical models. Ann. For. Res. 2022, 65, 8902–8922. [Google Scholar]
- Zimmermann, G.G.; Jasper, S.P.; Savi, D.; Francetto, T.R.; Cortez, J.W. Full-powershift energy behavior tractor in soil tillage operation. Eng. Agrícola 2023, 43, e20230054. [Google Scholar] [CrossRef]
- Grisso, R. Predicting Tractor Diesel Fuel Consumption. Virginia Cooperative Extension; Publication 442-073; Virginia Tech: Blacksburg, VA, USA, 2020; 11p. [Google Scholar]
- Nagar, H.; Rajendra Machavaram, A.; Soni, P.; Mahore, V.; Patidar, P. Cloud-driven serverless framework for generalised tractor fuel consumption prediction model using machine learning. Cogent Eng. 2024, 11, 2311810. [Google Scholar] [CrossRef]


| Parameters | Statistical Criteria | ||||||
|---|---|---|---|---|---|---|---|
| Average | Maximum | Minimum | Standard Deviation | Coefficient of Variation (%) | Kurtosis | Skewness | |
| OEE (%) | 16.77 | 19.92 | 11.49 | 2.53 | 15.11 | −1.12 | −0.46 |
| Plowing speed (km/h) | 3.62 | 6.30 | 2.24 | 0.77 | 21.21 | 0.74 | 0.46 |
| Draft force (kN) | 11.09 | 19.52 | 6.88 | 3.00 | 27.05 | 0.15 | 0.85 |
| Plowing depth (cm) | 13.87 | 23.00 | 10.00 | 3.64 | 26.27 | 0.60 | 1.08 |
| Fuel rate (L/h) | 16.13 | 17.61 | 11.36 | 1.39 | 8.64 | 4.06 | −1.92 |
| Drawbar power (kW) | 10.70 | 17.84 | 6.96 | 1.98 | 18.49 | 2.40 | 0.83 |
| Specific fuel consumption (L/kWh) | 1.57 | 2.42 | 0.64 | 0.35 | 22.22 | 0.55 | 0.03 |
| Tractor power (kW) | 79.50 | 86.79 | 56.00 | 6.87 | 8.64 | 4.06 | −1.92 |
| Initial soil moisture content (db, %) | 16.47 | 20.50 | 6.80 | 3.83 | 23.26 | −0.39 | −0.98 |
| Initial soil bulk density (g/cm3) | 1.35 | 1.40 | 1.20 | 0.06 | 4.19 | 1.01 | −1.39 |
| Soil texture index (-) | 0.30 | 0.66 | 0.10 | 0.16 | 53.29 | 0.80 | 0.87 |
| Implement width (m) | 2.09 | 3.85 | 1.75 | 0.72 | 34.39 | 2.25 | 2.00 |
| No. of data points | 89 | 89 | 89 | 89 | 89 | 89 | 89 |
| Parameters | Statistical Criteria | ||||||
|---|---|---|---|---|---|---|---|
| Average | Maximum | Minimum | Standard Deviation | Coefficient of Variation (%) | Kurtosis | Skewness | |
| OEE (%) | 18.76 | 20.00 | 14.43 | 1.10 | 5.88 | −0.52 | −0.82 |
| Plowing speed (km/h) | 4.05 | 5.25 | 2.57 | 0.59 | 14.68 | 0.52 | 0.17 |
| Draft force (kN) | 14.12 | 18.63 | 8.23 | 3.17 | 22.44 | −0.15 | −0.51 |
| Plowing depth (cm) | 16.93 | 21.00 | 7.30 | 2.61 | 15.40 | 2.81 | −0.85 |
| Fuel rate (L/h) | 13.27 | 21.19 | 9.84 | 4.85 | 36.50 | 1.32 | 1.70 |
| Drawbar power (kW) | 16.06 | 21.73 | 7.89 | 4.66 | 28.99 | −1.06 | −0.51 |
| Specific fuel consumption (L/kWh) | 1.04 | 2.69 | 0.45 | 0.78 | 74.82 | 1.59 | 1.71 |
| Tractor power (kW) | 65.42 | 104.44 | 48.49 | 23.88 | 36.50 | 1.32 | 1.70 |
| Initial soil moisture content (db, %) | 14.56 | 19.80 | 8.26 | 2.98 | 20.44 | −0.97 | 0.25 |
| Initial soil bulk density (g/cm3) | 1.27 | 1.52 | 1.08 | 0.10 | 8.25 | −0.73 | 0.40 |
| Soil texture index (-) | 0.67 | 0.84 | 0.37 | 0.12 | 17.87 | 0.44 | −1.28 |
| Implement width (m) | 1.04 | 1.35 | 0.80 | 0.16 | 15.04 | 5.24 | −1.90 |
| No. of data points | 408 | 408 | 408 | 408 | 408 | 408 | 408 |
| Parameters | Value 1 | Value 2 | Value 3 |
|---|---|---|---|
| Sand content (%) | 28.6 | 28.6 | 28.6 |
| Silt content (%) | 17.7 | 17.7 | 17.7 |
| Clay content (%) | 53.7 | 53.7 | 53.7 |
| Soil texture index (-) | 0.306 | 0.306 | 0.306 |
| Tractor power (kW) | 82 | 82 | 82 |
| Plowing depth (cm) | 16 | 16 | 16 |
| Plowing speed (km/h) | 3.7 | 4.7 | 6.9 |
| Initial soil moisture content (%db) | 19.8 | 19.8 | 19.8 |
| Initial soil bulk density (g/cm3) | 1.36 | 1.36 | 1.36 |
| Implement width (m) | 1.75 | 1.75 | 1.75 |
| Draft force (kN) | 18.76 | 19.67 | 21.68 |
| Drawbar or draft power (kW) | 19.28 | 25.68 | 41.55 |
| Fuel consumption (L/h) | 15.18 | 16.15 | 21.81 |
| Specific fuel consumption per draft power (L/kWh) | 0.787 | 0.629 | 0.525 |
| Overall energy efficiency (%) | 12.44 | 15.57 | 18.66 |
| Statistical Criteria | Training Dataset | Testing Dataset |
|---|---|---|
| RMSE (L/kWh) | 0.080 | 0.075 |
| MAE (L/kWh) | 0.057 | 0.054 |
| R2 | 0.985 | 0.983 |
| Hidden-Layer Neurons | W1 = Weight between Inputs and Hidden Layer | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Chisel Plow | Moldboard Plow | Tractor Power | Soil Texture Index | Plowing Depth | Plowing Speed | Initial Soil Moisture Content | Initial Soil Bulk Density | Implement Width | |
| (-) | (-) | (kW) | (-) | (cm) | (km/h) | (db, %) | (g/cm3) | (m) | |
| 1 | 0.19035 | 0.19717 | −0.066 | −0.35153 | −0.08198 | −0.39646 | −0.04227 | −0.08694 | −0.15066 |
| 2 | −0.85962 | 0.72751 | −0.40716 | −0.03638 | 1.50896 | 1.0031 | 0.50304 | 0.16612 | 0.08197 |
| 3 | 0.00233 | 0.02025 | −0.05847 | 0.26385 | 0.26267 | 0.38647 | 0.11467 | 0.18132 | 0.18917 |
| 4 | 0.38077 | −0.21469 | −0.26129 | −0.502 | −0.34415 | −0.91834 | −0.07168 | −0.19367 | −0.15324 |
| 5 | −0.06246 | −0.01446 | −0.31216 | 0.57808 | 0.73648 | 1.168 | −0.11966 | −0.47513 | 0.96697 |
| 6 | −0.19697 | −0.07868 | −0.16973 | 0.43001 | 0.58962 | 0.8332 | −0.23802 | −0.46489 | 0.83826 |
| 7 | −0.33345 | 0.27957 | −0.39279 | 0.4924 | 0.8537 | 0.33519 | −0.05576 | −0.15482 | 0.64401 |
| 8 | −0.01909 | −0.31904 | −0.09156 | −0.08692 | −0.7128 | −0.51896 | 0.17518 | 0.23999 | −0.56896 |
| 9 | −0.41839 | −0.11352 | −0.33347 | 0.34396 | 1.00388 | 0.98626 | −0.14585 | −0.10698 | 0.9686 |
| 10 | −0.41947 | −0.10327 | −0.17008 | 0.08392 | 0.53608 | 0.55534 | 0.05861 | −0.387 | 0.75625 |
| 11 | 0.43118 | −0.29121 | 0.14553 | −0.67883 | −0.52845 | −0.46833 | −0.08864 | 0.31176 | −0.42124 |
| 12 | −0.22067 | −0.0067 | −0.45759 | 0.50522 | 1.02118 | 0.52727 | 0.25051 | −0.47065 | 0.68776 |
| 13 | 0.13672 | −0.09198 | 0.19434 | −0.555 | −1.1652 | −0.8032 | 0.09824 | 0.46372 | −0.5922 |
| 14 | 0.35919 | −0.11701 | 0.00218 | 0.00115 | −0.09005 | −0.05033 | −0.14423 | 0.04469 | −0.07174 |
| 15 | 0.09815 | 0.08976 | −0.33991 | 0.36695 | 0.12448 | 0.61201 | 0.1112 | −0.45562 | 0.40137 |
| 16 | −0.00078 | −0.37508 | −0.20905 | 0.01447 | −0.51086 | −0.67855 | 0.20613 | −0.21273 | −0.39427 |
| 17 | 0.03141 | 0.13665 | −0.28487 | −0.13061 | 0.28313 | 0.01639 | −0.04468 | 0.1166 | −0.2194 |
| 18 | 0.06939 | 0.24756 | −0.50143 | 0.02617 | 0.16886 | 0.29653 | 0.12143 | 0.06383 | 0.12486 |
| 19 | 0.43712 | −0.08713 | −0.08521 | −0.1167 | −0.11657 | −0.88368 | −0.15611 | −0.28614 | −0.40588 |
| 20 | −0.20107 | −0.20741 | −0.28109 | 0.14172 | 0.09101 | −0.25293 | 0.21062 | −0.08701 | −0.23752 |
| 21 | 0.15758 | −0.26284 | −0.19279 | −0.35602 | −0.30383 | −0.25393 | 0.01294 | −0.22675 | 0.03401 |
| 22 | −0.89838 | 0.0991 | 1.16689 | 1.44052 | −0.29635 | 0.63546 | −0.02438 | −0.47725 | −5.30476 |
| Hidden-Layer Neurons | B1 = Hidden-Layer Biases | W2 = Weight between Output and Hidden Layer | B2 = Output-Layer Biases |
|---|---|---|---|
| 1 | 0.16048 | 0.77215 | 0.85011 |
| 2 | 0.11971 | −1.52163 | |
| 3 | −0.16271 | −0.16302 | |
| 4 | 0.29622 | 1.29996 | |
| 5 | −0.37419 | −1.55898 | |
| 6 | −0.14713 | −1.13387 | |
| 7 | −0.20668 | −0.95499 | |
| 8 | 0.21623 | 1.28453 | |
| 9 | −0.04239 | −1.46011 | |
| 10 | 0.08792 | −0.8132 | |
| 11 | 0.11282 | 1.46147 | |
| 12 | 0.0023 | −1.14313 | |
| 13 | 0.0854 | 1.85898 | |
| 14 | 0.3168 | 0.5853 | |
| 15 | −0.19352 | −0.53014 | |
| 16 | 0.14068 | 1.10854 | |
| 17 | −0.19475 | 0.31311 | |
| 18 | −0.19155 | −0.09952 | |
| 19 | 0.10089 | 1.20881 | |
| 20 | −0.16293 | 0.40959 | |
| 21 | −0.19571 | 0.64424 | |
| 22 | −0.72726 | 4.84614 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Sager, S.M.; Almady, S.S.; Marey, S.A.; Al-Hamed, S.A.; Aboukarima, A.M. Prediction of Specific Fuel Consumption of a Tractor during the Tillage Process Using an Artificial Neural Network Method. Agronomy 2024, 14, 492. https://doi.org/10.3390/agronomy14030492
Al-Sager SM, Almady SS, Marey SA, Al-Hamed SA, Aboukarima AM. Prediction of Specific Fuel Consumption of a Tractor during the Tillage Process Using an Artificial Neural Network Method. Agronomy. 2024; 14(3):492. https://doi.org/10.3390/agronomy14030492
Chicago/Turabian StyleAl-Sager, Saleh M., Saad S. Almady, Samy A. Marey, Saad A. Al-Hamed, and Abdulwahed M. Aboukarima. 2024. "Prediction of Specific Fuel Consumption of a Tractor during the Tillage Process Using an Artificial Neural Network Method" Agronomy 14, no. 3: 492. https://doi.org/10.3390/agronomy14030492
APA StyleAl-Sager, S. M., Almady, S. S., Marey, S. A., Al-Hamed, S. A., & Aboukarima, A. M. (2024). Prediction of Specific Fuel Consumption of a Tractor during the Tillage Process Using an Artificial Neural Network Method. Agronomy, 14(3), 492. https://doi.org/10.3390/agronomy14030492









