A Novel Three-Segment Model to Describe the Entire Soil–Water Characteristic Curve
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the SWCC
2.2. Three-Segmented SWCC Model
2.3. Predicting SWD within the Interval Where 0 ≤ θ ≤ θPWP
2.4. Experimental Data
2.5. Fitting the Entire SWCC
2.6. Statistical Analyses
3. Results
3.1. Test of the Three-Segmented Model for the Entire SWCC
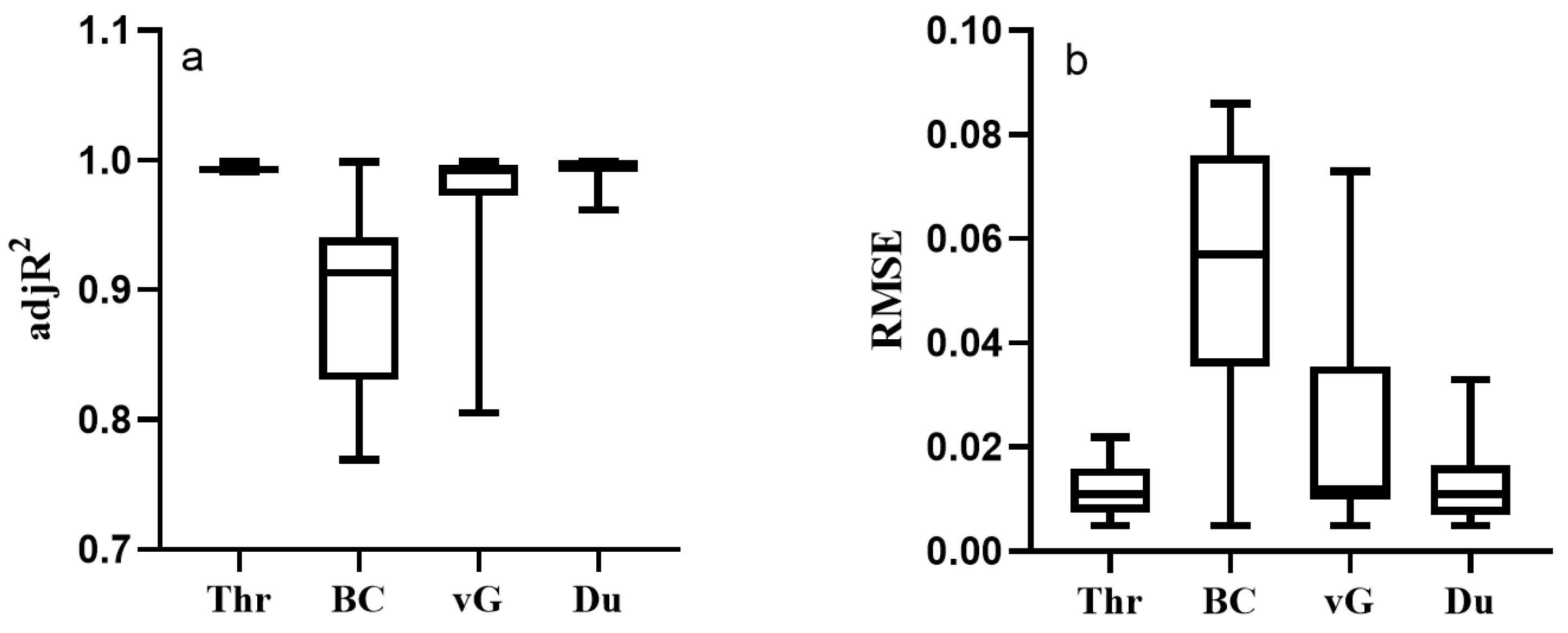
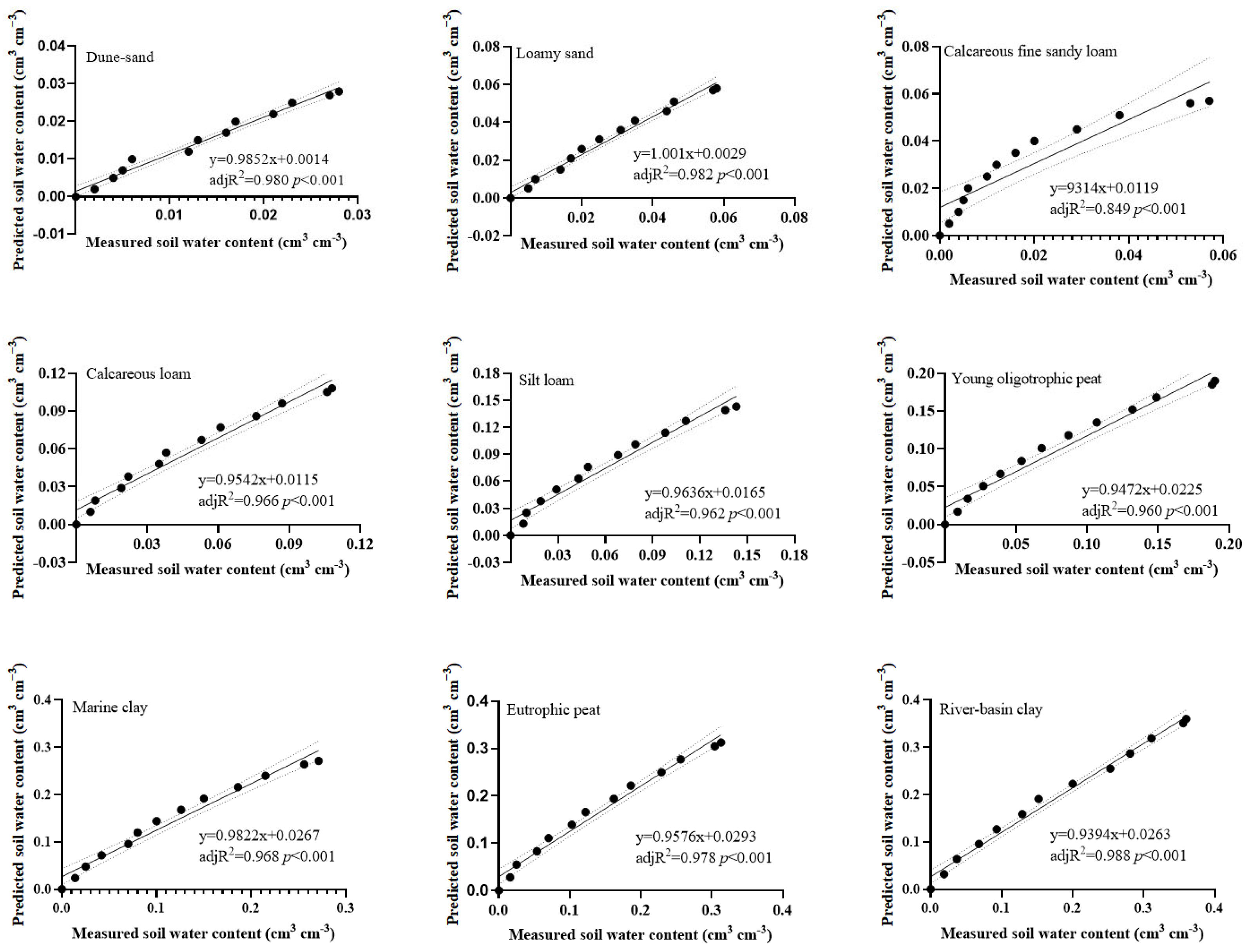
3.2. Comparison of SWCC Models
3.3. Predicting the Soil Water Content within the Interval of 0 ≤ θ ≤ θPWP
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Brooks, R.H.; Corey, A.T. Hydraulic Properties of Porous Media and Their Relation to Drainage Design. Trans. ASAE 1964, 92, 26–28. [Google Scholar]
- Campbell, G. A simple method for determining unsaturated conductivity from moisture retention data. Soil Sci. 1974, 117, 311–314. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Ikechukwu, A.F.; Hassan, M.M.; Moubarak, A. Resilient modulus and microstructure of unsaturated expansive subgrade stabilized with activated fly ash. Int. J. Geotech. Eng. 2021, 15, 915–938. [Google Scholar] [CrossRef]
- Onyelowe, K.C.; Mojtahedi, F.F.; Azizi, S.; Mahdi, H.A.; Sujatha, E.R.; Ebid, A.M.; Darzi, A.G.; Aneke, F.I. Innovative Overview of SWRC Application in Modeling Geotechnical Engineering Problems. Designs 2022, 6, 69. [Google Scholar] [CrossRef]
- Terleev, V.V.; Mirschel, W.; Badenko, V.L.; Guseva, I.Y. An improved Mualem–Van Genuchten method and its verification using data on Beit Netofa clay. Eurasian Soil Sci. 2017, 50, 445–455. [Google Scholar] [CrossRef]
- Kuang, X.; Jiao, J.J. A new equation for the soil water retention curve. Eur. J. Soil Sci. 2014, 65, 584–593. [Google Scholar] [CrossRef]
- Richards, L.A.; Weaver, L.R. Fifteen-atmosphere percentage as related to the permanent wilting point. Soil Sci. 1943, 56, 331–339. [Google Scholar] [CrossRef]
- Mualem, Y. A Catalogue of the Hydraulic Properties of Unsaturated Soils; Technical Report; Israel Institute of Technology: Haifa, Israel, 1976; pp. 28–70. [Google Scholar]
- Vogel, T.; Cislerova, M. On the reliability of unsaturated hydraulic conductivity calculated from the moisture retention curve. Transp. Porous Media 1988, 3, 1–15. [Google Scholar] [CrossRef]
- Webb, S.W. A simple extension of two-phase characteristic curves to include the dry region. Water Resour. Res. 2000, 36, 1425–1430. [Google Scholar] [CrossRef]
- Silva, O.; Grifoll, J. A soil-water retention function that includes the hyper-dry region through the BET adsorption isotherm. Water Resour. Res. 2007, 431, 398–408. [Google Scholar] [CrossRef]
- Groenevelt, P.H.; Grant, C.D. A new model for the soil-water retention curve that solves the problem of residual water contents. Eur. J. Soil Sci. 2004, 55, 479–485. [Google Scholar] [CrossRef]
- Ciocca, F.; Lunati, I.; Parlange, M.B. Effects of the water retention curve on evaporation from arid soils. Geophys. Res. Lett. 2014, 41, 3110–3116. [Google Scholar] [CrossRef]
- Rossi, C.; Nimmo, J.R. Modeling of soil water retention from saturation to oven dryness. Water Resour. Res. 1994, 30, 701–708. [Google Scholar] [CrossRef]
- Du, C. A novel segmental model to describe the complete soil water retention curve from saturation to oven dryness. J. Hydrol. 2020, 584, 124649. [Google Scholar] [CrossRef]
- Koorevaar, P.; Menelik, G.; Dirksen, C. Elements of Soil Physics; Elsevier: Amsterdam, The Netherlands, 1983. [Google Scholar]
- Chi, C. Two Models to Describe the Entire Soil Water Retention Curve. Eurasian Soil Sci. 2023, 56, 447–452. [Google Scholar] [CrossRef]
- Fredlund, D.G.; Xing, A. Equations for the soil-water characteristic curve. Can. Geotech. J. 1994, 31, 521–532. [Google Scholar] [CrossRef]
- Ross, P.J.; Williams, J.; Bristow, K.L. Equation for extending water-retention curves to dryness. Soil Sci. Soc. Am. J. 1991, 55, 923–927. [Google Scholar] [CrossRef]
- Fayer, M.J.; Simmons, C.S. Modified soil water retention functions for all matric suctions. Water Resour. Res. 1995, 31, 1233–1238. [Google Scholar] [CrossRef]
- Morel-Seytoux, H.J.; Nimmo, J.R. Soil water retention and maximum capillary drive from saturation to oven dryness. Water Resour. Res. 1999, 35, 2031–2041. [Google Scholar] [CrossRef]
- Zhang, Z.F. Soil Water Retention and Relative Permeability for Conditions from Oven-Dry to Full Saturation. Vadose Zone J. 2011, 10, 1299–1308. [Google Scholar] [CrossRef]
- Tuller, M.; Or, D. Water films and scaling of soil characteristic curves at low water contents. Water Resour. Res. 2005, 41, W09403. [Google Scholar] [CrossRef]
- Guan, L. General Soil Science, 2nd ed.; Agricultural University Press: Beijing, China, 2016. [Google Scholar]
- Smagin, A.V. Thermogravimetric determination of specific surface area for soil colloids. Colloid J. Russ. Acad. Sci. 2016, 78, 391–396. [Google Scholar] [CrossRef]
- Smagin, A.V. Thermodynamic Concept of Water Retention and Physical Quality of the Soil. Agronomy 2021, 11, 1686. [Google Scholar] [CrossRef]
- Schofield, R.K. The pF of the water in soil. Trans. 3rd Int. Congr. Soil Sci. 1935, 2, 37–48. [Google Scholar]
- Vanderlinden, K.; Pachepsky, Y.A.; Pederera-Parrilla, A.; Martínez, G.; Espejo-Pérez, A.J.; Perea, F.; Giráldez, J.V. Water Retention and Preferential States of Soil Moisture in a Cultivated Vertisol. Soil Sci. Soc. Am. J. 2017, 81, 1–9. [Google Scholar] [CrossRef]

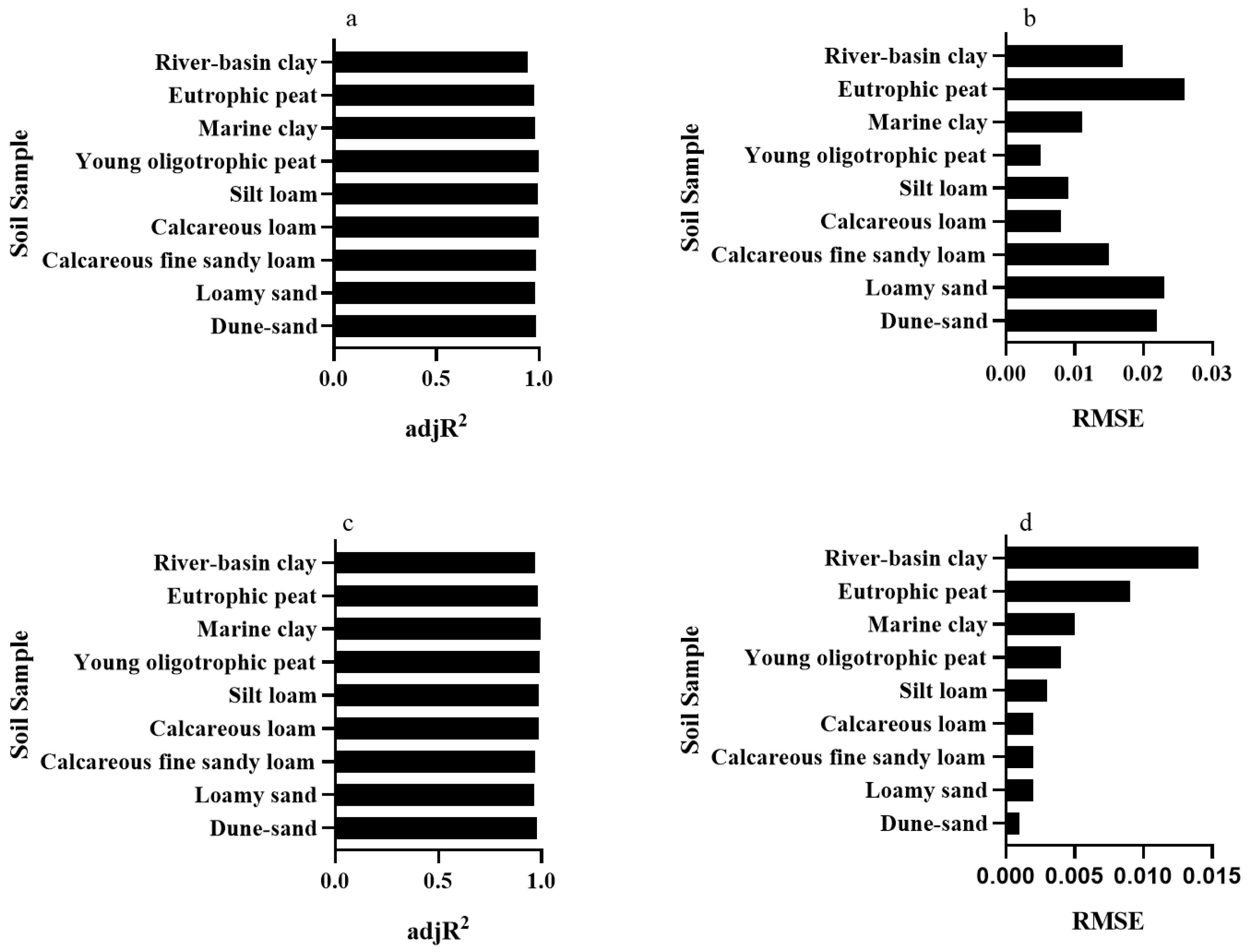
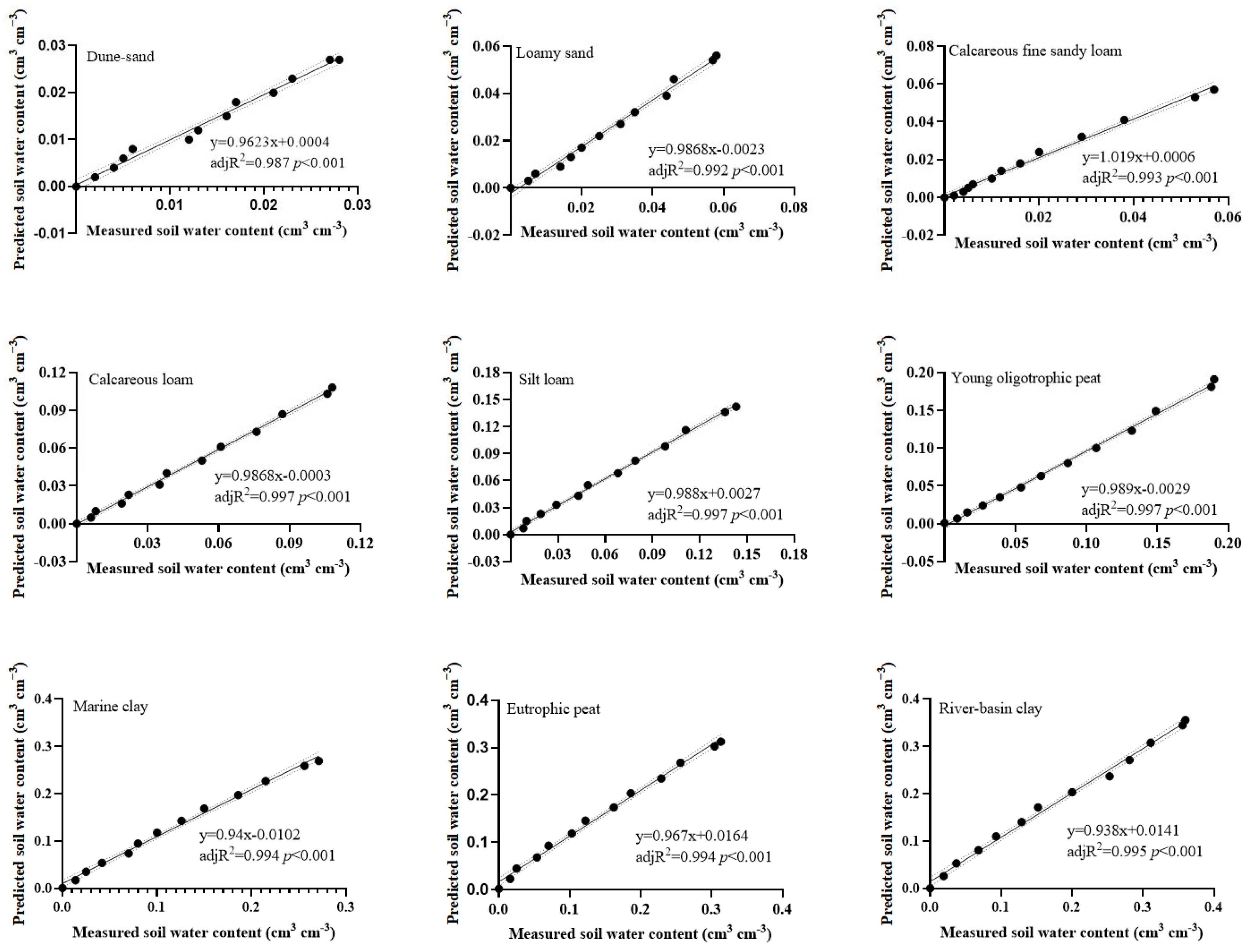
| Soil | θS | θR | θMH | θADC | ha | m | ω | λ | adjR2 | RMSE |
|---|---|---|---|---|---|---|---|---|---|---|
| cm3 cm−3 | cm | cm3 cm−3 | ||||||||
| Dune sand | 0.430 | 0.023 | 0.023 | 0.004 | 30 | 0.917 | 0.432 | 0.800 | 0.993 | 0.011 |
| Loamy sand | 0.469 | 0.043 | 0.046 | 0.010 | 146.7 | 0.938 | 0.401 | 0.740 | 0.991 | 0.016 |
| Calcareous fine sandy loam | 0.420 | 0.000 | 0.038 | 0.004 | 55 | 0.380 | 0.600 | 0.740 | 0.992 | 0.013 |
| Calcareous loam | 0.505 | 0.000 | 0.087 | 0.013 | 25 | 0.246 | 0.484 | 0.680 | 0.998 | 0.007 |
| Silt loam | 0.479 | 0.000 | 0.111 | 0.016 | 165 | 0.278 | 0.494 | 0.640 | 0.998 | 0.008 |
| Young oligotrophic peat | 0.835 | 0.029 | 0.149 | 0.021 | 50 | 0.35 | 0.498 | 0.540 | 0.999 | 0.013 |
| Marine clay | 0.474 | 0.000 | 0.215 | 0.034 | 1849 | 0.273 | 0.470 | 0.505 | 0.997 | 0.010 |
| Eutrophic peat | 0.777 | 0.000 | 0.256 | 0.040 | 39 | 0.165 | 0.472 | 0.502 | 0.992 | 0.022 |
| River-basin clay | 0.547 | 0.000 | 0.311 | 0.052 | 936 | 0.159 | 0.456 | 0.430 | 0.992 | 0.016 |
| SWCC Model | Function | Parameters | Reference |
|---|---|---|---|
| BC model | θ = (h/hd)−β(θS − θR) + θR | θR, hd, β | [1] |
| vG model | θ = [1 + (αh)N]1/(N−1)(θS − θR) + θR | θR, α, N | [3] |
| Du model | θI = [1 + (αh)N]1/(N−1)(θS − θR) + θR (0 ≤ h ≤ ha) θII = (hd/h)βθS (ha ≤ h ≤ hb) θIII = (hb ≤ h ≤ hZ) | θR, N, α, β, hZ, hb, θb | [16] |
| Soil | θc | θd | he | γ | adjR2 | RMSE |
|---|---|---|---|---|---|---|
| cm3 cm−3 | cm | cm3 cm−3 | ||||
| Dune sand | 0.163 | −0.028 | 0.104 | 0.104 | 0.992 | 0.003 |
| Loamy sand | 0.654 | −0.022 | 0.229 | 0.194 | 0.971 | 0.012 |
| Calcareous fine sandy loam | 2.896 | −0.004 | 1.169 | 0.408 | 0.993 | 0.007 |
| Calcareous loam | 1.229 | −0.037 | 0.473 | 0.209 | 0.997 | 0.008 |
| Silt loam | 1.267 | −0.064 | 0.474 | 0.180 | 0.996 | 0.012 |
| Young oligotrophic peat | 2.675 | −0.029 | 31620 | 0.35 | 0.999 | 0.005 |
| Marine clay | 1.530 | −0.24 | 0.294 | 0.115 | 0.982 | 0.042 |
| Eutrophic peat | 1.302 | −0.407 | 0.730 | 0.087 | 0.983 | 0.051 |
| River-basin clay | 1.230 | −0.689 | 1.131 | 0.064 | 0.992 | 0.042 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chi, C.; Zhao, C.; Zhi, J. A Novel Three-Segment Model to Describe the Entire Soil–Water Characteristic Curve. Agronomy 2024, 14, 707. https://doi.org/10.3390/agronomy14040707
Chi C, Zhao C, Zhi J. A Novel Three-Segment Model to Describe the Entire Soil–Water Characteristic Curve. Agronomy. 2024; 14(4):707. https://doi.org/10.3390/agronomy14040707
Chicago/Turabian StyleChi, Chunming, Changwei Zhao, and Jinhu Zhi. 2024. "A Novel Three-Segment Model to Describe the Entire Soil–Water Characteristic Curve" Agronomy 14, no. 4: 707. https://doi.org/10.3390/agronomy14040707
APA StyleChi, C., Zhao, C., & Zhi, J. (2024). A Novel Three-Segment Model to Describe the Entire Soil–Water Characteristic Curve. Agronomy, 14(4), 707. https://doi.org/10.3390/agronomy14040707






