Calibration and Evaluation of the SIMPLE Crop Growth Model Applied to the Common Bean under Irrigation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of the Study Area
2.2. Genetic Material and Crop Management
2.3. Irrigation Treatments and Experimental Design
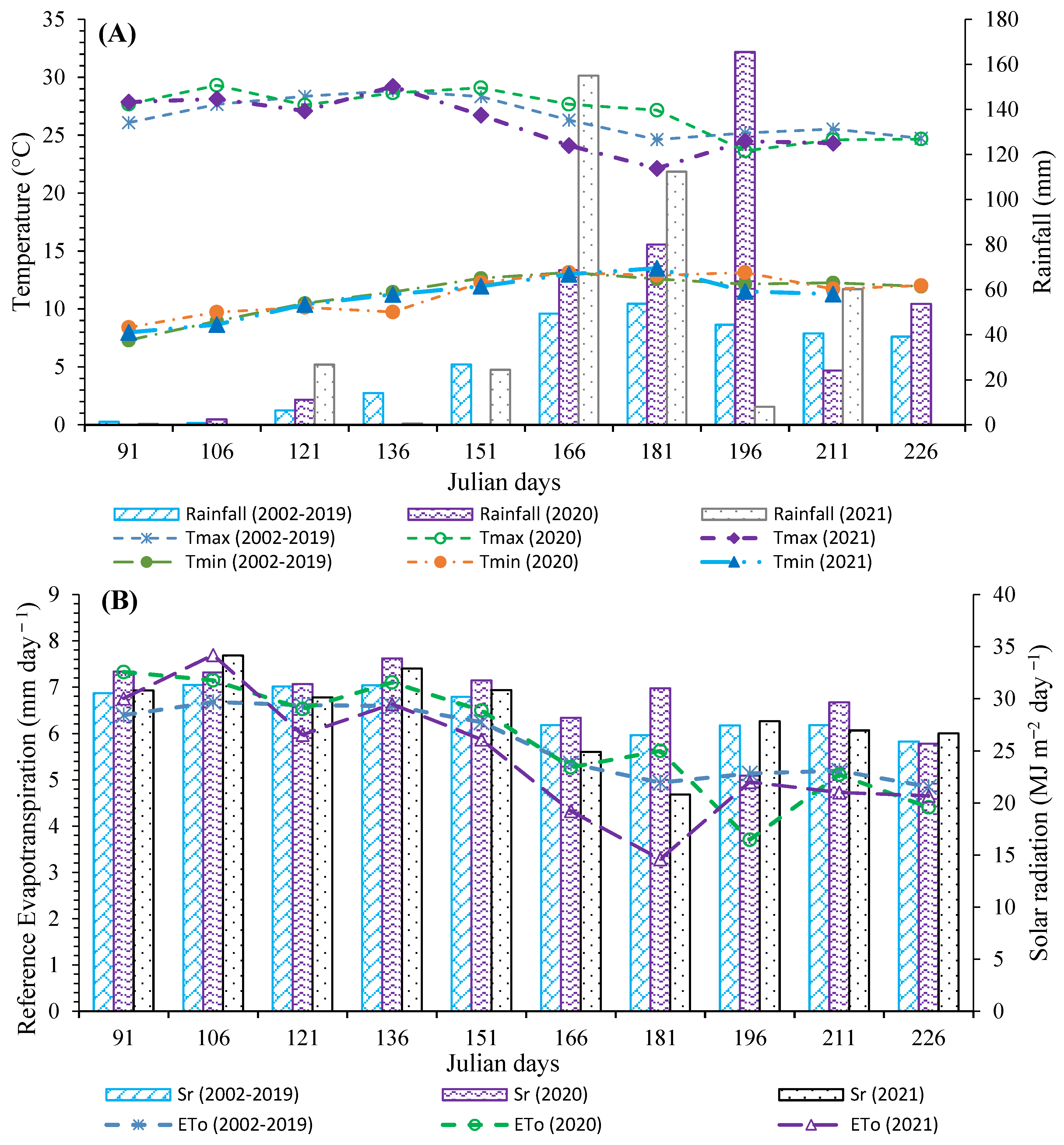
2.4. Climate Information
2.5. Description of the SIMPLE Model
2.6. Model Calibration
| Parameter | Description | Nominal | Threshold * | Units | Cite |
|---|---|---|---|---|---|
| Tsum | Cumulative temperature from sowing to maturity | 1200 | 1047–1356 & | °C d ** | B-G |
| HI | Harvest index | 0.36 | 0.29–0.43 | - | B-G |
| I50A | The cumulative temperature required for leaf area development to intercept 50% of radiation | 450 | 360–540 | °C d | Z |
| I50B | Cumulative temperature till maturity to reach 50% radiation interception due to leaf senescence | 200 | 160–240 | °C d | Z |
| Tb | Baseline temperature for phenology development and growth | 8 | 6.4–9.6 | °C | B-G |
| Topt | The optimal temperature for biomass growth | 30 | 22–30 | °C | B-G |
| RUE | Radiation use efficiency (above ground only and no respiration) | 3.21 | 2.57–3.85 | g MJ−1 m−2 | K |
| I50maxH | Maximum daily reduction in I50B due to heat stress | 90 | 72–108 | °C d | Z |
| I50maxW | Maximum daily reduction in I50B due to drought stress | 20 | 16–24 | °C d | Z |
| Tmax | Threshold temperature to start accelerating heat-stress senescence | 35 | 32.1–42 | °C | O |
| Text | Extreme temperature threshold when RUE becomes 0 due to heat stress | 45 | 42.1–52.5 | °C | Z |
| SCO2 | The relative increase in RUE per ppm of CO2 after 350 ppm | 0.07 | 0.06–0.08 | ppm | Z |
| Swater | Sensitivity of RUE to drought stress | 0.9 | 0.48–1.28 & | - | Z |
2.6.1. Differential-Evolution Algorithms
2.6.2. Objective Function
2.7. Model Evaluation
2.8. Measures for the Degree of Fit
3. Results
3.1. Climate and Irrigation Schedule
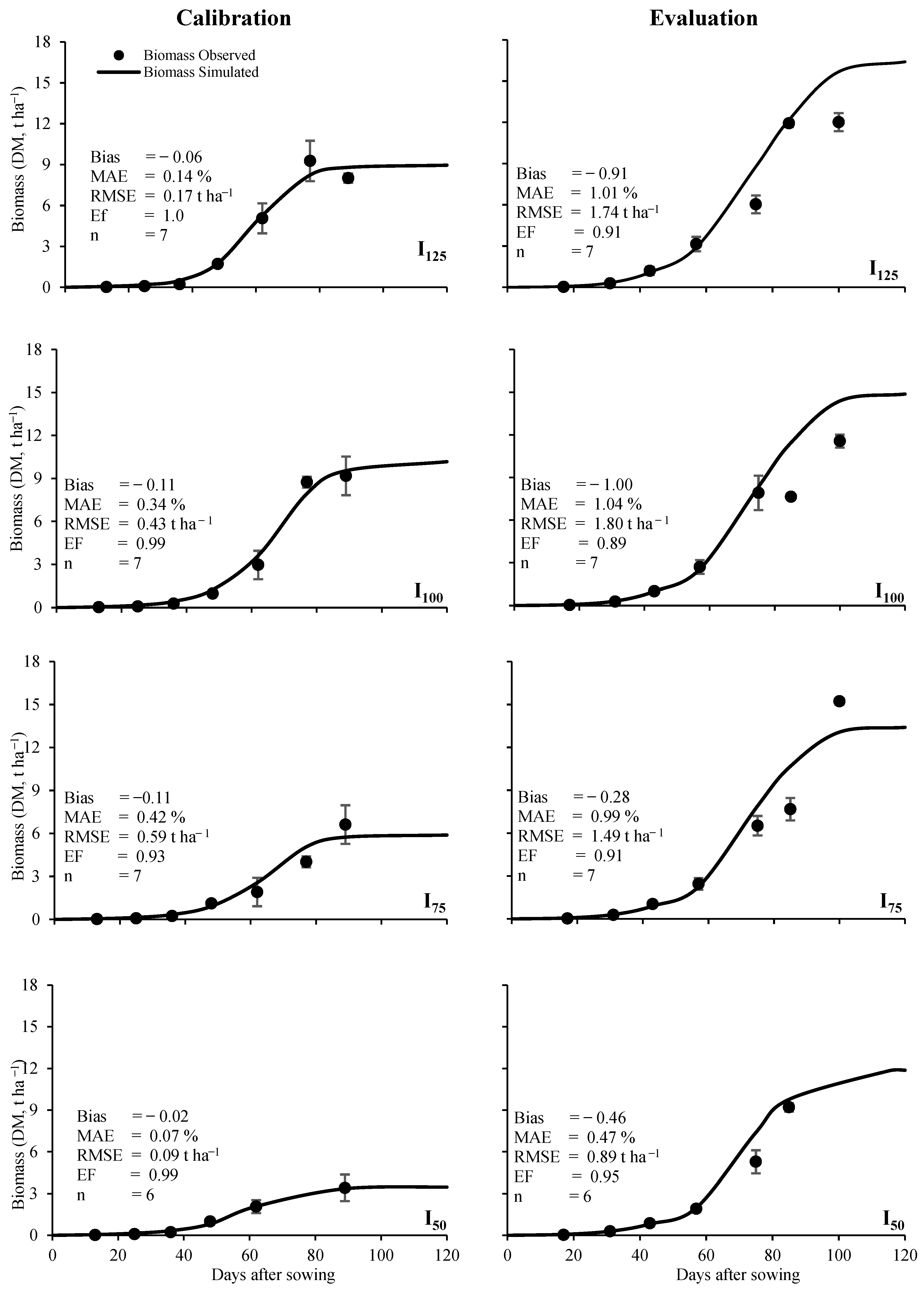
3.2. Biomass Accumulation Curve
3.3. Calibration and Evaluation
3.4. Harvest Index
4. Discussion
4.1. Climate and Irrigation Schedule
4.2. Cumulative Biomass Curve
4.3. Calibrated Parameters
4.4. Calibration and Evaluation
4.5. Harvest Index
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAOSTAT. FAO Statistics, Food and Agriculture Organization of the United Nations. 2022. Available online: http://www.fao.org/faostat/en/ (accessed on 20 January 2022).
- INEGI (Instituto Nacional De Estadistica y Geografia). Censo Agropecuario 2007. 2012. Available online: http://www3.inegi.org.mx (accessed on 15 May 2022).
- García, E. Modificaciones al Sistema de Clasificación Climática de Köppen (Quinta ed.). Instituto de Geografía-Universidad Nacional Autónoma de México (UNAM): México, DF, México, 2004. Available online: http://www.publicaciones.igg.unam.mx/index.php/ig/catalog/view/83/82/251-1 (accessed on 22 June 2022).
- Schwartz, H.F.; Brick, M.A. Dry Bean Pest Management and Production, 3rd ed.; Cooperative Extension Resource Center, Colorado State University: Fort Collins, CO, USA, 2015. [Google Scholar]
- SIAP. Servicio de Información y Estadística Agroalimentaria y Pesquera Información Agrícola. Avances Mensuales por Estado. 2015. Available online: http://www.siap.sagarpa.gob.mx (accessed on 15 May 2022).
- Seidel, S.J.; Palosuo, T.; Thorburn, P.; Wallach, D. Towards improved calibration of crop models—Where are we now and where should we go? Eur. J. Agron. 2018, 94, 25–35. [Google Scholar] [CrossRef]
- Chalabi, Z.; Zhou, W. Optimal control methods for agricultural systems. Acta Hortic. 1996, 406, 221–228. [Google Scholar] [CrossRef]
- Bhar, A.; Kumar, R.; Qi, Z.; Malone, R. Coordinate descent based agricultural model calibration and optimized input management. Comput. Electron. Agric. 2020, 172, 105353. [Google Scholar] [CrossRef]
- Wallach, D. Crop model calibration: A statistical perspective. Agron. J. 2011, 103, 1144–1151. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Hoogenboom, G.; White, J.W.; Jones, J.W.; Boote, K.J. Beangro V1. 01 Dry Bean Crop Growth Simulation Model: Users Guide; Department of Agricultural Engineering, University of Florida: Gainesville, FL, USA, 1991. [Google Scholar]
- White, J.W.; Hoogenboom, G. Simulating effects of genes for physiological traits in a process-oriented crop model. Agron. J. 1996, 88, 416–422. [Google Scholar] [CrossRef]
- Hoogenboom, G.; White, J.W.; Jones, J.W.; Boote, K.J. BEANGRO: A process-oriented dry bean model with a versatile user interface. Agron. J. 1994, 86, 182–190. [Google Scholar] [CrossRef]
- van Keulen, E.L.; Wolf, J. Modelling of Ugricultural Production: Weather, Soil and Crops; Simulation Monographs, Pudoc: Wageningen, The Netherlands, 1986. [Google Scholar]
- O’Callaghan, J.R.; Maende, C.; Wyseure, G.C.L. Modelling the intercropping of maize and beans in Kenya. Comput. Electron. Agric. 1994, 11, 351–365. [Google Scholar] [CrossRef]
- Van Keulen, H.; Penning de Vries, E.W.T.; Drees, E.M. A summary model for crop growth. In Simulation of Plant Growth and Crop Production; de Vries, E.W.T.P., Laar, H.H., Eds.; Simulation Monograph, Pudoc: Wageningen, The Netherlands, 1982; pp. 87–99. [Google Scholar]
- Verdoodt, A.; Van Ranst, E.; Ye, L. Daily simulation of potential dry matter production of annual field crops in tropical environments. Agron. J. 2004, 96, 1739–1753. [Google Scholar] [CrossRef]
- Soltani, A.; Sinclair, T.R. Modeling Physiology of Crop Development, Growthand Yield; CABI: Wallingford, UK, 2012. [Google Scholar]
- Seidel, S.J.; Rachmilevitch, S.; Schütze, N.; Lazarovitch, N. Modelling the impact of drought and heat stress on common bean with two different photosynthesis model approaches. Environ. Model. Softw. 2016, 81, 111–121. [Google Scholar] [CrossRef]
- Yuan, M.; Ruark, M.D.; Bland, W.L. A simple model for snap bean (Phaseolus vulgaris L.) development, growth and yield in response to nitrogen. Field Crops Res. 2017, 211, 125–136. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, B.; Xiao, L.; Hoogenboom, G.; Boote, K.J.; Kassie, B.T.; Pavan, W.; Shelia, V.; Kim, K.S.; Hernandez-Ochoa, I.M.; et al. A SIMPLE crop model. Eur. J. Agron. 2019, 104, 97–106. [Google Scholar] [CrossRef]
- Annandale, J.G.; Benadé, N.; Jovanovic, N.Z.; Steyn, J.M.; Du Sautoy, N. Facilitating Irrigation Scheduling by Means of the Soil Water Balance Model; Water Research Commission Report No. 753/1/99; Water SA Publishes: Pretoria, South Africa, 1999. [Google Scholar]
- Ragab, R. A holistic generic integrated approach for irrigation, crop and field management: The SALTMED model. Environ. Model. Softw. 2002, 17, 345–361. [Google Scholar] [CrossRef]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop—The FAO Crop Model to Simulate Yield Response to Water: I. Concepts Underlying Principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef]
- Wang, J.; Li, X.; Lu, L.; Fang, F. Parameter sensitivity analysis of crop growth models based on the extended Fourier Amplitude Sensitivity Test method. Environ. Model. Softw. 2013, 48, 171–182. [Google Scholar] [CrossRef]
- Martínez-Ruiz, A.; López-Cruz, I.L.; Ruiz-García, A.; Pineda-Pineda, J.; Prado-Hernández, J.V. HortSyst: A dynamic model to predict growth, nitrogen uptake, and transpiration of greenhouse tomatoes. Chil. J. Agric. Res. 2019, 79, 89–102. [Google Scholar] [CrossRef]
- Pham, Q.V.; Nguyen, T.T.; Vo, T.T.; Le, P.H.; Nguyen, X.T.; Duong, N.V.; Le, C.T. Applying the SIMPLE crop model to assess soybean (Glicine max.(L.) Merr.) biomass and yield in tropical climate variation. Agronomy 2023, 13, 1180. [Google Scholar] [CrossRef]
- Suliansyah, I.; Arlius, F.; Chaniago, I.; Xuan NT, T.; Duong VT, H.; Dung, N.P.; Van Quang, P. Simulation of Maize Biomass and Yield in An Giang, Vietnam, under Climate Variabilities. Trends Sci. 2024, 21, 7490. [Google Scholar] [CrossRef]
- Suliansyah, I.; Arlius, F.; Chaniago, I.; Xuan NT, T.; Van Quang, P. Literature Review Crop Modeling and Introduction a Simple Crop Model. J. Appl. Agric. Sci. Technol. 2023, 7, 197–216. [Google Scholar] [CrossRef]
- Medina-García, G.; Rumayor-Rodríguez, A.F.; Cabañas-Cruz, B.; Luna-Flores, M.; Ruiz-Corral, J.A.; Gallegos-Valdez, C.; Madero-Tamargo, J.; Gutiérrez-Sánchez, J.R.; Rubio-Díaz, S.; Bravo-Lozano, A.G. Potencial Productivo de Especies Agrícolas en el Estado de Zacatecas; Libro Técnico Núm. 2; Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias. Centro de Investigación Regional Norte Centro: Zacatecas, Mexico, 2003; 157p.
- Palacios, V.E. Por Qué, Cuándo, Cuánto y Cómo Regar? Para Lograr Mejores Cosechas; DF Editorial Trillas: México City, Mexico, 2002; 214p. [Google Scholar]
- Serna-Pérez, A.; Zegbe, J.A.; Mena-Covarrubias, J. Rendimiento y calidad de chile seco Mirasol cultivado bajo riego parcial de la raíz. Rev. Chapingo Ser. Hortic. 2011, 17, 19–24. Available online: http://www.scielo.org.mx/pdf/rcsh/v17nspe1/v17nspe1a4.pdf (accessed on 10 April 2022). [CrossRef]
- Servín-Palestina, M.; Tijerina Chávez, L.; Medina García, G.; Palacios Velez, O.; Flores Magdaleno, H. Sistema para programar y calendarizar el riego de los cultivos en tiempo real. Rev. Mex. De Cienc. Agrícolas 2017, 8, 423–430. [Google Scholar] [CrossRef]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Evapotranspiración del Cultivo: Guía Para la Determinación de Los Requerimientos de Agua de Los Cultivos. Estudio FAO Riego y Drenaje; FAO: Roma, Italy, 2006; pp. 56–323. Available online: http://www.fao.org/docrep/009/x0490s/x0490s00.htm (accessed on 1 April 2024).
- SAS Institute Inc. SAS 9.3 System Options: Reference, 2nd ed.; SAS Institute Inc.: Cary, NC, USA, 2011. [Google Scholar]
- Ritchie, J.T.; Godwin, D.C.; Otter-Nacke, S. CERES-Wheat: A User-Oriented Wheat Yield Model. Preliminary Documentation; AGRISTARS Publication No. YM-U3-04442-JSC-18892; Michigan State University: East Lansing, MI, USA, 1985; Available online: https://cir.nii.ac.jp/crid/1573387449661175552 (accessed on 1 April 2024).
- Monteith, J.L. Light distribution and photosynthesis in field crops. Ann. Bot. 1965, 29, 17–37. [Google Scholar] [CrossRef]
- Amir, J.; Sinclair, T.R. A model of water limitation on spring wheat growth and yield. Field Crops Res. 1991, 28, 59–69. [Google Scholar] [CrossRef]
- SCS. Soil Conservation Service, National Engineering Handbook, Section 4: Hydrology; US Department of Agriculture: Washington, DC, USA, 1972.
- Woli, P.; Jones, J.; Ingram, K.; Fraisse, C. Agricultural reference index for drought (ARID). Agron. J. 2012, 104, 287–300. [Google Scholar] [CrossRef]
- Ljung, L.; Glad, T. Modeling of Dynamic Systems; PTR Prentice Hall: Englewood Cliffs, NJ, USA, 1994. [Google Scholar]
- Voinov, A.; Gaddis, E.J.B. Lessons for successful participatory watershed modeling: A perspective from modeling practitioners. Ecol. Model. 2008, 216, 197–207. [Google Scholar] [CrossRef]
- Bala, B.K.; Arshad, F.M.; Noh, K.M. System Dynamics. Modelling and Simulation; Springer: Singapore, 2017; 278p. [Google Scholar] [CrossRef]
- Saltelli, A.; Tarantola, S.; Campolongo, F.; Ratto, M. Sensitivity Analysis in Practice. A Guide to Assesing Scientific Models; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2004; 219p. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Tarantola, S.; Campolongo, F. Sensitivity analysis practices: Strategies for model-based inference. Reliab. Eng. Syst. Saf. 2006, 91, 1109–1125. [Google Scholar] [CrossRef]
- Saltelli, A.; Ratto, M.; Andres, T.; Campolongo, F.; Cariboni, J.; Gatelli, D.; Tarantola, S. Global Sensitivity Analysis: The Primer; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar] [CrossRef]
- Baez-Gonzalez, A.D.; Fajardo-Díaz, R.; Garcia-Romero, G.; Osuna-Ceja, E.; Kiniry, J.R.; Meki, M.N. High Sowing Densities in Rainfed Common Beans (Phaseolus vulgaris L.) in Mexican Semi-Arid Highlands under Future Climate Change. Agronomy 2020, 10, 442. [Google Scholar] [CrossRef]
- Karimzadeh Soureshjani, H.; Nezami, A.; Kafi, M.; Tadayon, M. Responses of two common bean (Phaseolus vulgaris L.) genotypes to deficit irrigation. Agric. Water Manag. 2019, 213, 270–279. [Google Scholar] [CrossRef]
- Omae, H.; Kumar, A.; Shono, M. Adaptation to high temperature and water deficit in the common bean (Phaseolus vulgaris L.) during the reproductive period. J. Bot. 2012, 2012, 803413. [Google Scholar] [CrossRef]
- Price, K.V.; Storn, R.M.; Lampinen, J.A. Differential Evolution. A Practical Approach to Global Optimization; Springer: Berlin/Heidelberg, Germany, 2005; 538p. [Google Scholar]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Working with Dynamic Crop Models: Methods, Tools and Examples for Agriculture and Environment, 3rd ed.; Academic Press: London, UK, 2019. [Google Scholar]
- Krause, P.; Boyle, D.P.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Luo, Q. Temperature thresholds and crop production: A review. Clim. Chang. 2011, 109, 583–598. [Google Scholar] [CrossRef]
- Barrios Gómez, E.J.; López Castañeda, C.; Kohashi Shibata, J.; Acosta Gallegos, J.A.; Miranda Colín, S.; Mayek Pérez, N. Avances en el mejoramiento genético del frijol en México por tolerancia a temperatura alta ya sequía. Rev. Fitotec. Mex. 2011, 34, 247–255. Available online: http://www.scielo.org.mx/pdf/rfm/v34n4/v34n4a6.pdf (accessed on 1 April 2024).
- Beebe, S.; Ramirez, J.; Jarvis, A.; Rao, I.M.; Mosquera, G.; Bueno, J.M.; Blair, M.W. Genetic Improvement of Common Beans and the Challenges of Climate Change Crop Adaptation to Climate Change; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; pp. 356–369. [Google Scholar]
- Martínez-Gamiño, M.A.; Osuna-Ceja, E.S.; Padilla-Ramírez, J.S.; Acosta-Gallegos, J.A.; Loredo-Osti, C. Tecnología Para la Producción de Frijol en el Norte Centro de México; Libro Técnico No. 4; Instituto Nacional de Investigaciones Forestales, Agrícolas y Pecuarias Publication Series: San Luis Potosí, Mexico, 2008.
- Lynch, J.; van Beem, J.J. Growth and architecture of seedling roots of common bean genotypes. Crop Sci. 1993, 33, 1253–1257. [Google Scholar] [CrossRef]
- Boutraa, T.; Sanders, F.E. Influence of water stress on grain yield and vegetative growth of two cultivars of bean (Phaseolus vulgaris L.). J. Agron. Crop Sci. 2001, 187, 251–257. [Google Scholar] [CrossRef]
- Rai, A.; Sharma, V.; Heitholt, J. Dry bean [Phaseolus vulgaris L.] growth and yield response to variable irrigation in the arid to semi-arid climate. Sustainability 2020, 12, 3851. [Google Scholar] [CrossRef]
- Munier-Jolain, N.G.; Munier-Jolain, N.M.; Roche, R.; Ney, B.; Duthion, C. Seed growth rate in grain legumes I. Effect of photoassimilate availability on seed growth rate. J. Exp. Bot. 1998, 49, 1963–1969. [Google Scholar] [CrossRef]
- Trejo-Zúñiga, E.C.; López-Cruz, I.L.; Ruíz-García, A. Parameter estimation for crop growth model using evolutionary and bio-inspired algorithms. Agrociencia 2013, 47, 671–682. Available online: http://www.scielo.org.mx/pdf/agro/v47n7/v47n7a4.pdf (accessed on 1 April 2024).
- Civicioglu, P.; Besdok, E. A conceptual comparison of the Cuckoo-search, particle swarm optimization, differential evolution and artificial bee colony algorithms. Artif. Intell. Rev. 2013, 39, 315–346. [Google Scholar] [CrossRef]
- Ghassemi-Golezani, K.; Mardfar, R.A. Effects of limited irrigation on growth and grain yield of common bean. J. Plant Sci. 2008, 3, 230–235. [Google Scholar] [CrossRef]
- Ghassemi-Golezani, K.; Abriz, S.F.; Hassanpour-Bourkheili, S. Development of mung-bean seed vigour under different irrigations and plant densities. Int. J. Plant Anim. Environ. Sci. 2014, 4, 208–211. [Google Scholar]
- Masaya, P.; White, J.W. Adaptation to photoperiod and temperature. In Common Beans: Research for Crop Improvement; Schoonhoven, A.V., Voysest, O., Eds.; Centre for Agricultural Bioscience International and Centro Internacional de Agricultura Tropical (Cali, Colombia): Oxford, UK, 1991; pp. 445–500. [Google Scholar]
- Fernandez, F.; Gepts, P.; Lopez, M. Etapas de desarrollo en la planta de frijol. In Frijol: Investigación y producción. Programa de las Naciones Unidas (PNUD); López Genes, M., Fernández, O., Fernando, O., van Schoonhoven, A., Eds.; Centro Internacional de Agricultura Tropical (CIAT): Cali, Colombia, 1985; pp. 61–78. [Google Scholar]
- Bulatewicz, T.; Jin, W.; Staggenborg, S.; Lauwo, S.; Miller, M.; Das, S.; Andresen, D.; Peterson, J.; Steward, D.R.; Welch, S.M. Calibration of a crop model to irrigated water use using a genetic algorithm. Hydrol. Earth Syst. Sci. 2009, 13, 1467–1483. [Google Scholar] [CrossRef]
- Teweldebrhan, A.T.; Burkhart, J.F.; Schuler, T.V. Parameter uncertainty analysis for an operational hydrological model using residual-based and limits of acceptability approaches. Hydrol. Earth Syst. Sci. 2018, 22, 5021–5039. [Google Scholar] [CrossRef]
- White, J.W.; Izquierdo, J. Physiology of yield potential and stress tolerance. In Common Beans. Research for Crop Improvement; van Schoonhoven, A., Voysest, O., Eds.; CAB International: Wallingford, UK, 1991; pp. 287–382. [Google Scholar]
- Silva, V.M.; Andrade, M.J.; Moraes, A.R.; Vieira, N.M.; Alves, J., Jr. Dry matter accumulation by common bean cv. BRS MG Talismã. Bean Improv. Coop. 2005, 48, 154–155. [Google Scholar]
- Lépiz-Ildefonso, R.; Chavarín-Espinoza, I.E.; López-Alcocer JD, J.; Rodríguez-Guzmán, E. Dry matter accumulation during developmental stages of common bean cultivars. Rev. Fitotec. Mex. 2018, 41, 275–282. [Google Scholar] [CrossRef]
- Soltani, A.; Alimagham, S.M.; Nehbandani, A.; Torabi, B.; Zeinali, E.; Dadrasi, A.; Zand, E.; Ghassemi, S.; Pourshirazi, S.; Alasti, O.; et al. SSM-iCrop2: A simple model for diverse crop species over large areas. Agric. Syst. 2020, 182, 102855. [Google Scholar] [CrossRef]
- Mathobo, R.; Marais, D.; Steyn, J.M. Calibration and validation of the SWB model for dry beans (Phaseolus vulgaris L.) at different drought stress levels. Agric. Water Manag. 2018, 202, 113–121. [Google Scholar] [CrossRef]
- Dewedar, O.; Plauborg, F.; Marwa, M.; El-shafie, A.; Ragab, R. Improving water saving, yield, and water productivity of bean under deficit drip irrigation: Field and modelling study using the SALTMED model. Irrig. Drain. 2020, 70, 224–242. [Google Scholar] [CrossRef]
- Emam, Y.; Shekoofa, A.; Salehi, F.; Jalali, A.H. Water stress effects on two common bean cultivars with contrasting growth habits. Am. Eurasian J. Agric. Environ. Sci. 2010, 9, 495–499. [Google Scholar]
- Morales-Rosales, E.J.; Escalante-Estrada JA, S.; López-Sandoval, J.A. Crecimiento, índice de cosecha y rendimiento de frijol (Phaseolus vulgaris L.) en unicultivo y asociado con girasol (Helianthus annuus L.). Univ. Cienc. 2008, 24, 1–10. [Google Scholar]
- Acosta-Gallegos, J.A.; Rosales-Serna, R. Biomasa y sus componentes en variedades indeterminadas de frijol. Memoria. In 35a Reunion Anual de PCCMCA; Programa Cooperativo Centroamericano para Mejoramiento de Cultivos y Animales: San Perdo Sula, Honduras, 1989. [Google Scholar]
- Debaeke, P.; Aboudrare, A. Adaptation of crop management to water-limited environments. Eur. J. Agron. 2004, 21, 433–446. [Google Scholar] [CrossRef]
- Kemanian, A.R.; Stöckle, C.O.; Huggins, D.R.; Viega, L.M. A simple method to estimate harvest index in grain crops. Field Crops Res. 2007, 103, 208–216. [Google Scholar] [CrossRef]
- Ranjan, R.; Chandel, A.K.; Khot, L.R.; Bahlol, H.Y.; Zhou, J.; Boydston, R.A.; Miklas, P.N. Irrigated pinto bean crop stress and yield assessment using ground based low altitude remote sensing technology. Inf. Process. Agric. 2019, 6, 502–514. [Google Scholar] [CrossRef]
- Dallacort, R.; de Freitas, P.S.L.; Faria, R.T.; Goncalves, A.C.A.; Rezende, R.; Guimaraes, R.M.L. Simulation of bean crop growth, evapotranspiration and yield in Paraná State by the CROPGRO-Drybean model. Acta Sci. Agron. 2011, 33, 429–436. [Google Scholar] [CrossRef]
- Mompremier, R.; Her, Y.; Hoogenboom, G.; Migliaccio, K.; Muñoz-Carpena, R.; Brym, Z.; Colbert, R.W.; Jeune, W. Modeling the response of dry bean yield to irrigation water availability controlled by watershed hydrology. Agric. Water Manag. 2021, 243, 106429. [Google Scholar] [CrossRef]
- Marrou, H.; Sinclair, T.R.; Metral, R. Assessment of irrigation scenarios to improve performances of Lingot bean (Phaseolus vulgaris) in southwest France. Eur. J. Agron. 2014, 59, 22–28. [Google Scholar] [CrossRef]
- Espadafor, M.; Couto, L.; Resende, M.; Henderson, D.W.; Garcia-Vila, M.; Fereres, E. Simulation of the responses of dry beans (Phaseolus vulgaris L.) to irrigation. Trans. ASABE 2017, 60, 1983–1994. [Google Scholar] [CrossRef]


| Description | Equation |
|---|---|
| for leaf growth and senescence period is based on the Beer–Lambert law, | |
| The impact of temperature on the growth rate of biomass | |
| The impact of heat stress on the biomass growth rate | |
| The cumulative temperature required to achieve 50% radiation interception during canopy senescence (I50B) is increased by heat stress | |
| The impact of CO2 on the RUE | |
| Drought stress based on water retention. | |
| Standardized Drought Stress Index | |
| Drought stress reduces RUE | |
| Radiation interception affected by drought stress |
| Year/IT | AID (mm) | ER (mm) | TWA (mm) | Y (t ha−1) | WUE (kg m−3) | WP (kg m−3) |
|---|---|---|---|---|---|---|
| 2020 | ||||||
| I125 | 349 | 244.1 | 593.1 | 4.88 | 1.4 | 0.8 |
| I100 | 293 | 537.1 | 4.64 | 1.6 | 0.9 | |
| I75 | 234 | 478.2 | 3.12 | 1.3 | 0.7 | |
| I50 | 183 | 427.1 | 3.27 | 1.8 | 0.8 | |
| 2021 | ||||||
| I125 | 276 | 270.4 | 546.5 | 4.30 | 1.6 | 0.8 |
| I100 | 219 | 489.5 | 4.75 | 2.2 | 1.1 | |
| I75 | 174 | 444.5 | 3.95 | 2.3 | 0.9 | |
| I50 | 133 | 403.5 | 3.74 | 2.8 | 0.9 |
| Days after Sowing | |||||||
|---|---|---|---|---|---|---|---|
| IT | 13 | 25 | 36 | 48 | 62 | 77 | 89 |
| I125 | 0.021 ± 0.002 | 0.082 ± 0.006 | 0.222 ± 0.016 b | 1.714 ± 0.028 a | 5.06 ± 1.1 a | 9.27 ± 1.48 a | 8.01 ± 0.33 a |
| I100 | 0.021 ± 0.002 | 0.082 ± 0.006 | 0.277 ± 0.011 a | 0.972 ± 0.135 b | 2.96 ± 0.99 ab | 8.74 ± 0.38 a | 9.18 ± 1.35 a |
| I75 | 0.021 ± 0.002 | 0.082 ± 0.006 | 0.239 ± 0.01 ab | 1.119 ± 0.175 b | 1.91 ± 0.12 b | 4.02 ± 1.02 b | 6.62 ± 1.93 ab |
| I50 | 0.021 ± 0.002 | 0.082 ± 0.006 | 0.22 ± 0.028 b | 0.989 ± 0.223 b | 2.07 ± 0.47 b | -- | 3.41 ± 0.95 b |
| CV | 7.987 | 11.703 | 28.865 | 17.449 | 21.315 | ||
| RMSE | 0.019 | 0.140 | 0.866 | 1.035 | 1.450 | ||
| LSD | 0.049 | 0.360 | 2.222 | 2.655 | 3.718 | ||
| Days after Sowing | |||||||
|---|---|---|---|---|---|---|---|
| IT | 17 | 31 | 43 | 57 | 75 | 85 | 100 |
| I125 | 0.029 ± 0.009 | 0.287 ± 0.015 a | 1.19 ± 0.29 a | 3.16 ± 0.52 a | 6.03 ± 0.65 ab | 11.92 ± 0.27 a | 12.01 ± 0.66 b |
| I100 | 0.029 ± 0.009 | 0.273 ± 0.015 a | 0.10 ± 0.16 a | 2.70 ± 0.48 ab | 7.91 ± −1.21 a | 7.63 ± 0.19 c | 11.55 ± 0.45 b |
| I75 | 0.029 ± 0.009 | 0.286 ± 0.054 a | 1.04 ± 0.10 a | 2.45 ± 0.41 ab | 6.52 ± 0.68 ab | 7.67 ± 0.79 c | 15.23 ± 0.23 a |
| I50 | 0.029 ± 0.009 | 0.285 ± 0.027 a | 0.863 ± 0.02 a | 1.91 ± 0.15 b | 5.28 ± 0.83 b | 9.20 ± 0.30 b | -- |
| CV | 12.33 | 18.133 | 18.283 | 14.126 | 5.589 | 3.698 | |
| RMSE | 0.035 | 0.185 | 0.466 | 0.909 | 0.509 | 0.507 | |
| LSD | 0.090 | 0.48 | 1.196 | 2.331 | 1.305 | 1.300 | |
| Calibration Treatment | Optimal Parameters | Statistics | ||||||
|---|---|---|---|---|---|---|---|---|
| Tsum | I50A | Tb | Topt | I50maxW | Swater | RMSE | S | |
| I125 | 1356 | 540 | 8.7 | 24.0 | 16 | 1.00 | 0.51 | 3 × 10−17 |
| I100 | 1356 | 540 | 9.6 | 27.1 | 16 | 0.74 | 0.43 | 0.0 |
| I75 | 1354 | 540 | 9.6 | 29.8 | 16 | 0.79 | 0.59 | 1 × 10−16 |
| I50 | 1356 | 526 | 9.5 | 30.0 | 16 | 0.85 | 0.09 | 0.0 |
| Average | 1356 | 536 | 9.3 | 27.8 | 16 | 0.84 | 0.40 | 4 × 10−17 |
| Statistics | Calibration | Evaluation | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| I125 | I100 | I75 | I50 | Average | I125 | I100 | I75 | I50 | Average | |
| Bias | −0.06 | −0.11 | −0.11 | −0.02 | −0.08 | −0.91 | −1 | −0.28 | −0.46 | −0.66 |
| MAE | 0.36 | 0.34 | 0.43 | 0.07 | 0.30 | 1.01 | 1.04 | 0.99 | 0.47 | 0.88 |
| RMSE | 0.51 | 0.43 | 0.59 | 0.09 | 0.41 | 1.74 | 1.8 | 1.49 | 0.89 | 1.48 |
| EF | 0.98 | 0.99 | 0.93 | 0.99 | 0.97 | 0.91 | 0.89 | 0.91 | 0.95 | 0.92 |
| Year | IT | Yobs (t ha−1) | STsim (mm) | BioSim (t ha−1) | YSim (t ha−1) | CRE (%) | |
|---|---|---|---|---|---|---|---|
| 2020 | I125 | 4.88 ± 0.82 a * | 483.0 | 10.2 | 0.48 | 4.89 | 0.08 |
| I100 | 4.64 ± 0.79 ab | 456.3 | 8.1 | 0.52 | 4.24 | 8.69 | |
| I75 | 3.12 ± 0.66 b | 423.4 | 5.8 | 0.59 | 3.40 | 8.34 | |
| I50 | 3.27 ± 0.69 ab | 391.5 | 4.1 | 0.64 | 2.62 | 19.90 | |
| CV | 16.39 | ||||||
| RMSE | 0.65 | 0.17 t ha−1 | |||||
| 2021 | I125 | 4.30 ± 0.69 ab | 479.9 | 19.0 | 0.26 | 4.30 | 0.00 |
| I100 | 4.75 ± 0.51 a | 457.0 | 17.7 | 0.27 | 4.06 | 14.57 | |
| I75 | 3.95 ± 0.53 ab | 437.2 | 16.4 | 0.29 | 3.95 | 0.04 | |
| I50 | 3.74 ± 0.48 b | 417.7 | 15.2 | 0.33 | 3.88 | 3.58 | |
| CV | 13.00 | ||||||
| RMSE | 0.12 | 0.12 t ha−1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Servín-Palestina, M.; López-Cruz, I.; Zegbe, J.A.; Ruiz-García, A.; Salazar-Moreno, R.; Cid-Ríos, J.Á. Calibration and Evaluation of the SIMPLE Crop Growth Model Applied to the Common Bean under Irrigation. Agronomy 2024, 14, 917. https://doi.org/10.3390/agronomy14050917
Servín-Palestina M, López-Cruz I, Zegbe JA, Ruiz-García A, Salazar-Moreno R, Cid-Ríos JÁ. Calibration and Evaluation of the SIMPLE Crop Growth Model Applied to the Common Bean under Irrigation. Agronomy. 2024; 14(5):917. https://doi.org/10.3390/agronomy14050917
Chicago/Turabian StyleServín-Palestina, Miguel, Irineo López-Cruz, Jorge A. Zegbe, Agustín Ruiz-García, Raquel Salazar-Moreno, and José Ángel Cid-Ríos. 2024. "Calibration and Evaluation of the SIMPLE Crop Growth Model Applied to the Common Bean under Irrigation" Agronomy 14, no. 5: 917. https://doi.org/10.3390/agronomy14050917
APA StyleServín-Palestina, M., López-Cruz, I., Zegbe, J. A., Ruiz-García, A., Salazar-Moreno, R., & Cid-Ríos, J. Á. (2024). Calibration and Evaluation of the SIMPLE Crop Growth Model Applied to the Common Bean under Irrigation. Agronomy, 14(5), 917. https://doi.org/10.3390/agronomy14050917








