Inversion of Soybean Net Photosynthetic Rate Based on UAV Multi-Source Remote Sensing and Machine Learning
Abstract
:1. Introduction
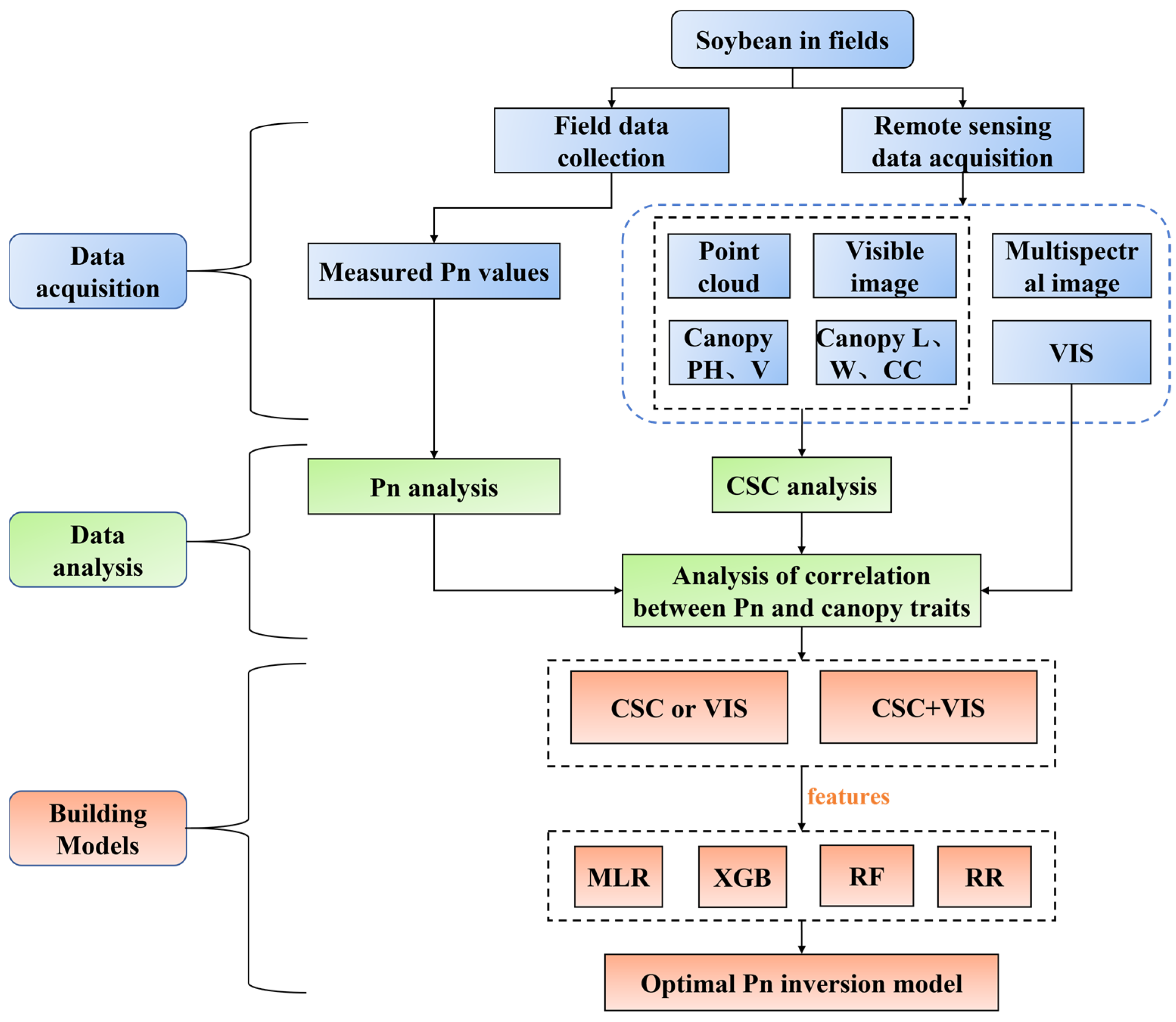
2. Materials and Methods
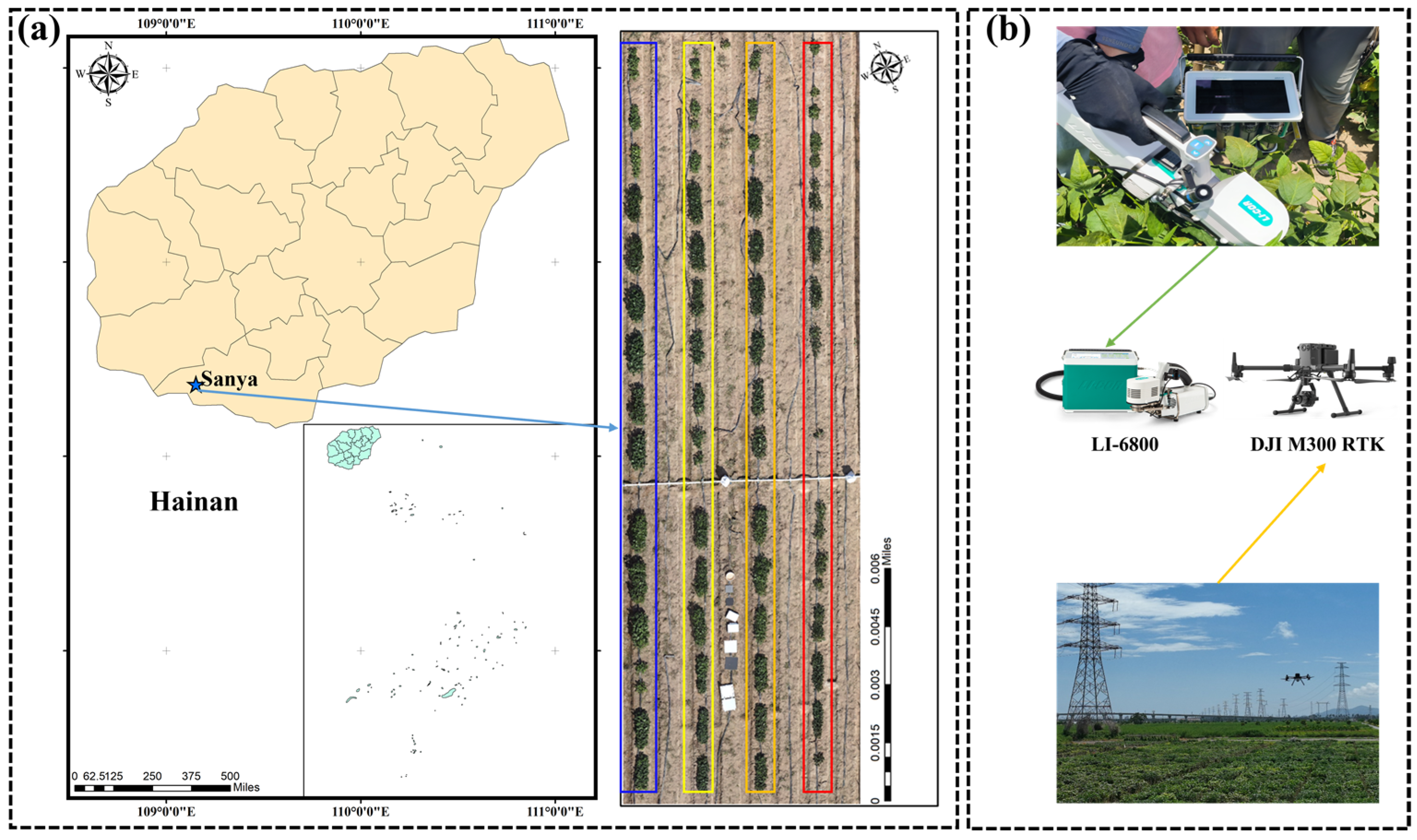
2.1. Study Region and Experimental Design
2.2. Photosynthetic Rate and Unmanned Aerial Vehicle Data Collection
2.3. Canopy Structure Characteristics Data Processing
2.4. Calculation of Vegetation Index
2.5. Construction and Evaluation of Regression Models
- (1)
- Multiple linear regression (MLR): MLR is a basic regression analysis method that establishes a relationship between the independent and dependent variables by fitting a linear relationship. It is simple and easy to understand and implement, fast to compute, and suitable for situations where the dataset exhibits a clear linear relationship.
- (2)
- Random forest regression (RF): RF is an integrated learning method that improves the model’s accuracy by constructing multiple decision trees and combining their prediction results [34]. It is highly robust, can handle high-dimensional data and large feature sets, is insensitive to outliers, and effectively reduces overfitting. It is widely used in various regression and classification problems, and is especially effective in the case of complex datasets and more features.
- (3)
- Extreme gradient-boosting tree regression (XGB): XGB is a gradient-boosting tree algorithm that improves the model’s accuracy by iteratively training the decision tree and optimising the loss function [35]. It is efficient, flexible, capable of handling large-scale datasets and complex features, and performs well in modelling non-linear relationships.
- (4)
- Ridge regression (RR): RR is a regularised linear regression method that prevents overfitting by adding a regular term to the loss function, thereby improving the generalisation ability of the model [36,37]. It is suitable for dealing with the presence of collinearity among features, effectively reducing the variance of the model and improving the stability of the model.
3. Results and Discussion
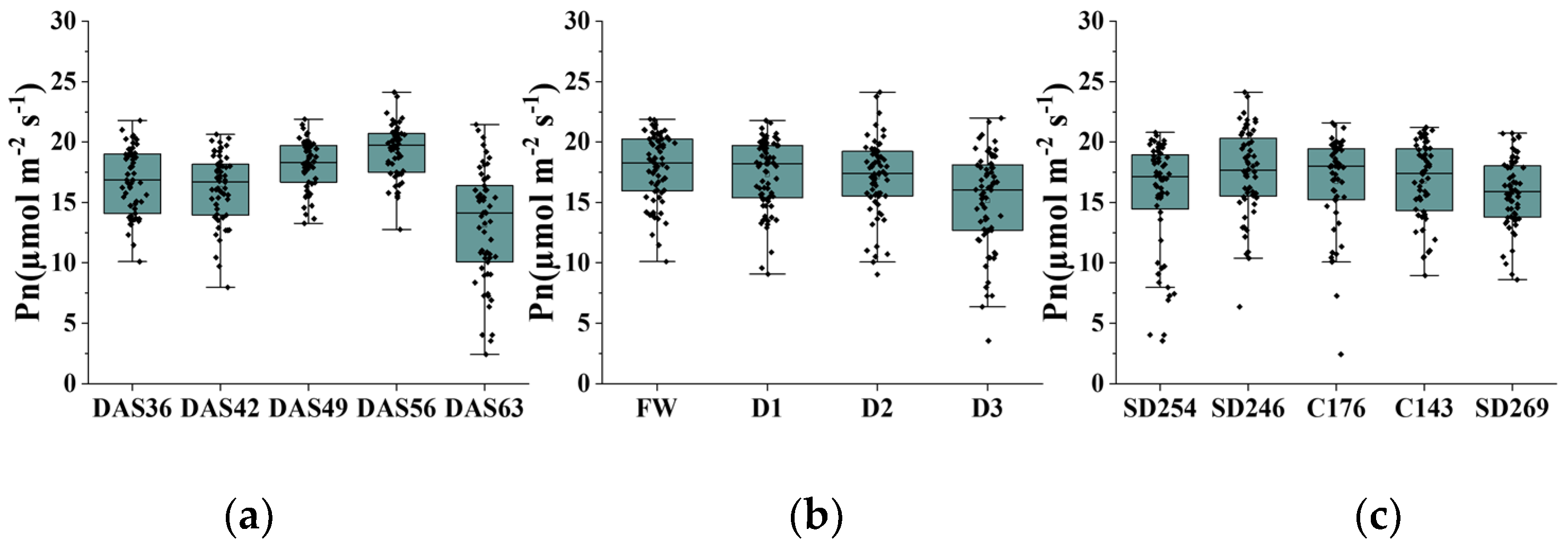
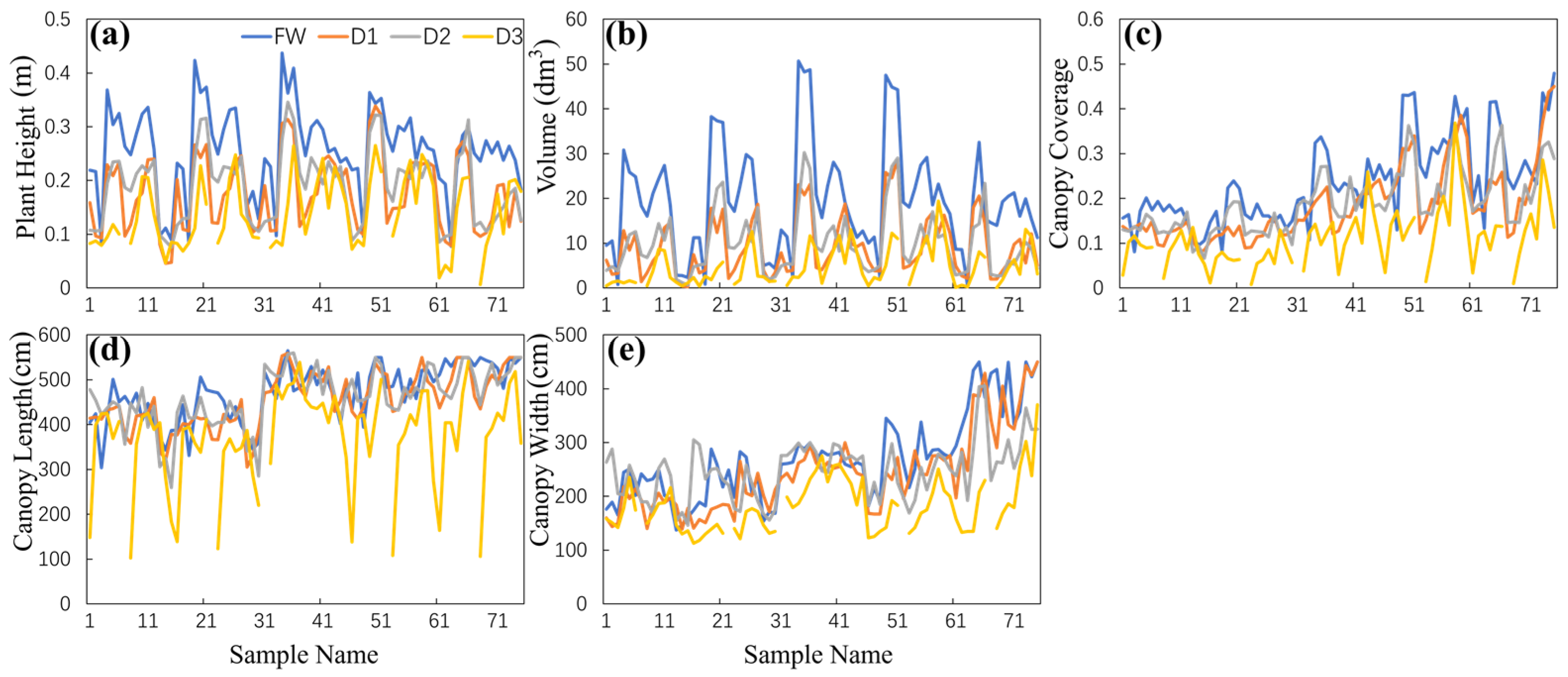
3.1. Trends in Photosynthetic Rate and Canopy Structure Charateristics
3.1.1. Trends in Photosynthetic Rate
3.1.2. Trends in Canopy Structure Characteristics
3.2. Analysis and Inversion of Photosynthetic Rate Using Vegetation Index and Canopy Structure Characteristics
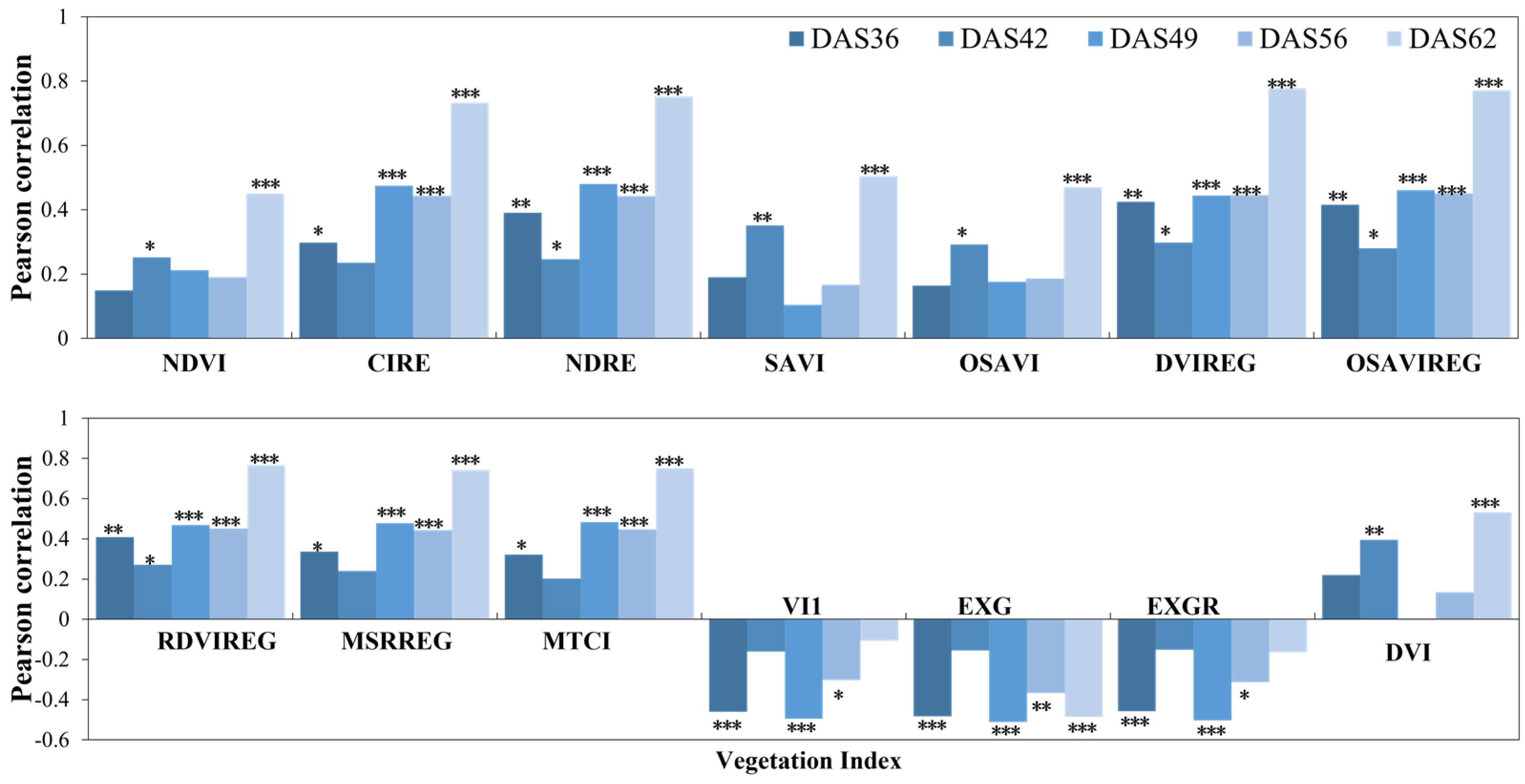
3.2.1. Correlation analysis between Photosynthetic Rate and Vegetation Index
3.2.2. Inversion of Photosynthetic Rate Using Vegetation Index
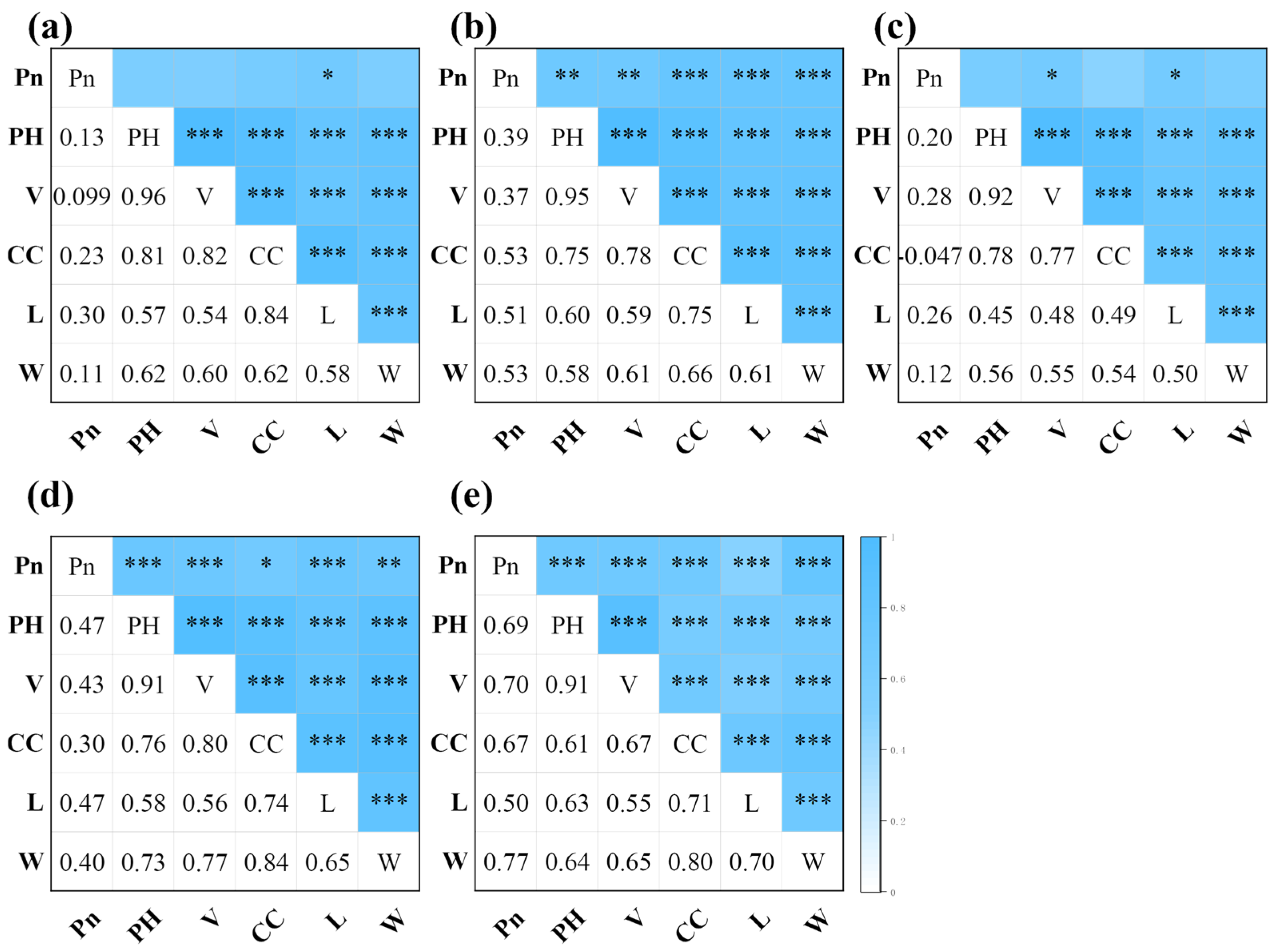
3.2.3. Correlation Analysis between Photosynthetic Rate and Canopy Structure Characteristics
3.2.4. Inversion of Photosynthetic Rate Using Canopy Structure Characteristics
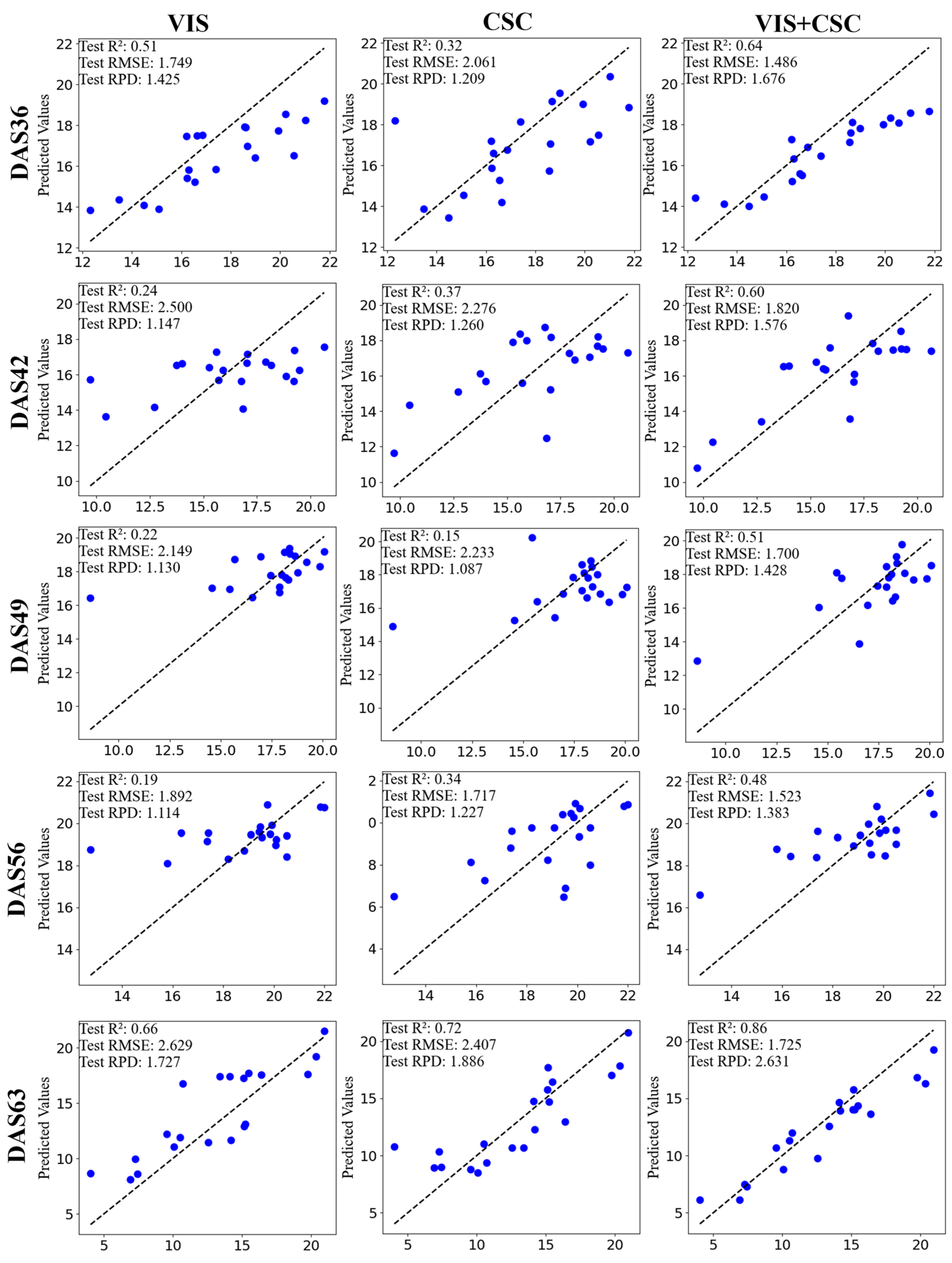
3.3. Fusion of Canopy Structure Characterisitcs and Vegetation Index for Photosynthetic Rate Inversion
3.4. Comparison of the Best Inversion Results for Vegetation Index, Canopy Structure Characteristics, and Vegetation Index + Canopy Structure Characteristics
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Stirbet, A.; Lazár, D.; Guo, Y.; Govindjee, G. Photosynthesis: Basics, history and modelling. Ann. Bot. 2020, 126, 511–537. [Google Scholar] [CrossRef] [PubMed]
- Blankenship, R.E. Early evolution of photosynthesis. Plant Physiol. 2010, 154, 434–438. [Google Scholar] [CrossRef] [PubMed]
- Evans, J.R. Improving photosynthesis. Plant Physiol. 2013, 162, 1780–1793. [Google Scholar] [CrossRef] [PubMed]
- Zhirenko, N.G.; Kurbatova, J.A. CO2 exchange of seedlings of Rhizophora Apiculata Bl. In Artificial and Natural Mangrove Forests of Southern Vietnam. Geogr. Environ. Sustain. 2023, 16, 102–109. [Google Scholar] [CrossRef]
- Narváez, F.J.Y.; del Pedregal, J.S.; Prieto, P.A.; Torres-Torriti, M.; Cheein, F.A.A. LiDAR and thermal images fusion for ground-based 3D characterisation of fruit trees. Biosyst. Eng. 2016, 151, 479–494. [Google Scholar] [CrossRef]
- Xie, C.; Yang, C. A review on plant high-throughput phenotyping traits using UAV-based sensors. Comput. Electron. Agric. 2020, 178, 105731. [Google Scholar] [CrossRef]
- Li, Y.; Shen, F.; Hu, L.; Lang, Z.; Liu, Q.; Cai, F.; Fu, L. A Stare-down video-rate high-throughput hyperspectral imaging system and its applications in biological sample sensing. IEEE Sens. J. 2023, 23, 23629–23637. [Google Scholar] [CrossRef]
- Feng, L.; Chen, S.; Zhang, C.; Zhang, Y.; He, Y. A comprehensive review on recent applications of unmanned aerial vehicle remote sensing with various sensors for high-throughput plant phenotyping. Comput. Electron. Agric. 2021, 182, 106033. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, K.; Wu, S.; Shi, H.; Sun, Y.; Zhao, Y.; Fu, E.; Chen, S.; Bian, C.; Ban, W. An investigation of winter wheat leaf area index fitting model using spectral and canopy height model data from unmanned aerial vehicle imagery. Remote Sens. 2022, 14, 5087. [Google Scholar] [CrossRef]
- Li, M.; Shamshiri, R.R.; Schirrmann, M.; Weltzien, C.; Shafian, S.; Laursen, M.S. UAV oblique imagery with an adaptive micro-terrain model for estimation of leaf area index and height of maize canopy from 3D point clouds. Remote Sens. 2022, 14, 585. [Google Scholar] [CrossRef]
- Gong, Y.; Yang, K.; Lin, Z.; Fang, S.; Wu, X.; Zhu, R.; Peng, Y. Remote estimation of leaf area index (LAI) with unmanned aerial vehicle (UAV) imaging for different rice cultivars throughout the entire growing season. Plant Methods 2021, 17, 88. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Yang, G.; Dai, H.; Xu, B.; Yang, H.; Feng, H.; Li, Z.; Yang, X. Modeling maize above-ground biomass based on machine learning approaches using UAV remote-sensing data. Plant Methods 2019, 15, 10. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Han, W.; Niu, Y.; Chavez, J.L.; Shao, G.; Zhang, H. Evaluating the sensitivity of water stressed maize chlorophyll and structure based on UAV derived vegetation indices. Comput. Electron. Agric. 2021, 185, 106174. [Google Scholar] [CrossRef]
- Maimaitijiang, M.; Sagan, V.; Sidike, P.; Daloye, A.M.; Erkbol, H.; Fritschi, F.B. Crop monitoring using satellite/UAV data fusion and machine learning. Remote Sens. 2020, 12, 1357. [Google Scholar] [CrossRef]
- Zhang, J.; Sun, B.; Yang, C.; Wang, C.; You, Y.; Zhou, G.; Liu, B.; Wang, C.; Kuai, J.; Xie, J. A novel composite vegetation index including solar-induced chlorophyll fluorescence for seedling rapeseed net photosynthesis rate retrieval. Comput. Electron. Agric. 2022, 198, 107031. [Google Scholar] [CrossRef]
- Wu, T.; Zhang, W.; Wu, S.; Cheng, M.; Qi, L.; Shao, G.; Jiao, X. Retrieving rice (Oryza sativa L.) net photosynthetic rate from UAV multispectral images based on machine learning methods. Front. Plant Sci. 2023, 13, 1088499. [Google Scholar] [CrossRef]
- Zhang, N.; Su, X.; Zhang, X.; Yao, X.; Cheng, T.; Zhu, Y.; Cao, W.; Tian, Y. Monitoring daily variation of leaf layer photosynthesis in rice using UAV-based multi-spectral imagery and a light response curve model. Agric. For. Meteorol. 2020, 291, 108098. [Google Scholar] [CrossRef]
- Zhang, X.-Y.; Huang, Z.; Su, X.; Siu, A.; Song, Y.; Zhang, D.; Fang, Q. Machine learning models for net photosynthetic rate prediction using poplar leaf phenotype data. PLoS ONE 2020, 15, e0228645. [Google Scholar] [CrossRef] [PubMed]
- Mao, W.; Wang, Y.; Wang, Y. Real-time detection of between-row weeds using machine vision. In 2003 ASAE Annual Meeting; American Society of Agricultural and Biological Engineers: St. Joseph, MI, USA, 2003; p. 1. [Google Scholar]
- Otsu, N. A threshold selection method from gray-level histograms. Automatica 1975, 11, 23–27. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martínez, Á.; Walther, S.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Muñoz-Marí, J.; García-Haro, F.J.; Guanter, L. A unified vegetation index for quantifying the terrestrial biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring vegetation systems in the Great Plains with ERTS. NASA Spec. Publ. 1974, 351, 309. [Google Scholar]
- Jiang, Z.; Huete, A.R.; Didan, K.; Miura, T. Development of a two-band enhanced vegetation index without a blue band. Remote Sens. Environ. 2008, 112, 3833–3845. [Google Scholar] [CrossRef]
- Song, Y.; Birch, C.; Qu, S.; Doherty, A.; Hanan, J. Analysis and modelling of the effects of water stress on maize growth and yield in dryland conditions. Plant Prod. Sci. 2010, 13, 199–208. [Google Scholar] [CrossRef]
- Sishodia, R.P.; Ray, R.L.; Singh, S.K. Applications of remote sensing in precision agriculture: A review. Remote Sens. 2020, 12, 3136. [Google Scholar] [CrossRef]
- Rondeaux, G.; Steven, M.; Baret, F. Optimization of soil-adjusted vegetation indices. Remote Sens. Environ. 1996, 55, 95–107. [Google Scholar] [CrossRef]
- Wang, F.; Yang, M.; Ma, L.; Zhang, T.; Qin, W.; Li, W.; Zhang, Y.; Sun, Z.; Wang, Z.; Li, F. Estimation of above-ground biomass of winter wheat based on consumer-grade multi-spectral UAV. Remote Sens. 2022, 14, 1251. [Google Scholar] [CrossRef]
- Liu, Y.; An, L.; Wang, N.; Tang, W.; Liu, M.; Liu, G.; Sun, H.; Li, M.; Ma, Y. Leaf area index estimation under wheat powdery mildew stress by integrating UAV-based spectral, textural and structural features. Comput. Electron. Agric. 2023, 213, 108169. [Google Scholar] [CrossRef]
- He-Ya, S.; Huang, X.; Zhou, D.; Zhang, J.; Bao, G.; Tong, S.; Bao, Y.; Ganbat, D.; Tsagaantsooj, N.; Altanchimeg, D. Identification of Larch Caterpillar Infestation Severity Based on Unmanned Aerial Vehicle Multispectral and LiDAR Features. Forests 2024, 15, 191. [Google Scholar] [CrossRef]
- Qiao, L.; Tang, W.; Gao, D.; Zhao, R.; An, L.; Li, M.; Sun, H.; Song, D. UAV-based chlorophyll content estimation by evaluating vegetation index responses under different crop coverages. Comput. Electron. Agric. 2022, 196, 106775. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, L. The potential of the MERIS Terrestrial Chlorophyll Index for crop yield prediction. Remote Sens. Lett. 2014, 5, 733–742. [Google Scholar] [CrossRef]
- Woebbecke, D.M.; Meyer, G.E.; Von Bargen, K.; Mortensen, D.A. Color indices for weed identification under various soil, residue, and lighting conditions. Trans. ASAE 1995, 38, 259–269. [Google Scholar] [CrossRef]
- Huete, A.; Justice, C.; Liu, H. Development of vegetation and soil indices for MODIS-EOS. Remote Sens. Environ. 1994, 49, 224–234. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Biased estimation for nonorthogonal problems. Technometrics 1970, 12, 55–67. [Google Scholar] [CrossRef]
- Hoerl, A.E.; Kennard, R.W. Ridge regression: Applications to nonorthogonal problems. Technometrics 1970, 12, 69–82. [Google Scholar] [CrossRef]
- Lawlor, D.W. Limitation to photosynthesis in water-stressed leaves: Stomata vs. metabolism and the role of ATP. Ann. Bot. 2002, 89, 871–885. [Google Scholar] [CrossRef] [PubMed]
- Dornhoff, G.M.; Shibles, R.M. Varietal Differences in Net Photosynthesis of Soybean Leaves 1. Crop Sci. 1970, 10, 42–45. [Google Scholar] [CrossRef]
- Emmel, C.; D’Odorico, P.; Revill, A.; Hörtnagl, L.; Ammann, C.; Buchmann, N.; Eugster, W. Canopy photosynthesis of six major arable crops is enhanced under diffuse light due to canopy architecture. Glob. Chang. Biol. 2020, 26, 5164–5177. [Google Scholar] [CrossRef]


| VIS | Abbreviations and Calculation Formulas | References |
|---|---|---|
| Normalised Difference Vegetation Index | NDVI = (NIR − R)/(NIR + R) | [22] |
| Canopy Intercepted Radiation Estimator | CIRE = NIR − REG | [23] |
| Normalised Difference Red Edge | NDRE = (NIR − REG)/(NIR + REG) | [24] |
| Soil-Adjusted Vegetation Index | SAVI = 1.5(NIR − R)/(NIR + R + 0.5) | [25] |
| Optimised Soil-Adjusted Vegetation Index | OSAVI = 1.16(NIR − R)/(NIR + R + 0.16) | [26] |
| Difference Vegetation Index | DVIREG = NIR − G | [27] |
| Optimised Soil-Adjusted Vegetation Index Regression | OSAVIREG = (1 + 0.16)(NIR − G)(NIR + G + 0.16) | [28] |
| Regression of Ratio Vegetation Index | RDVIREG = (NIR − REG)/(NIR + REG)0.5 | [29] |
| Modified Simple Ratio Regression | MSRREG = (NIR/REG − 1)/(NIR/REG + 1)0.5 | [30] |
| Modified Triangular Vegetation Index | MTCI = (NIR − REG)/(NIR − R) | [31] |
| VI1 | VI1 = G − R | / |
| Excess Green | EXG = 2 × G − R − B | [32] |
| Excess Green Ratio | EXGR = 3 × G − 2.4×R − B | [19] |
| Difference Vegetation Index | DVI = NIR − R | [33] |
| Time | Sample Size | Minimum (µmol m−2 s−1) | Maximum (µmol m−2 s−1) | Mean (µmol m−2 s−1) | STDEV (µmol m−2 s−1) | CV (%) |
|---|---|---|---|---|---|---|
| DAS36 | 59 | 10.101 | 21.781 | 16.751 | 2.736 | 16.335 |
| DAS42 | 59 | 7.975 | 20.634 | 16.174 | 2.811 | 17.377 |
| DAS49 | 59 | 8.607 | 21.895 | 17.846 | 2.487 | 13.936 |
| DAS56 | 59 | 12.762 | 24.13 | 19.284 | 2.195 | 11.38 |
| DAS63 | 59 | 2.421 | 21.449 | 13.114 | 4.632 | 35.323 |
| Growth Period | Characteristics |
|---|---|
| DAS36 | DVIREG, OSAVIREG, RDVIREG, EXG, EXGR |
| DAS42 | SAVI, DVI |
| DAS49 | CIRE, NDRE, DVIREG, OSAVIREG, RDVIREG, MSRREG, MTCIVI1, EXG, EXGR |
| ADS56 | CIRE, NDRE, DVIREG, OSAVIREG, RDVIREG, MSRREG, MTCI |
| DAS63 | CIRE, NDRE, DVIREG, OSAVIREG, RDVIREG, MSRREG, MTCI |
| Period | Model | R2 | RMSE | RPD |
|---|---|---|---|---|
| DAS36 | RF | 0.51 | 1.75 | 1.43 |
| MLR | 0.10 | 2.36 | 1.06 | |
| XGB | 0.48 | 1.80 | 1.38 | |
| RR | 0.07 | 2.40 | 1.03 | |
| DAS42 | RF | 0.11 | 3.01 | 0.95 |
| MLR | 0.24 | 2.50 | 1.15 | |
| XGB | 0.11 | 3.07 | 0.93 | |
| RR | 0.02 | 2.84 | 1.01 | |
| DAS49 | RF | 0.20 | 2.47 | 1.12 |
| MLR | 0.11 | 2.59 | 1.06 | |
| XGB | 0.08 | 2.63 | 1.05 | |
| RR | 0.22 | 2.15 | 1.13 | |
| DAS56 | RF | 0.08 | 2.19 | 0.96 |
| MLR | 0.08 | 2.20 | 0.96 | |
| XGB | 0.01 | 2.35 | 1.00 | |
| RR | 0.19 | 1.89 | 1.11 | |
| DAS63 | RF | 0.65 | 2.70 | 1.68 |
| MLR | 0.61 | 2.85 | 1.59 | |
| XGB | 0.26 | 3.90 | 1.16 | |
| RR | 0.66 | 2.63 | 1.73 |
| Period | Model | R2 | RMSE | RPD |
|---|---|---|---|---|
| DAS36 | RF | 0.26 | 2.14 | 1.16 |
| MLR | 0.07 | 2.58 | 0.97 | |
| XGB | 0.32 | 2.06 | 1.21 | |
| RR | 0.09 | 2.60 | 0.96 | |
| DAS42 | RF | 0.37 | 2.28 | 1.26 |
| MLR | 0.27 | 2.34 | 1.17 | |
| XGB | 0.11 | 2.70 | 1.06 | |
| RR | 0.35 | 2.31 | 1.24 | |
| DAS49 | RF | 0.03 | 2.48 | 0.98 |
| MLR | 0.15 | 2.23 | 1.09 | |
| XGB | 0.05 | 2.67 | 1.03 | |
| RR | 0.02 | 2.79 | 0.99 | |
| DAS56 | RF | 0.04 | 2.15 | 0.98 |
| MLR | 0.34 | 1.72 | 1.23 | |
| XGB | 0.10 | 2.25 | 1.05 | |
| RR | 0.32 | 1.73 | 1.22 | |
| DAS63 | RF | 0.66 | 2.64 | 1.72 |
| MLR | 0.72 | 2.41 | 1.89 | |
| XGB | 0.46 | 3.34 | 1.36 | |
| RR | 0.66 | 2.63 | 1.73 |
| Period | Model | R2 | RMSE | RPD |
|---|---|---|---|---|
| DAS36 | RF | 0.64 | 1.49 | 1.68 |
| MLR | 0.39 | 1.95 | 1.28 | |
| XGB | 0.48 | 1.80 | 1.38 | |
| RR | 0.10 | 2.36 | 1.06 | |
| DAS42 | RF | 0.48 | 2.07 | 1.39 |
| MLR | 0.38 | 2.26 | 1.27 | |
| XGB | 0.60 | 1.82 | 1.58 | |
| RR | 0.35 | 2.31 | 1.24 | |
| DAS49 | RF | 0.21 | 2.16 | 1.12 |
| MLR | 0.21 | 2.15 | 1.12 | |
| XGB | 0.51 | 1.70 | 1.43 | |
| RR | 0.17 | 2.51 | 1.09 | |
| DAS56 | RF | 0.11 | 1.99 | 1.06 |
| MLR | 0.14 | 2.25 | 0.94 | |
| XGB | 0.28 | 2.01 | 1.18 | |
| RR | 0.48 | 1.52 | 1.38 | |
| DAS63 | RF | 0.86 | 1.73 | 2.63 |
| MLR | 0.83 | 1.90 | 2.39 | |
| XGB | 0.61 | 2.84 | 1.60 | |
| RR | 0.76 | 2.23 | 2.03 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, Z.; Yao, W.; Pei, S.; Lu, Y.; Liang, H.; Xu, D.; Li, H.; Yu, L.; Zhou, Y.; Liu, Q. Inversion of Soybean Net Photosynthetic Rate Based on UAV Multi-Source Remote Sensing and Machine Learning. Agronomy 2024, 14, 1493. https://doi.org/10.3390/agronomy14071493
Lu Z, Yao W, Pei S, Lu Y, Liang H, Xu D, Li H, Yu L, Zhou Y, Liu Q. Inversion of Soybean Net Photosynthetic Rate Based on UAV Multi-Source Remote Sensing and Machine Learning. Agronomy. 2024; 14(7):1493. https://doi.org/10.3390/agronomy14071493
Chicago/Turabian StyleLu, Zhen, Wenbo Yao, Shuangkang Pei, Yuwei Lu, Heng Liang, Dong Xu, Haiyan Li, Lejun Yu, Yonggang Zhou, and Qian Liu. 2024. "Inversion of Soybean Net Photosynthetic Rate Based on UAV Multi-Source Remote Sensing and Machine Learning" Agronomy 14, no. 7: 1493. https://doi.org/10.3390/agronomy14071493
APA StyleLu, Z., Yao, W., Pei, S., Lu, Y., Liang, H., Xu, D., Li, H., Yu, L., Zhou, Y., & Liu, Q. (2024). Inversion of Soybean Net Photosynthetic Rate Based on UAV Multi-Source Remote Sensing and Machine Learning. Agronomy, 14(7), 1493. https://doi.org/10.3390/agronomy14071493





