Evaluation of the Possibility of Using Fuzzy C-Means Clustering, AMMI Analysis and GGE Biplot Methods to Predict the Yield of Chickpea Genotypes Cultivated in Different Environments
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
Climate Data for Experimental Areas
2.2. Methods
2.2.1. Methodology of GGE Biplot
2.2.2. Methodology of AMMI Biplot
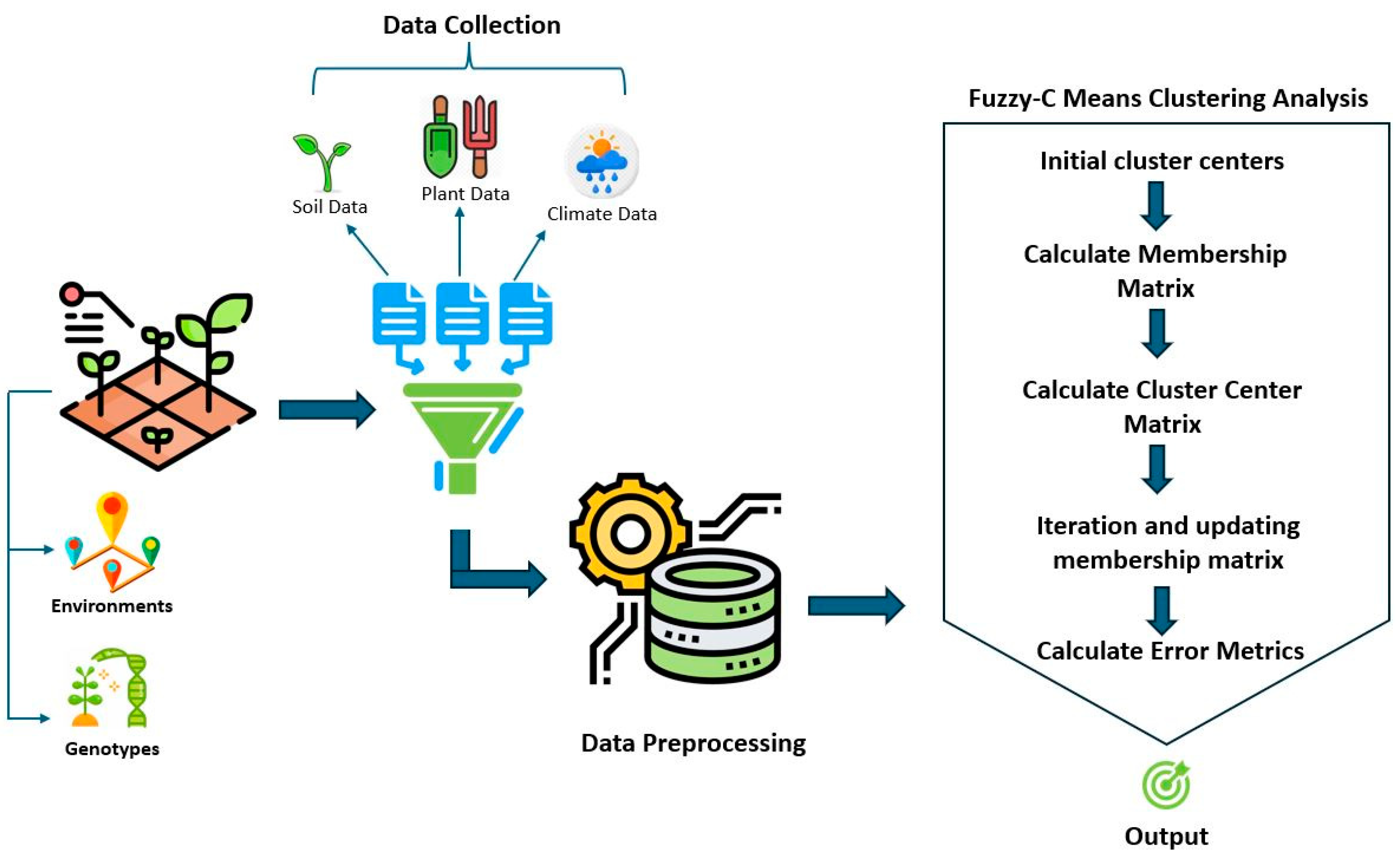
2.2.3. Architecture of Fuzzy C-Means Clustering
Fuzzy Partition Coefficient (FPC)
Davies–Bouldin Index (D-B Index)
Dunn Index
Silhouette Score
Root Mean Square Error (RMSE)
Partition Entropy (PE)
2.2.4. Statistical Analysis
3. Results
3.1. Analysis of Variance
3.2. Comparison of Environments Based on Discriminating Ability
3.3. Ranking Performance of Genotypes in Environments
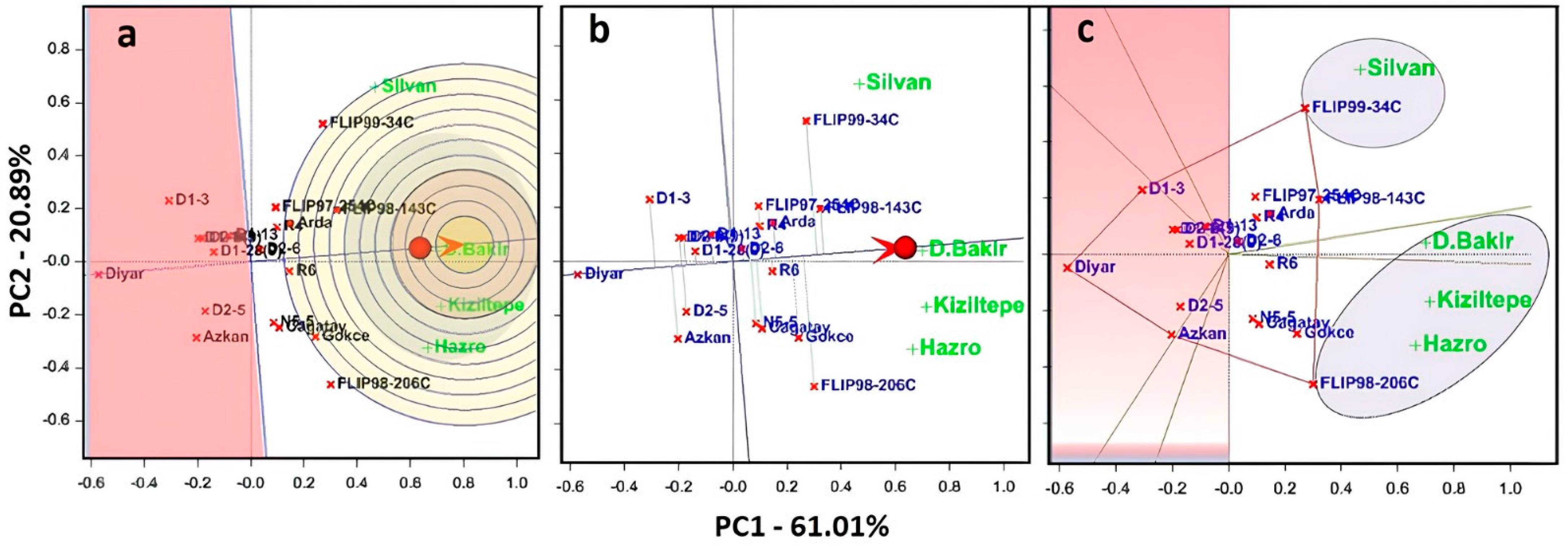
3.4. Detection of the Best Which-Won-Where Performance of Genotypes
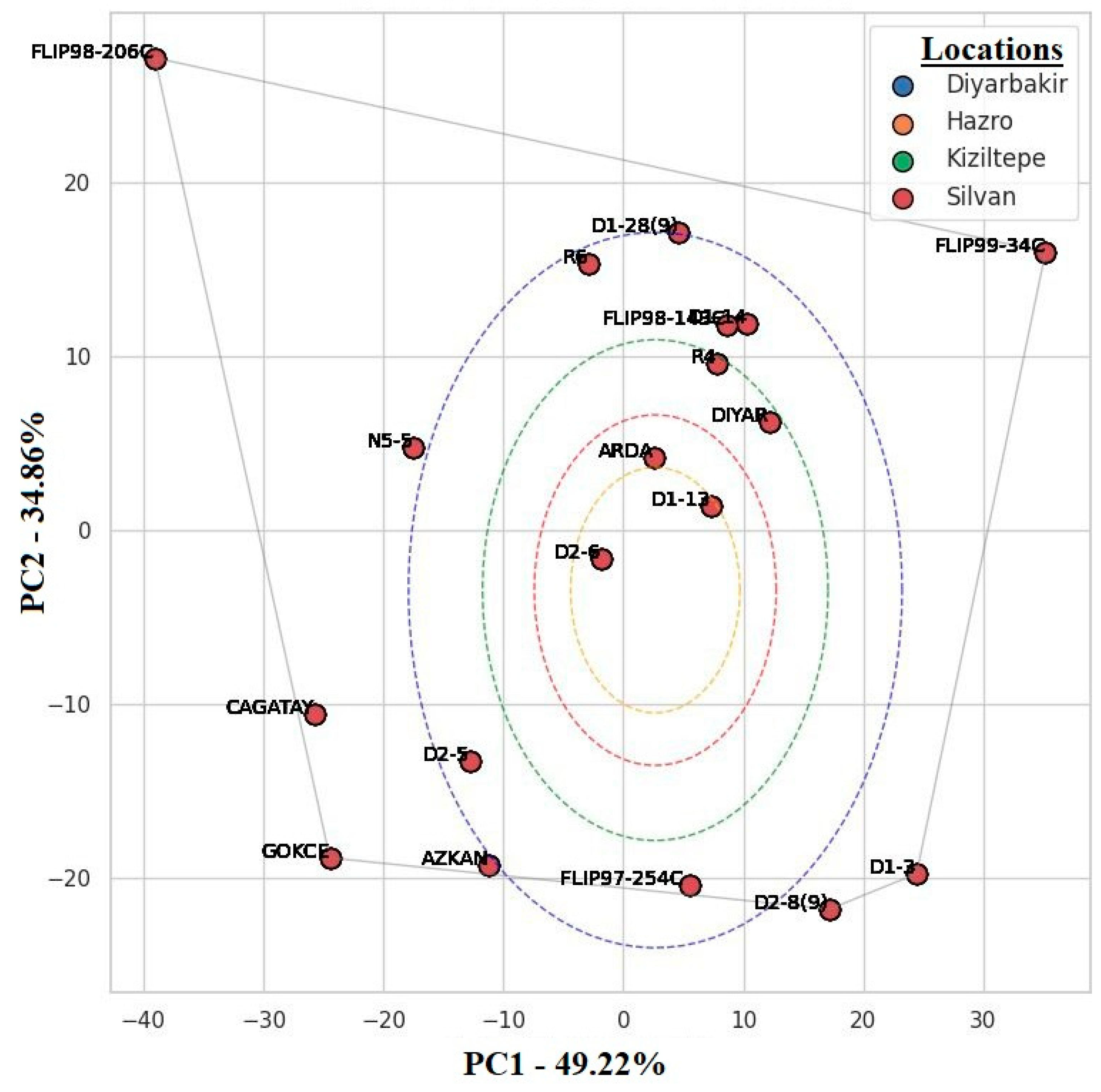
3.5. AMMI Biplot
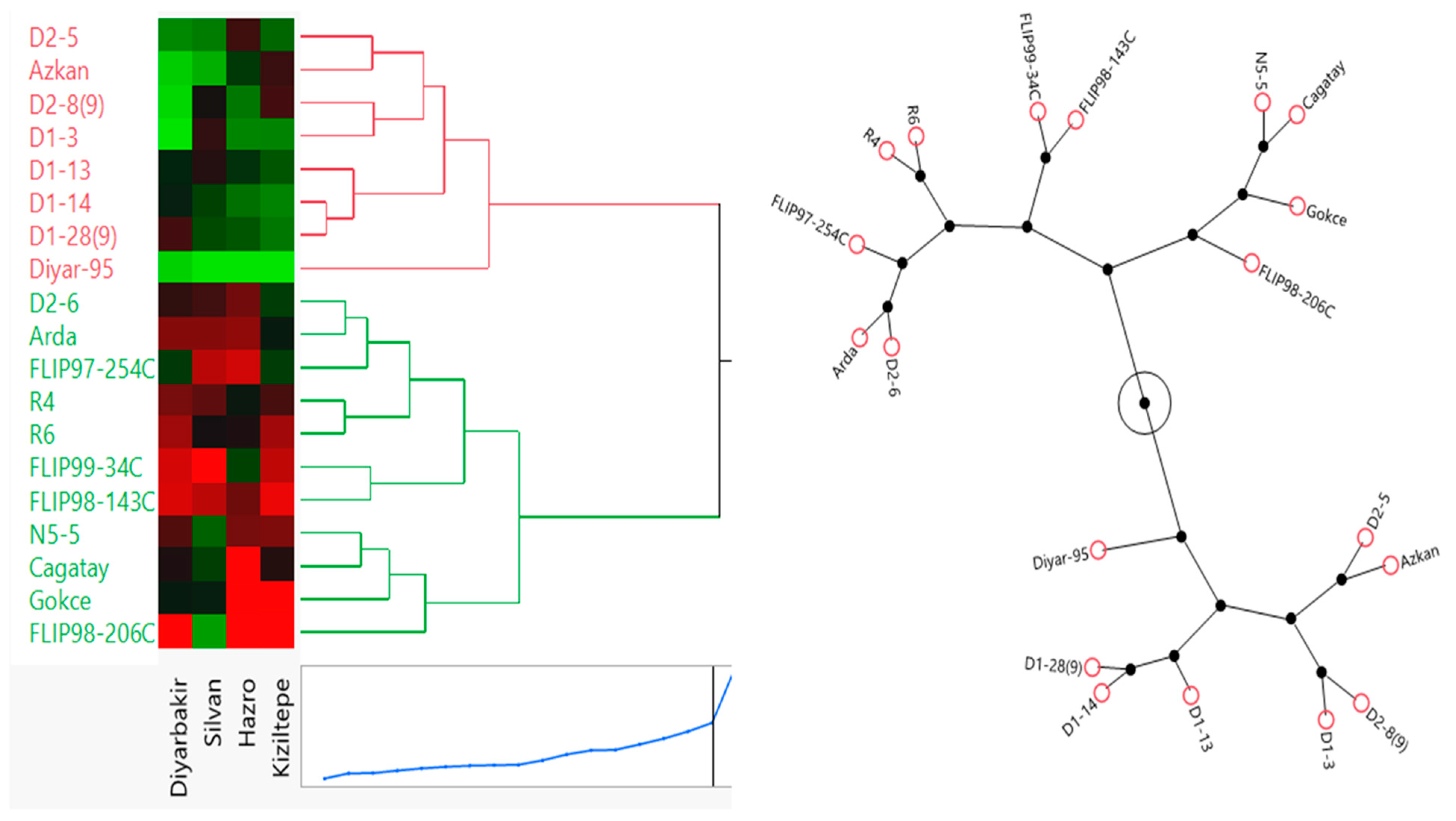
3.6. Ward’s Method Clustering
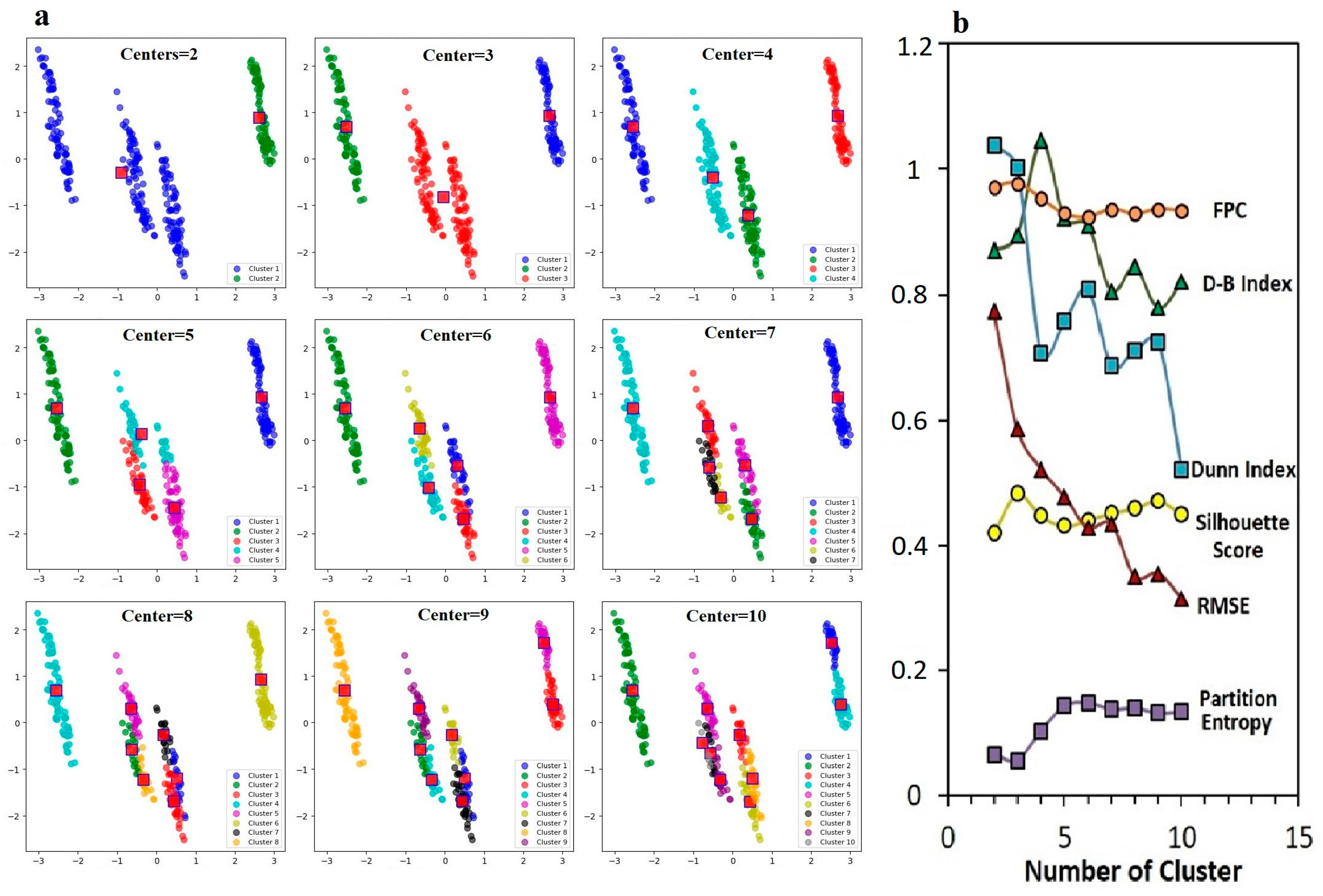
3.7. Fuzzy C-Means Clustering
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jendoubi, W.; Bouhadida, M.; Boukteb, A.; Béji, M.; Kharrat, M. Fusarium wilt affecting chickpea crop. Agriculture 2017, 7, 23. [Google Scholar] [CrossRef]
- Ipekesen, S.; Basdemir, F.; Tunc, M.; Bicer, B.T. Minerals, vitamins, protein and amino acids in wild Cicer species and pure line chickpea genotypes selected from a local population. J. Elem. 2022, 27, 127–140. [Google Scholar] [CrossRef]
- FAOSTAT. 2022. Available online: https://www.fao.org/faostat/en/#data/QCL (accessed on 10 October 2024).
- Shah, T.M.; Imran, M.; Atta, B.M.; Ashraf, M.Y.; Hameed, A.; Waqar, I.; Shafiq, M.; Hussain, K.; Naveed, M.; Aslam, M.; et al. Selection and screening of drought tolerant high yielding chickpea genotypes based on physio-biochemical indices and multi-environmental yield trials. BMC Plant Biol. 2020, 20, 171. [Google Scholar] [CrossRef] [PubMed]
- Padi, F.K. The relationship between stress tolerance and grain yield stability in cowpea. J. Agri. Sci. Camb. 2007, 142, 431–444. [Google Scholar] [CrossRef]
- Ebdon, J.S.; Gauch, H.G. Additive main effect and multiplicative interaction analysis of national turfgrass performance trials: I. Interpretation of genotype 3 environment interaction. Crop Sci. 2002, 42, 489–496. [Google Scholar] [CrossRef]
- Sabaghnia, N.; Dehghani, H.; Sabaghpour, S.H. Nonparametric methods for interpreting genotype× environment interaction of lentil genotypes. Crop Sci. 2006, 46, 1100–1106. [Google Scholar] [CrossRef]
- Yan, W. Singular-value partitioning in biplot analysis of multi-environment trial data. Agron. J. 2002, 94, 990–996. [Google Scholar] [CrossRef]
- Gower, J.C. Multivariate analysis and multivariate geometry. Statistician 1967, 17, 13–28. [Google Scholar] [CrossRef]
- Mungomery, V.E.; Shorter, R.; Byth, D.E. Genotype × environment interactions and environment adaptation. I. Pattern analysis—Application to soya bean populations. Aust. J. Agric. Res. 1974, 25, 59–72. [Google Scholar] [CrossRef]
- Gauch, H.G.; Zobel, R.W. Predictive and postdictive success of statistical analyses of yield trials. Theor. Appl. Genet. 1988, 76, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Ambuel, J.R.; Colvin, T.S.; Karlen, D.L. A fuzzy logic yield simulator for prescription farming. Trans. ASAE 1994, 37, 1999–2009. [Google Scholar] [CrossRef]
- Gauch, G. Statistical Analysis of Regional Yield Trials: AMMI Analysis of Factorial Designs; Elsevier Science Publishers: Amsterdam, The Netherlands, 1992. [Google Scholar] [CrossRef]
- Bezdek, J. Pattern Recognition with Fuzzy Objective Function Algorithms; Plenum Press: New York, NY, USA, 1981. [Google Scholar] [CrossRef]
- Jelacic, M. Unsupervised Learning for Plant Recognition. Master’s Thesis, School of Information Science, Computer and Electrical Engineering, Halmstad University, Halmstad, Sweden, 2006. [Google Scholar]
- Gabriel, K.R. Le biplot: Outil d’exploration de données multidimensionnelles [Biplot—Tool for exploration of data]. J. Société Française Stat. 2002, 143, 5–55. [Google Scholar]
- Yang, C.H.; Chuang, L.Y.; Lin, Y.D. Epistasis analysis using an improved fuzzy C-means-based entropy approach. IEEE Trans. Fuzzy Syst. 2019, 28, 718–730. [Google Scholar] [CrossRef]
- Yan, W.; Tinker, N.A. Biplot analysis of multi-environment trial data: Principles and applications. Can. J. Plant Sci. 2006, 86, 623–645. [Google Scholar] [CrossRef]
- Gollob, H.F. A Statistical Model Which Combines Features of Factor Analytic and Analysis of Variance Techniques. Psychometrika 1968, 33, 73–115. [Google Scholar] [CrossRef]
- Dunn, J.C. A Fuzzy Relative of the ISODATA Process and Its Use in Detecting Compact Well-Separated Clusters. J. Cybern. 1973, 3, 32–57. [Google Scholar] [CrossRef]
- Davies, D.L.; Bouldin, D.W. A Cluster Separation Measure. IEEE Trans. Pattern Anal. Mach. Intell. 1979, 1, 224–227. [Google Scholar] [CrossRef] [PubMed]
- Rousseeuw, P.J. Silhouettes: A Graphical Aid to the Interpretation and Validation of Cluster Analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- van der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- McKinney, W. Data Structures for Statistical Computing in Python. In Proceedings of the 9th Python in Science Conference, Austin, TX, USA, 28 June–3 July 2010. [Google Scholar] [CrossRef]
- Yousefabadi, V.A.; Mehdikhani, P.; Nadali, F.; Sharifi, M.; Azizi, H.; Ahmadi, M.; Fasahat, P. Evaluation of yield and stability of sugar beet (beta vulgaris L.) genotypes using GGE biplot and AMMI analysis. Sci. Rep. 2024, 14, 27384. [Google Scholar] [CrossRef] [PubMed]
- Asadi, B.; Shobeiri, S.S.; Asadi, A.A. Investigating of the Genotype× Environment Interaction Effect for Grain Yield in Red Bean Genotypes Using AMMI and GGE Biplot Methods. J. Crop Breed. 2024, 16, 86–102. [Google Scholar] [CrossRef]
- Supriadi, D.; Bimantara, Y.M.; Zendrato, Y.M.; Widaryanto, E.; Kuswanto, K.; Waluyo, B. Assessment of genotype by environment and yield performance of tropical maize hybrids using stability statistics and graphical biplots. PeerJ 2024, 12, e18624. [Google Scholar] [CrossRef] [PubMed]
- Daemo, B.B.; Ashango, Z. Application of AMMI and GGE biplot for genotype by environment interaction and yield stability analysis in potato genotypes grown in Dawuro zone, Ethiopia. J. Agric. Food Res. 2024, 18, 101287. [Google Scholar] [CrossRef]
- Rahmati, S.; Azizi-Nezhad, R.; Pour-Aboughadareh, A.; Etminan, A.; Shooshtari, L. Analysis of genotype-by-environment interaction effect in barley genotypes using AMMI and GGE biplot methods. Heliyon 2024, 10, e38131. [Google Scholar] [CrossRef] [PubMed]
- Vinu, V.; Alarmelu, S.; Elayaraja, K.; Appunu, C.; Hemaprabha, G.; Parthiban, S.; Shanmugasundaram, K.; Rajamadhan, R.; Saravanan, K.G.; Kathiravan, S.; et al. Multi-environment Analysis of Yield and Quality Traits in Sugarcane (Saccharum sp.) through AMMI and GGE Biplot Analysis. Sugar Tech. 2024, 1–19. [Google Scholar] [CrossRef]
- Demelash, H. Genotype by environment interaction, AMMI, GGE biplot, and mega environment analysis of elite Sorghum bicolor (L.) Moench genotypes in humid lowland areas of Ethiopia. Heliyon 2024, 10, e26528. [Google Scholar] [CrossRef]
- Mahmood, M.T.; Akhtar, M.; Cheema, K.L.; Ghaffar, A.; Ali, I.; Khalid, M.J.; Ali, Z. Genetic studies for detection of most diverse and high yielding genotypes among chickpea (Cicer arientinum L.) germplasm. Pak. J. Agric. Res. 2022, 35, 115. [Google Scholar] [CrossRef]
- Bezdek, J.C.; Ehrlich, R.; Full, W. FCM: The fuzzy c-means clustering algorithm. Comput. Geosci. 1984, 10, 191–203. [Google Scholar] [CrossRef]
- Cardoso, D.B.O.; Oliveira, L.F.; de Souza, G.S.; Garcia, M.F.; Medeiros, L.A.; Faria, P.N.; Cruz, C.D.; de Sousa, L.B. Using fuzzy logic to select coloured-fibre cotton genotypes based on adaptability and yield stability. Acta Scientiarum. Agron. 2021, 43, e50530. [Google Scholar] [CrossRef]
- Carneiro, V.Q.; Mencalha, J.; Sant’anna, I.d.C.; Silva, G.N.; Miguel, J.A.d.C.; Carneiro, P.C.S.; Nascimento, M.; Cruz, C.D. A novel fuzzy approach to identify the phenotypic adaptability of common bean lines. Acta Scientiarum. Agron. 2023, 45, e59854. [Google Scholar] [CrossRef]
- Yang, C.H.; Chuang, L.Y.; Lin, Y.D. An improved fuzzy set-based multifactor dimensionality reduction for detecting epistasis. Artif. Intell. Med. 2020, 102, 101768. [Google Scholar] [CrossRef]
- Zhou, X.; Chan, K.C. Detecting gene-gene interactions for complex quantitative traits using generalized fuzzy classification. BMC Bioinform. 2018, 19, 1–13. [Google Scholar] [CrossRef]



| Locations | Soil Properties | Altitude (a.s.l) | Latitude | Longitude |
|---|---|---|---|---|
| Dicle University | Saturation: 66 pH: 7.19 Lime: 11.40% Organic matter: 0.79% | 640 m | 37° 53′ | 40° 16′ |
| Yasarkoy, Kiziltepe, Mardin | Saturation: 59.4 pH: 7.71 Lime: 19.14% Organic matter: 2.10% | 480 m | 37°07′ | 40°16′ |
| Yenikoy, Silvan, Diyarbakir | Saturation: 72 pH: 7.36 Lime: 3.16%, Organic matter: 1.63% | 811 m | 38°07′ | 41°03′ |
| Hazro, Diyarbakir | Saturation: 65 pH: 7.41 Lime: 1.48% Organic matter: 1.74% | 1090 m | 38°15′ | 40°47′ |
| Source | DF | Mean of Squares | Probability |
|---|---|---|---|
| Replication | 3 | 103.9237 | 0.6860 |
| Genotype | 18 | 3928.26 | 34.8162 ** |
| Location | 3 | 5274.433 | 25.9302 ** |
| Genotype × Location | 54 | 906.776 | 5.9856 ** |
| Error | 225 | 34,086.08 | 151.49 |
| C. Total | 303 | 169,895.74 | |
| CV (%) | 10.24 |
| Genotypes | Environments | Mean | |||
|---|---|---|---|---|---|
| Diyarbakir | Silvan | Hazro | Kiziltepe | ||
| Arda | 1465.0 a–g | 1282.3 b–p | 1387.5 a–j | 1129.8 g–t | 1316.1 ab |
| Azkan | 957.3 n–u | 879.3 r–u | 1150.8 f–t | 1175.0 e–s | 1040.6 f |
| Cagatay | 1312.5 b–n | 1056.0 ı–u | 1571.8 a–d | 1158.8 e–t | 1274.8 abc |
| D1-13 | 1266.5 b–q | 1143.5 f–t | 1170.8 e–s | 1041.5 ı–u | 1155.6 c–f |
| D1-14 | 1274.8 b–q | 1053.3 ı–u | 1020.0 j–u | 969.0 m–u | 1079.3 f |
| D1-28(9) | 1365.0 a–k | 1039.3 ı–u | 1083.0 h–u | 987.8 l–u | 1118.8 def |
| D1-3 | 913.5 p–u | 1162.8 e–t | 965.8 n–u | 966.8 n–u | 1002.2 f |
| D2-5 | 1087.5 h–u | 961.5 n–u | 1289.3 b–o | 1015.5 k–u | 1088.4 ef |
| D2-6 | 1336.8 b–m | 1180.8 e–r | 1351.5 b–l | 1080.5 h–u | 1237.4 b–e |
| D2-8(9) | 938.5 o–u | 1125.5 g–t | 1001.8 k–u | 1183.8 e–r | 1062.4 f |
| Diyar 95 | 951.5 n–u | 794.8 tu | 723.5 u | 810.3 stu | 820.0 g |
| FLIP97-254C | 1230.5 c–r | 1360.3 a–k | 1467.5 a–g | 1080.8 h–u | 1284.8 abc |
| FLIP98-143C | 1605.0 ab | 1364.3 a–k | 1347.0 b–l | 1345.8 b–l | 1415.5 a |
| FLIP98-206C | 1727.3 a | 907.5 q–u | 1528.3 a–e | 1368.3 a–k | 1382.8 ab |
| FLIP99-34C | 1596.3 abc | 1528.0 a–e | 1131.5 g–t | 1301.0 b–o | 1389.2 ab |
| Gokce | 1282.3 b–p | 1103.0 g–t | 1576.8 a–d | 1402.5 a–ı | 1341.1 ab |
| N5-5 | 1388.5 a–j | 1004.5 k–u | 1356.0 b–l | 1238.3 b–r | 1246.8 bcd |
| R4 | 1445.0 a–h | 1225.3 d–r | 1225.8 d–r | 1186.0 e–r | 1270.5 a–d |
| R6 | 1509.0 a–f | 1124.0 g–t | 1253.3 b–q | 1273.0 b–q | 1289.8 abc |
| Mean | 129.75 a | 124.21 b | 114.28 c | 112.08 c | |
| LSD(0.05) Genotype:15.44 ** Location: 5.13 ** Genotype × Location: 36.88 ** | |||||
| Source of Variation | DF | SS | MS | SS Explained (%) | GE Explained (%) |
|---|---|---|---|---|---|
| Genotypes | 18 | 70708.69 | 3928.26 *** | 41.62 | |
| Environments | 3 | 15823.30 | 5274.43 *** | 9.31 | |
| Interactions | 54 | 48965.90 | 906.78 *** | 28.82 | 100.00 |
| PCA 1 | 1 | 31104.22 | 31104.22 *** | 63.52 | |
| PCA 2 | 1 | 9142.84 | 9142.84 *** | 18.67 | |
| Residuals | 52 | 8718.84 | 167.67 *** | 17.81 | |
| Error | 92340 | 34397.85 | 0.37 | ||
| Total | 92415 | 169895.74 | 100.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tunc, M.; Rufaioglu, S.B.; Ipekesen, S.; Yakar, M.; Yorulmaz, L.; Bicer, B.T. Evaluation of the Possibility of Using Fuzzy C-Means Clustering, AMMI Analysis and GGE Biplot Methods to Predict the Yield of Chickpea Genotypes Cultivated in Different Environments. Agronomy 2025, 15, 300. https://doi.org/10.3390/agronomy15020300
Tunc M, Rufaioglu SB, Ipekesen S, Yakar M, Yorulmaz L, Bicer BT. Evaluation of the Possibility of Using Fuzzy C-Means Clustering, AMMI Analysis and GGE Biplot Methods to Predict the Yield of Chickpea Genotypes Cultivated in Different Environments. Agronomy. 2025; 15(2):300. https://doi.org/10.3390/agronomy15020300
Chicago/Turabian StyleTunc, Murat, Süreyya Betül Rufaioglu, Sibel Ipekesen, Murat Yakar, Levent Yorulmaz, and Behiye Tuba Bicer. 2025. "Evaluation of the Possibility of Using Fuzzy C-Means Clustering, AMMI Analysis and GGE Biplot Methods to Predict the Yield of Chickpea Genotypes Cultivated in Different Environments" Agronomy 15, no. 2: 300. https://doi.org/10.3390/agronomy15020300
APA StyleTunc, M., Rufaioglu, S. B., Ipekesen, S., Yakar, M., Yorulmaz, L., & Bicer, B. T. (2025). Evaluation of the Possibility of Using Fuzzy C-Means Clustering, AMMI Analysis and GGE Biplot Methods to Predict the Yield of Chickpea Genotypes Cultivated in Different Environments. Agronomy, 15(2), 300. https://doi.org/10.3390/agronomy15020300






