Effect of Cell Age and Membrane Rigidity on Red Blood Cell Shape in Capillary Flow
Abstract
1. Introduction
2. Methods
2.1. In Vivo RBC Imaging
2.2. In Vitro RBC Sample Preparation
2.2.1. RBC Density Separation
2.2.2. Membrane Rigidification
2.2.3. Ektacytometry
2.3. Microfluidic Setup
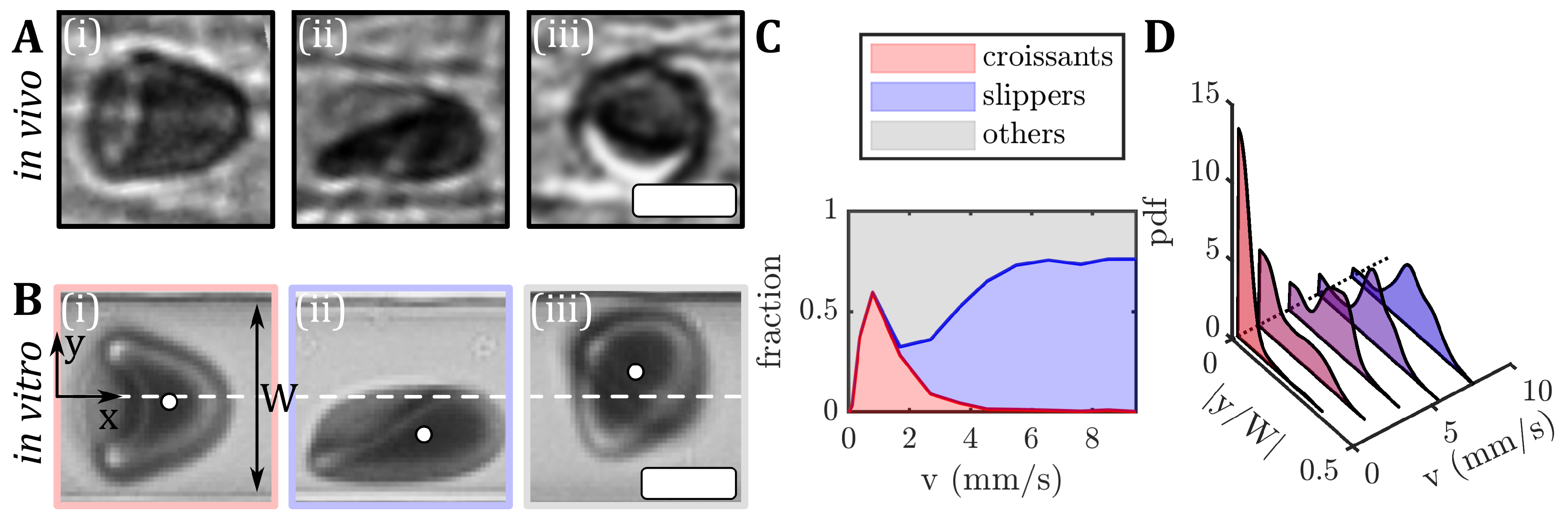
3. Results
3.1. Stable RBC Shapes in Straight Microchannels
3.2. RBC Equilibrium Position in the Channel Cross-Section
3.3. Fraction of Stable RBC Shapes
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| BSA | bovine serum albumin |
| EI | elongation index |
| Ht | hematocrit |
| Lx | layer no. x |
| PBS | phosphate-buffered saline |
| PD | phase diagram |
| probability density distribution | |
| PDMS | polydimethylsiloxane |
| RBC | red blood cell |
Appendix A



References
- Mohandas, N.; Evans, E. Mechanical Properties of the Red Cell Membrane in Relation to Molecular Structure and Genetic Defects. Annu. Rev. Biophys. Biomol. Struct. 1994, 23, 787–818. [Google Scholar] [CrossRef] [PubMed]
- Secomb, T.W. Blood Flow in the Microcirculation. Annu. Rev. Fluid Mech. 2017, 49, 443–461. [Google Scholar] [CrossRef]
- Skalak, R.; Branemark, P.I. Deformation of Red Blood Cells in Capillaries. Science 1969, 164, 717–719. [Google Scholar] [CrossRef] [PubMed]
- Bagge, U.; Brånemark, P.; Karlsson, R.; Skalak, R. Three-dimensional observations of red blood cell deformation in capillaries. Blood Cells 1980, 6, 231–239. [Google Scholar]
- Suzuki, Y.; Tateishi, N.; Soutani, M.; Maeda, N. Deformation of Erythrocytes in Microvessels and Glass Capillaries: Effects of Erythrocyte Deformability. Microcirculation 1996, 3, 49–57. [Google Scholar] [CrossRef]
- Freund, J.B. The flow of red blood cells through a narrow spleen-like slit. Phys. Fluids 2013, 25, 110807. [Google Scholar] [CrossRef]
- Salehyar, S.; Zhu, Q. Deformation and internal stress in a red blood cell as it is driven through a slit by an incoming flow. Soft Matter 2016, 12, 3156–3164. [Google Scholar] [CrossRef]
- Stuart, J.; Nash, G. Red cell deformability and haematological disorders. Blood Rev. 1990, 4, 141–147. [Google Scholar] [CrossRef]
- Symeonidis, A.; Athanassiou, G.; Psiroyannis, A.; Kyriazopoulou, V.; Kapatais-Zoumbos, K.; Missirlis, Y.; Zoumbos, N. Impairment of erythrocyte viscoelasticity is correlated with levels of glycosylated haemoglobin in diabetic patients. Clin. Lab. Haematol. 2001, 23, 103–109. [Google Scholar] [CrossRef]
- Dondorp, A.; Nyanoti, M.; Kager, P.; Mithwani, S.; Vreeken, J.; Marsh, K. The role of reduced red cell deformability in the pathogenesis of severe falciparum malaria and its restoration by blood transfusion. Trans. R. Soc. Trop. Med. Hyg. 2002, 96, 282–286. [Google Scholar] [CrossRef]
- Mannino, R.; Myers, D.R.; Sakurai, Y.; Ware, R.E.; Barabino, G.; Lam, W. Increased Erythrocyte Rigidity Is Sufficient to Cause Endothelial Dysfunction in Sickle Cell Disease. Blood 2012, 120, 818. [Google Scholar] [CrossRef]
- Rabe, A.; Kihm, A.; Darras, A.; Peikert, K.; Simionato, G.; Dasanna, A.K.; Glaß, H.; Geisel, J.; Quint, S.; Danek, A.; et al. The Erythrocyte Sedimentation Rate and Its Relation to Cell Shape and Rigidity of Red Blood Cells from Chorea-Acanthocytosis Patients in an Off-Label Treatment with Dasatinib. Biomolecules 2021, 11, 727. [Google Scholar] [CrossRef]
- Pries, A.R.; Secomb, T.W. Blood Flow in Microvascular Networks. In Microcirculation; Elsevier: Amsterdam, The Netherlands, 2008; pp. 3–36. [Google Scholar] [CrossRef]
- Lanotte, L.; Mauer, J.; Mendez, S.; Fedosov, D.A.; Fromental, J.M.; Claveria, V.; Nicoud, F.; Gompper, G.; Abkarian, M. Correction for Lanotte et al., Red cells’ dynamic morphologies govern blood shear thinning under microcirculatory flow conditions. Proc. Natl. Acad. Sci. USA 2016, 113, E8207. [Google Scholar] [CrossRef]
- Gaehtgens, P.; Dührssen, C.; Albrecht, K. Motion, deformation, and interaction of blood cells and plasma during flow through narrow capillary tubes. Blood Cells 1980, 6, 799–817. [Google Scholar]
- Abkarian, M.; Faivre, M.; Stone, H.A. High-speed microfluidic differential manometer for cellular-scale hydrodynamics. Proc. Natl. Acad. Sci. USA 2006, 103, 538–542. [Google Scholar] [CrossRef]
- Tomaiuolo, G.; Simeone, M.; Martinelli, V.; Rotoli, B.; Guido, S. Red blood cell deformation in microconfined flow. Soft Matter 2009, 5, 3736. [Google Scholar] [CrossRef]
- Guido, S.; Tomaiuolo, G. Microconfined flow behavior of red blood cells in vitro. Comptes Rendus Phys. 2009, 10, 751–763. [Google Scholar] [CrossRef]
- Braunmüller, S.; Schmid, L.; Sackmann, E.; Franke, T. Hydrodynamic deformation reveals two coupled modes/time scales of red blood cell relaxation. Soft Matter 2012, 8, 11240–11248. [Google Scholar] [CrossRef]
- Cluitmans, J.C.A.; Chokkalingam, V.; Janssen, A.M.; Brock, R.; Huck, W.T.S.; Bosman, G.J.C.G.M. Alterations in Red Blood Cell Deformability during Storage: A Microfluidic Approach. Biomed Res. Int. 2014, 2014, 764268. [Google Scholar] [CrossRef]
- Saadat, A.; Huyke, D.A.; Oyarzun, D.I.; Escobar, P.V.; vreeide, I.H.; Shaqfeh, E.S.G.; Santiago, J.G. A system for the high-throughput measurement of the shear modulus distribution of human red blood cells. Lab Chip 2020, 20, 2927–2936. [Google Scholar] [CrossRef]
- Kaoui, B.; Biros, G.; Misbah, C. Why Do Red Blood Cells Have Asymmetric Shapes Even in a Symmetric Flow? Phys. Rev. Lett. 2009, 103, 188101. [Google Scholar] [CrossRef] [PubMed]
- Fedosov, D.A.; Caswell, B.; Karniadakis, G.E. A Multiscale Red Blood Cell Model with Accurate Mechanics, Rheology, and Dynamics. Biophys. J. 2010, 98, 2215–2225. [Google Scholar] [CrossRef]
- Tahiri, N.; Biben, T.; Ez-Zahraouy, H.; Benyoussef, A.; Misbah, C. On the problem of slipper shapes of red blood cells in the microvasculature. Microvasc. Res. 2013, 85, 40–45. [Google Scholar] [CrossRef] [PubMed]
- Fedosov, D.A.; Noguchi, H.; Gompper, G. Multiscale modeling of blood flow: From single cells to blood rheology. Biomech. Model. Mechanobiol. 2014, 13, 239–258. [Google Scholar] [CrossRef]
- Lázaro, G.R.; Hernández-Machado, A.; Pagonabarraga, I. Rheology of red blood cells under flow in highly confined microchannels: I. effect of elasticity. Soft Matter 2014, 10, 7195. [Google Scholar] [CrossRef]
- Fedosov, D.A.; Peltomäki, M.; Gompper, G. Deformation and dynamics of red blood cells in flow through cylindrical microchannels. Soft Matter 2014, 10, 4258–4267. [Google Scholar] [CrossRef] [PubMed]
- Ye, T.; Shi, H.; Peng, L.; Li, Y. Numerical studies of a red blood cell in rectangular microchannels. J. Appl. Phys. 2017, 122, 084701. [Google Scholar] [CrossRef]
- Fischer, T.M. Tank-Tread Frequency of the Red Cell Membrane: Dependence on the Viscosity of the Suspending Medium. Biophys. J. 2007, 93, 2553–2561. [Google Scholar] [CrossRef]
- Fischer, T.M. Shape Memory of Human Red Blood Cells. Biophys. J. 2004, 86, 3304–3313. [Google Scholar] [CrossRef]
- Abkarian, M.; Faivre, M.; Viallat, A. Swinging of red blood cells under shear flow. Phys. Rev. Lett. 2007, 98, 188302. [Google Scholar] [CrossRef]
- Dupire, J.; Socol, M.; Viallat, A. Full dynamics of a red blood cell in shear flow. Proc. Natl. Acad. Sci. USA 2012, 109, 20808–20813. [Google Scholar] [CrossRef]
- Guckenberger, A.; Kihm, A.; John, T.; Wagner, C.; Gekle, S. Numerical–experimental observation of shape bistability of red blood cells flowing in a microchannel. Soft Matter 2018, 14, 2032–2043. [Google Scholar] [CrossRef]
- Recktenwald, S.M.; Lopes, M.G.M.; Peter, S.; Hof, S.; Simionato, G.; Peikert, K.; Hermann, A.; Danek, A.; van Bentum, K.; Eichler, H.; et al. Erysense, a Lab-on-a-Chip-Based Point-of-Care Device to Evaluate Red Blood Cell Flow Properties With Multiple Clinical Applications. Front. Physiol. 2022, 13, 884690. [Google Scholar] [CrossRef]
- Recktenwald, S.M.; Simionato, G.; Lopes, M.G.; Gamboni, F.; Dzieciatkowska, M.; Meybohm, P.; Zacharowski, K.; von Knethen, A.; Wagner, C.; Kaestner, L.; et al. Cross-talk between red blood cells and plasma influences blood flow and omics phenotypes in severe COVID-19. eLife 2022, 11, e81316. [Google Scholar] [CrossRef]
- Quint, S.; Christ, A.F.; Guckenberger, A.; Himbert, S.; Kaestner, L.; Gekle, S.; Wagner, C. 3D tomography of cells in micro-channels. Appl. Phys. Lett. 2017, 111, 103701. [Google Scholar] [CrossRef]
- Kihm, A.; Kaestner, L.; Wagner, C.; Quint, S. Classification of red blood cell shapes in flow using outlier tolerant machine learning. PLoS Comput. Biol. 2018, 14, e1006278. [Google Scholar] [CrossRef]
- Martin-Wortham, J.; Recktenwald, S.M.; Lopes, M.G.M.; Kaestner, L.; Wagner, C.; Quint, S. A deep learning-based concept for high throughput image flow cytometry. Appl. Phys. Lett. 2021, 118, 123701. [Google Scholar] [CrossRef]
- Reichel, F.; Kräter, M.; Peikert, K.; Glaß, H.; Rosendahl, P.; Herbig, M.; Rivera Prieto, A.; Kihm, A.; Bosman, G.; Kaestner, L.; et al. Changes in Blood Cell Deformability in Chorea-Acanthocytosis and Effects of Treatment With Dasatinib or Lithium. Front. Physiol. 2022, 13, 852946. [Google Scholar] [CrossRef]
- Lopes, M.G.M.; Recktenwald, S.M.; Simionato, G.; Murciano, N.; Eichler, H.; Wagner, C.; Quint, S.; Kaestner, L. Big data in transfusion medicine and artificial intelligence analysis for red blood cell quality control. Transfus. Med. Hemotherapy 2023. [Google Scholar]
- Reichel, F.; Mauer, J.; Ahsan Nawaz, A.; Gompper, G.; Guck, J.R.; Fedosov, D. High Troughput Microfluidic Characterization of Erythrocyte Shapes and Mechanical Variability. Biophys. J. 2019, 116, 123a–124a. [Google Scholar] [CrossRef]
- Matthews, K.; Lamoureux, E.S.; Myrand-Lapierre, M.E.; Duffy, S.P.; Ma, H. Technologies for measuring red blood cell deformability. Lab Chip 2022, 22, 1254–1274. [Google Scholar] [CrossRef] [PubMed]
- Duez, J.; Holleran, J.; Ndour, P.; Pionneau, C.; Diakité, S.; Roussel, C.; Dussiot, M.; Amireault, P.; Avery, V.; Buffet, P. Mechanical clearance of red blood cells by the human spleen: Potential therapeutic applications of a biomimetic RBC filtration method. Transfus. Clin. Biol. 2015, 22, 151–157. [Google Scholar] [CrossRef]
- Kaestner, L.; Minetti, G. The potential of erythrocytes as cellular aging models. Cell Death Differ. 2017, 24, 1475–1477. [Google Scholar] [CrossRef] [PubMed]
- Thiagarajan, P.; Parker, C.J.; Prchal, J.T. How Do Red Blood Cells Die? Front. Physiol. 2021, 12, 8–10. [Google Scholar] [CrossRef]
- Li, H.; Liu, Z.L.; Lu, L.; Buffet, P.; Karniadakis, G.E. How the spleen reshapes and retains young and old red blood cells: A computational investigation. PLoS Comput. Biol. 2021, 17, e1009516. [Google Scholar] [CrossRef]
- Linderkamp, O.; Meiselman, H. Geometric, osmotic, and membrane mechanical properties of density- separated human red cells. Blood 1982, 59, 1121–1127. [Google Scholar] [CrossRef]
- Waugh, R.; Narla, M.; Jackson, C.; Mueller, T.; Suzuki, T.; Dale, G. Rheologic properties of senescent erythrocytes: Loss of surface area and volume with red blood cell age. Blood 1992, 79, 1351–1358. [Google Scholar] [CrossRef]
- Bosch, F.H.; Werre, J.M.; Schipper, L.; Roerdinkholder-Stoelwinder, B.; Huls, T.; Willekens, F.; Wichers, G.; Halie, M.R. Determinants of red blood cell deformability in relation to cell age. Eur. J. Haematol. 2009, 52, 35–41. [Google Scholar] [CrossRef]
- Gifford, S.C.; Derganc, J.; Shevkoplyas, S.S.; Yoshida, T.; Bitensky, M.W. A detailed study of time-dependent changes in human red blood cells: From reticulocyte maturation to erythrocyte senescence. Br. J. Haematol. 2006, 135, 395–404. [Google Scholar] [CrossRef]
- Antonelou, M.H.; Kriebardis, A.G.; Papassideri, I.S. Aging and death signalling in mature red cells: From basic science to transfusion practice. Blood Transfus. 2010, 8, 39–47. [Google Scholar] [CrossRef]
- Bosman, G.; Lasonder, E.; Groenen-Döpp, Y.; Willekens, F.; Werre, J.; Novotný, V. Comparative proteomics of erythrocyte aging in vivo and in vitro. J. Proteom. 2010, 73, 396–402. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.X.; Wu, Z.J.; Mehrishi, J.; Huang, B.T.; Chen, X.Y.; Zheng, X.J.; Liu, W.J.; Luo, M. Human red blood cell aging: Correlative changes in surface charge and cell properties. J. Cell. Mol. Med. 2011, 15, 2634–2642. [Google Scholar] [CrossRef] [PubMed]
- Bizjak, D.A.; Brinkmann, C.; Bloch, W.; Grau, M. Increase in Red Blood Cell-Nitric Oxide Synthase Dependent Nitric Oxide Production during Red Blood Cell Aging in Health and Disease: A Study on Age Dependent Changes of Rheologic and Enzymatic Properties in Red Blood Cells. PLoS ONE 2015, 10, e0125206. [Google Scholar] [CrossRef] [PubMed]
- Guglietta, F.; Behr, M.; Biferale, L.; Falcucci, G.; Sbragaglia, M. On the effects of membrane viscosity on transient red blood cell dynamics. Soft Matter 2020, 16, 6191–6205. [Google Scholar] [CrossRef] [PubMed]
- Recktenwald, S.M.; Graessel, K.; Maurer, F.M.; John, T.; Gekle, S.; Wagner, C. Red blood cell shape transitions and dynamics in time-dependent capillary flows. Biophys. J. 2022, 121, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Gürbüz, A.; Pak, O.S.; Taylor, M.; Sivaselvan, M.V.; Sachs, F. Effects of membrane viscoelasticity on the red blood cell dynamics in a microcapillary. Biophys. J. 2023, 1–12. [Google Scholar] [CrossRef]
- Bosch, F.; Werre, J.; Roerdinkholder-Stoelwinder, B.; Huls, T.; Willekens, F.; Halie, M. Characteristics of red blood cell populations fractionated with a combination of counterflow centrifugation and Percoll separation. Blood 1992, 79, 254–260. [Google Scholar] [CrossRef]
- D’Alessandro, A.; Blasi, B.; D’Amici, G.M.; Marrocco, C.; Zolla, L. Red blood cell subpopulations in freshly drawn blood: Application of proteomics and metabolomics to a decades-long biological issue. Blood Transfus. 2013, 11, 75–87. [Google Scholar] [CrossRef]
- Ermolinskiy, P.; Lugovtsov, A.; Yaya, F.; Lee, K.; Kaestner, L.; Wagner, C.; Priezzhev, A. Effect of Red Blood Cell Aging In Vivo on Their Aggregation Properties In Vitro: Measurements with Laser Tweezers. Appl. Sci. 2020, 10, 7581. [Google Scholar] [CrossRef]
- Maurer, F.; John, T.; Makhro, A.; Bogdanova, A.; Minetti, G.; Wagner, C.; Kaestner, L. Continuous Percoll Gradient Centrifugation of Erythrocytes—Explanation of Cellular Bands and Compromised Age Separation. Cells 2022, 11, 1296. [Google Scholar] [CrossRef]
- Faivre, M.; Renoux, C.; Bessaa, A.; Da Costa, L.; Joly, P.; Gauthier, A.; Connes, P. Mechanical Signature of Red Blood Cells Flowing Out of a Microfluidic Constriction Is Impacted by Membrane Elasticity, Cell Surface-to-Volume Ratio and Diseases. Front. Physiol. 2020, 11, 576. [Google Scholar] [CrossRef]
- Rashidi, Y.; Simionato, G.; Zhou, Q.; John, T.; Kihm, A.; Bendaoud, M.; Krüger, T.; Bernabeu, M.O.; Kaestner, L.; Laschke, M.W.; et al. Red blood cell lingering modulates hematocrit distribution in the microcirculation. Biophys. J. 2023, 122, 1526–1537. [Google Scholar] [CrossRef]
- Fischer, T.; Haest, C.; Stöhr, M.; Kamp, D.; Deuticke, B. Selective alteration of erythrocyte deformability by SH-reagents. Evidence for an involvement of spectrin in membrane shear elasticity. Biochim. Biophys. Acta (BBA)-Biomembr. 1978, 510, 270–282. [Google Scholar] [CrossRef]
- Clavería, V.; Aouane, O.; Thiébaud, M.; Abkarian, M.; Coupier, G.; Misbah, C.; John, T.; Wagner, C. Clusters of red blood cells in microcapillary flow: Hydrodynamic versus macromolecule induced interaction. Soft Matter 2016, 12, 8235–8245. [Google Scholar] [CrossRef]
- Bogdanova, A.; Kaestner, L.; Simionato, G.; Wickrema, A.; Makhro, A. Heterogeneity of Red Blood Cells: Causes and Consequences. Front. Physiol. 2020, 11, 392. [Google Scholar] [CrossRef]
- Pfafferott, C.; Nash, G.; Meiselman, H. Red blood cell deformation in shear flow. Effects of internal and external phase viscosity and of in vivo aging. Biophys. J. 1985, 47, 695–704. [Google Scholar] [CrossRef] [PubMed]
- Shiga, T.; Sekiya, M.; Maeda, N.; Kon, K.; Okazaki, M. Cell age-dependent changes in deformability and calcium accumulation of human erythrocytes. Biochim. Biophys. Acta (BBA)-Biomembr. 1985, 814, 289–299. [Google Scholar] [CrossRef]
- Danker, G.; Vlahovska, P.M.; Misbah, C. Vesicles in Poiseuille Flow. Phys. Rev. Lett. 2009, 102, 148102. [Google Scholar] [CrossRef]
- Yazdani, A.Z.K.; Bagchi, P. Phase diagram and breathing dynamics of a single red blood cell and a biconcave capsule in dilute shear flow. Phys. Rev. E 2011, 84, 026314. [Google Scholar] [CrossRef] [PubMed]
- Kaoui, B.; Tahiri, N.; Biben, T.; Ez-Zahraouy, H.; Benyoussef, A.; Biros, G.; Misbah, C. Complexity of vesicle microcirculation. Phys. Rev. E 2011, 84, 041906. [Google Scholar] [CrossRef] [PubMed]
- Kaoui, B.; Krüger, T.; Harting, J. How does confinement affect the dynamics of viscous vesicles and red blood cells? Soft Matter 2012, 8, 9246. [Google Scholar] [CrossRef]
- Cordasco, D.; Yazdani, A.; Bagchi, P. Comparison of erythrocyte dynamics in shear flow under different stress-free configurations. Phys. Fluids 2014, 26, 041902. [Google Scholar] [CrossRef]
- Farutin, A.; Misbah, C. Symmetry breaking and cross-streamline migration of three-dimensional vesicles in an axial Poiseuille flow. Phys. Rev. E 2014, 89, 042709. [Google Scholar] [CrossRef]
- Sinha, K.; Graham, M.D. Dynamics of a single red blood cell in simple shear flow. Phys. Rev. E 2015, 92, 042710. [Google Scholar] [CrossRef]
- Mauer, J.; Mendez, S.; Lanotte, L.; Nicoud, F.; Abkarian, M.; Gompper, G.; Fedosov, D.A. Flow-Induced Transitions of Red Blood Cell Shapes under Shear. Phys. Rev. Lett. 2018, 121, 118103. [Google Scholar] [CrossRef]
- Lehmann, M.; Müller, S.J.; Gekle, S. Efficient viscosity contrast calculation for blood flow simulations using the lattice Boltzmann method. Int. J. Numer. Methods Fluids 2020, 92, 1463–1477. [Google Scholar] [CrossRef]
- Dasanna, A.K.; Mauer, J.; Gompper, G.; Fedosov, D.A. Importance of Viscosity Contrast for the Motion of Erythrocytes in Microcapillaries. Front. Phys. 2021, 9, 666913. [Google Scholar] [CrossRef]
- Skalak, R.; Tozeren, A.; Zarda, R.; Chien, S. Strain Energy Function of Red Blood Cell Membranes. Biophys. J. 1973, 13, 245–264. [Google Scholar] [CrossRef]
- Helfrich, W. Elastic Properties of Lipid Bilayers: Theory and Possible Experiments. Z. Naturforschung C 1973, 28, 693–703. [Google Scholar] [CrossRef] [PubMed]
- Barthès-Biesel, D.; Diaz, A.; Dhenin, E. Effect of Constitutive Laws for Two-Dimensional Membranes on Flow-Induced Capsule Deformation. J. Fluid Mech. 2002, 460, 211–222. [Google Scholar] [CrossRef]
- Skotheim, J.M.; Secomb, T.W. Red Blood Cells and Other Nonspherical Capsules in Shear Flow: Oscillatory Dynamics and the Tank-Treading-to-Tumbling Transition. Phys. Rev. Lett. 2007, 98, 078301. [Google Scholar] [CrossRef]
- Aouane, O.; Thiébaud, M.; Benyoussef, A.; Wagner, C.; Misbah, C. Vesicle dynamics in a confined Poiseuille flow: From steady state to chaos. Phys. Rev. E 2014, 90, 033011. [Google Scholar] [CrossRef] [PubMed]
- Mignon, T.; Mendez, S. A theoretical investigation of the frisbee motion of red blood cells in shear flow. Math. Model. Nat. Phenom. 2021, 16, 23. [Google Scholar] [CrossRef]
- Hochmuth, R.; Worthy, P.; Evans, E. Red cell extensional recovery and the determination of membrane viscosity. Biophys. J. 1979, 26, 101–114. [Google Scholar] [CrossRef]
- Evans, E.A. methods. In Methods Enzymology; Elsevier Inc.: Amsterdam, The Netherlands, 1989; Volume 173, pp. 3–35. [Google Scholar] [CrossRef]
- Matteoli, P.; Nicoud, F.; Mendez, S. Impact of the membrane viscosity on the tank-treading behavior of red blood cells. Phys. Rev. Fluids 2021, 6, 043602. [Google Scholar] [CrossRef]
- Tomaiuolo, G.; Guido, S. Start-up shape dynamics of red blood cells in microcapillary flow. Microvasc. Res. 2011, 82, 35–41. [Google Scholar] [CrossRef] [PubMed]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nouaman, M.; Darras, A.; John, T.; Simionato, G.; Rab, M.A.E.; van Wijk, R.; Laschke, M.W.; Kaestner, L.; Wagner, C.; Recktenwald, S.M. Effect of Cell Age and Membrane Rigidity on Red Blood Cell Shape in Capillary Flow. Cells 2023, 12, 1529. https://doi.org/10.3390/cells12111529
Nouaman M, Darras A, John T, Simionato G, Rab MAE, van Wijk R, Laschke MW, Kaestner L, Wagner C, Recktenwald SM. Effect of Cell Age and Membrane Rigidity on Red Blood Cell Shape in Capillary Flow. Cells. 2023; 12(11):1529. https://doi.org/10.3390/cells12111529
Chicago/Turabian StyleNouaman, Mohammed, Alexis Darras, Thomas John, Greta Simionato, Minke A. E. Rab, Richard van Wijk, Matthias W. Laschke, Lars Kaestner, Christian Wagner, and Steffen M. Recktenwald. 2023. "Effect of Cell Age and Membrane Rigidity on Red Blood Cell Shape in Capillary Flow" Cells 12, no. 11: 1529. https://doi.org/10.3390/cells12111529
APA StyleNouaman, M., Darras, A., John, T., Simionato, G., Rab, M. A. E., van Wijk, R., Laschke, M. W., Kaestner, L., Wagner, C., & Recktenwald, S. M. (2023). Effect of Cell Age and Membrane Rigidity on Red Blood Cell Shape in Capillary Flow. Cells, 12(11), 1529. https://doi.org/10.3390/cells12111529








