Information–Thermodynamic Method for the Study of Proliferation of Organized Cellular Structure
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mathematical Methods for the Studying of Cellular Environment
2.2. Experimental Methods for the Studying of Cell Proliferation
2.3. Entropy-Structural Method for the Dynamic Assessing of Cell Proliferation
Energy Balance of the Cellular Structure
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
References
- Gluschenkov, V.A.; Volova, L.T.; Belyaeva, I.A.; Boltovskaya, V.V.; Rossinskaya, V.V.; Ignatenko, A.I.; Nefedova, I.F.; Kulagina, L.N. Impact of pulsed magnetic field of high intensity on human dermal fibroblasts in culture. Tidings Samara Sci. Cent. Russ. Acad. Sci. 2020, 22, 5. (In Russian) [Google Scholar]
- Rybakov, U.L.; Kizhaev, E.V.; Letyagin, V.P.; Nikolaeva, T.G. System-wide Magnetotherapy in Oncology. Med. Phys. 2005, 2, 70–76. (In Russian) [Google Scholar]
- Rudykina, O.A.; Grekhov, R.A.; Suleimanova, G.P.; Adamovich, E.I. Electromagnetic field and its influence on physiological processes in human body. Vest. Volgogr. State Univ. Ser. 11 Nat. Sci. 2016, 3, 17. (In Russian) [Google Scholar] [CrossRef]
- Perov, S.Y. The study of the functional state of individual systems of the body under the influence of low-intensity radiofrequency electromagnetic field. Bull. New Med. Technol. 2015, 9, 3. (In Russian) [Google Scholar]
- Pletnev, A.S. Magnetic Fields in Experimental and Clinical Oncology; Belarusian Science: Minsk, Belarus, 2016; p. 229. (In Russian)
- France, E.M. Antitumor effect of magnetic fields and their effect on pain in experimental and clinical oncology. Res. Pract. Med. 2019, 6, 86–89. (In Russian) [Google Scholar]
- Maximov, A.V.; Kiryanova, V.V.; Maximova, M.A. Therapeutic use of magnetic fields. Physiother. Balneol. Rehabil. 2013, 3, 34–39. (In Russian) [Google Scholar]
- Gluschenkov, V.A. Technology of Magnetic Pulse Processing of Materials; Publishing house “Fedorov”: Samara, Russia, 2014; p. 208. (In Russian) [Google Scholar]
- Rubner, M. Das Problem der Lebensdauer und Seine Beziehungen zu Wachstum und Ernährung; Oldenbourg: München, Germany; Berlin, Germany, 1908. (In German) [Google Scholar]
- Bauer, E.S. Theoretical Biology; VIEM: Moscow-Leningrad, Russia, 1935; p. 206. (In Russian) [Google Scholar]
- Backman, G. Wachstum und Organiche Zeit; J.A.: Barth, Germany; Leipzig, Germany, 1943. (In German) [Google Scholar]
- Du Noüy, L.P. Biological Time; Methuen: London, UK, 1936. [Google Scholar]
- Brody, D.A.; Cox, J.W.; Horan, L.G. Hexadecapolar shift equations applicable to equivalent cardiac generators of lower degree. Ann. Biomed. Eng. 1973, 1, 481–488. [Google Scholar] [CrossRef]
- Brody, S. Bioenergetics and Growth; Reinhold Publishing Corporation: New York, NY, USA, 1945. [Google Scholar]
- Zotin, A.I. Thermodynamic Approach to the Problems of Mothers of Development, Growth and Aging; Nauka: Moscow, Russia, 1974. (In Russian) [Google Scholar]
- Zotin, A.I. Biology of Aging; Nauka: Moscow, Russia, 1982; pp. 116–129. (In Russian) [Google Scholar]
- Zotin, A.I. Thermodynamic Basis of the Influence of Organs on External and Internal Factors; Nauka: Moscow, Russia, 1988. (In Russian) [Google Scholar]
- Zotin, A.I.; Zotin, A.A. The Thermodynamic Foundation of Development. Ontogenez 1996, 27, 147–152. (In Russian) [Google Scholar]
- Zotin, A.I.; Zotina, R.S. Phenomenological Theory of Development, Growth, and Aging of the Organism; Nauka: Moscow, Russia, 1993. [Google Scholar]
- Zotin, A.I.; Alekseeva, T.A. Rubner’s constant as a criterion for species lifespan. Fiziol. Mag. 1984, 30, 59. (In Russian) [Google Scholar]
- Zotin, A.A. Vladimirova IG. Respiration rate and species-specific lifespan in fresh water bivalves of Margaritiferidae and Unionidae families. Izv. Akad. Nauk Ser. Biol. 2001, 3, 331–338. (In Russian) [Google Scholar]
- Alimov, A.F.; Kazantseva, T.I. Definition of unit internal (physiological) time. Biol. Bull. 2007, 34, 286–291. (In Russian) [Google Scholar] [CrossRef]
- Alimov, A.F.; Kazantseva, T.I. The basic life history parameters and their relationships. Zhurnal Obs. Biol. 2004, 65, 3–18. [Google Scholar]
- Reiss, J.O. The meaning of developmental time: A metric for comparative embryology. Am. Nat. 1989, 134, 170–189. [Google Scholar] [CrossRef]
- Boddington, M.J. An absolute metabolic scope for activity. J. Theor. Biol. 1978, 75, 443–449. [Google Scholar] [CrossRef] [PubMed]
- Prigogine, I.; Glansdorff, P. Thermodynamic Theory of Structure, Stability and Fluctuations; MIR: Moscow, Russia, 1973; p. 280. (In Russian) [Google Scholar]
- Volov, V.T. Hypothesis of the Entropy Invariant for Biological Organisms. Biophysics 2021, 66, 520–530. [Google Scholar] [CrossRef]
- Martin, N.F.; England, J.W. Mathematical Theory of Entropy; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Feder, J. Fractals; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Terekhov, S.V. Fractals and Physics of Similarity; Digital Printing House: Donetsk, Ukraine, 2011; p. 255. (In Russian) [Google Scholar]
- Mandelbrot, B.B.; Mandelbrot, B.B. The Fractal Geometry of Nature; WH Freeman: New York, NY, USA, 1982; Volume 1. [Google Scholar]
- Greenberg, K.N. Cultivation of human fibroblasts for diagnostics of hereditary diseases. In Methods of Cell Cultivation: Collection of Scientific Works; Nauka: Leningrad, Russia, 1988; pp. 250–257. [Google Scholar]
- Volova, L.T.; Pugachev, E.I.; Rossinskaya, V.V.; Boltovskaya, V.V.; Dolgushkin, D.A.; Ossina, N. Rheumatoid Arthritis: Applicability of Ready-to-Use Human Cartilaginous Cells for Screening of Compounds with TNF-Alpha Inhibitory Activity. Biomolecules 2020, 10, 1563. [Google Scholar] [CrossRef] [PubMed]
- Osina, N.K.; Pugachev, E.I.; Koliadenko, I.A.; Pryazhkina, V.V.; Shakurov, E.G.; Orlov, E.V.; Volova, L.T. In vitro test system for screening drugs with IL-17A inhibitory activity. Genes Cells 2021, XVI, 43–48. (In Russian) [Google Scholar] [CrossRef]
- Zorin, V.; Zorina, A.; Petrakova, O.; Cherkasov, V. Dermal Fibroblasts for Treatment of Skin Defects. Genes Cells 2009, 4, 26–40. (In Russian) [Google Scholar]
- Kuzmicheva, V.I.; Volova, L.T.; Gilmiyarova, F.N.; Bykov, I.M.; Avdeeva, E.V.; Kolotieva, N.A. Fibroblasts as an object for studying proliferative activity in vitro. Sci. Innov. Med. 2020, 5, 210–215. (In Russian) [Google Scholar] [CrossRef]
- Kotelnikov, G.P.; Kolsanov, A.V.; Nikolaenko, A.N.; Volova, L.T.; Rossinskaya, V.V.; Boltovskaya, V.V.; Popov, N.V.; Shcherbovskikh, A.E.; Prikhodko, S. Testing of additive materials on human fibroblast cell cultures. Clin. Exp. Surg. J. Acad. B.V. Petrovsk. 2018, 6, 67–73. (In Russian) [Google Scholar] [CrossRef]
- Coburn, J. FDA Additive Manufacturing Working Group. Technical Considerations for Additive Manufactured Devices. In FDA/RSNA Joint Meeting on 3D Printed Patient-Specific Anatomic Models; U.S. Food Drug: Silver Spring, MD, USA, 2017. [Google Scholar]
- Hesuani, Y.D.; Pereira, F.D.A.S.; Parfenov, V.; Koudan, E.; Mitryashkin, A.; Replyanski, N.; Kasyanov, V.; Knyazeva, A.; Bulanova, E.; Mironov, V. Design and implementation of novel multifunctional 3D bioprinter. 3D Print. Addit. Manuf. 2016, 3, 65–68. [Google Scholar] [CrossRef]
- Shafiee, A.; Atala, A. Printing Technologies for Medical Applications. Trends Mol. Med. 2016, 22, 254–265. [Google Scholar] [CrossRef] [PubMed]
- Leberfinger, A.N.; Ravnic, D.J.; Dhawan, A.; Ozbolat, I.T. Concise Review: Bioprinting of Stem Cells for Transplantable Tissue Fabrication. Stem Cells Transl. Med. 2017, 6, 1940–1948. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rocca, M.; Fragasso, A.; Liu, W.; Heinrich, M.A.; Zhang, Y.S. Embedded Multimaterial Extrusion Bioprinting. SLAS Technol. 2017, 1, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mandrycky, C.; Wang, Z.; Kim, K.; Kim, D.H. 3D bioprinting for engineering complex tissues. Biotechnol. Adv. 2016, 34, 422–434. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boyd-Moss, M.; Fox, K.; Brandt, M.; Nisbet, D.; Williams, R. Bioprinting and Biofabrication with Peptide and Protein Biomaterials. Adv. Exp. Med. Biol. 2017, 1030, 95–129. [Google Scholar]

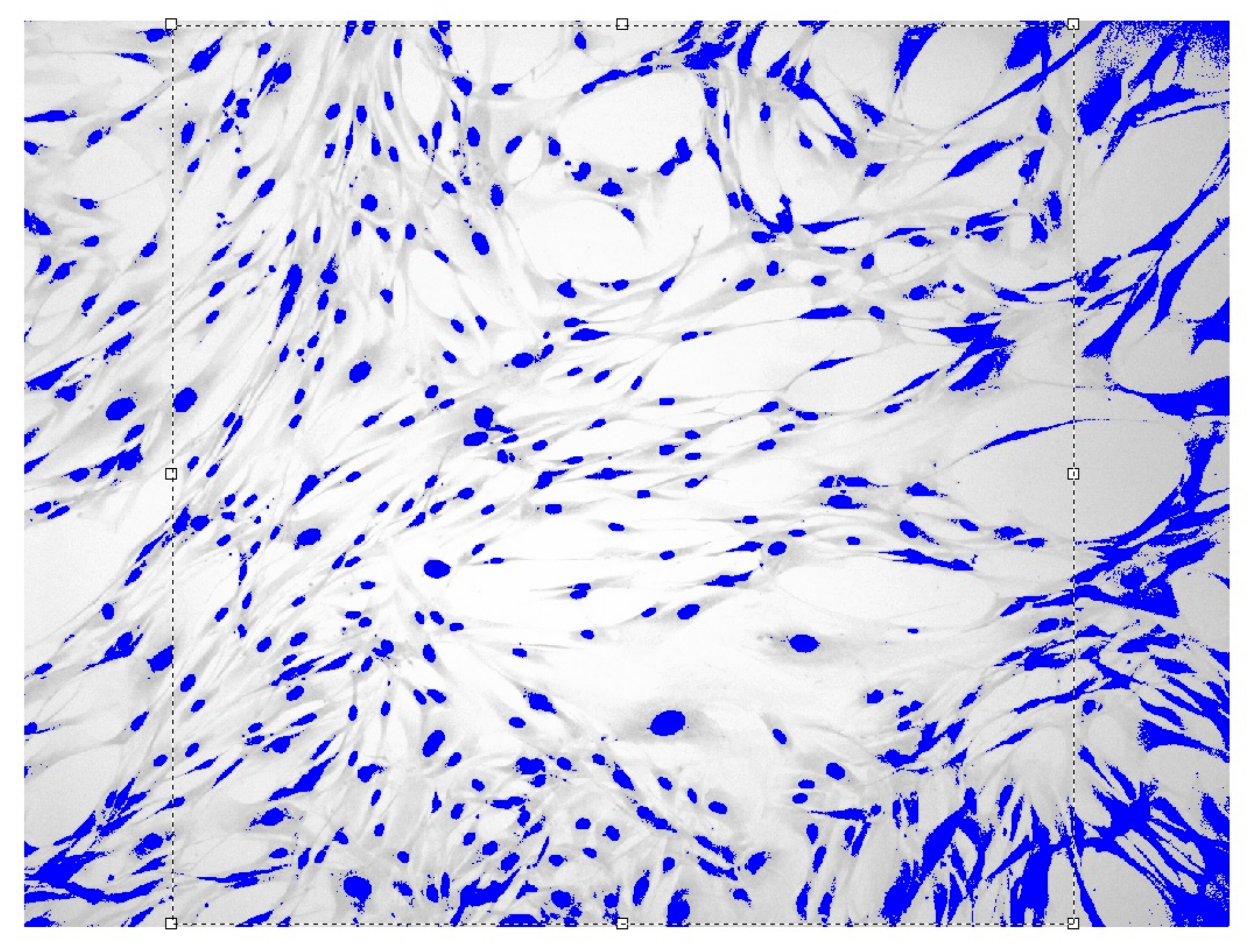
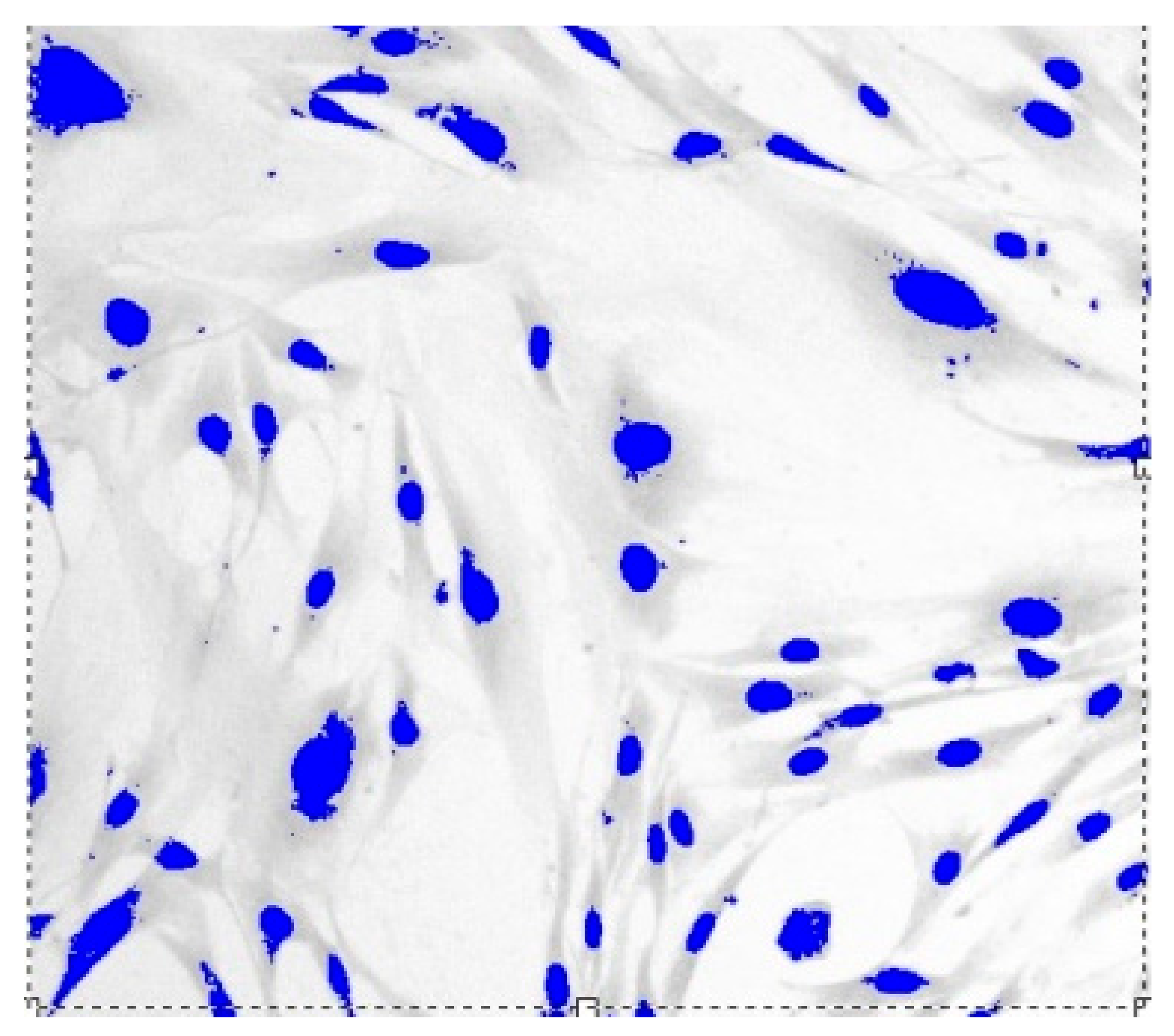
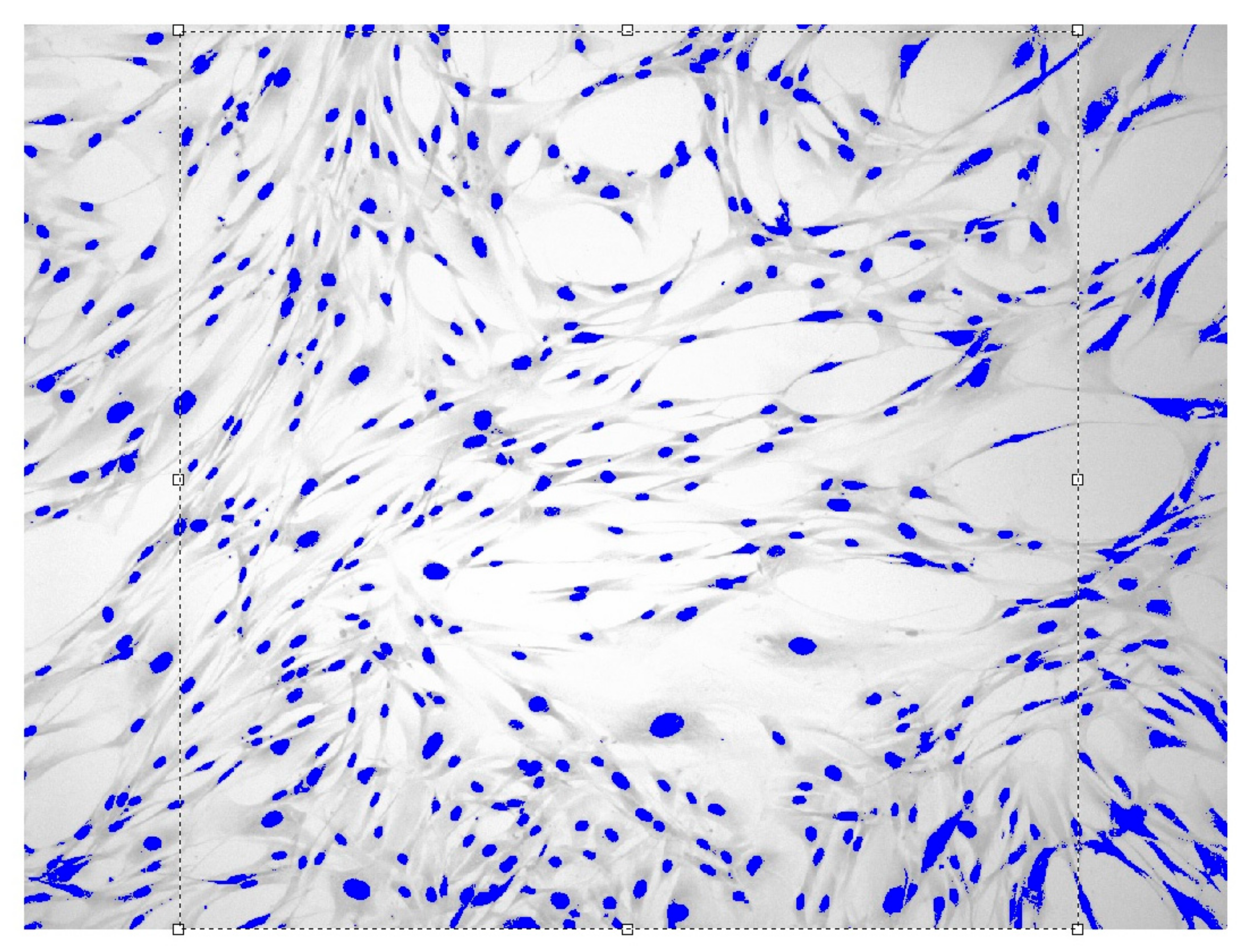
| Term of Experiment, Sowing Day/Experiment Day after Exposure | Monolayer Density, Cell/1 mm2 | IP, Rel. Units | Time Doubling, h | Quantity Doublings, Rel. Units |
|---|---|---|---|---|
| Initial data (1 day after sowing) | 42.9 ± 5.2 | |||
| 2 days/1 day | 114.9 ± 7.5 | 2.6 | 17.4 | |
| 3 days/2 days | 134.7 ± 6.4 | 1.1 | 106.3 | |
| 4 days/3 days | 163.3 ± 17.5 | 1.3 | 93 | |
| 5 days/4 days | 208.9 ± 18.1 | 1.1 | 69.5 | |
| 6 days/5 days | 263.3 ± 15.6 | 1.1 | 74.4 | |
| 7 days/6 days | 338.6 ± 25.3 | 1.2 | 68.3 | 3 |
| , Days | -Criterion | , J | |
|---|---|---|---|
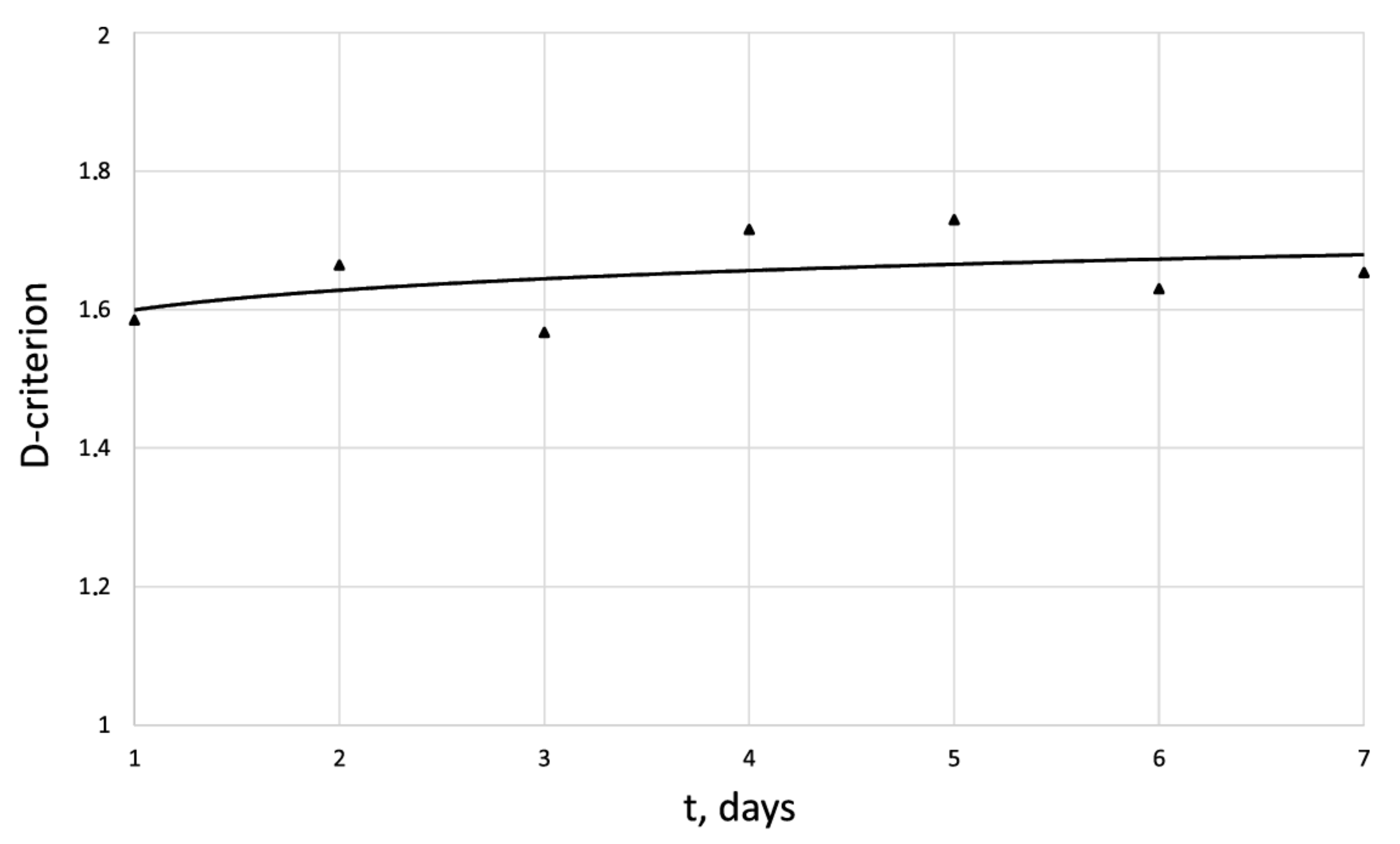
| 1 | 1.55 | 500 | 100 |
| 1 | 1.58 | 500 | 200 |
| 1 | 1.51 | 500 | 400 |
| 6 | 1.65 | 500 | 100 |
| 6 | 1.59 | 500 | 200 |
| 6 | 1.67 | 500 | 400 |
| , Day | -Criterion | , J | |
|---|---|---|---|
| 1 | 1.56 | 500 | 200 |
| 1 | 1.55 | 500 | 200 |
| 1 | 1.60 | 500 | 200 |
| 1 | 1.55 | 500 | 200 |
| 1 | 1.52 | 500 | 200 |
| 1 | 1.55 | 500 | 200 |
| 1 | 1.56 | 500 | 200 |
| = 500 J | |||||||
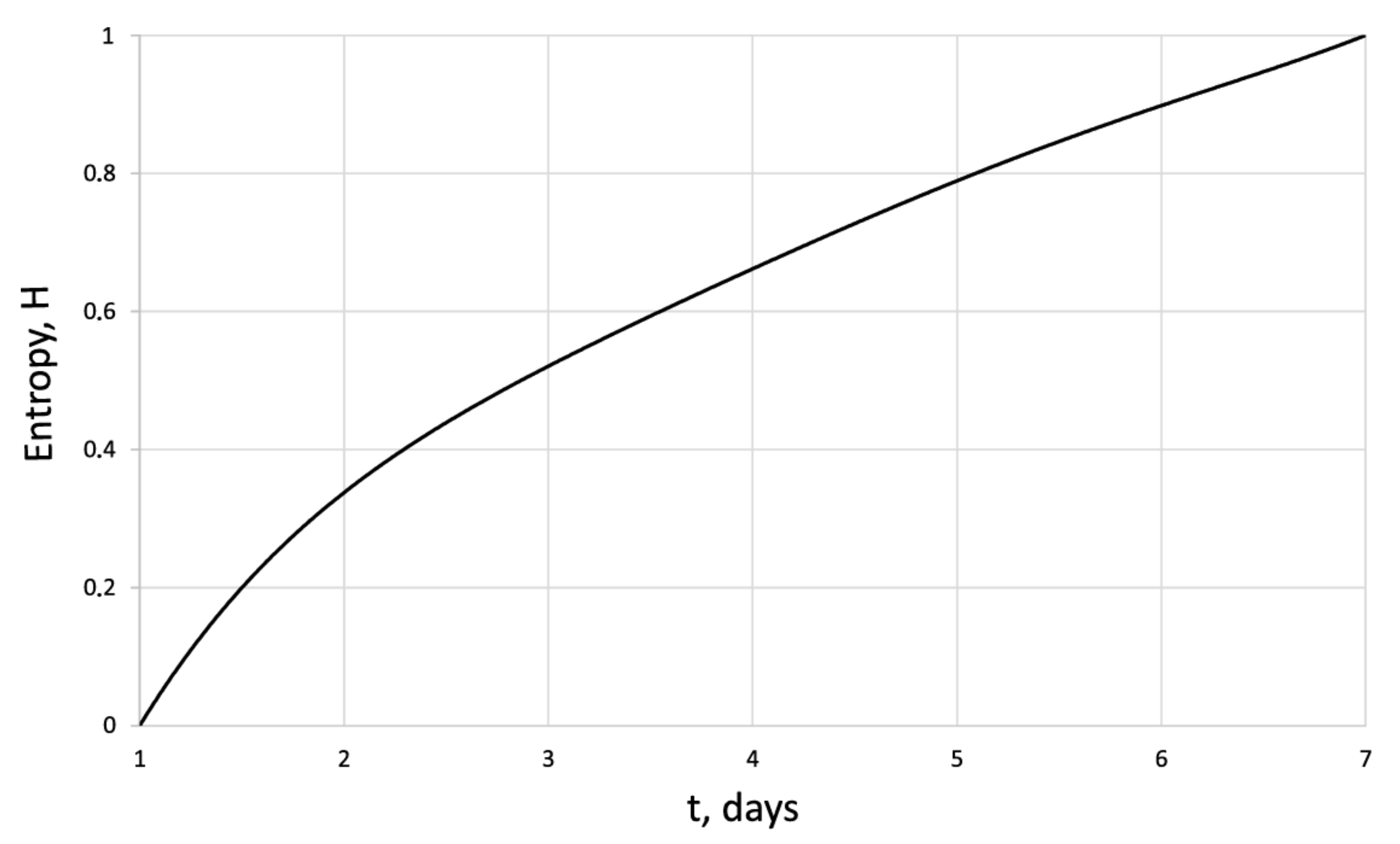
| Days | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 42.8 | 114 | 134.7 | 163.2 | 208 | 263 | 338.5 | |
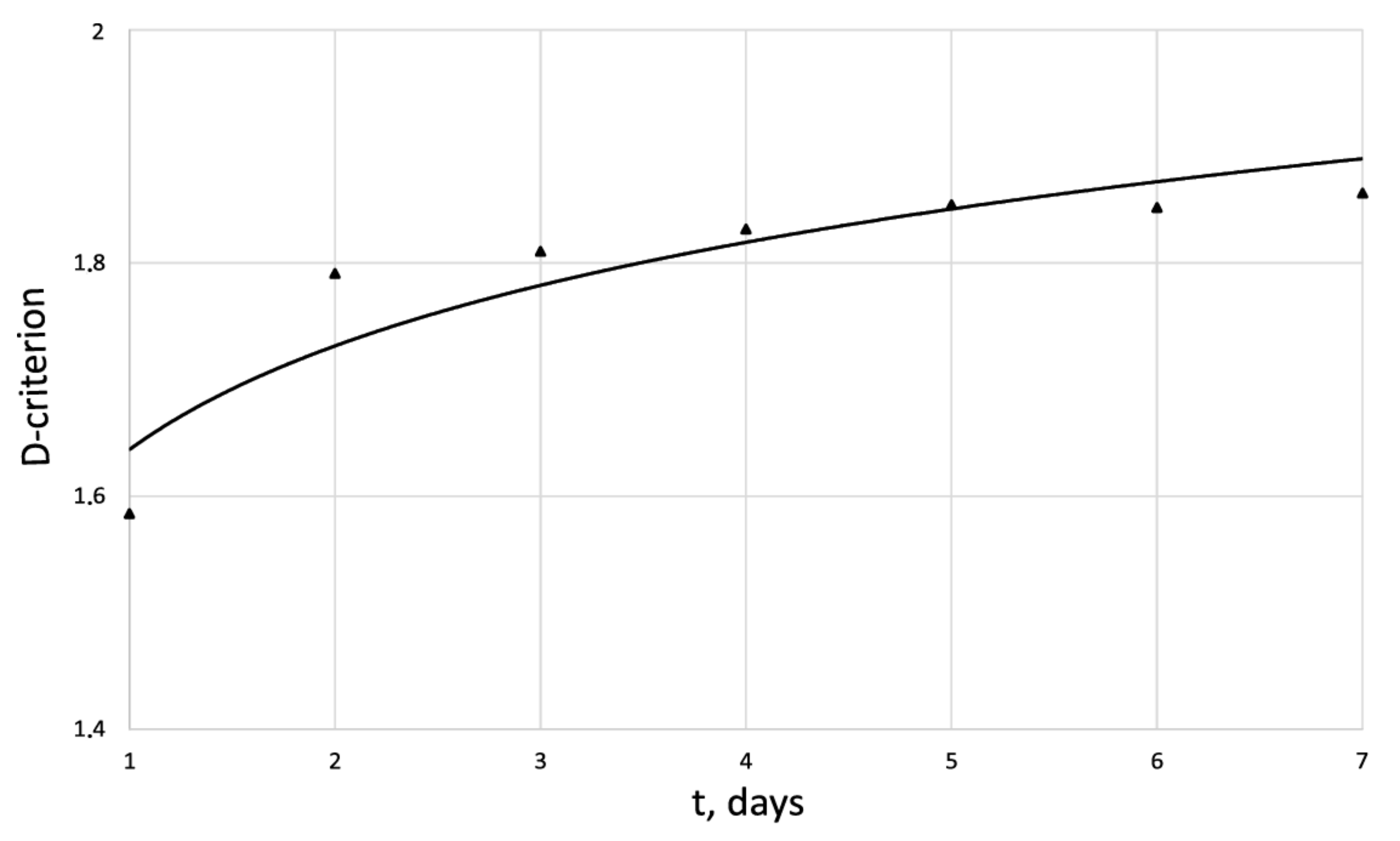
| 1.58 | 1.56 | 1.57 | 1.71 | 1.72 | 1.62 | 1.67 | |
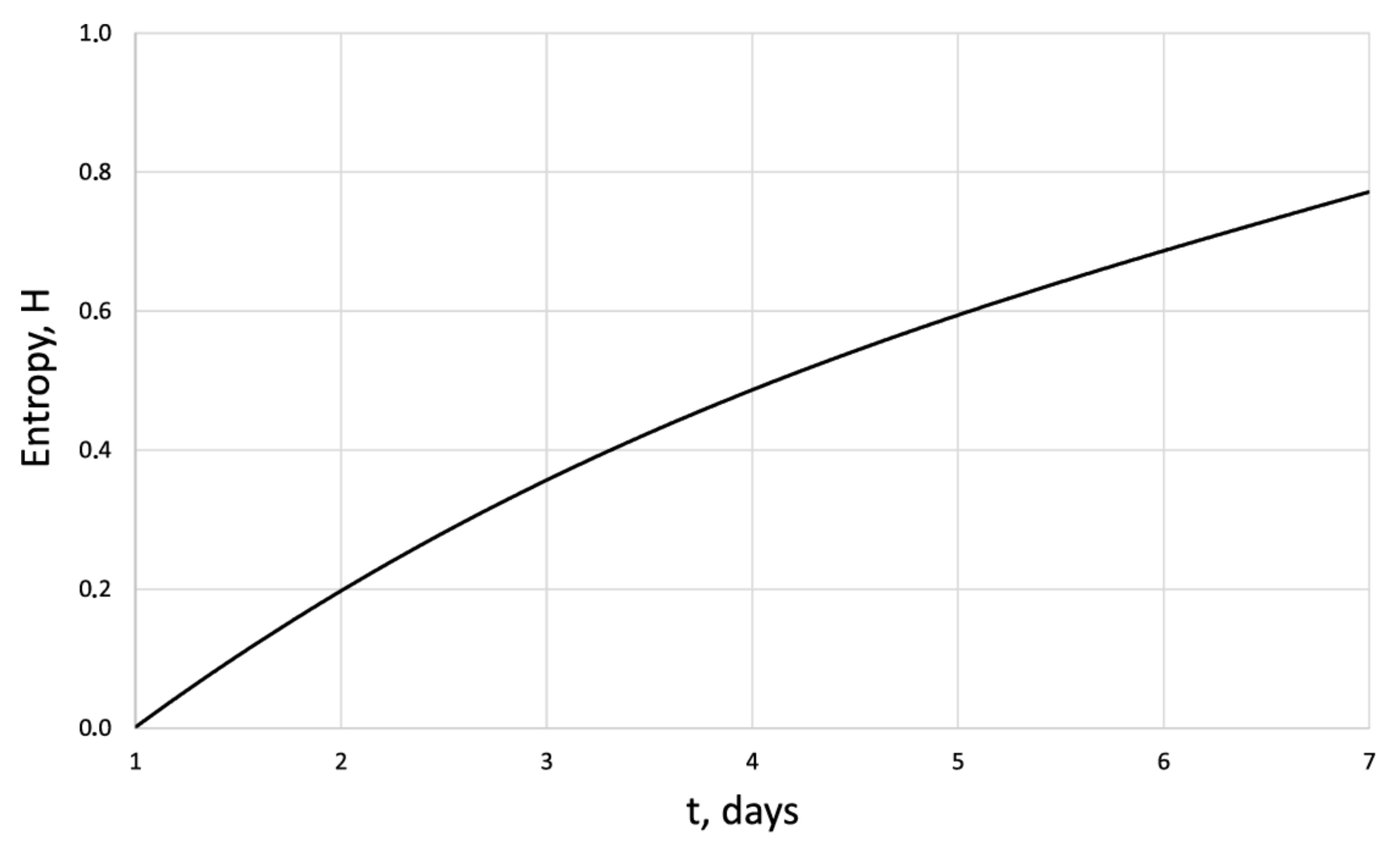
| 0 | 0.41 | 0.48 | 0.54 | 0.64 | 0.72 | 0.8 | |
| = 500 J | |||||||
| Days | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 42.2 | 132.1 | 201.33 | 385.2 | 426.7 | 499.7 | 562.8 | |
| 1.58 | 1.80 | 1.69 | 1.87 | 1.79 | 1.81 | 1.86 | |
| 0 | 0.48 | 0.62 | 0.84 | 0.87 | 0.92 | 0.96 | |
| Control | |||||||
| Days | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 44 | 90.7 | 142 | 201 | 286.5 | 442.7 | 630.5 | |
| 1.58 | 1.79 | 1.81 | 1.82 | 1.85 | 1.84 | 1.86 | |
| 0 | 0.34 | 0.50 | 0.57 | 0.7 | 0.86 | 1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Volov, V.T.; Volova, L.T.; Kolsanov, A.V. Information–Thermodynamic Method for the Study of Proliferation of Organized Cellular Structure. Cells 2023, 12, 731. https://doi.org/10.3390/cells12050731
Volov VT, Volova LT, Kolsanov AV. Information–Thermodynamic Method for the Study of Proliferation of Organized Cellular Structure. Cells. 2023; 12(5):731. https://doi.org/10.3390/cells12050731
Chicago/Turabian StyleVolov, Vyacheslav T., Larisa T. Volova, and Alexander V. Kolsanov. 2023. "Information–Thermodynamic Method for the Study of Proliferation of Organized Cellular Structure" Cells 12, no. 5: 731. https://doi.org/10.3390/cells12050731
APA StyleVolov, V. T., Volova, L. T., & Kolsanov, A. V. (2023). Information–Thermodynamic Method for the Study of Proliferation of Organized Cellular Structure. Cells, 12(5), 731. https://doi.org/10.3390/cells12050731







