Lung Cancers: Parenchymal Biochemistry and Mechanics
Abstract
1. Introduction
2. Materials and Methods
2.1. Ethics
2.2. Specimen
2.3. Immuno-Histochemistry
2.4. Mechanical Studies
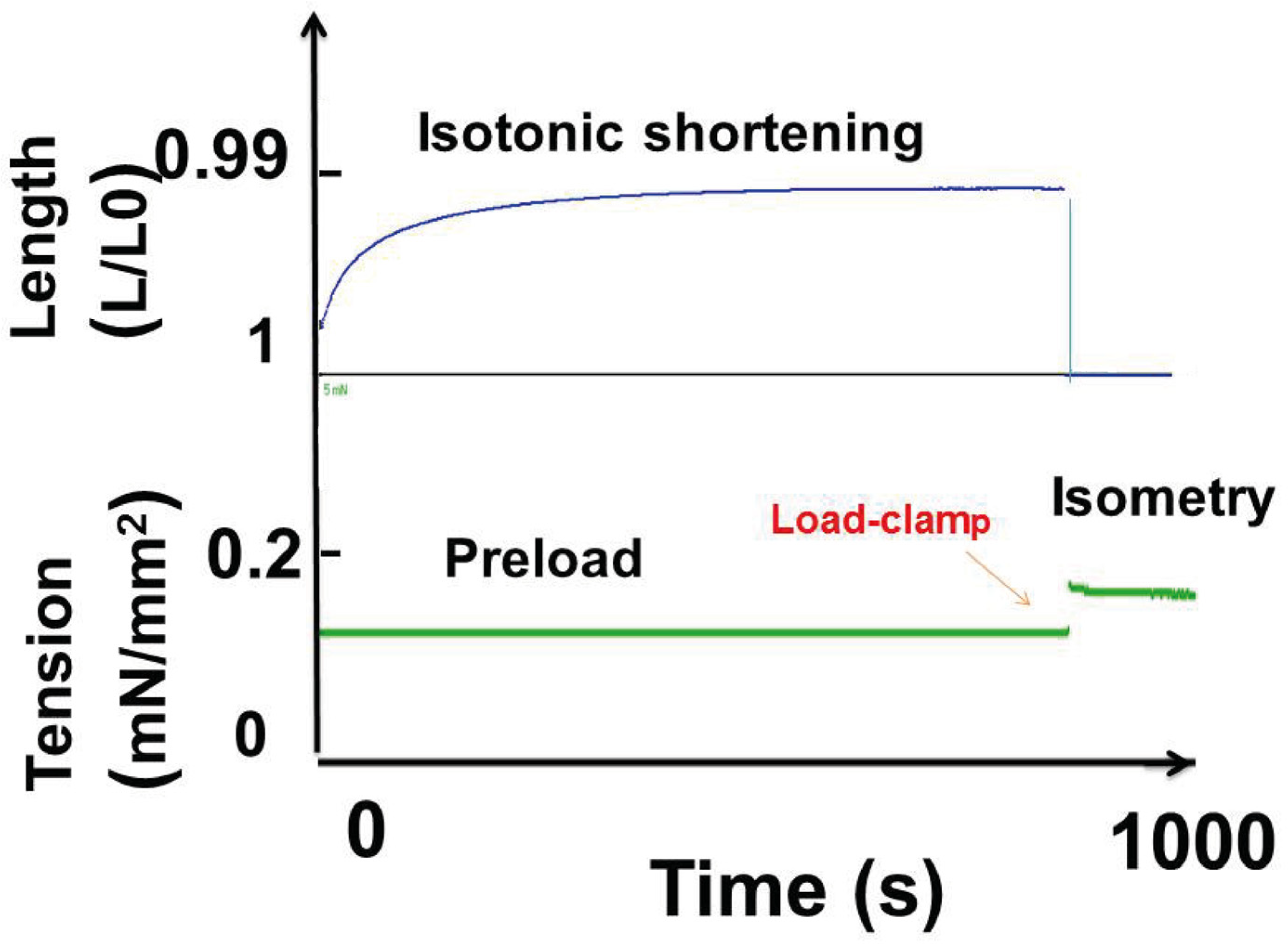
2.4.1. Experimental Protocol
2.4.2. A. Huxley Formalism
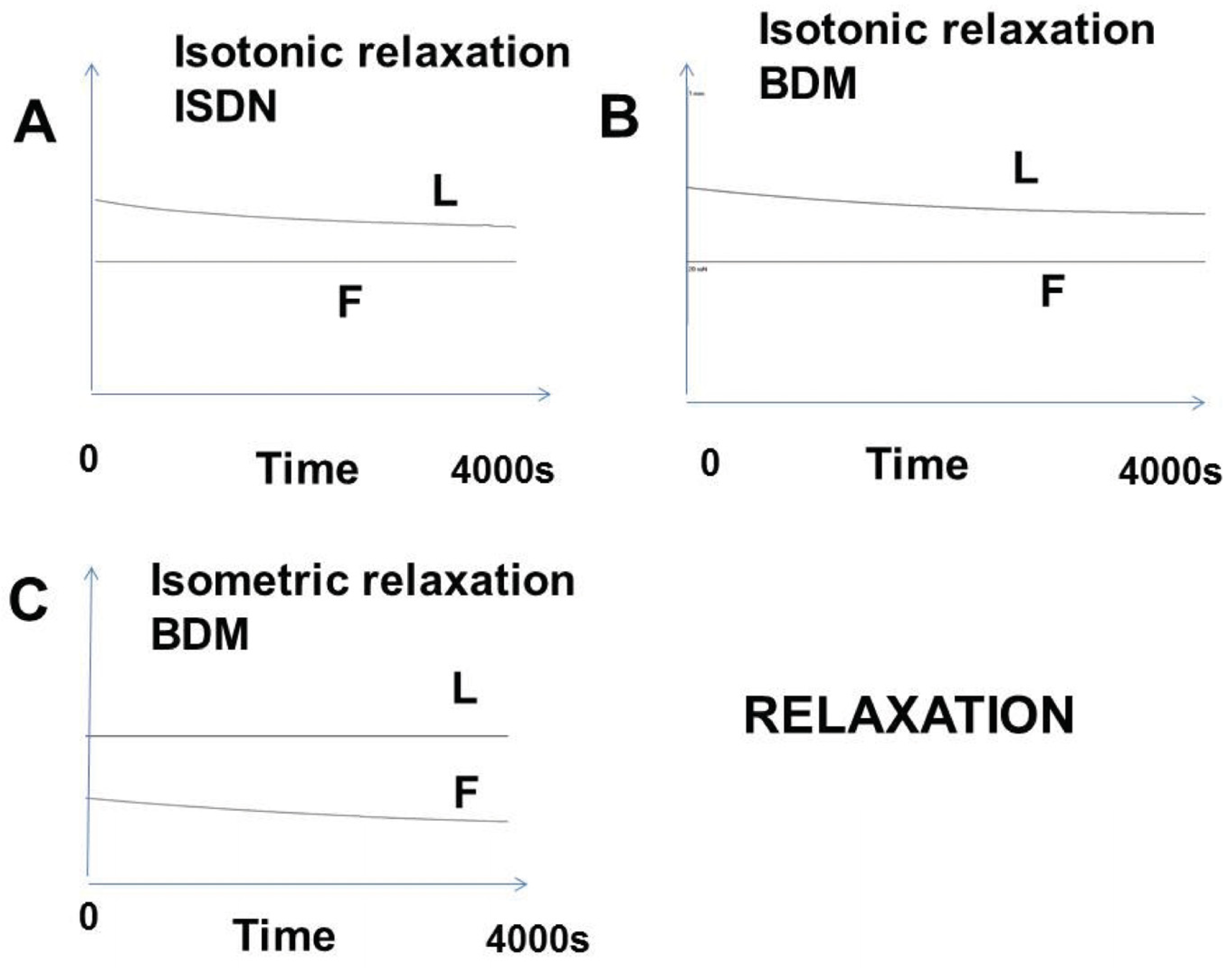
2.4.3. Relaxation
2.4.4. Statistical Analysis
3. Results
3.1. Immuno-Histochemistry
3.2. Mechanics
3.2.1. Contraction
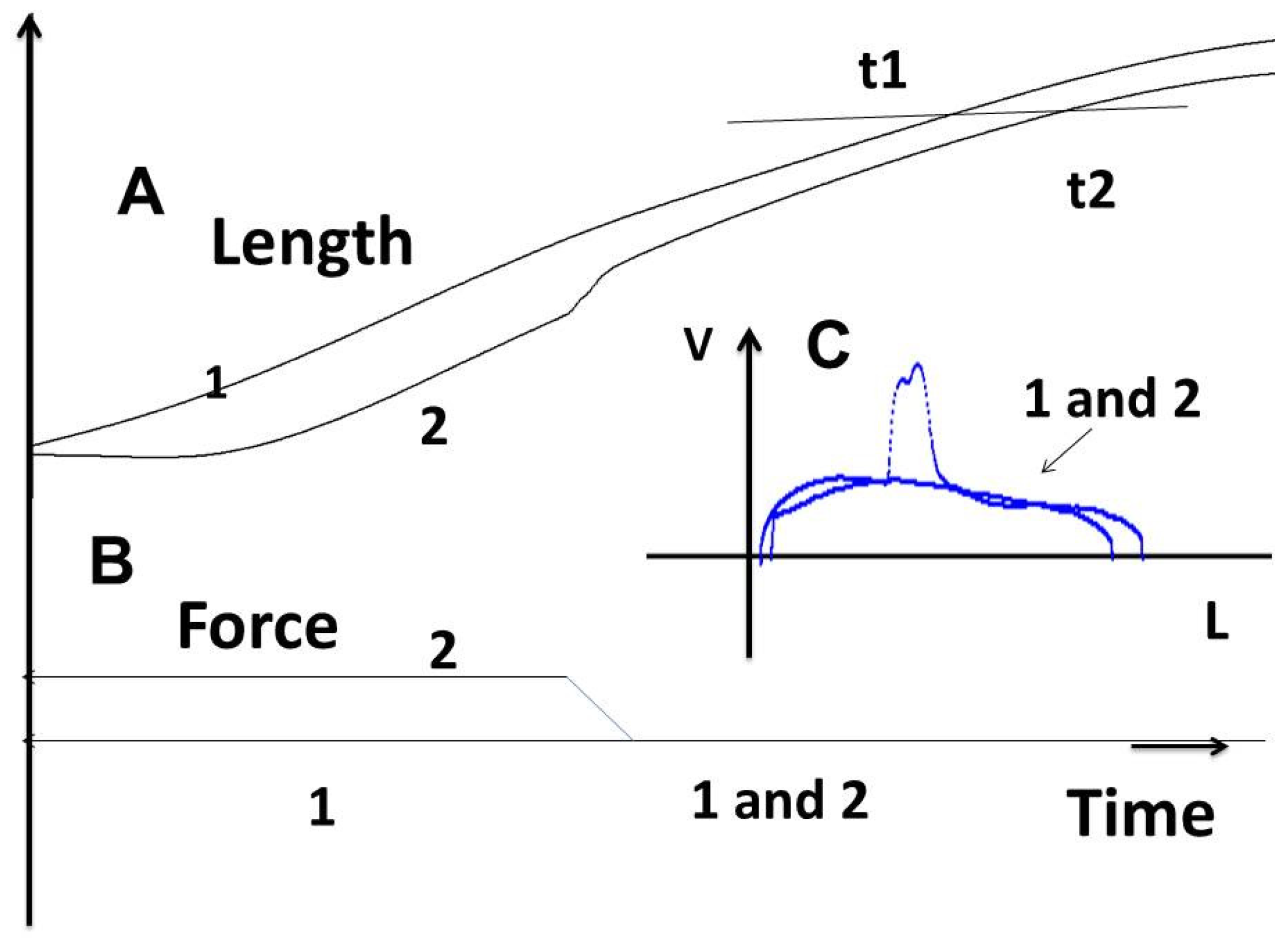
3.2.2. The Frank–Starling Mechanism and Hyperbolic Hill Relationship
3.2.3. Tridimensional Tension–Velocity–Shortening-Length Relationship
3.2.4. Relaxation
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Conti, M.A.; Adelstein, R.S. Nonmuscle myosin II moves in new directions. J. Cell Sci. 2008, 121 Pt 1, 11–18. [Google Scholar] [CrossRef] [PubMed]
- Frank, O. Zur Dynamik des Herzmuskels. Z. Biol. 1895, 32, 273–277. [Google Scholar]
- Starling, E.H. The Arris and Gale Lectures on some points in the pathology of heart disease. Lecture I. The compensating mechanism of the heart. Lancet 1897, 1, 569–572. [Google Scholar] [CrossRef]
- Hill, A.V. The heat of shortening and the dynamic constants of muscle. Proc. R. Soc. Lond. Biol. Sci. 1938, 126, 136–195. [Google Scholar]
- Brutsaert, D.L.; Sonnenblick, E.H. Force-velocity-length-time relations of the contractile elements in heart muscle of the cat. Circ. Res. 1969, 24, 137–149. [Google Scholar] [CrossRef]
- Kovacs, M.; Wang, F.; Hu, A.; Zhang, Y.; Sellers, J.R. Functional divergence of human cytoplasmic myosin II: Kinetic characterization of the non-muscle IIA isoform. J. Biol. Chem. 2003, 278, 38132–38140. [Google Scholar] [CrossRef] [PubMed]
- Lecarpentier, E.; Claes, V.; Timbely, O.; Hebert, J.L.; Arsalane, A.; Moumen, A.; Guerin, C.; Guizard, M.; Michel, F.; Lecarpentier, Y. Role of both actin-myosin cross bridges and NO-cGMP pathway modulators in the contraction and relaxation of human placental stem villi. Placenta 2013, 34, 1163–1169. [Google Scholar] [CrossRef]
- Matsumura, S.; Sakurai, K.; Shinomiya, T.; Fujitani, N.; Key, K.; Ohashi, M. Biochemical and immunohistochemical characterization of the isoforms of myosin and actin in human placenta. Placenta 2011, 32, 347–355. [Google Scholar] [CrossRef]
- Lecarpentier, Y.; Schussler, O.; Sakic, A.; Rincon-Garriz, J.M.; Soulie, P.; Bochaton-Piallat, M.L.; Kindler, V. Human Bone Marrow Contains Mesenchymal Stromal Stem Cells That Differentiate In Vitro into Contractile Myofibroblasts Controlling T Lymphocyte Proliferation. Stem Cells Int. 2018, 2018, 6134787. [Google Scholar] [CrossRef]
- Lecarpentier, Y.; Schussler, O.; Hebert, J.L.; Vallee, A. Multiple Targets of the Canonical WNT/beta-Catenin Signaling in Cancers. Front. Oncol. 2019, 9, 1248. [Google Scholar] [CrossRef]
- Murray, A.W. Cyclin synthesis and degradation and the embryonic cell cycle. J. Cell Sci. Suppl. 1989, 12, 65–76. [Google Scholar] [CrossRef] [PubMed]
- Murray, A.W. Cell biology: The cell cycle as a cdc2 cycle. Nature 1989, 342, 14–15. [Google Scholar] [CrossRef] [PubMed]
- Nurse, P. Cyclin dependent kinases and cell cycle control (nobel lecture). Chembiochem 2002, 3, 596–603. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.S.; Mellman, I. Oncology meets immunology: The cancer-immunity cycle. Immunity 2013, 39, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Savvidis, C.; Koutsilieris, M. Circadian rhythm disruption in cancer biology. Mol. Med. 2012, 18, 1249–1260. [Google Scholar] [CrossRef] [PubMed]
- Hinz, B. The myofibroblast: Paradigm for a mechanically active cell. J. Biomech. 2010, 43, 146–155. [Google Scholar] [CrossRef] [PubMed]
- Otranto, M.; Sarrazy, V.; Bonte, F.; Hinz, B.; Gabbiani, G.; Desmouliere, A. The role of the myofibroblast in tumor stroma remodeling. Cell Adhes. Migr. 2012, 6, 203–219. [Google Scholar] [CrossRef] [PubMed]
- Warburg, O. On the origin of cancer cells. Science 1956, 123, 309–314. [Google Scholar] [CrossRef]
- Shao, J.; Jung, C.; Liu, C.; Sheng, H. Prostaglandin E2 Stimulates the beta-catenin/T cell factor-dependent transcription in colon cancer. J. Biol. Chem. 2005, 280, 26565–26572. [Google Scholar] [CrossRef]
- Castellone, M.D.; Teramoto, H.; Williams, B.O.; Druey, K.M.; Gutkind, J.S. Prostaglandin E2 promotes colon cancer cell growth through a Gs-axin-beta-catenin signaling axis. Science 2005, 310, 1504–1510. [Google Scholar] [CrossRef]
- Li, A.; Chen, M.; Jiang, T.X.; Wu, P.; Nie, Q.; Widelitz, R.; Chuong, C.M. Shaping organs by a wingless-int/Notch/nonmuscle myosin module which orients feather bud elongation. Proc. Natl. Acad. Sci. USA 2013, 110, E1452–E1461. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Bao, J.; Adelstein, R.S. Loss of cell adhesion causes hydrocephalus in nonmuscle myosin II-B-ablated and mutated mice. Mol. Biol. Cell 2007, 18, 2305–2312. [Google Scholar] [CrossRef] [PubMed]
- Huxley, A.F. Muscle structure and theories of contraction. Prog. Biophys. Biophys. Chem. 1957, 7, 255–318. [Google Scholar] [CrossRef] [PubMed]
- Veech, R.L.; Lawson, J.W.; Cornell, N.W.; Krebs, H.A. Cytosolic phosphorylation potential. J. Biol. Chem. 1979, 254, 6538–6547. [Google Scholar] [CrossRef]
- Sheterline, P.; Clayton, J.; Sparrow, J.C. Protein Profile, 3rd ed.; Academic Press: London, UK, 1996. [Google Scholar]
- Huxley, A.F.; Simmons, R.M. Mechanical properties of the cross-bridges of frog striated muscle. J. Physiol. 1971, 218, 59P–60P. [Google Scholar] [PubMed]
- Rayment, I.; Holden, H.M.; Whittaker, M.; Yohn, C.B.; Lorenz, M.; Holmes, K.C.; Milligan, R.A. Structure of the actin-myosin complex and its implications for muscle contraction. Science 1993, 261, 58–65. [Google Scholar] [CrossRef]
- Dominguez, R.; Freyzon, Y.; Trybus, K.M.; Cohen, C. Crystal structure of a vertebrate smooth muscle myosin motor domain and its complex with the essential light chain: Visualization of the pre-power stroke state. Cell 1998, 94, 559–571. [Google Scholar] [CrossRef]
- Lecarpentier, Y.; Kindler, V.; Krokidis, X.; Bochaton-Piallat, M.L.; Claes, V.; Hebert, J.L.; Vallee, A.; Schussler, O. Statistical Mechanics of Non-Muscle Myosin IIA in Human Bone Marrow-Derived Mesenchymal Stromal Cells Seeded in a Collagen Scaffold: A Thermodynamic Near-Equilibrium Linear System Modified by the Tripeptide Arg-Gly-Asp (RGD). Cells 2020, 9, 1510. [Google Scholar] [CrossRef]
- Gabbiani, G.; Ryan, G.B.; Majne, G. Presence of modified fibroblasts in granulation tissue and their possible role in wound contraction. Experientia 1971, 27, 549–550. [Google Scholar] [CrossRef]
- Hinz, B. Masters and servants of the force: The role of matrix adhesions in myofibroblast force perception and transmission. Eur. J. Cell Biol. 2006, 85, 175–181. [Google Scholar] [CrossRef]
- Hinz, B. Mechanical aspects of lung fibrosis: A spotlight on the myofibroblast. Proc. Am. Thorac. Soc. 2012, 9, 137–147. [Google Scholar] [CrossRef]


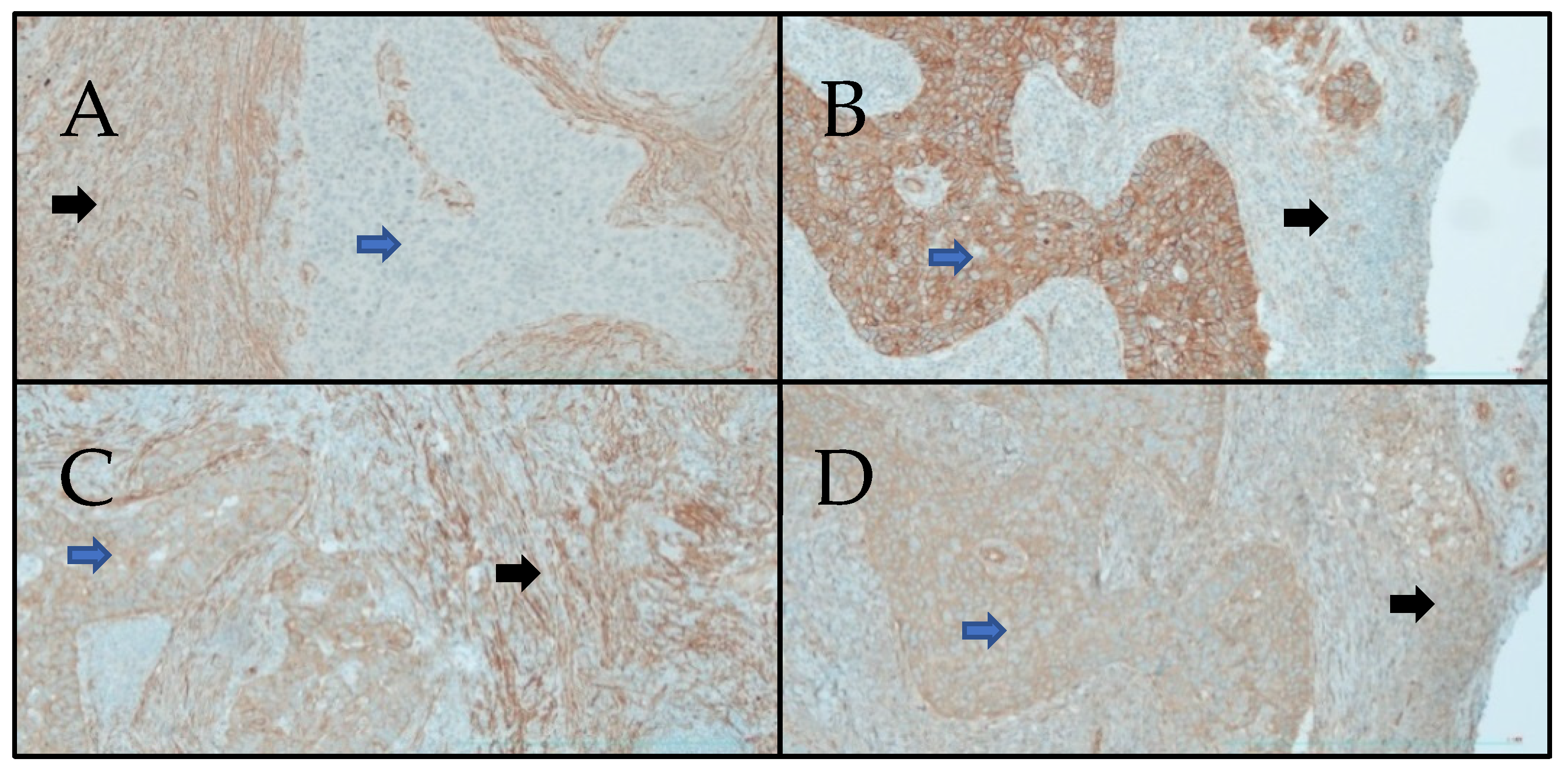

| NM-IIA | NM-IIB | SMA | β-Catenin | ||||||
|---|---|---|---|---|---|---|---|---|---|
| n° | Histological Type | Tumor | Stroma | Tumor | Stroma | Tumor | Stroma | Tumor | Stroma |
| 1 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 2 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 3 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 4 | Squamous cell carcinoma | - | + | + | + | - | + | + | + |
| 5 | Adenocarcinoma | + | + | - | + | - | + | + | + |
| 6 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 7 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 8 | Carcinoid carcinoma | + | + | + | + | - | + | + | + |
| 9 | Adenocarcinoma | + | - | + | - | - | + | + | + |
| 10 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 11 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 12 | Squamous cell carcinoma | + | + | + | + | - | + | + | + |
| 13 | Prostatic adenocarcinoma | - | + | + | - | - | + | + | + |
| 14 | Squamous cell carcinoma | + | + | + | + | - | + | + | + |
| 15 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 16 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 17 | Squamous cell carcinoma | + | + | + | + | - | + | + | + |
| 18 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 19 | Adenocarcinoma | + | + | + | + | - | + | + | + |
| 20 | Squamous cell carcinoma | + | + | + | - | - | + | + | + |
| 21 | Adenocarcinoma | + | + | - | + | - | + | + | + |
| Lung Cancer | Placenta | MSC | Heart | |
|---|---|---|---|---|
| Vmax | 0.003 | 0.002 | 0.002 | 3.7 |
| Tension | 0.2 | 1.5 | 0.3 | 42 |
| kcat | 0.004 | 0.003 | 0.004 | 20.6 |
| CB force | 2.0 | 2.0 | 2.1 | 1.6 |
| max.Eff (%) | 36 | 36 | 38 | 28 |
| MC | 0.01 | 0.14 | 0.07 | 12.5 |
| G | 4.5 | 3.7 | 4.1 | 1.6 |
| f1 | 0.09 | 0.08 | 0.08 | 308 |
| g1 | 0.04 | 0.03 | 0.03 | 194 |
| g2 | 0.52 | 0.34 | 0.35 | 731 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lecarpentier, Y.; Tremblay, B.; Locher, C.; Schussler, O.; Vallée, A.; Locher, C.; Pho, D. Lung Cancers: Parenchymal Biochemistry and Mechanics. Cells 2024, 13, 427. https://doi.org/10.3390/cells13050427
Lecarpentier Y, Tremblay B, Locher C, Schussler O, Vallée A, Locher C, Pho D. Lung Cancers: Parenchymal Biochemistry and Mechanics. Cells. 2024; 13(5):427. https://doi.org/10.3390/cells13050427
Chicago/Turabian StyleLecarpentier, Yves, Bruno Tremblay, Christèle Locher, Olivier Schussler, Alexandre Vallée, Christophe Locher, and David Pho. 2024. "Lung Cancers: Parenchymal Biochemistry and Mechanics" Cells 13, no. 5: 427. https://doi.org/10.3390/cells13050427
APA StyleLecarpentier, Y., Tremblay, B., Locher, C., Schussler, O., Vallée, A., Locher, C., & Pho, D. (2024). Lung Cancers: Parenchymal Biochemistry and Mechanics. Cells, 13(5), 427. https://doi.org/10.3390/cells13050427





