An Approach for Studying the Direct Effects of Shock Waves on Neuronal Cell Structure and Function
Abstract
:1. Introduction
2. Methods
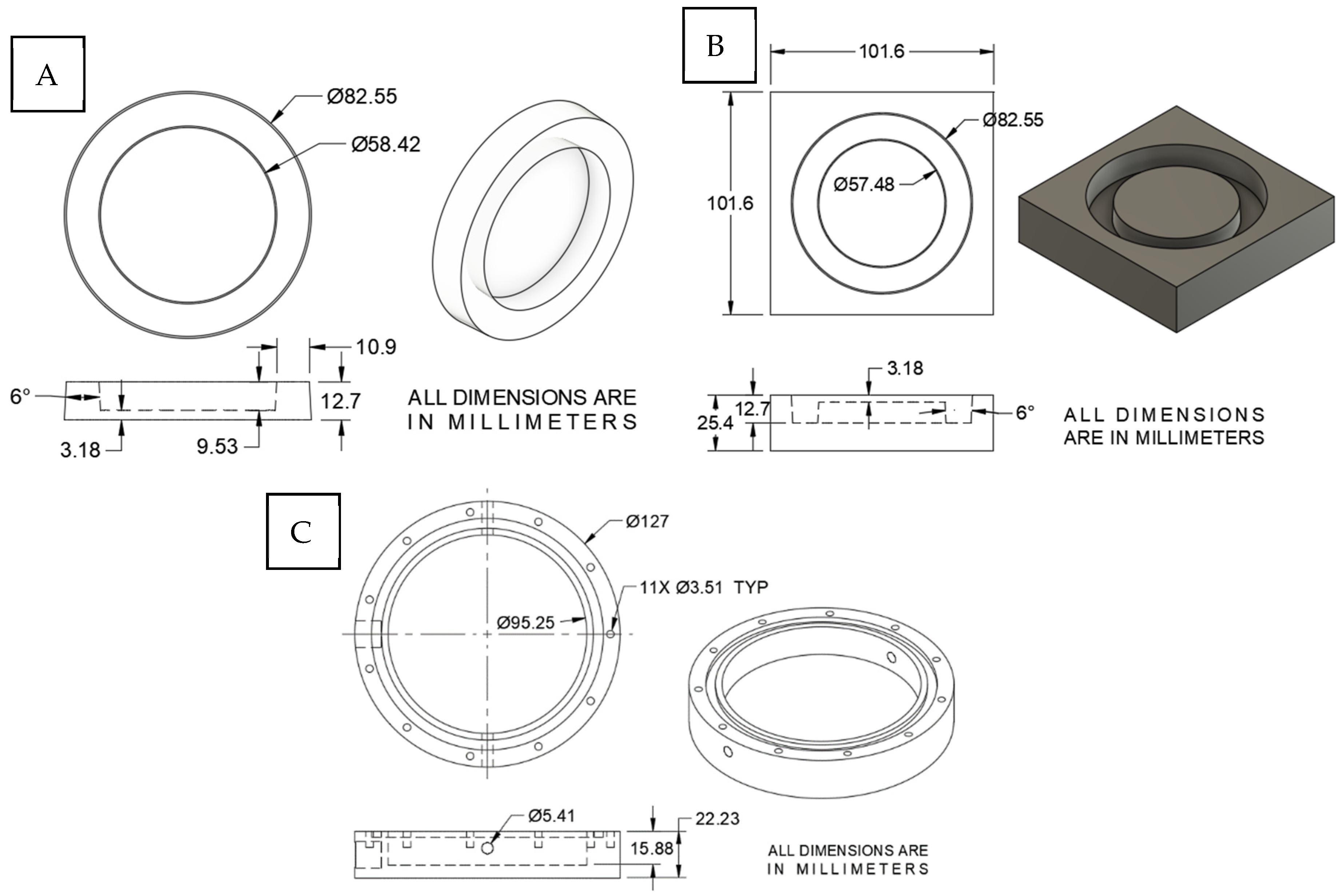
2.1. In Vitro Blast Injury Apparatus
2.2. Primary Neuronal Culture
2.3. Shock Wave Exposure
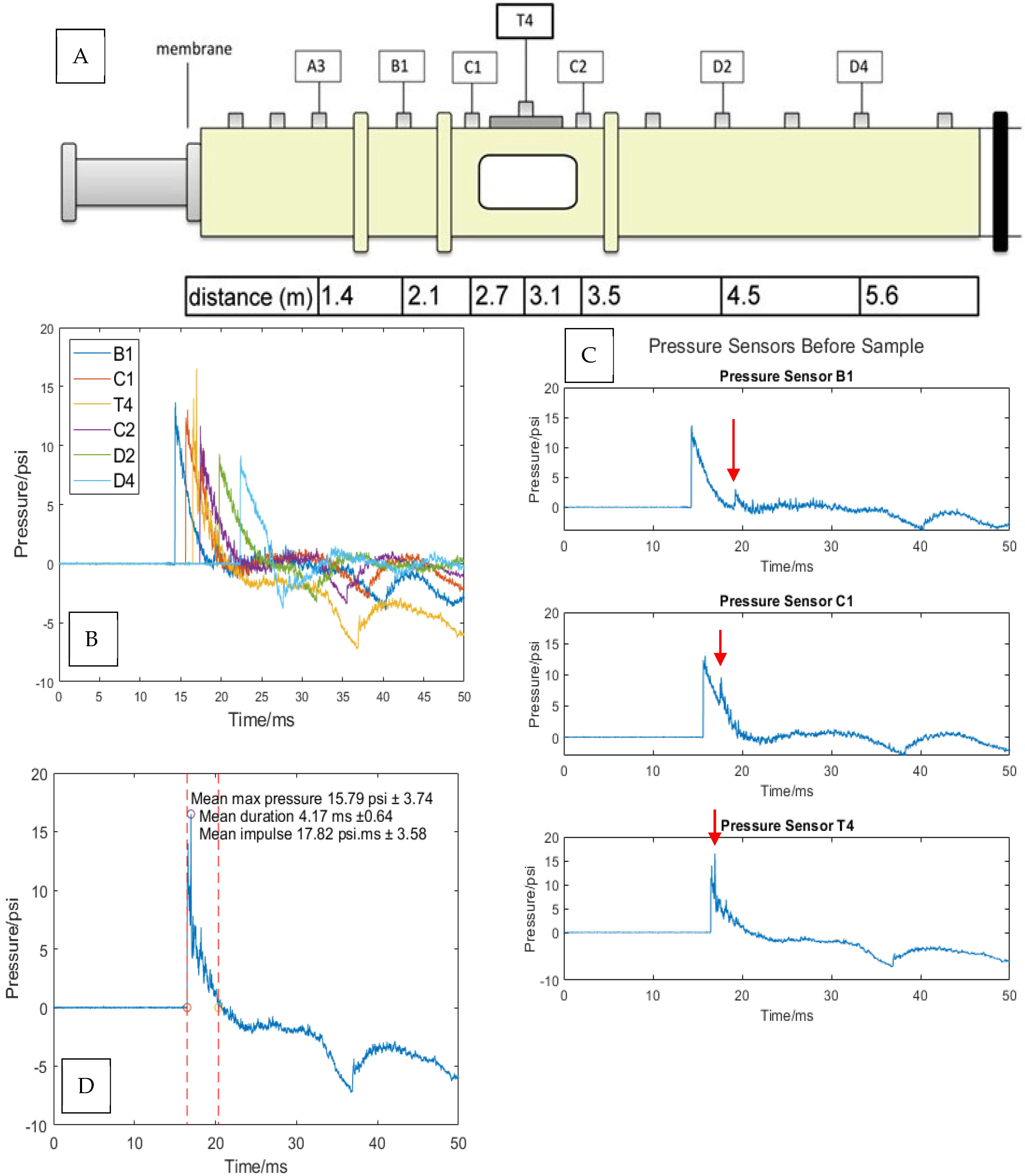
2.4. Pressure Wave Analysis
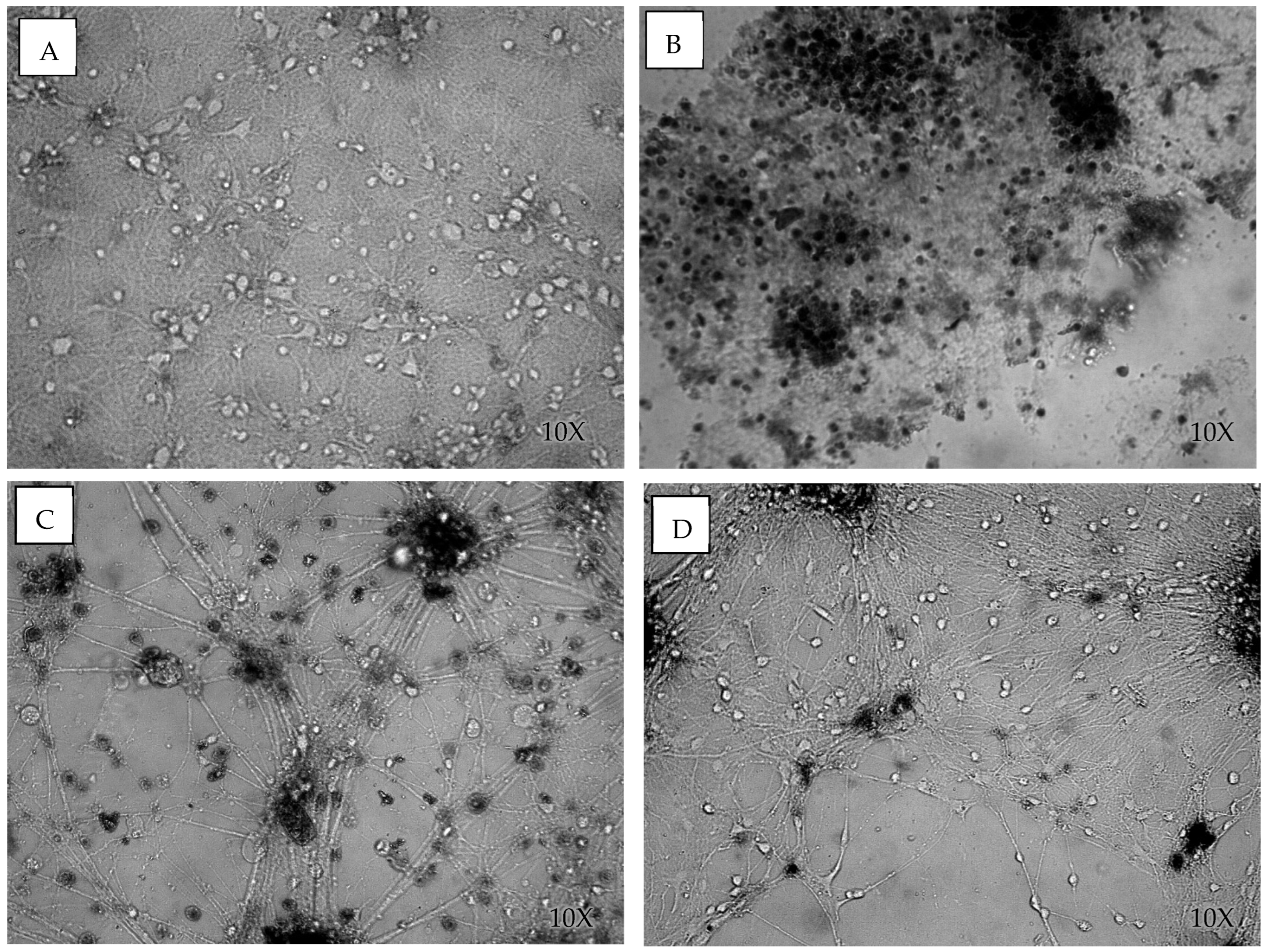
2.5. Cell Viability
2.6. Statistics
3. Results
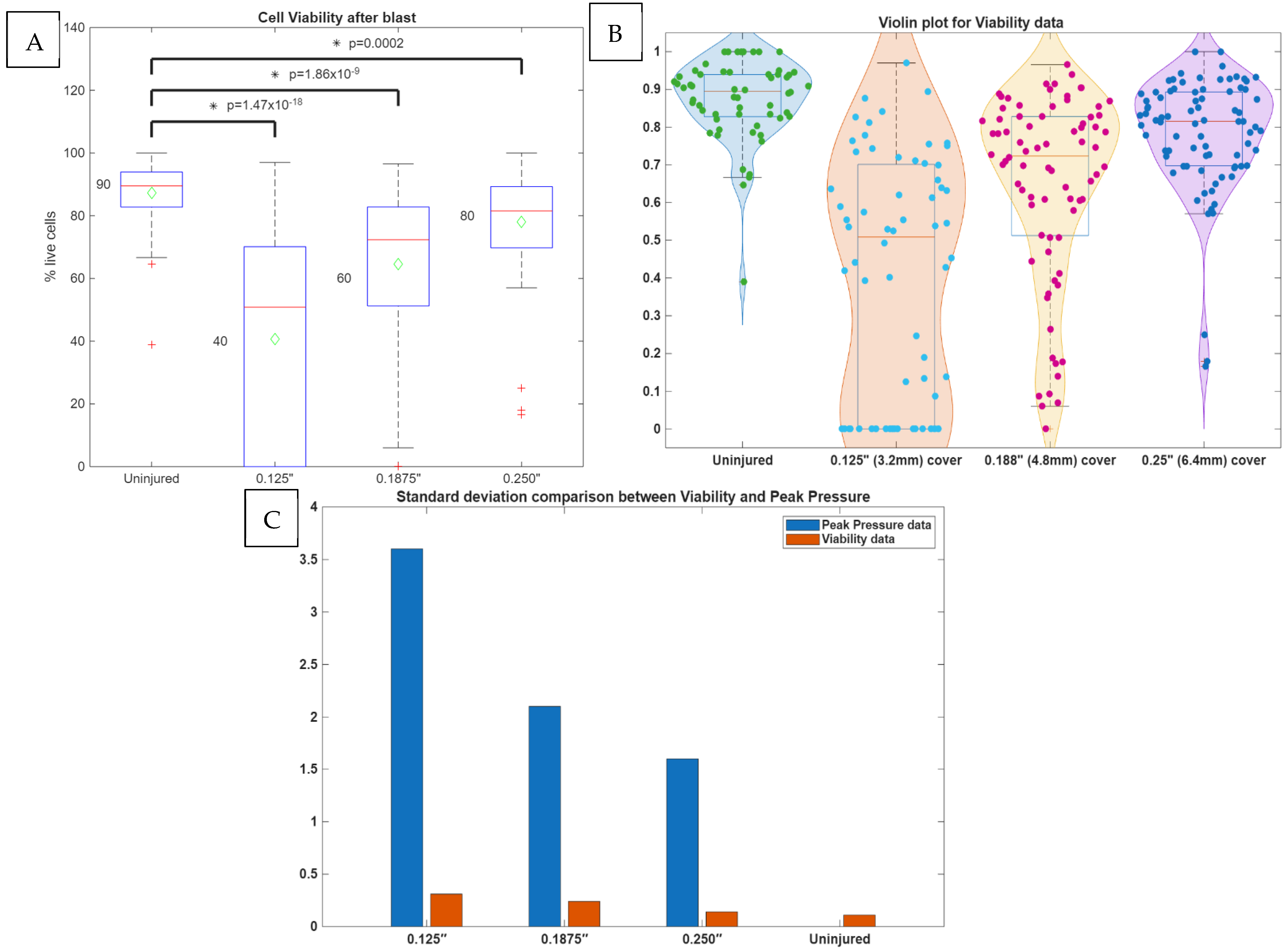
3.1. Cell Viability After Blast
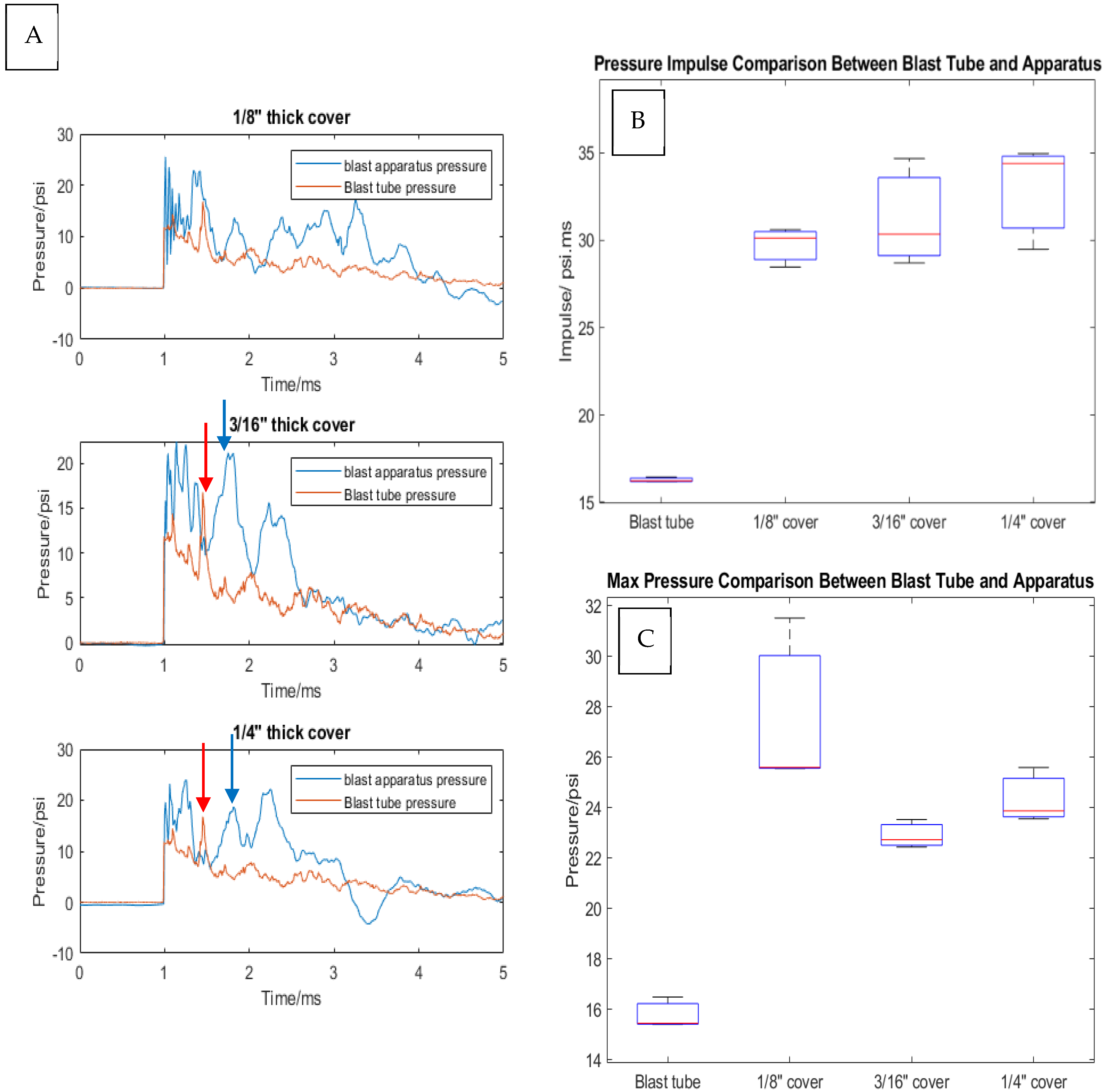
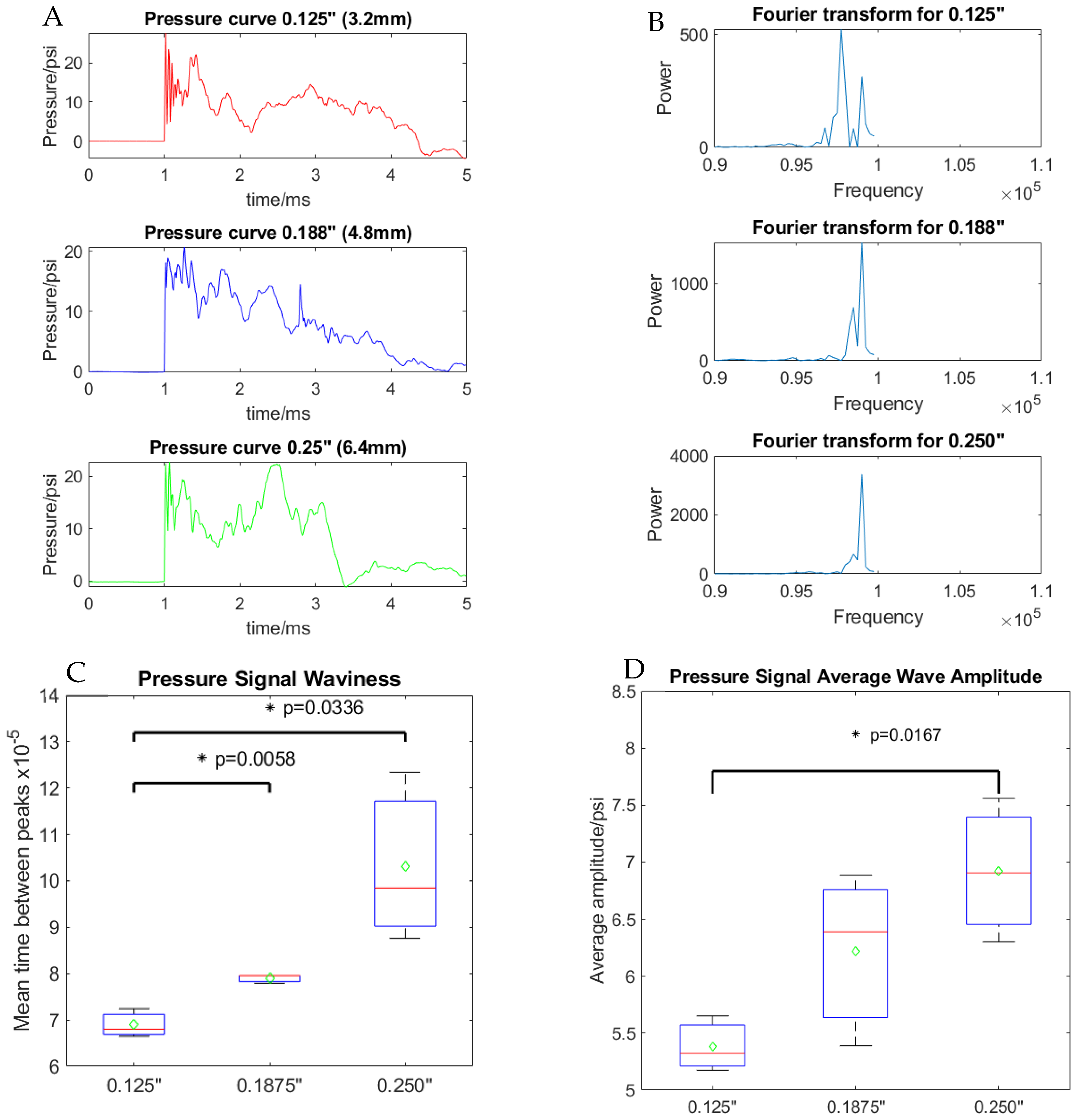
3.2. Analysis of Shock Wave Transmission
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Effgen, G.B.; Hue, C.D.; Vogel, E., 3rd; Panzer, M.B.; Meaney, D.F.; Bass, C.R.; Morrison, B., 3rd. A Multiscale Approach to Blast Neurotrauma Modeling: Part Ii: Methodology for Inducing Blast Injury to In Vitro Models. Front. Neurol. 2012, 3, 23. [Google Scholar] [CrossRef]
- Zander, N.E.; Piehler, T.; Banton, R.; Boggs, M. The Effect of Explosive Blast Loading on Human Neuroblastoma Cells. Anal. Biochem. 2016, 504, 4–6. [Google Scholar] [CrossRef] [PubMed]
- Adams, J.; Graham, D.; Doyle, D.; Lawrence, A.; Mclellan, D. Diffuse Axonal Injury in Head Injuries Caused by a Fall. Lancet 1984, 2, 1420–1422. [Google Scholar] [CrossRef] [PubMed]
- Gennarelli, T.A. Mechanisms of Brain Injury. J. Emerg. Med. 1993, 11 (Suppl. 1), 5–11. [Google Scholar]
- Grady, M.S.; McLaughlin, M.R.; Christman, C.W.; Valadka, A.B.; Fligner, C.L.; Povlishock, J.T. The Use of Antibodies Targeted against the Neurofilament Subunits for the Detection of Diffuse Axonal Injury in Humans. J. Neuropathol. Exp. Neurol. 1993, 52, 143–152. [Google Scholar] [CrossRef]
- Smith, D.H.; Meaney, D.F. Axonal Damage in Traumatic Brain Injury. Neuroscientist 2000, 6, 483–495. [Google Scholar] [CrossRef]
- Thibault, L.E.; Gennarelli, T.A.; Margulies, S.S.; Marcus, J.; Eppinger, R. The Strain Dependent Pathophysiological Consequences of Inertial Loading on Central Nervous System Tissue. In Proceedings of the International Conference on the Biomechanics of Impact, Lyon, France, 12–14 September 1990; pp. 191–202. [Google Scholar]
- Walter Reed Army Medical Center. Traumatic Brain Injury Program. [Website] 2006 [Retrieved in 2007]. Available online: https://walterreed.tricare.mil/News-Gallery/Articles/Article/3427538/neuropsychiatrytbi-unit-at-walter-reed-unique-in-dod (accessed on 1 June 2020).
- Holbourn, A.H.S. Mechanics of Head Injury. Lancet 1943, 2, 438–441. [Google Scholar] [CrossRef]
- Holbourn, A.H.S. The Mechanics of Brain Injuries. Br. Med. Bull. 1945, 3, 147–149. [Google Scholar] [CrossRef]
- Strich, S.J. Shearing of Nerve Fibres as a Cause of Brain Damage Due to Head Injury. Lancet 1961, 278, 443–448. [Google Scholar] [CrossRef]
- Martin, R.M.; Wright, M.J.; Lutkenhoff, E.S.; Ellingson, B.M.; Van Horn, J.D.; Tubi, M.; Alger, J.R.; McArthur, D.L.; Vespa, P.M. Traumatic Hemorrhagic Brain Injury: Impact of Location and Resorption on Cognitive Outcome. J. Neurosurg. 2017, 126, 796–804. [Google Scholar] [CrossRef]
- Mychasiuk, R.; Hehar, H.; Candy, S.; Ma, I.; Esser, M.J. The Direction of the Acceleration and Rotational Forces Associated with Mild Traumatic Brain Injury in Rodents Effect Behavioural and Molecular Outcomes. J. Neurosci. Methods 2016, 257, 168–178. [Google Scholar] [CrossRef] [PubMed]
- Post, A.; Hoshizaki, T.B.; Gilchrist, M.D.; Brien, S.; Cusimano, M.; Marshall, S. Traumatic Brain Injuries: The Influence of the Direction of Impact. Neurosurgery 2015, 76, 81–91. [Google Scholar] [CrossRef] [PubMed]
- Aravind, A.; Ravula, A.R.; Chandra, N.; Pfister, B.J. Behavioral Deficits in Animal Models of Blast Traumatic Brain Injury. Front. Neurol. 2020, 11, 990. [Google Scholar] [CrossRef]
- Ravula, A.R.; Das, T.; Gosain, A.; Dolalas, T.; Padhi, S.; Chandra, N.; Pfister, B.J. An Update on Repeated Blast Traumatic Brain Injury. Curr. Opin. Biomed. Eng. 2022, 24, 100409. [Google Scholar] [CrossRef]
- Chen, Y.C.; Smith, D.H.; Meaney, D.F. In-Vitro Approaches for Studying Blast-Induced Traumatic Brain Injury. J. Neurotrauma 2009, 26, 861–876. [Google Scholar] [CrossRef]
- Abdul-Muneer, P.M.; Conte, A.A.; Haldar, D.; Long, M.; Patel, R.K.; Santhakumar, V.; Overall, C.M.; Pfister, B.J. Traumatic Brain Injury Induced Matrix Metalloproteinase2 Cleaves Cxcl12alpha (Stromal Cell Derived Factor 1alpha) and Causes Neurodegeneration. Brain Behav. Immun. 2017, 59, 190–199. [Google Scholar] [CrossRef] [PubMed]
- Abdul-Muneer, P.M.; Long, M.; Conte, A.A.; Santhakumar, V.; Pfister, B.J. High Ca2+ Influx During Traumatic Brain Injury Leads to Caspase-1-Dependent Neuroinflammation and Cell Death. Mol. Neurobiol. 2016, 54, 3964–3975. [Google Scholar] [CrossRef]
- Magou, G.C.; Guo, Y.; Choudhury, M.; Chen, L.; Hususan, N.; Masotti, S.; Pfister, B.J. Engineering a High Throughput Axon Injury System. J. Neurotrauma 2011, 28, 2203–2218. [Google Scholar] [CrossRef]
- Magou, G.C.; Pfister, B.J.; Berlin, J.R. Effect of Acute Stretch Injury on Action Potential and Network Activity of Rat Neocortical Neurons in Culture. Brain Res. 2015, 1624, 525–535. [Google Scholar] [CrossRef]
- Hanna, M.E.; Pfister, B.J. Advancements in In vitro Models of Traumatic Brain Injury. Curr. Opin. Biomed. Eng. 2023, 25, 100430. [Google Scholar] [CrossRef]
- Zander, N.E.; Piehler, T.; Boggs, M.E.; Banton, R.; Benjamin, R. In Vitro Studies of Primary Explosive Blast Loading on Neurons. J. Neurosci. Res. 2015, 93, 1353–1363. [Google Scholar] [CrossRef] [PubMed]
- Logan, N.J.; Arora, H.; Higgins, C.A. Evaluating Primary Blast Effects In Vitro. J. Vis. Exp. JoVE 2017, 55618. [Google Scholar] [CrossRef]
- Campos-Pires, R.; Yonis, A.; Macdonald, W.; Harris, K.; Edge, C.J.; Mahoney, P.F.; Dickinson, R. A Novel In Vitro Model of Blast Traumatic Brain Injury. J. Vis. Exp. 2018, e58400. [Google Scholar] [CrossRef]
- Ravin, R.; Morgan, N.Y.; Blank, P.S.; Ravin, N.; Guerrero-Cazares, H.; Quinones-Hinojosa, A.; Zimmerberg, J. Response to Blast-Like Shear Stresses Associated with Mild Blast-Induced Brain Injury. Biophys. J. 2019, 117, 1167–1178. [Google Scholar] [CrossRef]
- Xu, D.; Zhang, N.; Wang, S.; Yu, Y.; Zhang, P.; Li, Y.; Yang, H. A Novel In Vitro Platform Development in the Lab for Modeling Blast Injury to Microglia. Front. Bioeng. Biotechnol. 2022, 10, 883545. [Google Scholar] [CrossRef]
- Snapper, D.M.; Reginauld, B.; Liaudanskaya, V.; Fitzpatrick, V.; Kim, Y.; Georgakoudi, I.; Kaplan, D.L.; Symes, A.J. Development of a Novel Bioengineered 3d Brain-Like Tissue for Studying Primary Blast-Induced Traumatic Brain Injury. J. Neurosci. Res. 2023, 101, 3–19. [Google Scholar] [CrossRef]
- Zander, N.E.; Piehler, T.; Banton, R.; Benjamin, R. Effects of Repetitive Low-Pressure Explosive Blast on Primary Neurons and Mixed Cultures. J. Neurosci. Res. 2016, 94, 827–836. [Google Scholar] [CrossRef]
- Zander, N.E.; Piehler, T.; Hogberg, H.; Pamies, D. Explosive Blast Loading on Human 3d Aggregate Minibrains. Cell. Mol. Neurobiol. 2017, 37, 1331–1334. [Google Scholar] [CrossRef]
- Hanna, M.; Ali, A.; Bhatambarekar, P.; Modi, K.; Lee, C.; Morrison, B.; Klienberger, M.; Pfister, B.J. Anatomical Features and Material Properties of Human Surrogate Head Models Affect Spatial and Temporal Brain Motion under Blunt Impact. Bioengineering 2024, 11, 650. [Google Scholar] [CrossRef]
- Wu, J.Z.; Pan, C.S.; Wimer, B.M.; Rosen, C.L. An Improved Finite Element Modeling of The cerebrospinal Fluid Layer in the Head Impact analysis. Bio-Med. Mater. Eng. 2017, 28, 187–199. [Google Scholar] [CrossRef]
- Selvan, V.; Chandra, N. Relationship between Blast Overpressure and Shell Thickness on the Fluid Pressure on a Cylinder under Blast Loading. In Proceedings of the ASME 2013 Summer Bioengineering Conference, Sunriver, OR, USA, 26–29 June 2013. [Google Scholar]
- Del Razo, M.J.; LeVeque, R.J. Computational Study of Shock Waves Propagating through Air-Plastic-Water Interfaces. Bull. Braz. Math. Soc. New Ser. 2016, 47, 685–700. [Google Scholar] [CrossRef]
- Sutar, S.; Ganpule, S. Investigation of Wave Propagation through Head Layers with Focus on Understanding Blast Wave Transmission. Biomech. Model. Mechanobiol. 2020, 19, 875–892. [Google Scholar] [CrossRef] [PubMed]
- Skotak, M.; Alay, E.; Chandra, N. On the Accurate Determination of Shock Wave Time-Pressure Profile in the Experimental Models of Blast-Induced Neurotrauma. Front. Neurol. 2018, 9, 52. [Google Scholar] [CrossRef]
- Ganpule, S.; Alai, A.; Plougonven, E.; Chandra, N. Mechanics of Blast Loading on the Head Models in the Study of Traumatic Brain Injury Using Experimental and Computational Approaches. Biomech. Model. Mechanobiol. 2013, 12, 511–531. [Google Scholar] [CrossRef]
- Kuriakose, M.; Skotak, M.; Misistia, A.; Kahali, S.; Sundaramurthy, A.; Chandra, N. Tailoring the Blast Exposure Conditions in the Shock Tube for Generating Pure, Primary Shock Waves: The End Plate Facilitates Elimination of Secondary Loading of the Specimen. PLoS ONE 2016, 11, e0161597. [Google Scholar] [CrossRef]
- Michael, H.; Ali, A.; Klienberger, M.; Pfister, B.J. A Method for Evaluating Brain Deformation under Sagittal Blunt Impacts Using a Half-Skull Human-Scale Surrogate. J. Biomech. Eng. 2022, 145, 061001. [Google Scholar]
- Thielen, P.; Mehoke, T.; Gleason, J.; Iwaskiw, A.; Paulson, J.; Wester, A.M.B.; Dymond, J. Exploration of the Molecular Basis of Blast Injury in a Biofidelic Model of Traumatic Brain Injury. Shock. Waves 2018, 28, 115–126. [Google Scholar] [CrossRef]
- Kim, J.; Adams, A.A.; Gokina, P.; Zambrano, B.; Jayakumaran, J.; Dobrowolski, R.; Maurel, P.; Pfister, B.J.; Kim, H.A.-O. Mechanical Stretch Induces Myelin Protein Loss in Oligodendrocytes by Activating Erk1/2 in a Calcium-Dependent Manner. Glia 2020, 68, 2070–2085. [Google Scholar] [CrossRef]
- Pfister, B.J.; Weihs, T.P.; Betenbaugh, M.; Bao, G. An In Vitro Uniaxial Stretch Model for Axonal Injury. Ann. Biomed. Eng. 2003, 31, 589–598. [Google Scholar] [CrossRef]
- Miranda, I.; Souza, A.; Sousa, P.; Ribeiro, J.; Castanheira, E.M.S.; Lima, R.; Minas, G. Properties and Applications of Pdms for Biomedical Engineering: A Review. J. Funct. Biomater. 2021, 13, 2. [Google Scholar] [CrossRef]
- Jones, D.A.; Urban, J.E.; Lillie, E.M.; Stitzel, J.D. Skull Thickness Morphing for an Age and Sex Specific Fe Model of the Skull. Biomed. Sci. Instrum. 2015, 51, 173–180. [Google Scholar] [PubMed]
- Lillie, E.M.; Urban, J.E.; Lynch, S.K.; Weaver, A.A.; Stitzel, J.D. Evaluation of Skull Cortical Thickness Changes with Age and Sex from Computed Tomography Scans. Of. J. Am. Soc. Bone Miner. Res. 2016, 31, 299–307. [Google Scholar] [CrossRef] [PubMed]
- Delye, H.; Verschueren, P.; Depreitere, B.; Verpoest, I.; Berckmans, D.; Sloten, J.V.; Van Der Perre, G.; Goffin, J. Biomechanics of Frontal Skull Fracture. J. Neurotrauma 2007, 24, 1576–1586. [Google Scholar] [CrossRef]
- Zhai, X.; Nauman, E.A.; Moryl, D.; Lycke, R.; Chen, W.W. The Effects of Loading-Direction and Strain-Rate on the Mechanical Behaviors of Human Frontal Skull Bone. J. Mech. Behav. Biomed. Mater. 2020, 103, 103597. [Google Scholar] [CrossRef]
- Yoganandan, N.; Pintar, F.A.; Sances, A., Jr.; Walsh, P.R.; Ewing, C.L.; Thomas, D.J.; Snyder, R.G. Biomechanics of Skull Fracture. J. Neurotrauma 1995, 12, 659–668. [Google Scholar] [CrossRef]
- McElhaney, J.H.; Fogle, J.L.; Melvin, J.W.; Haynes, R.R.; Roberts, V.L.; Alem, N.M. Mechanical Properties on Cranial Bone. J. Biomech. 1970, 3, 495–511. [Google Scholar] [CrossRef] [PubMed]
- Motherway, J.A.; Verschueren, P.; Van der Perre, G.; Sloten, J.V.; Gilchrist, M.D. The Mechanical Properties of Cranial Bone: The Effect of Loading Rate and Cranial Sampling Position. J. Biomech. 2009, 42, 2129–2135. [Google Scholar] [CrossRef]
- Alexander, S.L.; Gunnarsson, C.A.; Rafaels, K.; Weerasooriya, T. Multiscale Response of the Human Skull to Quasi-Static Compression. J. Mech. Behav. Biomed. Mater. 2020, 102, 103492. [Google Scholar] [CrossRef]
- Bloomfield, I.G.; Johnston, I.H.; Bilston, L.E. Effects of Proteins, Blood Cells and Glucose on the Viscosity of Cerebrospinal Fluid. Pediatr. Neurosurg. 1998, 28, 246–251. [Google Scholar] [CrossRef]
- Thomas, J.H. Fluid Dynamics of Cerebrospinal Fluid Flow in Perivascular Spaces. J. R. Soc. Interface 2019, 16, 20190572. [Google Scholar] [CrossRef]
- Sundaramurthy, A.; Chandra, N. A Parametric Approach to Shape Field-Relevant Blast Wave Profiles in Compressed-Gas-Driven Shock Tube. Front. Neurol. 2014, 5, 253. [Google Scholar] [CrossRef] [PubMed]
- Ruan, J.; Prasad, P. The Effects of Skull Thickness Variations on Human Head Dynamic Impact Responses. Stapp Car Crash J. 2001, 45, 395–414. [Google Scholar]
- Jeon, H.; Eliasson, V. Shock Wave Interactions with Liquid Sheets. Exp. Fluids 2017, 58, 24. [Google Scholar] [CrossRef]
- Courtney, A.; Courtney, M. The Complexity of Biomechanics Causing Primary Blast-Induced Traumatic Brain Injury: A Review of Potential Mechanisms. Front. Neurol. 2015, 6, 221. [Google Scholar] [CrossRef]
- Azar, A.; Bhagavathula, K.B.; Hogan, J.; Ouellet, S.; Satapathy, S.; Dennison, C.R. Protective Headgear Attenuates Forces on the Inner Table and Pressure in the Brain Parenchyma During Blast and Impact: An Experimental Study Using a Simulant-Based Surrogate Model of the Human Head. J. Biomech. Eng. 2019, 142, 041009. [Google Scholar] [CrossRef]
- Du, Z.; Li, Z.; Wang, P.; Wang, X.; Zhang, J.; Zhuang, Z.; Liu, Z. Revealing the Effect of Skull Deformation on Intracranial Pressure Variation During the Direct Interaction between Blast Wave and Surrogate Head. Ann. Biomed. Eng. 2022, 50, 1038–1052. [Google Scholar] [CrossRef] [PubMed]
- Bir, C.A. Measuring Blast-Related Intracranial Pressure within the Human Head; Technology Information Center Technical Report; Wayne State University: Detroit, MI, USA, 2011. [Google Scholar]
- Elkin, B.S.; Fau-Morrison, B.I.A., 3rd; Morrison, B., 3rd. Viscoelastic Properties of the P17 and Adult Rat Brain from Indentation in the Coronal Plane. J. Biomech. Eng. 2013, 135, 114507. [Google Scholar] [CrossRef]
- Elkin, B.S.; Ilankova, A.; Morrison, B., III. Dynamic, Regional Mechanical Properties of the Porcine Brain: Indentation in the Coronal Plane. J. Biomech. Eng. 2011, 133, 071009. [Google Scholar] [CrossRef]
- Budday, S.; Sommer, G.; Birkl, C.; Langkammer, C.; Haybaeck, J.; Kohnert, J.; Bauer, M.; Paulsen, F.; Steinmann, P.; Kuhl, E.; et al. Mechanical Characterization of Human Brain Tissue. Acta Biomater. 2017, 48, 319–340. [Google Scholar] [CrossRef]
- Finan, J.D.; Sundaresh, S.N.; Elkin, B.S.; McKhann, G.M.; Morrison, B. Regional Mechanical Properties of Human Brain Tissue for Computational Models of Traumatic Brain Injury. Acta Biomater. 2017, 55, 333–339. [Google Scholar] [CrossRef]
- Procès, A.; Luciano, M.; Kalukula, Y.; Ris, L.; Gabriele, S. Multiscale Mechanobiology in Brain Physiology and Diseases. Front. Cell Dev. Biol. 2022, 10, 823857. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Zhu, F.; Mao, H.; Shen, M.; Yang, K.H. A Comprehensive Experimental Study on Material Properties of Human Brain Tissue. J. Biomech. 2013, 46, 2795–2801. [Google Scholar] [CrossRef] [PubMed]
- Chandra, N.; Ganpule, S.; Kleinschmit, N.N.; Feng, R.; Holmberg, A.D.; Sundaramurthy, A.; Selvan, V.; Alai, A. Evolution of Blast Wave Profiles in Simulated Air Blasts: Experiment and Computational Modeling. Shock. Waves 2012, 22, 403–415. [Google Scholar] [CrossRef]
- Needham, C.E.; Ritzel, D.; Rule, G.T.; Wiri, S.; Young, L. Blast Testing Issues and Tbi: Experimental Models That Lead to Wrong Conclusions. Front. Neurol. 2015, 6, 72. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hanna, M.; Pfister, B.J. An Approach for Studying the Direct Effects of Shock Waves on Neuronal Cell Structure and Function. Cells 2025, 14, 563. https://doi.org/10.3390/cells14080563
Hanna M, Pfister BJ. An Approach for Studying the Direct Effects of Shock Waves on Neuronal Cell Structure and Function. Cells. 2025; 14(8):563. https://doi.org/10.3390/cells14080563
Chicago/Turabian StyleHanna, Michael, and Bryan J. Pfister. 2025. "An Approach for Studying the Direct Effects of Shock Waves on Neuronal Cell Structure and Function" Cells 14, no. 8: 563. https://doi.org/10.3390/cells14080563
APA StyleHanna, M., & Pfister, B. J. (2025). An Approach for Studying the Direct Effects of Shock Waves on Neuronal Cell Structure and Function. Cells, 14(8), 563. https://doi.org/10.3390/cells14080563



