The Roles of Signaling in Cytoskeletal Changes, Random Movement, Direction-Sensing and Polarization of Eukaryotic Cells
Abstract
:1. Introduction
2. The Primary Modes of Cell Movement
3. The Signal-Transduction Network in Eukaryotic Cells
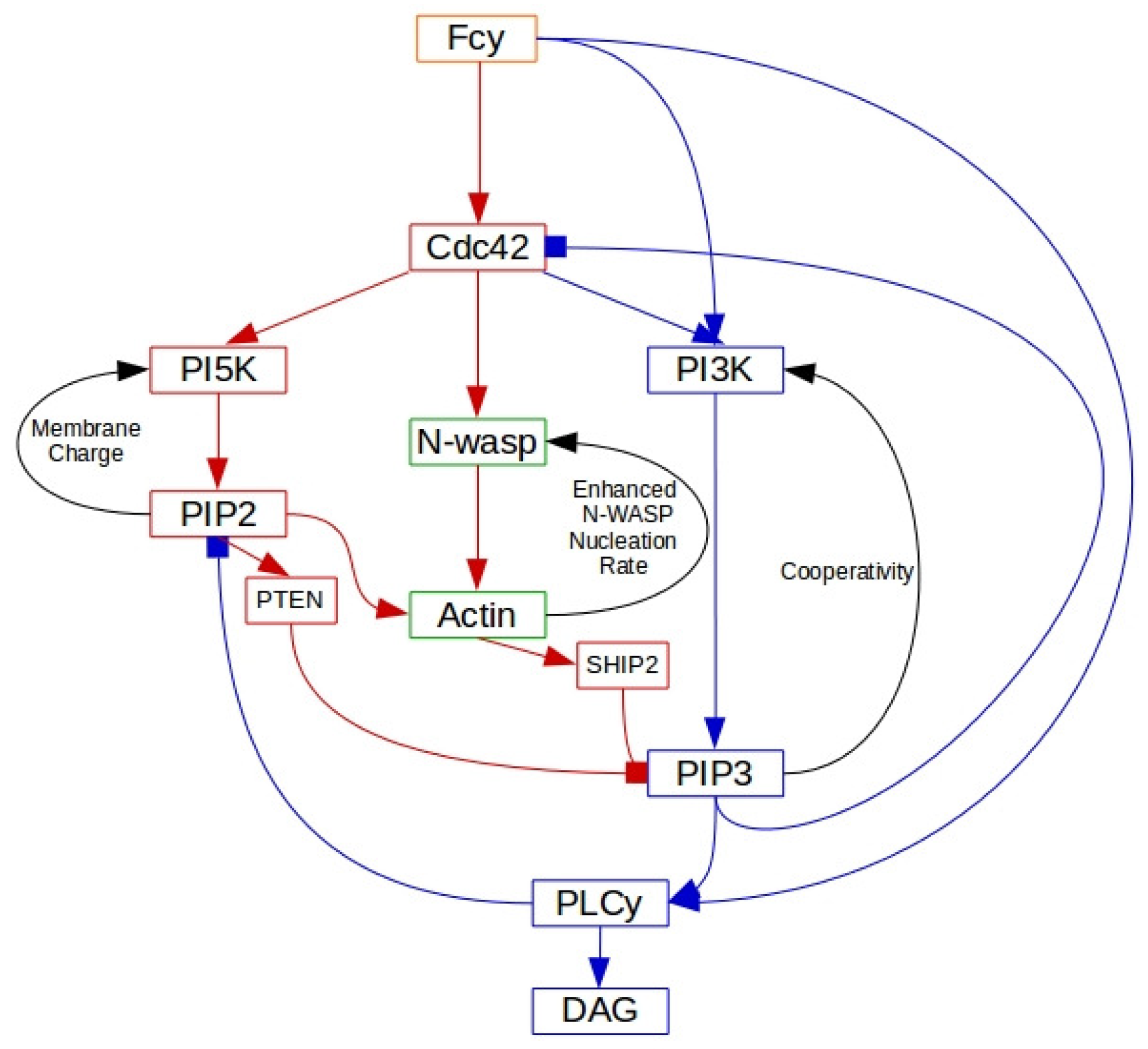
3.1. The Signal-Transduction Networks in Dictyostelium and Neutrophils
3.2. The Dynamics of the Ras-PI3K-PTEN Pathway
4. Intracellular Actin Waves in the Absence of Directional Signals
4.1. Models of Intracellular Waves in Dicty
4.2. Intracellular Waves in Frustrated Phagocytosis
5. Models for Polarization and Direction Sensing
5.1. Mathematical Models for Polarization
5.1.1. Localization of ‘Hotspots’ for Wave Initiation and Polarization
5.1.2. Reaction-Diffusion Models for Gradient Establishment
5.2. A Model for Direction-Sensing in Dictyostelium in cAMP Gradients
6. The Integration of Signaling, Polarization and Structural Changes in the CSK
- Detection of the chemical and mechanical signals in the ME with membrane receptors, adhesive sites, and other detection mechanisms.
- Transduction of the extracellular signals into spatially biased intracellular signals that reflect the external signals and activate one or more downstream signaling pathways.
- Translation of the output of these signaling pathways into the changes in the CSK needed to begin directed motion.
6.1. How Graded Chemical Signals Lead to Polarization
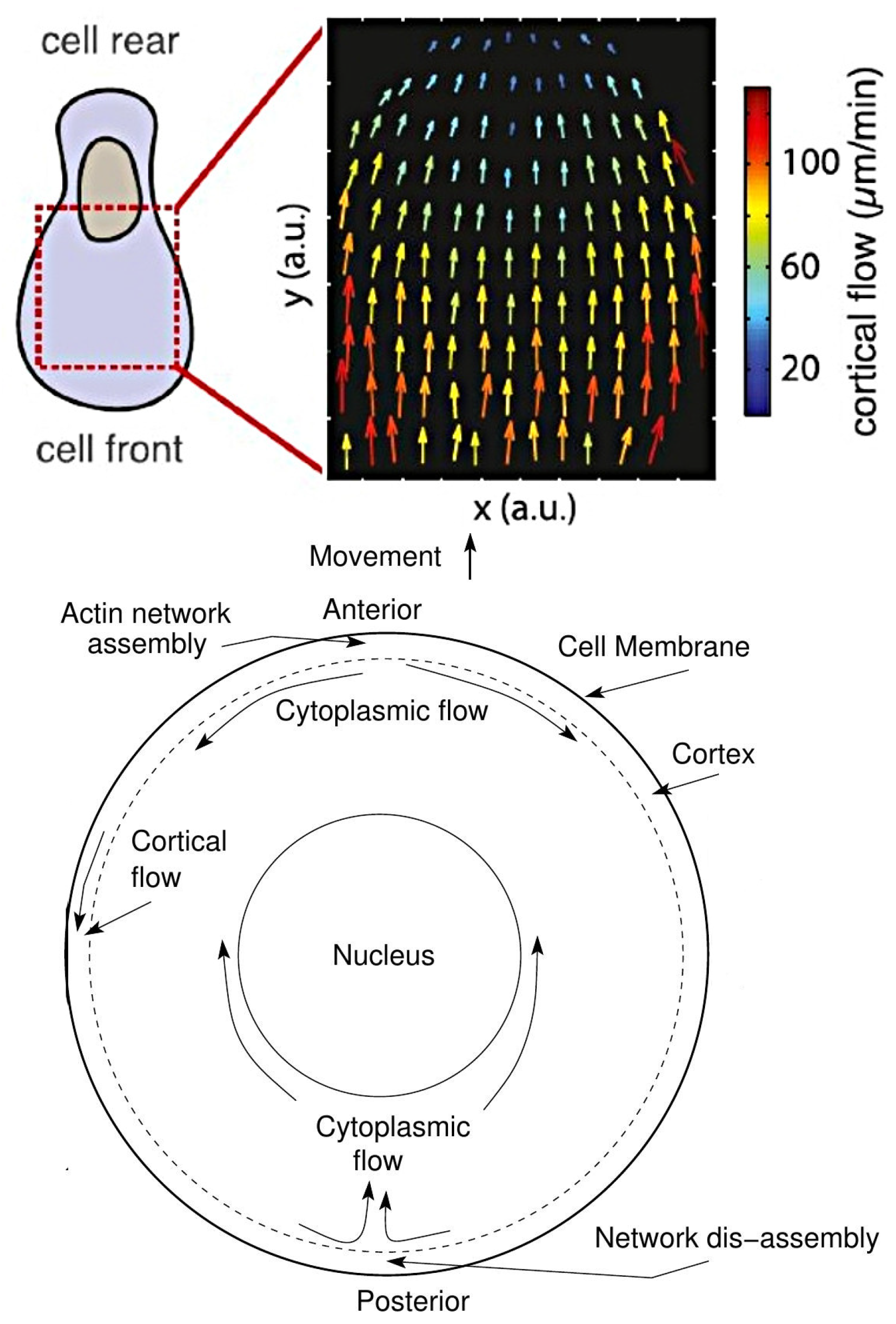
6.2. The Role of Membrane and Cortical Tension in Polarization
7. Epilogue and Open Problems
- What is the minimal set of components of the network shown in Figure 5 that can control the random initiation of intracellular waves in un-stimulated cells? Experimental work described earlier suggests that a minimal set in Dicty may be SCAR/WAVE, Arp 2/3 and actin-binding proteins, but there are presently no models that can replicate the experimental results. A related question is what controls the initiation sites for pseudopodia. Is it randomness in the wave generation, or are there randomly located sites of decreased membrane tension that facilitate membrane deformation, or both?
- A question raised earlier concerns how cells establish a sharp demarcation between ‘frontness’ and ‘backness’ in the presence of an extracellular signal. This involves the spatial distribution of numerous species, and a minimal set of components to produce the demarcation is not yet known. A related question is how the strength of the signal determines whether the cell turns in response to a change in direction of the signal, or whether it completely rebuilds the CSK.
- There are as yet no models that integrate mechanical and chemical pathways to predict actin flows and structural changes in the CSK—even within a fixed cell shape. In the previous sections we simply described how some of the separate components may be involved in polarization, but their integration remains to be addressed.
- A larger question is how these pathways control the mode of migration used by a cell. Cells moving on flat surfaces often use lamellipodia, but movement in confined spaces can prevent the extension of lateral membrane protrusions, which may account in part for the use of blebs in confined spaces. The coexistence of blebs and pseudopods in Dicty suggests that the balance can be subtle, but there are experimental conditions under which one or the other dominates. Since cells often move in a spatially variable environment, the feedback from the ME can affect the mode of movement dynamically, and far more work is needed to understand how the cell-ME interaction controls the mode of movement. Significant progress has been made on simpler systems such as keratocytes moving on a flat surface [169], and recent techniques that can capture more dynamic shape changes in 3D via interface tracking shows promise [170], but much remains to be done. In the context of swimmers such as shown in Figure 3, a model in which protrusions propagate along the body length can replicate swimming speeds under various conditions [28], but how extension of protrusions is controlled by local fluid properties and other factors is not yet known.
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| F-actin | Branched and linear actin or either |
| CON | CSK oscillatory network |
| Dicty | Dictyostelium discoideum |
| G beta-gamma complex | |
| G-protein alpha-subunit | |
| GEF | GTP exchange factor |
| GAP | GTPase-activating factor |
| DGAP1 | IQGAP-related protein |
| PHP | PH domain proteins |
| Akt | PI3 kinase and protein kinase B |
| WRC | SCAR/WAVE regulatory complex |
| SHIP | SH2-containing inositol 5-phosphatase |
| WAVE | WASP-family verprolin-homologous protein |
| WASP | Wiskott–Aldrich syndrome protein |
| Arp2/3 | actin-related protein 2 and 3 complex |
| AC | adenylate cyclase |
| B-actin | branched actin |
| calcium | |
| CaM | calmodulin |
| CapP | capping proteins |
| Ctx | cortexilin |
| CAR | cyclic AMP receptor |
| cGMP | cyclic GMP |
| cAMP | cyclic AMP |
| CSK | cytoskeleton |
| CRAC | cytosolic regulator of adenylyl cyclase |
| DAG | diacylglycerol |
| ELMO | eukaryotic engulfment and cell motility proteins |
| ECM | extracellular matrix |
| G-actin | free actin monomer |
| GFP | green-fluorescent-protein |
| GDI | guanine dissociation inhibitor |
| GDP | guanosine diphosphate |
| GTP | guanosine triphosphate |
| GC | guanylate cyclase |
| IP3 | inositol 1,4,5-trisphosphate |
| LatA | latrunculin A |
| L-actin | linear actin |
| LEGI | local excitation and global inhibition |
| MAT | mesenchymal-to-amoeboid transition |
| ME | microenvironment |
| MHCK | myosin heavy-chain kinase |
| MLCK | myosin light chain kinase |
| myo-IB | myosin-IB |
| myo-II | non-muscle myosin-II |
| PakA | p21-activated kinase A |
| PTEN | phosphatase and tensin homologue |
| PIP3 | phosphatidylinositol 3,4,5-trisphosphate |
| PI3K | phosphatidylinositol-3 kinase |
| PIP2 | phosphatidylinositol-4,5-diphosphate |
| PI5K | phosphatidylinositol-5 kinase |
| PLA2 | phospholipase |
| PLC | phospholipase C |
| PH | pleckstrin homology |
| STEN | signal-transduction excitable network |
| TORC2 | target of rapamycin complex 2 |
| WT | wild-type |
References
- Nürnberg, A.; Kitzing, T.; Grosse, R. Nucleating actin for invasion. Nat. Rev. Cancer 2011, 11, 177–187. [Google Scholar] [CrossRef] [PubMed]
- Othmer, H.G. Eukaryotic cell dynamics from crawlers to swimmers. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2019, 9, e1376. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Haeger, A.; Wolf, K.; Zegers, M.M.; Friedl, P. Collective cell migration: Guidance principles and hierarchies. Trends Cell Biol. 2015, 25, 556–566. [Google Scholar] [CrossRef] [PubMed]
- Artemenko, Y.; Lampert, T.J.; Devreotes, P.N. Moving towards a paradigm: Common mechanisms of chemotactic signaling in Dictyostelium and mammalian leukocytes. Cell. Mol. Life Sci. 2014, 71, 3711–3747. [Google Scholar] [CrossRef] [Green Version]
- Charras, G.; Sahai, E. Physical influences of the extracellular environment on cell migration. Nat. Rev. Mol. Cell Biol. 2014, 15, 813–824. [Google Scholar] [CrossRef]
- Hind, L.E.; Vincent, W.J.; Huttenlocher, A. Leading from the back: The role of the uropod in neutrophil polarization and migration. Dev. Cell 2016, 38, 161–169. [Google Scholar] [CrossRef] [Green Version]
- Petri, B.; Sanz, M.J. Neutrophil chemotaxis. Cell Tissue Res. 2018, 371, 425–436. [Google Scholar] [CrossRef]
- Weiner, O.D.; Marganski, W.A.; Wu, L.F.; Altschuler, S.J.; Kirschner, M.W. An actin-based wave generator organizes cell motility. PLoS Biol. 2007, 5, 2053–2063. [Google Scholar] [CrossRef] [Green Version]
- Asano, Y.; Nagasaki, A.; Uyeda, T.Q.P. Correlated waves of actin filaments and PIP3 in Dictyostelium cells. Cell Motil. Cytoskelet. 2008, 65, 923–934. [Google Scholar] [CrossRef]
- Huang, C.H.; Tang, M.; Shi, C.; Iglesias, P.A.; Devreotes, P.N. An excitable signal integrator couples to an idling cytoskeletal oscillator to drive cell migration. Nat. Cell Biol. 2013, 15, 1307–1316. [Google Scholar] [CrossRef] [Green Version]
- Goryachev, A.B.; Leda, M. Many roads to symmetry breaking: Molecular mechanisms and theoretical models of yeast cell polarity. Mol. Biol. Cell 2017, 28, 370–380. [Google Scholar] [CrossRef]
- Friedl, P.; Wolf, K. Plasticity of cell migration: A multiscale tuning model. J. Cell Biol. 2010, 188, 11–19. [Google Scholar] [CrossRef] [Green Version]
- Binamé, F.; Pawlak, G.; Roux, P.; Hibner, U. What makes cells move: Requirements and obstacles for spontaneous cell motility. Mol. BioSyst. 2010, 6, 648–661. [Google Scholar] [CrossRef]
- Pollard, T.D.; Blanchoin, L.; Mullins, R.D. Molecular mechanisms controlling actin filament dynamics in nonmuscle cells. Ann. Rev. Biophys. Biomol. Struct. 2000, 29, 545–576. [Google Scholar] [CrossRef] [Green Version]
- Sanz-Moreno, V.; Gadea, G.; Ahn, J.; Paterson, H.; Marra, P.; Pinner, S.; Sahai, E.; Marshall, C.J. Rac activation and inactivation control plasticity of tumor cell movement. Cell 2008, 135, 510–523. [Google Scholar] [CrossRef] [Green Version]
- Lämmermann, T.; Bader, B.L.; Monkley, S.J.; Worbs, T.; Wedlich-Söldner, R.; Hirsch, K.; Keller, M.; Förster, R.; Critchley, D.R.; Fässler, R.; et al. Rapid leukocyte migration by integrin-independent flowing and squeezing. Nature 2008, 453, 51–55. [Google Scholar] [CrossRef]
- Wu, H.; De Leon, M.A.P.; Othmer, H.G. Getting in shape and swimming: The role of cortical forces and membrane heterogeneity in eukaryotic cells. J. Math. Biol. 2018, 1–32. [Google Scholar] [CrossRef]
- Driscoll, M.K.; McCann, C.; Kopace, R.; Homan, T.; Fourkas, J.T.; Parent, C.; Losert, W. Cell shape dynamics: From waves to migration. PLoS Comp. Biol. 2012, 8. [Google Scholar] [CrossRef] [Green Version]
- Friedl, P.; Alexander, S. Cancer Invasion and the Microenvironment: Plasticity and Reciprocity. Cell 2011, 147, 992–1009. [Google Scholar] [CrossRef] [Green Version]
- Van Zijl, F.; Krupitza, G.; Mikulits, W. Initial steps of metastasis: Cell invasion and endothelial transmigration. Mutat. Res. Mutat. Res. 2011, 728, 23–34. [Google Scholar] [CrossRef]
- Wolf, K.; Mazo, I.; Leung, H.; Engelke, K.; Andrian, U.H.V.; Deryugina, E.I.; Strongin, A.Y.; Bröcker, E.B.; Friedl, P. Compensation mechanism in tumor cell migration: Mesenchymal-amoeboid transition after blocking of pericellular proteolysis. J. Cell Biol. 2003, 160, 267–277. [Google Scholar] [CrossRef] [Green Version]
- Friedl, P.; Wolf, K. Tumour-cell invasion and migration: Diversity and escape mechanisms. Nat. Rev. Cancer 2003, 3, 362–374. [Google Scholar] [CrossRef]
- Zatulovskiy, E.; Tyson, R.; Bretschneider, T.; Kay, R.R. Bleb-driven chemotaxis of Dictyostelium cells. J. Cell Biol. 2014, 204, 1027–1044. [Google Scholar] [CrossRef] [Green Version]
- Tyson, R.A.; Zatulovskiy, E.; Kay, R.R.; Bretschneider, T. How blebs and pseudopods cooperate during chemotaxis. Proc. Nat. Acad. Sci. USA 2014, 111, 11703–11708. [Google Scholar] [CrossRef] [Green Version]
- Bergert, M.; Chandradoss, S.D.; Desai, R.A.; Paluch, E. Cell mechanics control rapid transitions between blebs and lamellipodia during migration. Proc. Nat. Acad. Sci. USA 2012, 109, 14434–14439. [Google Scholar] [CrossRef] [Green Version]
- Charras, G.T.; Paluch, E. Blebs lead the way: How to migrate without lamellipodia. Nat. Revs Molec Cell Biol. 2008, 9, 730–736. [Google Scholar] [CrossRef] [PubMed]
- Barry, N.P.; Bretscher, M.S. Dictyostelium amoebae and neutrophils can swim. Proc. Nat. Acad. Sci. USA 2010, 107, 11376–11380. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Othmer, H.G. Computational analysis of amoeboid swimming at low Reynolds number. J. Math. Biol. 2015, 72, 1893–1926. [Google Scholar] [CrossRef] [Green Version]
- Howe, J.D.; Barry, N.P.; Bretscher, M.S. How do amoebae swim and crawl? PLoS ONE 2013, 8, e74382. [Google Scholar] [CrossRef]
- Renkawitz, J.; Sixt, M. Mechanisms of force generation and force transmission during interstitial leukocyte migration. EMBO Rep. 2010, 11, 744–750. [Google Scholar] [CrossRef] [Green Version]
- Van Haastert, P.J.M. Amoeboid Cells Use Protrusions for Walking, Gliding and Swimming. PLoS ONE 2011, 6, e27532. [Google Scholar] [CrossRef] [Green Version]
- Parkinson, J.S. Bacterial chemotaxis: A new player in response regulator dephosphorylation. J. Bacteriol. 2003, 185, 1492–1494. [Google Scholar] [CrossRef] [Green Version]
- Xin, X.; Othmer, H.G. A Trimer of Dimers-Based Model for the Chemotactic Signal Transduction Network in Bacterial Chemotaxis. Bull. Math. Biol. 2012, 74, 2339–2382. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sasaki, A.T.; Janetopoulos, C.; Lee, S.; Charest, P.G.; Takeda, K.; Sundheimer, L.W.; Meili, R.; Devreotes, P.N.; Firtel, R.A. G protein-independent Ras/PI3K/F-actin circuit regulates basic cell motility. J. Cell Biol. 2007, 178, 185–191. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wessels, D.; Soll, D.; Knecht, D.; Loomis, W.; Lozanne, A.D.; Spudich, J. Cell Motility and Chemotaxis in Dictyostelium Amebae Lacking Myosin Heavy Chain. Dev. Biol. 1988, 128, 164–177. [Google Scholar] [CrossRef]
- Condeelis, J.; Segall, J.E. Intravital imaging of cell movement in tumours. Nat. Rev. Cancer 2003, 3, 921–930. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Nørrelykke, S.F.; Cox, E.C. Persistent cell motion in the absence of external signals: A search strategy for eukaryotic cells. PLoS ONE 2008, 3, e2093. [Google Scholar] [CrossRef] [Green Version]
- Devreotes, P.; Horwitz, A.R. Signaling networks that regulate cell migration. Cold Spring Harb. Perspect. Biol. 2015, 7, a005959. [Google Scholar] [CrossRef] [Green Version]
- Bretschneider, T.; Othmer, H.G.; Weijer, C.J. Progress and perspectives in signal transduction, actin dynamics, and movement at the cell and tissue level: Lessons from Dictyostelium. Interface Focus 2016, 6, 20160047. [Google Scholar] [CrossRef] [Green Version]
- Wennerberg, K.; Rossman, K.L.; Der, C.J. The Ras superfamily at a glance. J. Cell Sci. 2005, 118, 843–846. [Google Scholar] [CrossRef] [Green Version]
- Etienne-Manneville, S. Cdc42–the centre of polarity. J. Cell Sci. 2004, 117, 1291. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sanz-Moreno, V.; Marshall, C.J. The plasticity of cytoskeletal dynamics underlying neoplastic cell migration. Curr. Opin. Cell Biol. 2010, 22, 690–696. [Google Scholar] [CrossRef]
- Charest, P.G.; Firtel, R.A. Big roles for small GTPases in the control of directed cell movement. Biochem. J. 2007, 401, 377–390. [Google Scholar] [CrossRef] [PubMed]
- Katoh, K.; Kano, Y.; Amano, M.; Onishi, H.; Kaibuchi, K.; Fujiwara, K. Rho-kinase-mediated contraction of isolated stress fibers. J. Cell Biol. 2001, 153, 569–583. [Google Scholar] [CrossRef] [PubMed]
- Kolsch, V.; Charest, P.G.; Firtel, R.A. The regulation of cell motility and chemotaxis by phospholipid signaling. J. Cell Sci. 2008, 121, 551–559. [Google Scholar] [CrossRef] [Green Version]
- King, J.S.; Insall, R.H. Chemotaxis: Finding the way forward with Dictyostelium. Trends Cell Biol. 2009, 19, 523–530. [Google Scholar] [CrossRef]
- Othmer, H.G.; Schaap, P. Oscillatory cAMP signaling in the development of Dictyostelium discoideum. CMTS Theor. Biol. 1998, 5, 175–282. [Google Scholar]
- Chung, C.Y.; Firtel, R.A. PAKa, a putative PAK family member, is required for cytokinesis and the regulation of the cytoskeleton in Dictyostelium discoideum cells during chemotaxis. J. Cell Biol. 1999, 147, 559–576. [Google Scholar] [CrossRef] [Green Version]
- Jilkine, A.; Edelstein-Keshet, L. A comparison of mathematical models for polarization of single eukaryotic cells in response to guided cues. PLoS Comp. Biol. 2011, 7, e1001121. [Google Scholar] [CrossRef] [Green Version]
- Allard, J.; Mogilner, A. Traveling waves in actin dynamics and cell motility. Curr. Opin. Cell Biol. 2012, 25, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Sept, D.; Carlsson, A.E. Modeling large-scale dynamic processes in the cell: Polarization, waves, and division. Q. Rev. Biophys. 2014, 47, 221. [Google Scholar] [CrossRef] [PubMed]
- Condeelis, J.; Bresnick, A.; Demma, M.; Dharmawardhane, S.; Eddy, R.; Hall, A.L.; Sauterer, R.; Warren, V. Mechanisms of amoeboid chemotaxis: An evaluation of the cortical expansion model. Dev. Genet. 1990, 11, 333–340. [Google Scholar] [CrossRef] [PubMed]
- Postma, M.; Roelofs, J.; Goedhart, J.; Gadella, T.W.; Visser, A.J.; Haastert, P.J.V. Uniform cAMP stimulation of Dictyostelium cells induces localized patches of signal transduction and pseudopodia. Mol. Biol. Cell 2003, 14, 5019–5027. [Google Scholar] [CrossRef] [Green Version]
- Chen, L.; Janetopoulos, C.; Huang, Y.E.; Iijima, M.; Borleis, J.; Devreotes, P.N. Two phases of actin polymerization display different dependencies on PI(3,4,5)P3 accumulation and have unique roles during chemotaxis. Mol. Biol. Cell 2003, 14, 5028–5037. [Google Scholar] [CrossRef] [Green Version]
- Yan, J.; Mihaylov, V.; Xu, X.; Brzostowski, J.A.; Li, H.; Liu, L.; Veenstra, T.D.; Parent, C.A.; Jin, T. A Gβγ Effector, ElmoE, Transduces GPCR Signaling to the Actin Network during Chemotaxis. Dev. Cell 2012, 22, 92–103. [Google Scholar] [CrossRef] [Green Version]
- Varnum, B.; Edwards, K.B.; Soll, D.R. Dictyostelium Amebae Alter Motil. Differ. Response Increasing Versus Decreasing Temporal Gradients cAMP. J. Cell Biol. 1985, 101, 1–5. [Google Scholar] [CrossRef]
- Hall, A.L.; Schlein, A.; Condeelis, J. Relationship of pseudopod extension to chemotactic hormone-induced actin polymerization in amoeboid cells. J. Cell Biol. 1988, 37, 285–299. [Google Scholar] [CrossRef]
- Wessels, D.; Murray, J.; Soll, D.R. Behavior of Dictyostelium amoebae is regulated primarily by the temporal dynamic of the natural cAMP wave. Cell Motil. Cytoskelet. 1992, 23, 145–156. [Google Scholar] [CrossRef]
- Swanson, J.; Taylor, D.L. Local and spatially coordinated movements in Dictyostelium Discoideum Amoedae Chemotaxis. Cell 1982, 28, 225–232. [Google Scholar] [CrossRef]
- Chung, C.Y.; Funamoto, S.; Firtel, R.A. Signaling pathways controlling cell polarity and chemotaxis. Trends Biochem. Sci. 2001, 26, 557–566. [Google Scholar] [CrossRef]
- Takeda, K.; Sasaki, A.T.; Ha, H.; Seung, H.A.; Firtel, R.A. Role of phosphatidylinositol 3-kinases in chemotaxis in Dictyostelium. J. Biol. Chem. 2007, 282, 11874–11884. [Google Scholar] [CrossRef] [Green Version]
- Iijima, M.; Huang, Y.E.; Devreotes, P. Temporal and spatial regulation of chemotaxis. Dev. Cell 2002, 3, 469–478. [Google Scholar] [CrossRef] [Green Version]
- Parent, C.A.; Devreotes, P.N. A cell’s sense of direction. Science 1999, 284, 765–770. [Google Scholar] [CrossRef] [Green Version]
- Janetopoulos, C.; Jin, T.; Devreotes, P. Receptor-mediated activation of heterotrimeric G-proteins in living cells. Science 2001, 291, 2408–2411. [Google Scholar] [CrossRef] [Green Version]
- Janetopoulos, C.; Firtel, R.A. Directional sensing during chemotaxis. FEBS Lett. 2008, 582, 2075–2085. [Google Scholar] [CrossRef] [Green Version]
- Fets, L.; Nichols, J.M.; Kay, R.R. A PIP5 kinase essential for efficient chemotactic signaling. Curr. Biol. 2014, 24, 415–421. [Google Scholar] [CrossRef] [Green Version]
- Killich, T.; Plath, P.J.; Haß, E.C.; Xiang, W.; Bultmann, H.; Rensing, L.; Vicker, M.G. Cell movement and shape are non-random and determined by intracellular, oscillatory rotating waves in Dictyostelium amoebae. Biosystems 1994, 33, 75–87. [Google Scholar] [CrossRef]
- Killich, T.; Plath, P.J.; Wei, X.; Bultmann, H.; Rensing, L.; Vicker, M.G. The locomotion, shape and pseudopodial dynamics of unstimulated Dictyostelium cells are not random. J. Cell Sci. 1993, 106, 1005–1013. [Google Scholar]
- Vicker, M.G. Eukaryotic cell locomotion depends on the propagation of self-organized reaction–diffusion waves and oscillations of actin filament assembly. Exp. Cell Res. 2002, 275, 54–66. [Google Scholar] [CrossRef] [PubMed]
- Vicker, M.G. Reaction-diffusion waves of actin filament polymerization/depolymerization in Dictyostelium pseudopodium extension and cell locomotion. Biophys. Chem. 2000, 84, 87–98. [Google Scholar] [CrossRef]
- Bretschneider, T.; Anderson, K.; Ecke, M.; Müller-Taubenberger, A.; Schroth-Diez, B.; Ishikawa-Ankerhold, H.C.; Gerisch, G. The three-dimensional dynamics of actin waves, a model of cytoskeletal self-organization. Biophys. J. 2009, 96, 2888–2900. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schroth-Diez, B.; Gerwig, S.; Ecke, M.; Hegerl, R.; Diez, S.; Gerisch, G. Propagating waves separate two states of actin organization in living cells. HFSP J. 2009, 3, 412–427. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Arai, Y.; Shibata, T.; Matsuoka, S.; Sato, M.J.; Yanagida, T.; Ueda, M. Self-organization of the phosphatidylinositol lipids signaling system for random cell migration. Proc. Natl. Acad. Sci. USA 2010, 107, 12399–12404. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xiong, Y.; Huang, C.H.; Iglesias, P.A.; Devreotes, P.N. Cells navigate with a local-excitation, global-inhibition-biased excitable network. Proc. Nat. Acad. Sci. USA 2010, 107, 17079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nishikawa, M.; Hörning, M.; Ueda, M.; Shibata, T. Excitable signal transduction induces both spontaneous and directional cell asymmetries in the phosphatidylinositol lipid signaling system for eukaryotic chemotaxis. Biophys. J. 2014, 106, 723–734. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Masters, T.A.; Sheetz, M.P.; Gauthier, N.C. F-actin waves, actin cortex disassembly and focal exocytosis driven by actin-phosphoinositide positive feedback. Cytoskeleton 2016, 73, 180–196. [Google Scholar] [CrossRef] [PubMed]
- Miao, Y.; Bhattacharya, S.; Edwards, M.; Cai, H.; Inoue, T.; Iglesias, P.A.; Devreotes, P.N. Altering the threshold of an excitable signal transduction network changes cell migratory modes. Nat. Cell Biol. 2017, 19, 329–340. [Google Scholar] [CrossRef] [Green Version]
- Inagaki, N.; Katsuno, H. Actin waves: Origin of cell polarization and migration? Trends Cell Biol. 2017, 27, 515–526. [Google Scholar] [CrossRef] [Green Version]
- Gerisch, G. Self-organizing actin waves that simulate phagocytic cup structures. PMC Biophys. 2010, 3, 7. [Google Scholar] [CrossRef] [Green Version]
- Dai, J.; Ting-Beall, H.P.; Hochmuth, R.M.; Sheetz, M.P.; Titus, M.A. Myosin I contributes to the generation of resting cortical tension. Biophys. J. 1999, 77, 1168–1176. [Google Scholar] [CrossRef] [Green Version]
- Brzeska, H.; Pridham, K.; Chery, G.; Titus, M.A.; Korn, E.D. The association of myosin IB with actin waves in Dictyostelium requires both the plasma membrane-binding site and actin-binding region in the myosin tail. PLoS ONE 2014, 9, e94306. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cai, L.; Marshall, T.W.; Uetrecht, A.C.; Schafer, D.A.; Bear, J.E. Coronin 1B coordinates Arp2/3 complex and cofilin activities at the leading edge. Cell 2007, 128, 915–929. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ecke, M.; Prassler, J.; Tanribil, P.; Müller-Taubenberger, A.; Körber, S.; Faix, J.; Gerisch, G. Formins specify membrane patterns generated by propagating actin waves. Mol. Biol. Cell 2020. [Google Scholar] [CrossRef] [PubMed]
- Othmer, H.G. Nonlinear wave propagation in reacting systems. J. Math. Biol. 1976, 2, 133–163. [Google Scholar] [CrossRef]
- Mori, Y.; Jilkine, A.; Edelstein-Keshet, L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophys. J. 2008, 94, 3684–3697. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Haastert, P.J.; Keizer-Gunnink, I.; Kortholt, A. Coupled excitable Ras and F-actin activation mediates spontaneous pseudopod formation and directed cell movement. Mol. Biol. Cell 2017, 28, 922–934. [Google Scholar] [CrossRef] [PubMed]
- De León, M.A.A.P.; Othmer, H.G. A phosphoinositide-based model of actin waves in frustrated phagocytosis. PLoS Comput. Biol. 2020, submitted. [Google Scholar]
- Fukushima, S.; Matsuoka, S.; Ueda, M. Excitable dynamics of Ras triggers spontaneous symmetry breaking of PIP3 signaling in motile cells. J. Cell Sci. 2019, 132, jcs224121. [Google Scholar] [CrossRef] [Green Version]
- Shibata, T.; Nishikawa, M.; Matsuoka, S.; Ueda, M. Modeling the self-organized phosphatidylinositol lipid signaling system in chemotactic cells using quantitative image analysis. J. Cell Sci. 2012, 125, 5138–5150. [Google Scholar] [CrossRef] [Green Version]
- Taniguchi, D.; Ishihara, S.; Oonuki, T.; Honda-Kitahara, M.; Kaneko, K.; Sawai, S. Phase geometries of two-dimensional excitable waves govern self-organized morphodynamics of amoeboid cells. Proc. Natl. Acad. Sci. USA 2013, 110, 5016–5021. [Google Scholar] [CrossRef] [Green Version]
- Vazquez, F.; Matsuoka, S.; Sellers, W.R.; Yanagida, T.; Ueda, M.; Devreotes, P.N. Tumor suppressor PTEN acts through dynamic interaction with the plasma membrane. Proc. Natl. Acad. Sci. USA 2006, 103, 3633–3638. [Google Scholar] [CrossRef] [Green Version]
- Gerisch, G.; Schroth-Diez, B.; Müller-Taubenberger, A.; Ecke, M. PIP3 waves and PTEN dynamics in the emergence of cell polarity. Biophys. J. 2012, 103, 1170–1178. [Google Scholar] [CrossRef] [Green Version]
- Charest, P.G.; Firtel, R.A. Feedback signaling controls leading-edge formation during chemotaxis. Curr. Opin. Genet. Dev. 2006, 16, 339–347. [Google Scholar] [CrossRef] [PubMed]
- Sasaki, A.T.; Chun, C.; Takeda, K.; Firtel, R.A. Localized Ras signaling at the leading edge regulates PI3K, cell polarity, and directional cell movement. J. Cell Biol. 2004, 167, 505–518. [Google Scholar] [CrossRef] [PubMed]
- Tuosto, L.; Capuano, C.; Muscolini, M.; Santoni, A.; Galandrini, R. The multifaceted role of PIP2 in leukocyte biology. Cell. Mol. Life Sci. 2015, 72, 4461–4474. [Google Scholar] [CrossRef] [PubMed]
- Funamoto, S.; Meili, R.; Lee, S.; Parry, L.; Firtel, R.A. Spatial and temporal regulation of 3-phosphoinositides by PI 3-kinase and PTEN mediates chemotaxis. Cell 2002, 109, 611–623. [Google Scholar] [CrossRef] [Green Version]
- Iijima, M.; Devreotes, P. Tumor suppressor PTEN mediates sensing of chemoattractant gradients. Cell 2002, 109, 599–610. [Google Scholar] [CrossRef] [Green Version]
- Song, M.S.; Salmena, L.; Pandolfi, P.P. The functions and regulation of the PTEN tumour suppressor. Nat. Rev. Mol. Cell Biol. 2012, 13, 283–296. [Google Scholar] [CrossRef]
- Das, S.; Dixon, J.E.; Cho, W. Membrane-binding and activation mechanism of PTEN. Proc. Natl. Acad. Sci. USA 2003, 100, 7491–7496. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.O.; Yang, H.; Georgescu, M.M.; Cristofano, A.D.; Maehama, T.; Shi, Y.; Dixon, J.E.; Pandolfi, P.; Pavletich, N.P. Crystal structure of the PTEN tumor suppressor: Implications for its phosphoinositide phosphatase activity and membrane association. Cell 1999, 99, 323–334. [Google Scholar] [CrossRef] [Green Version]
- Lumb, C.N.; Sansom, M.S. Defining the membrane-associated state of the PTEN tumor suppressor protein. Biophys. J. 2013, 104, 613–621. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, H.N.; Yang, J.M.; Miyamoto, T.; Itoh, K.; Rho, E.; Zhang, Q.; Inoue, T.; Devreotes, P.N.; Sesaki, H.; Iijima, M. Opening the conformation is a master switch for the dual localization and phosphatase activity of PTEN. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rahdar, M.; Inoue, T.; Meyer, T.; Zhang, J.; Vazquez, F.; Devreotes, P.N. A phosphorylation-dependent intramolecular interaction regulates the membrane association and activity of the tumor suppressor PTEN. Proc. Natl. Acad. Sci. USA 2009, 106, 480–485. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nguyen, H.N.; Yang, J.M.; Afkari, Y.; Park, B.H.; Sesaki, H.; Devreotes, P.N.; Iijima, M. Engineering ePTEN, an enhanced PTEN with increased tumor suppressor activities. Proc. Natl. Acad. Sci. USA 2014, 111, E2684–E2693. [Google Scholar] [CrossRef] [Green Version]
- Walker, S.M.; Leslie, N.R.; Perera, N.M.; Batty, I.H.; Downes, C.P. The tumour-suppressor function of PTEN requires an N-terminal lipid-binding motif. Biochem. J. 2004, 379, 301–307. [Google Scholar] [CrossRef] [Green Version]
- Denning, G.; Jean-Joseph, B.; Prince, C.; Durden, D.; Vogt, P. A short N-terminal sequence of PTEN controls cytoplasmic localization and is required for suppression of cell growth. Oncogene 2007, 26, 3930–3940. [Google Scholar] [CrossRef] [Green Version]
- Khamviwath, V.; Hu, J.; Othmer, H.G. A continuum model of actin waves in D Ictyostelium discoideum. PLoS ONE 2013, 8, e64272. [Google Scholar] [CrossRef] [Green Version]
- Hoeller, O.; Toettcher, J.E.; Cai, H.; Sun, Y.; Huang, C.H.; Freyre, M.; Zhao, M.; Devreotes, P.N.; Weiner, O.D. Gβ regulates coupling between actin oscillators for cell polarity and directional migration. PLoS Biol. 2016, 14. [Google Scholar] [CrossRef] [Green Version]
- Rosales, C.; Uribe-Querol, E. Phagocytosis: A fundamental process in immunity. Biomed Res. Int. 2017, 2017. [Google Scholar] [CrossRef] [Green Version]
- Campanale, J.P.; Sun, T.Y.; Montell, D.J. Development and dynamics of cell polarity at a glance. J. Cell Sci. 2017, 130, 1201–1207. [Google Scholar] [CrossRef] [Green Version]
- Goryachev, A.B.; Pokhilko, A.V. Dynamics of Cdc42 network embodies a Turing-type mechanism of yeast cell polarity. FEBS Lett. 2008, 582, 1437–1443. [Google Scholar] [CrossRef] [Green Version]
- Muller, N.; Piel, M.; Calvez, V.; Voituriez, R.; Goncalves-Sá, J.; Guo, C.L.; Jiang, X.; Murray, A.; Meunier, N. A predictive model for yeast cell polarization in pheromone gradients. PLoS Comp. Biol. 2016, 12. [Google Scholar] [CrossRef] [Green Version]
- Chiou, J.G.; Balasubramanian, M.K.; Lew, D.J. Cell polarity in yeast. Annu. Rev. Cell Dev. Biol. 2017, 33, 77–101. [Google Scholar] [CrossRef]
- Chiou, J.G.; Ramirez, S.A.; Elston, T.C.; Witelski, T.P.; Schaeffer, D.G.; Lew, D.J. Principles that govern competition or co-existence in Rho-GTPase driven polarization. PLoS Comp. Biol. 2018, 14, e1006095. [Google Scholar] [CrossRef] [Green Version]
- Vendel, K.J.; Tschirpke, S.; Shamsi, F.; Dogterom, M.; Laan, L. Minimal in vitro systems shed light on cell polarity. J. Cell Sci. 2019, 132, jcs217554. [Google Scholar] [CrossRef] [Green Version]
- Woods, B.; Lew, D.J. Polarity establishment by Cdc42: Key roles for positive feedback and differential mobility. Small GTPases 2019, 10, 130–137. [Google Scholar] [CrossRef] [Green Version]
- Sartorel, E.; Ünlü, C.; Jose, M.; Massoni-Laporte, A.; Meca, J.; Sibarita, J.B.; McCusker, D. Phosphatidylserine and GTPase activation control Cdc42 nanoclustering to counter dissipative diffusion. Mol. Biol. Cell 2018, 29, 1299–1310. [Google Scholar] [CrossRef]
- Meca, J.; Massoni-Laporte, A.; Martinez, D.; Sartorel, E.; Loquet, A.; Habenstein, B.; McCusker, D. Avidity-driven polarity establishment via multivalent lipid–GTPase module interactions. EMBO J. 2019, 38, e99652. [Google Scholar] [CrossRef]
- Hu, J.; Kang, H.W.W.; Othmer, H.G. Stochastic analysis of reaction–diffusion processes. Bull. Math. Biol. 2013, 1–41. [Google Scholar] [CrossRef] [Green Version]
- Turner, M.S.; Sens, P.; Socci, N.D. Nonequilibrium raftlike membrane domains under continuous recycling. Phys. Rev. Lett. 2005, 95, 168301. [Google Scholar] [CrossRef] [Green Version]
- Richardson, G.; Cummings, L.J.; Harris, H.; O’Shea, P. Toward a mathematical model of the assembly and disassembly of membrane microdomains: Comparison with experimental models. Biophys. J. 2007, 92, 4145–4156. [Google Scholar] [CrossRef] [Green Version]
- Altschuler, S.J.; Angenent, S.B.; Wang, Y.; Wu, L.F. On the spontaneous emergence of cell polarity. Nature 2008, 454, 886–889. [Google Scholar] [CrossRef] [Green Version]
- Houk, A.R.; Jilkine, A.; Mejean, C.O.; Boltyanskiy, R.; Dufresne, E.R.; Angenent, S.B.; Altschuler, S.J.; Wu, L.F.; Weiner, O.D. Membrane tension maintains cell polarity by confining signals to the leading edge during neutrophil migration. Cell 2012, 148, 175–188. [Google Scholar] [CrossRef] [Green Version]
- Marco, E.; Wedlich-Soldner, R.; Li, R.; Altschuler, S.J.; Wu, L.F. Endocytosis optimizes the dynamic localization of membrane proteins that regulate cortical polarity. Cell 2007, 129, 411–422. [Google Scholar] [CrossRef] [Green Version]
- Meinhardt, H. Orientation of chemotactic cells and growth cones: Models and mechanisms. J. Cell Sci. 1999, 17, 2867–2874. [Google Scholar]
- Tang, M.; Wang, M.; Shi, C.; Iglesias, P.A.; Devreotes, P.N.; Huang, C.H. Evolutionarily conserved coupling of adaptive and excitable networks mediates eukaryotic chemotaxis. Nat. Commun. 2014, 5. [Google Scholar] [CrossRef] [Green Version]
- Umulis, D.; O’Connor, M.B.; Othmer, H.G. Robustness of Embryonic Spatial Patterning in Dros. melanogater. Curr. Top Dev. Biol. 2008, 81, 65–111. [Google Scholar]
- Otsuji, M.; Ishihara, S.; Co, C.; Kaibuchi, K.; Mochizuki, A.; Kuroda, S. A mass conserved reaction—Diffusion system captures properties of cell polarity. PLoS Comp. Biol. 2007, 3. [Google Scholar] [CrossRef] [Green Version]
- Mori, Y.; Jilkine, A.; Edelstein-Keshet, L. Asymptotic and bifurcation analysis of wave-pinning in a reaction-diffusion model for cell polarization. SIAM J. Appl. Math. 2011, 71, 1401–1427. [Google Scholar] [CrossRef] [Green Version]
- Edelstein-Keshet, L.; Holmes, W.R.; Zajac, M.; Dutot, M. From simple to detailed models for cell polarization. Philos. Trans. R. Soc. B 2013, 368, 20130003. [Google Scholar] [CrossRef] [Green Version]
- Dallon, J.C.; Othmer, H.G. A discrete cell model with adaptive signalling for aggregation of Dictyostelium discoideum. Phil. Trans. R. Soc. Lond. 1997, B352, 391–417. [Google Scholar] [CrossRef] [Green Version]
- Dallon, J.C.; Othmer, H.G. A continuum analysis of the chemotactic signal seen by Dictyostelium discoideum. J. Theor. Biol. 1998, 194, 461–483. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Cheng, Y.; Othmer, H.G. A model for direction sensing in Dictyostelium discoideum: Ras activity and symmetry breaking driven by a Gβγ-mediated, Gα2-Ric8—Dependent signal transduction network. PLoS Comp. Biol. 2016. [Google Scholar] [CrossRef] [Green Version]
- Takeda, K.; Shao, D.; Adler, M.; Charest, P.G.; Loomis, W.F.; Levine, H.; Groisman, A.; Rappel, W.J.; Firtel, R.A. Incoherent feedforward control governs adaptation of activated Ras in a eukaryotic chemotaxis pathway. Sci. Signal 2012, 5, ra2. [Google Scholar] [CrossRef] [Green Version]
- Kortholt, A.; Keizer-Gunnink, I.; Kataria, R.; Haastert, P.J.M. Ras activation and symmetry breaking during Dictyostelium chemotaxis. J. Cell Sci. 2013, 126, 4502–4513. [Google Scholar] [CrossRef] [Green Version]
- Kataria, R.; Xu, X.; Fusetti, F.; Keizer-Gunnink, I.; Jin, T.; Van Haastert, P.J.; Kortholt, A. Dictyostelium Ric8 is a nonreceptor guanine exchange factor for heterotrimeric G proteins and is important for development and chemotaxis. Proc. Nat. Acad. Sci. USA 2013, 110, 6424–6429. [Google Scholar] [CrossRef] [Green Version]
- Jin, T.; Zhang, N.; Long, Y.; Parent, C.A.; Devreotes, P.N. Localization of the G protein βγ complex in living cells during chemotaxis. Science 2000, 287, 1034–1036. [Google Scholar] [CrossRef] [Green Version]
- Postma, M.; Van Haastert, P.J. Mathematics of experimentally generated chemoattractant gradients. In Chemotaxis; Springer: Berlin, Germany, 2009; pp. 473–488. [Google Scholar]
- Nichols, J.M.; Veltman, D.; Kay, R.R. Chemotaxis of a model organism: Progress with Dictyostelium. Curr. Opin. Cell Biol. 2015, 36, 7–12. [Google Scholar] [CrossRef]
- Hohmann, T.; Dehghani, F. The cytoskeleton—A complex interacting meshwork. Cells 2019, 8, 362. [Google Scholar] [CrossRef] [Green Version]
- Artemenko, Y.; Axiotakis, L.; Borleis, J.; Iglesias, P.A.; Devreotes, P.N. Chemical and mechanical stimuli act on common signal transduction and cytoskeletal networks. Proc. Nat. Acad. Sci. USA 2016, 113, E7500–E7509. [Google Scholar] [CrossRef] [Green Version]
- Meili, R.; Ellsworth, C.; Lee, S.; Reddy, T.B.; Ma, H.; Firtel, R.A. Chemoattractant-mediated transient activation and membrane localization of Akt/PKB is required for efficient chemotaxis to cAMP in Dictyostelium. EMBO J. 1999, 18, 2092–2105. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, X.; Meier-Schellersheim, M.; Yan, J.; Jin, T. Locally controlled inhibitory mechanisms are involved in eukaryotic GPCR-mediated chemosensing. J. Cell Biol. 2007, 178, 141–153. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lebensohn, A.M.; Kirschner, M.W. Activation of the WAVE complex by coincident signals controls actin assembly. Mol. Cell 2009, 36, 512–524. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Veltman, D.M.; King, J.S.; Machesky, L.M.; Insall, R.H. SCAR knockouts in Dictyostelium: WASP assumes SCAR’s position and upstream regulators in pseudopods. J. Cell Biol. 2012, 198, 501–508. [Google Scholar] [CrossRef] [Green Version]
- Filić, V.; Marinović, M.; Faix, J.; Weber, I. The IQGAP-related protein DGAP1 mediates signaling to the actin cytoskeleton as an effector and a sequestrator of Rac1 GTPases. Cell. Mol. Life Sci. 2014, 71, 2775–2785. [Google Scholar] [CrossRef]
- Matsuoka, S.; Ueda, M. Mutual inhibition between PTEN and PIP3 generates bistability for polarity in motile cells. Nat. Commun. 2018, 9, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Jeon, T.J.; Lee, D.J.; Merlot, S.; Weeks, G.; Firtel, R.A. Rap1 controls cell adhesion and cell motility through the regulation of myosin II. J. Cell Biol. 2007, 176, 1021–1033. [Google Scholar] [CrossRef]
- Parent, C.A. Making all the right moves: Chemotaxis in neutrophils and Dictyostelium. Curr. Opin. Cell Biol. 2004, 16, 4–13. [Google Scholar] [CrossRef]
- Pramanik, M.K.; Iijima, M.; Iwadate, Y.; Yumura, S. PTEN is a mechanosensing signal transducer for myosin II localization in Dictyostelium cells. Genes Cells 2009, 14, 821–834. [Google Scholar] [CrossRef]
- Yoshioka, D.; Fukushima, S.; Koteishi, H.; Okuno, D.; Ide, T.; Matsuoka, S.; Ueda, M. Single-molecule imaging of PI (4,5) P2 and PTEN in vitro reveals a positive feedback mechanism for PTEN membrane binding. Commun. Biol. 2020, 3, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Bosgraaf, L.; Van Haastert, P.J.M. The regulation of myosin II in Dictyostelium. Eur. J. Cell Biol. 2006, 85, 969–979. [Google Scholar] [CrossRef] [Green Version]
- Sugiyama, T.; Pramanik, M.K.; Yumura, S. Microtubule-Mediated Inositol Lipid Signaling Plays Critical Roles in Regulation of Blebbing. PLoS ONE 2015, 10, e0137032. [Google Scholar] [CrossRef] [PubMed]
- Fernandez-Gonzalez, R.; Simoes, S.M.; Röper, J.C.; Eaton, S.; Zallen, J.A. Myosin II dynamics are regulated by tension in intercalating cells. Dev. Cell 2009, 17, 736–743. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Amato, C.; Thomason, P.A.; Davidson, A.J.; Swaminathan, K.; Ismail, S.; Machesky, L.M.; Insall, R.H. WASP restricts active Rac to maintain cells’ front-rear polarization. Curr. Biol. 2019, 29, 4169–4182. [Google Scholar] [CrossRef] [Green Version]
- Byrne, K.M.; Monsefi, N.; Dawson, J.C.; Degasperi, A.; Bukowski-Wills, J.C.; Volinsky, N.; Dobrzyński, M.; Birtwistle, M.R.; Tsyganov, M.A.; Kiyatkin, A.; et al. Bistability in the Rac1, PAK, and RhoA signaling network drives actin cytoskeleton dynamics and cell motility switches. Cell Syst. 2016, 2, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Sidani, M.; Wessels, D.; Mouneimne, G.; Ghosh, M.; Goswami, S.; Sarmiento, C.; Wang, W.; Kuhl, S.; El-Sibai, M.; Backer, J.M.; et al. Cofilin determines the migration behavior and turning frequency of metastatic cancer cells. J. Cell Biol. 2007, 179, 777–791. [Google Scholar] [CrossRef] [Green Version]
- Funk, J.; Merino, F.; Venkova, L.; Heydenreich, L.; Kierfeld, J.; Vargas, P.; Raunser, S.; Piel, M.; Bieling, P. Profilin and formin constitute a pacemaker system for robust actin filament growth. Elife 2019, 8. [Google Scholar] [CrossRef]
- Carlier, M.F.; Shekhar, S. Global treadmilling coordinates actin turnover and controls the size of actin networks. Nat. Rev. Mol. Cell Biol. 2017, 18, 389–401. [Google Scholar] [CrossRef]
- Bieling, P.; Weichsel, J.; McGorty, R.; Jreij, P.; Huang, B.; Fletcher, D.A.; Mullins, R.D. Force feedback controls motor activity and mechanical properties of self-assembling branched actin networks. Cell 2016, 164, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Gerisch, G. Chemotaxis in Dictyostelium. Annu. Rev. Physiol. 1982, 44, 535–552. [Google Scholar] [CrossRef]
- Faix, J.; Weber, I. A dual role model for active Rac1 in cell migration. Small GTPases 2013, 4, 110–115. [Google Scholar] [CrossRef] [Green Version]
- Yamazaki, D.; Itoh, T.; Miki, H.; Takenawa, T. srGAP1 regulates lamellipodial dynamics and cell migratory behavior by modulating Rac1 activity. Mol. Biol. Cell 2013, 24, 3393–3405. [Google Scholar] [CrossRef] [PubMed]
- Aspenström, P. BAR domain proteins regulate Rho GTPase signaling. Small GTPases 2014, 5, e972854. [Google Scholar] [CrossRef] [Green Version]
- Dalous, J.; Burghardt, E.; Müller-Taubenberger, A.; Bruckert, F.; Gerisch, G.; Bretschneider, T. Reversal of cell polarity and actin-myosin cytoskeleton reorganization under mechanical and chemical stimulation. Biophys. J. 2008, 94, 1063–1074. [Google Scholar] [CrossRef] [Green Version]
- Ruprecht, V.; Wieser, S.; Callan-Jones, A.; Smutny, M.; Morita, H.; Sako, K.; Barone, V.; Ritsch-Marte, M.; Sixt, M.; Voituriez, R.; et al. Cortical contractility triggers a stochastic switch to fast amoeboid cell motility. Cell 2015, 160, 673–685. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.J.; Berre, M.L.; Lautenschlaeger, F.; Maiuri, P.; Callan-Jones, A.; Heuzé, M.; Takaki, T.; Voituriez, R.; Piel, M. Confinement and low adhesion induce fast amoeboid migration of slow mesenchymal cells. Cell 2015, 160, 659–672. [Google Scholar] [CrossRef] [Green Version]
- Callan-Jones, A.; Ruprecht, V.; Wieser, S.; Heisenberg, C.P.; Voituriez, R. Cortical Flow-Driven Shapes of Nonadherent Cells. Phys. Rev. Lett. 2016, 116, 028102. [Google Scholar] [CrossRef]
- Keren, K.; Pincus, Z.; Allen, G.M.; Barnhart, E.L.; Marriott, G.; Mogilner, A.; Theriot, J.A. Mechanism of shape determination in motile cells. Nature 2008, 453, 475–481. [Google Scholar] [CrossRef] [Green Version]
- Stinner, B.; Bretschneider, T. Mathematical modelling in cell migration: Tackling biochemistry in changing geometries. Biochem. Soc. Trans. 2020, 48, 419–428. [Google Scholar] [CrossRef]
- Traynor, D.; Milne, J.L.; Insall, R.H.; Kay, R.R. Ca2+ signalling is not required for chemotaxis in Dictyostelium. EMBO J. 2000, 19, 4846–4854. [Google Scholar] [CrossRef] [Green Version]
- Lusche, D.F.; Wessels, D.; Soll, D.R. The effects of extracellular calcium on motility, pseudopod and uropod formation, chemotaxis, and the cortical localization of myosin II in Dictyostelium discoideum. Cell Motil. Cytoskelet. 2009, 66, 567–587. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Melchionda, M.; Pittman, J.K.; Mayor, R.; Patel, S. Ca2+/H+ exchange by acidic organelles regulates cell migration in vivo. J. Cell Biol. 2016, 212, 803–813. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tsai, F.C.; Seki, A.; Yang, H.W.; Hayer, A.; Carrasco, S.; Malmersjö, S.; Meyer, T. A polarized Ca2+, diacylglycerol and STIM1 signalling system regulates directed cell migration. Nat. Cell Biol. 2014, 16, 133–144. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Evans, J.H.; Falke, J.J. Ca2+ influx is an essential component of the positive-feedback loop that maintains leading-edge structure and activity in macrophages. Proc. Nat. Acad. Sci. USA 2007, 104, 16176–16181. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wei, C.; Wang, X.; Chen, M.; Ouyang, K.; Song, L.S.; Cheng, H. Calcium flickers steer cell migration. Nature 2009, 457, 901–905. [Google Scholar] [CrossRef] [Green Version]
- Valeyev, N.V.; Kim, J.S.; Heslop-Harrison, J.P.; Postlethwaite, I.; Kotov, N.V.; Bates, D.G. Computational modelling suggests dynamic interactions between Ca2+, IP3 and G protein-coupled modules are key to robust Dictyostelium aggregation. Mol. BioSyst. 2009, 5, 612–628. [Google Scholar] [CrossRef] [Green Version]
- Catacuzzeno, L.; Franciolini, F. Role of KCa3.1 channels in modulating Ca2+ oscillations during glioblastoma cell migration and invasion. Int. J. Mol. Sci. 2018, 19, 2970. [Google Scholar] [CrossRef] [Green Version]
- Cuddapah, V.A.; Robel, S.; Watkins, S.; Sontheimer, H. A neurocentric perspective on glioma invasion. Nat. Rev. Neurosci. 2014, 15, 455–465. [Google Scholar] [CrossRef] [Green Version]
- Bominaar, A.A.; Haastert, P.J.V. Phospholipase C in Dictyostelium discoideum. Identification of stimulatory and inhibitory surface receptors and G-proteins. Biochem. J. 1994, 297, 189–193. [Google Scholar] [CrossRef] [Green Version]
- Gresset, A.; Sondek, J.; Harden, T.K. The phospholipase C isozymes and their regulation. In Phosphoinositides I: Enzymes of Synthesis and Degradation; Springer: Berlin, Germany, 2012; pp. 61–94. [Google Scholar]
- Kortholt, A.; King, J.S.; Keizer-Gunnink, I.; Harwood, A.J.; Haastert, P.J.M.V. Phospholipase C regulation of phosphatidylinositol 3,4,5-trisphosphate-mediated chemotaxis. Mol. Biol. Cell 2007, 18, 4772–4779. [Google Scholar] [CrossRef] [Green Version]
- Falcke, M. Reading the patterns in living cells—The physics of Ca2+ signaling. Adv. Phys. 2004, 53, 255–440. [Google Scholar] [CrossRef]
- Cohen, R.; Torres, A.; Ma, H.T.; Holowka, D.; Baird, B. Ca2+ waves initiate antigen-stimulated Ca2+ responses in mast cells. J. Immunol. 2009, 183, 6478–6488. [Google Scholar] [CrossRef] [Green Version]
- Lechleiter, J.; Girard, S.; Peralta, E.; Clapham, D. Spiral Calcium wave propagation and annihilation in Xenopus laevis Oocytes. Science 1991, 252, 123–126. [Google Scholar] [CrossRef]
- Hu, J.; Khamviwath, V.; Othmer, H. A Stochastic Model for Actin Waves in Eukaryotic Cells. bioRxiv 2019. [Google Scholar] [CrossRef] [Green Version]






















© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Felix, B.; Othmer, H.G. The Roles of Signaling in Cytoskeletal Changes, Random Movement, Direction-Sensing and Polarization of Eukaryotic Cells. Cells 2020, 9, 1437. https://doi.org/10.3390/cells9061437
Cheng Y, Felix B, Othmer HG. The Roles of Signaling in Cytoskeletal Changes, Random Movement, Direction-Sensing and Polarization of Eukaryotic Cells. Cells. 2020; 9(6):1437. https://doi.org/10.3390/cells9061437
Chicago/Turabian StyleCheng, Yougan, Bryan Felix, and Hans G. Othmer. 2020. "The Roles of Signaling in Cytoskeletal Changes, Random Movement, Direction-Sensing and Polarization of Eukaryotic Cells" Cells 9, no. 6: 1437. https://doi.org/10.3390/cells9061437
APA StyleCheng, Y., Felix, B., & Othmer, H. G. (2020). The Roles of Signaling in Cytoskeletal Changes, Random Movement, Direction-Sensing and Polarization of Eukaryotic Cells. Cells, 9(6), 1437. https://doi.org/10.3390/cells9061437





