1. Introduction
The rapid development of single-cell RNA sequencing technologies allows us to study tissue heterogeneity at the cellular level [
1,
2]. Cell clustering and annotation are two fundamental steps in analyzing single-cell RNA-seq data [
3]. For example, exploring cell-to-cell interactions and gene-to-gene interactions are often based on specific cell types [
4,
5]. In the past few years, a large volume of single-cell transcriptome unsupervised clustering algorithms have emerged based on the similarity of gene expression patterns [
6,
7,
8,
9]. However, in the absence of a unified standard, the clustering results of different algorithms usually show a little degree of overlap and even vary widely [
10]. The typical cell annotation method finds differential expression genes between the identified clusters [
11] and then annotates cells by leveraging the function of these differential expression genes [
12]. However, the process can be complicated by the low sensitivity of the well-known marker genes. In addition, as the number of mapped cells increases, such as the Human Cell Project (HCA) [
13] and Mouse Organogenesis Cell Atlas (MOCA) [
14], this method of cell annotation also becomes a highly labor-intensive task.
Recently, researchers have tried to use prior information to guide cell clustering and annotation on the target dataset (see
Table 1). For example, Zhang et al. proposed CellAssign, a probabilistic model that leverages prior knowledge of cell type marker genes to annotate single-cell RNA sequencing data into predefined or de novo cell types [
15]. Similarly, Pliner et al. proposed Garnett, a tool for rapidly annotating cell types in single-cell transcriptional profiling datasets, based on an interpretable, hierarchical markup language of cell type specific marker genes [
16]. However, these two methods require users to provide a list of marker genes corresponding to the cell types in advance. For non-experts, this is not a trivial matter, because ample knowledge of the marker genes usually requires a large amount of literature review and long-term accumulation.
With more and more large-scale, well-annotated datasets becoming available, it is feasible to apply supervised classification techniques for categorizing cells into known cell types [
17,
18]. For example, SingleR performs cell type classification by calculating the Spearman correlation between query cells and one representative gene expression per cell type in reference datasets [
19]; Moana classifies cells in the target data by using a support-vector-machine (SVM) with a linear kernel that is well-trained on the labeled source data [
20]. In this way, much time and effort are saved in matching marker genes. However, although classification techniques do not require domain knowledge of the cell types, they usually require the reference dataset to cover all cell types contained in the target dataset, thus limiting the ability to discover novel cell types. Similar problems also arise in mapping strategies. To illustrate, scmapCluster assigns cell types by calculating the maximum similarity between unannotated cells and the cluster centers of well-annotated cell types in the reference dataset [
21]. Although scmapCluster can predict certain cells as "unassigned" when the similarity score is lower than a predefined threshold, subjectively selecting threshold parameters, coupled with the failure to consider the global structure of clusters, usually makes the annotation results less satisfactory. In addition, technical biases, such as batch effects, also invalidate these projection algorithms [
22].
Deep learning has achieved impressive performance over traditional machine learning algorithms on many bioinformatics tasks over the past few years [
23]. Lopez et al. developed a ready-to-use scalable framework, scVI, for the probabilistic representation and analysis of gene expression in single cells [
24]. Xu et al. developed scANVI, a semi-supervised variant of scVI designed to leverage any available cell state annotations for annotating new datasets [
25]. However, the extra latent space assumption like mixture Gaussian distribution cannot perfectly portray the low-dimensional manifolds where data resides most of the time. Moreover, variational inference requires advanced optimization techniques; otherwise, the objective function can easily fall into local extreme values. Hu et al. developed ItClust, an iterative transfer learning algorithm with deep neural network for scRNA-seq clustering [
26]. ItClust learns cell type knowledge from well-annotated source datasets, but it also leverages information in the target dataset to make it less dependent on the quality of the source dataset. Nevertheless, transfer learning based on cluster centers is easily infected by batch effects, resulting in false cell type annotations. When the target dataset holds the cell types that do not exist in the source dataset, it is also difficult for ItClust to peform accurate discovery. Furthermore, neither scANVI nor ItClust considers the affinity constraint of pairwise similar cells, which can often improve the effect of cell clustering and annotation [
7].
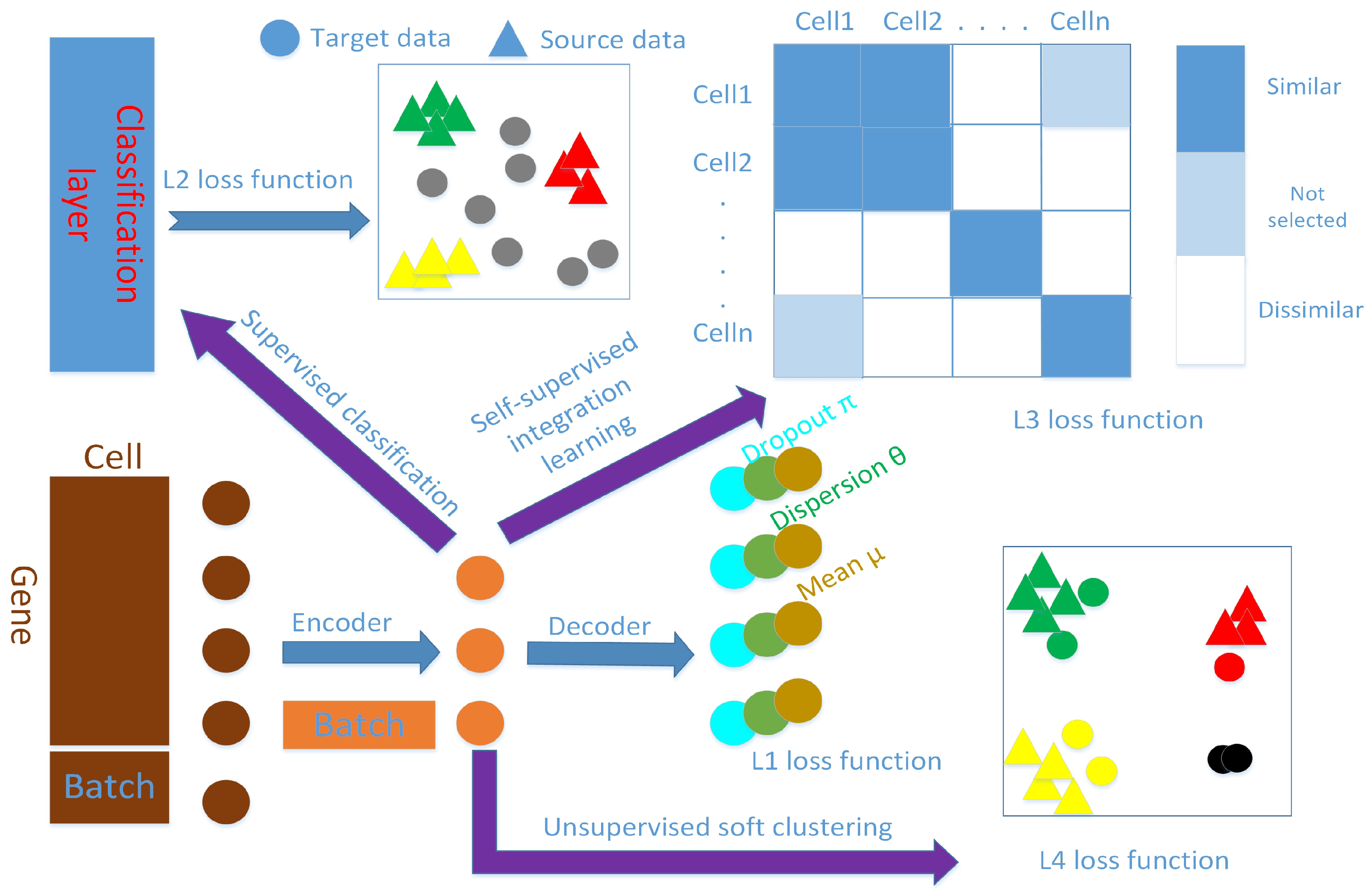
In this paper, we combine deep learning technique with statistical modeling and propose an end-to-end single-cell RNA-seq data supervised clustering and annotation framework, named scAnCluster, based on our previous unsupervised clustering works scDMFK [
6] and scziDesk [
7]. The three methods adhere to similar modeling concepts, namely simultaneous denoising, dimensionality reduction and clustering. The difference is that the main purpose of scAnCluster is to implement automatic cell type annotation based on clustering. In addition to transferring cell type knowledge, scAnCluster also needs to balance the importance of the label information on the reference data and the unique characteristics of the target data. In this regard, we dismember this semi-supervised learning task as the integration of supervised learning, self-supervised learning and unsupervised learning. First, we model the count data distribution in the mixed annotated source dataset and unannotated target dataset. Then we use the deep autoencoder to learn the low-dimensional manifold where the distribution parameters are located, giving us the joint latent representation of different datasets. Second, we learn a classifier on the well-labeled data to enhance and aggregate each known cell type, at the same time equipping the latent space with basic cluster recognition ability. Third, we calculate the pairwise similarity among all cells and obtain pairwise pseudo-labels by determining whether each cell pair is similar or not, thereby constructing a pairwise classification task to fuse labeled and unlabeled cells. This step uses a meta-learning technique and can be regarded as a proxy for clustering, which also provides guidance for subsequent clustering. Finally, we use an iterative soft k-means model with entropy regularization based on spherical distance to perform clustering on the mixed datasets. After that, we can assign known cell types in the source dataset to those clusters with a high confidence level. In order to prevent overfitting and destroying the global structure of the data, our training process carries the decoder for data reconstruction and denoising from beginning to end. In addition, our model only requires users to provide the total cluster number of the joint datasets, and it imposes no constraints or restrictions on the number of clusters for the target dataset to be annotated.
2. Materials and Methods
2.1. Zero-Inflated Negative Binomial Distribution for scRNA-seq Data Modeling
Assume a single-cell RNA-seq data matrix is
where
n represents total cell number, and
m refers to the gene feature number. Furthermore,
x includes the source dataset matrix
and target dataset matrix
. The source dataset is well labeled with cell type number
, and its label set is
. Our goal is to automatically cluster the unlabeled target dataset by mixing two datasets together and leveraging the known label information in the source dataset. We construct the one-hot encoded batch matrix
where its non-zero element position in each row
represents the corresponding batch index, namely source dataset and target dataset. Since the mean of gene expression data is usually larger than its dispersion [
27], we assume that this discrete count data follow negative binomial distribution (NB), as
Based on the low sensitivity of massive genes, namely “dropout” events, we use mass density
to account for dropout probability of the
j-th gene in the
i-th cell, thereby making data distribution a natural mixture distribution, i.e., zero-inflated negative binomial distribution (ZINB), as
Complex gene-to-gene interactions do not completely free the parameter sets
from one another. Furthermore, they are actually located on an inenarrable low-dimensional manifold. Therefore, we use the deep autoencoder representation to approximate this parameter space and estimate three groups of parameters by three output layers in a manner similar to that of the DCA and scziDesk model [
7,
28]. To take the batch effects into account, we merge the expression data matrix
x with batch matrix
b as the input of the encoder network. Similarly, we also concatenate the latent space representation matrix
z and batch matrix
b as the input of the decoder network to output the estimation of batch-related parameters
. This approach is interpretable because it is equivalent to treating the batch effect as a covariate and using the nonlinear regression capability of the neural network to eliminate this part of the deviation. Finally, we take the negative log-likelihood function of ZINB distribution as data reconstruction loss, as
2.2. Supervised Classification on Well-Labeled Source Dataset
Before aligning and integrating the joint low-dimensional representation of the source dataset and target dataset, we should first ensure that cells from the same type in the source dataset are aggregated together [
29]. In other words, the latent space representation
of the cells in the source dataset should be clearly separable. To accomplish this, we connect a classification layer to the last layer of the encoder network. Its node number is the known cell type number in the source dataset
, and its activation function is selected as the softmax function. For convenience, we assume that the one-hot matrix form of label vector
is
and that the classification prediction probability matrix is
. We take the classification loss function as the standard cross-entropy function, which only operates on the well-labeled source dataset.
This step actually also ensures that the encoder can map cells in the target dataset that are close to the expression pattern of known cell types into the vicinity of the corresponding cell type location.
2.3. Self-Supervised Integration Learning on the Union of Source and Target Dataset
To transfer the cell type label of the source dataset to the unlabeled target dataset, we construct a pairwise-classification task on their union by determining whether the cell pair is similar or not, which can be regarded as the surrogate for clustering [
30,
31]. Specifically, we first use the joint latent space representation
z to compute the pairwise similarity matrix
S measured by the cosine distance, as
Then we iteratively go through a self-supervised meta-learning step to refine these similarities. Technically, we construct a pseudo-labeled matrix by applying dynamic thresholds on a similarity matrix
S:
where
. We use the dynamic upper threshold
and lower threshold
to determine whether the cell pair is similar or dissimilar. Furthermore, because we have the gold standard label information on the source dataset, which can be treated as prior knowledge to guide clustering, we can extend the self-labeled matrix
as,
where
y is defined as
on the source dataset and unknown on the target dataset. We then combine this self-labeled matrix
with the similarity matrix
S to compute the self-supervised loss
, as
It contains items for both the labeled and unlabeled subsets, using the given labels and generated pseudo-labels, thus avoiding the forgetting the issue that may arise with a sequence approach. In the specific implementation, we gradually decrease the value, while increasing the value during the training process. This step allows us to gradually select more cell pairs to participate in the similarity fusion training. As the thresholds change, we train our model from easy-to-classify cell pairs to hard-to-classify cell pairs iteratively to pursue and bootstrap the cluster-friendly joint latent space representation. When , we stop this iterative similarity fusion process. Most importantly, as the training iterations proceed, target cells that are similar to the cell types in the source dataset can gradually move to the vicinity of where they are located, while those target cells that are dissimilar to source cells would naturally form new diverse populations due to their inherent high similarity in the target dataset.
2.4. Unsupervised Soft Clustering Upon the Union of Source and Target Dataset
After self-supervised fusion training, we expected to learn a joint latent space representation
z suitable for clustering. That is, similar cells are aggregated together and dissimilar cells are separated from each other. Therefore, in the latent space, in order to further enforce cluster compactness, we propose a soft k-means clustering model with entropy regularization to perform cell clustering [
32]. Suppose total
k clusters with cluster centers
; then the optimization objective function for clustering is
where
is one kind of distance measurement. In the last section, we used the cosine distance for similarity calculation. Since this soft clustering was found to work well under sphere distance, rather than
distance in scziDesk or
adaptive distance in scDMFK, between
z and
v, we assume that all
and
have a unity norm. Then the above clustering model can be re-written as a dot product, as follows:
In fact, when the
z and
v are known,
has a closed form, which is
In this paper, the default value of
is 1. We can see that weight
is a decreasing function of distance between
and
. We give greater attention to cells close to the cluster center. To a certain extent,
also gives the membership probability that the
i-th cell
belongs to the
j-th cluster(
). As such, we can assign cluster labels to each cell according to the maximum membership probability. Finally, we give the following clustering loss for training, as
This continuous loss function can benefit from the efficiency of stochastic gradient descent.
2.5. Model Training Strategy and Parameter Setting
We summarize our end-to-end clustering model below: denoising autoencoder for estimating data distribution parameters, deep supervised classification for aggregating cells of the same type in the source dataset, deep self-supervised pairwise classification with dynamic similarity threshold for distinguishing highly similar and dissimilar cell pairs, and deep soft k-means clustering with cosine distance for refining clusters. In this paper, we train the whole multi-task model by matching different loss functions in an orderly manner. First, we pretrain the model by uniting
and
loss, as
Then we turn to similarity fusion training by combining
and
loss, as
where
is a weight hyperparameter that controls relative balance between two loss parts. Finally, we perform cell clustering training by assembling
and
loss, as
Similarly,
is also a weight hyperparameter. Without any preference, we expect that the contribution of each part of the loss to the gradients is at the same level. In the specific algorithm implementation,
is averaged over all cells and genes, while
and
are averaged over all cells such that
and
are naturally larger than
. We use the grid search method to determine these two hyperparameter values from the candidate sets
. Our guiding principle holds that the weights can make the loss function values of both parts the same order of magnitude.
Supplementary Table S1 gives their setting in all experiments. We add reconstruction loss
to each training step because we want to preserve the global structure of the data through it, which can also avoid model overfitting. We implement our method in Python3 with Tensorflow software. The two layers of the encoder are sized as 256 and 64, respectively, and the decoder has the reverse structure of the encoder. The bottleneck layer (namely, the latent space) has a size of 32. The training minibatch size is 256, and the stochastic gradient optimizer is Adam with learning rate 1e-4. The epochs of pretraining and fusion training are 500 and 100, respectively. The dynamic thresholds
and
are set to
and
, respectively. After similarity fusion training, we take out the latent space representation and use the standard k-means algorithm to obtain cluster centers as the initial values of
. We stop the clustering training when the cluster label assignments no longer change. The schematic diagram is shown in
Figure 1, and we name our method scAnCluster. An implementation of scAnCluster is available from
https://github.com/xuebaliang/scAnCluster.
2.6. Cell Type Annotation for Target Dataset
After completing the clustering, we obtained the cluster label of each cell by the union of the source dataset and target dataset. In order to leverage the cell type information in the source dataset to help annotate each cluster, we define the cluster clarity score. For cluster i, we can summarize the cell composition of the source dataset contained in this cluster. When the cell number of a given cell type in the i-th cluster is larger than half of its total number in the source dataset, we set it as the candidate reference cell type of the i-th cluster and record its corresponding percentage (). Finally, we take the reference cell type corresponding to the largest percentage as the annotation of the i-th cluster, and this largest percentage is regarded as the clarity score of i-th cluster. In the meantime, we can also annotate all cells in the target dataset contained in the i-th cluster. For those clusters that cannot be annotated through the information of the source dataset, namely "unassigned", we supply their cluster labels, and the user can further apply differential expression analysis and find highly expressed marker genes to annotate these clusters.
2.7. Data Preprocessing
All datasets we used have passed through quality control and are in the formats of counts. We unify raw cell type annotation by Cell Ontology [
22,
33], a structured controlled vocabulary for cell types. We merge the source dataset and target dataset according to their shared gene names. We first normalize the total expression value of each cell to its median value and then take a natural log-transformation on data. Then we select the top 1000 highly variable genes according to their normalized dispersion value ranking. Finally we transform the data into z-score data. That is, each selected gene has zero mean and unit variance. All three steps can be completed using the Scanpy package [
34]. We take the preprocessed data as neural network input and use its corresponding original count data for modeling.
4. Discussion and Conclusions
Single-cell transcriptome sequencing technologies have brought unprecedented capabilities to the study of tissue heterogeneity. Two essential analytical procedures are cell clustering and annotation, and they have always been very challenging and labor-intensive. In this paper, based on scDMFK and scziDesk, we use the available cell label information to develop a novel deep learning model that integrates single-cell clustering and annotation. Our method, scAnCluster, has the following highlights. Firstly, our model can perform both cell clustering and annotation for intra-datasets, as well as for inter-datasets. Secondly, our model shows strong discriminatory power in discovering novel cell types that are absent in the reference data. Thirdly, our model is end-to-end so that it does not require intensive feature engineering. It incorporates some mainstream deep learning techniques, including supervised learning, self-supervised learning and unsupervised learning. In order to better demonstrate the robustness and reliability of our method, we also implemented several groups of control experiments.
4.1. Influence of Highly Variable Genes Number
Single-cell RNA-seq data is usually highly noisy. Consequently, selecting some informative, highly variable genes for clustering analysis helps to improve the clustering performance. During the experiments in the text, we selected 1000 highly variable genes by default. To illustrate the effect of highly variable genes on the results, we conducted control experiments on two groups of inter-datasets. The number of highly variable genes changed from 500 and 1000 to 1500 and 2000. From the results in
Figure 6A, we find that the ARI value of 500 genes on the “Macosko+Shekhar” dataset is significantly lower than that of the other three conditions, while the difference of annotation accuracy is not evident. For “Baron_human+Enge”, a similar phenomenon occurs with 500 genes in terms of ARI value, but the selection of 1000 genes is unique for annotation accuracy. Therefore, considering the calculation time and memory limitations, we selected 1000 highly variable genes by default for clustering analysis. Certainly, for complex datasets with massive cell types, we also recommend that users select more highly variable genes for clustering analysis.
4.2. Influence of Total Cluster Number
Inferring the number of categories in the dataset has always been a challenging problem for statisticians and machine learning researchers. However, in single-cell clustering analysis, it seems that confusion over how to choose cell type number is essentially settled since this decision depends on the investigator’s concerns and aims. In previous experiments, we took the total cell type number by default as the true one of the whole mixed dataset and recorded it as
k. To explore the impact of the total number of cell types on the ARI and annotation accuracy, we let the total cell type number to be selected from
and implemented experiments on two groups of inter-datasets. From the results in
Figure 6B, the changes in ARI and annotation accuracy values are relatively small, fully demonstrating the robustness of scAnCluster to total cell type number. Therefore, we recommend that users employ a rough estimation of the cell type number on the mixed dataset before applying our method.
4.3. Importance of Three Parts of Learning Strategies
So far, we have not discussed the contribution and significance of supervised learning, self-supervised learning and unsupervised learning in our model because in previous experiments, we always combined them together for training. In order to show the indispensability of these three parts of the learning process, we consider the method of controlling variables, as a kind of loss/gain-of-function exercise, by removing one of the three parts and retaining the other two parts for training. From the results on simulation datasets, when we remove supervised learning, which is classification learning on the source dataset, the ARI and annotation accuracy values seriously collapse (see
Figure 7). Similarly, when we remove the self-supervised similarity fusion training on the mixed datasets, these two evaluation indicators also show a significant decline. In the real data of “Macosko” and “Shekhar”, we can see that removing unsupervised soft clustering training will make clustering and annotations less ideal (see
Figure 6C). For “Baron_human” and “Enge”, throwing away any of the three parts will lead to unsatisfactory results (see
Figure 6C). Further, we also show the results of these comparative experiments on the “Baron_human + Enge” dataset with a two-dimensional visualization in
Figure 8. Specifically, we use UMAP (Uniform Manifold Approximation and Projection) [
44] to reduce the latent space representation obtained in each case to a two-dimensional plane. In order to distinguish these two datasets, we have also produced corresponding visualizations of the batch index. We focused on the four main cell types common to both datasets, namely “type B pancreatic cell”, “pancreatic A cell”, “pancreatic ductal cell” and “pancreatic acinar cell”. When combining the three learning techniques, these four cell types in the “Enge” dataset are well mapped near the corresponding cell types in the “Baron_human” dataset. However, removing supervised classification learning will result in improper annotation of “type B pancreatic cell”, “pancreatic A cell” and “pancreatic ductal cell”. A similar phenomenon also occurred when self-supervised similarity learning was removed. When eliminating unsupervised soft clustering learning, type B pancreatic cells and pancreatic A cells in the “Enge” dataset could not be well separated, which affected cell type annotations. Overall, the three parts of our model are complementary. Supervised classification learning affords the latent space needed to obtain basic discriminative ability, thus guaranteeing the smooth progress of annotation. The use of self-supervised learning for bootstrapping the cell latent representation trades off the representation quality with its generality for discovering novel cell types. Jointly carrying out unsupervised clustering on both labeled reference data and unlabeled target data can reinforce the annotation task, while avoiding forgetting. When they function together, they can facilitate cell clustering and annotation more accurately and convincingly.
Based on previous discussion, our method, scAnCluster, whether in simulation data or real data analysis, has shown competitive performance compared to that of each existing single-cell RNA-seq supervised clustering algorithm tested. In the simulation experiments, our method is robust to various settings of dataset size, cluster size and dropout probability. On intra-datasets and inter-datasets, our method shows a strong ability to explore and discover new cell types with the only partial overlap in cell type compositions. Such evidence ensures that our method will stand out among existing single-cell clustering and annotation algorithms. The combination experiments of multiple datasets from the same tissue also validate the stability and robustness of our method for integrating data generated by different sequencing technologies. In addition, although scAnCluster is not as fast as scmap, it still has an advantage over ItClust and scANVI in calculation efficiency (see
Supplementary Table S3). Considering the running speed, clustering and annotation performance, scAnCluster is an ideal choice for users. With the rise and maturity of single-cell multiomics sequencing technologies, we can recommend applying our algorithm ideas to the design of integrated multiomics analysis methods. Of course, our method also has some potential faults. For example, the strong batch effect between source dataset and target dataset may not be completely eliminated by simply concatenating the gene expression data with the batch ID. Therefore, we suggest that users take advantage of other scRNA-seq customized batch correction softwares, such as pagoda2 [
45] (see
Supplementary Table S4), before using our method.