The Consequences of Budding versus Binary Fission on Adaptation and Aging in Primitive Multicellularity
Abstract
:1. Introduction
2. Materials and Methods
2.1. Population Growth and Reproduction
2.2. Mutations
2.3. Aging
2.4. Resource Sharing
2.5. Noise
2.6. Code
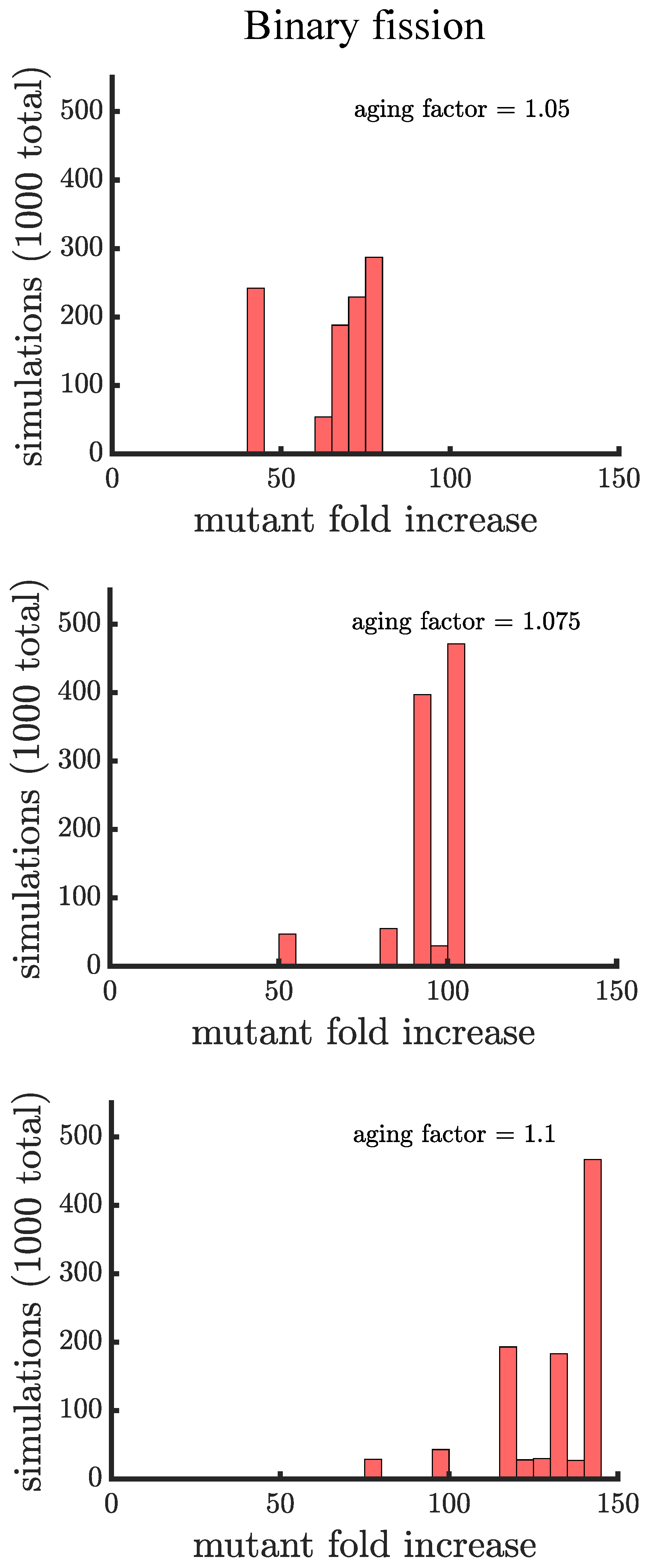
3. Results
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Noise Versus Aging

Appendix B. Defining Age in Binary Fission Populations

Appendix C. Robustness of Findings to Mutant Growth Rate Differences



Appendix D. Robustness of Findings to When the Mutation Is Introduced




Appendix E. Robustness of Findings to Carrying Capacity


Appendix F. Age Structure for Different Populations

References
- Maynard Smith, J.; Szathmary, E. The Major Transitions in Evolution; Oxford University Press: New York, NY, USA, 1997. [Google Scholar]
- Grosberg, R.K.; Strathmann, R.R. The evolution of multicellularity: A minor major transition? Annu. Rev. Ecol. Evol. Syst. 2007, 38, 621–654. [Google Scholar] [CrossRef] [Green Version]
- Rokas, A. The origins of multicellularity and the early history of the genetic toolkit for animal development. Annu. Rev. Genet. 2008, 42, 235–251. [Google Scholar] [CrossRef] [Green Version]
- Domazet-Lošo, T.; Tautz, D. Phylostratigraphic tracking of cancer genes suggests a link to the emergence of multicellularity in metazoa. BMC Biol. 2010, 8, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Aktipis, C.A.; Boddy, A.M.; Jansen, G.; Hibner, U.; Hochberg, M.E.; Maley, C.C.; Wilkinson, G.S. Cancer across the tree of life: Cooperation and cheating in multicellularity. Philos. Trans. R. Soc. Biol. Sci. 2015, 370, 20140219. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Libby, E.; Ratcliff, W.C. Ratcheting the evolution of multicellularity. Science 2014, 346, 426–427. [Google Scholar] [CrossRef] [PubMed]
- Rebolleda-Gómez, M.; Travisano, M. The cost of being big: Local competition, importance of dispersal, and experimental evolution of reversal to unicellularity. Am. Nat. 2018, 192, 731–744. [Google Scholar] [CrossRef]
- Rebolleda-Gómez, M.; Travisano, M. Adaptation, chance, and history in experimental evolution reversals to unicellularity. Evolution 2019, 73, 73–83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Libby, E.; Conlin, P.L.; Kerr, B.; Ratcliff, W.C. Stabilizing multicellularity through ratcheting. Philos. Trans. R. Soc. Biol. Sci. 2016, 371, 20150444. [Google Scholar] [CrossRef] [Green Version]
- Duran-Nebreda, S.; Solé, R. Emergence of multicellularity in a model of cell growth, death and aggregation under size-dependent selection. J. R. Soc. Interface 2015, 12, 20140982. [Google Scholar] [CrossRef]
- Libby, E.; Ratcliff, W.; Travisano, M.; Kerr, B. Geometry shapes evolution of early multicellularity. PLoS Comput. Biol. 2014, 10, e1003803. [Google Scholar] [CrossRef] [Green Version]
- Jacobeen, S.; Pentz, J.T.; Graba, E.C.; Brandys, C.G.; Ratcliff, W.C.; Yunker, P.J. Cellular packing, mechanical stress and the evolution of multicellularity. Nat. Phys. 2018, 14, 286–290. [Google Scholar] [CrossRef] [Green Version]
- Ratcliff, W.C.; Herron, M.; Conlin, P.L.; Libby, E. Nascent life cycles and the emergence of higher-level individuality. Philos. Trans. R. Soc. Biol. Sci. 2017, 372, 20160420. [Google Scholar] [CrossRef] [Green Version]
- Staps, M.; van Gestel, J.; Tarnita, C.E. Emergence of diverse life cycles and life histories at the origin of multicellularity. Nat. Ecol. Evol. 2019, 3, 1197–1205. [Google Scholar] [CrossRef] [Green Version]
- Pentz, J.T.; Márquez-Zacarías, P.; Bozdag, G.O.; Burnetti, A.; Yunker, P.J.; Libby, E.; Ratcliff, W.C. Ecological advantages and evolutionary limitations of aggregative multicellular development. Curr. Biol. 2020, 30, 4155–4164. [Google Scholar] [CrossRef]
- Pichugin, Y.; Peña, J.; Rainey, P.B.; Traulsen, A. Fragmentation modes and the evolution of life cycles. PLoS Comput. Biol. 2017, 13, e1005860. [Google Scholar] [CrossRef] [Green Version]
- Libby, E.; Rainey, P.B. Eco-evolutionary feedback and the tuning of proto-developmental life cycles. PLoS ONE 2013, 8, e82274. [Google Scholar] [CrossRef] [PubMed]
- Black, A.J.; Bourrat, P.; Rainey, P.B. Ecological scaffolding and the evolution of individuality. Nat. Ecol. Evol. 2020, 4, 426–436. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.; Shik, J.; Boomsma, J. The evolution of multicellular complexity: The role of relatedness and environmental constraints. Proc. R. Soc. 2020, 287, 20192963. [Google Scholar] [CrossRef] [PubMed]
- Niklas, K.J.; Newman, S.A. The origins of multicellular organisms. Evol. Dev. 2013, 15, 41–52. [Google Scholar] [CrossRef]
- King, N.; Hittinger, C.T.; Carroll, S.B. Evolution of key cell signaling and adhesion protein families predates animal origins. Science 2003, 301, 361–363. [Google Scholar] [CrossRef] [PubMed]
- Nedelcu, A.M.; Michod, R.E. The evolutionary origin of an altruistic gene. Mol. Biol. Evol. 2006, 23, 1460–1464. [Google Scholar] [CrossRef] [PubMed]
- Ritchie, A.V.; van Es, S.; Fouquet, C.; Schaap, P. From drought sensing to developmental control: Evolution of cyclic AMP signaling in social amoebas. Mol. Biol. Evol. 2008, 25, 2109–2118. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hanschen, E.R.; Marriage, T.N.; Ferris, P.J.; Hamaji, T.; Toyoda, A.; Fujiyama, A.; Neme, R.; Noguchi, H.; Minakuchi, Y.; Suzuki, M.; et al. The Gonium pectorale genome demonstrates co-option of cell cycle regulation during the evolution of multicellularity. Nat. Commun. 2016, 7, 1–10. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kiss, E.; Hegedüs, B.; Virágh, M.; Varga, T.; Merényi, Z.; Kószó, T.; Bálint, B.; Prasanna, A.N.; Krizsán, K.; Kocsubé, S.; et al. Comparative genomics reveals the origin of fungal hyphae and multicellularity. Nat. Commun. 2019, 10, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Mikhailov, K.V.; Konstantinova, A.V.; Nikitin, M.A.; Troshin, P.V.; Rusin, L.Y.; Lyubetsky, V.A.; Panchin, Y.V.; Mylnikov, A.P.; Moroz, L.L.; Kumar, S.; et al. The origin of Metazoa: A transition from temporal to spatial cell differentiation. Bioessays 2009, 31, 758–768. [Google Scholar] [CrossRef]
- Brunet, T.; King, N. The origin of animal multicellularity and cell differentiation. Dev. Cell 2017, 43, 124–140. [Google Scholar] [CrossRef] [Green Version]
- Schaap, P. From environmental sensing to developmental control: Cognitive evolution in dictyostelid social amoebas. Philos. Trans. R. Soc. 2021, 376, 20190756. [Google Scholar] [CrossRef]
- Ratcliff, W.C.; Denison, R.F.; Borrello, M.; Travisano, M. Experimental evolution of multicellularity. Proc. Natl. Acad. Sci. USA 2012, 109, 1595–1600. [Google Scholar] [CrossRef] [Green Version]
- Libby, E.; Rainey, P.B. A conceptual framework for the evolutionary origins of multicellularity. Phys. Biol. 2013, 10, 035001. [Google Scholar] [CrossRef] [Green Version]
- Herron, M.D.; Borin, J.M.; Boswell, J.C.; Walker, J.; Chen, I.C.K.; Knox, C.A.; Boyd, M.; Rosenzweig, F.; Ratcliff, W.C. De novo origins of multicellularity in response to predation. Sci. Rep. 2019, 9, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Koschwanez, J.H.; Foster, K.R.; Murray, A.W. Sucrose utilization in budding yeast as a model for the origin of undifferentiated multicellularity. PLoS Biol. 2011, 9, e1001122. [Google Scholar] [CrossRef]
- Boraas, M.E.; Seale, D.B.; Boxhorn, J.E. Phagotrophy by a flagellate selects for colonial prey: A possible origin of multicellularity. Evol. Ecol. 1998, 12, 153–164. [Google Scholar] [CrossRef]
- Shelton, D.E.; Michod, R.E. Group and individual selection during evolutionary transitions in individuality: Meanings and partitions. Philos. Trans. R. Soc. 2020, 375, 20190364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Goldsby, H.J.; Knoester, D.B.; Ofria, C.; Kerr, B. The evolutionary origin of somatic cells under the dirty work hypothesis. PLoS Biol. 2014, 12, e1001858. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gavrilets, S. Rapid transition towards the division of labor via evolution of developmental plasticity. PLoS Comput. Biol. 2010, 6, e1000805. [Google Scholar] [CrossRef] [PubMed]
- Yanni, D.; Jacobeen, S.; Márquez-Zacarías, P.; Weitz, J.S.; Ratcliff, W.C.; Yunker, P.J. Topological constraints in early multicellularity favor reproductive division of labor. Elife 2020, 9, e54348. [Google Scholar] [CrossRef]
- Michod, R.E.; Nedelcu, A.M. On the reorganization of fitness during evolutionary transitions in individuality. Integr. Comp. Biol. 2003, 43, 64–73. [Google Scholar] [CrossRef] [PubMed]
- Gruenheit, N.; Parkinson, K.; Stewart, B.; Howie, J.A.; Wolf, J.B.; Thompson, C.R. A polychromatic ‘greenbeard’locus determines patterns of cooperation in a social amoeba. Nat. Commun. 2017, 8, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Velicer, G.J.; Kroos, L.; Lenski, R.E. Developmental cheating in the social bacterium Myxococcus xanthus. Nature 2000, 404, 598–601. [Google Scholar] [CrossRef]
- Ratcliff, W.C.; Herron, M.D.; Howell, K.; Pentz, J.T.; Rosenzweig, F.; Travisano, M. Experimental evolution of an alternating uni-and multicellular life cycle in Chlamydomonas reinhardtii. Nat. Commun. 2013, 4, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Sebé-Pedrós, A.; Roger, A.J.; Lang, F.B.; King, N.; Ruiz-Trillo, I. Ancient origin of the integrin-mediated adhesion and signaling machinery. Proc. Natl. Acad. Sci. USA 2010, 107, 10142–10147. [Google Scholar] [CrossRef] [Green Version]
- Wolinsky, E.; Libby, E. Evolution of regulated phenotypic expression during a transition to multicellularity. Evol. Ecol. 2016, 30, 235–250. [Google Scholar] [CrossRef] [Green Version]
- Lachmann, M.; Libby, E. Epigenetic inheritance systems contribute to the evolution of a germline. Philos. Trans. R. Soc. Biol. Sci. 2016, 371, 20150445. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sebé-Pedrós, A.; Degnan, B.M.; Ruiz-Trillo, I. The origin of Metazoa: A unicellular perspective. Nat. Rev. Genet. 2017, 18, 498. [Google Scholar] [CrossRef]
- Dodds, W.K.; Gudder, D.A.; Mollenhauer, D. The ecology of Nostoc. J. Phycol. 1995, 31, 2–18. [Google Scholar] [CrossRef]
- Lloyd, C.; Chan, J. Not so divided: The common basis of plant and animal cell division. Nat. Rev. Mol. Cell Biol. 2006, 7, 147–152. [Google Scholar] [CrossRef]
- Walker, G.M.; White, N.A. Introduction to fungal physiology. Fungi Biol. Appl. 2017, 1–35. [Google Scholar] [CrossRef] [Green Version]
- Steinkraus, K.; Kaeberlein, M.; Kennedy, B.K. Replicative aging in yeast: The means to the end. Annu. Rev. Cell Dev. Biol. 2008, 24, 29–54. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Stewart, E.J.; Madden, R.; Paul, G.; Taddei, F. Aging and death in an organism that reproduces by morphologically symmetric division. PLoS Biol. 2005, 3, e45. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tarnita, C.E.; Taubes, C.H.; Nowak, M.A. Evolutionary construction by staying together and coming together. J. Theor. Biol. 2013, 320, 10–22. [Google Scholar] [CrossRef] [PubMed]
- Fisher, R.M.; Cornwallis, C.K.; West, S.A. Group formation, relatedness, and the evolution of multicellularity. Curr. Biol. 2013, 23, 1120–1125. [Google Scholar] [CrossRef] [Green Version]
- Knoll, A.H. The multiple origins of complex multicellularity. Annu. Rev. Earth Planet. Sci. 2011, 39, 217–239. [Google Scholar] [CrossRef] [Green Version]
- Cairney, J. Translocation of solutes in ectomycorrhizal and saprotrophic rhizomorphs. Mycol. Res. 1992, 96, 135–141. [Google Scholar] [CrossRef]
- Lew, R.R. How does a hypha grow? The biophysics of pressurized growth in fungi. Nat. Rev. Microbiol. 2011, 9, 509–518. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bonner, J.T. Why Size Matters: From Bacteria to Blue Whales; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Schlichting, C.D. Origins of differentiation via phenotypic plasticity. Evol. Dev. 2003, 5, 98–105. [Google Scholar] [CrossRef]
- Travisano, M.; Mongold, J.A.; Bennett, A.F.; Lenski, R.E. Experimental tests of the roles of adaptation, chance, and history in evolution. Science 1995, 267, 87–90. [Google Scholar] [CrossRef]
- Ratcliff, W.C.; Fankhauser, J.D.; Rogers, D.W.; Greig, D.; Travisano, M. Origins of multicellular evolvability in snowflake yeast. Nat. Commun. 2015, 6, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Longo, V.D.; Shadel, G.S.; Kaeberlein, M.; Kennedy, B. Replicative and chronological aging in Saccharomyces cerevisiae. Cell Metab. 2012, 16, 18–31. [Google Scholar] [CrossRef] [Green Version]
- Wessel, A.K.; Arshad, T.A.; Fitzpatrick, M.; Connell, J.L.; Bonnecaze, R.T.; Shear, J.B.; Whiteley, M. Oxygen limitation within a bacterial aggregate. MBio 2014, 5. [Google Scholar] [CrossRef] [Green Version]
- Roberts, M.E.; Stewart, P.S. Modeling antibiotic tolerance in biofilms by accounting for nutrient limitation. Antimicrob. Agents Chemother. 2004, 48, 48–52. [Google Scholar] [CrossRef] [Green Version]
- Hallatschek, O.; Hersen, P.; Ramanathan, S.; Nelson, D.R. Genetic drift at expanding frontiers promotes gene segregation. Proc. Natl. Acad. Sci. USA 2007, 104, 19926–19930. [Google Scholar] [CrossRef] [Green Version]
- Gralka, M.; Stiewe, F.; Farrell, F.; Möbius, W.; Waclaw, B.; Hallatschek, O. Allele surfing promotes microbial adaptation from standing variation. Ecol. Lett. 2016, 19, 889–898. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fusco, D.; Gralka, M.; Kayser, J.; Anderson, A.; Hallatschek, O. Excess of mutational jackpot events in expanding populations revealed by spatial Luria–Delbrück experiments. Nat. Commun. 2016, 7, 1–9. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Farrell, F.D.; Gralka, M.; Hallatschek, O.; Waclaw, B. Mechanical interactions in bacterial colonies and the surfing probability of beneficial mutations. J. R. Soc. Interface 2017, 14, 20170073. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Flemming, H.C.; Wuertz, S. Bacteria and archaea on Earth and their abundance in biofilms. Nat. Rev. Microbiol. 2019, 17, 247–260. [Google Scholar] [CrossRef] [PubMed]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Isaksson, H.; Conlin, P.L.; Kerr, B.; Ratcliff, W.C.; Libby, E. The Consequences of Budding versus Binary Fission on Adaptation and Aging in Primitive Multicellularity. Genes 2021, 12, 661. https://doi.org/10.3390/genes12050661
Isaksson H, Conlin PL, Kerr B, Ratcliff WC, Libby E. The Consequences of Budding versus Binary Fission on Adaptation and Aging in Primitive Multicellularity. Genes. 2021; 12(5):661. https://doi.org/10.3390/genes12050661
Chicago/Turabian StyleIsaksson, Hanna, Peter L. Conlin, Ben Kerr, William C. Ratcliff, and Eric Libby. 2021. "The Consequences of Budding versus Binary Fission on Adaptation and Aging in Primitive Multicellularity" Genes 12, no. 5: 661. https://doi.org/10.3390/genes12050661
APA StyleIsaksson, H., Conlin, P. L., Kerr, B., Ratcliff, W. C., & Libby, E. (2021). The Consequences of Budding versus Binary Fission on Adaptation and Aging in Primitive Multicellularity. Genes, 12(5), 661. https://doi.org/10.3390/genes12050661






