A Genomic Quantitative Study on the Contribution of the Ancestral-State Bases Relative to Derived Bases in the Divergence and Local Adaptation of Populus davidiana
Abstract
:1. Introduction
2. Materials and Methods
2.1. Population Sampling, Sequencing, Quality Control, and Read Mapping
2.2. Site Filtering and SNP Calling
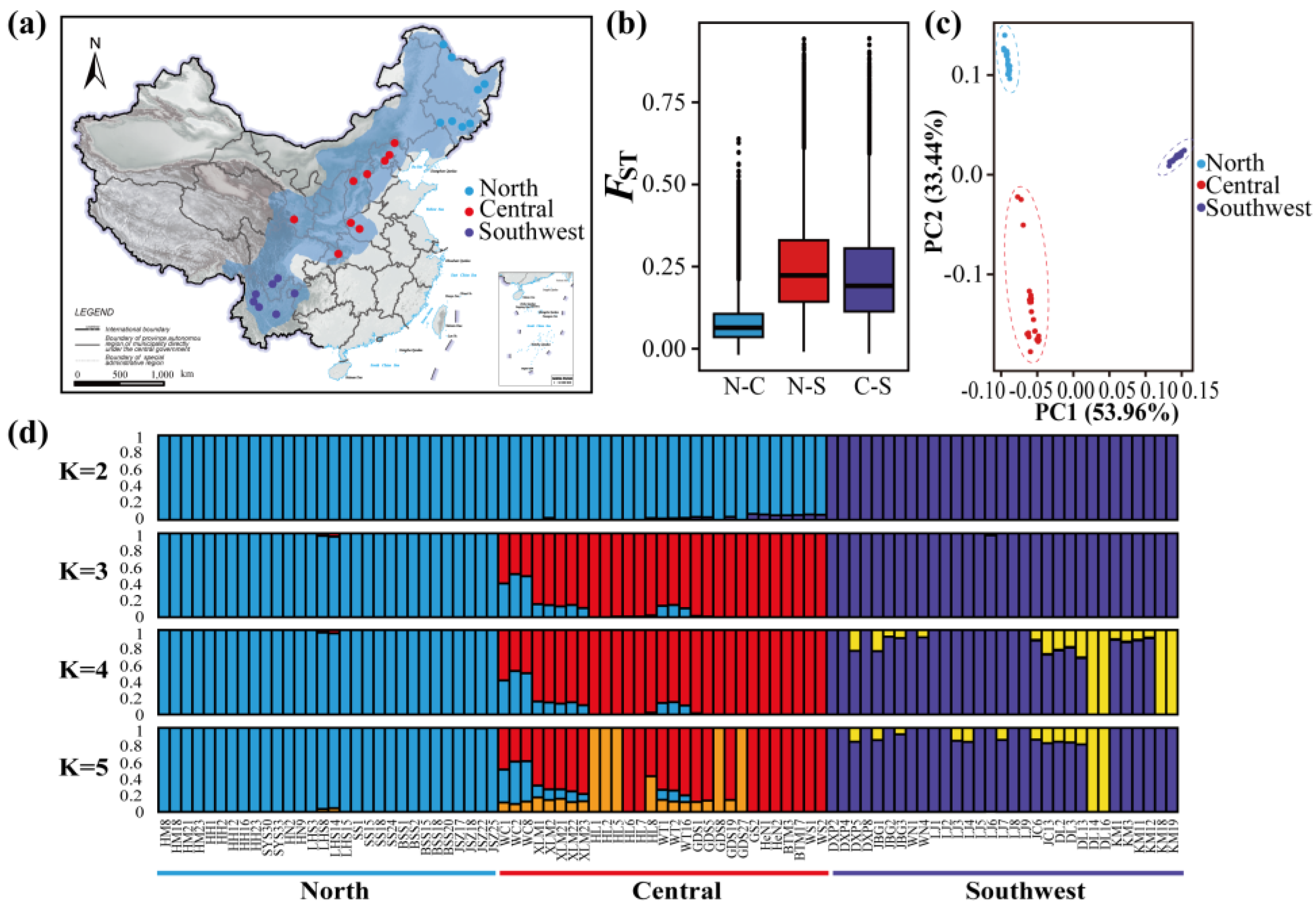
2.3. Population Structure
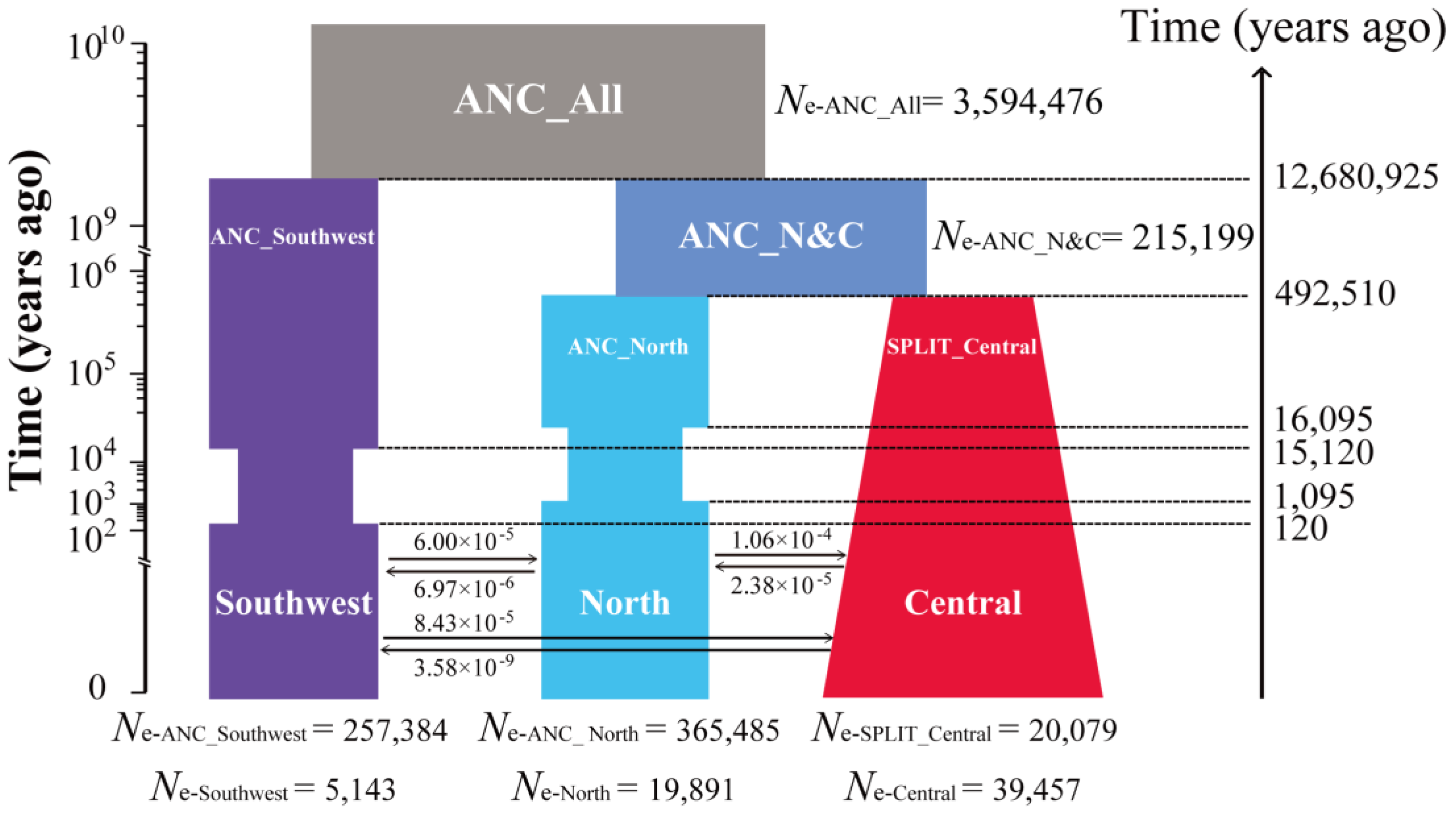
2.4. Demographic Modelling
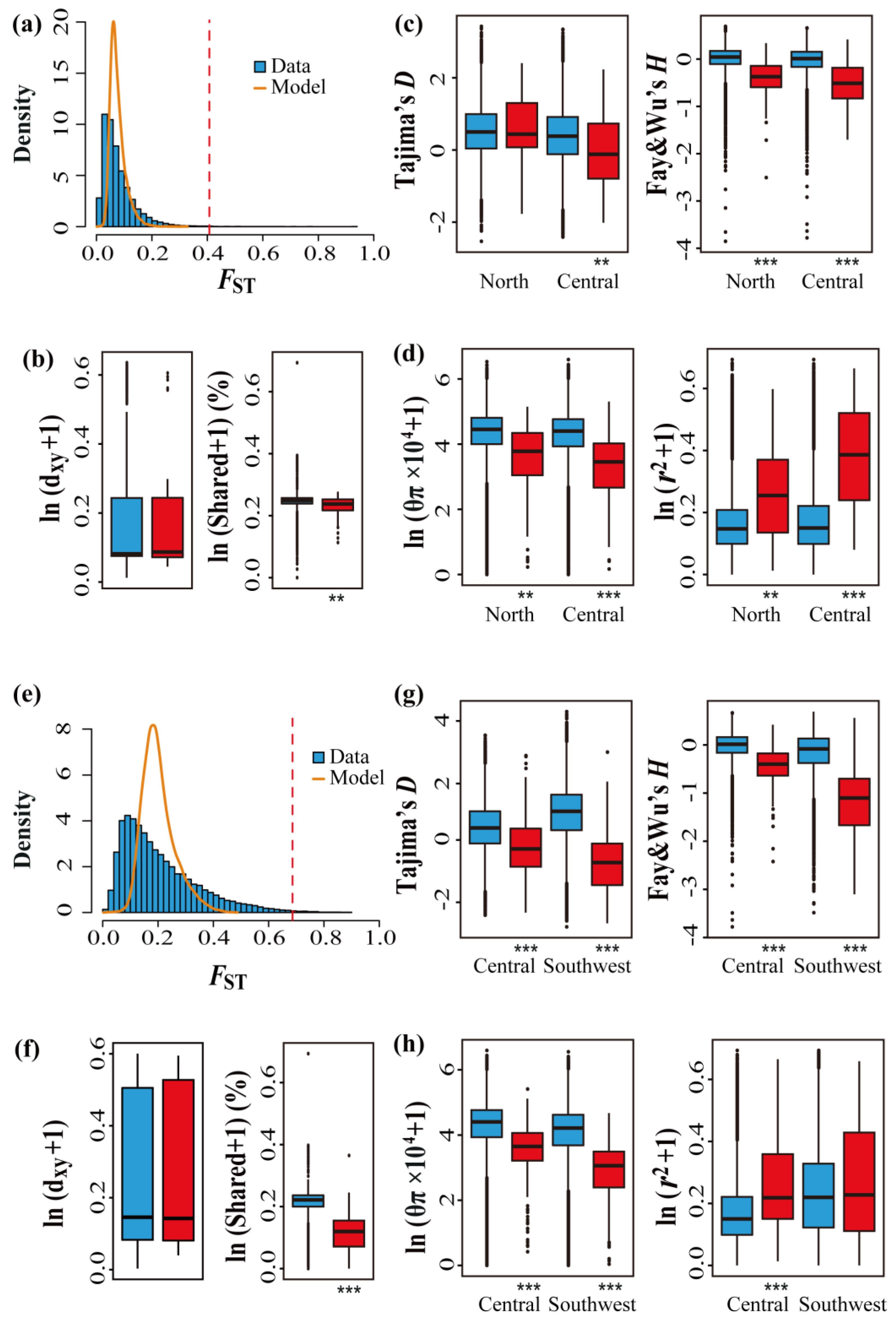
2.5. Genome-Wide Patterns of Differentiation
2.6. Identification of Outlier Regions and Signatures of Selection
2.7. Proportion Calculations of ASB and DB
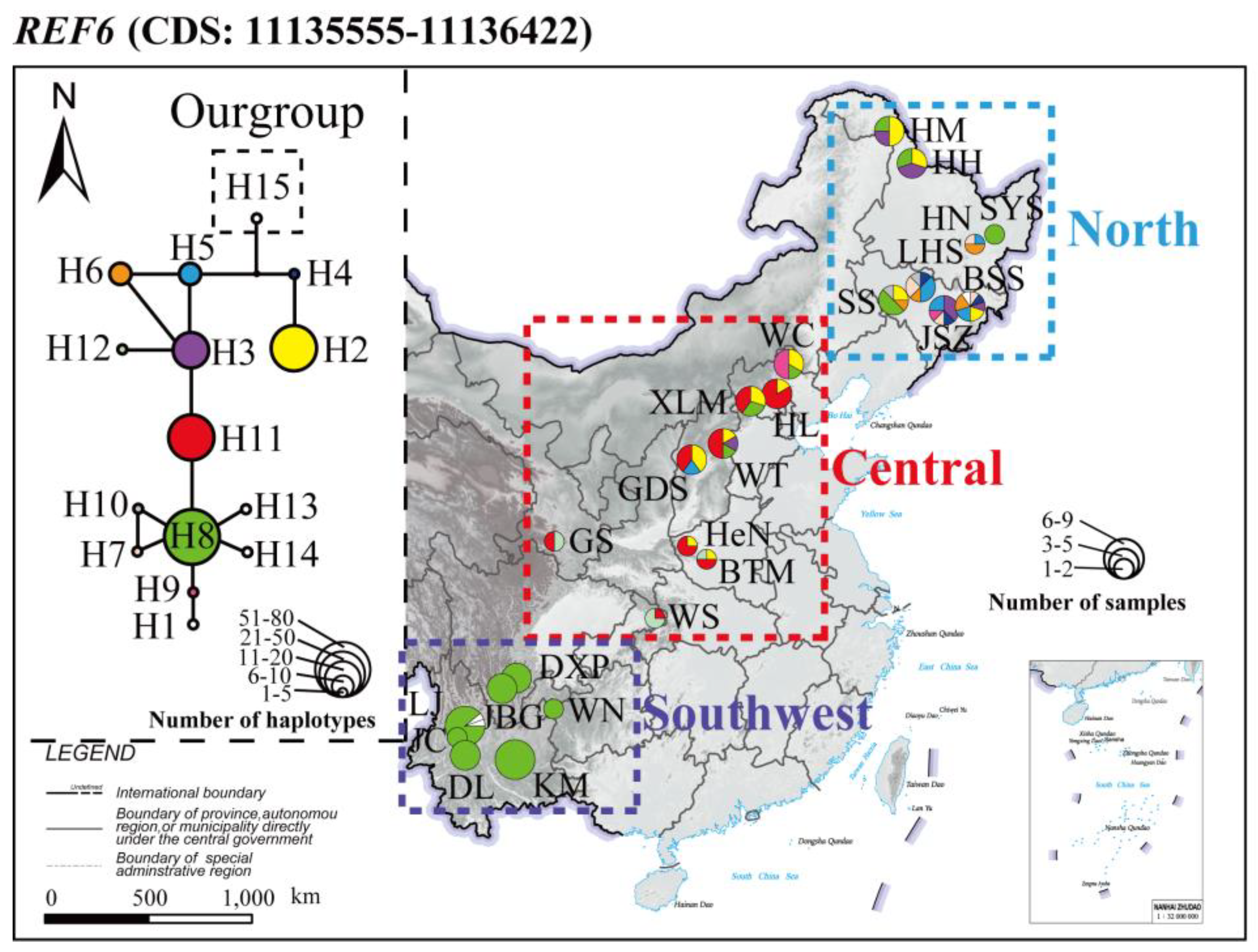
2.8. Gene Identification and Sequence Analysis in Highly Differentiated Regions
3. Results
3.1. Population Structure
3.2. Divergence and Demographic Reconstructions
3.3. Genome-Wide Patterns of Differentiation and Identification of Outlier Regions
3.4. Contribution of ASBs and DBs
3.5. Genes under Selection
4. Discussion
4.1. Reconstruction of Historical Demography as Relates to East Asian Geology and Climate Fluctuations
4.2. ASBs and DBs in the Adaptation to Changing Selective Pressures
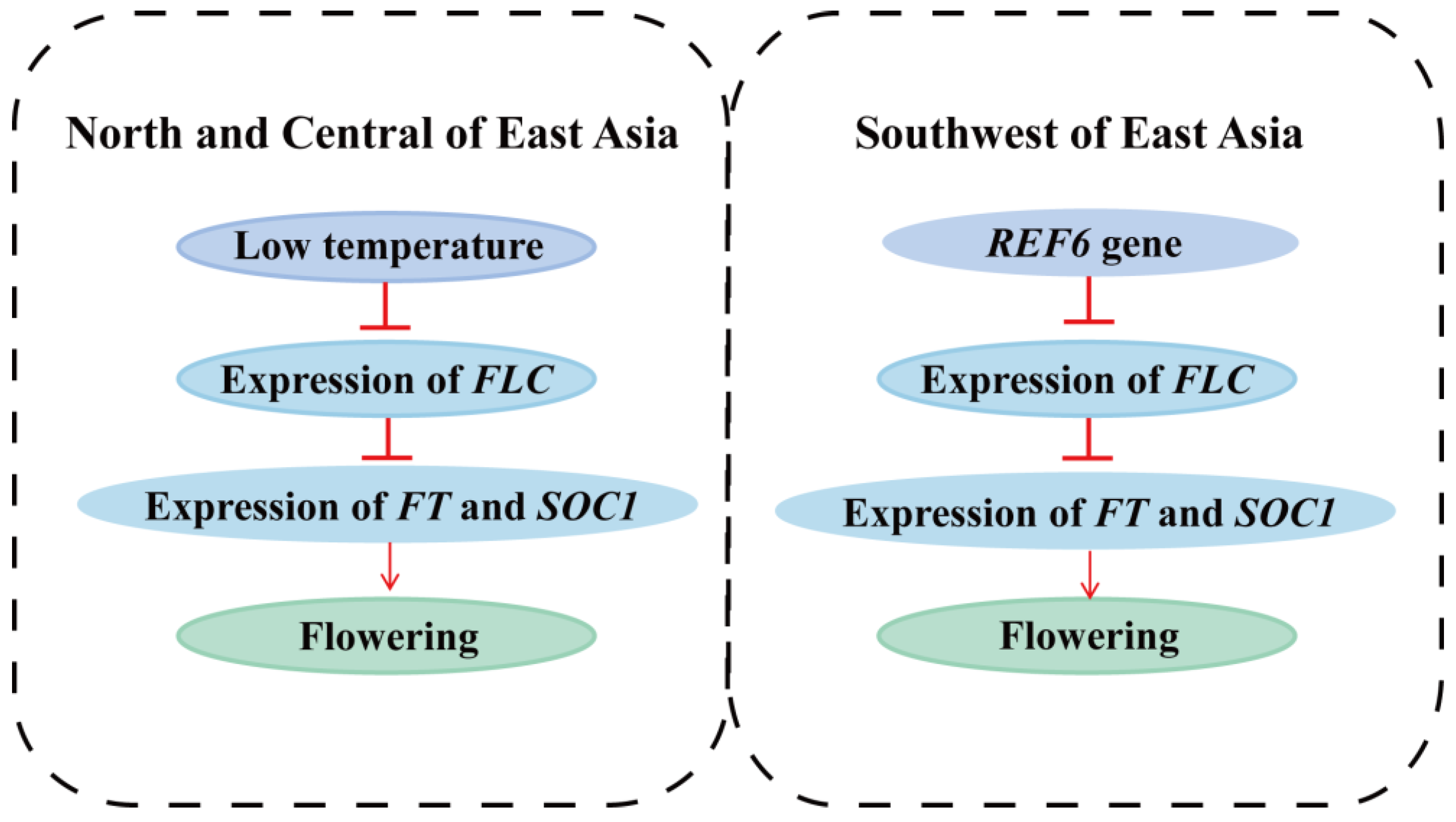
4.3. Genes Related to Environmental Adaptation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fan, W.-B.; Wu, Y.; Yang, J.; Shahzad, K.; Li, Z.-H. Comparative Chloroplast Genomics of Dipsacales Species: Insights Into Sequence Variation, Adaptive Evolution, and Phylogenetic Relationships. Front. Plant Sci. 2018, 9, 689. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ellegren, H. Genome sequencing and population genomics in non-model organisms. Trends Ecol. Evol. 2014, 29, 51–63. [Google Scholar] [CrossRef] [PubMed]
- Presgraves, D.C.; Balagopalan, L.; Abmayr, S.M.; Orr, H.A. Adaptive evolution drives divergence of a hybrid inviability gene between two species of Drosophila. Nature 2003, 423, 715–719. [Google Scholar] [CrossRef]
- Aitken, S.N.; Yeaman, S.; Holliday, J.A.; Wang, T.; Curtis-McLane, S. Adaptation, migration or extirpation: Climate change outcomes for tree populations. Evol. Appl. 2008, 1, 95–111. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Wan, Z.Y.; Lim, H.S.; Yue, G.H. Genetic variability, local selection and demographic history: Genomic evidence of evolving towards allopatric speciation in Asian seabass. Mol. Ecol. 2016, 25, 3605–3621. [Google Scholar] [CrossRef]
- Wang, J.; Street, N.R.; Scofield, D.G.; Ingvarsson, P.K. Variation in Linked Selection and Recombination Drive Genomic Divergence during Allopatric Speciation of European and American Aspens. Mol. Biol. Evol. 2016, 33, 1754–1767. [Google Scholar] [CrossRef] [Green Version]
- Luikart, G.; England, P.R.; Tallmon, D.; Jordan, S.; Taberlet, P. The power and promise of population genomics: From genotyping to genome typing. Nat. Rev. Genet. 2003, 4, 981–994. [Google Scholar] [CrossRef]
- Via, S. Natural selection in action during speciation. Proc. Natl. Acad. Sci. USA 2009, 106, 9939–9946. [Google Scholar] [CrossRef] [Green Version]
- Noor, M.A.F.; Bennett, S.M. Islands of speciation or mirages in the desert? Examining the role of restricted recombination in maintaining species. Heredity 2009, 103, 439–444. [Google Scholar] [CrossRef] [Green Version]
- Nachman, M.W.; Payseur, B.A. Recombination rate variation and speciation: Theoretical predictions and empirical results from rabbits and mice. Philos. Trans. R. Soc. B Biol. Sci. 2012, 367, 409–421. [Google Scholar] [CrossRef] [Green Version]
- Wright, S. Evolution in Mendelian Populations. Genetics 1931, 16, 97–159. [Google Scholar] [CrossRef]
- Renaut, S.; Grassa, C.J.; Yeaman, S.; Moyers, B.T.; Lai, Z.; Kane, N.C.; Bowers, J.E.; Burke, J.M.; Rieseberg, L.H. Genomic islands of divergence are not affected by geography of speciation in sunflowers. Nat. Commun. 2013, 4, 1827. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gartside, D.W.; McNeilly, T. The potential for evolution of heavy metal tolerance in plants. II. Copper tolerance in normal populations of different plant species. Heredity 1974, 32, 335–348. [Google Scholar] [CrossRef]
- A Walley, K.; I Khan, M.S.; Bradshaw, A.D. The potential for evolution of heavy metal tolerance in plants. I. Copper and zinc tolerance in Agrostis Tenuis. Heredity 1974, 32, 309–319. [Google Scholar] [CrossRef] [Green Version]
- Barrett, R.D.; Schluter, D. Adaptation from standing genetic variation. Trends Ecol. Evol. 2008, 23, 38–44. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Josephs, E.B.; Lee, K.M.; Roberts, L.M.; Rellán-Álvarez, R.; Ross-Ibarra, J.; Hufford, M.B. Molecular Parallelism Underlies Convergent Highland Adaptation of Maize Landraces. Mol. Biol. Evol. 2021, 38, 3567–3580. [Google Scholar] [CrossRef]
- Urban, S.; Nater, A.; Meyer, A.; Kratochwil, C.F. Different Sources of Allelic Variation Drove Repeated Color Pattern Divergence in Cichlid Fishes. Mol. Biol. Evol. 2020, 38, 465–477. [Google Scholar] [CrossRef] [PubMed]
- Prezeworski, M.; Coop, G.; Wall, J.D. The signature of positive selection on standing genetic variation. Evolution 2005, 59, 2312–2323. [Google Scholar] [CrossRef]
- Cayuela, H.; Rougemont, Q.; Laporte, M.; Mérot, C.; Normandeau, E.; Dorant, Y.; Tørresen, O.K.; Hoff, S.N.K.; Jentoft, S.; Sirois, P.; et al. Standing genetic variation and chromosomal rearrangements facilitate local adaptation in a marine fish. bioRxiv 2019. [Google Scholar] [CrossRef]
- A Tishkoff, S.; Reed, F.; Ranciaro, A.; Voight, B.F.; Babbitt, C.C.; Silverman, J.S.; Powell, K.; Mortensen, H.M.; Hirbo, J.B.; Osman, M.; et al. Convergent adaptation of human lactase persistence in Africa and Europe. Nat. Genet. 2006, 39, 31–40. [Google Scholar] [CrossRef]
- Pelz, H.-J.; Rost, S.; Hünerberg, M.; Fregin, A.; Heiberg, A.-C.; Baert, K.; MacNicoll, A.D.; Prescott, C.V.; Walker, A.-S.; Oldenburg, J.; et al. The Genetic Basis of Resistance to Anticoagulants in Rodents. Genetics 2005, 170, 1839–1847. [Google Scholar] [CrossRef] [Green Version]
- Feder, J.L.; Berlocher, S.H.; Roethele, J.B.; Dambroski, H.; Smith, J.J.; Perry, W.L.; Gavrilovic, V.; Filchak, K.E.; Rull, J.; Aluja, M. Allopatric genetic origins for sympatric host-plant shifts and race formation in Rhagoletis. Proc. Natl. Acad. Sci. USA 2003, 100, 10314–10319. [Google Scholar] [CrossRef] [Green Version]
- Colosimo, P.F.; Hosemann, K.E.; Balabhadra, S.; Villarreal, G.; Dickson, M.; Grimwood, J.; Schmutz, J.; Myers, R.M.; Schluter, D.; Kingsley, D.M. Widespread Parallel Evolution in Sticklebacks by Repeated Fixation of Ectodysplasin Alleles. Science 2005, 307, 1928–1933. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Steiner, C.C.; Weber, J.; Hoekstra, H.E. Adaptive Variation in Beach Mice Produced by Two Interacting Pigmentation Genes. PLoS Biol. 2007, 5, e219. [Google Scholar] [CrossRef] [PubMed]
- Ben Stern, D.; Lee, C.E. Evolutionary origins of genomic adaptations in an invasive copepod. Nat. Ecol. Evol. 2020, 4, 1084–1094. [Google Scholar] [CrossRef] [PubMed]
- Innan, H.; Kim, Y. Pattern of polymorphism after strong artificial selection in a domestication event. Proc. Natl. Acad. Sci. USA 2004, 101, 10667–10672. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chhatre, V.E.; Evans, L.M.; DiFazio, S.P.; Keller, S.R. Adaptive introgression and maintenance of a trispecies hybrid complex in range-edge populations of Populus. Mol. Ecol. 2018, 27, 4820–4838. [Google Scholar] [CrossRef]
- Suarez-Gonzalez, A.; Hefer, C.A.; Lexer, C.; Douglas, C.J.; Cronk, Q.C.B. Introgression from Populus balsamifera underlies adaptively significant variation and range boundaries in P. trichocarpa. New Phytol. 2018, 217, 416–427. [Google Scholar] [CrossRef] [Green Version]
- Rendón-Anaya, M.; Wilson, J.; Sveinsson, S.; Fedorkov, A.; Cottrell, J.; Bailey, M.E.S.; Ruņǵis, D.; Lexer, C.; Jansson, S.; Robinson, K.M.; et al. Adaptive Introgression Facilitates Adaptation to High Latitudes in European Aspen (Populus tremula L.). Mol. Biol. Evol. 2021, 38, 5034–5050. [Google Scholar] [CrossRef]
- Oakley, C.G.; Ågren, J.; Schemske, D.W. Heterosis and outbreeding depression in crosses between natural populations of Arabidopsis thaliana. Heredity 2015, 115, 73–82. [Google Scholar] [CrossRef] [Green Version]
- Christin, P.-A.; Salamin, N.; Savolainen, V.; Duvall, M.R.; Besnard, G. C4 Photosynthesis Evolved in Grasses via Parallel Adaptive Genetic Changes. Curr. Biol. 2007, 17, 1241–1247. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Besnard, G.; Muasya, A.M.; Russier, F.; Roalson, E.H.; Salamin, N.; Christin, P.-A. Phylogenomics of C4 Photosynthesis in Sedges (Cyperaceae): Multiple Appearances and Genetic Convergence. Mol. Biol. Evol. 2009, 26, 1909–1919. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carrasco, P.; de la Iglesia, F.; Elena, S.F. Distribution of Fitness and Virulence Effects Caused by Single-Nucleotide Substitutions in Tobacco Etch Virus. J. Virol. 2007, 81, 12979–12984. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ravikumar, A.; Arzumanyan, G.A.; Obadi, M.K.; Javanpour, A.A.; Liu, C.C. Scalable, Continuous Evolution of Genes at Mutation Rates above Genomic Error Thresholds. Cell 2018, 175, 1946–1957.e13. [Google Scholar] [CrossRef] [Green Version]
- Katju, V.; Bergthorsson, U. Old Trade, New Tricks: Insights into the Spontaneous Mutation Process from the Partnering of Classical Mutation Accumulation Experiments with High-Throughput Genomic Approaches. Genome Biol. Evol. 2018, 11, 136–165. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Wang, Z.; Ye, Z.; Du, S.; Liu, S.; Zhang, J. Phylogeographic analyses of a widely distributed Populus davidiana: Further evidence for the existence of glacial refugia of cool-temperate deciduous trees in northern East Asia. Ecol. Evol. 2018, 8, 13014–13026. [Google Scholar] [CrossRef] [Green Version]
- Keller, S.R.; E Chhatre, V.; Fitzpatrick, M.C. Influence of Range Position on Locally Adaptive Gene-Environment Associations in Populus Flowering Time Genes. J. Hered. 2017, 109, 47–58. [Google Scholar] [CrossRef]
- Wang, J.; Ding, J.; Tan, B.; Robinson, K.M.; Michelson, I.H.; Johansson, A.; Nystedt, B.; Scofield, D.G.; Nilsson, O.; Jansson, S.; et al. A major locus controls local adaptation and adaptive life history variation in a perennial plant. Genome Biol. 2018, 19, 72. [Google Scholar] [CrossRef] [Green Version]
- Tembrock, L.R.; Stevens, J.E.; Schuhmann, A.; Walton, J.A. Genetic characterization and comparison of three disjunct Populus tremuloides Michx. (Salicaceae) stands across a latitudinal gradient. Nat. Resour. Rep. NPS/NRSS/IMD/NRR 2020, 2020/2073, 1–74. [Google Scholar]
- Zheng, H.; Fan, L.; Milne, R.I.; Zhang, L.; Wang, Y.; Mao, K. Species Delimitation and Lineage Separation History of a Species Complex of Aspens in China. Front. Plant Sci. 2017, 8, 375. [Google Scholar] [CrossRef] [Green Version]
- Lohse, M.; Bolger, A.M.; Nagel, A.; Fernie, A.R.; Lunn, J.E.; Stitt, M.; Usadel, B. RobiNA: A user-friendly, integrated software solution for RNA-Seq-based transcriptomics. Nucleic Acids Res. 2012, 40, W622–W627. [Google Scholar] [CrossRef]
- Tuskan, G.A.; DiFazio, S.; Jansson, S.; Bohlmann, J.; Grigoriev, I.; Hellsten, U.; Putnam, N.; Ralph, S.; Rombauts, S.; Salamov, A.; et al. The Genome of Black Cottonwood, Populus trichocarpa (Torr. & Gray). Science 2006, 313, 1596–1604. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.-J.; Wang, X.-R.; Zeng, Q.-Y. De novo assembly of white poplar genome and genetic diversity of white poplar population in Irtysh River basin in China. Sci. China Life Sci. 2019, 62, 609–618. [Google Scholar] [CrossRef] [PubMed]
- Pakull, B.; Groppe, K.; Meyer, M.; Markussen, T.; Fladung, M. Genetic linkage mapping in aspen (Populus tremula L. and Populus tremuloides Michx.). Tree Genet. Genomes 2009, 5, 505–515. [Google Scholar] [CrossRef]
- Li, H. Aligning Sequence Reads, Clone Sequences and Assembly Contigs with BWA-MEM. Available online: http://arxiv.org/abs/1303.3997 (accessed on 25 June 2020).
- Korneliussen, T.S.; Albrechtsen, A.; Nielsen, R. ANGSD: Analysis of Next Generation Sequencing Data. BMC Bioinform. 2014, 15, 1–13. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, H.; Handsaker, B.; Wysoker, A.; Fennell, T.; Ruan, J.; Homer, N.; Marth, G.; Abecasis, G.; Durbin, R. The Sequence Alignment/Map format and SAMtools. Bioinformatics 2009, 25, 2078–2079. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, S.Y.; E Lohmueller, K.; Albrechtsen, A.; Li, Y.; Korneliussen, T.; Tian, G.; Grarup, N.; Jiang, T.; Andersen, G.; Witte, D.; et al. Estimation of allele frequency and association mapping using next-generation sequencing data. BMC Bioinform. 2011, 12, 231. [Google Scholar] [CrossRef] [Green Version]
- Danecek, P.; Auton, A.; Abecasis, G.; Albers, C.A.; Banks, E.; DePristo, M.A.; Handsaker, R.E.; Lunter, G.; Marth, G.T.; Sherry, S.T.; et al. The variant call format and VCFtools. Bioinformatics 2011, 27, 2156–2158. [Google Scholar] [CrossRef]
- Skotte, L.; Korneliussen, T.S.; Albrechtsen, A. Estimating Individual Admixture Proportions from Next Generation Sequencing Data. Genetics 2013, 195, 693–702. [Google Scholar] [CrossRef] [Green Version]
- Alexander, D.H.; Novembre, J.; Lange, K. Fast model-based estimation of ancestry in unrelated individuals. Genome Res. 2009, 19, 1655–1664. [Google Scholar] [CrossRef] [Green Version]
- Purcell, S.; Neale, B.; Todd-Brown, K.; Thomas, L.; Ferreira, M.A.R.; Bender, D.; Maller, J.; Sklar, P.; de Bakker, P.I.W.; Daly, M.J.; et al. PLINK: A Tool Set for Whole-Genome Association and Population-Based Linkage Analyses. Am. J. Hum. Genet. 2007, 81, 559–575. [Google Scholar] [CrossRef] [Green Version]
- Fumagalli, M.; Vieira, F.G.; Linderoth, T.; Nielsen, R. ngsTools: Methods for population genetics analyses from next-generation sequencing data. Bioinformatics 2014, 30, 1486–1487. [Google Scholar] [CrossRef]
- Excoffier, L.; Dupanloup, I.; Huerta-Sánchez, E.; Sousa, V.C.; Foll, M. Robust Demographic Inference from Genomic and SNP Data. PLoS Genet. 2013, 9, e1003905. [Google Scholar] [CrossRef] [Green Version]
- Levsen, N.D.; Tiffin, P.; Olson, M.S. Pleistocene Speciation in the Genus Populus (Salicaceae). Syst. Biol. 2012, 61, 401–412. [Google Scholar] [CrossRef] [Green Version]
- Ewing, G.; Hermisson, J. MSMS: A coalescent simulation program including recombination, demographic structure and selection at a single locus. Bioinformatics 2010, 26, 2064–2065. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tajima, F. Statistical Method for Testing the Neutral Mutation Hypothesis by DNA Polymorphism. Genetics 1989, 3, 607–612. [Google Scholar] [CrossRef]
- Fay, J.; Wu, C.-I. Hitchhiking Under Positive Darwinian Selection. Genetics 2000, 155, 1405–1413. [Google Scholar] [CrossRef] [PubMed]
- McVean, G.A.T.; Myers, S.R.; Hunt, S.; Deloukas, P.; Bentley, D.R.; Donnelly, P. The Fine-Scale Structure of Recombination Rate Variation in the Human Genome. Science 2004, 304, 581–584. [Google Scholar] [CrossRef] [Green Version]
- Watterson, G. On the number of segregating sites in genetical models without recombination. Theor. Popul. Biol. 1975, 7, 256–276. [Google Scholar] [CrossRef]
- Fu, Y.X.; Li, W.H. Statistical tests of neutrality of mutations. Genetics 1993, 133, 693–709. [Google Scholar] [CrossRef] [PubMed]
- Librado, P.; Rozas, J. DnaSP v5: A software for comprehensive analysis of DNA polymorphism data. Bioinformatics 2009, 25, 1451–1452. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bandelt, H.J.; Forster, P.; Rohl, A. Median-joining networks for inferring intraspecific phylogenies. Mol. Biol. Evol. 1999, 16, 37–48. [Google Scholar] [CrossRef]
- Ding, W.-N.; Ree, R.H.; Spicer, R.A.; Xing, Y.-W. Ancient orogenic and monsoon-driven assembly of the world’s richest temperate alpine flora. Science 2020, 369, 578–581. [Google Scholar] [CrossRef] [PubMed]
- Ji, J.L.; Hong, H.L.; Xiao, G.Q.; Lin, X.; Xu, Y.D. Evolutionary sequences of the Neogene major climatic events in the Tibetan Plateau. Geol. Bull. China 2013, 32, 120–129. [Google Scholar]
- Qiu, Y.; Lu, Q.; Zhang, Y.; Cao, Y. Phylogeography of East Asia’s Tertiary relict plants: Current progress and future prospects. Biodivers. Sci. 2017, 25, 24–28. [Google Scholar] [CrossRef] [Green Version]
- Su, T.; Farnsworth, A.; Spicer, R.A.; Huang, J.; Wu, F.-X.; Liu, J.; Li, S.-F.; Xing, Y.-W.; Huang, Y.-J.; Deng, W.-Y.; et al. No high Tibetan Plateau until the Neogene. Sci. Adv. 2019, 5, eaav2189. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, K.X.; Wang, G.C.; Luo, M.S.; Ji, J.L.; Xu, Y.D.; Chen, R.M.; Chen, F.N.; Song, B.W.; Liang, Y.P.; Zhang, J.Y.; et al. Evolution of Tectonic Lithofacies Paleogeography of Cenozoic of Qinghai-Tibet Plateau and Its Response to Uplift of the Plateau. Earth Sci. 2010, 35, 697–712. [Google Scholar] [CrossRef]
- Raymo, M.E.; Ruddiman, W.F. Tectonic forcing of late Cenozoic climate. Nature 1992, 359, 117–122. [Google Scholar] [CrossRef]
- Riebe, C.S.; Kirchner, J.W.; Granger, D.E. Strong tectonic and weak climatic control of long-term chemical weathering rates. Geology 2001, 29, 511–514. [Google Scholar] [CrossRef]
- Gettelman, A.; Kinnison, D.E.; Dunkerton, T.J.; Brasseur, G.P. Impact of monsoon circulations on the upper troposphere and lower stratosphere. J. Geophys. Res. Atmos. 2004, 109, 51–67. [Google Scholar] [CrossRef]
- Ma, Y.; Zhong, L.; Su, Z.; Ishikawa, H.; Menenti, M.; Koike, T. Determination of regional distributions and seasonal variations of land surface heat fluxes from Landsat-7 Enhanced Thematic Mapper data over the central Tibetan Plateau area. J. Geophys. Res. Atmos. 2006, 111, 1843–1852. [Google Scholar] [CrossRef] [Green Version]
- Dupont-Nivet, G.; Hoorn, C.; Konert, M. Tibetan uplift prior to the Eocene-Oligocene climate transition: Evidence from pollen analysis of the Xining Basin. Geology 2008, 36, 987–990. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.; Ma, W.-X.; He, X.; Zhao, T.-T.; Yang, X.-H.; Wang, L.-J.; Ma, Q.-H.; Liang, L.-S.; Wang, G.-X. Species divergence and phylogeography of Corylus heterophylla Fisch complex (Betulaceae): Inferred from molecular, climatic and morphological data. Mol. Phylogenetics Evol. 2022, 168, 107413. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.; Yin, Q.; Crucifix, M.; Clemens, S.C.; Araya-Melo, P.; Liu, W.; Qiang, X.; Liu, Q.; Zhao, H.; Liang, L.; et al. Diverse manifestations of the mid-Pleistocene climate transition. Nat. Commun. 2019, 10, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.Y. Effects of Quaternary Ice Age on flora and vegetation in China. China Place Name 2020, 324, 51+53. Available online: https://kns.cnki.net/kcms2/article/abstract?v=6NQcqlsMs0jY9w0g-b2_cO1audgqnrIaoHmkfI80ibdl2V3j_DUzG7_0I7EcvUAMul_kajlArAW5EumSbm5ZLeJyFRIAKfka64BJ5YinhjE00BY-Z0zszFXHhJoK_8g_&uniplatform=NZKPT&language=CHS (accessed on 12 March 2021).
- Guo, G.X.; Jiang, H.C.; Cai, X.M. A quaternary pollen record from the X5 core in Beijing and its response to the pleistocene climate change. Quat. Sci. 2013, 33, 1160–1170. [Google Scholar] [CrossRef]
- Tang, L.Y.; Shen, C.M.; Kong, Z.Z.; Wang, F.B.; Liu, K.B. Pollen Evidence of Climate during the Last Glacial Maximum in Eastern Tibetan Plateau. J. Glaciol. Geocryol. 1998, 20, 133–140. [Google Scholar]
- Xiao, M.Q. Quaternary Geology Research in Ning Cheng County Chifeng City Inner Mongolia. Master’s Thesis, China University of Geoscience, Beijing, China, 2010. [Google Scholar]
- Cruickshank, T.E.; Hahn, M.W. Reanalysis suggests that genomic islands of speciation are due to reduced diversity, not reduced gene flow. Mol. Ecol. 2014, 23, 3133–3157. [Google Scholar] [CrossRef] [Green Version]
- Burri, R. Linked selection, demography and the evolution of correlated genomic landscapes in birds and beyond. Mol. Ecol. 2017, 26, 3853–3856. [Google Scholar] [CrossRef] [Green Version]
- Zhou, Q.; Wang, W. Detecting Natural Selection at the DNA Level. Zool. Res. 2004, 25, 73–80. [Google Scholar] [CrossRef]
- Nielsen, R. Molecular Signatures of Natural Selection. Annu. Rev. Genet. 2005, 39, 197–218. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ahrens, C.W.; Byrne, M.; Rymer, P.D. Standing genomic variation within coding and regulatory regions contributes to the adaptive capacity to climate in a foundation tree species. Mol. Ecol. 2019, 28, 2502–2516. [Google Scholar] [CrossRef] [PubMed]
- Stephan, W.; Song, Y.S.; Langley, C.H. The Hitchhiking Effect on Linkage Disequilibrium Between Linked Neutral Loci. Genetics 2006, 172, 2647–2663. [Google Scholar] [CrossRef] [Green Version]
- Ravinet, M.; Yoshida, K.; Shigenobu, S.; Toyoda, A.; Fujiyama, A.; Kitano, J. The genomic landscape at a late stage of stickleback speciation: High genomic divergence interspersed by small localized regions of introgression. PLoS Genet. 2018, 14, e1007358. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sheldon, C.C.; Burn, J.E.; Perez, P.P.; Metzger, J.; Edwards, J.A.; Peacock, W.J.; Dennis, E.S. The FLF MADS Box Gene: A Repressor of Flowering in Arabidopsis Regulated by Vernalization and Methylation. Plant Cell 1999, 11, 445. [Google Scholar] [CrossRef] [Green Version]
- Sheldon, C.C.; Rouse, D.T.; Finnegan, E.J.; Peacock, W.J.; Dennis, E.S. The molecular basis of vernalization: The central role of FLOWERING LOCUS C (FLC). Proc. Natl. Acad. Sci. USA 2000, 97, 3753–3758. [Google Scholar] [CrossRef]
- Noh, B.; Lee, S.-H.; Kim, H.-J.; Yi, G.; Shin, E.-A.; Lee, M.; Jung, K.-J.; Doyle, M.R.; Amasino, R.M.; Noh, Y.-S. Divergent Roles of a Pair of Homologous Jumonji/Zinc-Finger–Class Transcription Factor Proteins in the Regulation of Arabidopsis Flowering Time. Plant Cell 2004, 16, 2601–2613. [Google Scholar] [CrossRef] [Green Version]

| Point Estimation | 95% CI a | ||
|---|---|---|---|
| Parameters | Lower Bound | Upper Bound | |
| Ne−ANCAll | 3,594,476 | 152,843 | 4,630,207 |
| Ne−ANC−N&C | 215,199 | 62,862 | 1,454,818 |
| Ne−ANC_Southwest | 257,384 | 135,586 | 461,135 |
| Ne−ANC_North | 365,485 | 105,719 | 453,562 |
| Ne−SPLIT_Central | 20,079 | 8815 | 29,231 |
| Ne−BOT−Southwest | 1065 | 916 | 1164 |
| Ne−BOT−North | 3698 | 3468 | 8946 |
| Ne−North | 19,891 | 5271 | 54,619 |
| Ne−Central | 39,457 | 28,082 | 57,748 |
| Ne−Southwest | 5143 | 5082 | 10,794 |
| MIGCentral→Southwest | 3.58 × 10−9 | 2.62 × 10−11 | 2.97 × 10−6 |
| MIGSouthwest→Central | 8.43 × 10−5 | 3.00 × 10−5 | 2.40 × 10−4 |
| MIGCentral→North | 2.38 × 10−5 | 5.25 × 10−6 | 4.68 × 10−5 |
| MIGNorth→Central | 1.06 × 10−4 | 8.81 × 10−5 | 1.40 × 10−4 |
| MIGSouthwest→North | 6.00 × 10−5 | 4.63 × 10−11 | 1.73 × 10−4 |
| MIGNorth→Southwest | 6.97 × 10−6 | 6.30 × 10−6 | 1.51 × 10−5 |
| TDIV− Southwest _ANC−N&C | 12,680,925 | 4,323,255 | 14,781,162 |
| TDIV−North−Central | 492,510 | 214,723.80 | 680,931 |
| TBOT−Nend−Southwest | 120 | 30 | 1629 |
| TBOT−Nstart−Southwest | 15,120 | 15,030 | 16,629 |
| TBOT−Nend−North | 1095 | 97 | 37,751 |
| TBOT−Nstart−North | 16,095 | 15,097 | 52,751 |
| GrowthP−Central | −2.06 × 10−5 | −8.00 × 10−5 | −4.34 × 10−6 |
| Parameters | Population | Spearman’s ρ | p-Value | |
|---|---|---|---|---|
| FST and ρ | North-Central | North | −0.362 | <0.01 |
| Central | −0.337 | <0.01 | ||
| Central-Southwest | Central | −0.369 | <0.01 | |
| Southwest | −0.346 | <0.01 | ||
| dxy and ρ | North-Central | North | 0.018 | <0.01 |
| Central | 0.016 | <0.01 | ||
| Central-Southwest | Central | 0.012 | <0.05 | |
| Southwest | 0.027 | <0.01 |
| Population | Highly Differentiated | Background | Whole Genome | |
|---|---|---|---|---|
| N-C | North | 13.15 (5.82, 16.30) | 19.03 (8.49, 23.75) | 19.03 (8.49, 23.74) |
| Central | 10.04 (4.21, 12.64) | 17.90 (7.85, 21.69) | 17.89 (7.84, 21.67) | |
| C-S | Central | 4.64 (1.69, 4.39) | 17.87 (7.46, 22.03) | 17.79 (7.40, 21.92) |
| Southwest | 6.66 (2.02, 8.25) | 13.22 (5.64, 15.13) | 13.19 (5.61, 15.08) |
| Region | CDS | S | π | θw | Nh | D | D * | F * |
|---|---|---|---|---|---|---|---|---|
| North | 11135555–11136422 | 7 | 0.0027 | 0.0020 | 10 | 0.95 | 0.55 | 0.80 |
| 11137806–11137884 | 0 | 0.0000 | 0.0000 | 1 | / | 0.00 | 0.00 | |
| 11138254–11138321 | 1 | 0.0031 | 0.0032 | 2 | −0.03 | 0.53 | 0.42 | |
| 11138432–11138582 | 0 | 0.0000 | 0.0000 | 1 | / | 0.00 | 0.00 | |
| 11139034–11139707 | 7 | 0.0016 | 0.0022 | 9 | −0.74 | −0.38 | −0.59 | |
| 11140636–11141367 | 16 | 0.0066 | 0.0082 | 29 | −0.64 | 0.94 | 0.43 | |
| 11142487–11144538 | 43 | 0.0040 | 0.0045 | 39 | −0.36 | 1.35 | 0.85 | |
| 11144758–11144891 | 3 | 0.0047 | 0.0048 | 4 | −0.05 | 0.87 | 0.69 | |
| Mean | 9.63 | 0.0028 | 0.0031 | 11.88 | −0.15 | 0.48 | 0.33 | |
| Central | 11135555–11136422 | 7 | 0.0021 | 0.0017 | 7 | 0.57 | 1.23 | 1.20 |
| 11137806–11137884 | 1 | 0.0027 | 0.0027 | 2 | 0.00 | 0.53 | 0.44 | |
| 11138254–11138321 | 0 | 0.0000 | 0.0000 | 1 | / | 0.00 | 0.00 | |
| 11138432–11138582 | 2 | 0.0017 | 0.0029 | 3 | −0.72 | −0.93 | −1.01 | |
| 11139034–11139707 | 4 | 0.0014 | 0.0013 | 5 | 0.15 | 0.99 | 0.85 | |
| 11140636–11141367 | 14 | 0.0061 | 0.0097 | 26 | −1.23 | −0.19 | −0.68 | |
| 11142487–11144538 | 47 | 0.0050 | 0.0055 | 34 | −0.30 | −0.28 | −0.34 | |
| 11144758–11144891 | 2 | 0.0035 | 0.0032 | 3 | 0.17 | 0.73 | 0.66 | |
| Mean | 9.63 | 0.0028 | 0.0034 | 10.13 | −0.19 | 0.26 | 0.14 | |
| Southwest | 11135555–11136422 | 2 | 0.0001 | 0.0005 | 3 | −1.44 | −2.63 * | −2.64 * |
| 11137806–11137884 | 0 | 0.0000 | 0.0000 | 1 | / | 0.00 | 0.00 | |
| 11138254–11138321 | 0 | 0.0000 | 0.0000 | 1 | / | 0.00 | 0.00 | |
| 11138432–11138582 | 1 | 0.0006 | 0.0014 | 2 | −0.71 | 0.53 | 0.19 | |
| 11139034–11139707 | 0 | 0.0000 | 0.0000 | 1 | / | 0.00 | 0.00 | |
| 11140636–11141367 | 8 | 0.0117 | 0.0134 | 16 | −0.42 | 1.61 * | 1.01 | |
| 11142487–11144538 | 9 | 0.0006 | 0.0009 | 11 | −1.07 | −2.10 | −2.08 | |
| 11144758–11144891 | 1 | 0.0005 | 0.0016 | 2 | −0.89 | 0.53 | 0.13 | |
| Mean | 2.63 | 0.0017 | 0.0022 | 4.63 | −0.9 | −0.26 | −0.42 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Zhang, J.; Hui, N.; Wang, L.; Tian, Y.; Ni, W.; Long, J.; Jiang, L.; Li, Y.; Diao, S.; et al. A Genomic Quantitative Study on the Contribution of the Ancestral-State Bases Relative to Derived Bases in the Divergence and Local Adaptation of Populus davidiana. Genes 2023, 14, 821. https://doi.org/10.3390/genes14040821
Zhao D, Zhang J, Hui N, Wang L, Tian Y, Ni W, Long J, Jiang L, Li Y, Diao S, et al. A Genomic Quantitative Study on the Contribution of the Ancestral-State Bases Relative to Derived Bases in the Divergence and Local Adaptation of Populus davidiana. Genes. 2023; 14(4):821. https://doi.org/10.3390/genes14040821
Chicago/Turabian StyleZhao, Dandan, Jianguo Zhang, Nan Hui, Li Wang, Yang Tian, Wanning Ni, Jinhua Long, Li Jiang, Yi Li, Songfeng Diao, and et al. 2023. "A Genomic Quantitative Study on the Contribution of the Ancestral-State Bases Relative to Derived Bases in the Divergence and Local Adaptation of Populus davidiana" Genes 14, no. 4: 821. https://doi.org/10.3390/genes14040821
APA StyleZhao, D., Zhang, J., Hui, N., Wang, L., Tian, Y., Ni, W., Long, J., Jiang, L., Li, Y., Diao, S., Li, J., Tembrock, L. R., Wu, Z., & Wang, Z. (2023). A Genomic Quantitative Study on the Contribution of the Ancestral-State Bases Relative to Derived Bases in the Divergence and Local Adaptation of Populus davidiana. Genes, 14(4), 821. https://doi.org/10.3390/genes14040821






