Inferring Cell–Cell Communications from Spatially Resolved Transcriptomics Data Using a Bayesian Tweedie Model
Abstract
:1. Introduction
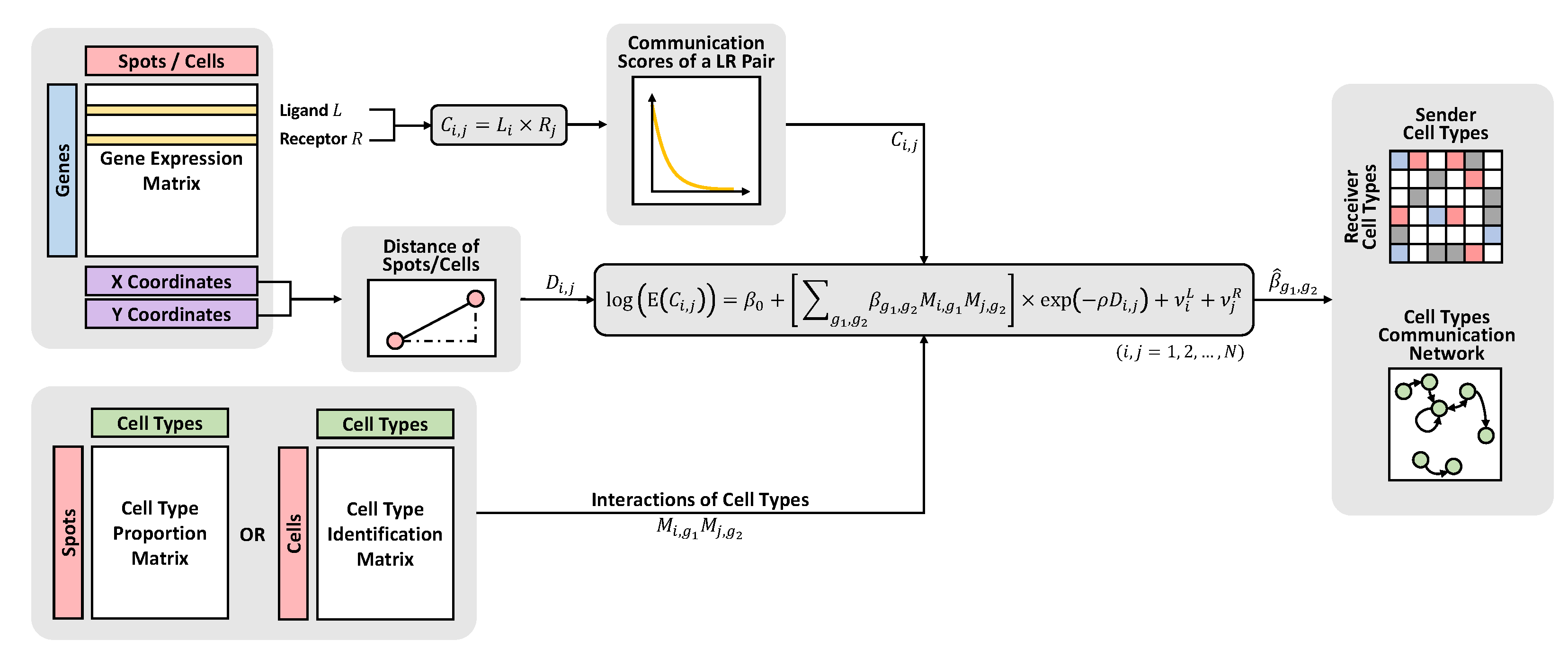
2. Materials and Methods
2.1. Spot-to-Spot Communication Score
2.2. BATCOM Model Structure
2.3. Compound Poisson–Gamma Distribution
2.4. Model Inference
2.4.1. Parameter Estimation
2.4.2. Hypothesis Testing
3. Results
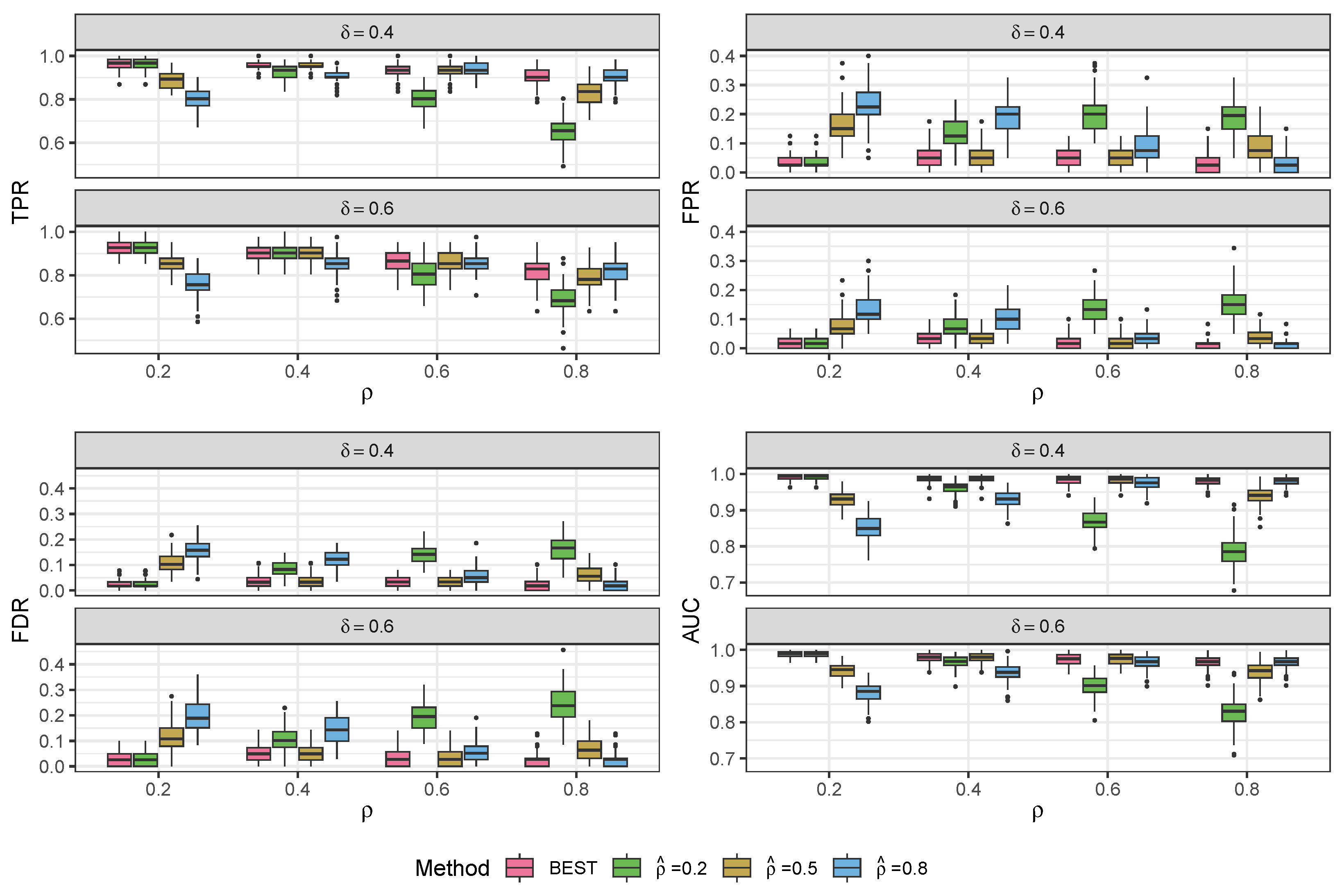
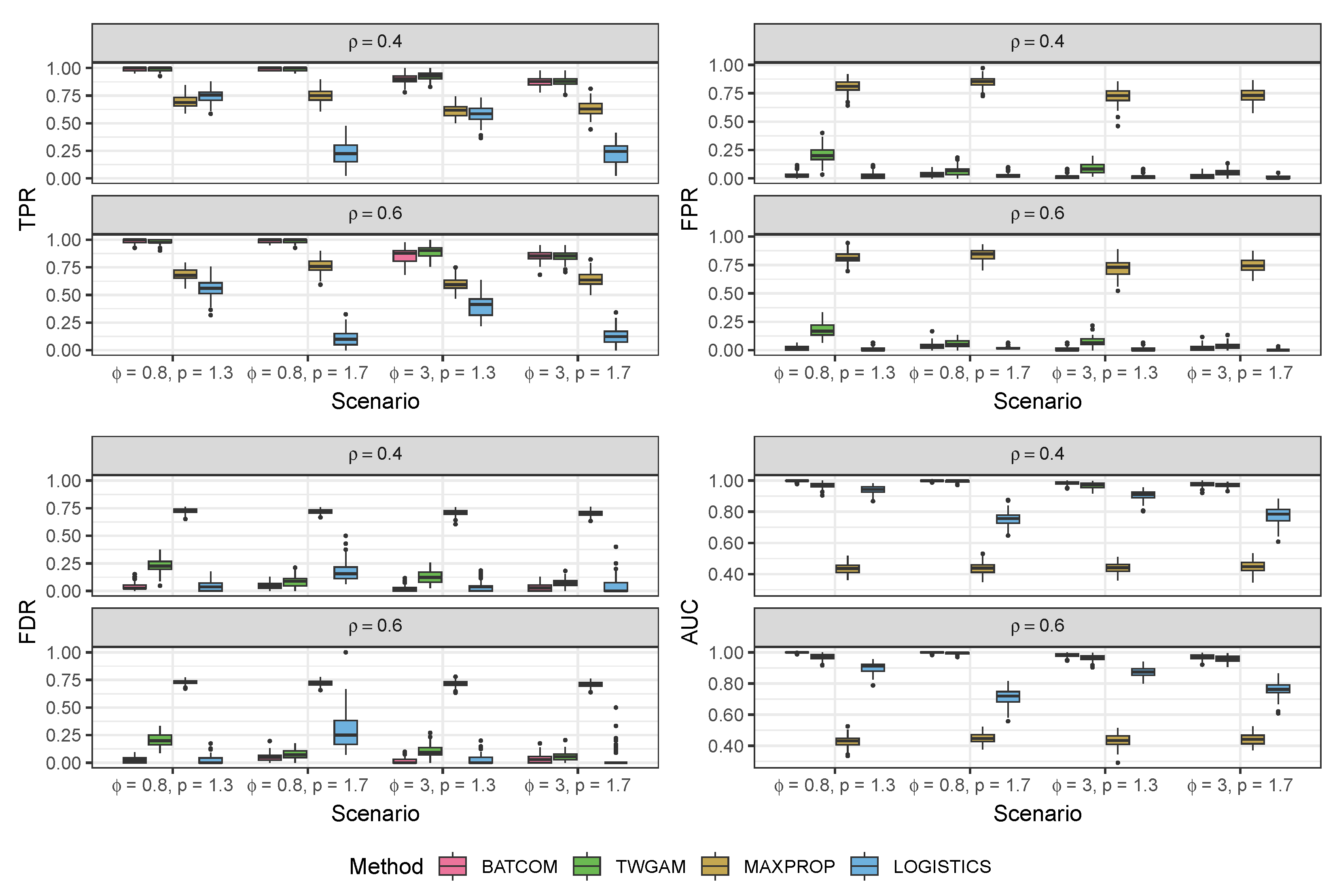
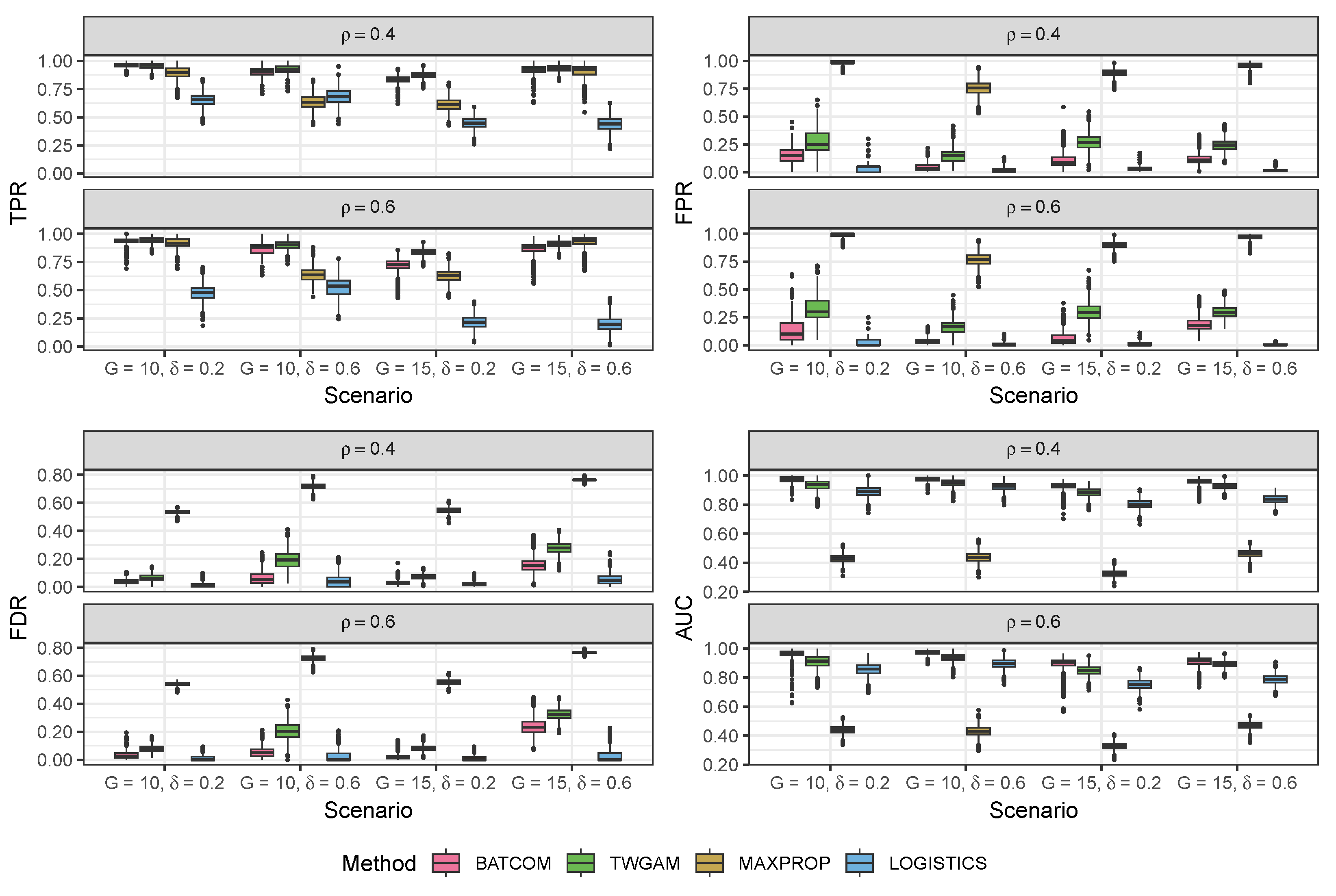
3.1. Simulation Study
3.1.1. Data Generated from the Compound Poisson-Gamma Model
3.1.2. Data Generated from the Pseudo-Hurdle Gamma Model
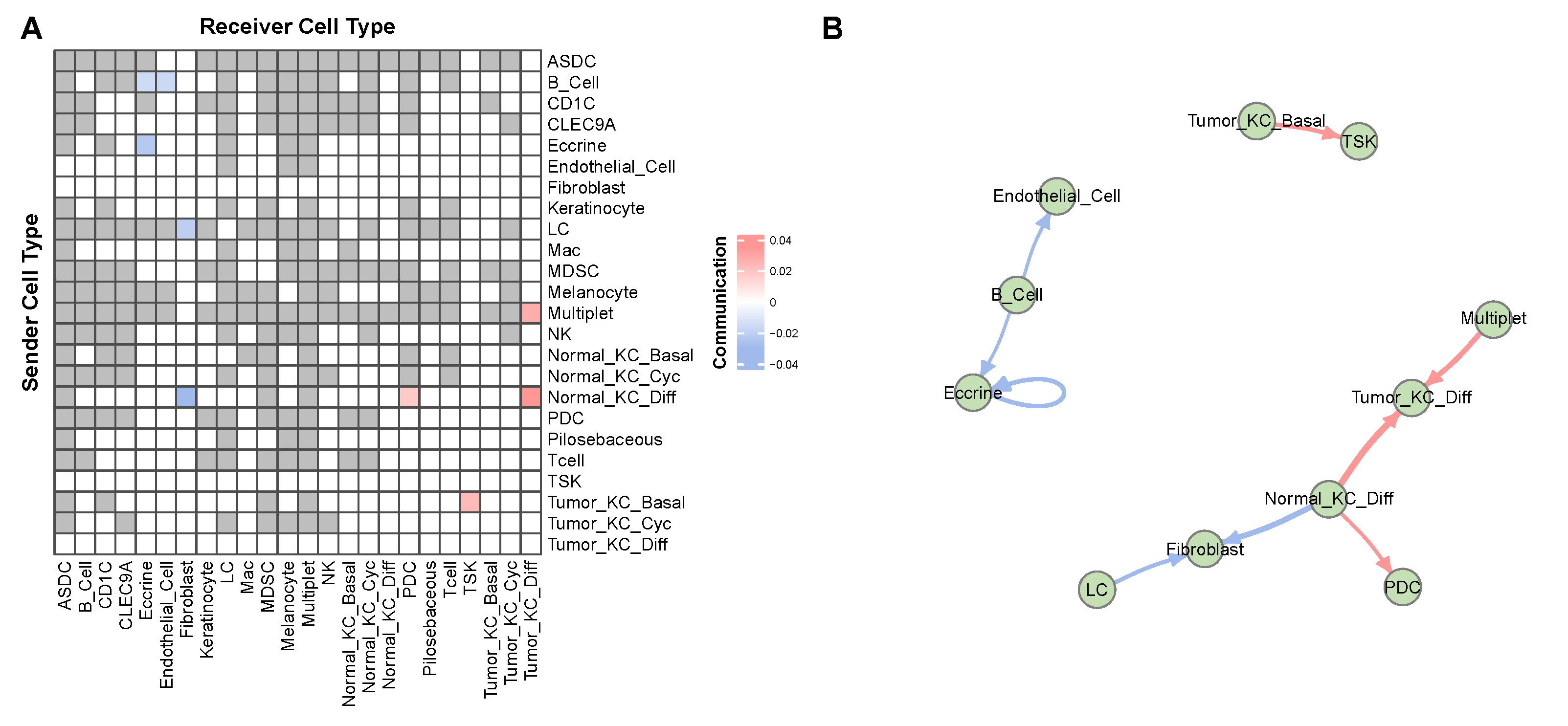
3.2. Case Study
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Closed Form of the Gradient of the Log-Posterior Density Function
Appendix B. The Detailed Numerical Results of Simulation Studies
| TPR | FPR | FDR | AUC | TPR | FPR | FDR | AUC | ||
|---|---|---|---|---|---|---|---|---|---|
| , , , | |||||||||
| BEST | 0.96 (0.03) | 0.04 (0.03) | 0.03 (0.02) | 0.99 (0.01) | 0.92 (0.03) | 0.02 (0.02) | 0.03 (0.03) | 0.99 (0.01) | |
| 0.96 (0.03) | 0.04 (0.03) | 0.03 (0.02) | 0.99 (0.01) | 0.92 (0.03) | 0.02 (0.02) | 0.03 (0.03) | 0.99 (0.01) | ||
| 0.89 (0.04) | 0.17 (0.06) | 0.11 (0.04) | 0.93 (0.02) | 0.85 (0.05) | 0.08 (0.04) | 0.12 (0.05) | 0.94 (0.02) | ||
| 0.81 (0.05) | 0.23 (0.07) | 0.16 (0.04) | 0.85 (0.03) | 0.76 (0.06) | 0.13 (0.06) | 0.20 (0.07) | 0.88 (0.03) | ||
| , , , | |||||||||
| BEST | 0.96 (0.02) | 0.06 (0.04) | 0.04 (0.03) | 0.99 (0.01) | 0.89 (0.04) | 0.03 (0.02) | 0.05 (0.04) | 0.98 (0.01) | |
| 0.93 (0.03) | 0.13 (0.05) | 0.08 (0.03) | 0.96 (0.02) | 0.90 (0.04) | 0.08 (0.04) | 0.11 (0.05) | 0.97 (0.02) | ||
| 0.96 (0.02) | 0.06 (0.04) | 0.04 (0.03) | 0.99 (0.01) | 0.89 (0.04) | 0.03 (0.02) | 0.05 (0.04) | 0.98 (0.01) | ||
| 0.91 (0.03) | 0.20 (0.06) | 0.12 (0.03) | 0.93 (0.02) | 0.85 (0.05) | 0.10 (0.05) | 0.14 (0.06) | 0.94 (0.02) | ||
| , , , | |||||||||
| BEST | 0.93 (0.04) | 0.05 (0.03) | 0.03 (0.02) | 0.98 (0.01) | 0.86 (0.05) | 0.02 (0.02) | 0.04 (0.03) | 0.97 (0.02) | |
| 0.80 (0.06) | 0.20 (0.06) | 0.14 (0.03) | 0.87 (0.03) | 0.80 (0.06) | 0.14 (0.05) | 0.20 (0.06) | 0.90 (0.03) | ||
| 0.93 (0.04) | 0.05 (0.03) | 0.03 (0.02) | 0.98 (0.01) | 0.86 (0.05) | 0.02 (0.02) | 0.04 (0.04) | 0.97 (0.02) | ||
| 0.94 (0.03) | 0.09 (0.05) | 0.05 (0.03) | 0.97 (0.02) | 0.86 (0.05) | 0.03 (0.03) | 0.05 (0.04) | 0.96 (0.02) | ||
| , , , | |||||||||
| BEST | 0.91 (0.04) | 0.03 (0.03) | 0.02 (0.02) | 0.98 (0.01) | 0.81 (0.06) | 0.02 (0.02) | 0.03 (0.03) | 0.97 (0.02) | |
| 0.65 (0.06) | 0.19 (0.06) | 0.16 (0.05) | 0.79 (0.04) | 0.69 (0.07) | 0.15 (0.05) | 0.24 (0.07) | 0.83 (0.04) | ||
| 0.83 (0.05) | 0.09 (0.05) | 0.06 (0.03) | 0.94 (0.02) | 0.78 (0.06) | 0.04 (0.03) | 0.07 (0.05) | 0.94 (0.03) | ||
| 0.91 (0.04) | 0.03 (0.03) | 0.02 (0.02) | 0.98 (0.01) | 0.81 (0.06) | 0.02 (0.02) | 0.03 (0.03) | 0.97 (0.02) | ||
| TPR | FPR | FDR | AUC | TPR | FPR | FDR | AUC | ||
|---|---|---|---|---|---|---|---|---|---|
| , , , | |||||||||
| BATCOM | 0.99 (0.01) | 0.03 (0.03) | 0.04 (0.04) | 1.00 (0.00) | 0.99 (0.02) | 0.02 (0.02) | 0.03 (0.02) | 1.00 (0.00) | |
| TWGAM | 0.99 (0.02) | 0.20 (0.06) | 0.23 (0.06) | 0.97 (0.02) | 0.98 (0.02) | 0.18 (0.06) | 0.21 (0.06) | 0.97 (0.02) | |
| MAXPROP | 0.69 (0.06) | 0.81 (0.06) | 0.73 (0.02) | 0.43 (0.04) | 0.68 (0.05) | 0.81 (0.05) | 0.73 (0.02) | 0.43 (0.04) | |
| LOGISTICS | 0.75 (0.06) | 0.03 (0.03) | 0.05 (0.04) | 0.94 (0.03) | 0.56 (0.08) | 0.01 (0.01) | 0.03 (0.04) | 0.90 (0.03) | |
| , , , | |||||||||
| BATCOM | 0.99 (0.01) | 0.04 (0.02) | 0.05 (0.03) | 1.00 (0.00) | 0.99 (0.01) | 0.03 (0.03) | 0.05 (0.03) | 1.00 (0.00) | |
| TWGAM | 0.99 (0.01) | 0.06 (0.04) | 0.08 (0.05) | 1.00 (0.01) | 0.98 (0.02) | 0.06 (0.03) | 0.08 (0.04) | 0.99 (0.01) | |
| MAXPROP | 0.75 (0.06) | 0.85 (0.05) | 0.72 (0.02) | 0.44 (0.04) | 0.76 (0.06) | 0.84 (0.05) | 0.72 (0.02) | 0.45 (0.03) | |
| LOGISTICS | 0.22 (0.10) | 0.03 (0.02) | 0.17 (0.09) | 0.75 (0.04) | 0.10 (0.07) | 0.02 (0.01) | 0.34 (0.25) | 0.72 (0.05) | |
| , , , | |||||||||
| BATCOM | 0.90 (0.05) | 0.01 (0.02) | 0.02 (0.03) | 0.98 (0.01) | 0.86 (0.06) | 0.01 (0.02) | 0.02 (0.03) | 0.98 (0.01) | |
| TWGAM | 0.92 (0.04) | 0.09 (0.05) | 0.13 (0.06) | 0.97 (0.02) | 0.89 (0.05) | 0.07 (0.04) | 0.10 (0.05) | 0.96 (0.02) | |
| MAXPROP | 0.61 (0.06) | 0.72 (0.07) | 0.71 (0.02) | 0.44 (0.03) | 0.60 (0.06) | 0.73 (0.07) | 0.72 (0.02) | 0.43 (0.04) | |
| LOGISTICS | 0.59 (0.08) | 0.02 (0.02) | 0.04 (0.04) | 0.91 (0.03) | 0.40 (0.09) | 0.01 (0.01) | 0.02 (0.04) | 0.87 (0.03) | |
| , , , | |||||||||
| BATCOM | 0.87 (0.04) | 0.02 (0.02) | 0.04 (0.03) | 0.98 (0.01) | 0.85 (0.05) | 0.02 (0.02) | 0.04 (0.03) | 0.97 (0.02) | |
| TWGAM | 0.88 (0.04) | 0.04 (0.03) | 0.06 (0.04) | 0.97 (0.01) | 0.85 (0.05) | 0.04 (0.03) | 0.06 (0.04) | 0.96 (0.02) | |
| MAXPROP | 0.63 (0.06) | 0.73 (0.06) | 0.70 (0.03) | 0.45 (0.04) | 0.64 (0.06) | 0.75 (0.06) | 0.71 (0.03) | 0.44 (0.03) | |
| LOGISTICS | 0.23 (0.09) | 0.01 (0.01) | 0.05 (0.08) | 0.78 (0.06) | 0.12 (0.08) | 0.00 (0.01) | 0.04 (0.08) | 0.76 (0.05) | |
| TPR | FPR | FDR | AUC | TPR | FPR | FDR | AUC | ||
|---|---|---|---|---|---|---|---|---|---|
| , , , | |||||||||
| 0.99 (0.01) | 0.03 (0.03) | 0.04 (0.04) | 1.00 (0.00) | 0.99 (0.02) | 0.02 (0.02) | 0.03 (0.02) | 1.00 (0.00) | ||
| 0.99 (0.01) | 0.03 (0.03) | 0.04 (0.03) | 1.00 (0.00) | 0.99 (0.01) | 0.02 (0.02) | 0.03 (0.03) | 1.00 (0.00) | ||
| 0.99 (0.02) | 0.03 (0.03) | 0.04 (0.03) | 1.00 (0.00) | 0.99 (0.02) | 0.02 (0.02) | 0.03 (0.03) | 1.00 (0.00) | ||
| 0.98 (0.02) | 0.03 (0.03) | 0.04 (0.03) | 1.00 (0.00) | 0.98 (0.02) | 0.02 (0.02) | 0.03 (0.03) | 1.00 (0.00) | ||
| , , , | |||||||||
| 0.99 (0.01) | 0.04 (0.02) | 0.05 (0.03) | 1.00 (0.00) | 0.99 (0.01) | 0.03 (0.03) | 0.05 (0.03) | 1.00 (0.00) | ||
| 0.99 (0.01) | 0.04 (0.02) | 0.05 (0.03) | 1.00 (0.00) | 0.99 (0.01) | 0.03 (0.03) | 0.05 (0.03) | 1.00 (0.00) | ||
| 0.99 (0.01) | 0.04 (0.02) | 0.05 (0.03) | 1.00 (0.00) | 0.99 (0.01) | 0.03 (0.03) | 0.05 (0.03) | 1.00 (0.00) | ||
| 0.99 (0.02) | 0.04 (0.03) | 0.05 (0.04) | 1.00 (0.01) | 0.99 (0.02) | 0.03 (0.03) | 0.04 (0.03) | 1.00 (0.00) | ||
| , , , | |||||||||
| 0.90 (0.05) | 0.01 (0.02) | 0.02 (0.03) | 0.98 (0.01) | 0.86 (0.06) | 0.01 (0.02) | 0.02 (0.03) | 0.98 (0.01) | ||
| 0.90 (0.05) | 0.02 (0.02) | 0.02 (0.03) | 0.98 (0.01) | 0.86 (0.06) | 0.01 (0.02) | 0.02 (0.03) | 0.98 (0.01) | ||
| 0.90 (0.05) | 0.02 (0.02) | 0.03 (0.03) | 0.98 (0.01) | 0.86 (0.06) | 0.01 (0.02) | 0.02 (0.03) | 0.98 (0.01) | ||
| 0.88 (0.05) | 0.02 (0.02) | 0.03 (0.03) | 0.98 (0.01) | 0.84 (0.06) | 0.01 (0.02) | 0.02 (0.03) | 0.97 (0.02) | ||
| , , , | |||||||||
| 0.87 (0.04) | 0.02 (0.02) | 0.04 (0.03) | 0.98 (0.01) | 0.85 (0.05) | 0.02 (0.02) | 0.04 (0.03) | 0.97 (0.02) | ||
| 0.87 (0.04) | 0.02 (0.02) | 0.04 (0.03) | 0.98 (0.01) | 0.85 (0.05) | 0.02 (0.02) | 0.04 (0.03) | 0.97 (0.02) | ||
| 0.86 (0.04) | 0.02 (0.02) | 0.04 (0.04) | 0.97 (0.02) | 0.84 (0.05) | 0.02 (0.02) | 0.03 (0.03) | 0.97 (0.02) | ||
| 0.83 (0.05) | 0.02 (0.02) | 0.03 (0.03) | 0.97 (0.02) | 0.81 (0.06) | 0.02 (0.02) | 0.03 (0.03) | 0.96 (0.02) | ||
| TPR | FPR | FDR | AUC | TPR | FPR | FDR | AUC | ||
|---|---|---|---|---|---|---|---|---|---|
| , | |||||||||
| BATCOM | 0.96 (0.02) | 0.16 (0.09) | 0.04 (0.02) | 0.97 (0.02) | 0.94 (0.03) | 0.13 (0.08) | 0.03 (0.02) | 0.96 (0.03) | |
| TWGAM | 0.96 (0.02) | 0.27 (0.11) | 0.07 (0.02) | 0.93 (0.04) | 0.94 (0.03) | 0.32 (0.11) | 0.08 (0.03) | 0.91 (0.04) | |
| MAXPROP | 0.89 (0.05) | 0.98 (0.02) | 0.53 (0.01) | 0.43 (0.03) | 0.92 (0.05) | 0.99 (0.02) | 0.54 (0.01) | 0.44 (0.03) | |
| LOGISTICS | 0.65 (0.06) | 0.04 (0.05) | 0.01 (0.02) | 0.89 (0.03) | 0.48 (0.07) | 0.02 (0.03) | 0.01 (0.01) | 0.86 (0.04) | |
| , | |||||||||
| BATCOM | 0.90 (0.04) | 0.04 (0.03) | 0.06 (0.04) | 0.97 (0.02) | 0.87 (0.05) | 0.03 (0.03) | 0.05 (0.04) | 0.97 (0.02) | |
| TWGAM | 0.92 (0.04) | 0.15 (0.06) | 0.19 (0.06) | 0.95 (0.02) | 0.90 (0.04) | 0.16 (0.06) | 0.21 (0.06) | 0.94 (0.03) | |
| MAXPROP | 0.63 (0.06) | 0.76 (0.06) | 0.72 (0.02) | 0.44 (0.03) | 0.64 (0.06) | 0.77 (0.06) | 0.72 (0.02) | 0.43 (0.04) | |
| LOGISTICS | 0.69 (0.07) | 0.02 (0.02) | 0.04 (0.04) | 0.92 (0.03) | 0.53 (0.08) | 0.01 (0.01) | 0.03 (0.04) | 0.90 (0.03) | |
| , | |||||||||
| BATCOM | 0.84 (0.03) | 0.10 (0.05) | 0.03 (0.01) | 0.93 (0.02) | 0.72 (0.05) | 0.06 (0.05) | 0.02 (0.02) | 0.90 (0.04) | |
| TWGAM | 0.87 (0.03) | 0.27 (0.08) | 0.07 (0.02) | 0.88 (0.03) | 0.84 (0.03) | 0.30 (0.08) | 0.08 (0.02) | 0.85 (0.03) | |
| MAXPROP | 0.61 (0.05) | 0.89 (0.03) | 0.55 (0.02) | 0.33 (0.02) | 0.63 (0.06) | 0.90 (0.03) | 0.56 (0.02) | 0.33 (0.02) | |
| LOGISTICS | 0.45 (0.05) | 0.03 (0.03) | 0.02 (0.02) | 0.80 (0.03) | 0.21 (0.06) | 0.01 (0.01) | 0.01 (0.02) | 0.75 (0.04) | |
| , | |||||||||
| BATCOM | 0.92 (0.03) | 0.12 (0.04) | 0.16 (0.05) | 0.96 (0.02) | 0.87 (0.05) | 0.18 (0.06) | 0.24 (0.06) | 0.91 (0.03) | |
| TWGAM | 0.93 (0.03) | 0.24 (0.05) | 0.28 (0.04) | 0.93 (0.02) | 0.91 (0.03) | 0.30 (0.05) | 0.32 (0.04) | 0.89 (0.02) | |
| MAXPROP | 0.91 (0.06) | 0.96 (0.03) | 0.76 (0.01) | 0.46 (0.03) | 0.94 (0.05) | 0.97 (0.02) | 0.77 (0.01) | 0.47 (0.02) | |
| LOGISTICS | 0.44 (0.06) | 0.02 (0.01) | 0.05 (0.04) | 0.84 (0.03) | 0.20 (0.06) | 0.00 (0.01) | 0.03 (0.04) | 0.79 (0.03) | |
References
- Almet, A.A.; Cang, Z.; Jin, S.; Nie, Q. The landscape of cell–cell communication through single-cell transcriptomics. Curr. Opin. Syst. Biol. 2021, 26, 12–23. [Google Scholar] [CrossRef]
- Armingol, E.; Officer, A.; Harismendy, O.; Lewis, N.E. Deciphering cell–cell interactions and communication from gene expression. Nat. Rev. Genet. 2021, 22, 71–88. [Google Scholar] [CrossRef]
- Efremova, M.; Vento-Tormo, M.; Teichmann, S.A.; Vento-Tormo, R. CellPhoneDB: Inferring cell–cell communication from combined expression of multi-subunit ligand–receptor complexes. Nat. Protoc. 2020, 15, 1484–1506. [Google Scholar] [CrossRef]
- Cabello-Aguilar, S.; Alame, M.; Kon-Sun-Tack, F.; Fau, C.; Lacroix, M.; Colinge, J. SingleCellSignalR: Inference of intercellular networks from single-cell transcriptomics. Nucleic Acids Res. 2020, 48, e55. [Google Scholar] [CrossRef] [Green Version]
- Jin, S.; Guerrero-Juarez, C.F.; Zhang, L.; Chang, I.; Ramos, R.; Kuan, C.H.; Myung, P.; Plikus, M.V.; Nie, Q. Inference and analysis of cell-cell communication using CellChat. Nat. Commun. 2021, 12, 1088. [Google Scholar] [CrossRef]
- Dries, R.; Zhu, Q.; Dong, R.; Eng, C.H.L.; Li, H.; Liu, K.; Fu, Y.; Zhao, T.; Sarkar, A.; Bao, F.; et al. Giotto: A toolbox for integrative analysis and visualization of spatial expression data. Genome Biol. 2021, 22, 78. [Google Scholar] [CrossRef]
- Cang, Z.; Nie, Q. Inferring spatial and signaling relationships between cells from single cell transcriptomic data. Nat. Commun. 2020, 11, 2084. [Google Scholar] [CrossRef] [PubMed]
- Cang, Z.; Zhao, Y.; Almet, A.A.; Stabell, A.; Ramos, R.; Plikus, M.V.; Atwood, S.X.; Nie, Q. Screening cell–cell communication in spatial transcriptomics via collective optimal transport. Nat. Methods 2023, 20, 218–228. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.; Li, C.; Yang, H.; Lu, X.; Liao, J.; Qian, J.; Wang, K.; Cheng, J.; Yang, P.; Chen, H.; et al. Knowledge-graph-based cell-cell communication inference for spatially resolved transcriptomic data with SpaTalk. Nat. Commun. 2022, 13, 4429. [Google Scholar] [CrossRef] [PubMed]
- Heydari, A.A.; Sindi, S.S. Deep learning in spatial transcriptomics: Learning from the next next-generation sequencing. Biophys. Rev. 2023, 4, 011306. [Google Scholar] [CrossRef]
- Eng, C.H.L.; Lawson, M.; Zhu, Q.; Dries, R.; Koulena, N.; Takei, Y.; Yun, J.; Cronin, C.; Karp, C.; Yuan, G.C.; et al. Transcriptome-scale super-resolved imaging in tissues by RNA seqFISH+. Nature 2019, 568, 235–239. [Google Scholar] [CrossRef]
- Wang, X.; Allen, W.E.; Wright, M.A.; Sylwestrak, E.L.; Samusik, N.; Vesuna, S.; Evans, K.; Liu, C.; Ramakrishnan, C.; Liu, J.; et al. Three-dimensional intact-tissue sequencing of single-cell transcriptional states. Science 2018, 361, eaat5691. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ståhl, P.L.; Salmén, F.; Vickovic, S.; Lundmark, A.; Navarro, J.F.; Magnusson, J.; Giacomello, S.; Asp, M.; Westholm, J.O.; Huss, M.; et al. Visualization and analysis of gene expression in tissue sections by spatial transcriptomics. Science 2016, 353, 78–82. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Salmén, F.; Ståhl, P.L.; Mollbrink, A.; Navarro, J.F.; Vickovic, S.; Frisen, J.; Lundeberg, J. Barcoded solid-phase RNA capture for Spatial Transcriptomics profiling in mammalian tissue sections. Nat. Protoc. 2018, 13, 2501–2534. [Google Scholar] [CrossRef]
- Stickels, R.R.; Murray, E.; Kumar, P.; Li, J.; Marshall, J.L.; Di Bella, D.J.; Arlotta, P.; Macosko, E.Z.; Chen, F. Highly sensitive spatial transcriptomics at near-cellular resolution with Slide-seqV2. Nat. Biotechnol. 2021, 39, 313–319. [Google Scholar] [CrossRef] [PubMed]
- Cable, D.M.; Murray, E.; Zou, L.S.; Goeva, A.; Macosko, E.Z.; Chen, F.; Irizarry, R.A. Robust decomposition of cell type mixtures in spatial transcriptomics. Nat. Biotechnol. 2022, 40, 517–526. [Google Scholar] [CrossRef]
- Elosua-Bayes, M.; Nieto, P.; Mereu, E.; Gut, I.; Heyn, H. SPOTlight: Seeded NMF regression to deconvolute spatial transcriptomics spots with single-cell transcriptomes. Nucleic Acids Res. 2021, 49, e50. [Google Scholar] [CrossRef]
- Sun, D.; Liu, Z.; Li, T.; Wu, Q.; Wang, C. STRIDE: Accurately decomposing and integrating spatial transcriptomics using single-cell RNA sequencing. Nucleic Acids Res. 2022, 50, e42. [Google Scholar] [CrossRef]
- Shao, X.; Liao, J.; Li, C.; Lu, X.; Cheng, J.; Fan, X. CellTalkDB: A manually curated database of ligand–receptor interactions in humans and mice. Briefings Bioinform. 2021, 22, bbaa269. [Google Scholar] [CrossRef] [PubMed]
- Finak, G.; McDavid, A.; Yajima, M.; Deng, J.; Gersuk, V.; Shalek, A.K.; Slichter, C.K.; Miller, H.W.; McElrath, M.J.; Prlic, M.; et al. MAST: A flexible statistical framework for assessing transcriptional changes and characterizing heterogeneity in single-cell RNA sequencing data. Genome Biol. 2015, 16, 278. [Google Scholar] [CrossRef] [Green Version]
- Sekula, M.; Gaskins, J.; Datta, S. Detection of differentially expressed genes in discrete single-cell RNA sequencing data using a hurdle model with correlated random effects. Biometrics 2019, 75, 1051–1062. [Google Scholar] [CrossRef] [PubMed]
- Miao, Z.; Deng, K.; Wang, X.; Zhang, X. DEsingle for detecting three types of differential expression in single-cell RNA-seq data. Bioinformatics 2018, 34, 3223–3224. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dunn, P.K.; Smyth, G.K. Series evaluation of Tweedie exponential dispersion model densities. Stat. Comput. 2005, 15, 267–280. [Google Scholar] [CrossRef] [Green Version]
- Dunn, P.K.; Smyth, G.K. Evaluation of Tweedie exponential dispersion model densities by Fourier inversion. Stat. Comput. 2008, 18, 73–86. [Google Scholar] [CrossRef] [Green Version]
- Bonat, W.H.; Kokonendji, C.C. Flexible Tweedie regression models for continuous data. J. Stat. Comput. Simul. 2017, 87, 2138–2152. [Google Scholar] [CrossRef] [Green Version]
- Mallick, H.; Chatterjee, S.; Chowdhury, S.; Chatterjee, S.; Rahnavard, A.; Hicks, S.C. Differential expression of single-cell RNA-seq data using Tweedie models. Stat. Med. 2022, 41, 3492–3510. [Google Scholar] [CrossRef]
- Zhang, Y. Likelihood-based and Bayesian methods for Tweedie compound Poisson linear mixed models. Stat. Comput. 2013, 23, 743–757. [Google Scholar] [CrossRef]
- Smyth, G.K. Regression analysis of quantity data with exact zeros. In Proceedings of the Second Australia-Japan Workshop on Stochastic Models in Engineering, Technology and Management, Gold Coast, Australia, 17–19 July 1996; pp. 17–19. [Google Scholar]
- Gelman, A.; Carlin, J.; Stern, H.; Dunson, D.; Vehtari, A.; Rubin, D. Bayesian Data Analysis, 3rd ed.; Chapman and Hall/CRC: Boca Raton, FL, USA, 2013. [Google Scholar] [CrossRef]
- Matz, M.V.; Wright, R.M.; Scott, J.G. No control genes required: Bayesian analysis of qRT-PCR data. PLoS ONE 2013, 8, e71448. [Google Scholar] [CrossRef]
- Benjamini, Y.; Hochberg, Y. Controlling the false discovery rate: A practical and powerful approach to multiple testing. J. R. Stat. Soc. Ser. (Methodol.) 1995, 57, 289–300. [Google Scholar] [CrossRef]
- Wood, S.N. Generalized Additive Models: An Introduction with R; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Ji, A.L.; Rubin, A.J.; Thrane, K.; Jiang, S.; Reynolds, D.L.; Meyers, R.M.; Guo, M.G.; George, B.M.; Mollbrink, A.; Bergenstråhle, J.; et al. Multimodal analysis of composition and spatial architecture in human squamous cell carcinoma. Cell 2020, 182, 497–514. [Google Scholar] [CrossRef]
- Klein, R.M.; Bernstein, D.; Higgins, S.P.; Higgins, C.E.; Higgins, P.J. SERPINE 1 expression discriminates site-specific metastasis in human melanoma. Exp. Dermatol. 2012, 21, 551–554. [Google Scholar] [CrossRef] [Green Version]
- Jayachandran, A.; Anaka, M.; Prithviraj, P.; Hudson, C.; McKeown, S.J.; Lo, P.H.; Vella, L.J.; Goding, C.R.; Cebon, J.; Behren, A. Thrombospondin 1 promotes an aggressive phenotype through epithelial-to-mesenchymal transition in human melanoma. Oncotarget 2014, 5, 5782. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Keller-Pinter, A.; Gyulai-Nagy, S.; Becsky, D.; Dux, L.; Rovo, L. Syndecan-4 in tumor cell motility. Cancers 2021, 13, 3322. [Google Scholar] [CrossRef] [PubMed]
- Rezaie, Y.; Fattahi, F.; Mashinchi, B.; Kamyab Hesari, K.; Montazeri, S.; Kalantari, E.; Madjd, Z.; Saeednejad Zanjani, L. High expression of Talin-1 is associated with tumor progression and recurrence in melanoma skin cancer patients. BMC Cancer 2023, 23, 302. [Google Scholar] [CrossRef] [PubMed]
- Chen, G.; Sun, J.; Xie, M.; Yu, S.; Tang, Q.; Chen, L. PLAU promotes cell proliferation and epithelial-mesenchymal transition in head and neck squamous cell carcinoma. Front. Genet. 2021, 12, 651882. [Google Scholar] [CrossRef]
- Fang, L.; Che, Y.; Zhang, C.; Huang, J.; Lei, Y.; Lu, Z.; Sun, N.; He, J. PLAU directs conversion of fibroblasts to inflammatory cancer-associated fibroblasts, promoting esophageal squamous cell carcinoma progression via uPAR/Akt/NF-κB/IL8 pathway. Cell Death Discov. 2021, 7, 32. [Google Scholar] [CrossRef]
- Zhou, C.; Shen, Y.; Wei, Z.; Shen, Z.; Tang, M.; Shen, Y.; Deng, H. ITGA5 is an independent prognostic biomarker and potential therapeutic target for laryngeal squamous cell carcinoma. J. Clin. Lab. Anal. 2022, 36, e24228. [Google Scholar] [CrossRef]
- Fan, Q.C.; Tian, H.; Wang, Y.; Liu, X.B. Integrin-α5 promoted the progression of oral squamous cell carcinoma and modulated PI3K/AKT signaling pathway. Arch. Oral Biol. 2019, 101, 85–91. [Google Scholar] [CrossRef]
- McMillen, P.; Oudin, M.J.; Levin, M.; Payne, S.L. Beyond neurons: Long distance communication in development and cancer. Front. Cell Dev. Biol. 2021, 9, 739024. [Google Scholar] [CrossRef]
- Li, B.; Zhang, W.; Guo, C.; Xu, H.; Li, L.; Fang, M.; Hu, Y.; Zhang, X.; Yao, X.; Tang, M.; et al. Benchmarking spatial and single-cell transcriptomics integration methods for transcript distribution prediction and cell type deconvolution. Nat. Methods 2022, 19, 662–670. [Google Scholar] [CrossRef]


| Ligand | Receptor | Sender Cell Type | Receiver Cell Type |
|---|---|---|---|
| SERPINE1 | ITGB5 | Fibroblast | TSK |
| SERPINE1 | ITGB5 | TSK | Fibroblast |
| THBS1 | SDC4 | Fibroblast | TSK |
| PLAU | ITGB5 | TSK | Fibroblast |
| TLN1 | ITGB5 | TSK | Tumor KC Diff |
| PLAU | MRC2 | TSK | Fibroblast |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, D.; Gaskins, J.T.; Sekula, M.; Datta, S. Inferring Cell–Cell Communications from Spatially Resolved Transcriptomics Data Using a Bayesian Tweedie Model. Genes 2023, 14, 1368. https://doi.org/10.3390/genes14071368
Wu D, Gaskins JT, Sekula M, Datta S. Inferring Cell–Cell Communications from Spatially Resolved Transcriptomics Data Using a Bayesian Tweedie Model. Genes. 2023; 14(7):1368. https://doi.org/10.3390/genes14071368
Chicago/Turabian StyleWu, Dongyuan, Jeremy T. Gaskins, Michael Sekula, and Susmita Datta. 2023. "Inferring Cell–Cell Communications from Spatially Resolved Transcriptomics Data Using a Bayesian Tweedie Model" Genes 14, no. 7: 1368. https://doi.org/10.3390/genes14071368
APA StyleWu, D., Gaskins, J. T., Sekula, M., & Datta, S. (2023). Inferring Cell–Cell Communications from Spatially Resolved Transcriptomics Data Using a Bayesian Tweedie Model. Genes, 14(7), 1368. https://doi.org/10.3390/genes14071368



_Wang.jpg)



