coiTAD: Detection of Topologically Associating Domains Based on Clustering of Circular Influence Features from Hi-C Data
Abstract
1. Introduction
Background
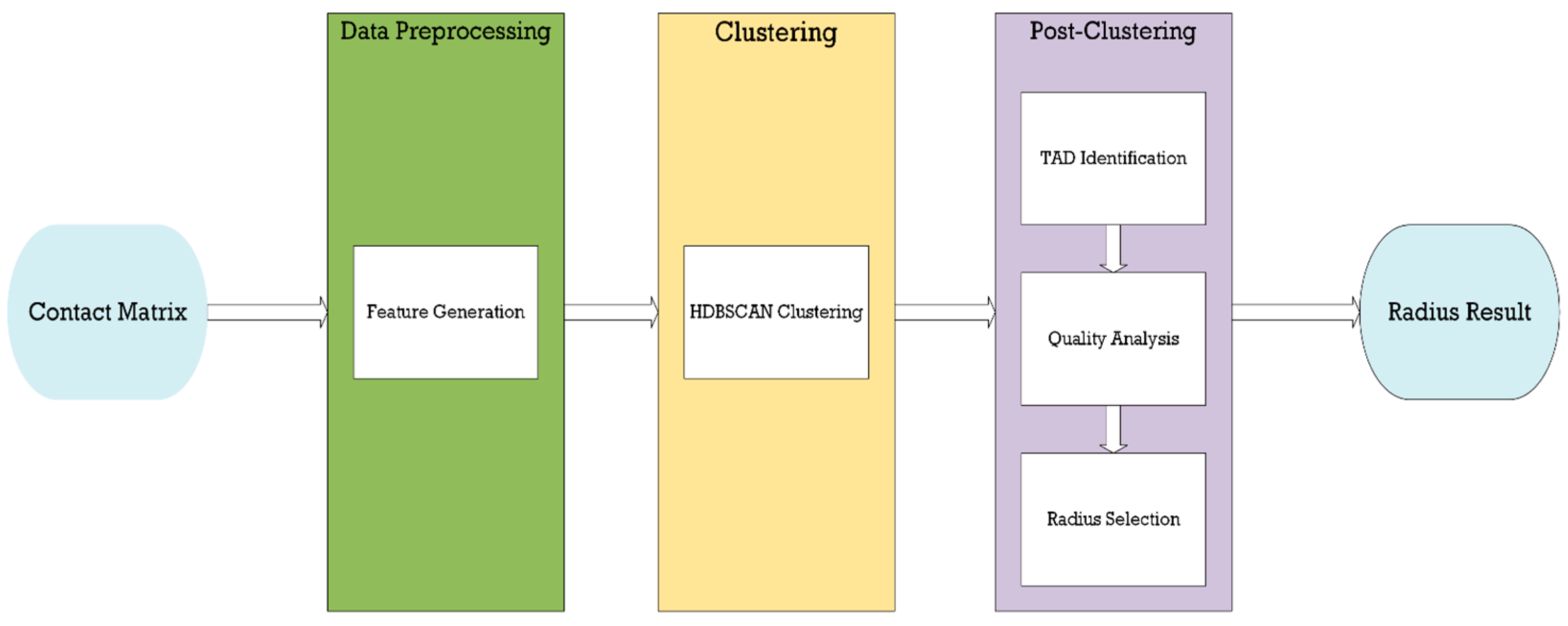
2. Methods
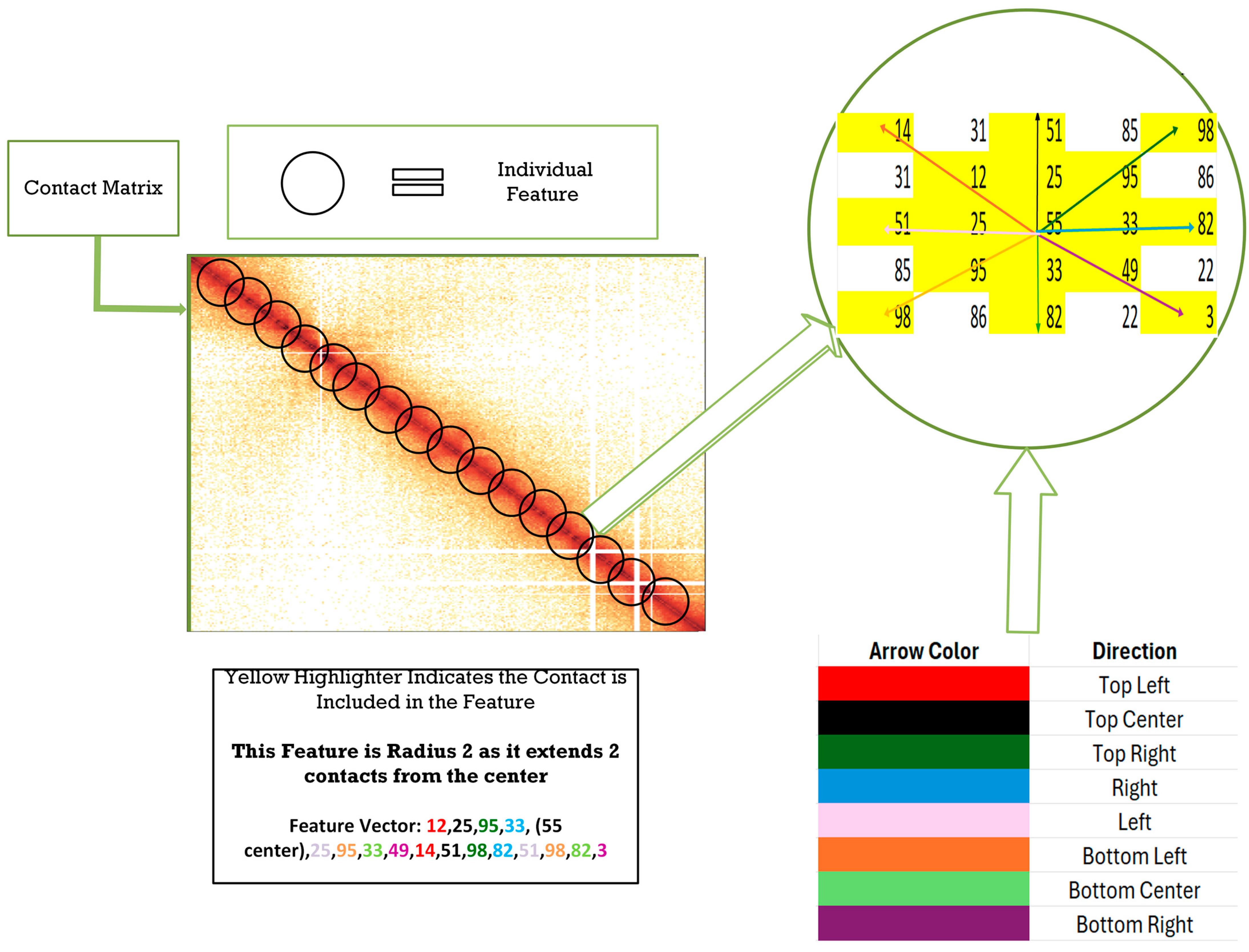
2.1. Feature Generation
2.2. Circle Feature
2.3. Semi-Circle Feature
2.4. HDBSCAN Clustering
2.5. TAD Identification
2.6. Radius Selection/TAD Quality
3. Results and Discussion
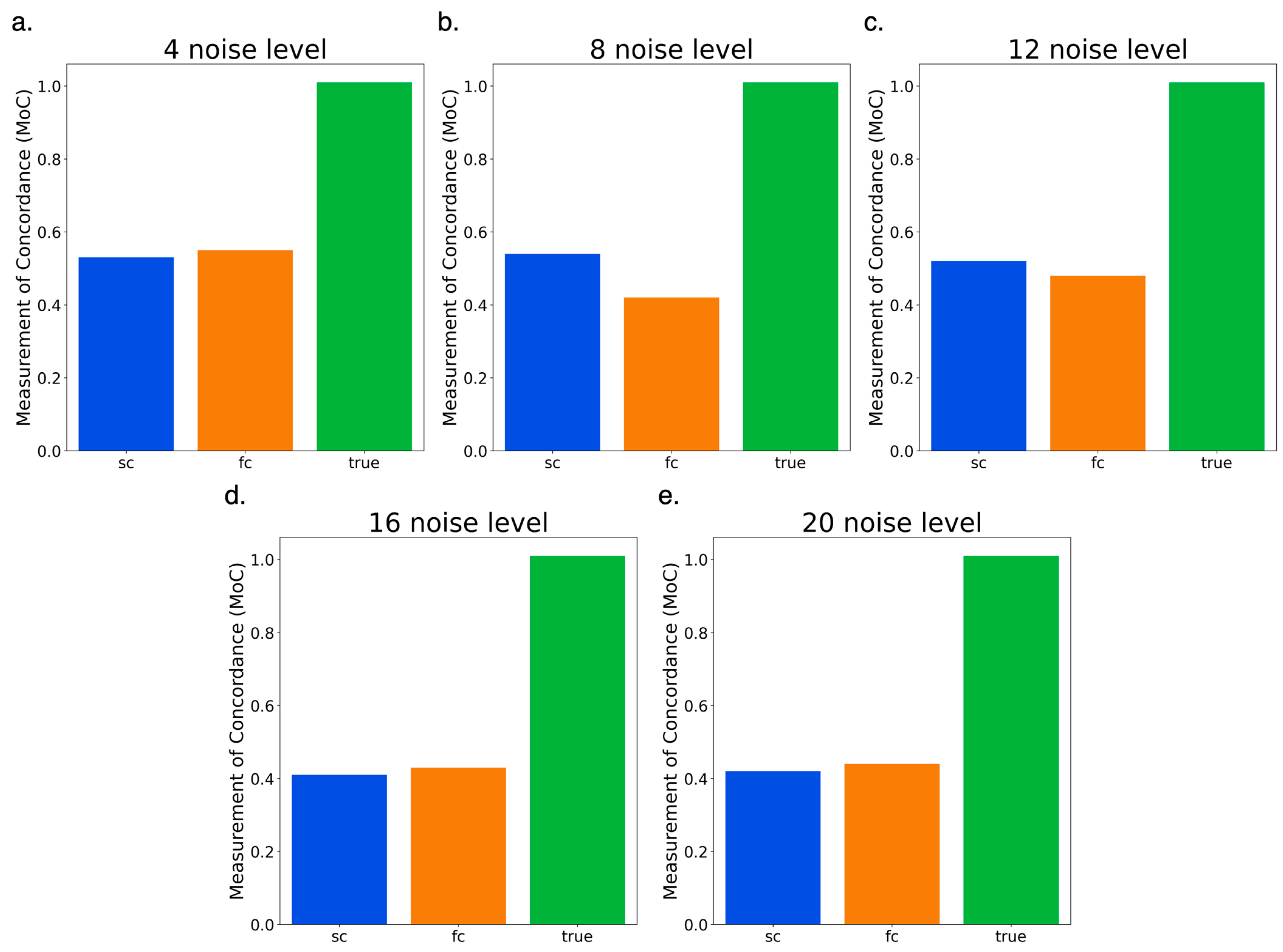
3.1. Assessment on Simulated Dataset
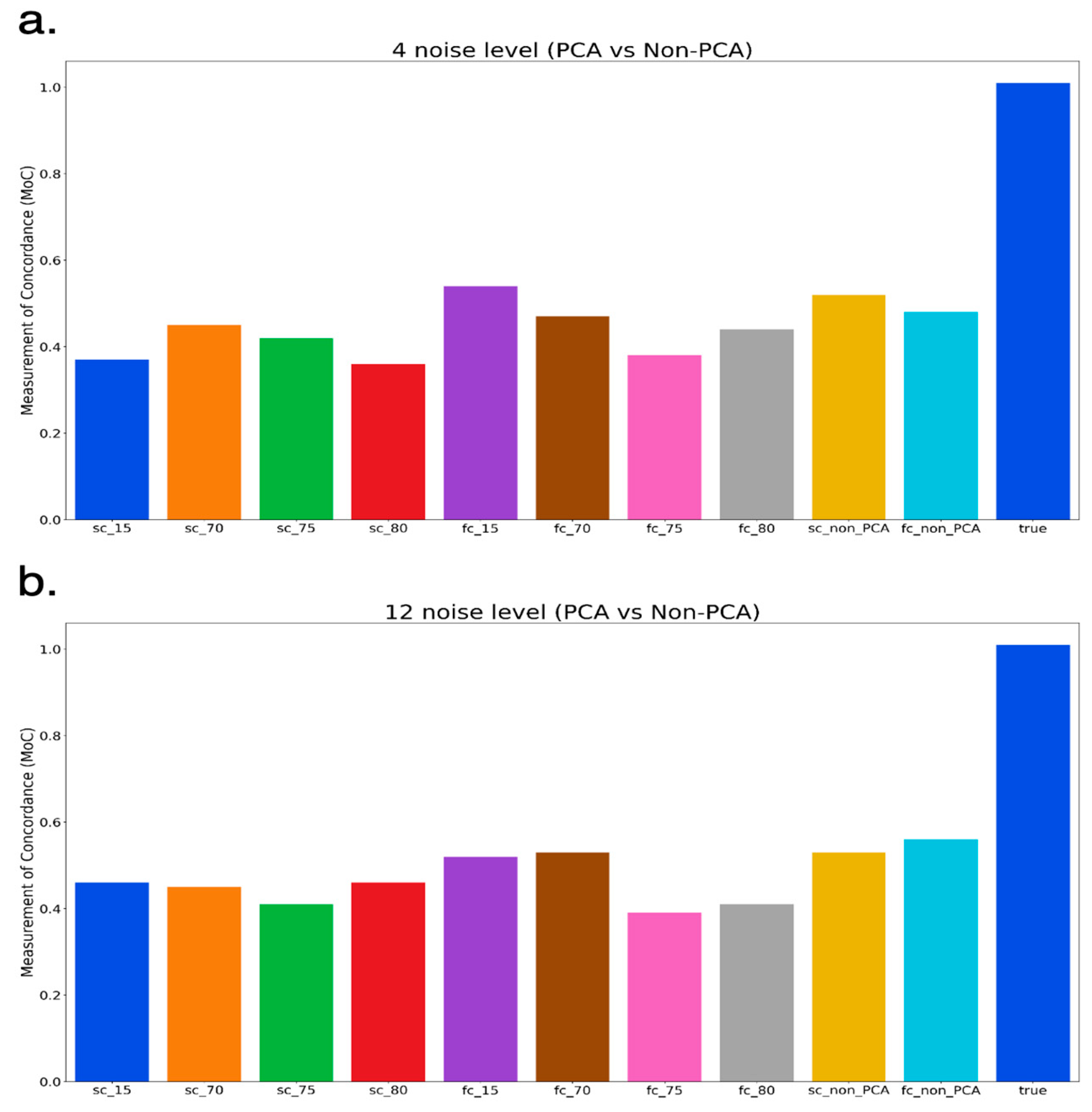
3.2. Comparison of PCA and Non-PCA Applied Results
3.3. Non-PCA Results
3.4. PCA-Applied Results
3.5. Testing Full Circle vs. Semi-Circle Features
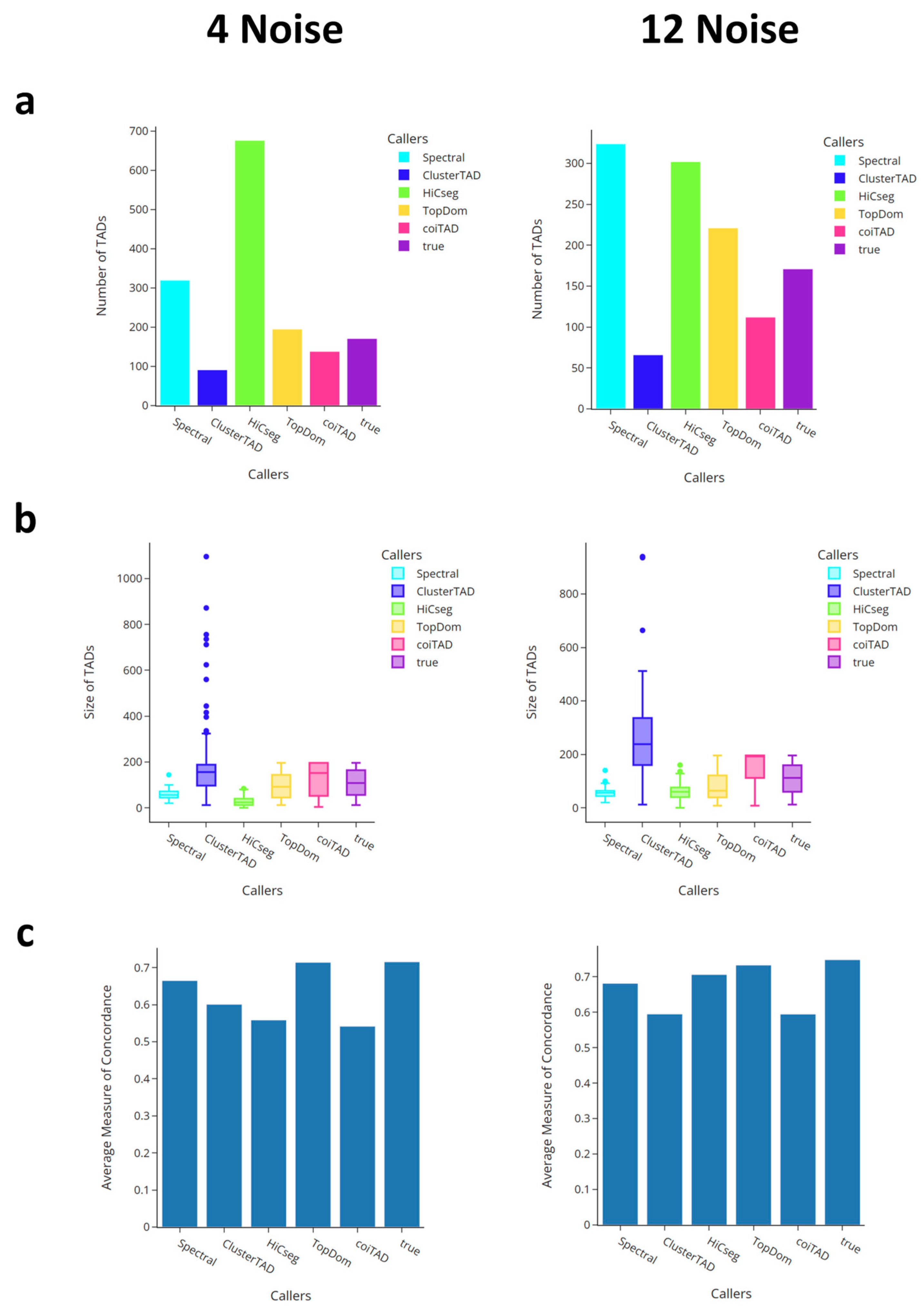
3.6. Comparison with Callers on Simulated Data
3.6.1. Number of TADs for Simulated Data
3.6.2. Size Distribution of TADs for Simulated Data
3.6.3. Comparison of Average Domain Overlap for Simulated Data
3.7. Assessment on Real Hi-C Datasets
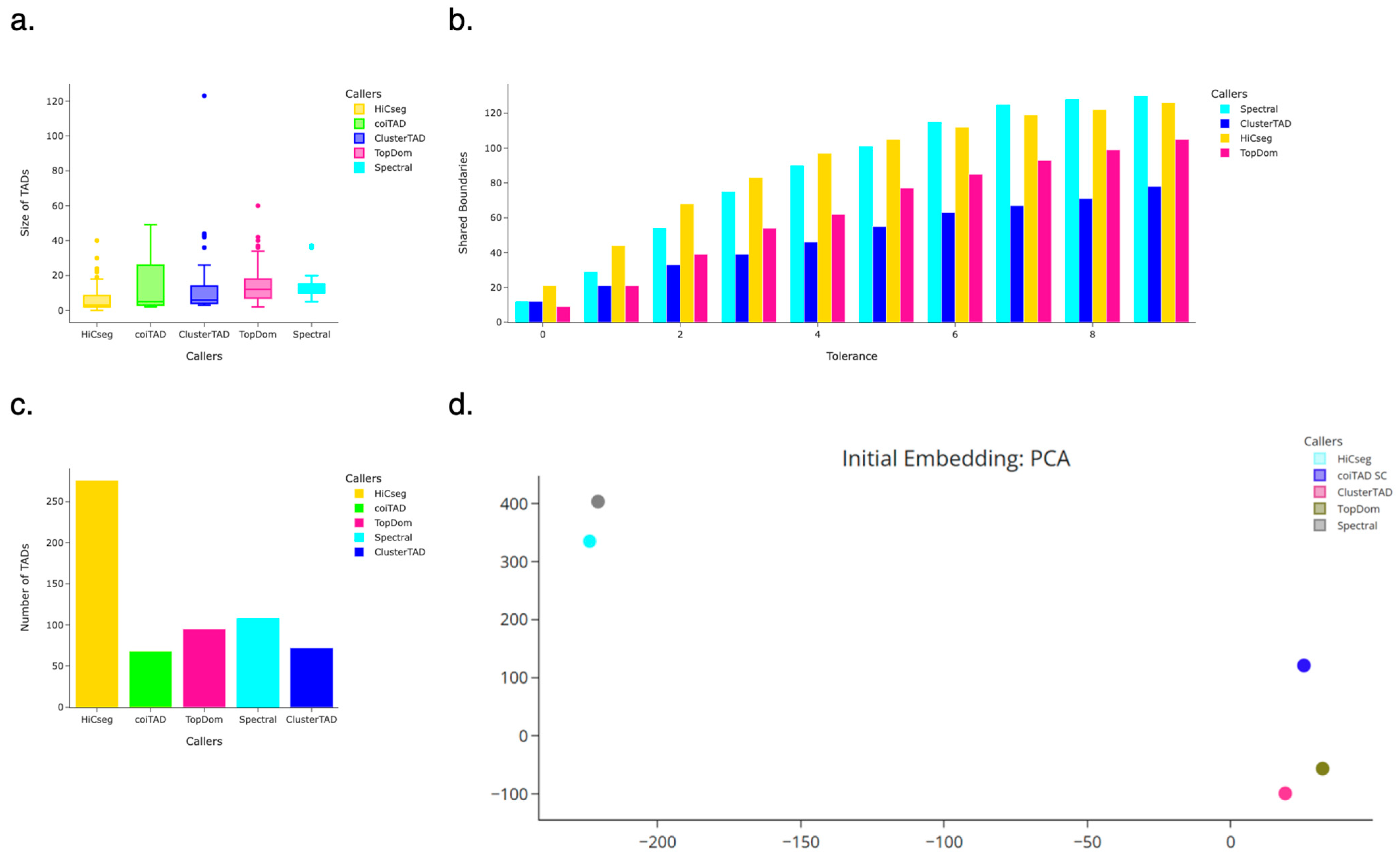
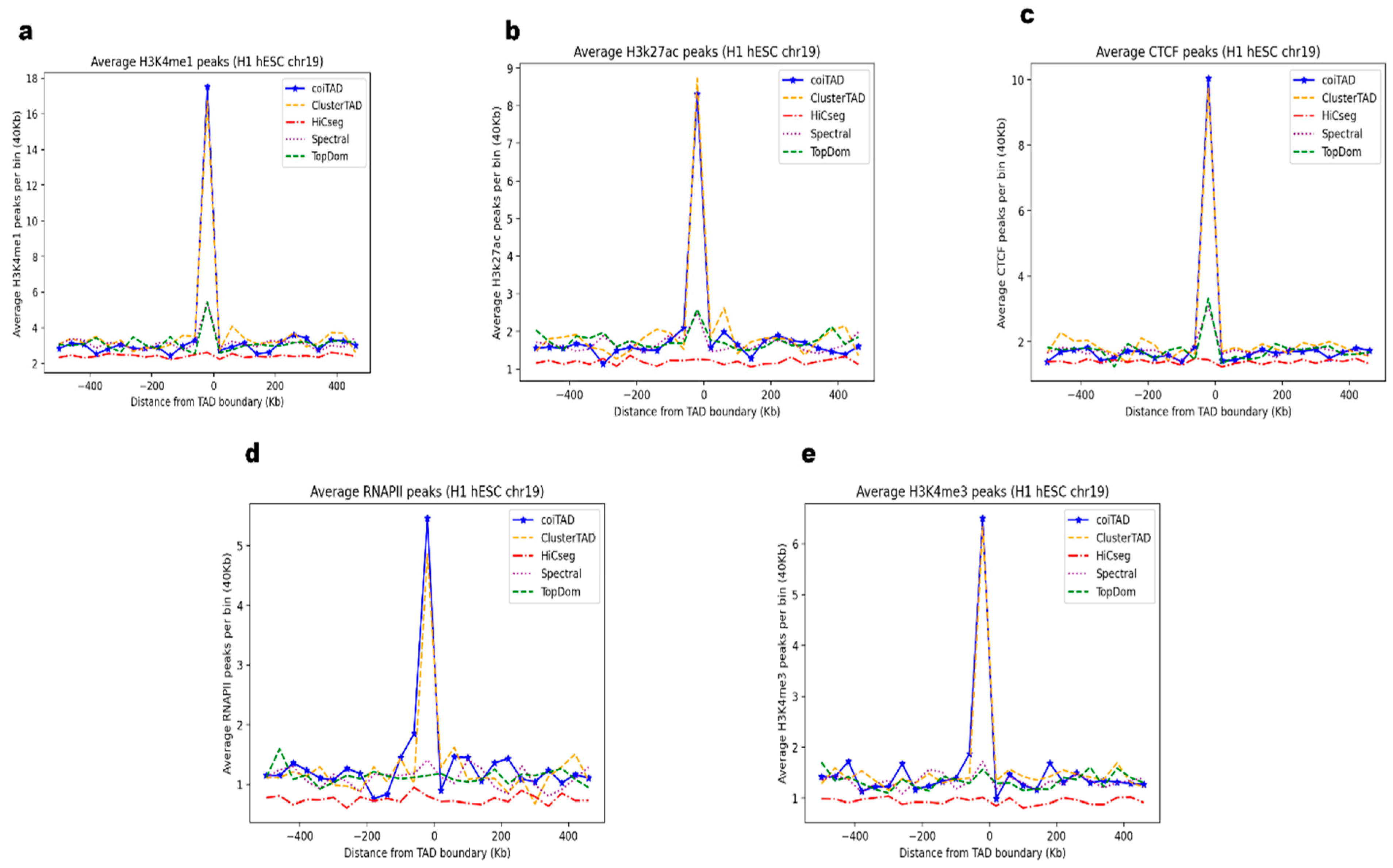
3.8. hESC 40 kb Chromosome 19 Hi-C Dataset
3.8.1. Number of TADs Identified for 40 kb HhESC Chromosome 19 Hi-C Dataset
3.8.2. Size Distribution of TADs for 40 kb hESC Chromosome 19 Hi-C Dataset
3.8.3. Number of Shared Boundaries for 40 kb hESC Chromosome 19 Hi-C Dataset
3.8.4. PCA Embedding for 40 kb hESC Chromosome 19 Hi-C Dataset
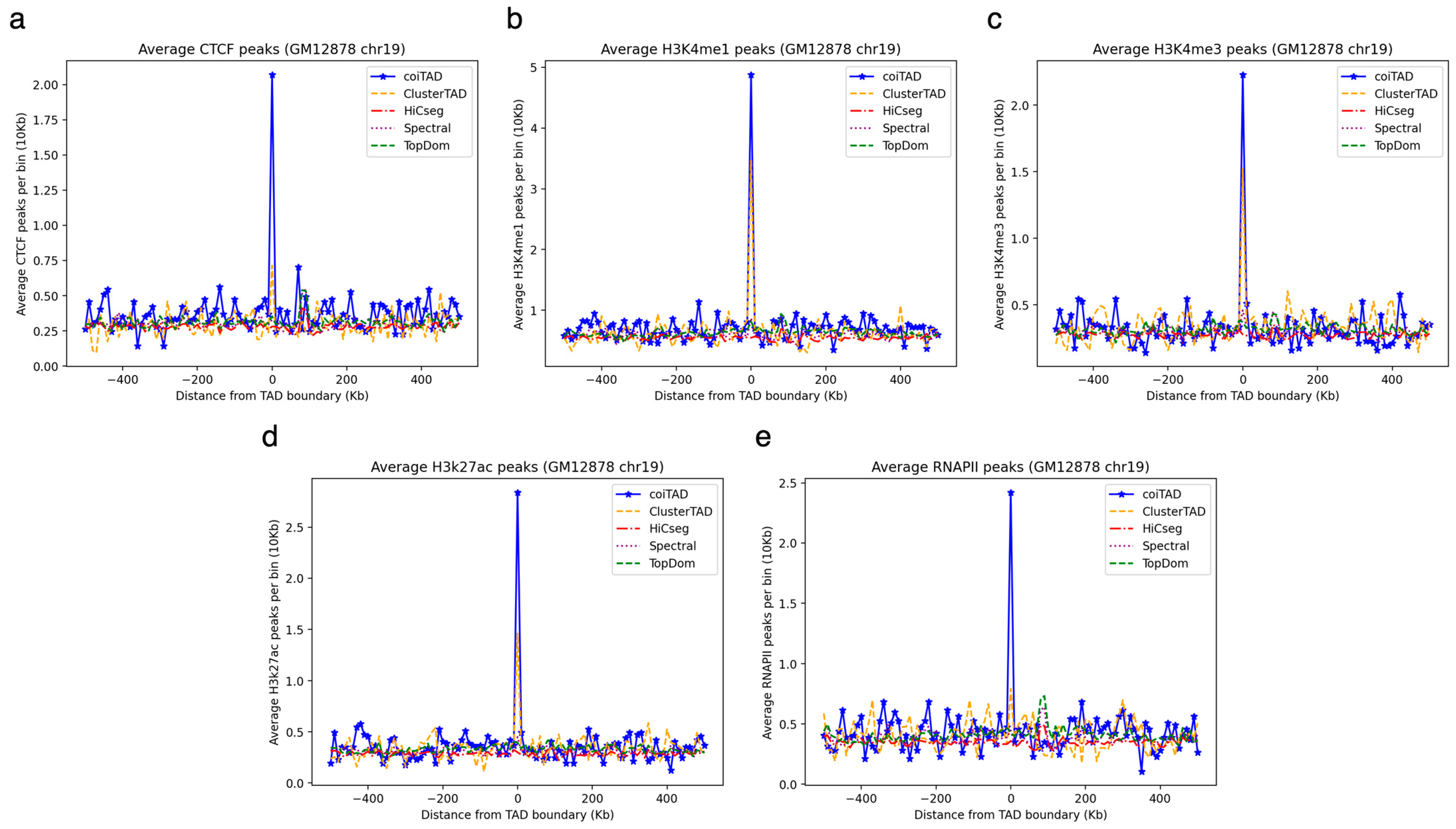
3.9. Chromosome 19 at 10 kb GM12878 Hi-C Dataset
3.9.1. Numbers of TADs Identified for 10 kb GM12878 Chromosome 19 Hi-C Dataset
3.9.2. Size Distribution of TADs for 10 kb GM12878 Chromosome 19 Hi-C Dataset
3.9.3. Number of Shared Boundaries for 10 kb GM12878 Chromosome 19 Hi-C Dataset
3.10. Chromosome 1 at 10 kb GM12878 Hi-C Dataset
3.10.1. Numbers of TADs Identified for 10 kb GM12878 Chromosome 1 Hi-C Dataset
3.10.2. Size Distribution of TADs for 10 kb GM12878 Chromosome 1 Hi-C Dataset
3.10.3. Number of Shared Boundaries for 10 kb GM12878 Chromosome 1 Hi-C Dataset
3.11. Biological Validation of coiTAD
3.12. Computational Performance Benchmarking
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SC | Semi-Circle |
| FC | Full circle |
| PCA | Principal component analysis |
| COI | Circle of influence |
| MOC | Measure of concordance |
References
- Lieberman-Aiden, E.; Van Berkum, N.L.; Williams, L.; Imakaev, M.; Ragoczy, T.; Telling, A.; Amit, I.; Lajoie, B.R.; Sabo, P.J.; Dorschner, M.O.; et al. Comprehensive Mapping of Long-Range Interactions Reveals Folding Principles of the Human Genome. Science 2009, 326, 289–293. [Google Scholar] [CrossRef]
- Dixon, J.R.; Selvaraj, S.; Yue, F.; Kim, A.; Li, Y.; Shen, Y.; Hu, M.; Liu, J.S.; Ren, B. Topological Domains in Mammalian Genomes Identified by Analysis of Chromatin Interactions. Nature 2012, 485, 376–380. [Google Scholar] [CrossRef]
- Nora, E.P.; Lajoie, B.R.; Schulz, E.G.; Giorgetti, L.; Okamoto, I.; Servant, N.; Piolot, T.; Van Berkum, N.L.; Meisig, J.; Sedat, J.; et al. Spatial Partitioning of the Regulatory Landscape of the X-inactivation Centre. Nature 2012, 485, 381–385. [Google Scholar] [CrossRef]
- Dixon, J.R.; Jung, I.; Selvaraj, S.; Shen, Y.; Antosiewicz-Bourget, J.E.; Lee, A.Y.; Ye, Z.; Kim, A.; Rajagopal, N.; Xie, W.; et al. Chromatin Architecture Reorganization during Stem Cell Differentiation. Nature 2015, 518, 331–336. [Google Scholar] [CrossRef]
- Wang, H.; Maurano, M.T.; Qu, H.; Varley, K.E.; Gertz, J.; Pauli, F.; Lee, K.; Canfield, T.; Weaver, M.; Sandstrom, R.; et al. Widespread plasticity in CTCF occupancy linked to DNA methylation. Genome Res. 2012, 22, 1680–1688. [Google Scholar] [CrossRef]
- Heinz, S.; Benner, C.; Spann, N.; Bertolino, E.; Lin, Y.C.; Laslo, P.; Cheng, J.X.; Murre, C.; Singh, H.; Glass, C.K. Simple Combinations of Lineage-Determining Transcription Factors Prime Cis-Regulatory Elements Required for Macrophage and B Cell Identities. Mol. Cell 2010, 38, 576–589. [Google Scholar] [CrossRef] [PubMed]
- Xiao, T.; Wallace, J.; Felsenfeld, G. Specific sites in the C terminus of CTCF interact with the SA2 subunit of the cohesin complex and are required for cohesin-dependent insulation activity. Mol Cell Biol. 2011, 31, 2174–2183. [Google Scholar] [CrossRef] [PubMed]
- Sanborn, A.L.; Rao, S.S.; Huang, S.C.; Durand, N.C.; Huntley, M.H.; Jewett, A.I.; Bochkov, I.D.; Chinnappan, D.; Cutkosky, A.; Li, J.; et al. Chromatin extrusion explains key features of loop and domain formation in wild-type and engineered genomes. Proc. Natl. Acad. Sci. USA 2015, 112, E6456–E6465. [Google Scholar] [CrossRef] [PubMed]
- Parelho, V.; Hadjur, S.; Spivakov, M.; Leleu, M.; Sauer, S.; Gregson, H.C.; Jarmuz, A.; Canzonetta, C.; Webster, Z.; Nesterova, T.; et al. Cohesins functionally associate with CTCF on mammalian chromosome arms. Cell 2008, 132, 422–433. [Google Scholar] [CrossRef]
- Cuddapah, S.; Jothi, R.; Schones, D.E.; Roh, T.Y.; Cui, K.; Zhao, K. Global analysis of the insulator binding protein CTCF in chromatin barrier regions reveals demarcation of active and repressive domains. Genome Res. 2009, 19, 24–32. [Google Scholar] [CrossRef]
- Kagey, M.H.; Newman, J.J.; Bilodeau, S.; Zhan, Y.; Orlando, D.A.; Van Berkum, N.L.; Ebmeier, C.C.; Goossens, J.; Rahl, P.B.; Levine, S.S.; et al. Mediator and Cohesin Connect Gene Expression and Chromatin Architecture. Nature 2010, 467, 430–435. [Google Scholar] [CrossRef]
- Jin, F.; Li, Y.; Dixon, J.R.; Selvaraj, S.; Ye, Z.; Lee, A.Y.; Yen, C.A.; Schmitt, A.D.; Espinoza, C.A.; Ren, B. A high-resolution map of the three-dimensional chromatin interactome in human cells. Nature 2013, 503, 290–294. [Google Scholar] [CrossRef] [PubMed]
- Lupianez, D.G.; Kraft, K.; Heinrich, V.; Krawitz, P.; Brancati, F.; Klopocki, E.; Horn, D.; Kayserili, H.; Opitz, J.M.; Laxova, R.; et al. Disruptions of Topological Chromatin Domains Cause Pathogenic Rewiring of Gene-Enhancer Interactions. Cell 2015, 161, 1012–1025. [Google Scholar] [CrossRef] [PubMed]
- Franke, M.; Ibrahim, D.M.; Andrey, G.; Schwarzer, W.; Heinrich, V.; Schöpflin, R.; Kraft, K.; Kempfer, R.; Jerković, I.; Chan, W.-L.; et al. Formation of New Chromatin Domains Determines Pathogenicity of Genomic Duplications. Nature 2016, 538, 265–269. [Google Scholar] [CrossRef] [PubMed]
- Flavahan, W.A.; Drier, Y.; Johnstone, S.E.; Hemming, M.L.; Tarjan, D.R.; Hegazi, E.; Shareef, S.J.; Javed, N.M.; Raut, C.P.; Eschle, B.K.; et al. Altered Chromosomal Topology Drives Oncogenic Programs in SDH-Deficient GISTs. Nature 2017, 548, 110–114. [Google Scholar] [CrossRef]
- Fraser, J.; Ferrai, C.; Chiariello, A.M.; Schueler, M.; Rito, T.; Laudanno, G.; Barbieri, M.; Moore, B.L.; Kraemer, D.C.; Aitken, S.; et al. Hierarchical Folding and Reorganization of Chromosomes Are Linked to Transcriptional Changes in Cellular Differentiation. Mol. Syst. Biol. 2015, 11, 852. [Google Scholar] [CrossRef]
- Rao, S.S.P.; Huntley, M.H.; Durand, N.C.; Stamenova, E.K.; Bochkov, I.D.; Robinson, J.T.; Sanborn, A.L.; Machol, I.; Omer, A.D.; Lander, E.S.; et al. A 3D Map of the Human Genome at Kilobase Resolution Reveals Principles of Chromatin Looping. Cell 2014, 159, 1665–1680. [Google Scholar] [CrossRef]
- Han, J.; Jian, P.; Kamber, M. Data mining: Concepts and Techniques; Elsevier: Amsterdam, The Netherlands, 2011. [Google Scholar]
- Berkhin, P. A Survey of Clustering Data Mining Techniques. In Grouping Multidimensional Data; Kogan, J., Nicholas, C., Teboulle, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar] [CrossRef]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1988. [Google Scholar]
- Xu, D.; Tian, Y. A comprehensive survey of clustering algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Gong, H.; Yang, Y.; Zhang, X.; Li, M.; Zhang, S.; Chen, Y. CASPIAN: A method to identify chromatin topological associated domains based on spatial density cluster. Comput. Struct. Biotechnol. J. 2022, 20, 4816–4824. [Google Scholar] [CrossRef]
- Oluwadare, O.; Cheng, J. ClusterTAD: An unsupervised machine learning approach to detecting topologically associated domains of chromosomes from Hi-C data. BMC Bioinform. 2017, 18, 480. [Google Scholar] [CrossRef] [PubMed]
- Lévy-Leduc, C.; Delattre, M.; Mary-Huard, T.; Robin, S. Two-dimensional segmentation for analyzing hi-C data. Bioinformatics 2014, 30, i386–i392. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Li, Y.; Gao, J.; Zhang, M.Q. A novel method to identify topological domains using hi-C data. Quant. Biol. 2015, 3, 81–89. [Google Scholar] [CrossRef]
- Zufferey, M.; Tavernari, D.; Oricchio, E.; Ciriello, G. Comparison of computational methods for the identification of topologically associating domains. Genome Biol. 2018, 19, 217. [Google Scholar] [CrossRef] [PubMed]
- Shin, H.; Shi, Y.; Dai, C.; Tjong, H.; Gong, K.; Alber, F.; Zhou, X.J. TopDom: An efficient and deterministic method for identifying topological domains in genomes. Nucleic Acids Res. 2016, 44, e70. [Google Scholar] [CrossRef]
- Cresswell, K.G.; Stansfield, J.C.; Dozmorov, M.G. SpectralTAD: An R package for defining a hierarchy of topologically associated domains using spectral clustering. BMC Bioinform. 2020, 21, 319. [Google Scholar] [CrossRef]
- Higgins, S.; Akpokiro, V.; Westcott, A.; Oluwadare, O. TADMaster: A comprehensive web-based tool for the analysis of topologically associated domains. BMC Bioinform. 2022, 23, 463. [Google Scholar] [CrossRef] [PubMed]
- Mizuguchi, T.; Fudenberg, G.; Mehta, S.; Belton, J.-M.; Taneja, N.; Folco, H.D.; FitzGerald, P.; Dekker, J.; Mirny, L.; Barrowman, J.; et al. Cohesin-dependent globules and heterochromatin shape 3D genome architecture in S. pombe. Nature 2014, 516, 432–435. [Google Scholar] [CrossRef]
- Lajoie, B.R.; Dekker, J.; Kaplan, N. The Hitchhiker’s guide to hi-C analysis: Practical guidelines. Methods 2015, 72, 65–75. [Google Scholar] [CrossRef]
- Crane, E.; Bian, Q.; McCord, R.P.; Lajoie, B.R.; Wheeler, B.S.; Ralston, E.J.; Uzawa, S.; Dekker, J.; Meyer, B.J. Condensin-driven remodelling of X chromosome topology during dosage compensation. Nature 2015, 523, 240–244. [Google Scholar] [CrossRef] [PubMed]
- Van Bortle, K.; Nichols, M.H.; Li, L.; Ong, C.-T.; Takenaka, N.; Qin, Z.S.; Corces, V.G. Insulator function and topological domain border strength scale with architectural protein occupancy. Genome Biol. 2014, 15, R82. [Google Scholar] [CrossRef] [PubMed]
- Phillips, J.E.; Corces, V.G. CTCF: Master weaver of the genome. Cell 2009, 137, 1194–1211. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]
- Guelen, L.; Pagie, L.; Brasset, E.; Meuleman, W.; Faza, M.B.; Talhout, W.; Eussen, B.H.; De Klein, A.; Wessels, L.; De Laat, W.; et al. Domain organization of human chromosomes revealed by mapping of nuclear lamina interactions. Nature 2008, 453, 948–951. [Google Scholar] [CrossRef] [PubMed]
- Handoko, L.; Xu, H.; Li, G.; Ngan, C.Y.; Chew, E.; Schnapp, M.; Lee, C.W.H.; Ye, C.; Ping, J.L.H.; Mulawadi, F.; et al. CTCF-mediated functional chromatin interactome in pluripotent cells. Nat. Genet. 2011, 43, 630–638. [Google Scholar] [CrossRef] [PubMed]
- Holwerda, S.J.; de Laat, W. CTCF: The protein, the binding partners, the binding sites and their chromatin loops. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2013, 368, 20120369. [Google Scholar] [CrossRef] [PubMed]
- Raney, B.J.; Barber, G.P.; Benet-Pagès, A.; Casper, J.; Clawson, H.; Cline, M.S.; Diekhans, M.; Fischer, C.; Navarro Gonzalez, J.; Hickey, G.; et al. The UCSC Genome Browser database: 2024 update. Nucleic Acids Res. 2024, 52, D1082–D1088. [Google Scholar] [CrossRef] [PubMed] [PubMed Central]



| Semi-Circle Results | Full-Circle Results | ||
|---|---|---|---|
| PCA RL (%) | MoC (%) | PCA RL (%) | MoC (%) |
| 5 | 0.091 | 5 | 0.117 |
| 10 | 0.121 | 10 | 0.132 |
| 15 | 0.621 | 15 | 0.592 |
| 20 | 0.601 | 20 | 0.564 |
| 25 | 0.095 | 25 | 0.543 |
| 30 | 0.089 | 30 | 0.521 |
| 35 | 0.122 | 35 | 0.532 |
| 40 | 0.102 | 40 | 0.493 |
| 45 | 0.615 | 45 | 0.536 |
| 50 | 0.602 | 50 | 0.419 |
| 55 | 0.412 | 55 | 0.466 |
| 60 | 0.597 | 60 | 0.406 |
| 65 | 0.466 | 65 | 0.394 |
| 70 | 0.593 | 70 | 0.534 |
| 75 | 0.612 | 75 | 0.391 |
| 80 | 0.582 | 80 | 0.409 |
| 85 | 0.465 | 85 | 0.453 |
| 90 | 0.532 | 90 | 0.467 |
| 95 | 0.524 | 95 | 0.582 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Houchens, D.; Chowdhury, H.M.A.M.; Oluwadare, O. coiTAD: Detection of Topologically Associating Domains Based on Clustering of Circular Influence Features from Hi-C Data. Genes 2024, 15, 1293. https://doi.org/10.3390/genes15101293
Houchens D, Chowdhury HMAM, Oluwadare O. coiTAD: Detection of Topologically Associating Domains Based on Clustering of Circular Influence Features from Hi-C Data. Genes. 2024; 15(10):1293. https://doi.org/10.3390/genes15101293
Chicago/Turabian StyleHouchens, Drew, H. M. A. Mohit Chowdhury, and Oluwatosin Oluwadare. 2024. "coiTAD: Detection of Topologically Associating Domains Based on Clustering of Circular Influence Features from Hi-C Data" Genes 15, no. 10: 1293. https://doi.org/10.3390/genes15101293
APA StyleHouchens, D., Chowdhury, H. M. A. M., & Oluwadare, O. (2024). coiTAD: Detection of Topologically Associating Domains Based on Clustering of Circular Influence Features from Hi-C Data. Genes, 15(10), 1293. https://doi.org/10.3390/genes15101293






