Independent Aridity and Drought Pieces of Evidence Based on Meteorological Data and Tree Ring Data in Southeast Banat, Vojvodina, Serbia
Abstract
1. Introduction
2. Study Area and Data
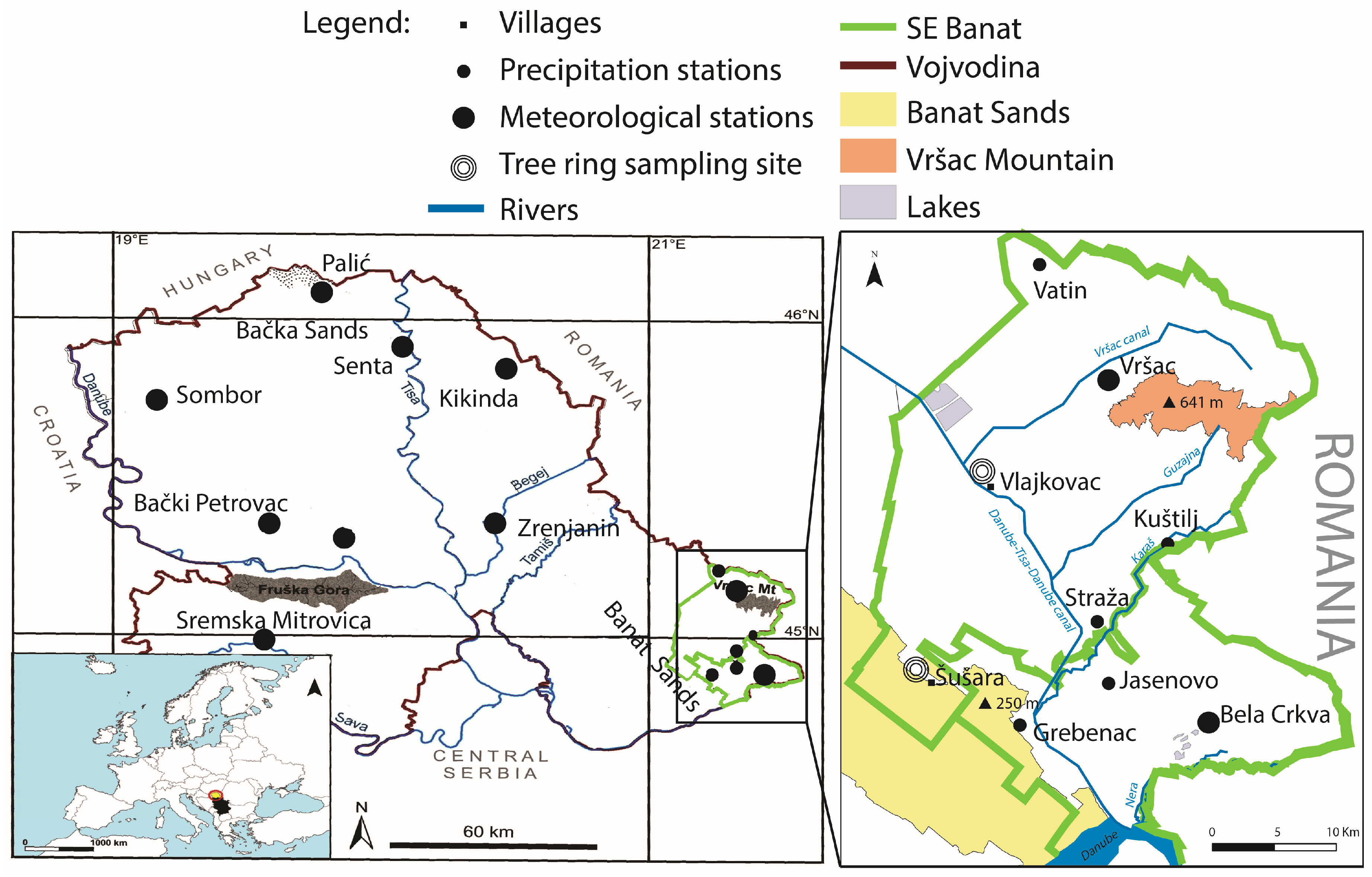
2.1. Study Area
2.2. Data
3. Methods
3.1. The De Martonne Aridity Index
3.2. Forestry Aridity Index
3.3. The Palmer Drought Severity Index
3.4. The Tree Ring Width Index
3.5. Data Analysis
3.6. Software
4. Results
4.1. Annual Distributions and Trends
4.1.1. The De Martonne Aridity Index
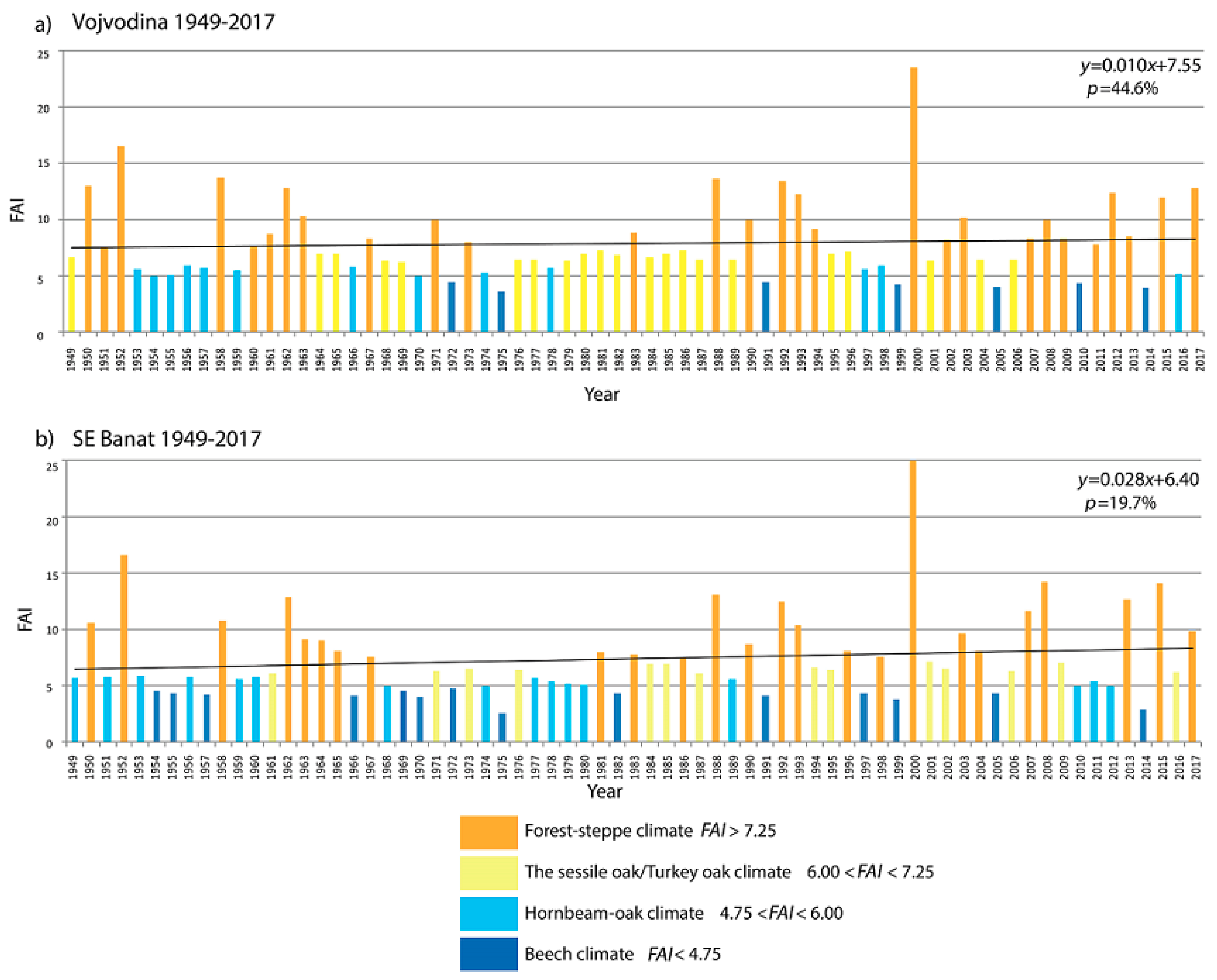
4.1.2. The Forestry Aridity Index
4.1.3. The Palmer Drought Severity Index
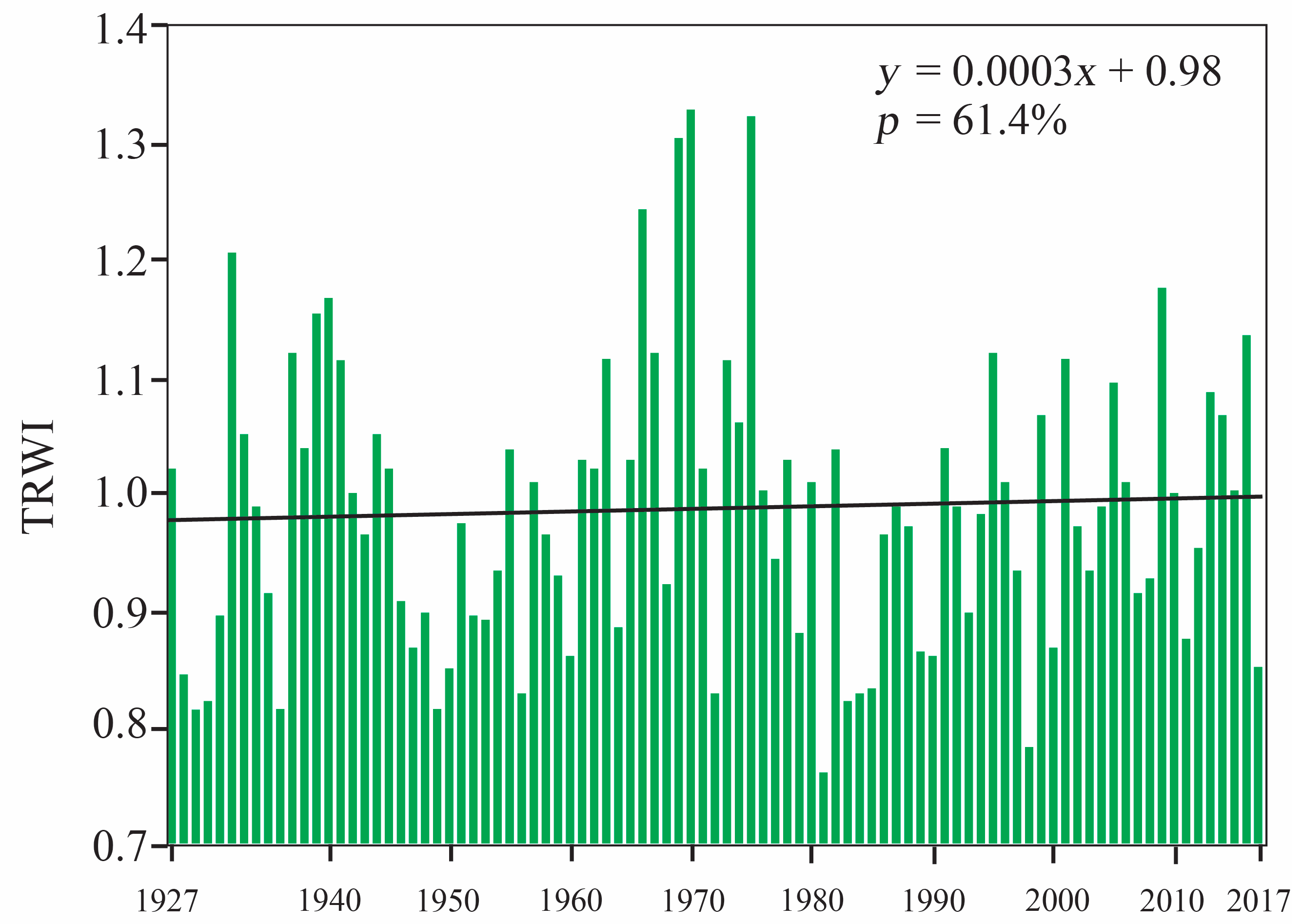
4.1.4. The Tree Ring Width Index
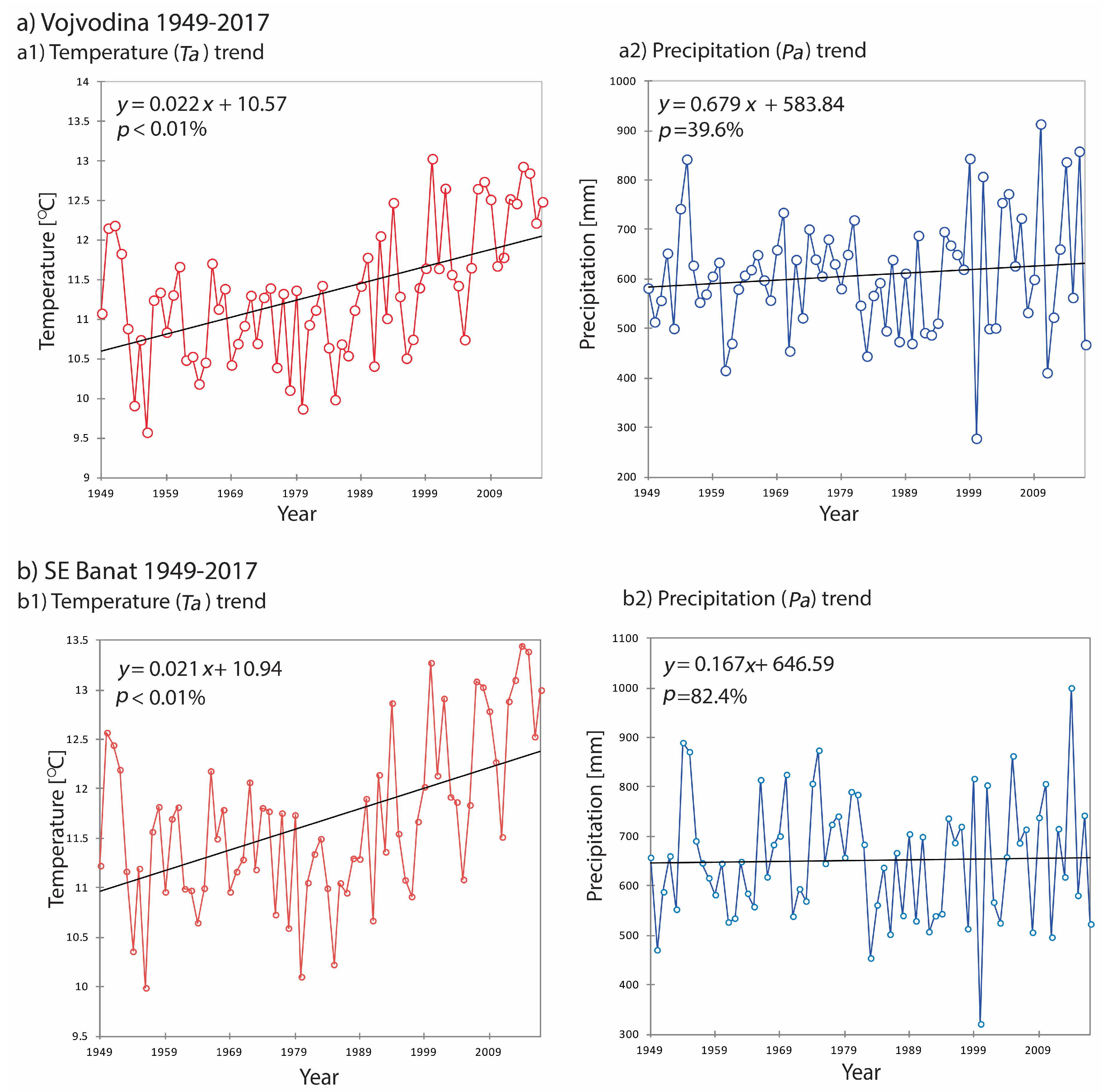
4.1.5. Temperature and Precipitation
4.2. Correlation Analysis
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hulme, M.; Barrow, E.M.; Arnell, N.W.; Harrisson, P.A.; Johns, T.C.; Downing, T.E. Relative impacts of human-induced climate change and natural climate variability. Nature 1999, 397, 688–691. [Google Scholar] [CrossRef]
- Kenny, G.J.; Ye, W.; Flux, T.; Warrick, R.A. Climate variations and New Zealand agriculture: The CLIMPACTS system and issues of spatial and temporal scale. Environ. Int. 2001, 27, 189–194. [Google Scholar] [CrossRef]
- Baltas, E.; Mimikou, M. Climate change impacts on the water supply of Thessaloniki. Int. J. Water Resour. Dev. 2005, 21, 341–353. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Global Warming of 1.5 °C; World Meteorological Organization: Geneva, Switzerland, 2018. [Google Scholar]
- Gavrilov, M.B.; Marković, S.B.; Mladjan, D.; Zarić, M.; Pešić, A.; Janc, N.; Todorović, N. Global Warning—Between the Myth and Reality. In Proceedings of the International Scientific Conference “Archibald Reiss Days”, Zemun, Serbia, 10–11 March 2016; Kolarić, D., Ed.; Academy of Criminalistic And Police Studies: Belgrade, Serbia, 2016. [Google Scholar]
- Climatic Research Unit. Global Average Temperature Change 1856–2003. Available online: https://crudata.uea.ac.uk/cru/data/temperature/ (accessed on 6 March 2012).
- Diaz, H.F.; Bradley, R.; Eischeid, J.K. Precipitation fluctuation over global land areas since the late 1800s. J. Geophys. Res. 1989, 94, 1195–1210. [Google Scholar] [CrossRef]
- American Meteorological Society, Glossary of Meteorology. Available online: http://glossary.ametsoc.org/wiki/Aridity (accessed on 15 September 2019).
- Deniz, A.; Toros, H.; Incecik, S. Spatial variations of climate indices in Turkey. Int. J. Climatol. 2011, 3, 394–403. [Google Scholar] [CrossRef]
- Arora, V.K. The use of the aridity index to assess climate change effect on annual runoff. J. Hydrol. 2002, 265, 164–177. [Google Scholar] [CrossRef]
- De Martonne, E. Traité de géographie physique, Vol. I: Notions generales, climat, hydrographie. Geogr. Rev. 1925, 15, 336–337. [Google Scholar] [CrossRef]
- Baltas, E. Spatial distribution of climatic indices in northern Greece. Meteorol. Appl. 2007, 14, 69–78. [Google Scholar] [CrossRef]
- Croitoru, А.Е.; Piticar, А.; Imbroane, А.М.; Burada, D.C. Spatiotemporal distribution of aridity indices based on temperature and precipitation in the extra-Carpathian regions of Romania. Theor. Appl. Climatol. 2013, 112, 597–607. [Google Scholar] [CrossRef]
- Moral, F.J.; Paniagua, L.L.; Rebollo, F.J.; García-Martín, A. Spatial analysis of the annual and seasonal aridity trends in Extremadura, southwestern Spain. Theor. Appl. Climatol. 2017, 130, 917–932. [Google Scholar] [CrossRef]
- Nistor, M.M. Spatial distribution of climate indices in the Emilia-Romagna region. Meteorol. Appl. 2016, 23, 304–313. [Google Scholar] [CrossRef]
- Gebremedhin, M.A.; Hailu Kahsay, G.H.; Fanta, H.G. Assessment of spatial distribution of aridity indices in Raya valley, northern Ethiopia. Appl. Water Sci. 2018, 8, 217–224. [Google Scholar] [CrossRef]
- Hrnjak, I.; Lukić, T.; Gavrilov, M.B.; Marković, S.B.; Unkašević, M.; Tošić, I. Aridity in Vojvodina, Serbia. Theor. Appl. Climatol. 2014, 115, 323–332. [Google Scholar] [CrossRef]
- Bačević, N.; Vukoičić, D.; Nikolić, M.; Janc, N.; Milentijević, N.; Gavrilov, M.B. Aridity in Kosovo and Metohija, Serbia. Carpathian J. Earth Environ. Sci. 2017, 12, 563–570. [Google Scholar]
- Radaković, M.G.; Tošić, I.; Bačević, N.; Mladjan, D.; Gavrilov, M.B.; Marković, S.B. The analysis of aridity in Central Serbia from 1949 to 2015. Theor.Appl. Climatol. 2018, 133, 887–898. [Google Scholar] [CrossRef]
- Zambakas, J. General Climatology; Department of Geology, National & Kapodistrian University of Athens: Athens, Greece, 1992. [Google Scholar]
- Thornthwaite, C.W. An approach toward a rational classification of climate. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Palmer, W.C. Meteorological Drought; U.S. Department of Commerce: Washington, DC, USA, 1965.
- Ben-Gai, T.; Bitan, A.; Manes, A.; Alpert, P. Long-term changes in annual rainfall patterns in southern Israel. Theor. Appl. Climatol. 1994, 49, 59–67. [Google Scholar] [CrossRef]
- Cook, E.R.; Woodhouse, C.A.; Mark, E.C.; Meko, D.M.; Stahle, D.W. Long-term aridity changes in the western United States. Science 2004, 306, 1015–1018. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Yin, Y.; Zheng, D.; Yang, Q. Moisture conditions and climate trends in China during the period 1971–2000. Int. J. Climatol. 2006, 26, 193–206. [Google Scholar] [CrossRef]
- Tabari, H.; Aghajanloo, M.-B. Temporal pattern of monthly aridity index in Iran with considering precipitation and evapotranspiration trends. Int. J. Climatol. 2013, 33, 396–409. [Google Scholar] [CrossRef]
- Johansson, O.V. Die Hauptcharakteristika des jahrlichen Temperaturganges. Gerlands Beitr. Z. J. Geophys. 1931, 33, 406–428. [Google Scholar]
- Kerner, F.V. Thermoisodromen, Versuch einer kartographischen Darstellung des jahrlichen Ganges der Lufttemperatur; Geographische Gesellschaft: Österreich, Wien, 1905. [Google Scholar]
- Emberger, E. Sur une formule climatique et ses applications en botanique. La Météorologie 1932, 92, 423–432. [Google Scholar]
- Food and Agriculture Organization of the United Nations. World Map of Desertification; United Nations: Rome, Italy, 1977. [Google Scholar]
- Führer, E.; Horvath, L.; Jagodics, A.; Machon, A.; Szabados, I. Application of new aridity index in Hungarian forestry practice. Időjárás 2011, 115, 205–216. [Google Scholar]
- Gavrilov, M.B.; Lukić, T.; Janc, N.; Basarin, B.; Marković, S.B. Forestry Aridity Index in Vojvodina, North Serbia. Open Geosci. 2019, 11, 367–377. [Google Scholar] [CrossRef]
- Alley, W. The Palmer Drought Severity Index: Limitations and Assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Cufar, K.; Grabner, M.; Morgás, A.; Martínez del Castillo, E.; Merela, M.; De Luis, M. Common climatic signals affecting oak tree-ring growth in SE Central Europe. Trees 2014, 28, 1267–1277. [Google Scholar] [CrossRef]
- Stojanović, D.; Levanič, T.; Matović, B.; Bravo-Oviedo, A. Climate change impact on a mixed lowland oak stand in Serbia. Ann. Silvic. Res. 2015, 39, 94–99. [Google Scholar]
- Marković, S.B.; Bokhorst, M.; Vandenberghe, J.; Oches, E.A.; Zöller, L.; McCoy, W.D.; Gaudenyi, T.; Jovanović, M.; Hambach, U.; Machalett, B. Late Pleistocene loess-paleosol sequences in the Vojvodina region, North Serbia. J. Quat. Sci. 2008, 23, 73–84. [Google Scholar] [CrossRef]
- Marković, S.B.; Hambach, U.; Catto, N.; Jovanović, M.; Buggle, B.; Machalett, B.; Zöller, L.; Glaser, B.; Frechen, M. The middle and late Pleistocene loess-paleosol sequences at Batajanica, Vojvodina, Serbia. Quat. Int. 2009, 198, 255–266. [Google Scholar]
- Marković, S.B.; Hambach, U.; Stevens, T.; Kukla, G.J.; Heller, F.; William, D.; McCoy, W.D.; Oches, E.A.; Buggle, B.; Zöller, L. The last million years recorded at the Stari Slankamen loess-palaeosol sequence: Revised chronostratigraphy and long-term environmental trends. Quat. Sci. Rev. 2011, 30, 1142–1154. [Google Scholar] [CrossRef]
- Marković, S.B.; Stevens, T.; Kukla, G.J.; Hambach, U.; Fitzsimmons, K.E.; Gibbard, P.; Buggle, B.; Zech, M.; Guo, Z.T.; Hao, Q.Z.; et al. The Danube loess stratigraphy—New steps towards the development of a pan-European loess stratigraphic model. Earth Sci. Rev. 2015, 148, 228–258. [Google Scholar] [CrossRef]
- Gavrilov, M.B.; Marković, S.B.; Schaetzl, R.J.; Tošić, I.A.; Zeeden, C.; Obreht, I.; Sipos, G.; Ruman, A.; Putniković, S.; Emunds, K.; et al. Prevailing surface winds in Northern Serbia in the recent and past time periods; modern- and past dust deposition. Aeolian Res. 2018, 31, 117–129. [Google Scholar] [CrossRef]
- Tošić, I.; Gavrilov, M.B.; Marković, S.B.; Ruman, A.; Putniković, S. Seasonal prevailing surface winds in Northern Serbia. Theor. Appl. Climatol. 2018, 131, 1273–1284. [Google Scholar] [CrossRef]
- Gavrilov, M.B.; Marković, S.B.; Korać, V.; Jarad, A. The analysis of temperature trends in Vojvodina (Serbia) from 1949 to 2006. Therm. Sci. 2015, 19, 339–350. [Google Scholar] [CrossRef]
- Gavrilov, M.B.; Tošić, I.; Marković, S.B.; Unkašević, M.; Petrović, P. The analysis of annual and seasonal temperature trends using the Mann-Kendall test in Vojvodina, Serbia. Időjárás 2016, 120, 183–198. [Google Scholar]
- Tošić, I.; Hrnjak, I.; Gavrilov, M.B.; Unkašević, M.; Marković, S.B.; Lukić, T. Annual and seasonal variability of precipitation in Vojvodina, Serbia. Theor. Appl. Climatol. 2014, 117, 331–341. [Google Scholar] [CrossRef]
- Milovanov, D. Hydrosystem Danube-Tisa-Danube; Water Management: Novi Sad, Serbia, 1972. (In Serbian)
- Javno preduzeće za gazdovanje šumama, VOJVODINAŠUME, Šumsko gazdinstvo “BANAT” Pančevo. Available online: http://www.banatsume.rs/ (accessed on 1 May 2019).
- RHMZ-RepubličkiHidrometeorološkizavodSrbijeKnezaVišeslava 66 Beograd. Available online: http://www.hidmet.gov.rs/ (accessed on 17 March 2019).
- Alexandersson, H. A homogeneity test applied to precipitation data. J. Climatol. 1986, 6, 661–675. [Google Scholar] [CrossRef]
- Dai, A.; Trenberth, K.E.; Qian, T. A global dataset of Palmer Drought Severity Index for 1870–2002: Relationship with soil moisture and effects of surface warming. J. Hydrometeorol. 2004, 5, 1117–1130. [Google Scholar] [CrossRef]
- Palmer Drought Severity Index (PDSI) | NCAR - Climate Data Guide. Available online: http://www.cgd.ucar.edu/cas/catalog/climind/pdsi.html (accessed on 22 May 2019).
- Tabari, H.; Talaee, P.H.; Nadoushani, S.M.; Willems, P.; Marchetto, A. A survey of temperature and precipitation based aridity indices in Iran. Quat. Int. 2014, 345, 158–166. [Google Scholar] [CrossRef]
- Marriott, F.H.C. Dictionary of Statistical Terms; International Statistical Institute by Longman Scientific and Technical &Wiley: New York, NY, USA, 2002. [Google Scholar]
- Dai, A. Characteristics and trends in various forms of the Palmer Drought Severity Index during 1900–2008. J. Geophys. Res. 2011, 116, D12115. [Google Scholar] [CrossRef]
- Stokes, M.A.; Smiley, T.L. An Introduction to Tree-Ring Dating; The University of Arizona Press: Tucson, AZ, USA, 1996. [Google Scholar]
- Holmes, R.L. Computer-assisted quality control in tree-ring dating and measurement. Tree-Ring Bull. 1983, 43, 69–78. [Google Scholar]
- Cook, E.R. A Time-Series Analysis Approach to Tree-Ring Standardization. Ph.D. Thesis, University of Arizona, Tucson, AZ, USA, 1985. [Google Scholar]
- Osborn, T.J.; Briffa, K.R.; Jones, P.D. Adjusting variance for sample-size in tree-ring chronologies and other regional-mean time series. Dendrochronologia 1997, 15, 89–99. [Google Scholar]
- Wigley, T.M.L.; Briffa, K.R.; Jones, P.D. On the average value of correlated time series, with applications in dendroclimatology and hydrometeorology. J. Clim. Appl. Meteorol. 1984, 23, 201–213. [Google Scholar] [CrossRef]
- Grissino-Mayer, H.D. Evaluating crossdating accuracy: A manual and tutorial for the computer program COFECHA. Tree-Ring Res. 2001, 57, 205–221. [Google Scholar]
- Draper, N.R.; Smith, H. Applied Regression Analysis; John Wiley and Sons: New York, NY, USA, 1966. [Google Scholar]
- Kendall, M.G. New Measure of Rank Correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Kendall, M.G. Rank Correlation Methods, 4th ed.; Charles Griffin: London, England, 1975. [Google Scholar]
- Mann, H.B. Non-parametric Tests Against Trend. Econometrica 1945, 13, 245–259. [Google Scholar] [CrossRef]
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring; Van Nostrand Reinhold Company Inc.: New York, NY, USA, 1987. [Google Scholar]
- Onoz, B.; Bayazit, M. The Power of Statistical Tests for Trend Detection. Turkish J. Engineer. Environ. Sci. 2003, 27, 247–251. [Google Scholar]
- Karmeshu, N. Trend Detection in Annual Temperature & precipitation Using the Mann Kendall Test—A Case Study to Assess Climate Change on Select States in the Northeastern United States. Master’s Thesis, University of Pennsylvania, Philadelphia, PA, USA, 2012. [Google Scholar]
- Gavrilov, M.B.; Marković, S.B.; Janc, N.; Nikolić, M.; Valjarević, A.; Komac, B.; Zorn, M.; Punišić, M.; Bačević, N. Assessing average annual air temperature trends using the Mann–Kendall test in Kosovo. Acta Geogr. Slov. 2018, 58, 7–25. [Google Scholar] [CrossRef]
- Marin, L.; Birsan, M.V.; Bojariu, R.; Dumitrescu, A.; Micu, D.M.; Manea, A. An Overview of annual climatic changes in Romania: Trends in air temperature, precipiutation, sunshine hours, cloud cover, relative humidity nd wind speed duration the 1961–2013 period. Carpathian J. Earth Environ. Sci. 2014, 9, 253–258. [Google Scholar]
- Çiçek, İ.; Duman, N. Seasonal and annual precipitation trends in Turkey. Carpathian J. Earth Environ. Sci. 2015, 10, 77–84. [Google Scholar]
- Serra, C.; Burgueño, A.; Lana, X. Analysis of maximum and minimum daily temperatures recorded at Fabra Observatory (Barcelona, NE Spain) in the period 1917–1998. Int. J. Climatol. 2001, 21, 617–636. [Google Scholar] [CrossRef]
- Gavrilov, M.B.; Lazić, L.; Pešić, A.; Milutinović, M.; Marković, D.; Stanković, A.; Gavrilov, M.M. Influence of Hail Suppression on the Hail Trend in Serbia. Phys. Geogr. 2010, 31, 441–454. [Google Scholar] [CrossRef]
- Gavrilov, M.B.; Lazić, L.; Milutinović, M.; Gavrilov, M.M. Influence of Hail Suppression on the Hail Trend in Vojvodina, Serbia. Geogr. Pannonica 2011, 15, 36–41. [Google Scholar] [CrossRef]
- Gavrilov, M.B.; Marković, S.B.; Zorn, M.; Komac, B.; Lukić, T.; Milošević, M.; Janićević, S. Is hail suppression useful in Serbia?—General review and new results. Acta Geogr. Slov. 2013, 53, 165–179. [Google Scholar] [CrossRef]
- Janc, N.; Gavrilov, M.B. History of Hail Suppression in Serbia; LAP LAMBERT Academic Publishing: Saarbrücken, Germany, 2017. [Google Scholar]
- Ahmed, K.; Shahid, S.; Wang, X.-J..; Nawaz, N.; Khan, N. Spatiotemporal Changes in Aridity of Pakistan during 1901–2016. Hydrol. Earth Syst. Sci. 2019, 23, 3081–3096. [Google Scholar] [CrossRef]
- Tabari, H.; Marofi, S.; Aeini, A.; Talaee, P.H.; Mohammadi, K. Trend analysis of reference evapotranspirationin the western half of Iran. Agric. For. Meteorol. 2011, 151, 128–136. [Google Scholar] [CrossRef]
- Drapela, K.; Drapelova, I. Application of Mann-Kendall test and the Sen’s slope estimates for trend detection in deposition data from Bílý Kříž (Beskydy Mts., the Czech Republic) 1997–2010. Beskydy 2011, 4, 133–146. [Google Scholar]
- Statistical Software & Data Analysis Add-on for Excel | XLSTAT. Available online: https://www.xlstat.com/en/ (accessed on 17 March 2019).
- Sümegi, P.; Krolopp, E. Quatermalacological analyses modelling of the Upper Weichselian palaeoenviromental changes in the Carpathian Basin. Quat. Int. 2002, 91, 53–63. [Google Scholar] [CrossRef]
- Marković, S.B.; McCoy, W.D.; Oches, E.A.; Savić, S.; Gaudenyi, T.; Jovanović, M.; Stevens, T.; Walther, R.; Ivanišević, P.; Galić, Z. Paleoclimate record in the Late Pleistocene loess-paleosol sequence at Petrovaradin Brickyard (Vojvodina, Serbia). Geol. Carpathica 2005, 56, 483–491. [Google Scholar]
- Marković, S.B.; Oches, E.; Sümegi, P.; Jovanović, M.; Gaudenyi, T. An introduction to the Upper and Middle Pleistocene loess-paleosol sequences of Ruma section (Vojvodina, Serbia). Quat. Int. 2006, 149, 80–86. [Google Scholar] [CrossRef]
- Marković, S.B.; Oches, E.A.; McCoy, W.D.; Gaudenyi, T.; Frechen, M. Malacological and sedimentological evidence for “warm” climate from the Irig loess sequence (Vojvodina, Serbia). Geochem. Geophys. Geosyst. 2007, 8, Q09008. [Google Scholar] [CrossRef]
- Marković, S.B.; Sümegi, P.; Stevens, T.; Schaetzl, R.J.; Obreht, I.; Chu, W.; Buggle, B.; Zech, M.; Zech, R.; Zeeden, C.; et al. The Crvenka loess-paleosol sequence: A record of continuous grassland domination in the southern Carpathian Basin during the Late Pleistocene. Palaeogeogr. Palaeoclimatol. Palaeoecol. 2018, 509, 33–46. [Google Scholar] [CrossRef]
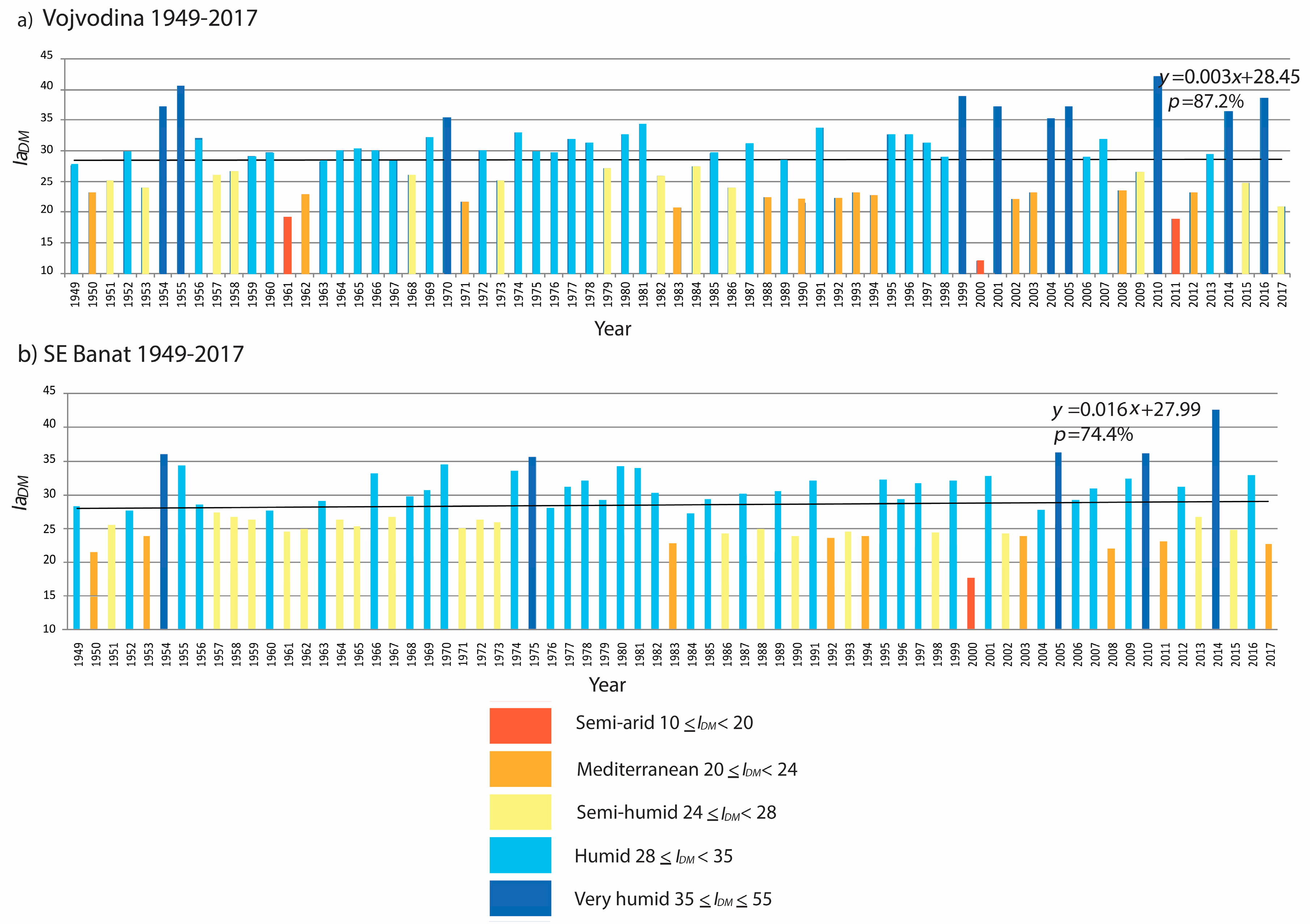





| Types of Climate | Values of IaDM |
|---|---|
| Arid | IaDM < 10 |
| Semi-arid | 10 ≤ IaDM < 20 |
| Mediterranean | 20 ≤ IaDM < 24 |
| Semi-humid | 24 ≤ IaDM < 28 |
| Humid | 28 ≤ IaDM < 35 |
| Very humid | 35 ≤ IaDM ≤ 55 |
| Extremely humid | IaDM > 55 |
| FAI Values | Forestry Climate Categories |
|---|---|
| Less than 4.75 | Beech climate |
| 4.75–6.00 | Hornbeam-oak climate |
| 6.00–7.25 | The sessile oak/Turkey oak climate |
| More than 7.25 | Forest-steppe climate |
| Site | SE Banat |
|---|---|
| Altitude (m AMSL) | 83–181 |
| Standard deviation (SD) | 0.29 |
| First-order autocorrelation (AC1) | 0.18 |
| Length of chronology (CL, years) | 99 |
| Mean tree ring width (mm) | 3.31 |
| Mean inter-series correlation (Rbar) | 0.40 |
| Expressed population signal (EPS) | 0.92 |
| Ordinar | Climate Parameters | Periods | Trends | |
|---|---|---|---|---|
| SE Banat | Vojvodina | |||
| 1. | TRWI | 1927–2017 | No | - |
| 2. | Ta | 1949–2017 | Yes | Yes |
| 3. | Pa | 1949–2017 | No | No |
| 4. | DM Aridity Index | 1949–2017 | No | No |
| 5. | FAI | 1949–2017 | No | No |
| 6. | PDSI | 1927–2016 | No | No |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gavrilov, M.B.; An, W.; Xu, C.; Radaković, M.G.; Hao, Q.; Yang, F.; Guo, Z.; Perić, Z.; Gavrilov, G.; Marković, S.B. Independent Aridity and Drought Pieces of Evidence Based on Meteorological Data and Tree Ring Data in Southeast Banat, Vojvodina, Serbia. Atmosphere 2019, 10, 586. https://doi.org/10.3390/atmos10100586
Gavrilov MB, An W, Xu C, Radaković MG, Hao Q, Yang F, Guo Z, Perić Z, Gavrilov G, Marković SB. Independent Aridity and Drought Pieces of Evidence Based on Meteorological Data and Tree Ring Data in Southeast Banat, Vojvodina, Serbia. Atmosphere. 2019; 10(10):586. https://doi.org/10.3390/atmos10100586
Chicago/Turabian StyleGavrilov, Milivoj B., Wenling An, Chenxi Xu, Milica G. Radaković, Qingzhen Hao, Fan Yang, Zhengtang Guo, Zoran Perić, Gavrilo Gavrilov, and Slobodan B. Marković. 2019. "Independent Aridity and Drought Pieces of Evidence Based on Meteorological Data and Tree Ring Data in Southeast Banat, Vojvodina, Serbia" Atmosphere 10, no. 10: 586. https://doi.org/10.3390/atmos10100586
APA StyleGavrilov, M. B., An, W., Xu, C., Radaković, M. G., Hao, Q., Yang, F., Guo, Z., Perić, Z., Gavrilov, G., & Marković, S. B. (2019). Independent Aridity and Drought Pieces of Evidence Based on Meteorological Data and Tree Ring Data in Southeast Banat, Vojvodina, Serbia. Atmosphere, 10(10), 586. https://doi.org/10.3390/atmos10100586







