The South Atlantic–South Indian Ocean Pattern: a Zonally Oriented Teleconnection along the Southern Hemisphere Westerly Jet in Austral Summer
Abstract
:1. Introduction
2. Data and Methods
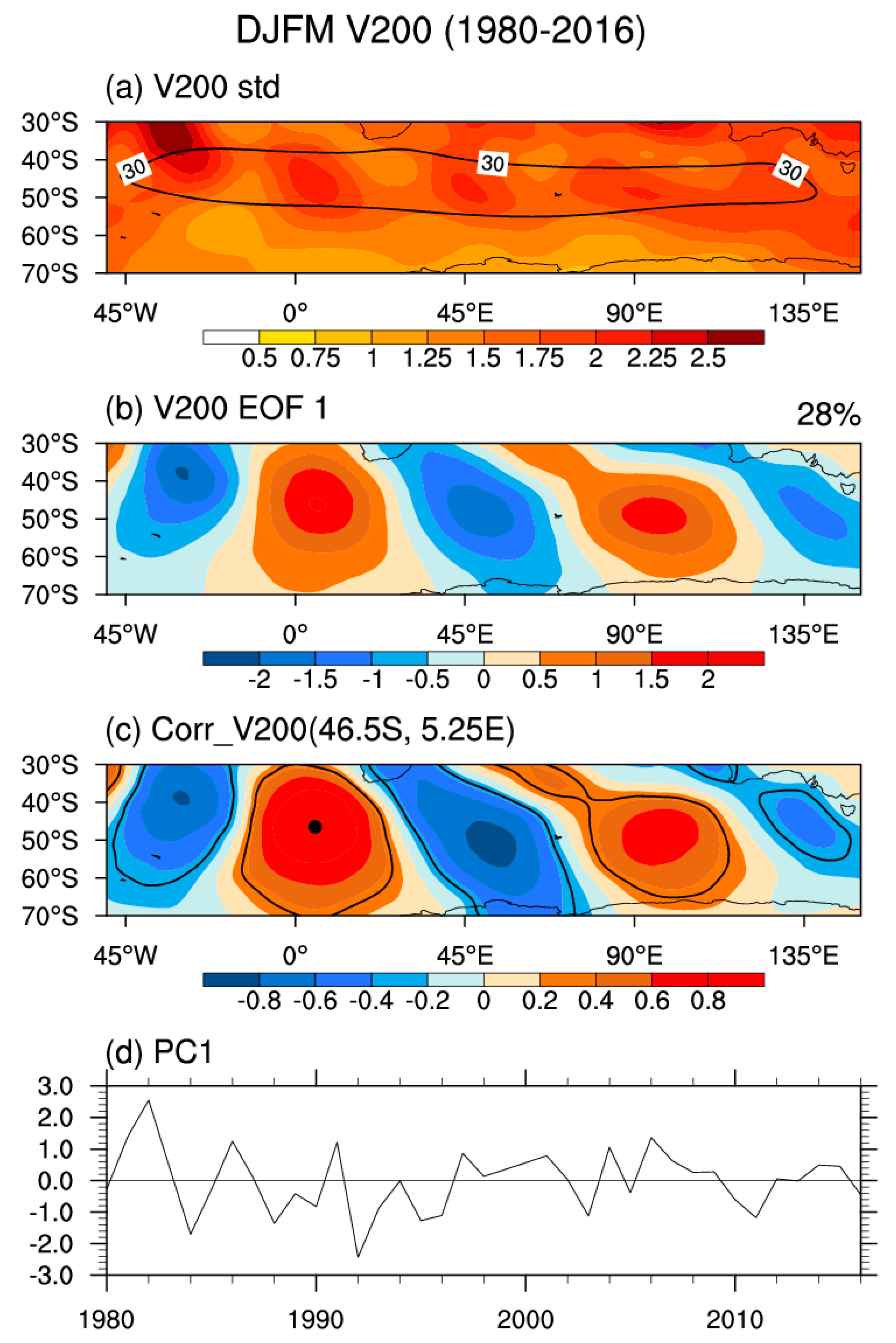
3. Identification of the SAIO Teleconnection Pattern
4. Dynamical Processes of the SAIO Pattern
4.1. Waveguide Effect of the Southern Hemisphere Westerly Jet
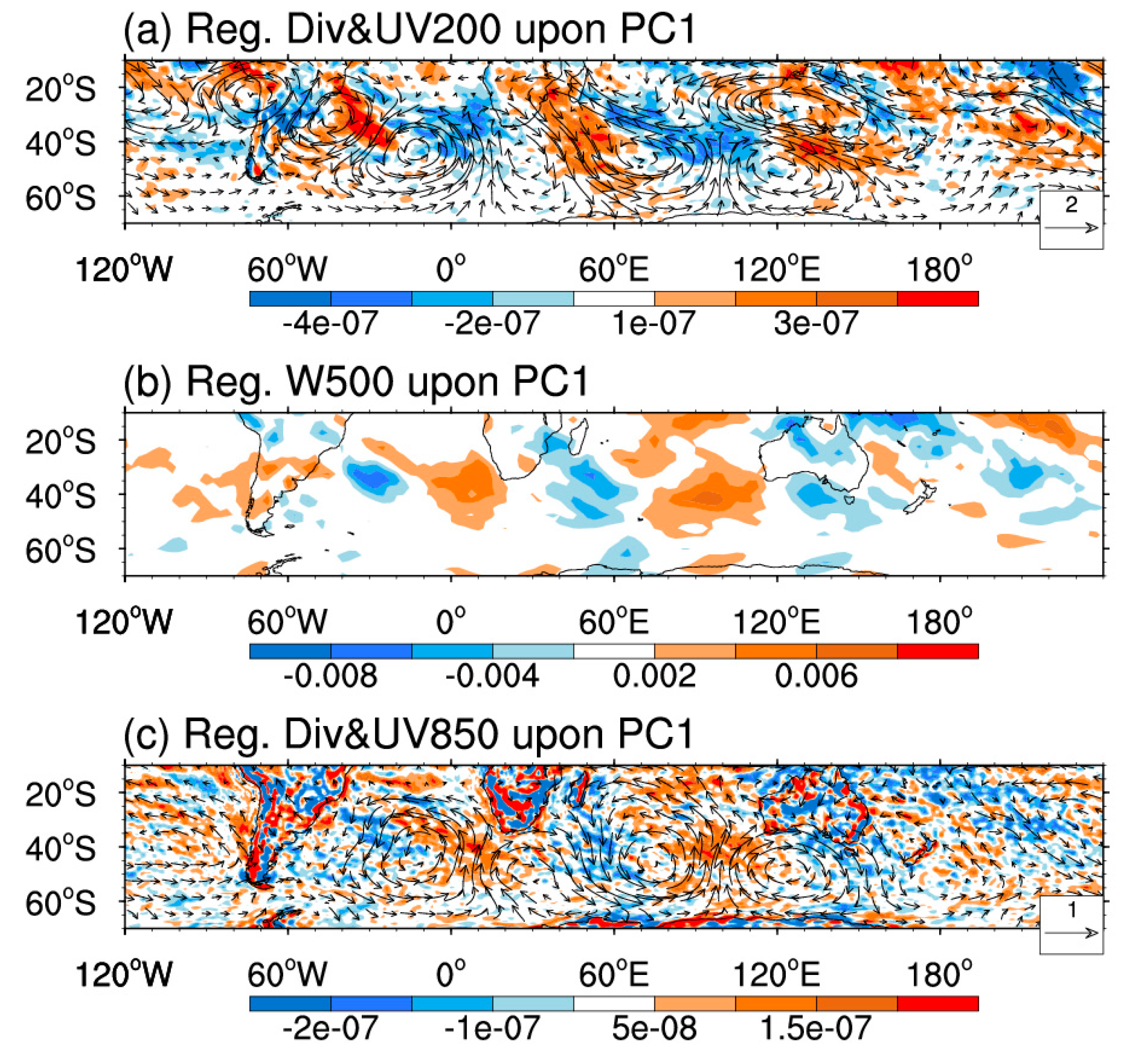
4.2. Anomalous Rossby Wave Source Related to the SAIO Pattern
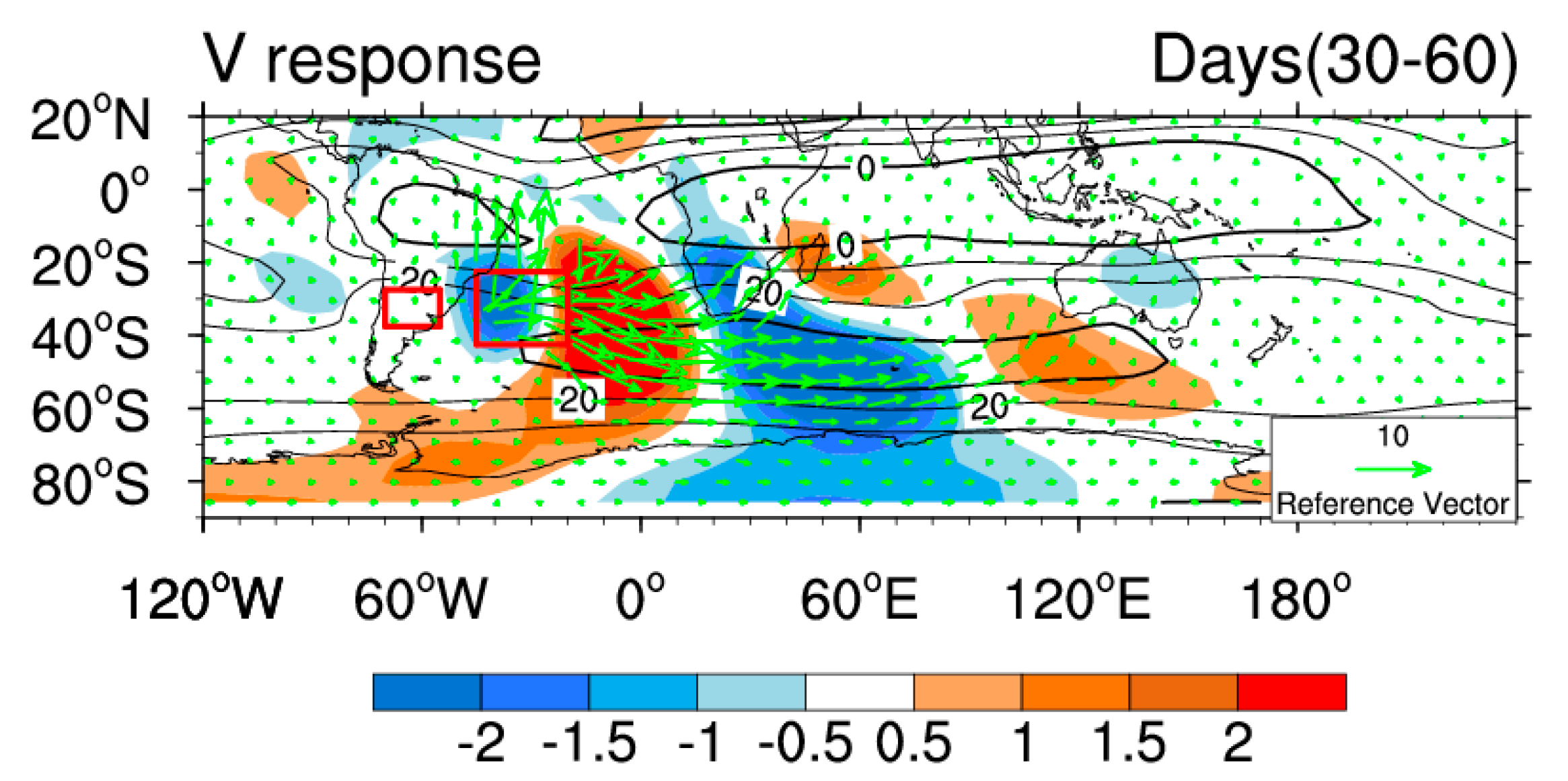
4.3. Tropical Connection of the SAIO Pattern
4.4. Relation to the Southern Annular Mode
5. Conclusion and Discussion
Funding
Acknowledgments
Conflicts of Interest
References
- Wallace, J.M.; Gutzler, D.S. Teleconnections in the geopotential height field during the northern hemisphere winter. Mon. Weather Rev. 1981, 109, 784–812. [Google Scholar] [CrossRef]
- Barnston, A.; Livezey, R. Classification, seasonality and persistence of low-frequency atmospheric circulation patterns. Mon. Weather Rev. 1987, 115, 1083–1126. [Google Scholar] [CrossRef]
- Wakabayashi, S.; Kawamura, R. Extraction of major teleconnection patterns possibly associated with the anomalous summer climate in japan. J. Meteorol. Soc. Jpn. 2004, 82, 1577–1588. [Google Scholar] [CrossRef]
- Mo, K.C.; Higgins, R.W. The pacific–south american modes and tropical convection during the southern hemisphere winter. Mon. Weather Rev. 1998, 126, 1581–1596. [Google Scholar] [CrossRef]
- O’Kane, T.J.; Monselesan, D.P.; Risbey, J.S. A multiscale reexamination of the pacific–south american pattern. Mon. Weather Rev. 2016, 145, 379–402. [Google Scholar] [CrossRef]
- Mo, K.C.; Paegle, J.N. The pacific-south american modes and their downstream effects. Int. J. Climatol. 2001, 21, 1211–1229. [Google Scholar] [CrossRef]
- Cai, W.; van Rensch, P.; Cowan, T.; Hendon, H.H. Teleconnection pathways of enso and the iod and the mechanisms for impacts on australian rainfall. J. Clim. 2011, 24, 3910–3923. [Google Scholar] [CrossRef]
- McIntosh, P.C.; Hendon, H.H. Understanding rossby wave trains forced by the indian ocean dipole. Clim. Dyn. 2018, 50, 2783–2798. [Google Scholar] [CrossRef]
- Shimizu, M.H.; de Albuquerque Cavalcanti, I.F. Variability patterns of rossby wave source. Clim. Dyn. 2011, 37, 441–454. [Google Scholar] [CrossRef]
- Grimm, A.M.; Reason, C.J.C. Does the south american monsoon influence african rainfall? J. Clim. 2011, 24, 1226–1238. [Google Scholar] [CrossRef]
- DeBlander, E.; Shaman, J. Teleconnection between the south atlantic convergence zone and the southern indian ocean: Implications for tropical cyclone activity. J. Geophys. Res. Atmos. 2017, 122, 728–740. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Karoly, D.J. The steady linear response of a spherical atmosphere to thermal and orographic forcing. J. Atmos. Sci. 1981, 38, 1179–1196. [Google Scholar] [CrossRef]
- Hoskins, B.J.; Ambrizzi, T. Rossby wave propagation on a realistic longitudinally varying flow. J. Atmos. Sci. 1993, 50, 1661–1671. [Google Scholar] [CrossRef]
- Hu, K.; Huang, G.; Wu, R.; Wang, L. Structure and dynamics of a wave train along the wintertime asian jet and its impact on east asian climate. Clim. Dyn. 2018, 51, 4123–4137. [Google Scholar] [CrossRef]
- Branstator, G. Circumglobal teleconnections, the jet stream waveguide, and the north atlantic oscillation. J. Clim. 2002, 14, 1893–1910. [Google Scholar] [CrossRef]
- Lu, R.-Y.; Oh, J.-H.; Kim, B.-J. A teleconnection pattern in upper-level meridional wind over the north african and eurasian continent in summer. Tellus Ser. A 2002, 54, 44–55. [Google Scholar] [CrossRef]
- Enomoto, T.; Hoskins, B.J.; Matsuda, Y. The formation mechanism of the bonin high in august. Q. J. R. Meteorol. Soc. 2003, 129, 157–178. [Google Scholar] [CrossRef]
- Ding, Q.; Wang, B. Circumglobal teleconnection in the northern hemisphere summer. J. Clim. 2005, 18, 3483–3505. [Google Scholar] [CrossRef]
- Huang, G.; Liu, Y.; Huang, R. The interannual variability of summer rainfall in the arid and semiarid regions of northern china and its association with the northern hemisphere circumglobal teleconnection. Adv. Atmos. Sci. 2011, 28, 257–268. [Google Scholar] [CrossRef]
- Huang, W.; Feng, S.; Chen, J.; Chen, F. Physical mechanisms of summer precipitation variations in the tarim basin in northwestern china. J. Clim. 2015, 28, 3579–3591. [Google Scholar] [CrossRef]
- Li, C.; Wu, L.; Chang, P. A far-reaching footprint of the tropical pacific meridional mode on the summer rainfall over the yellow river loop valley. J. Clim. 2010, 24, 2585–2598. [Google Scholar] [CrossRef]
- Small, D.; Islam, S.; Barlow, M. The impact of a hemispheric circulation regime on fall precipitation over north america. J. Hydrometeorol. 2010, 11, 1182–1189. [Google Scholar] [CrossRef]
- Syed, F.; Yoo, J.; Körnich, H.; Kucharski, F. Extratropical influences on the inter-annual variability of south-asian monsoon. Clim. Dyn. 2012, 38, 1661–1674. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, Y. Summertime atmospheric teleconnection pattern associated with a warming over the eastern tibetan plateau. Adv. Atmos. Sci. 2009, 26, 413–422. [Google Scholar] [CrossRef]
- Chen, G.; Huang, R. Excitation mechanisms of the teleconnection patterns affecting the july precipitation in northwest china. J. Clim. 2012, 25, 7834–7851. [Google Scholar] [CrossRef]
- Hong, X.; Lu, R.; Li, S. Amplified summer warming in europe–west asia and northeast asia after the mid-1990s. Environ. Res. Lett. 2017, 12, 094007. [Google Scholar] [CrossRef]
- Lin, Z.; Lu, R.; Wu, R. Weakened impact of the indian early summer monsoon on north china rainfall around the late 1970s. J. Clim. 2017, 30, 7991–8005. [Google Scholar] [CrossRef]
- Li, X.; Lu, R. Extratropical factors affecting the variability in summer precipitation over the yangtze river basin, china. J. Clim. 2017, 30, 8357–8374. [Google Scholar] [CrossRef]
- Lin, Z. Intercomparison of impacts of four summer teleconnections over eurasia on east asian rainfall. Adv. Atmos. Sci. 2014, 31, 1366–1376. [Google Scholar] [CrossRef]
- Yu, B.; Lin, H.; Soulard, N. A comparison of north american surface temperature and temperature extreme anomalies in association with various atmospheric teleconnection patterns. Atmosphere 2019, 10, 172. [Google Scholar] [CrossRef]
- Wu, R. Relationship between indian and east asian summer rainfall variations. Adv. Atmos. Sci. 2017, 34, 4–15. [Google Scholar] [CrossRef]
- Wu, R. A mid-latitude asian circulation anomaly pattern in boreal summer and its connection with the indian and east asian summer monsoons. Int. J. Climatol. 2002, 22, 1879–1895. [Google Scholar] [CrossRef]
- Ambrizzi, T.; Hoskins, B.J.; Hsu, H.H. Rossby wave propagation and teleconnection patterns in the austral winter. J. Atmos. Sci. 1995, 52, 3661–3672. [Google Scholar] [CrossRef]
- Risbey, J.S.; O’Kane, T.J.; Monselesan, D.P.; Franzke, C.L.E.; Horenko, I. On the dynamics of austral heat waves. J. Geophys. Res. Atmos. 2018, 123, 38–57. [Google Scholar] [CrossRef]
- Müller, G.V.; Ambrizzi, T. Teleconnection patterns and rossby wave propagation associated to generalized frosts over southern south america. Clim. Dyn. 2007, 29, 633–645. [Google Scholar] [CrossRef]
- Reeder, M.J.; Spengler, T.; Musgrave, R. Rossby waves, extreme fronts, and wildfires in southeastern australia. Geophys. Res. Lett. 2015, 42, 2015–2023. [Google Scholar] [CrossRef]
- Tozer, C.R.; Risbey, J.S.; O’Kane, T.J.; Monselesan, D.P.; Pook, M.J. The relationship between wave trains in the southern hemisphere storm track and rainfall extremes over tasmania. Mon. Weather Rev. 2018, 146, 4201–4230. [Google Scholar] [CrossRef]
- Zhao, C.; Li, T.; Zhou, T. Precursor signals and processes associated with mjo initiation over the tropical indian ocean. J. Clim. 2012, 26, 291–307. [Google Scholar] [CrossRef]
- Fauchereau, N.; Trzaska, S.; Richard, Y.; Roucou, P.; Camberlin, P. Sea-surface temperature co-variability in the southern atlantic and indian oceans and its connections with the atmospheric circulation in the southern hemisphere. Int. J. Climatol. 2003, 23, 663–677. [Google Scholar] [CrossRef]
- Jury, M.R.; Parker, B.A.; Raholijao, N.; Nassor, A. Variability of summer rainfall over madagascar: Climatic determinants at interannual scales. Int. J. Climatol. 1995, 15, 1323–1332. [Google Scholar] [CrossRef]
- Lin, Z.; Li, Y. Remote influence of the tropical atlantic on the variability and trend in north west australia summer rainfall. J. Clim. 2012, 25, 2408–2420. [Google Scholar] [CrossRef]
- Grimm, A.M.; Reason, C.J.C. Intraseasonal teleconnections between south america and south africa. J. Clim. 2015, 28, 9489–9497. [Google Scholar] [CrossRef]
- Xue, J.; Li, J.; Sun, C.; Zhao, S.; Mao, J.; Dong, D.; Li, Y.; Feng, J. Decadal-scale teleconnection between south atlantic sst and southeast australia surface air temperature in austral summer. Clim. Dyn. 2018, 50, 2687–2703. [Google Scholar] [CrossRef]
- Dee, D.; Uppala, S.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.; Balsamo, G.; Bauer, P. The era-interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Xie, P.P.; Arkin, P.A. Global precipitation: A 17-year monthly analysis based on gauge observations, satellite estimates, and numerical model outputs. Bull. Am. Meteorol. Soc. 1997, 78, 2539–2558. [Google Scholar] [CrossRef]
- Takaya, K.; Nakamura, H. A formulation of a phase-independent wave-activity flux for stationary and migratory quasigeostrophic eddies on a zonally varying basic flow. J. Atmos. Sci. 2001, 58, 608–627. [Google Scholar] [CrossRef]
- North, G.R.; Bell, T.L.; Cahalan, R.F.; Moeng, F.J. Sampling errors in the estimation of empirical orthogonal functions. Mon. Weather Rev. 1982, 110, 699–706. [Google Scholar] [CrossRef]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The ncep/ncar 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Timbal, B.; Fawcett, R. A historical perspective on southeastern australian rainfall since 1865 using the instrumental record. J. Clim. 2013, 26, 1112–1129. [Google Scholar] [CrossRef]
- Sardeshmukh, P.D.; Hoskins, B.J. The generation of global rotational flow by steady idealized tropical divergence. J. Atmos. Sci. 1988, 45, 1228–1251. [Google Scholar] [CrossRef]
- Paegle, J.N.; Mo, K.C. Linkages between summer rainfall variability over south america and sea surface temperature anomalies. J. Clim. 2002, 15, 1389–1407. [Google Scholar] [CrossRef]
- Zhou, J.; Lau, K.M. Principal modes of interannual and decadal variability of summer rainfall over south america. Int. J. Climatol. 2001, 21, 1623–1644. [Google Scholar] [CrossRef]
- Montecinos, A.; Díaz, A.; Aceituno, P. Seasonal diagnostic and predictability of rainfall in subtropical south america based on tropical pacific sst. J. Clim. 2000, 13, 746–758. [Google Scholar] [CrossRef]
- Thompson, D.W.J.; Wallace, J.M. Annular modes in the extratropical circulation. Part i: Month-to-month variability. J. Clim. 2000, 13, 1000–1016. [Google Scholar] [CrossRef]
- Gong, D.; Wang, S. Definition of antarctic oscillation index. Geophys. Res. Lett. 1999, 26, 459–462. [Google Scholar] [CrossRef]
- Ding, Q.; Steig, E.J.; Battisti, D.S.; Wallace, J.M. Influence of the tropics on the southern annular mode. J. Clim. 2012, 25, 6330–6348. [Google Scholar] [CrossRef]








© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, Z. The South Atlantic–South Indian Ocean Pattern: a Zonally Oriented Teleconnection along the Southern Hemisphere Westerly Jet in Austral Summer. Atmosphere 2019, 10, 259. https://doi.org/10.3390/atmos10050259
Lin Z. The South Atlantic–South Indian Ocean Pattern: a Zonally Oriented Teleconnection along the Southern Hemisphere Westerly Jet in Austral Summer. Atmosphere. 2019; 10(5):259. https://doi.org/10.3390/atmos10050259
Chicago/Turabian StyleLin, Zhongda. 2019. "The South Atlantic–South Indian Ocean Pattern: a Zonally Oriented Teleconnection along the Southern Hemisphere Westerly Jet in Austral Summer" Atmosphere 10, no. 5: 259. https://doi.org/10.3390/atmos10050259
APA StyleLin, Z. (2019). The South Atlantic–South Indian Ocean Pattern: a Zonally Oriented Teleconnection along the Southern Hemisphere Westerly Jet in Austral Summer. Atmosphere, 10(5), 259. https://doi.org/10.3390/atmos10050259




