Impacts of Green Vegetation Fraction Derivation Methods on Regional Climate Simulations
Abstract
:1. Introduction
2. Methods and Data
2.1. NDVI Data
2.2. Deriving FVC from NDVI Data
2.2.1. Wetzel Method
2.2.2. Gutman Method
2.2.3. Zeng Method
2.3. Regional Climate Model Experiments
3. Results
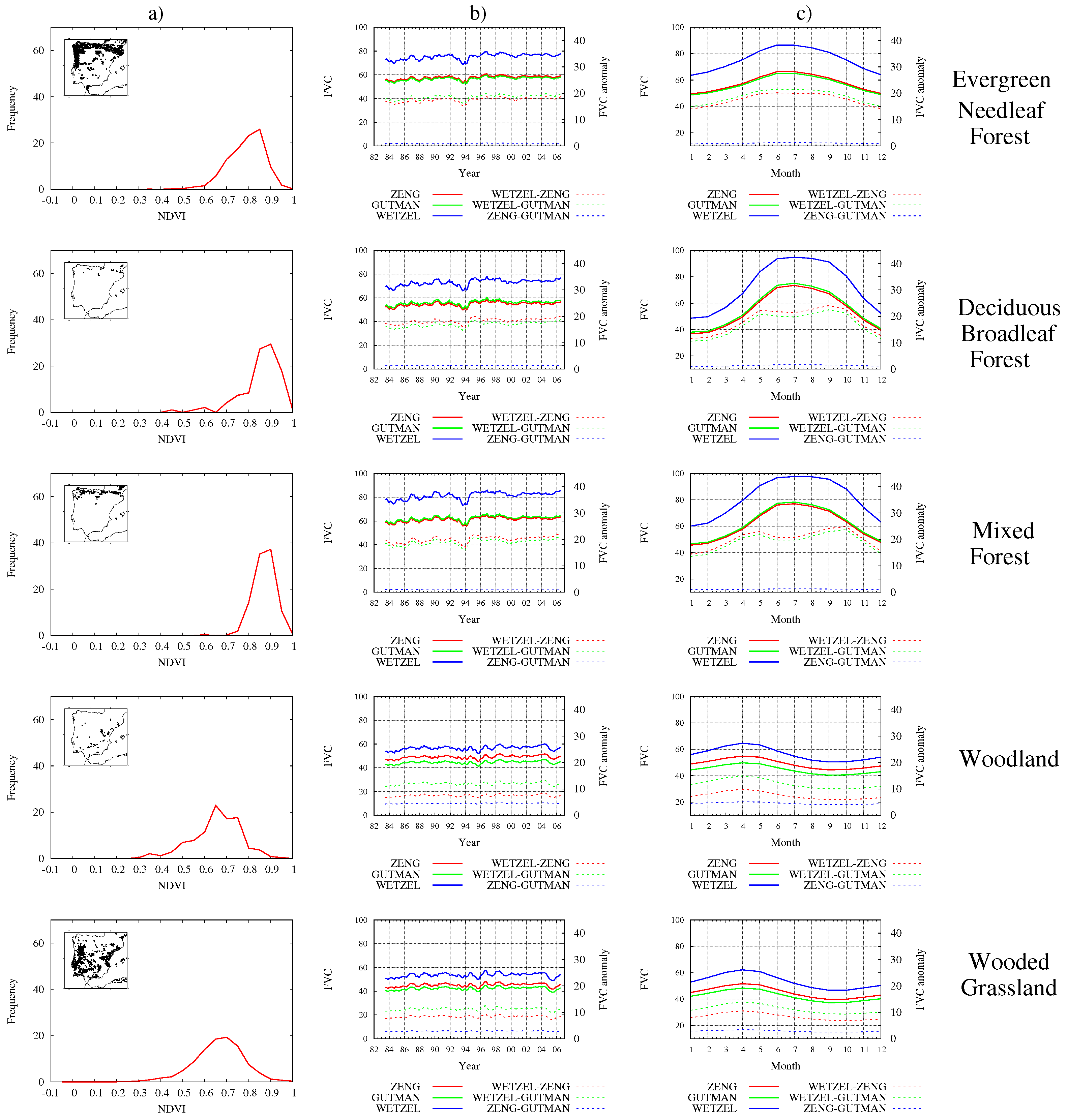
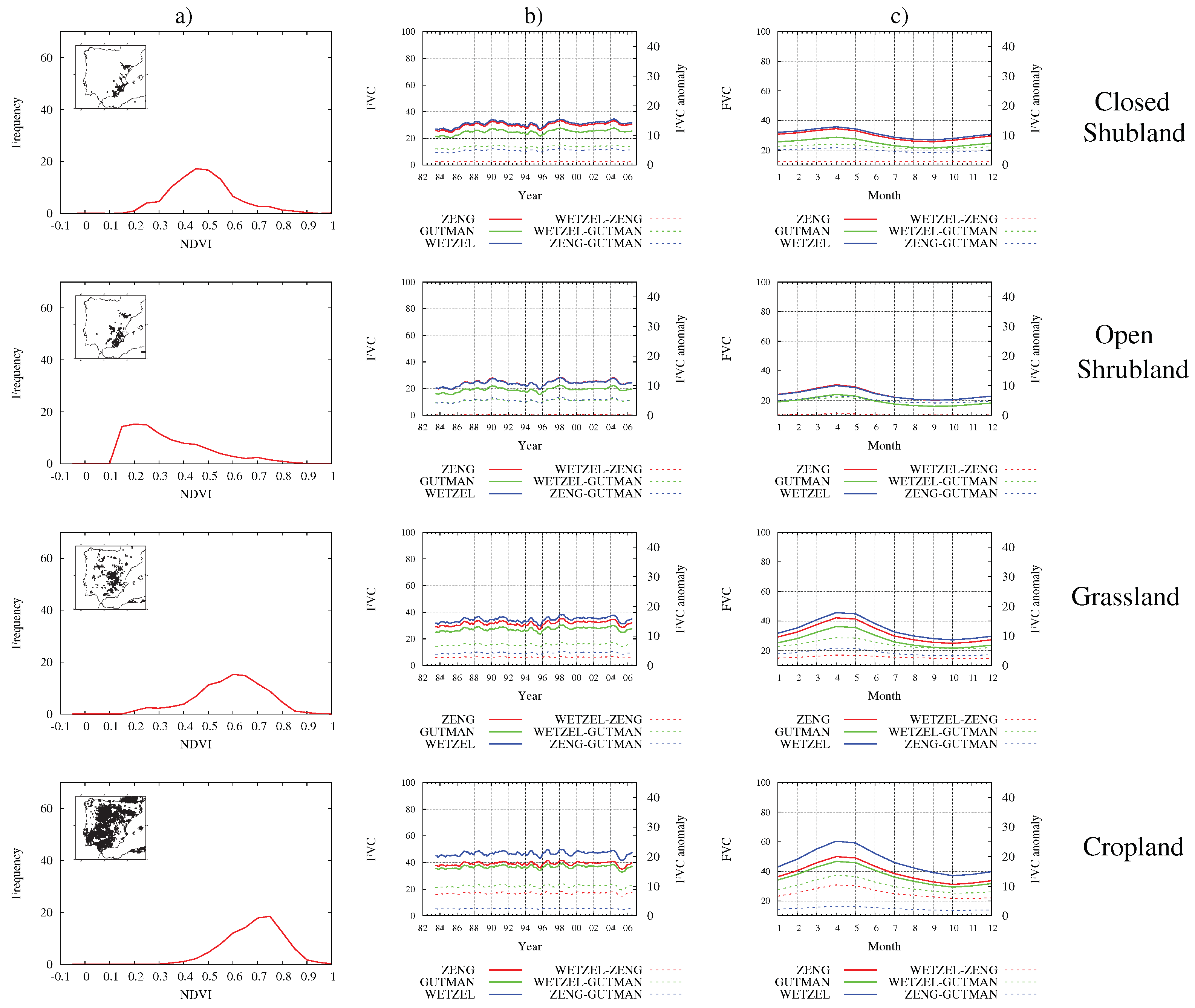
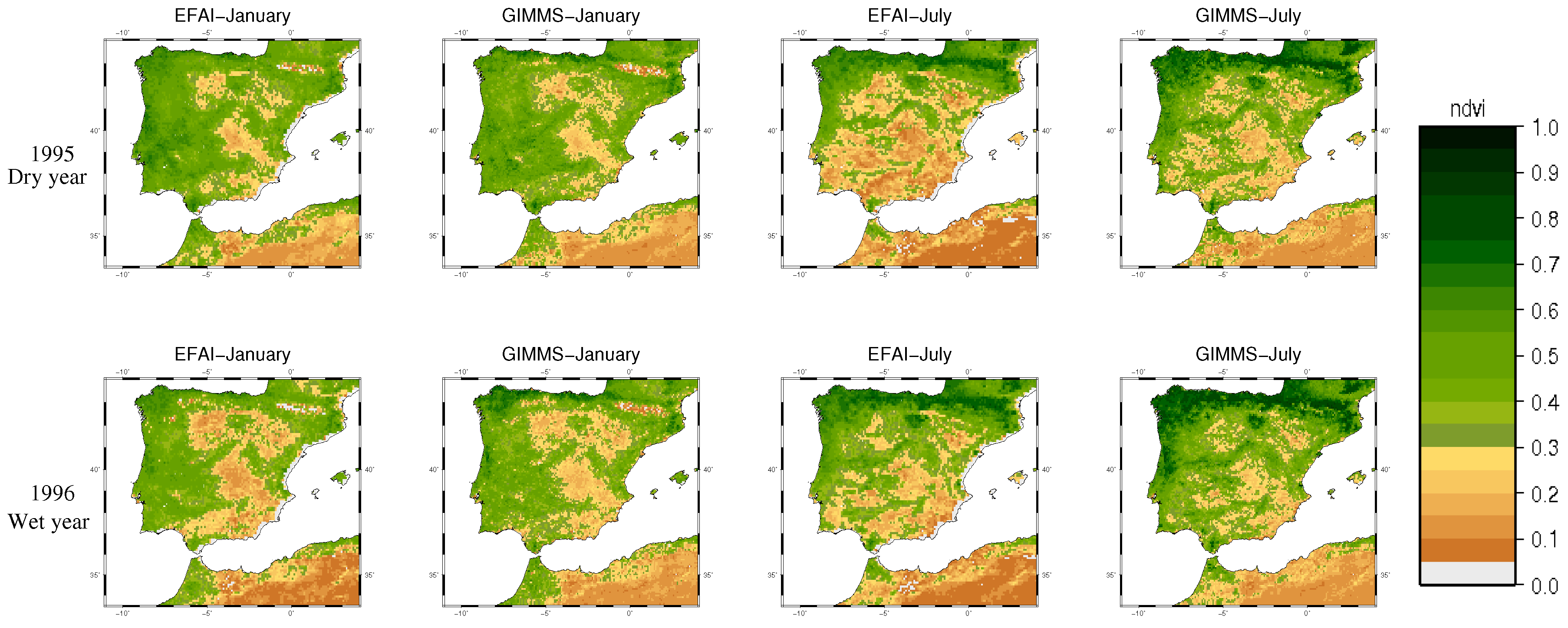
3.1. NDVI Database Comparison
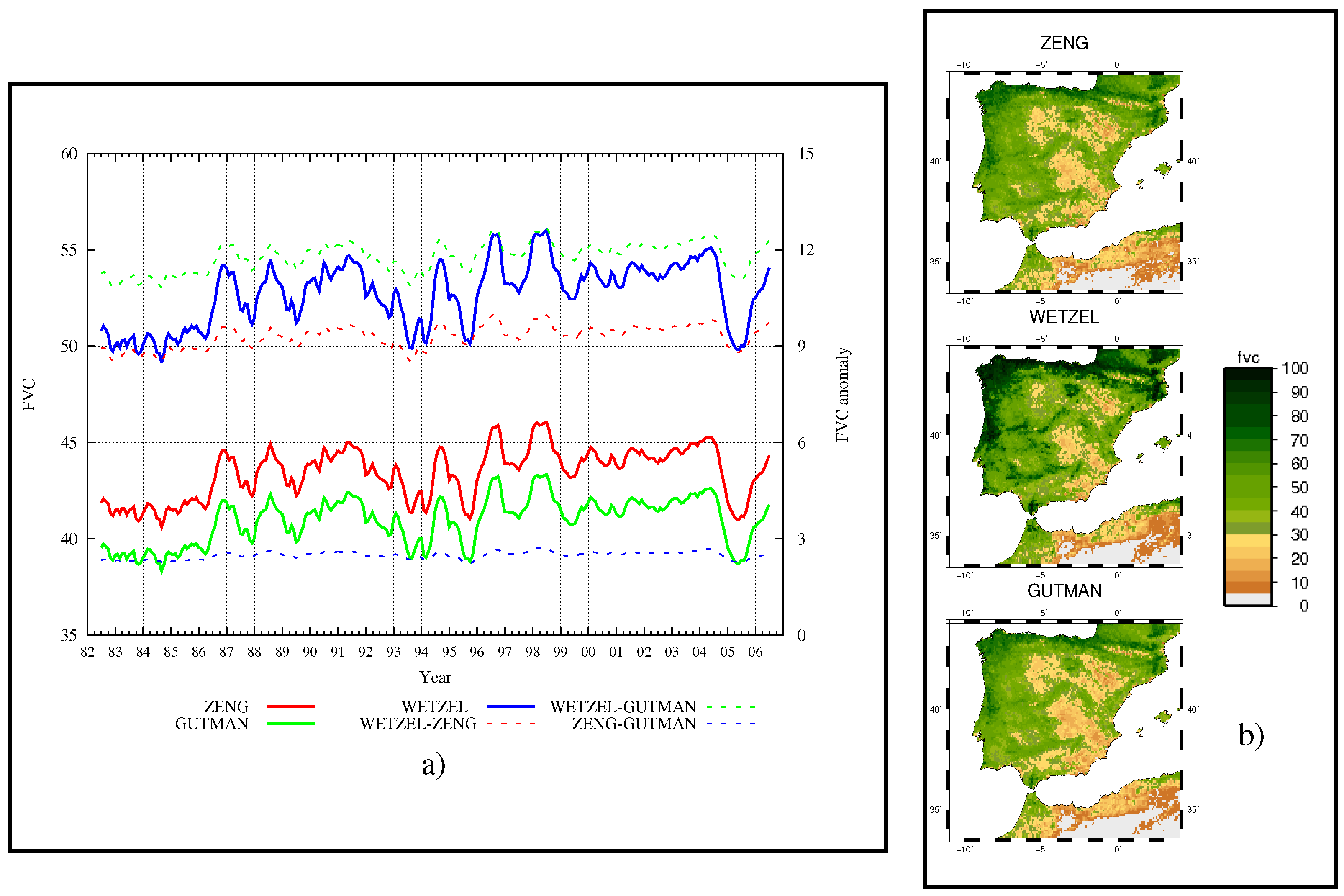
3.2. Analysis of FVC Retrieval Methods
3.3. Sensitivity to the FVC Estimation Method
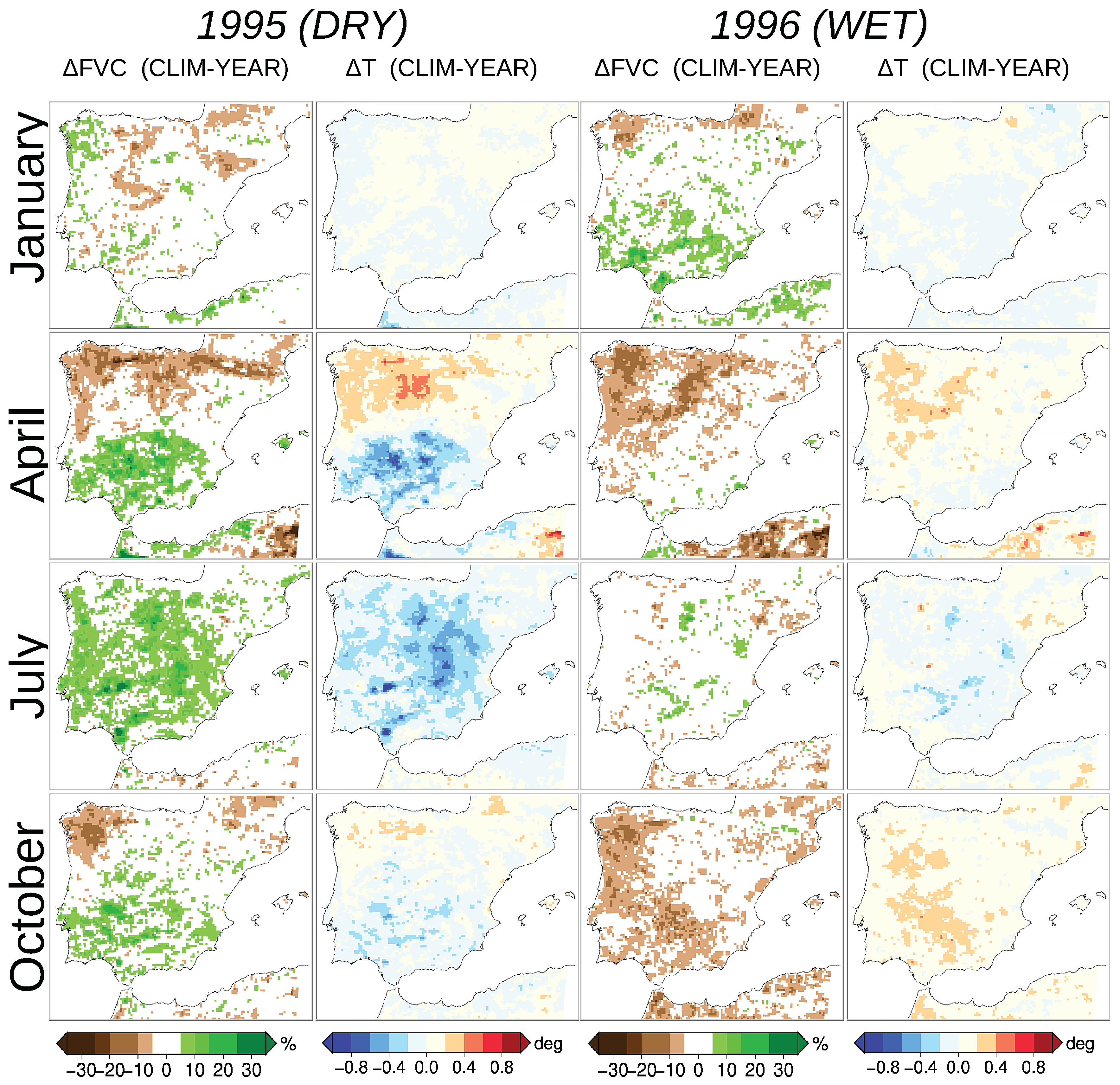
3.4. Sensitivity to FVC Interannual Variations
4. Discussion and Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pielke, R.A. Overlooked issues in the U.S. National Climate and IPCC assesments. Clim. Chang. 2002, 52, 1–11. [Google Scholar]
- Godfrey, C.M.; Stensrud, D.J.; Leslie, L.M. The influence of improved land surface and soil data on mesoscale model predictions. CD–ROM. In Proceedings of the 19th Conference on Hydrology; American Meteorological Society: Boston, MA, USA, 2002; Paper 4.7. [Google Scholar]
- Jerez, S.; Montavez, J.; Gomez-Navarro, J.; Jimenez, P.; Jimenez-Guerrero, P.; Lorente, R.; Gonzalez-Rouco, J.F. The role of the land-surface model for climate change projections over the Iberian Peninsula. J. Geophys. Res. Atmos. 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Stensrud, D.J. Parameterization Schemes: Keys to Understanding Numerical Weather Prediction Models; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Chang, J.T.; Wetzel, P.J. Effects of spatial variations of soil moisture and vegetation on the evolution of a prestorm environment: A numerical case study. Mon. Weather Rev. 1991, 119, 1368–1390. [Google Scholar] [CrossRef]
- Gutman, G.; Ignatov, A. The derivation of the green vegetation fraction from NOAA/AVHRR data for use in numerical weather prediction models. Int. J. Remote Sens. 1998, 19, 1533–1543. [Google Scholar] [CrossRef]
- Zeng, X.; Dickinson, R.E.; Walker, A.; Shaikh, M. Derivation and evaluation of global 1-km fractional vegetation cover data for land modelling. J. Appl. Meteorol. 2000, 39, 826–839. [Google Scholar] [CrossRef]
- Li, X.; Zhang, J. Derivation of the Green Vegetation Fraction of the Whole China from 2000 to 2010 from MODIS Data. Earth Interact. 2016, 20, 1–16. [Google Scholar] [CrossRef]
- Carlson, T.N.; Perry, E.M.; Schmugge, T.J. Remote estimates of soil moisture availability and fractional vegetation cover for agricultural fields. Remote Sens. Environ. 1990, 52, 45–70. [Google Scholar]
- Sellers, P.J.; Los, S.O.; Tucker, C.J.; Justice, C.O.; Dazlich, D.A.; Collatz, G.J.; Randall, D.A. A revised land surface parameterization (SiB2) for atmospheric GCMs. Part II: The generation of global fields of terrestrial biophysical parameters from satellite data. J. Clim. 1996, 9, 706–737. [Google Scholar] [CrossRef]
- Hanamean, J.M., Jr.; Pielke, R.A., Sr.; Castro, C.L.; Ojima, D.S.; Reed, B.C.; Gao, Z. Vegetation greenness impacts on maximum and minimum temperatures in northeast Colorado. Meteorol. Appl. 2003, 10, 203–215. [Google Scholar] [CrossRef] [Green Version]
- Ek, M.B.; Mitchell, K.E.; Lin, Y.; Rogers, E.; Grunmann, P.; Koren, V.; Gayno, G.; Tarpley, J.D. Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model. J. Geophys. Res. Atmos. 2003, 108, 8851. [Google Scholar] [CrossRef]
- Kurkowski, N.P.; Stensrud, D.J.; Baldwin, M.E. Assessment of Implementing Satellite-Derived Land Cover Data in the Eta Model. Weather Forecast. 2003, 18, 404–416. [Google Scholar] [CrossRef]
- Marshall, C.H.; Crawford, K.C.; Mitchell, K.E.; Stensrud, D.J. The impact of the land surface physics in the operational NCEP Eta model on simulating the diurnal cycle: Evaluation and testing using Oklahoma Mesonet data. Weather Forecast. 2003, 18, 748–768. [Google Scholar] [CrossRef]
- Hong, S.; Lakshmi, V.; Small, E.; Chen, F.; Tewari, M.; Manning, K.W. Effects of vegetation and soil moisture on the simulated land surface processes from the coupled WRF/Noah model. J. Geophys. Res. Atmos. 2009, 114, D18118. [Google Scholar] [CrossRef]
- Limei, R.; Gilliam, R.; Binkowski, F.; Xiu, A.; Pleim, J.; Band, L. Sensitivity of the Weather Research and Forecast/Community Multiscale Air Quality modeling system to MODIS LAI, FPAR, and albedo. J. Geophys. Res. Atmos. 2015, 120, 8491–8511. [Google Scholar] [Green Version]
- Cao, Q.; Yu, D.; Georgescu, M.; Han, Z.; Wu, J. Impacts of land use and land cover change on regional climate: A case study in the agro-pastoral transitional zone of China. Environ. Res. Lett. 2015, 10, 124025. [Google Scholar] [CrossRef]
- Xu, L.; Pyles, R.D.; Snyder, R.H.; Monier, E.; Falk, M.; Chen, S.-H. Impact of canopy representations on regional modeling of evapotranspiration using the WRF-ACASA coupled model. Agric. For. Meteorol. 2017, 247, 79–92. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Geping, L.; Maeyer, P.D.; Cai, P.; Kurban, A. Improved Atmospheric Modelling of the Oasis-Desert System in Central Asia Using WRF with Actual Satellite Products. Remote Sens. 2017, 9, 1273. [Google Scholar] [CrossRef]
- Wen, J.; Lai, X.; Shi, X.; Pan, X. Numerical simulations of fractional vegetation coverage influences on the convective environment over the source region of the Yellow River. Meteorol. Atmos. Phys. 2013, 120, 1–10. [Google Scholar] [CrossRef]
- Meng, X.H.; Evans, J.P.; McCabe, M.F. The Impact of Observed Vegetation Changes on Land–Atmosphere Feedbacks During Drought. J. Hydrometeorol. 2014, 15, 759–776. [Google Scholar] [CrossRef] [Green Version]
- Müller, O.V.; Berbery, E.H.; Alcaraz-Segura, D.; Ek, M.B. Regional model simulations of the 2008 drought in southern South America using a consistent set of land surface properties. J. Clim. 2014, 27, 6754–6778. [Google Scholar] [CrossRef]
- Matsui, T.; Lakshmi, V.; Small, E.E. The effects of satellite-derived vegetation cover variability on simulated land-atmosphere interactions in the NAMS. J. Clim. 2005, 18, 21–40. [Google Scholar] [CrossRef]
- Notaro, M.; Chen, G.; Yu, Y.; Wang, F.; Tawfik, A. Regional Climate Modeling of Vegetation Feedbacks on the Asian–Australian Monsoon Systems. J. Clim. 2017, 30, 1553–1582. [Google Scholar] [CrossRef]
- James, K.A.; Stensrud, D.J.; Yussouf, N. Value of real-time vegetation fraction to forecasts of severe convection in high-resolution models. Weather Forecast. 2009, 24, 187–210. [Google Scholar] [CrossRef]
- Zhang, G.; Zhou, G.; Chen, F.; Barlage, M.; Xue, L. A Trial to Improve Surface Heat Exchange Simulation through Sensitivity Experiments over a Desert Steppe Site. J. Hydrometeorol. 2014, 15, 664–684. [Google Scholar] [CrossRef]
- Vahmani, P.; Hogue, T. High-resolution land surface modeling utilizing remote sensing parameters and the Noah UCM: A case study in the Los Angeles Basin. Hydrol. Earth Syst. Sci. 2014, 18, 4791–4806. [Google Scholar] [CrossRef]
- Vahmani, P.; Ban-Weiss, G. Climatic consequences of adopting drought-tolerant vegetation over Los Angeles as a response to California drought. Geophys. Res. Lett. 2016, 43, 8240–8249. [Google Scholar] [CrossRef]
- Stockli, R.; Vidale, P.L. European plant phenology and climate as seen in a 20 year AVHRR land-surface parameter dataset. Int. J. Remote Sens. 2004, 17, 3303–3330. [Google Scholar] [CrossRef]
- Miller, J.; Barlage, M.; Zeng, X.; Wei, H.; Mitchell, K. Sensitivity of the NCEP/Noah land surface model to the MODIS green vegetation fraction data set. Geophys. Res. Lett. 2006, 33, 237–250. [Google Scholar] [CrossRef]
- Crawford, T.M.; Stensrud, D.J.; Mora, F.; Merchant, J.W.; Wetzel, P.J. Value of Incorporating Satellite-Derived Land Cover Data in MM5/PLACE for Simulating Surface Temperatures. J. Hydrometeorol. 2001, 2, 453–468. [Google Scholar] [CrossRef]
- Myneni, R.B.; Keeling, C.D.; Tucker, C.J.; Asrar, G.; Nemani, R.R. Increased plant growth in the northern high latitudes from 1981 to 1991. Nature 1997, 386, 698–702. [Google Scholar] [CrossRef]
- Refslund, J.; Dellwik, E.; Hahmann, A.; Barlage, M.; Boegh, E. Development of satellite green vegetation fraction time series for use in mesoscale modeling: Application to the European heat wave 2006. Theor. Appl. Clim. 2014, 117, 377–392. [Google Scholar] [CrossRef]
- Pettorelli, N.; Olav, V.J.; Atle, M.; Gaillard, J.M.; Tucker, C.J.; Stenseth, N.C. Using the satellite-derived NDVI to assess ecological responses to enviromental change. IEEE Trans. Geosci. Remote Sens. 2005, 20, 503–510. [Google Scholar]
- Myneni, R.B.; Hall, F.G.; Sellers, P.J.; Marshak, A.L. The interpretation of spectral vegetation indexes. IEEE Trans. Geosci. Remote Sens. 1995, 33, 481–486. [Google Scholar] [CrossRef]
- Zhou, L.; Kaufmann, R.K.; Tian, Y.; Mineny, R.B.; Tucker, C.J. Relation between interannual variations in satellite measures of northern forest greenness and climate between 1982 and 1999. J. Geophys. Res. 2003, 108. ACL 3-1–ACL 3-16. [Google Scholar] [CrossRef]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E.; Slayback, D.; Pak, E.W.; Mahoney, R.; Vermote, E.; Saleous, N.E. An Extended AVHRR 8-km NDVI Data Set Compatible with MODIS and SPOT Vegetation NDVI Data. Int. J. Remote Sens. 2005, 26, 4485–4498. [Google Scholar]
- Tarpley, J.P.; Schneider, S.R.; Money, R.L. Global vegetation indices from NOAA-7 meteorological satellite. J. Clim. Appl. Meteorol. 1984, 23, 491–494. [Google Scholar]
- Gutman, G.; Tarpley, D.; Ignatov, A.; Olson, S. The enhanced NOAA Global Land datasets from the Advanced Very High Resolution Radiometer. Int. J. Remote Sens. 1995, 76, 1141–1156. [Google Scholar] [CrossRef]
- James, M.E.; Kalluri, S.N.V. The Pathfinder AVHRR land dataset:an improved coarse resolution dataset for terrestrial monitoring. Int. J. Remote Sens. 1994, 15, 3347–3363. [Google Scholar] [CrossRef]
- Pinzon, J. Using HHT to successfully uncouple seasonal and interannual components in remotely sensed data. In Proceedings of the 6th World Multiconference on Systemics, Cybernetics and Informatics, Orlando, FL, USA, 14–18 July 2002. [Google Scholar]
- Tucker, C.J.; Pinzon, J.E.; Brown, M.E. Global Inventory Modeling and Mapping Studies 2.0, 2004. Digital Media. Available online: http://staff.glcf.umd.edu/sns/htdocs/data/gimms/ (accessed on 8 March 2019).
- Gallo, K.; Tarpley, D.; Mitchell, K.; Csiszar, I.; Owen, T.; Reed, B. Monthly fractional green vegetation cover associated with land cover classes of the Conterminous USA. Geophys. Res. Lett. 2001, 28, 2089–2092. [Google Scholar] [CrossRef]
- Montandon, L.M.; Small, E.E. The impact of soil reflectance on the quantification of the green vegetation fraction from NDVI. Remote Sens. Environ. 2008, 112, 1835–1845. [Google Scholar] [CrossRef]
- Carlson, T.N.; Rypley, D.A. On the relation between NDVI, fractional vegetation cover, and leaf area index. Remote Sens. Environ. 1997, 62, 241–252. [Google Scholar] [CrossRef]
- Price, J.C. Estimating vegetation amount from visible and near infrared reflectances. Remote Sens. Environ. 1992, 41, 29–34. [Google Scholar] [CrossRef]
- Hansen, M.; DeFries, R.; Townshend, J.R.G.; Sohlberg, R. UMD Global Land Cover Classification. 8 Kilometer. Version 1.0. 1981–1994; Department of Geography, University of Maryland: College Park, MD, USA, 1998. [Google Scholar]
- Hansen, M.; DeFries, R.; Townshend, J.R.G.; Sohlberg, R. Global land cover classification at 1km resolution using a decision tree classifier. Int. J. Remote Sens. 2000, 21, 1331–1365. [Google Scholar] [CrossRef]
- Grell, G.; Dudhia, J.; Stauffer, D. A Description of the Fifth-Generation Penn State/NCAR Mesoscale Model (MM5); NCAR Technik Note; NCAR: Boulder, CO, USA, 1994. [Google Scholar]
- Jerez, S.; Montavez, J.P.; Gomez-Navarro, J.J.; Jimenez-Guerrrero, P.; Jimenez, J.M.; Gonzalez-Rouco, J.F. Temperature sensitivity to the land-surface model in MM5 climate simulations over the Iberian Peninsula. Meteorol. Z. 2010, 19, 363–374. [Google Scholar] [CrossRef] [Green Version]
- Dee, D.P.; Uppala, S.M.; Simmons, A.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Quart. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Grell, G.A. Prognostic evaluation of assumptions used by cumulus parameterizations. Mon. Weather Rev. 1993, 121, 764–787. [Google Scholar] [CrossRef]
- Dudhia, J. Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model. J. Atmos. Sci. 1989, 46, 3077–3107. [Google Scholar] [CrossRef]
- Mlawer, E.; Taubman, S.; Brown, P.; Iacono, M.; Clough, S. Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave. J. Geophys. Res. 1997, 102, 16663–16682. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Pan, H. Nonlocal boundary layer vertical diffusion in a Medium-Range Forecast Model. Mon. Weather Rev. 1996, 124, 2322–2339. [Google Scholar] [CrossRef]
- Chen, F.; Dudhia, J. Coupling an advanced land-surface/hydrology model with the Penn State/NCAR MM5 modeling system. Part I: Model implementation and sensitivity. Mon. Weather Rev. 2001, 129, 569–585. [Google Scholar] [CrossRef]
- Mahrt, L.; Ek, M. The influence of atmospheric stability on potential evaporation. J. Appl. Meteorol. 1984, 23, 222–234. [Google Scholar] [CrossRef]
- Mahrt, L.; Pan, H. A two-layer model of soil hydrology. Bound. Layer Meteorol. 1984, 29, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Pan, H.L.; Mahrt, L. Interaction between soil hydrology and boundary-layer development. Bound. Layer Meteorol. 1987, 38, 185–202. [Google Scholar] [CrossRef]
- Chen, F.; Mitchell, K.; Schaake, J.; Xue, Y.; Pan, H.L.; Koren, V.; Duan, Q.Y.; Ek, M.; Betts, A. Modeling of land surface evaporation by four schemes and comparison with FIFE observations. J. Geophys. Res. Atmos. 1996, 101, 7251–7268. [Google Scholar] [CrossRef] [Green Version]
- Noilhan, J.; Planton, S. A simple parameterization of land surface processes for meteorological models. Mon. Weather Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Jacquemin, B.; Noilhan, J. Sensitivity study and validation of a land surface parameterization using the HAPEX-MOBILHY data set. Bound. Layer. Meteorol. 1990, 52, 93–134. [Google Scholar] [CrossRef]
- Gómez-Navarro, J.; Montávez, J.; Jiménez-Guerrero, P.; Jerez, S.; Lorente-Plazas, R.; González-Rouco, J.; Zorita, E. Internal and external variability in regional simulations of the Iberian Peninsula climate over the last millennium. Clim. Past 2012, 8, 25. [Google Scholar] [CrossRef]
- Jerez, S.; Montavez, J.P.; Jimenez-Guerrero, P.; Gomez-Navarro, J.J.; Lorente-Plazas, R.; Zorita, E. A multi-physics ensemble of present-day climate regional simulations over the Iberian Peninsula. Clim. Dyn. 2013, 40, 3023–3046. [Google Scholar] [CrossRef]
- Lorente-Plazas, R.; Montávez, J.; Jerez, S.; Gómez-Navarro, J.; Jiménez-Guerrero, P.; Jiménez, P. A 49 year hindcast of surface winds over the Iberian Peninsula. Int. J. Climatol. 2015, 35, 3007–3023. [Google Scholar] [CrossRef]
- Peters-Lidard, C.D.; Zion, M.S.; Wood, E.F. A soil-vegetation-atmosphere transfer scheme for modeling spatially variable water and energy balance processes. J. Geophys. Res. Atmos. 1997, 102, 4303–4324. [Google Scholar] [CrossRef] [Green Version]
- Gómez-Navarro, J.; Montávez, J.; Jerez, S.; Jiménez-Guerrero, P.; Zorita, E. What is the role of the observational dataset in the evaluation and scoring of climate models? Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef] [Green Version]
- Fernández, J.; Montávez, J.; Sáenz, J.; González-Rouco, J.; Zorita, E. Sensitivity of the MM5 mesoscale model to physical parameterizations for regional climate studies: Annual cycle. J. Geophys. Res. Atmos. 2007, 112. [Google Scholar] [CrossRef] [Green Version]




© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiménez-Gutiérrez, J.M.; Valero, F.; Jerez, S.; Montávez, J.P. Impacts of Green Vegetation Fraction Derivation Methods on Regional Climate Simulations. Atmosphere 2019, 10, 281. https://doi.org/10.3390/atmos10050281
Jiménez-Gutiérrez JM, Valero F, Jerez S, Montávez JP. Impacts of Green Vegetation Fraction Derivation Methods on Regional Climate Simulations. Atmosphere. 2019; 10(5):281. https://doi.org/10.3390/atmos10050281
Chicago/Turabian StyleJiménez-Gutiérrez, Jose Manuel, Francisco Valero, Sonia Jerez, and Juan Pedro Montávez. 2019. "Impacts of Green Vegetation Fraction Derivation Methods on Regional Climate Simulations" Atmosphere 10, no. 5: 281. https://doi.org/10.3390/atmos10050281
APA StyleJiménez-Gutiérrez, J. M., Valero, F., Jerez, S., & Montávez, J. P. (2019). Impacts of Green Vegetation Fraction Derivation Methods on Regional Climate Simulations. Atmosphere, 10(5), 281. https://doi.org/10.3390/atmos10050281






