Using Convective Available Potential Energy (CAPE) and Dew-Point Temperature to Characterize Rainfall-Extreme Events in the South-Central Andes

Abstract

The interactions between atmosphere and steep topography in the eastern south–central Andes result in complex relations with inhomogenous rainfall distributions. The atmospheric conditions leading to deep convection and extreme rainfall and their spatial patterns—both at the valley and mountain-belt scales—are not well understood. In this study, we aim to identify the dominant atmospheric conditions and their spatial variability by analyzing the convective available potential energy (CAPE) and dew-point temperature ($T_d$). We explain the crucial effect of temperature on extreme rainfall generation along the steep climatic and topographic gradients in the NW Argentine Andes stretching from the low-elevation eastern foreland to the high-elevation central Andean Plateau in the west. Our analysis relies on version 2.0 of the ECMWF’s (European Centre for Medium-Range Weather Forecasts) Re-Analysis (ERA-interim) data and TRMM (Tropical Rainfall Measuring Mission) data. We make the following key observations: First, we observe distinctive gradients along and across strike of the Andes in dew-point temperature and CAPE that both control rainfall distributions. Second, we identify a nonlinear correlation between rainfall and a combination of dew-point temperature and CAPE through a multivariable regression analysis. The correlation changes in space along the climatic and topographic gradients and helps to explain controlling factors for extreme-rainfall generation. Third, we observe more contribution (or higher importance) of $T_d$ in the tropical low-elevation foreland and intermediate-elevation areas as compared to the high-elevation central Andean Plateau for 90th percentile rainfall. In contrast, we observe a higher contribution of CAPE in the intermediate-elevation area between low and high elevation, especially in the transition zone between the tropical and subtropical areas for the 90th percentile rainfall. Fourth, we find that the parameters of the multivariable regression using CAPE and $T_d$ can explain rainfall with higher statistical significance for the 90th percentile compared to lower rainfall percentiles. Based on our results, the spatial pattern of rainfall-extreme events during the past ∼16 years can be described by a combination of dew-point temperature and CAPE in the south–central Andes.

1. Introduction

The south–central Andes are characterized by steep gradients in topography, climate, and ecology supporting a diverse environment with economic significance. This region is repeatedly affected by hydrometeorological extreme events that impact infrastructures through mass movements and cause flooding downstream in agricultural, societal important, and populated areas, e.g., [1,2,3].

The understanding and investigation of extreme rainfall in the south–central Andes of NW Argentina has been hampered by complex interaction between the atmosphere and steep topography that can be summarized by the following four specific challenges: (1) High relief and steep terrain with elevations ranging from ∼800 m in the foreland to >6000 m at mountain peaks cause complex rainfall patterns with strong, local impact [2,4]. Past studies describe the strong orographic rainfall effect of the south–central Andes [5]. The analysis of orographic rainfall and intense storms in the south–central Andes has been challenging because of sparse instrumental data [2,6,7] and high terrain variability that complicates deriving precipitation amounts from weather models [8]; (2) highly seasonal wind patterns control the moisture influx and rainfall intensity in this region [9,10]. Specifically, the strong warm and dry upper-level westerlies that occur east of the Andes during the austral summer trigger deep convection in connection with low-level wind flow and associated shear that cause extreme rainfall in this region [9,10,11,12,13]; (3) the region lies at the climatic transition zone between the tropical and subtropical atmospheric circulation regimes. Transfer of moisture and thermal energy occurs along and across the transition zone between these two climatic regimes [3,13,14,15]. The tropics are regions characterized by more humidity and lower frequencies of storm formation; however, the sub-tropical regions have a higher frequencies of deep convective storms and higher seasonal rainfall. Both moisture transport from the tropics and deep convective activity in the sub tropics, result in high convection and rainfall in this region [13]; and (4) formation of mesoscale convective systems (MCSs): the complex interplay of topography, moisture transport, and the wind and thermal fields mentioned above lead to the formation of deep convection [13] that results in extreme rainfall. Water vapour originates in the tropical North Atlantic and the Amazon, is transported through the trade winds westwards and travels southward to subtropical South America along the eastern Andes through the South American Low-Level Jet (SALLJ), a low-level wind system [16]. This moist and warm air is prevented from rising due to the subsidence of dry air coming through westerly wind systems to the south–central Andes. Because of the wind shear between upper level winds and the SALLJ, MCSs are formed. Once temperature rises, for example through solar heating, the associated thermal energy provides the condition for forming deep convective storms along the south–central Andes [11,12,13,15]. The combination of these atmospheric processes described above show that the south–central Andes are a region characterized by highly seasonal and extreme rainfall events.

As mentioned above, the temperature rise triggers the condition for formation of deep convective storms along the south–central Andes. Past studies indicate the crucial role of the atmospheric temperature on rainfall intensity. For example, references [17,18,19] investigated the strong impact of temperature on convective rainfall. In all of these studies, the changes in the intensity of rainfall with temperature were explained by the Clausius–Clapeyron (CC) relation. The CC relation explains the rate of about 6.8% ${}^{\circ }$C${}^{-1}$ increase of rainfall with increasing temperature [20,21]. The convective storms which are triggered by temperature rise increase the atmospheric water content and hence increase (extreme) rainfall amount. It has been suggested that dew-point temperature can be used as a meteorological variable to indicate the humidity rate and hence extreme rainfall amounts and also can be compared with the CC relation [20]. Lepore et al. [20] investigated the relationship between extreme rainfall and dew-point temperature in the east of the Rocky Mountains in the United States where orographic storms are similar to southeastern South America [22]. Haider et al. [23] also investigated the relation between dew-point temperature and precipitation extremes. They identified dew-point temperature as a reliable variable for understanding the extreme rainfall under a warming climate over the tropics.

The deep convection and rainfall extremes are not only triggered by available water content but by temperature effects on the atmospheric stability. The parameter describing atmospheric stability is the convective available potential energy (CAPE) [20]. CAPE indicates the amount of energy available for convection [24]. If CAPE is efficiently transferred to parcel kinetic energy the amount of energy of a rising air parcel and therefore the rainfall intensity are commensurate to $\sqrt{CAPE}$, which is defined by meteorological parcel theory [20,24,25] (assuming idealized conditions). Gettelman et al. [26] investigated a positive correlation between CAPE and surface temperature over the tropics. They show that an increase in surface temperature leads to higher CAPE. Other studies show the crucial role of convection associated with extreme rainfall over the tropical systems [27]. Furthermore, Mesgana et al. [28] defined CAPE as a proxy for extreme rainfall over the United States and Southern Canada. Thus, CAPE can be used as an atmospheric stability parameter to parameterize extreme rainfall.

Several previous studies analyzed the spatiotemporal distribution of annual and extreme rainfall in the greater NW Argentine Andes, but often do not take into account the atmospheric boundary conditions leading to deep convection and extreme rainfall e.g., [2,5,6,7,13,29,30].

The aim of our study is to identify the dominant atmospheric conditions and climatic variables leading to deep convection and rainfall extreme events in the south–central Andes by focusing on convective available potential energy (CAPE) and dew-point temperature ($T_d$).

2. Continental and Regional Climatic Setting

2.1. Climatic Setting of South America

The Andes are located along the west coast of South America and extend from about 10${}^{\circ }$ N to 53${}^{\circ }$ S [10]. Moisture transport in South America is controlled by the SALLJ and the activity of the South Atlantic Convergence Zone (SACZ). Both of these atmospheric circulation systems constitute the most important components of the South American Monsoon System (SAMS), e.g., [31,32]. The SAMS and its associated strong convective activity contribute to intense rainfall over tropical and sub-tropical regions in South America during the austral summer months (DJF), e.g., [31,32,33,34].

During the austral summer season, moist air flows from the Amazon and tropical North Atlantic to subtropical South America due to the southward shift of the intertropical convergence zone (ITCZ) and the thermal difference between land and ocean [29,34]. The ITCZ is a zone of wind convergence near the equatorial region (more detailed descriptions of the ITCZ can be found in, for example, [35]). The direction of this moist air flowing to the subtropical South America is associated with the South American rainfall dipole, which is often considered the most important component of SAMS [31,32].

The eastward anomalies of this flow generate heavy rainfall along the SACZ [36,37]. The SACZ is defined as the region with a strong convective activity band stretching from the northwest (Amazonia) into the southeast (south Atlantic), e.g., [36,37,38,39]. The southward anomalies (SALLJ) at the eastern flank of the Andes trigger heavy rainfall in south–eastern South America (SESA) [16,29]. The deep convection is triggered by temperature rise and thermal energy during the daytime through solar heating [15]. The diurnal timing investigated by [15] documents the strongest activity of SALLJ during the night, which was triggered by the deep convection during the afternoon and evening (local times).

In order to show the SALLJ activity during the austral summer and over the south–central Andes, we have used averaged austral summertime low-level (850 hPa) wind speed (1999–2013) (Figure 1).

The divergent circulation during the austral summer (Figure 2) represents the low-level convergence activity over both, the northern and southern central Andes as a result of extreme convection during afternoon and evening, which is followed by the early and mid-daytime thermal energy [15]. Divergent circulation is defined as [40]:

$$\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial p}\right)=0$$

(1)

$$\frac{\partial w}{\partial p}=-\nabla ·V,$$

(2)

where (Equation (1)) is the continuity equation in pressure coordinates. $\nabla ·V$ in (Equation (2)) is the horizontal component of divergence, w is the vertical velocity and p is pressure level. The horizontal divergence is defined as ($\nabla ·V$> 0) while ($\nabla ·V$< 0) shows the horizontal convergence.

The wind at upper levels in the study area is often controlled by the Bolivian High (BH) (Figure 2 and Figure 3), an upper-level anticyclone associated with both the condensational heating of the Amazon basin and the heat released by intensive convection and precipitation over the Bolivian Altiplano [41,42,43]. Anticyclonic upper level flow is formed parallel to the high with strong subsidence to the west of the high that modulates convection in connection with low level flow in the region [43]. This circulation system sits eastward of the central Andean Plateau above the low-elevation foreland area and significantly influences convective rainfall patterns in connection with SALLJ and SACZ [2,9,44,45,46,47,48,49].

2.2. Regional Geographic and Climatic Setting of NW Argentina

The south–central Andes in NW Argentina are characterized by a strong rainfall asymmetry (Figure 4B). In the east-west direction exists one of the steepest rainfall gradients on Earth [5], resulting from the high topography and latitudinal position. In the west, the central Andean Plateau (Altiplano-Puna Plateau), the second highest Plateau on the Earth, extends from about 15${}^{\circ }$ S to 27${}^{\circ }$ S with a mean elevation about 3700 m [50]. The northern central Andean Plateau is called Altiplano, whereas the southern Andean Plateau is referred to as the Puna Plateau (or Puna de Atacama Plateau) (Figure 4A, A1). The central Andean Plateau is internally drained and the geomorphic areas of the Altiplano and Puna delineate different hydrologic catchment regimes. The low-elevation foreland area with elevations of 800 m is located in the east of the south–central Andes (Figure 4A, A3). In the north-south direction, the rainfall intensity varies as the climatic regime shifts from the tropical central Andes to the subtropical south–central Andes [13,29].

Study Region: NW Argentina

In order to analyze the climatic conditions leading to extreme rainfall in the study area, we divide the region (63${}^{\circ }$–69${}^{\circ }$ W, 22${}^{\circ }$–28${}^{\circ }$ S) into nine boxes with equal areas (1.5${}^{\circ }$× 1.5${}^{\circ }$) along the steepest climatic and topographic gradient (Figure 4A). The boxes go from high elevation to low elevation (numbers) and from the tropical central Andes to the subtropical south–central Andes (letters): A1, B1 and C1 are located in the high-elevation Puna Plateau (the southern central Andean Plateau); A2, B2 and C2 characterize an intermediate-elevation area exhibiting intramontane basins and high relief, and A3, B3 and C3 indicate the low-elevation foreland area. The north-south gradient stretches from the tropics (A1, A2 and A3), a transition zone between tropic and subtropic (B1, B2 and B3) and the subtropics (C1, C2 and C3). In the study area both the dew-point temperature and CAPE east-west (from A3 to A1, B3 to B1 and C3 to C1) gradients (Figure 4C,D) coincide with the rainfall gradient (Figure 4B) from low elevation foreland regions to the high-elevation central Andean Plateau.

3. Data and Methods

3.1. Data

We used the version 2.0 of the ECMWF’s (European Centre for Medium-Range Weather Forecasts) Re-Analysis (ERA-interim) data [51,52] to analyze temperature, dew-point temperature and CAPE. Dew-point temperature indicates the absolute specific humidity of the atmosphere [53]. High values of dew-point temperature describes near saturated air and high-moisture availability in the air. CAPE is an area between the level of free convection (LFC) and the level of neutral buoyancy (LNB). The level of free convection is the pressure level with the positive buoyancy, where temperature of the surrounding air reduces faster than the moist adiabatic lapse rate of a saturated parcel. The level of neutral buoyancy is the pressure level where the temperature of the air parcel is equal to the surrounding air [54]. $T_{vp}$ and $T_{ve}$ are the temperature of the air parcel and surrounding environment, respectively. $R_d$ is the gas constant and P is pressure [55]:

$$CAPE={\int }_{LFC}^{LNB}{R}_d(T_{vp}-T_{ve})dln\left(P\right).$$

(3)

In addition to CAPE, convective inhibition (CIN) is also characterized as an important parameter which quantifies the energy provided by the triggering mechanisms for deep convection to be developed [11,56]. CIN is defined as the amount of energy that the rising air parcel needs to overcome in order to reach to the level of free convection from its stable layer [57]. The early and mid-daytime thermal energy causes the well-mixed boundary layer which leads to high CAPE and low CIN that favors the deep convection and extreme rainfall [11]. Since our study aims at understanding the effect of temperature rise through solar heating on deep convection, we put our focus on atmospheric stability parameter CAPE which is considered to be high as a result of daytime solar heating.

ERA-interim reanalysis data used in this study have a spatial resolution of 0.75${}^{\circ }$ × 0.75${}^{\circ }$ and a temporal resolution of 6 h. We calculated the mean daily values from six hourly data.

TRMM (Tropical Rainfall Measuring Mission) data [58], product 3B42 [59,60] (Version 7) with a spatial resolution of 0.25${}^{\circ }$ × 0.25${}^{\circ }$ and daily temporal resolution have been used to identify rainfall values. TRMM rainfall data are interpolated on the ERA-interim grid (0.75${}^{\circ }$). We have interpolated data using the bilinear interpolation method. TRMM data has been shown to be a reliable dataset for capturing mean and extreme rainfall in South America [29,33]. Our analysis was performed from 1998 to 2013. We defined an extreme event as rainfall above the 90th percentile of the rainfall time series. For example, for a daily 16 year time series, we used: 16 years of data × 365 days per year × 10% = 584 events at each study box, because we have calculated the mean value of all grid points for each study box. We have explored other methodologies (fitting gamma or stretched exponential distributions), but these were generally affected by statistic significance, because of the steep rainfall gradient in that region. See Figure 5 for the events above the 90th percentiles and Figure 4A for the boxes.

3.2. Identifying the Effect of Temperature on Deep Convective Storms and Extreme Rainfall Formation

We analyze the dominant climatic variables leading to extreme rainfall events by focusing on dew-point temperature and convective available potential energy to show the effect of temperature on atmospheric humidity ($T_d$) and on convection (CAPE) for deep convective storms [20]. We argue that these will help us to understand extreme rainfall events that are often triggered by deep convective storms along the steep climatic and topographic gradient in the eastern south–-central Andes (22–28${}^{\circ }$ S) [13]. Our study consists of the following steps:

First, we analyze the temporal correlation between temperature, dew-point temperature, and CAPE in conjunction with rainfall during the austral summer months. We also show the spatiotemporal correlation between both climatic variables and rainfall along the steep topographic gradient.

Second, we regress daily rainfall events that are above the 90th percentile onto daily values of CAPE and dew-point temperature in each box during event days using 16 years of data. This analysis indicates an exponential relationship between rainfall and dew-point temperature and suggests a power-law relation between rainfall and CAPE. Our regression coefficients undergo a comparison with the value ranges of CAPE and dew-point temperature in each box along the topographic and climatic gradient.

Previous research by [24] and based on the CC relationship and idealized parcel theory suggested a relation between rainfall and both climatic variables of the type:

$$lnrainfall=c+\alpha \ast T_d+\beta \ast lnCAPE.$$

(4)

Their model also reveals exponential sensitivity of rainfall to dew-point temperature and a power-law relationship between rainfall and CAPE [20].

Real data show that the slope coefficients $\alpha$ and $\beta$ deviate from their theoretical values of $\alpha$ = 0.068 (CC relationship coefficient) and $\beta$ = 0.5 (parcel-theory coefficient) due to different meteorological boundary conditions [20,24].

Third, we fit the regression model (Equation (4)) [20,24] which shows a log-linear relationship between rainfall and both variables based on meteorological data described by convective available potential energy (CAPE) and dew-point temperature ($T_d$) in our study region. We have used a linear model fitting function that uses the Wilkinson notation.

We divided the rainfall distributions into the 50th, 75th, and 90th percentiles and separately analyzed their relationship to the driving variables. For extreme (90th) and moderate (75th) rainfall percentiles, we regress daily values of these rainfall percentiles onto daily values of CAPE and dew-point-temperature during these days. For lower rainfall intensities, we regress daily rainfall that is above 50th percentile onto daily values of CAPE and dew-point-temperature during these days.

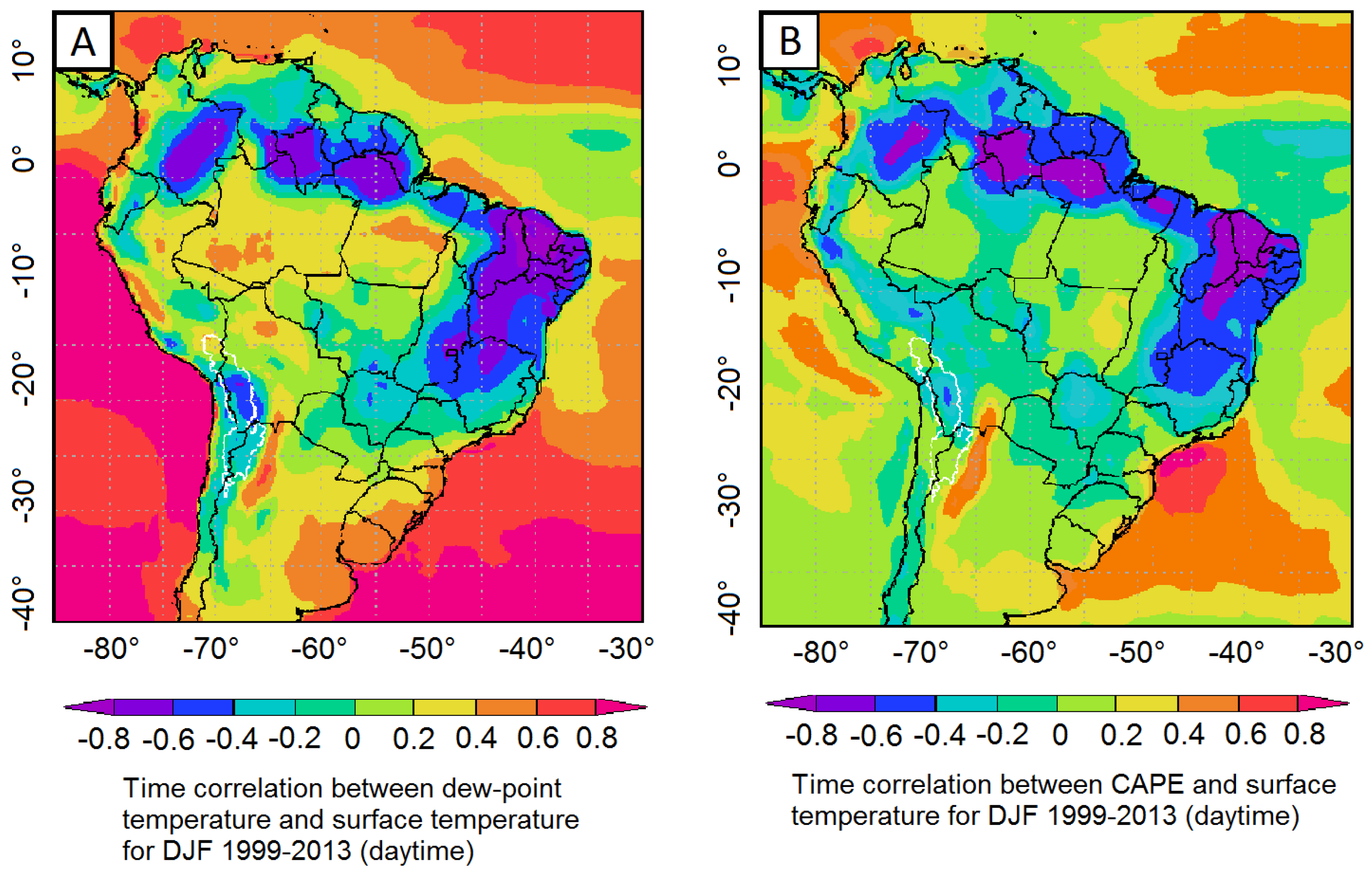
4. Results

The south–central Andes were characterized by extreme rainfall. We showed that the contribution of 90th percentile rainfall to total DJF rainfall was 70% and higher in this region (Figure 6) [29,61]. This highlights the significant contribution of deep convective storms to rainfall over this region. Our results showed the moderate to high temporal correlation between surface temperature and dew-point temperature and moderate correlation between surface temperature and CAPE east of the south–central Andes during the austral summer and during the daytime (Figure 7). Therefore, during the daytime, high solar heating and high temperatures trigger deep convection and extreme rainfall over the south–central Andes (Figure 6).

Our analysis of the spatial pattern of austral summer mean rainfall in conjunction with CAPE and dew-point temperature in each box in (Figure 4A–D) shows that both the dew-point temperature and CAPE east-west gradients (from A3 to A1, B3 to B1 and C3 to C1) (Figure 4C,D) coincide with the rainfall gradient from the wet, low elevation foreland regions to the dry, high-elevation central Andean Plateau (Figure 4B). Both, the spatial pattern shown by the area averaged boxes A3 and A2 compared to A1 (Figure 8A–C) and the temporal behavior, which is indicated by DJF seasonal mean from 1999 to 2013 (Figure 8A–C) of these climate variables, change along the steep topographic gradient in our study boxes in conjunction with rainfall.

Next, we analyze the relationship between CAPE, dew-point temperature, and 90th percentile rainfall along the steep topographic gradient. We observe a nonlinear relationship between 90th percentile rainfall and associated CAPE and dew-point temperature (Figure 9A–C) Boxes A3, A2, and A1.

We have separately regressed the daily rainfall events that are above the 90th percentile onto daily values of dew-point temperature (Figure 10) and CAPE (Figure 11) to quantify conditions leading to extreme rainfall. We show the effect of temperature with respect to atmospheric humidity ($T_d$) and also with respect to convection (CAPE) for deep-convective storms [20]. This is particularly pronounced in the eastern south–central Andes along the latitude 22–28${}^{\circ }$ S with a high distribution of MCS during austral summer months [62]. The regression coefficient (a) for the dew-point temperature and the regression coefficient (b) for CAPE reveal values around the CC relation and parcel theory, respectively. The regression coefficient (a) for the dew-point temperature is higher in the tropical and the transition zone between the tropical and subtropical areas and over intermediate-elevation (Box A2) and low-elevation foreland (Box A3) regions as compared to high-elevation Puna Plateau and subtropical regions (Figure 10). The regression coefficient (b) for the CAPE is higher in the transition zone between the tropical and subtropical and over the intermediate-elevation area as compared to all others regions (Figure 11).

The linear model defined in Equation (4) also indicates exponential sensitivity of rainfall to dew-point temperature and a power-law relationship between rainfall and CAPE [20]. We used the linear multivariable regression model (Equation (4)) [20] to show the joint effect of both climatic variables in our study region. The regression analysis reveals statistically significant relationships (p-value $<<$ 0.001) between the dew-point temperature and CAPE and 90th percentile rainfall over all nine areas. The regression coefficient ($\alpha$) for the dew-point temperature in (Equation (4)) is higher and it is close to CC relationship (0.068 ${}^{\circ }$C${}^{-1}$) for the extreme (90th percentile) rainfall in the tropical region and over intermediate-elevation (Box A2) and low-elevation foreland areas (Box A3) (Figure 12A). We show that the high contribution of dew-point temperature to extreme rainfall over these regions coincide with the higher dew-point temperature values (>10 ${}^{\circ }$C) for most of the events of the 90th percentiles rainfall over these boxes (Figure 13). We show that the dew-point temperature scaling of rainfall, based on our regression coefficients, are much higher than that derived from CC relation for the low rainfall percentile (50th percentile). This argues that the dew-point temperature scaling of rainfall for the lower rainfall percentiles cannot reliably explain rainfall amounts, likely because of the low rainfall intensities and other atmospheric driving processes.

The regression coefficient for CAPE ($\beta$ in Equation (4) indicates that CAPE is the more important climatic variable for extreme (90th percentile) rainfall in the transition zone between the tropical and subtropical region and over the intermediate-elevation area (Figure 12B, B2). Based on the regression coefficient for CAPE (Figure 12B) in all three topographic regions for 90th percentile rainfall and regarding the value ranges of CAPE in each box, we indicate that there is a high contribution of CAPE also over the Altiplano–Puna region (Figure 14) as the regression coefficient does not reveal much lower value as those over low-elevation foreland and intermediate-elevation areas. That is the case despite the low value ranges of CAPE for most of the events of 90th percentiles rainfall over Altiplano region.

Based on root mean squared error (RMSE) values, uncertainties decrease with increasing percentiles. This argues that rainfall can not be explained reasonably at the low percentile (50th) using CAPE and $T_d$ (Figure 15).

5. Discussion

Our observations show a strong dependence of extreme rainfall on CAPE and dew-point temperature (Figure 4). We have used a functional relationship (Equation (4)) to quantify their relative impacts.

Based on our regression coefficient ($\alpha$ in Equation (4)) dew-point temperature is the most important climatic variables for the extreme (90th percentile) rainfall in the tropical regions (Figure 12A) (A1, A2, and A3). This can be attributed to the fact that warmer tropical air can hold larger amounts of water vapor and hence can lead to higher occurrences and amounts of rainfall. Dew-point temperature is also a more important factor in the intermediate-elevation area and low-elevation foreland area (A2, B2, C2 and A3, B3, C3) compared to the high-elevation Puna Plateau (A1, B1 and C1) (Figure 12B). This is, because warmer air over these regions contains higher moisture availability and can lead to high convection and extreme rainfall (Figure 13). The highest contribution of dew-point temperature in the tropical intermediate-elevation area can be explained by the small differences between dew-point temperature and air temperature and consequently higher moisture availability (Figure 16).

The larger differences between coefficient $\alpha$ for dew-point temperature in (Equation (4)) and their expected CC relationship (0.068 ${}^{\circ }$C${}^{-1}$) in the high-elevation Puna Plateau compared to intermediate-elevation area and low-elevation foreland area for the extreme rainfall argues that the mechanism of converting atmospheric moisture to rainfall is less efficient in the high-elevation Puna Plateau. Several studies have shown and documented the super-CC scaling of extreme rainfall by variations in intensify of convection processes with temperature [17,19,20]. By comparing the regression coefficients of the 90th percentile (extreme rainfall) and the two lower percentiles at 75 and 50, the extreme 90th and moderate 75th rainfall percentiles in our analysis reveal a scale close to CC or in some cases super-CC (2×CC) which is supported by other studies as mentioned above. We emphasize that the temperature scaling of rainfall for the lower rainfall percentiles cannot be explained reliably because of the low rainfall intensities and this is supported by other studies [63]. Taken together, this suggests that the mechanism of transforming dew-point temperature to rainfall is more efficient when the rain intensity is higher [20].

The regression and coefficient $\beta$ for the CAPE (Equation (4)) indicates a high importance of CAPE for extreme rainfall in the study area (Figure 12B). This is of particular importance in the transition zone between the tropical and subtropical region and over intermediate elevations, because the transition zone is characterized by strong rising of warm and moist air and the formation of deep convective storms. The coefficient $\beta$ for CAPE in (Equation (4)) in the high-elevation Puna Plateau for extreme rainfall is not much lower than those over two other lower topographic regions, which have larger absolute values of CAPE (Figure 14). Therefore, even the lower values of CAPE play an important role for extreme rainfall over high-elevation Puna Plateau.

Past studies [20] investigated the relationship between extreme rainfall and CAPE and dew-point temperature in the Eastern United States. Their results show a power-law relationship between rainfall and CAPE with a regression coefficient of ≈0.2–0.4 changing with geographic regions. For the dew-point temperature the regression coefficient changes significantly depending on the rainfall percentile. Our study suggests similar results, but different coefficients $\alpha$ and $\beta$, which change depending on the rainfall percentile as well as the topographic and climatic sub-regions.

Some other studies used different modeling approaches on investigation of rainfall along the topographic gradient. Smith et al. [5,64,65,66] parameterized the mean orographic rainfall in south America and other regions where complex terrain is similar. These models rely on static climatic variables and allow reproducing an average rainfall patterns. But they do not allow for atmospheric variability along a larger geographic region. In our approach, we considered not only the topographic gradient, but also allow for atmospheric variability by including the dominant atmospheric conditions and climatic variables leading to deep convection and extreme rainfall events.

6. Conclusions

We analyzed extreme rainfall events by documenting the effect of temperature on atmospheric humidity (dew point temperature, $T_d$) and convective available potential energy (CAPE) on deep-convective storms in the south–central Andes in NW Argentina. We used a multivariable regression analysis to describe the correlation between rainfall percentiles and the two driving atmospheric variables: $T_d$ and CAPE. We have separately analyzed low-elevation frontal areas (Andean foreland), intermediate-elevation areas (intermontane basins), and high-elevation areas (central Andean Plateau). We obtained the following key results:

First, based on our spatial analysis, the rainfall distribution in the south–central Andes correspond to spatial differences in CAPE and $T_d$ (Figure 4B–D). The east-west gradients in both, dew-point temperature and CAPE (from A3 to A1, B3 to B1 and C3 to C1 in Figure 4C,D), correlate with the rainfall gradient (Figure 4B). Our temporal analysis indicates that the temporal differences in CAPE and $T_d$ correspond the rainfall distribution in the south–central Andes (Figure 8A–C).

Second, we find a correlation between extreme rainfall and a combination of dew-point temperature and CAPE through a multivariable regression analysis (Equation (4)). Our results based on p values $<<$ 0.001 show a statistically significant relationship between a non-linear combination of dew-point temperature and CAPE and 90th percentile rainfall. This suggests that spatial and temporal occurrences of rainfall at the 90th percentile (i.e., extreme rainfall) can be partially explained by combining dew-point temperature and CAPE.

Third, we observe that the atmospheric mechanism of transforming moisture to extreme rainfall is more efficient in the tropical low- and intermediate-elevation areas and the mechanism of transforming CAPE to extreme rainfall is more efficient in the transition zone between the tropical and subtropical and in the intermediate-elevation areas (Figure 12).

Fourth, we observe that the uncertainties (RMSE) of the model fit decrease with increasing rainfall percentiles (Figure 15). This suggests that the described modeling approach is more reliable for higher rainfall percentiles as these are primarily driven by CAPE and dew-point temperature variations.

Our study deciphers the important role of dew-point temperature and CAPE on extreme rainfall events in the south–central Andes. We show that hydrometeorological extreme events are triggered by different boundary conditions from north to south along the steep topographic gradient of the eastern Andes and that multiple conditions must be met before extreme rainfall events can be triggered.