Multiscale Spatio-Temporal Changes of Precipitation Extremes in Beijing-Tianjin-Hebei Region, China during 1958–2017
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Collection and Processing
2.2.1. Precipitation Data
2.2.2. Climate Indices
2.3. Methods
2.3.1. Definition of Extreme Precipitation Indices
2.3.2. Statistical Analysis
2.3.3. Wavelet Analysis
3. Results
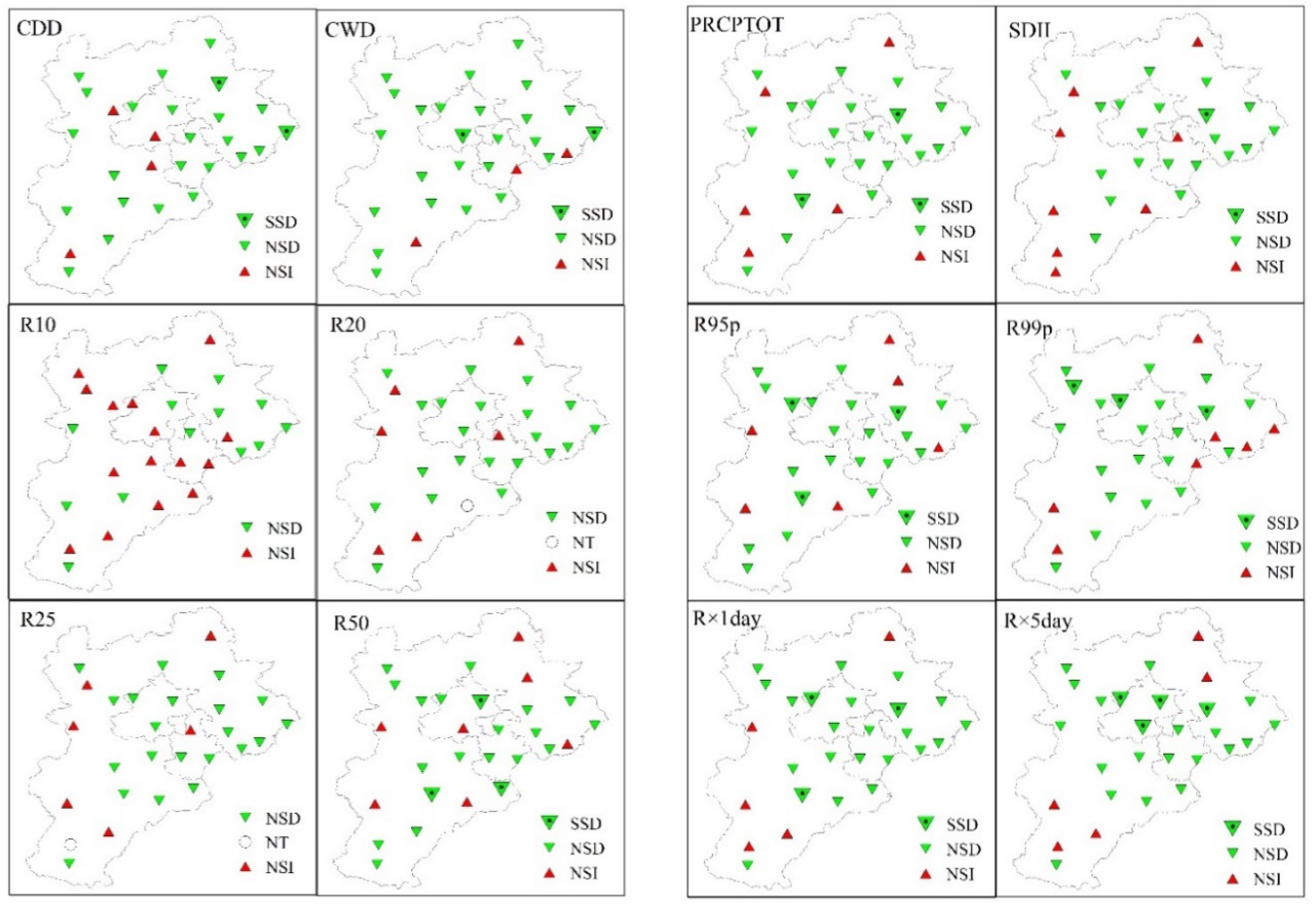
3.1. Spatial Variation of Extreme Precipitation Events
3.2. Temporal Variations Extreme Precipitation Events
3.2.1. Annual Scale Trends in Extreme Precipitation Indices
3.2.2. Monthly and Seasonal Changes in Precipitation Extremes
3.2.3. Decadal Variability in Precipitation Extremes
3.2.4. Periodicity Analysis of Extreme Precipitation Indices
3.3. Relationship Between Precipitation Extremes and Annual Total Precipitation
3.4. Possible Linkage to Large-Scale Atmospheric Circulation Patterns
4. Discussion
5. Summary and Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tong, S.Q.; Li, X.Q.; Zhang, J.Q.; Bao, Y.H.; Bao, Y.B.; Na, L.; Si, A. Spatial and temporal variability in extreme temperature and precipitation events in Inner Mongolia (China) during 1960–2017. Sci. Total Environ. 2019, 649, 75–89. [Google Scholar] [CrossRef] [PubMed]
- Boccolari, M.; Malmusi, S. Changes in temperature and precipitation extremes observed in Modena, Italy. Atmos. Res. 2013, 122, 16–31. [Google Scholar] [CrossRef]
- Hettiarachch, S.; Wasko, C.; Sharma, A. Increase in flood risk resulting from climate change in a developed urban watershed—The role of storm temporal patterns. Hydrol. Earth Syst. Sci. 2018, 22, 2041–2056. [Google Scholar] [CrossRef]
- Xie, Z.; Du, Y.; Zeng, Y.; Miao, Q. Classification of yearly extreme precipitation events and associated flood risk in the Yangtze-Huaihe River Valley. Sci. China Earth Sci. 2018, 61, 1341–1356. [Google Scholar] [CrossRef]
- Zheng, J.Y.; Yu, Y.Z.; Zhang, X.Z.; Hao, X.Z. Variation of extreme drought and flood in North China revealed by document-based seasonal precipitation reconstruction for the past 300 years. Clim. Past 2018, 14, 1135–1145. [Google Scholar] [CrossRef] [Green Version]
- Zhai, P.M.; Zhang, X.B.; Wan, H.; Pan, X.H. Trends in total precipitation and frequency of daily precipitation extremes over China. J. Clim. 2005, 18, 1096–1108. [Google Scholar] [CrossRef]
- Zhou, B.T.; Wen, Q.H.; Xu, Y.; Song, L.C.; Zhang, X.B. Projected Changes in Temperature and Precipitation Extremes in China by the CMIP5 Multimodel Ensembles. J. Clim. 2014, 27, 6591–6611. [Google Scholar] [CrossRef]
- Sigdel, M.; Ma, Y.M. Variability and trends in daily precipitation extremes on the northern and southern slopes of the central Himalaya. Theor. Appl. Climatol. 2017, 130, 571–581. [Google Scholar] [CrossRef]
- Turco, M.; Llasat, M.C. Trends in indices of daily precipitation extremes in Catalonia (NE Spain), 1951–2003. Nat. Hazards Earth Syst. 2011, 11, 3213–3226. [Google Scholar] [CrossRef]
- Xue, T.T.; Tang, G.P.; Sun, L.; Wu, Y.Z.; Liu, Y.L.; Dou, Y.F. Long-term trends in precipitation and precipitation extremes and underlying mechanisms in the US Great Basin during 1951–2013. J. Geophys. Res. Atmos. 2017, 122, 6152–6169. [Google Scholar] [CrossRef]
- Alexander, L.V.; Zhang, X.; Peterson, T.C.; Caesar, J.; Gleason, B.; Tank, A.M.G.K.; Haylock, M.; Collins, D.; Trewin, B.; Rahimzadeh, F.; et al. Global observed changes in daily climate extremes of temperature and precipitation. J. Geophys. Res. Atmos. 2006, 111, 1042–1063. [Google Scholar] [CrossRef]
- Frich, P.; Alexander, L.; Della-Marta, P.M.; Gleason, B.; Haylock, M.; Tank, A.K.; Peterson, T. Observed coherent changes in climatic extremes during the second half of the twentieth century. Clim. Res. 2002, 19, 193–212. [Google Scholar] [CrossRef] [Green Version]
- Asadieh, B.; Krakauer, N.Y. Global trends in extreme precipitation: Climate models versus observations. Hydrol. Earth Syst. Sci. 2015, 19, 877–891. [Google Scholar] [CrossRef]
- Zarekarizi, M.; Rana, A.; Moradkhani, H. Precipitation extremes and their relation to climatic indices in the Pacific Northwest USA. Clim. Dyn. 2018, 50, 4519–4537. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, G.H.; Wang, X.Q.; Cheng, G.H. Future Changes in Precipitation Extremes over Canada: Driving Factors and Inherent Mechanism. J. Geophys. Res. Atmos. 2018, 123, 5783–5803. [Google Scholar] [CrossRef]
- Wasko, C.; Lu, W.T.; Mehrotra, R. Relationship of extreme precipitation, dry-bulb temperature, and dew point temperature across Australia. Environ. Res. Lett. 2018, 13, 074031. [Google Scholar] [CrossRef]
- Tan, X.Z.; Gan, T.Y.; Chen, Y.D. Moisture sources and pathways associated with the spatial variability of seasonal extreme precipitation over Canada. Clim. Dyn. 2018, 50, 629–640. [Google Scholar] [CrossRef]
- Sedlmeier, K.; Feldmann, H.; Schadler, G. Compound summer temperature and precipitation extremes over central Europe. Theor. Appl. Climatol. 2018, 131, 1493–1501. [Google Scholar] [CrossRef]
- Marston, M.L.; Ellis, A.W. Extreme reversals in successive winter season precipitation anomalies across the Western United States, 1895–2015. Int. J. Climatol. 2018, 38, 1520–1532. [Google Scholar] [CrossRef]
- Bohlinger, P.; Sorteberg, A. A comprehensive view on trends in extreme precipitation in Nepal and their spatial distribution. Int. J. Climatol. 2018, 38, 1833–1845. [Google Scholar] [CrossRef]
- Kunkel, K.E. North American trends in extreme precipitation. Nat. Hazards 2003, 29, 291–305. [Google Scholar] [CrossRef]
- Khan, S.; Kuhn, G.; Ganguly, A.R.; Erickson, D.J.; Ostrouchov, G. Spatio-temporal variability of daily and weekly precipitation extremes in South America. Water Resour. Res. 2007, 43. [Google Scholar] [CrossRef] [Green Version]
- Vogel, M.M.; Zscheischler, J.; Seneviratne, S.I. Varying soil moisture-atmosphere feedbacks explain divergent temperature extremes and precipitation projections in central Europe. Earth Syst. Dyn. 2018, 9, 1107–1125. [Google Scholar] [CrossRef]
- Volosciuk, C.; Maraun, D.; Semenov, V.A.; Tilinina, N.; Gulev, S.K.; Latif, M. Rising Mediterranean Sea Surface Temperatures Amplify Extreme Summer Precipitation in Central Europe. Sci. Rep. 2016, 6, 32450. [Google Scholar] [CrossRef]
- Aguilar, E.; Barry, A.A.; Brunet, M.; Ekang, L.; Fernandes, A.; Massoukina, M.; Mbah, J.; Mhanda, A.; do Nascimento, D.H.; Peterson, T.C.; et al. Changes in temperature and precipitation extremes in western central Africa, Guinea Conakry, and Zimbabwe, 1955–2006. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Vincent, L.A.; Aguilar, E.; Saindou, M.; Hassane, A.F.; Jumaux, G.; Roy, D.; Booneeady, P.; Virasami, R.; Amelie, V.; Montfraix, B.; et al. Observed trends in indices of daily and extreme temperature and precipitation for the countries of the western Indian Ocean, 1961–2008. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Yuan, Z.; Yang, Z.Y.; Yan, D.H.; Yin, J. Historical changes and future projection of extreme precipitation in China. Theor. Appl. Climatol. 2017, 127, 393–407. [Google Scholar] [CrossRef]
- Chen, Y.; Zhai, P.M. Persistent extreme precipitation events in China during 1951–2010. Clim. Res. 2013, 57, 143–155. [Google Scholar] [CrossRef]
- Tao, Y.Y.; Wang, W.; Song, S.; Ma, J. Spatial and Temporal Variations of Precipitation Extremes and Seasonality over China from 1961–2013. Water 2018, 10, 719. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Lei, W.J. Complex patterns of precipitation and extreme events during 1951–2011 in Sichuan Basin, Southwestern China. J. Mt. Sci. Engl. 2018, 15, 340–356. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, X.D.; Zhao, T.L.; Xu, H.X.; Mao, F.; Sun, H.; Wang, Y. Extreme precipitation events in East China and associated moisture transport pathways. Sci. China Earth Sci. 2016, 59, 1854–1872. [Google Scholar] [CrossRef]
- Wang, F.; Yang, S.; Higgins, W.; Li, Q.; Zuo, Z.Y. Long-term changes in total and extreme precipitation over China and the United States and their links to oceanic-atmospheric features. Int. J. Climatol. 2014, 34, 286–302. [Google Scholar] [CrossRef]
- Mei, C.; Liu, J.H.; Chen, M.T.; Wang, H.; Li, M.; Yu, Y.D. Multi-decadal spatial and temporal changes of extreme precipitation patterns in northern China (Jing-Jin-Ji district, 1960–2013). Quat. Int. 2018, 476, 1–13. [Google Scholar] [CrossRef]
- Gao, T.; Xie, L. Multivariate Regression Analysis and Statistical Modeling for Summer Extreme Precipitation over the Yangtze River Basin, China. Adv. Meteorol. 2014. [Google Scholar] [CrossRef]
- Voskresenskaya, E.; Vyshkvarkova, E. Extreme precipitation over the Crimean peninsula. Quat. Int. 2016, 409, 75–80. [Google Scholar] [CrossRef]
- Zhang, D.D.; Yan, D.H.; Wang, Y.C.; Lu, F.; Liu, S.H. GAMLSS-based nonstationary modeling of extreme precipitation in Beijing-Tianjin-Hebei region of China. Nat. Hazards 2015, 77, 1037–1053. [Google Scholar] [CrossRef]
- Wei, W.; Shi, Z.J.; Yang, X.H.; Wei, Z.; Liu, Y.S.; Zhang, Z.Y.; Ge, G.; Zhang, X.; Guo, H.; Zhang, K.; et al. Recent Trends of Extreme Precipitation and Their Teleconnection with Atmospheric Circulation in the Beijing-Tianjin Sand Source Region, China, 1960–2014. Atmosphere 2017, 8, 83. [Google Scholar] [CrossRef]
- Shen, L.L.; Zhang, Y.X.; Long, L.X.; Sun, Y.; Kang, Z.M. Characteristics of extreme precipitation in Beijing-Tianjin-Hebei region from 1981 to 2016. Torrential Rain Dis. 2018, 37, 428–434. [Google Scholar]
- Du, H.; Xia, J.; Zeng, S.D.; She, D.X.; Liu, J.J. Variations and statistical probability characteristic analysis of extreme precipitation events under climate change in Haihe River Basin, China. Hydrol. Process 2014, 28, 913–925. [Google Scholar] [CrossRef]
- Zhou, X.; Bai, Z.; Yang, Y. Linking trends in urban extreme rainfall to urban flooding in China. Int. J. Climatol. 2017, 37, 4586–4593. [Google Scholar] [CrossRef]
- Xiao, M.Z.; Zhang, Q.; Singh, V.P. Spatiotemporal variations of extreme precipitation regimes during 1961-2010 and possible teleconnections with climate indices across China. Int. J. Climatol. 2017, 37, 468–479. [Google Scholar] [CrossRef]
- Chen, A.J.; He, X.G.; Guan, H.D.; Zhang, X.P. Variability of seasonal precipitation extremes over China and their associations with large-scale ocean-atmosphere oscillations. Int. J. Climatol. 2019, 1–16. [Google Scholar] [CrossRef]
- Gao, T.; Wang, H.L. Trends in precipitation extremes over the Yellow River basin in North China: Changing properties and causes. Hydrol. Process 2017, 31, 2412–2428. [Google Scholar] [CrossRef]
- Shi, J.; Cui, L.; Wen, K.; Tian, Z.; Wei, P.; Zhang, B. Trends in the consecutive days of temperature and precipitation extremes in China during 1961–2015. Environ. Res. 2018, 161, 381–391. [Google Scholar] [CrossRef]
- Duan, L.M.; Zheng, J.Y.; Li, W.; Liu, T.X.; Luo, Y.Y. Multivariate properties of extreme precipitation events in the Pearl River basin, China: Magnitude, frequency, timing, and related causes. Hydrol. Process 2017, 31, 3662–3671. [Google Scholar] [CrossRef]
- Li, C.L.; Filho, W.L.; Wang, J.; Fudjumdjum, H.; Fedoruk, M.; Hu, R.C.; Yin, S.; Bao, Y.H.; Yu, S.; Hunt, J. An Analysis of Precipitation Extremes in the Inner Mongolian Plateau: Spatial-Temporal Patterns, Causes, and Implications. Atmosphere 2018, 9, 322. [Google Scholar] [CrossRef]
- Talchabhadel, R.; Karki, R.; Thapa, B.R.; Maharjan, M.; Parajuli, B. Spatio-temporal variability of extreme precipitation in Nepal. Int. J. Climatol. 2018, 38, 4296–4313. [Google Scholar] [CrossRef]
- Huang, H.P.; Winter, J.M.; Osterberg, E.C. Mechanisms of Abrupt Extreme Precipitation Change over the Northeastern United States. J. Geophys. Res. Atmos. 2018, 123, 7179–7192. [Google Scholar] [CrossRef]
- Hoell, A.; Cheng, L.Y. Austral summer Southern Africa precipitation extremes forced by the El Nino-Southern oscillation and the subtropical Indian Ocean dipole. Clim. Dyn. 2018, 50, 3219–3236. [Google Scholar] [CrossRef]
- GDEMDEM 30M digital elevation model data. Available online: http://www.gscloud.cn/sources/list_dataset/310?cdataid=302&pdataid=10&datatype=gdem_utm#dlv=Wzg4LFswLDEwLDEsMF0sW1siZGF0YWlkIiwxXV0sW10sOTld (accessed on 12 April 2019).
- Daily Dataset of Surface Climate in China (V3.0). Available online: http://data.cma.cn/data/cdcdetail/dataCode/SURF_CLI_CHN_MUL_DAY_V3.0.html (accessed on 20 December 2018).
- El Nino/Southern Oscillation (ENSO), Cold & Warm Episodes by Season. Available online: https://origin.cpc.ncep.noaa.gov/products/analysis_monitoring/ensostuff/ONI_v5.php (accessed on 18 January 2019).
- North Atlantic Oscillation (NAO). Available online: https://www.cpc.ncep.noaa.gov/products/precip/CWlink/pna/nao.shtml (accessed on 18 January 2019).
- Moore, G.W.K.; Renfrew, I.A.; Pickart, R.S. Multidecadal Mobility of the North Atlantic Oscillation. J. Clim. 2013, 26, 2453–2466. [Google Scholar] [CrossRef] [Green Version]
- Indian Ocean Dipole (IOD). Available online: http://www.jamstec.go.jp/aplinfo/sintexf/DATA/dmi.monthly.txt (accessed on 18 January 2019).
- Pacific Decadal Oscillation (PDO). Available online: http://research.jisao.washington.edu/pdo/PDO.latest.txt (accessed on 18 January 2019).
- Indices calculation: RClimDex. Available online: http://etccdi.pacificclimate.org/software.shtml (accessed on 30 October 2018).
- Song, X.M.; Zhang, J.Y.; AghaKouchak, A.; Sen Roy, S.; Xuan, Y.; Wang, G.Q.; He, R.M.; Wang, X.J.; Liu, C.S. Rapid urbanization and changes in spatiotemporal characteristics of precipitation in Beijing metropolitan area. J. Geophys. Res. Atmos. 2014, 119, 11250–11271. [Google Scholar] [CrossRef]
- Zhao, Y.F.; Zou, X.Q.; Cao, L.G.; Xu, X.W.H. Changes in precipitation extremes over the Pearl River Basin, southern China, during 1960–2012. Quat. Int. 2014, 333, 26–39. [Google Scholar] [CrossRef]
- Penalba, O.C.; Vargas, W.M. Interdecadal and interannual variations of annual and extreme precipitation over central-northeastern Argentina. Int. J. Climatol. 2014, 24, 1565–1580. [Google Scholar] [CrossRef]
- Zhang, K.X.; Pan, S.M.; Cao, L.G.; Wang, Y.; Zhao, Y.F.; Zhang, W. Spatial distribution and temporal trends in precipitation extremes over the Hengduan Mountains region, China, from 1961 to 2012. Quat. Int. 2014, 349, 346–356. [Google Scholar] [CrossRef]
- Duan, W.L.; He, B.; Takara, K.; Luo, P.P.; Hu, M.C.; Alias, NE.; Nover, D. Changes of precipitation amounts and extremes over Japan between 1901 and 2012 and their connection to climate indices. Clim. Dyn. 2015, 45, 2273–2292. [Google Scholar] [CrossRef]
- Wang, X.L.; Hou, X.Y.; Wang, Y.D. Spatiotemporal variations and regional differences of extreme precipitation events in the Coastal area of China from 1961 to 2014. Atmos. Res. 2017, 197, 94–104. [Google Scholar] [CrossRef]
- Chen, A.J.; He, X.G.; Guan, H.D.; Cai, Y. Trends and periodicity of daily temperature and precipitation extremes during 1960-2013 in Hunan Province, central south China. Theor. Appl. Climatol. 2018, 132, 71–88. [Google Scholar] [CrossRef]
- Pedron, I.T.; Dias, M.A.F.S.; Dias, S.D.; Carvalho, L.M.V.; Freitas, E.D. Trends and variability in extremes of precipitation in Curitiba - Southern Brazil. Int. J. Climatol. 2017, 37, 1250–1264. [Google Scholar] [CrossRef]
- Tan, X.Z.; Gan, T.Y.; Shao, D.G. Wavelet analysis of precipitation extremes over Canadian ecoregions and teleconnections to large-scale climate anomalies. J. Geophys. Res. Atmos. 2006, 121, 14469–14486. [Google Scholar] [CrossRef]
- Yang, P.; Xia, J.; Zhang, Y.Y.; Hong, S. Temporal and spatial variations of precipitation in Northwest China during 1960–2013. Atmos. Res. 2017, 183, 283–295. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Zhao, N.; Yue, T.X.; Li, H.; Zhang, L.L.; Yin, X.Z.; Liu, Y. Spatio-temporal changes in precipitation over Beijing-Tianjin-Hebei region, China. Atmos. Res. 2018, 202, 156–168. [Google Scholar] [CrossRef]
- Gao, T.; Shi, X.H. Spatio-temporal characteristics of extreme precipitation events during 1951–2011 in Shandong, China and possible connection to the large scale atmospheric circulation. Stoch. Environ. Res. Risk Assess. 2016, 30, 1421–1440. [Google Scholar] [CrossRef]
- Huang, H.P.; Winter, J.M.; Osterberg, E.C.; Horton, R.M.; Beckage, B. Total and Extreme Precipitation Changes over the Northeastern United. J. Hydrometeorol. 2017, 18, 1783–1798. [Google Scholar] [CrossRef]
- Chen, F.L.; Chen, H.M.; Yang, Y.Y. Annual and seasonal changes in means and extreme events of precipitation and their connection to elevation over Yunnan Province, China. Quat. Int. 2015, 374, 46–61. [Google Scholar] [CrossRef]
- Song, X.M.; Zhang, J.Y.; Zou, X.J.; Zhang, C.H.; AghaKouchak, A.; Kong, F.Z. Changes in precipitation extremes in the Beijing metropolitan area during 1960–2012. Atmos. Res. 2019, 222, 134–153. [Google Scholar] [CrossRef]
- Jiang, D.; Wang, K.; Li, Z.; Wang, Q. Variability of extreme summer precipitation over Circum-Bohai-Sea region during 1961–2008. Theor. Appl. Climatol. 2011, 104, 501–509. [Google Scholar] [CrossRef]
- Gemmer, M.; Fischer, T.; Jiang, T.; Su, B.; Liu, L.L. Trends in precipitation extremes in the Zhujiang river basin, South China. J. Clim. 2011, 24, 750–761. [Google Scholar] [CrossRef]
- Casanueva, A.; Rodriguez-Puebla, C.; Frias, M.D.; Gonzalez-Reviriego, N. Variability of extreme precipitation over Europe and its relationships with teleconnection patterns. Hydrol. Earth Syst. Sci. 2014, 18, 709–725. [Google Scholar] [CrossRef] [Green Version]
- Moron, V.; Vautard, R.; Ghil, M. Trends, interdecadal and interannual oscillation in global sea-surface temperatures. Clim. Dyn. 1998, 14, 545–569. [Google Scholar] [CrossRef]
- Wang, F.; Yang, S. Regional characteristics of long-term changes in total and extreme precipitations over China and their links to atmospheric-oceanic features. Int. J. Climatol. 2017, 37, 751–769. [Google Scholar] [CrossRef]
- Gao, T.; Wang, H.; Zhou, T. Changes of extreme precipitation and nonlinear influence of climate variables over monsoon region in China. Atmos. Res. 2017, 197, 379–389. [Google Scholar] [CrossRef]
- Chen, H.S.; Zhang, Y. Sensitivity experiments of impacts of large-scale urbanization in East China on East Asian winter monsoon. Chin. Sci. Bull. 2013, 58, 809–815. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Zhou, L. Observed trends in extreme precipitation events in China during 1961–2001 and the associated changes in large-scale circulation. Geophys. Res. Lett. 2005, 32, 32. [Google Scholar] [CrossRef]
- Hamed, K.H. Trend detection in hydrologic data: The Mann-Kendall trend test under the scaling hypothesis. J. Hydrol. 2008, 349, 350–363. [Google Scholar] [CrossRef]
- Yue, S.; Pilon, P.; Cavadis, G. Power of the Mann-Kendall and Spearman’s rho tests for detecting monotonic trends in hydrological series. J. Hydrol. 2002, 259, 254–271. [Google Scholar] [CrossRef]
- Min, S.K.; Zhang, X.B.; Zwiers, F.W.; Hegerl, G.C. Human contribution to more-intense precipitation extremes. Nature 2011, 470, 378–381. [Google Scholar] [CrossRef]
- Nalley, D.; Adamowski, J.; Biswas, A.; Gharabaghi, B.; Hu, W. A multiscale and multivariate analysis of precipitation and streamflow variability in relation to ENSO, NAO and PDO. J. Hydrol. 2019, 574, 288–307. [Google Scholar] [CrossRef]
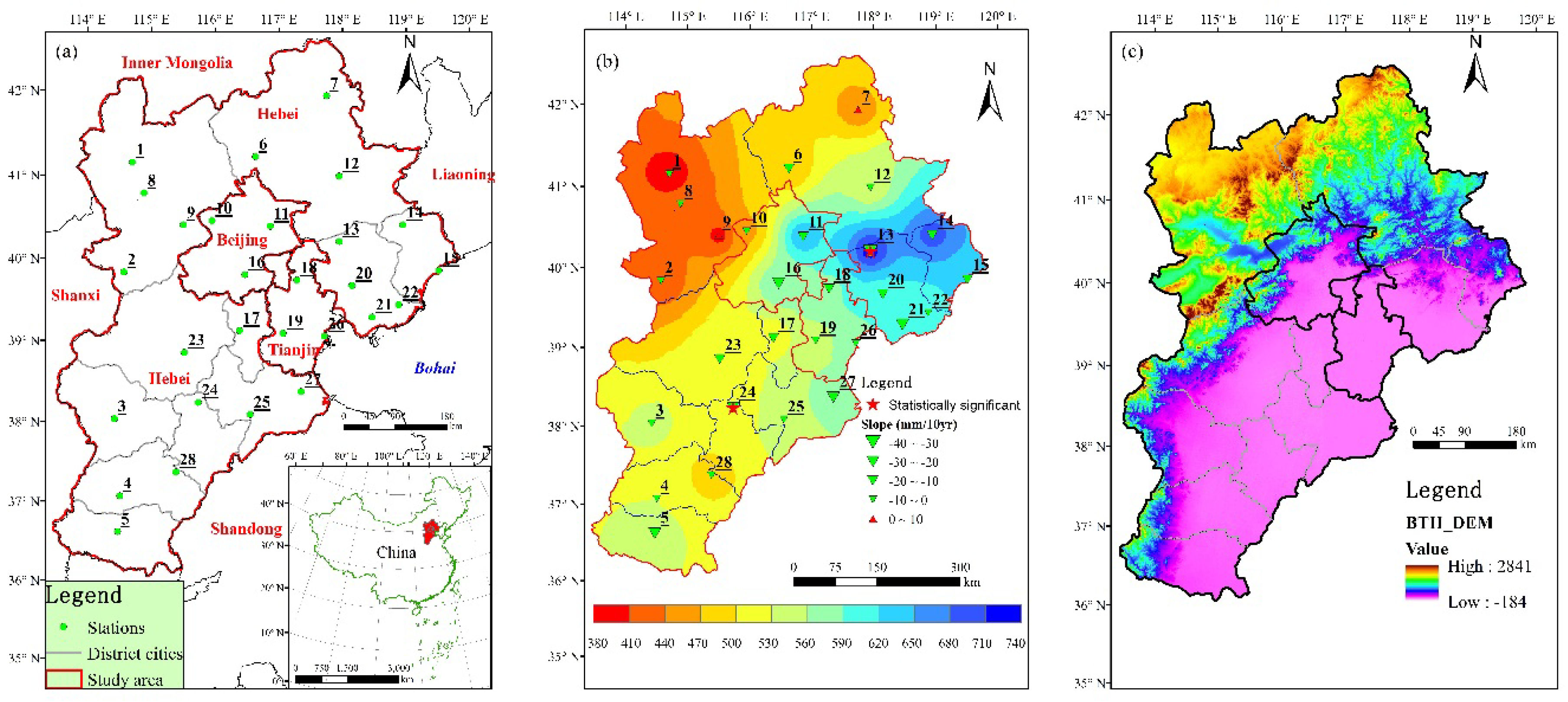













| No. | Station Code | Station Name | Latitude (N) | Longitude (E) | Elevation (m) |
|---|---|---|---|---|---|
| 1 | 53399 | Zhangbei | 41.15 | 114.70 | 1393.3 |
| 2 | 53593 | Yuxian | 39.83 | 114.57 | 909.5 |
| 3 | 53698 | Shijiazhuang | 38.03 | 114.42 | 81 |
| 4 | 53798 | Xingtai | 37.07 | 114.50 | 77.3 |
| 5 | 53892 | Handan | 36.62 | 114.47 | 66.6 |
| 6 | 54308 | Fengning | 41.22 | 116.63 | 661.2 |
| 7 | 54311 | Weichang | 41.93 | 117.75 | 842.8 |
| 8 | 54401 | Zhangjiakou | 40.78 | 114.88 | 724.2 |
| 9 | 54405 | Huailai | 40.40 | 115.50 | 536.8 |
| 10 | 54406 | Yanqing | 40.45 | 115.95 | 489 |
| 11 | 54416 | Miyun | 40.38 | 116.87 | 71.8 |
| 12 | 54423 | Chengde | 40.98 | 117.95 | 385.9 |
| 13 | 54429 | Zunhua | 40.20 | 117.95 | 54.9 |
| 14 | 54436 | Qinglong | 40.40 | 118.95 | 227.5 |
| 15 | 54449 | Qinhuadao | 39.85 | 119.52 | 2.4 |
| 16 | 54511 | Beijing | 39.80 | 116.47 | 31.3 |
| 17 | 54518 | Bazhou | 39.12 | 116.38 | 9 |
| 18 | 54525 | Baodi | 39.73 | 117.28 | 5.1 |
| 19 | 54527 | Tianjin | 39.08 | 117.07 | 2.5 |
| 20 | 54534 | Tangshan | 39.67 | 118.15 | 27.8 |
| 21 | 54535 | Caofeidian | 39.28 | 118.47 | 3.2 |
| 22 | 54539 | Laoting | 39.43 | 118.88 | 10.5 |
| 23 | 54602 | Baoding | 38.85 | 115.52 | 17.2 |
| 24 | 54606 | Raoyang | 38.23 | 115.73 | 19 |
| 25 | 54618 | Botou | 38.08 | 116.55 | 13.2 |
| 26 | 54623 | Tanggu | 39.05 | 117.72 | 4.8 |
| 27 | 54624 | Huanghua | 38.37 | 117.35 | 6.6 |
| 28 | 54705 | Nangong | 37.37 | 115.38 | 27.4 |
| Acronym. | Definition | Unit |
|---|---|---|
| R10 | Annual number of days with more than 10 mm/day | days |
| R20 | Annual number of days with more than 20 mm/day | days |
| R25 * | Annual number of days with more than 25 mm/day | days |
| R50 * | Annual number of days with more than 50 mm/day | days |
| CDD | Maximum number of consecutive dry days 1 | days |
| CWD | Maximum number of consecutive wet days 2 | days |
| R95p | Annual total precipitation when daily precipitation >95th percentile | mm |
| R99p | Annual total precipitation when daily precipitation >99th percentile | mm |
| R × 1day | Annual, seasonal and monthly maximum one-day precipitation | mm |
| R × 5day | Annual, seasonal and monthly maximum five-days precipitation | mm |
| SDII | Annual total precipitation divided by the number of wet days in the year | mm/d |
| PRCPTOT | Annual total amount of precipitation cumulated in wet days | mm |
| Index | Mann-Kendall Trend Test | Linear Regression Trend | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Z Score | Positive | Negative | No Trend | Slope of Change (b) | p Value | Positive | Negative | No Trend | |||||
| TT | SS | TT | SS | TT | SS | TT | SS | ||||||
| CDD | −0.778 | 4 | 0 | 24 | 2 | 0 | −0.143 | 0.337 | 10 | 0 | 18 | 0 | 0 |
| CWD | −1.843 | 3 | 0 | 25 | 2 | 0 | −0.007 | 0.06 | 3 | 0 | 25 | 6 | 0 |
| PRCPTOT | −0.887 | 5 | 0 | 23 | 2 | 0 | −1.027 | 0.183 | 2 | 0 | 26 | 2 | 0 |
| R10 | 0.070 | 15 | 0 | 13 | 0 | 0 | −0.009 | 0.684 | 8 | 0 | 20 | 0 | 0 |
| R20 | −0.472 | 6 | 0 | 21 | 0 | 1 | −0.012 | 0.377 | 4 | 0 | 24 | 0 | 0 |
| R25 | −0.619 | 6 | 0 | 21 | 0 | 1 | −0.013 | 0.261 | 4 | 0 | 23 | 3 | 1 |
| R50 | −2.398 | 7 | 0 | 21 | 3 | 0 | −0.01 | 0.025 | 3 | 0 | 22 | 5 | 3 |
| R95p | −2.137 | 6 | 0 | 22 | 3 | 0 | −0.85 | 0.041 | 5 | 0 | 23 | 4 | 0 |
| R99p | −2.749 | 7 | 0 | 21 | 3 | 0 | −0.478 | 0.036 | 5 | 0 | 23 | 5 | 0 |
| R×1day | −3.042 | 5 | 0 | 23 | 3 | 0 | −0.265 | 0.022 | 4 | 0 | 24 | 3 | 0 |
| R×5day | −2.532 | 5 | 0 | 23 | 4 | 0 | −0.505 | 0.021 | 3 | 0 | 25 | 5 | 0 |
| SDII | −0.874 | 8 | 0 | 20 | 1 | 0 | −0.009 | 0.361 | 8 | 0 | 19 | 1 | 1 |
| Indices | NAO-1 | NAO-0 | NINO3.4-1 | NINO3.4-0 | PDO-1 | PDO-0 |
|---|---|---|---|---|---|---|
| CDD | −0.132 | 0.135 | −0.373 | 0 | −0.152 | −0.208 |
| CWD | 0.03 | −0.2 | 0.273 | 0.034 | 0.204 | 0.038 |
| PRCPTOT | 0.09 | −0.123 | 0.379 | −0.153 | 0.074 | −0.067 |
| R10 | 0.111 | −0.038 | 0.397 | −0.13 | 0.129 | 0.005 |
| R20 | 0.128 | −0.103 | 0.337 | −0.183 | 0.076 | −0.095 |
| R25 | 0.11 | −0.108 | 0.336 | −0.18 | 0.067 | −0.109 |
| R50 | −0.026 | −0.217* | 0.251 | −0.181 | −0.089 | −0.201 |
| R95p | 0.012 | −0.213* | 0.254 | −0.247* | −0.04 | −0.2 |
| R99p | 0.019 | −0.235* | 0.122 | −0.236* | 0.093 | −0.152 |
| R × 1day | −0.016 | −0.229* | 0.205 | −0.223* | 0.039 | −0.198 |
| R × 5day | 0.082 | −0.188 | 0.222* | −0.258 | 0.052 | −0.152 |
| SDII | 0.064 | −0.19 | 0.295 | −0.329 | 0.065 | −0.142 |
| Indices | NINO3.4-0 | NINO3.4-1 | ||||||
| 2-year | 4-year | 8-year | 16-year | 2-year | 4-year | 8-year | 16-year | |
| CDD | 0.396 | −0.382 | −0.255 | −0.479 | −0.565 | −0.336 | −0.512 | −0.483 |
| CWD | −0.209 | 0.063 | 0.334 | −0.224 | 0.267 | 0.208 | 0.362 | −0.240 |
| PRCPTOT | −0.325 | −0.067 | 0.245 | −0.546 | 0.466 | 0.045 | 0.165 | −0.519 |
| R10 | −0.326 | 0.100 | 0.390 | −0.656 | 0.412 | 0.254 | 0.469 | −0.614 |
| R20 | −0.291 | −0.027 | 0.275 | −0.674 | 0.452 | 0.037 | 0.304 | −0.638 |
| R25 | −0.245 | −0.103 | 0.304 | −0.591 | 0.416 | −0.014 | 0.251 | −0.569 |
| R50 | −0.243 | −0.274 | 0.020 | −0.607 | 0.348 | −0.159 | −0.144 | −0.618 |
| R95p | −0.341 | −0.306 | 0.008 | −0.355 | 0.491 | −0.160 | −0.147 | −0.380 |
| R99p | −0.140 | −0.470 | 0.009 | 0.200 | 0.200 | −0.204 | −0.060 | 0.143 |
| R×1day | −0.260 | −0.531 | −0.174 | 0.070 | 0.281 | −0.018 | −0.163 | 0.021 |
| R×5day | −0.112 | −0.400 | −0.036 | −0.196 | 0.321 | 0.098 | −0.177 | −0.232 |
| SDII | −0.222 | −0.304 | 0.170 | −0.691 | 0.368 | 0.032 | 0.190 | −0.715 |
| Indices | NAO-0 | NAO-1 | ||||||
| 2-year | 4-year | 8-year | 16-year | 2-year | 4-year | 8-year | 16-year | |
| CDD | 0.097 | 0.376 | 0.015 | 0.705 | −0.208 | −0.017 | 0.287 | 0.561 |
| CWD | −0.377 | −0.219 | −0.224 | 0.278 | 0.276 | 0.179 | 0.208 | 0.368 |
| PRCPTOT | −0.212 | −0.065 | −0.309 | 0.626 | 0.334 | 0.321 | 0.097 | 0.569 |
| R10 | −0.207 | −0.083 | −0.262 | 0.653 | 0.301 | 0.209 | 0.126 | 0.554 |
| R20 | −0.188 | −0.065 | −0.287 | 0.678 | 0.250 | 0.307 | 0.146 | 0.592 |
| R25 | −0.194 | 0.014 | −0.301 | 0.681 | 0.220 | 0.350 | 0.123 | 0.586 |
| R50 | 0.026 | 0.017 | −0.314 | 0.602 | −0.023 | 0.441 | 0.047 | 0.633 |
| R95p | −0.110 | 0.038 | −0.321 | 0.488 | 0.071 | 0.415 | 0.072 | 0.527 |
| R99p | −0.366 | 0.151 | 0.127 | 0.110 | 0.225 | 0.360 | 0.423 | 0.207 |
| R×1day | −0.333 | 0.355 | 0.076 | 0.155 | 0.238 | 0.414 | 0.419 | 0.242 |
| R×5day | −0.323 | 0.207 | 0.098 | 0.285 | 0.277 | 0.430 | 0.427 | 0.410 |
| SDII | 0.270 | 0.193 | -0.101 | 0.702 | 0.093 | 0.395 | 0.331 | 0.746 |
| Indices | PDO-0 | PDO-1 | ||||||
| 2-year | 4-year | 8-year | 16-year | 2-year | 4-year | 8-year | 16-year | |
| CDD | −0.051 | −0.306 | −0.122 | −0.593 | −0.055 | 0.184 | −0.363 | −0.707 |
| CWD | −0.436 | 0.139 | 0.666 | 0.117 | 0.562 | −0.129 | 0.628 | −0.083 |
| PRCPTOT | −0.074 | −0.116 | 0.514 | −0.538 | 0.339 | −0.152 | 0.420 | −0.668 |
| R10 | −0.088 | 0.034 | 0.709 | −0.753 | 0.330 | −0.100 | 0.706 | −0.828 |
| R20 | −0.120 | −0.129 | 0.614 | −0.709 | 0.324 | −0.206 | 0.581 | −0.813 |
| R25 | −0.166 | −0.190 | 0.583 | −0.652 | 0.365 | −0.208 | 0.475 | −0.770 |
| R50 | −0.046 | −0.333 | 0.263 | −0.341 | 0.178 | −0.205 | 0.129 | −0.565 |
| R95p | −0.110 | −0.316 | 0.276 | −0.051 | 0.355 | −0.167 | 0.154 | −0.290 |
| R99p | −0.208 | −0.308 | 0.387 | 0.629 | 0.459 | 0.015 | 0.247 | 0.415 |
| R×1day | −0.239 | −0.320 | 0.271 | 0.448 | 0.499 | 0.106 | 0.232 | 0.232 |
| R×5day | −0.106 | −0.193 | 0.262 | 0.280 | 0.422 | 0.062 | 0.101 | 0.047 |
| SDII | −0.244 | −0.248 | 0.568 | −0.284 | 0.442 | −0.074 | 0.490 | −0.553 |
| Indices | IOD-0 | IOD-1 | ||||||
| 2-year | 4-year | 8-year | 16-year | 2-year | 4-year | 8-year | 16-year | |
| CDD | −0.273 | 0.191 | 0.029 | 0.939 | −0.396 | −0.017 | 0.488 | 0.925 |
| CWD | 0.015 | −0.217 | −0.266 | 0.078 | 0.008 | 0.435 | −0.196 | 0.027 |
| PRCPTOT | −0.018 | −0.210 | −0.235 | 0.598 | 0.206 | 0.404 | −0.052 | 0.569 |
| R10 | −0.064 | −0.188 | −0.368 | 0.689 | 0.262 | 0.422 | −0.353 | 0.691 |
| R20 | 0.027 | −0.153 | −0.232 | 0.699 | 0.303 | 0.417 | −0.149 | 0.698 |
| R25 | 0.104 | −0.117 | −0.292 | 0.748 | 0.252 | 0.433 | −0.141 | 0.727 |
| R50 | 0.115 | −0.211 | 0.093 | 0.506 | 0.130 | 0.414 | 0.229 | 0.489 |
| R95p | 0.024 | −0.147 | 0.043 | 0.385 | 0.160 | 0.423 | 0.239 | 0.334 |
| R99p | 0.001 | −0.099 | 0.358 | −0.086 | −0.047 | 0.400 | 0.451 | −0.158 |
| R×1day | 0.047 | 0.136 | 0.469 | −0.006 | 0.033 | 0.639 | 0.525 | −0.078 |
| R×5day | 0.048 | 0.078 | 0.329 | 0.011 | 0.014 | 0.704 | 0.442 | −0.028 |
| SDII | 0.108 | 0.073 | 0.047 | 0.539 | 0.247 | 0.617 | 0.102 | 0.545 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, X.; Zou, X.; Zhang, C.; Zhang, J.; Kong, F. Multiscale Spatio-Temporal Changes of Precipitation Extremes in Beijing-Tianjin-Hebei Region, China during 1958–2017. Atmosphere 2019, 10, 462. https://doi.org/10.3390/atmos10080462
Song X, Zou X, Zhang C, Zhang J, Kong F. Multiscale Spatio-Temporal Changes of Precipitation Extremes in Beijing-Tianjin-Hebei Region, China during 1958–2017. Atmosphere. 2019; 10(8):462. https://doi.org/10.3390/atmos10080462
Chicago/Turabian StyleSong, Xiaomeng, Xianju Zou, Chunhua Zhang, Jianyun Zhang, and Fanzhe Kong. 2019. "Multiscale Spatio-Temporal Changes of Precipitation Extremes in Beijing-Tianjin-Hebei Region, China during 1958–2017" Atmosphere 10, no. 8: 462. https://doi.org/10.3390/atmos10080462
APA StyleSong, X., Zou, X., Zhang, C., Zhang, J., & Kong, F. (2019). Multiscale Spatio-Temporal Changes of Precipitation Extremes in Beijing-Tianjin-Hebei Region, China during 1958–2017. Atmosphere, 10(8), 462. https://doi.org/10.3390/atmos10080462






