Nonlinear Effects on the Precessional Instability in Magnetized Turbulence
Abstract
:1. Introduction
2. Model Equations
2.1. Incompressible MHD Equations
2.2. Equations for the Kinetic and Magnetic Energies
3. Equations for Fourier Amplitudes
3.1. Time-Dependent Wave Vector
3.2. Equations for the Fourier Amplitudes
3.3. Linear Stability Analysis
3.4. Spectral Density of Energy
4. DNS Results and Discussions
4.1. Initial Conditions
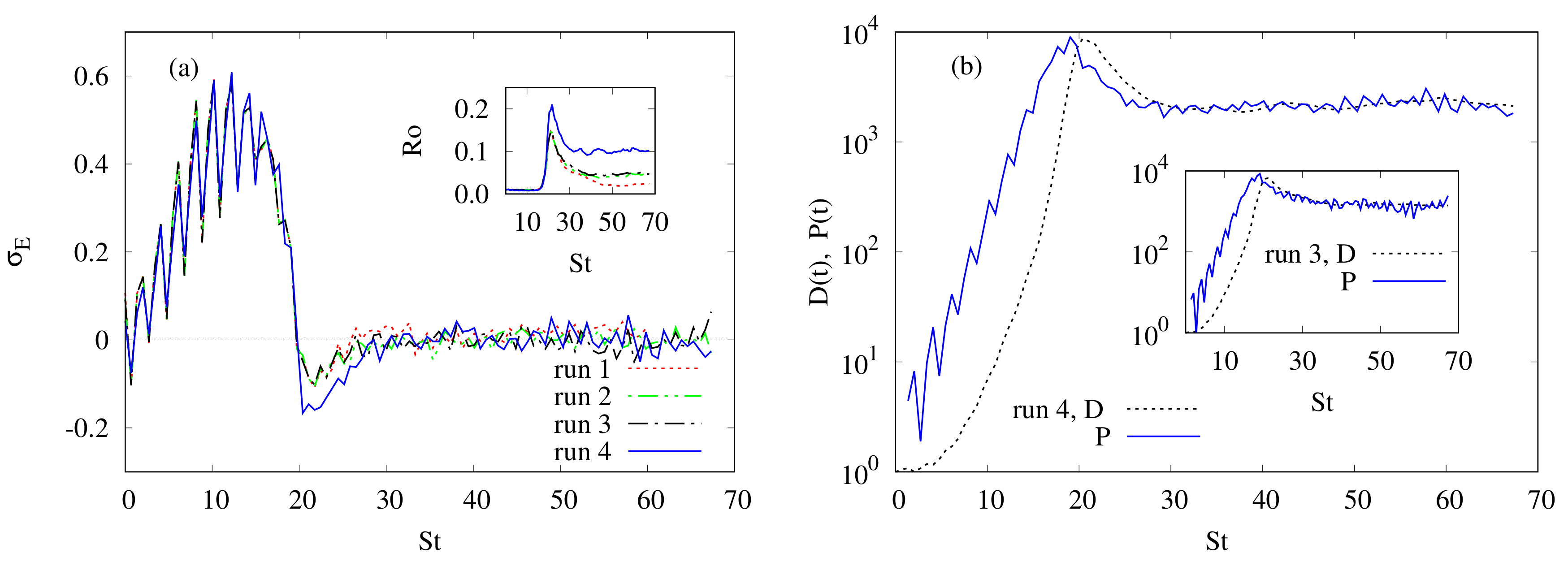
4.2. Time Evolution of Global Quantities
4.3. Spectra for Kinetic and Magnetic Energies
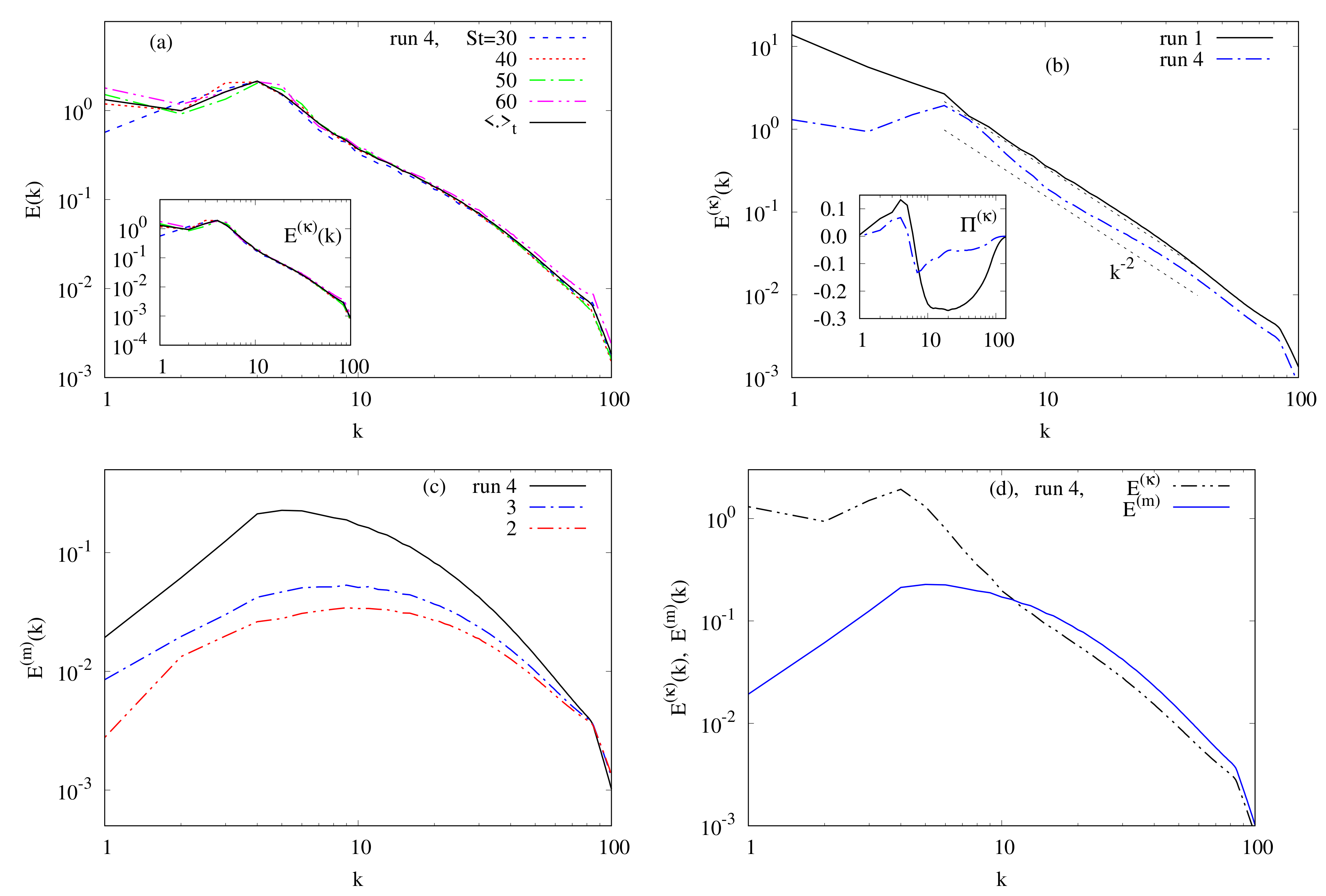
4.3.1. Radial Spectra
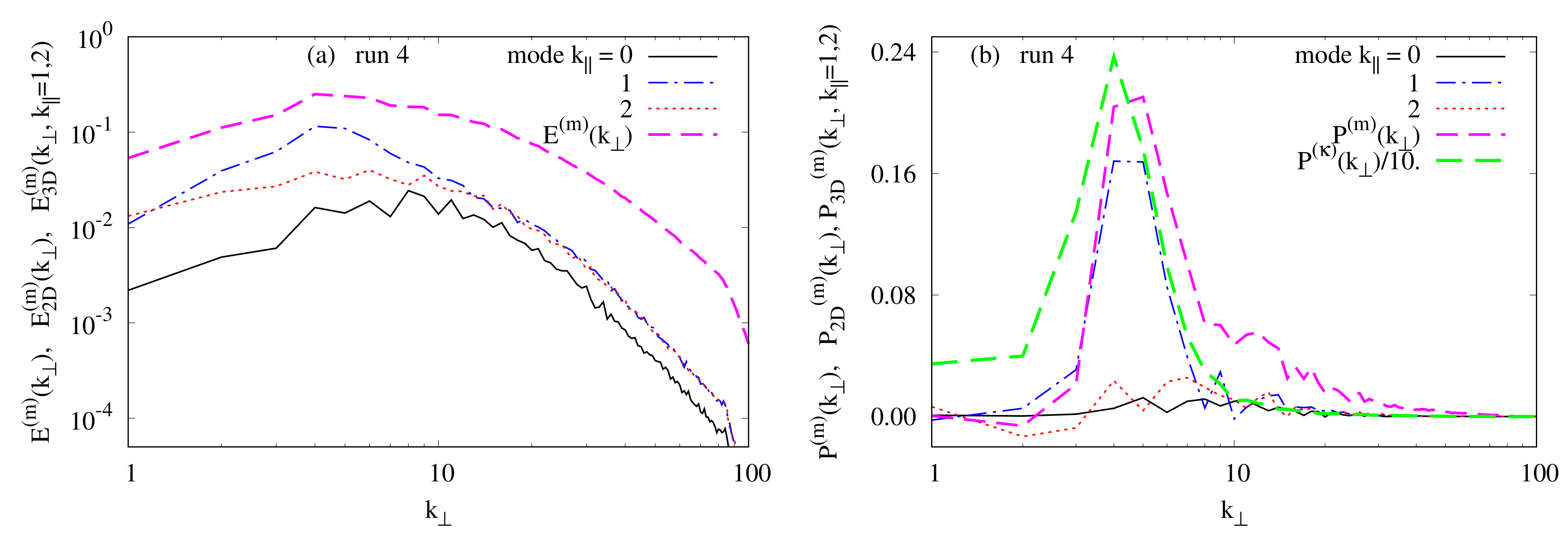
4.3.2. The Role of the Mode and Its Nearest Neighbors Modes
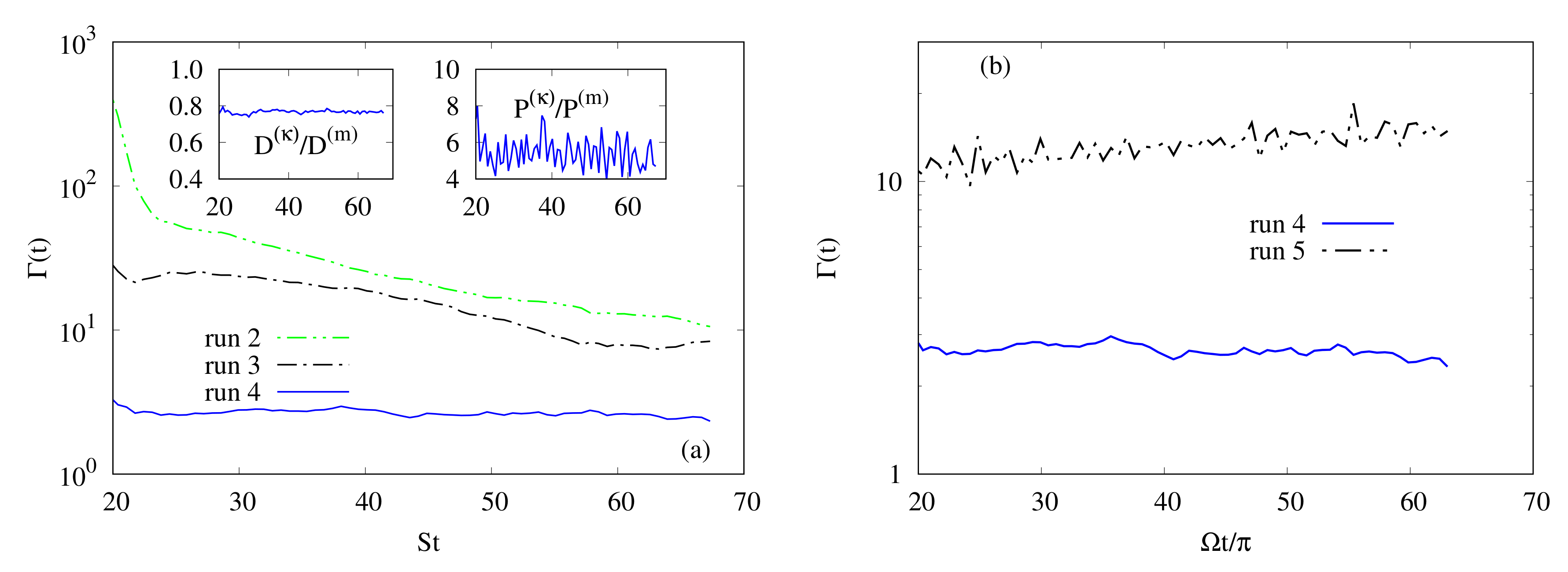
4.3.3. Alfvén Ratio between Kinetic and Magnetic Energies
5. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
References
- Pedlowsky, J. Geophysical Fluid Dynamics; Springer: New York, NY, USA; Berlin/Heidelberg, Germany, 1987. [Google Scholar]
- Maeder, A. Physics, Formation and Evolution of Rotating Stars; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Galperin, B.; Read, P.L. Zonal Jets Phenomenology, Genesis, and Physics; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Nastrom, G.D.; Gage, K.S. A climatology of atmospheric wavenumber spectra of wind and temperature observed by commercial aircraft. J. Atmos. Sci. 1985, 42, 950–960. [Google Scholar] [CrossRef] [Green Version]
- Cho, J.Y.N.; Lindborg, E. Horizontal velocity structure functions in the upper troposphere and lower stratosphere 1. Observations. J. Geophys. Res. 2001, 106, 10223–10232. [Google Scholar] [CrossRef]
- Galperin, B.; Sukoriansky, S. Turbulence in rotating fluids and the Nastrom & Gage spectrum. In Proceedings of the Sixth International Conference Turbulence Mixing and Beyond, ICTP, Trieste, Italy, 14–18 August 2017; pp. 14–18. [Google Scholar]
- Greenspan, H.P. The Theory of Rotating Fluids; Cambridge University Press: Cambridge, UK, 1968. [Google Scholar]
- Sagaut, P.; Cambon, C. Homogeneous Turbulence Dynamics; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Sukoriansky, S.; Galperin, B. QNSE theory of turbulence anisotropization and onset of the inverse energy cascade by solid-body rotation. J. Fluid Mech. 2016, 805, 384–421. [Google Scholar] [CrossRef]
- Khlifi, A.; Salhi, A.; Nasraoui, S.; Godeferd, F.; Cambon, C. Spectral energy scaling in precessing turbulence. Phys. Rev. E 2018, 98, 011102. [Google Scholar] [CrossRef]
- Kerswell, R.R. The instability of precessing flow. Geophys. Astrophys. Fluid Dyn. 1993, 72, 107–144. [Google Scholar] [CrossRef]
- Hollerbach, R.; Kerswell, R.R. Oscillatory internal shear layers in rotating and precessing flows. J. Fluid Mech. 1995, 298, 327–339. [Google Scholar] [CrossRef] [Green Version]
- Poincaré, H. Sur la précession des corps déformables. Bull. Astron. 1910, 27, 321–356. [Google Scholar]
- Malkus, W.V.R. Precession of the Earth as the cause of geomagnetism: Experiments lend support to the proposal that precessional torques drive the Earth’s dynamo. Science 1968, 160, 259–264. [Google Scholar] [CrossRef]
- Noir, J.; Cardin, P.; Jault, D.; Masson, J.-P. Experimental evidence of nonlinear resonance effects between retrograde precession and the tilt-over mode within a spheroid. Geophys. J. Int. 2003, 154, 407–416. [Google Scholar] [CrossRef] [Green Version]
- Herault, J.; Gundrum, T.; Giesecke, A.; Stefani, F. Subcritical transition to turbulence of a precessing flow in a cylindrical vessel. Phys. Fluids 2015, 27, 124102. [Google Scholar] [CrossRef] [Green Version]
- Horimoto, Y.; Goto, S. Sustaining mechanism of small-scale turbulent eddies in a precessing sphere. Phys. Rev. Fluids 2017, 2, 114603. [Google Scholar] [CrossRef]
- Horimoto, Y.; Simonet-Davin, G.; Katayama, A.; Goto, S. Impact of a small ellipticity on the sustainability condition of developed turbulence in a precessing spheroid. Phys. Rev. Fluids 2018, 3, 044603. [Google Scholar] [CrossRef]
- Wu, C.C.; Roberts, P.H. On a dynamo driven by topographic precession. Geophys. Astrophys. Fluid Dyn. 2009, 103, 467–501. [Google Scholar] [CrossRef]
- Glampedakis, K.; Andersson, N.; Jones, D.I. On the stability of precessing superfluid neutron stars. Phys. Rev. Lett. 2008, 100, 081101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bayly, B.J. Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 1986, 57, 2160–2163. [Google Scholar] [CrossRef] [PubMed]
- Kerswell, R.R. Elliptical instability. Annu. Rev. Fluid Mech. 2002, 34, 83–113. [Google Scholar] [CrossRef]
- Salhi, A.; Cambon, C. Precessing rotating flows with additional shear: Stability analysis. Phys. Rev. E 2009, 79, 036303. [Google Scholar] [CrossRef] [PubMed]
- Mahalov, A. The instability of rotating fluid columns subjected to a weak external Coriolis force. Phys. Fluids 1993, 5, 891–900. [Google Scholar] [CrossRef]
- Wiener, R.J.; Hammer, P.W.; Swanson, C.E.; Donnelly, R.J. Stability of Taylor-Couette Flow Subject to an External Coriolis Force. Phys. Rev. Lett. 1990, 64, 1115–1118. [Google Scholar] [CrossRef]
- Biferale, L.; Bonaccorso, F.; Mazzitelli, I.M.; van Hinsberg, M.A.T.; Lanotte, A.S.; Musacchio, S.; Perlekar, P.; Toschi, F. Coherent Structures and Extreme Events in Rotating Multiphase Turbulent Flows. Phys. Rev. X 2016, 6, 041036. [Google Scholar] [CrossRef] [Green Version]
- Craik, A.D.D.; Criminale, W.O. Evolution of wavelike disturbances in shear flows: A class of exact solutions of the Navier-Stokes equations. Proc. R. Soc. Lond. A 1986, 406, 13–26. [Google Scholar] [CrossRef]
- Salhi, A.; Lehner, T.; Cambon, C. Magnetohydrodynamic instabilities in rotating and precessing sheared flows: An asymptotic analysis. Phys. Rev. E 2010, 82, 016315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mason, R.M.; Kerswell, R.R. Chaotic dynamics in a strained rotating flow: A precessing plane fluid layer. J. Fluid Mech. 2002, 471, 71–106. [Google Scholar] [CrossRef]
- Barker, A.J. On turbulence driven by axial precession and tidal evolution of the spin-orbit angle of close-in giant planets. Mon. Not. R. Astron. Soc. 2016, 460, 2339–2350. [Google Scholar] [CrossRef] [Green Version]
- Godeferd, F.S.; Moisy, F. Structure and Dynamics of Rotating Turbulence: A Review of Recent Experimental and Numerical Results. Appl. Mech. Rev. 2015, 67, 030802. [Google Scholar] [CrossRef] [Green Version]
- Shirley, J.H.; Fairbridge, R.W. Encyclopedia of Planetary Sciences; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Babin, A.; Mahalov, A.; Nicolaenko, B. Global regularity of 3d rotating Navier-Stokes equations for resonant domains. Appl. Maths Lett. 2000, 13, 51–57. [Google Scholar] [CrossRef] [Green Version]
- Chen, Q.; Chen, S.; Eyink, G.L.; Holm, D.D. Resonant interactions in rotating homogeneous three-dimensional turbulence. J. Fluid Mech. 2005, 542, 139–164. [Google Scholar] [CrossRef] [Green Version]
- Thiele, M.; Muller, W.-C. Structure and decay of rotating homogeneous turbulence. J. Fluid Mech. 2009, 637, 425–442. [Google Scholar] [CrossRef] [Green Version]
- Bourouiba, L.; Straub, D.N.; Waite, M.L. Non-local energy transfers in rotating turbulence at intermediate Rossby number. J. Fluid Mech. 2012, 690, 129–147. [Google Scholar] [CrossRef]
- Julien, K.; Rubio, A.M.; Grooms, I.; Knobloch, E. Statistical and physical balances in low Rossby number Rayleigh-Bénard convection. Geophys. Astrophys. Fluid Dyn. 2012, 106, 392–428. [Google Scholar] [CrossRef]
- Rubio, A.M.; Julien, K.; Knobloch, E.; Jeffrey, B.W. Upscale Energy Transfer in three-dimensional rapidly rotating turbulent convection. Phys. Rev. Lett. 2014, 112, 144501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nastrom, G.; Jasperson, W.; Gage, K. Kinetic energy spectrum of large and mesoscale atmospheric processes. Nature 1984, 310, 36–38. [Google Scholar] [CrossRef]
- Byrne, D.; Zhang, J.A. Height-dependent transition from 3-D to 2-D turbulence in the hurricane boundary layer. Geophys. Res. Lett. 2013, 40, 1439–1442. [Google Scholar] [CrossRef]
- Sahoo, G.; Alexakis, A.; Biferale, L. Discontinuous transition from direct to inverse cascade in three-dimensional turbulence. Phys. Rev. Lett. 2017, 118, 164501. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Baklouti, F.S.; Khlifi, A.; Salhi, A.; Godeferd, G.; Cambon, C.; Lehner, T. Kinetic magnetic energy exchanges in rotating magnetohydrodynamic turbulence. J. Turbulence 2019, 20, 263–284. [Google Scholar] [CrossRef]
- Favier, B.; Godeferd, F.; Cambon, C. On the effect of rotation on magnetohydrodynamic turbulence at high magnetic Reynolds number. Geophys. Astrophys. Fluid Dyn. 2012, 106, 89–111. [Google Scholar] [CrossRef] [Green Version]
- Galtier, S. Weak turbulence theory for rotating magnetohydrodynamics and planetary dynamos. J. Fluid Mech. 2014, 757, 114–154. [Google Scholar] [CrossRef] [Green Version]
- Salhi, A.; Baklouti, F.S.; Godeferd, F.; Lehner, T.; Cambon, C. Energy partition, scale by scale, in magnetic Archimedes Coriolis weak wave turbulence. Phys. Rev. E. 2017, 95, 023112. [Google Scholar] [CrossRef] [Green Version]
- Menu, M.D.; Galtier, S.; Petitdemange, L. Inverse cascade of hybrid helicity in BΩ-MHD turbulence. Phys. Rev. Fluids 2019, 4, 073701. [Google Scholar] [CrossRef] [Green Version]
- Biskamp, D. Nonlinear Magnetohydrodynamics; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Baerenzung, J.; Politano, H.; Ponty, Y.; Pouquet, A. Spectral Modeling of Magnetohydrodynamic Turbulent Flows. Phys. Rev. E 2008, 78, 026310. [Google Scholar] [CrossRef] [Green Version]
- Lesur, G.; Longaretti, P.-Y. Impact of dimensionless numbers on the efficiency of magnetorotational instability induced turbulent transport. Mon. Not. R. Astron. Soc. 2007, 378, 1471–1480. [Google Scholar] [CrossRef] [Green Version]
- Orszag, S.A.; Patterson, G.S. Numerical Simulation of Three-Dimensional Homogeneous Isotropic Turbulence. Phys. Rev. Lett. 1972, 28, 76–79. [Google Scholar] [CrossRef]
- Yakubovich, V.A.; Starzhinskii, V.M. Linear Differential Equations with Periodic Coefficients; Wiley: New York, NY, USA, 1975; Volume 1. [Google Scholar]
- Lebovitz, N.R.; Zweibel, E. Magnetoelliptic instabilities. Astrophys. J. 2004, 609, 301–312. [Google Scholar] [CrossRef]
- Salhi, A.; Cambon, C. Stability of rotating stratified shear flow: An analytical study. Phys. Rev. E 2010, 81, 026302. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lehnert, B. The decay of magnetoturbulence in the presence of a magnetic field and Coriolis force. Q. Appl. Math. 1955, 12, 321–341. [Google Scholar] [CrossRef] [Green Version]
- Nornberg, M.D.; Ji, H.; Schartman, E.; Roach, A.; Goodman, J. Observation of Magnetocoriolis Waves in a Liquid Metal Taylor- Couette Experiment. Phys. Rev. Lett. 2010, 104, 074501. [Google Scholar] [CrossRef] [PubMed]
- Rogallo, R.S. Numerical Experiments in Homogeneous Turbulence; NASA Ames Research Center: Moffett Field, CA, USA, 1981. [Google Scholar]
- Salhi, A.; Jacobitz, F.G.; Schneider, K.; Cambon, C. Nonlinear dynamics and anisotropic structure of rotating sheared turbulence. Phys. Rev. E. 2014, 89, 013020. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Roberts, P.H.; King, E.M. On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 2013, 76, 096801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jones, C. Planetary magnetic fields and fluid dynamos. Annu. Rev. Fluid Mech. 2011, 43, 583–614. [Google Scholar] [CrossRef] [Green Version]
- Bigot, B.; Galtier, S.; Politano, H. Development of anisotropy in incompressible magnetohydrodynamic turbulence. Phys. Rev. E 2008, 78, 066301. [Google Scholar] [CrossRef] [Green Version]
- Cambon, C.; Rubinstein, R.; Godeferd, F. Advances in wave turbulence: Rapidly rotating flows. New J. Phys. 2004, 6, 1–30. [Google Scholar] [CrossRef]
- Goto, S.; Komoda, K.; Kanki, J. Turbulence in precessing containers. In Proceedings of the 11th International Symposium on Turbulence and Shear Flow Phenomena (TSFP11), Southampton, UK, 30 July–2 August 2019. [Google Scholar]
- Elmegreen, B.G.; Scalo, J. Interstellar Turbulence I: Observations and Processes. Ann. Rev. Astron. Astrophys. 2004, 42, 211–273. [Google Scholar] [CrossRef] [Green Version]
- Corrsin, S. On Local Isotropy in Turbulent Shear Flow; Technical Report 58B11; NACA R & M: Washington, DC, USA, 1958. [Google Scholar]
- Zeman, O. A note on the spectra and decay of rotating homogeneous turbulence. Phys. Fluids 1994, 6, 3221–3223. [Google Scholar] [CrossRef]
- Mininni, P.D.; Rosenberg, D.; Pouquet, A. Isotropisation at small scales of rotating helically driven turbulence. J. Fluid Mech. 2012, 699, 263–279. [Google Scholar] [CrossRef] [Green Version]
- Delache, A.; Cambon, C.; Godeferd, F. Scale by scale anisotropy in freely decaying rotating turbulence. Phys. Fluids 2014, 26, 025104. [Google Scholar] [CrossRef] [Green Version]
- Iyer, K.P.; Mazzitelli, I.; Bonaccorso, F.; Pouquet, A.; Biferale, L. Rotating turbulence under “precession-like” perturbation. Eur. Phys. J. E 2015, 38, 128–134. [Google Scholar] [CrossRef] [Green Version]
- Alexakis, A. On the 2D behavior of 3D MHD with a strong guiding field. Phys. Rev. E 2011, 84, 056330. [Google Scholar] [CrossRef] [Green Version]
- Smith, L.M.; Chasnov, J.R.; Waleffe, F. Crossover from two- to three-dimensional turbulence. Phys. Rev. Lett. 1996, 77, 2467–2470. [Google Scholar] [CrossRef] [Green Version]
- Smith, L.M.; Lee, Y. On near resonances and symmetry breaking in forced rotating flows at moderate Rossby number. J. Fluid Mech. 2005, 535, 111–142. [Google Scholar] [CrossRef]
- Sen, A.; Mininni, P.D.; Rosenberg, D.; Pouquet, A. Anisotropy and nonuniversality in scaling laws of the large-scale energy spectrum in rotating turbulence. Phys. Rev. E 2012, 86, 036319. [Google Scholar] [CrossRef] [Green Version]
- Pouquet, A.; Sen, A.; Rosenberg, D.; Mininni, P.D.; Baerenzung, J. Inverse cascades in turbulence and the case of rotating flows. Phys. Scr. 2013, 2013, 014032. [Google Scholar] [CrossRef] [Green Version]








| Run | B | ||||
|---|---|---|---|---|---|
| 1 (PHT) | 0.0025 | 20 | 0.17 | 0 | 0 |
| 2 (PMHDT) | 0.0025 | 20 | 0.17 | 0.1 | 0.1 |
| 3 (PMHDT) | 0.0025 | 20 | 0.17 | 0.5 | 2.5 |
| 4 (PMHDT) | 0.0025 | 20 | 0.17 | 2.5 | 62.5 |
| 5 (RMHDT) | 0.0025 | 20 | 0.0 | 2.5 | 62.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salhi, A.; Khlifi, A.; Cambon, C. Nonlinear Effects on the Precessional Instability in Magnetized Turbulence. Atmosphere 2020, 11, 14. https://doi.org/10.3390/atmos11010014
Salhi A, Khlifi A, Cambon C. Nonlinear Effects on the Precessional Instability in Magnetized Turbulence. Atmosphere. 2020; 11(1):14. https://doi.org/10.3390/atmos11010014
Chicago/Turabian StyleSalhi, Abdelaziz, Amor Khlifi, and Claude Cambon. 2020. "Nonlinear Effects on the Precessional Instability in Magnetized Turbulence" Atmosphere 11, no. 1: 14. https://doi.org/10.3390/atmos11010014
APA StyleSalhi, A., Khlifi, A., & Cambon, C. (2020). Nonlinear Effects on the Precessional Instability in Magnetized Turbulence. Atmosphere, 11(1), 14. https://doi.org/10.3390/atmos11010014






